Skip to main content
SpringerLink
Log in

A review of the deterministic and diffusion approximations for stochastic chemical reaction networks

  • Published:
Reaction Kinetics, Mechanisms and Catalysis Aims and scope Submit manuscript

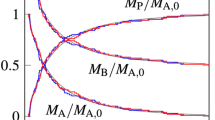
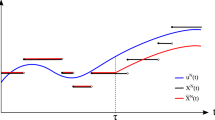
Abstract

This work reviews deterministic and diffusion approximations of the stochastic chemical reaction networks and explains their applications. We discuss the added value the diffusion approximation provides for systems with different phenomena, such as a deficiency and a bistability. It is advocated that the diffusion approximation can be considered as an alternative theoretical approach to study the reaction networks rather than a simulation shortcut. We discuss two examples in which the diffusion approximation is able to catch qualitative properties of reaction networks that the deterministic model misses. We provide an explicit construction of the original process and the diffusion approximation such that the distance between their trajectories is controlled and demonstrate this construction for the examples. We also discuss the limitations and potential directions of the developments.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Anderson D, Enciso G, Johnston M (2014) Stochastic analysis of biochemical reaction networks with absolute concentration robustness. J R Soc Interface 11(93) https://doi.org/10.1098/rsif.2013.0943

  2. Anderson DF, Cappelletti D, Koyama M, Kurtz TG (2017) Non-explosivity of stochastically modeled reaction networks that are complex balanced. arXiv preprint arXiv:1708.09356

  3. Anderson DF, Cappelletti D, Kurtz TG (2017) Finite time distributions of stochastically modeled chemical systems with absolute concentration robustness. SIAM J Appl Dyn Syst 16(3):1309–1339

    Article  Google Scholar 

  4. Anderson DF, Craciun G, Kurtz TG (2010) Product-form stationary distributions for deficiency zero chemical reaction networks. Bull Math Biol 72(8):1947–1970

    Article  CAS  Google Scholar 

  5. Anderson DF, Kurtz TG (2015) Stochastic analysis of biochemical systems. Mathematical biosciences Institute lecture series. Stochastics in biological systems, vol 1. Springer, MBI Mathematical Biosciences Institute, Ohio State University, Cham. https://doi.org/10.1007/978-3-319-16895-1

  6. Angius A, Balbo G, Beccuti M, Bibbona E, Horvath A, Sirovich R (2015) Approximate analysis of biological systems by hybrid switching jump diffusion. Theor Comput Sci 587:49–72

    Article  Google Scholar 

  7. Baxendale PH, Greenwood PE (2011) Sustained oscillations for density dependent markov processes. J Math Biol 63(3):433–457

    Article  Google Scholar 

  8. Beccuti M, Bibbona E, Horváth A, Sirovich R, Angius A, Balbo G (2014) Analysis of Petri net models through stochastic differential equation. In: Proc. of international conference on application and theory of Petri nets and other models of concurrency (ICATPN’14), Tunis, Tunisia

  9. Brémaud, P.: Point processes and queues. Martingale dynamics. Springer series in statistics. Springer, New York (1981).

  10. Cappelletti D, Wiuf C (2016) Product-form poisson-like distributions and complex balanced reaction systems. SIAM J Appl Math 76(1):411–432. https://doi.org/10.1137/15M1029916

    Article  Google Scholar 

  11. Csörgő M, Révész P (1975) A new method to prove strassen type laws of invariance principle. 1. Zeitschrift für Wahrscheinlichkeitstheorie und verwandte Gebiete 31(4):255–259

    Article  Google Scholar 

  12. E. Bibbona R (2017) Strong approximation of density dependent markov chains on bounded domains. ArXiv:1704.07481

  13. Érdi P, Lente G (2014) Stochastic chemical kinetics. Springer series in synergetics. Springer, New York. https://doi.org/10.1007/978-1-4939-0387-0. Theory and (mostly) systems biological applications

  14. Érdi P, Tóth J (1989) Mathematical models of chemical reactions. Nonlinear science: theory and applications. Princeton University Press, Princeton, NJ. Theory and applications of deterministic and stochastic models

  15. Ethier SN, Kurtz TG (1986) Markov processes. Wiley series in probability and mathematical statistics: probability and mathematical statistics. Wiley, New York. https://doi.org/10.1002/9780470316658. Characterization and convergence

  16. Feinberg M (1972) On chemical kinetics of a certain class. Arch Ration Mech Anal 46(1):1–41

    Article  Google Scholar 

  17. Feliu E, Wiuf C (2015) Finding the positive feedback loops underlying multi-stationarity. BMC Syst Biol 9(1). https://doi.org/10.1186/s12918-015-0164-0

  18. Gillespie DT (1977) Exact stochastic simulation of coupled chemical reactions. J Phys Chem 81(25):2340–2361

    Article  CAS  Google Scholar 

  19. Gillespie DT (2000) The chemical langevin equation. J Chem Phys 113(1):297–306. https://doi.org/10.1063/1.481811

    Article  CAS  Google Scholar 

  20. Jahnke T, Huisinga W (2007) Solving the chemical master equation for monomolecular reaction systems analytically. J Math Biol 54(1):1–26

    Article  Google Scholar 

  21. Joshi B, Shiu A (2013) Atoms of multistationarity in chemical reaction networks. J Math Chem 51(1):153–178

    CAS  Google Scholar 

  22. Komlós J, Major P, Tusnády G (1975) An approximation of partial sums of independent \({\rm RV}\)’s and the sample \({\rm DF}\). I Z Wahrscheinlichkeitstheorie und Verw. Gebiete 32:111–131

    Article  Google Scholar 

  23. Kurtz TG (1970) Solutions of ordinary differential equations as limits of pure jump Markov processes. J Appl Probab. 7:49–58

    Article  Google Scholar 

  24. Kurtz TG (1972) The relationship between stochastic and deterministic models for chemical reactions. J Chem Phys 57(7):2976–2978. https://doi.org/10.1063/1.1678692

    Article  CAS  Google Scholar 

  25. Kurtz TG (1976) Limit theorems and diffusion approximations for density dependent Markov chains. Springer, Berlin, pp 67–78

  26. Leite SC, Williams RJ (2017) A constrained langevin approximation for chemical reaction network. http://www.math.ucsd.edu/~williams/biochem/biochem.html

  27. Øksendal B (2003) Stochastic differential equations, 6th ed. Universitext. Springer, Berlin. https://doi.org/10.1007/978-3-642-14394-6. An introduction with applications

  28. Polettini M, Wachtel A, Esposito M (2005) Dissipation in noisy chemical networks: the role of deficiency. J Chem Phys 143(18), 11B606_1

  29. R Core Team (2017) R: a language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. https://www.R-project.org/

  30. Santillán M (2014) Chemical kinetics, stochastic processes, and irreversible thermodynamics. Lecture notes on mathematical modelling in the life sciences. Springer, Cham. https://doi.org/10.1007/978-3-319-06689-9

  31. Schlögl F (1972) Chemical reaction models for non-equilibrium phase transitions. Zeitschrift für Physik A Hadrons and Nuclei 253(2):147–161

    Google Scholar 

  32. Schnoerr D, Sanguinetti G, Grima R (2014) The complex chemical langevin equation. J Chem Phys 141(2):024103. https://doi.org/10.1063/1.4885345

  33. Schnoerr D, Sanguinetti G, Grima R (2017) Approximation and inference methods for stochastic biochemical kinetics—a tutorial review. J Phys A 50(9). https://doi.org/10.1088/1751-8121/aa54d9

  34. Stewart WJ (1994) Introduction to the numerical solutions of Markov chains. Princeton Univ, Press

    Google Scholar 

  35. Strassen V et al (1967) Almost sure behavior of sums of independent random variables and martingales. In: Proceedings of the fifth Berkeley symposium on mathematical statistics and probability. Contributions to probability theory, Part 1, vol 2. The Regents of the University of California

  36. Ullah M, Wolkenhauer O (2011) Stochastic approaches for systems biology. Springer, New York. https://doi.org/10.1007/978-1-4614-0478-1

  37. Wilhelm T (2009) The smallest chemical reaction system with bistability. BMC Syst Biol 3(1):90

    Article  Google Scholar 

Download references

Funding

P. Mozgunov and T. Jaki have received funding from the European Union‘s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie Grant Agreement No 633567.

Author information

Authors and Affiliations

  1. Medical and Pharmaceutical Statistics Research Unit, Department of Mathematics and Statistics, Lancaster University, Lancaster, UK

    Pavel Mozgunov & Thomas Jaki

  2. Dipartimento di Informatica, Università di Torino, Turin, Italy

    Marco Beccuti & Andras Horvath

  3. Dipartimento di Matematica G. Peano, Università di Torino, Turin, Italy

    Roberta Sirovich

  4. DISMA, Politecnico di Torino, Turin, Italy

    Enrico Bibbona

Authors
  1. Pavel Mozgunov
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Marco Beccuti
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Andras Horvath
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Thomas Jaki
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Roberta Sirovich
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Enrico Bibbona
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Enrico Bibbona.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mozgunov, P., Beccuti, M., Horvath, A. et al. A review of the deterministic and diffusion approximations for stochastic chemical reaction networks. Reac Kinet Mech Cat 123, 289–312 (2018). https://doi.org/10.1007/s11144-018-1351-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11144-018-1351-y

Keywords

Search

Navigation