Risk information, investor learning, and informational feedback

Abstract

This paper studies how public information regarding a firm’s riskiness affects investors’ incentives to acquire information about the firm and the firm’s ability to learn decision-useful information from its price. I find that risk information complements investor learning by informing investors of when it is most lucrative to investigate the firm, thereby reducing liquidity. Furthermore, risk information causes the firm’s price to contain more information when the firm’s investment decisions have the greatest impact on its value, thereby improving real efficiency. Extensions of the model suggest that the impact of risk information on real efficiency may deteriorate when the firm’s manager is excessively exposed to idiosyncratic risk, when the firm’s shareholders are excessively averse to such risk, or when the disclosure concerns a “downside risk.” In sum, my analysis suggests that information regarding firms’ expected values and information regarding firms’ risks significantly differ in their effects on the capital market.

1 Introduction

Regulatory authorities state that a core goal of financial reporting is to aid investors in the estimation of the riskiness of firms’ cash flows.¹ Consistent with this goal, financial disclosures contain risk information, and this information is often actively used by investors. Empirical research documents that risk metrics derived from the financial statements and footnotes potently predict future firm risk and influence investors’ trading behavior (Campbell et al. (2014), Sridharan (2015), Penman and Yehuda (2019), and Badia et al. (2020)). The risk information that firms provide extends beyond the 10-K to range forecasts, compensation risk disclosures, and 8-Ks, in which firms document the creation of off-balance-sheet liabilities, asset acquisitions and disposals, and loan defaults.

Ostensibly, the regulatory demand for financial reports that provide information on firm risk is founded upon the often-cited theories that public disclosure enhances liquidity and improves the efficiency of capital allocation (e.g., Diamond and Verrecchia (1991) and Goldstein and Yang (2017)). However, the existing models that support these benefits of disclosure assume that investors perfectly understand firms’ riskiness and focus exclusively on information concerning firms’ expected future values. In this paper, I build a model to analyze the impact of disclosure that provides information on a firm’s riskiness on liquidity and investment efficiency. I find that the impact of risk information on these market outcomes starkly differs from that of information on firms’ expected cash flows.

The model that I develop builds upon the standard framework of strategic trade in a firm’s stock by allowing the firm’s idiosyncratic risk to be unknown to the market (e.g., Glosten and Milgrom (1985) and Kyle (1985)). A sophisticated investor in the model can incur a cost to acquire information regarding the firm’s value and trades in the firm’s stock alongside a liquidity trader. The existing theoretical work that employs this framework to study disclosure often finds that higher-quality disclosure levels the playing field among investors by making public information that might otherwise have been acquired privately. Thus, it reduces the profits that sophisticated traders earn at the expense of liquidity traders (e.g., Diamond (1985) and Diamond and Verrecchia (1991)). As such, disclosure is often thought to enhance liquidity and reduce firms’ costs of capital.

In contrast, I find that public information concerning firm-specific risk increases the profits earned by sophisticated traders. The reason is that the firm’s riskiness determines the returns that are available to traders who study the firm: when a firm’s risk is higher, a fixed amount of private information can be exploited for greater profit, since it represents a greater relative information advantage (e.g., Grossman and Stiglitz (1980)). As a result, risk information assists traders who have the expertise and ability to acquire private information in determining when and where to focus their efforts at doing so. Thus, rather than “leveling the playing field,” risk information increases the degree of information asymmetry among investors and the losses incurred by liquidity traders. Importantly, this reduction in liquidity arises despite the fact that, on average, risk information has no impact on the amount of informed trade in the market: it simply causes traders to acquire more (less) information on a firm when it is of high (low) risk.

At first pass, the negative impact of risk information on liquidity might suggest that such information is detrimental to markets. However, this reduction in liquidity is driven purely by risk information’s influence on private information acquisition. Moreover, while private information in the marketplace can cause undesirable decreases in liquidity, it is well recognized that such information can have real effects on firm value through its impact on the efficiency of stock prices (e.g., Dow and Gorton (1997) and Bond et al. (2012)). I next study how risk information’s impact on investor learning influences firms’ real decisions. To do so, I assume the firm is run by a manager who decides whether to liquidate an investment (or whether to initiate a new investment). When making this decision, the manager possesses imperfect information regarding the investment’s profitability and observes the firm’s stock price. The manager bases their decision in part on the stock price, as this price reflects investors’ private information concerning the investment’s value.

In this setting, I show that risk information increases real efficiency by enhancing the usefulness of the information that the manager learns from the firm’s stock price. Intuitively, since risk information causes investors to expend more effort studying the firm when its risk is elevated, it leads the firm’s price to be more informative when investment risk is greater. While this is naturally offset by a less informative price when investment risk is low, the firm has a greater demand for information when risk is high: since riskier investments have both higher potential upside and downside, knowledge of whether such investments are destined to be successful is of greater importance in deciding whether to continue them. To summarize, risk information can enhance investment efficiency by leading investors to acquire more information precisely when it is more useful to the firm.

To contrast with existing studies of disclosure and investor learning, which study exclusively information on expected firm value, I focus on a disclosure that exclusively provides information on risk. However, in applying the model, it is essential to recognize that many, if not most, disclosures contain information on both the mean of future cash flows and their risk. The conventional wisdom that disclosure increases liquidity applies to the mean component of these disclosures, while the insights from my model apply to their risk component. To illustrate this point and to demonstrate how the insights in the model apply to existing disclosure regulation, consider the impact on liquidity of the SEC’s requirement that firms quickly disclose the arrival of unanticipated events with a material impact on firm value in a Form 8-K.² Existing models that assume disclosures contain exclusively mean information predict that this policy increases liquidity because it makes public the arrival of events that influence the firm’s expected value – knowledge which might otherwise be held privately and traded upon.

Note, however, that such a policy also provides investors with information on the firms’ riskiness. The reason is that material events (e.g., asset acquisitions, debt issuance, merger discussions, etc.) introduce uncertainty regarding the firm’s value, and thus knowledge of their arrival resolves uncertainty regarding the firm’s fundamental risk. As a result, my model suggests that the policy should have an offsetting negative impact on liquidity: the policy helps sophisticated investors decipher when it is worthwhile to investigate the firm and when it is better to invest their efforts elsewhere. This example also illustrates the effect of risk information on investment efficiency. Managers likely have a heightened desire for decision-relevant information around the types of events disclosed in 8-Ks, since their decisions have a precipitous impact on firm value around these events (Edmans et al. (2015)).³ Since the disclosure policy induces investors to acquire more information around these events, it makes prices more informative precisely when managers have a spike in their demand for information.

I conduct a series of additional analyses in the paper that provide a fuller picture on the relationship between risk information, investor learning, and informational feedback. First, I consider the case in which the firm is run by a manager who is risk averse in their investment decision, which reflects a setting where they are overly exposed to idiosyncratic risk as a result of their compensation policy. In this case, when the investment’s risk is sufficiently large, the manager liquidates the project unless the firm’s price reveals that investors have acquired positive information regarding the investment’s performance. Since investors tend to earn minimal profits when price reveals their information, this implies that when the firm discloses very high risk, investors reduce the amount of information they acquire, thereby leading to an inverse-U-shaped relationship between the amount of informed trade and the disclosed level of risk. I document conditions for which risk information reduces versus enhances investment efficiency and explore the impact of risk information on the expected level of firm investment.

Next, I consider a setting in which investors are averse to the idiosyncratic risk revealed by the disclosure, which corresponds to a setting in which a few players take large positions in the stock. In this case, I again find that risk information has an ambiguous impact on investment efficiency as, when risk is excessively high, investors may no longer find it optimal to take risky speculative positions on their information. Finally, I explore the case in which the firm’s disclosure concerns an asymmetric risk. For example, the firm may disclose a “downside risk,” such as the potential for an adverse litigation outcome, that both lowers expected cash flows and raises cash flow risk. In this case, I show that, because the disclosure that a downside risk is more severe indicates that the manager is more likely to act to mitigate the risk, such a disclosure may discourage investors from acquiring information about the risk. Thus, it is again possible that risk information reduces the efficacy of feedback and investment efficiency.

Related literature

A strand of prior literature also discusses the idea that disclosure may complement informed trade, typically focusing on settings in which investors’ private information has little or no value unless a disclosure is released (e.g., when their information concerns the error in or payoff-irrelevant component of a disclosure; see Alles and Lundholm (1993), Kim and Verrecchia (1994), Boot and Thakor (2001), and Cheynel and Levine (2020)).⁴ Within this literature, the economic mechanism driving the complementarity between disclosure and private information in Cheynel and Levine (2020) is the closest to the one I document. They study a setting in which a voluntary disclosure provides non-directional information that, when paired with the trader’s private information, can become directional. In this literature, disclosure increases informed traders’ ability to profit from a fixed level of information. In contrast, in my model, risk information has no impact on the ability of traders to profit from a fixed level of information acquisition; it increases their expected profits only when they choose the level of information they acquire as a function of the outcome of the disclosure. Related to the channel in my model, Fischer and Heinle (2020) also find that traders can use accounting data (in their case, the deviation between price and earnings) to learn about the value to acquiring information.

This article also relates to the significant empirical literature documenting that firms reveal information on their risk to capital markets through a variety of disclosure channels; I briefly review and discuss the model’s implications for this literature in Section 5. A much smaller body of prior theoretical work also examines the capital-market impacts of disclosure that provides information on firm risk (e.g., Jorgensen and Kirschenheiter (2003), Heinle et al. (2018)). Notably, Jorgensen and Kirschenheiter (2003) study a model in which firms voluntarily disclose information on their cash-flow risk, showing that there exists an equilibrium in which high-risk firms choose to withhold their information. In contrast, consistent with the existing literature that studies the impact of disclosure on informed trade, I focus on disclosure that the firm must release, such as regulated disclosure.

Finally, prior work also studies the equilibria that arise when firms use the information in price when making real decisions (e.g., Gao and Liang (2013), Edmans et al. (2015), Goldstein and Yang (2019), and Chen et al. (2021)). Especially relevant to this article, Gao and Liang (2013) and Goldstein and Yang (2019) study the impact of disclosure that concerns the level of a firm’s payoffs on the firm’s ability to learn from its price. These papers show that disclosure influences real efficiency by changing the amount of private information aggregated into prices. In contrast, in my model, risk information has no impact on the expected amount of information in prices, but nevertheless influences real efficiency by increasing the amount of information in prices when the firm benefits the most from this information. Relatedly, recent work by Schneemeier (2021), Petrov (2020), and Xiong and Yang (2021), and Lassak (2021) consider how voluntary disclosure on the level of cash flows influences managers’ ability to learn from price. Dye and Sridhar (2002) and Langberg and Sivaramakrishnan (2010) also study models in which disclosure enhances feedback. In these models, disclosure improves feedback because investors are only able to acquire information if the firm first makes a disclosure.⁵ In contrast, in my analysis, investors can always acquire information regarding the firm, and yet disclosure still can improve feedback.

In Section 2, I discuss the model’s assumptions and study how risk information affects private information acquisition. In Section 3, I study how risk information affects firm’s expected value and expected investment through the channel of learning from stock prices. In Section 4, I extend the model to consider investor risk aversion and information on the firm’s expected cash flows in addition to the firm’s risk. In Section 5, I discuss the relevance of the model to empirical research, and in Section 6 I conclude.

2 Model

2.1 Assumptions

The model consists of five periods, $t\in \left \{ 0,\ldots ,4\right \}$, and centers on a firm that holds an investment with uncertain future payoff $\tilde {x}$. At time 0, the firm releases a public disclosure $\tilde {\Delta }$ that concerns the risk of its investment. The model’s timeline following this disclosure draws on the informational feedback effects literature (e.g., Edmans et al. (2015)). At time 1, an investor expends unobservable effort $q\left (\tilde {\Delta }\right )$ to learn about the profitability of the investment. At time 2, the investor trades in the firm’s stock alongside a noise trader and risk-neutral market maker. The market maker sets price equal to the firm’s expected value given the disclosure $\tilde {\Delta }$ and the total order flow in the market. Next, at time 3, the firm’s manager decides whether to continue or liquidate the investment. Importantly, the manager observes the firm’s stock price when making this decision. Finally, at time 4, the firm’s payoffs are distributed to its shareholders.

The critical and novel features of the model concern the distribution of the investment’s payoff $\tilde {x}$ and the nature of the firm’s disclosure $\tilde {\Delta }$. The investment’s payoff $\tilde {x}$ depends on the outcome of two independent random variables, $\tilde {\omega }$ and $\tilde {V}$, that capture its expected value and risk, respectively. The variable $\tilde { \omega }$ takes on values of 1 or 0 with equal probabilities, where $\tilde {\omega }=1$ ($\tilde {\omega }=0$) corresponds to an investment that is profitable (unprofitable). Specifically, when $\tilde {\omega }=1$, the investment’s payoff is $\tilde {x}=\mu +\tilde {V}$, while when $\tilde {\omega } =0$, the investment’s payoff is $\tilde {x}=\mu -\tilde {V}$. Given this setup, an increase in $\tilde {\omega }$ raises the project’s expected payoff but has no impact on its risk. The parameter μ represents the ex ante expected payoff of the project. Assume that μ > 0 and that μ is known to all parties in the model.

On the other hand, the variable $\tilde {V}$ represents the risk of the investment in the sense that as $\tilde {V}$ increases, the investment’s expected value remains fixed, but the investment becomes more profitable on the upside and less profitable on the downside. I allow $\tilde {V}$ to have any distribution with finite expectation and support υ.⁶ The investment’s payoffs can be concisely expressed as follows:

$$ \tilde{x} = \mu+\tilde{V}\left( 2\tilde{\omega}-1\right). $$

Turning to the firm’s disclosure policy, I assume that the firm observes a signal $\tilde {s}$ that concerns the investment’s risk $\tilde {V}$ and is independent of its expected payoff, $\tilde {\omega }$. I allow this signal to have a general distribution with support S and assume that it orders the investment’s risk $\tilde {V}$ in the sense of first-order stochastic dominance, that is, for s₁ > s₂:

$$ \tilde{V}|\tilde{s}=s_{1}\succ_{FSD}\tilde{V}|\tilde{s}=s_{2}\text{.} $$

Thus, a higher value of the signal raises investors’ perception of the firm’s risk.⁷ In the appendix, I show that this assumption implies that an increase in the signal leads to a mean-preserving spread in the distribution of the firm’s cash flows.

I compare market outcomes under two disclosure policies, one in which $\tilde {s}$ is disclosed and one in which $\tilde {s}$ remains private to the firm: under the first policy, $\tilde {\Delta }=\tilde {s}$, and under the second policy, $\tilde {\Delta }=ND$. As a convenient way of referring to these policies, I term the first policy risk disclosure and the second nondisclosure. However, the results may apply more generally to the risk component of any disclosure, even those that do not explicitly discuss risk and those that also contain information on expected firm value. This includes, for instance, earnings and balance-sheet line items (e.g., Beyer and Smith (2021)) and the disclosure of potential adverse events such as lawsuits. To demonstrate this fact, in Section 4.2, I extend the model to consider the case in which the disclosure simultaneously alters perceptions of firm risk and expected firm cash flows.

The investor’s information acquisition choice $q\left (\tilde {\Delta }\right )$ causes them to incur a cost of $\frac {k q\left (\tilde {\Delta }\right )^{2}}{2}$, which represents the effort that they must exert investigating the firm. Given a choice of $q\left (\tilde {\Delta }\right )$, they learn the outcome of $\tilde {\omega }$ with probability $q\left (\tilde {\Delta }\right )$ and learn nothing otherwise. Whether the success or failure of their information acquisition is observable to the market is not important for the analysis.

The noise trader in the financial market randomly submits a demand of − 1 or 1 with probabilities $\frac {1}{2}$.⁸ In order to pool their order flows with the noise trader, the investor also either submits a demand of − 1 or 1, or refrains from trading. In order to rule out perverse equilibria, I assume that if the informed trader does not earn a positive expected profit from trading, they prefer not to trade; this reflects a small transaction cost to trading. To reiterate, the market maker sets price equal to the firm’s expected value, which rules out the possibility that the outcome of $\tilde {s}$ directly influences the firm’s price via a risk premium. Thus, the analysis captures the case in which $\tilde {V}$ is an idiosyncratic source of risk.

In deciding whether to liquidate the investment, the firm’s manager maximizes their expected utility $u_{m}\left (\cdot \right )$ as a function of the firm’s value, where $u_{m}^{\prime }>0$, $u_{m}^{\prime \prime }\leq 0$, and $u_{m}\left (0\right )$ is normalized to 0. This objective function captures a manager who aims to maximize the firm’s value but is risk averse, which is consistent with the manager maximizing their expected utility as a function of their long-term equity-based compensation. If the manager liquidates the investment, the firm’s payoffs are normalized to 0. To keep the analysis interesting, assume that, with positive probability, the manager’s risk signal is such that they find it optimal to continue the project when they rely on their prior beliefs regarding $\tilde {\omega }$: $E\left (u_{m}\left (\tilde {x}\right ) |\tilde {s}\right ) >0$. Furthermore, assume that ∀s ∈ S, $E\left (u_{m}\left (\mu -\tilde {V}\right ) |\tilde {s}=s\right ) <0$. This states that, when the manager is certain that $\tilde {\omega }=0$, they prefer to liquidate the project regardless of their risk signal.

Throughout the model, the equilibrium concept I use is perfect Bayesian Nash. This implies that in determining price, the market maker takes into account not only the information that the order flow contains but also how the price impacts the manager’s investment decision. Moreover, the manager and market maker must correctly anticipate the investor’s information acquisition choice. I solve the model via backwards induction, first considering the manager’s investment decision, then studying the financial market, and finally considering the investor’s learning decision.

2.2 Discussion of assumptions

Prior to moving to the analysis, I next discuss the model’s key assumptions.

Firm information

The model is founded on the assumption that the firm has private information on its idiosyncratic risk that it can disclose to the market. One conspicuous source of risk information firms possess is their knowledge of the scale and nature of their investments. For instance, the firm is the first to know about speculative investments in R&D, expansions into new markets, and divestitures. The firm is likely also the first to know about economic shocks that increase its risk, such as changes in strategy, potential litigation, potential M&As, and data breaches. In Section 5, I review the empirical literature that studies the various types of risk information firms disclose and the effects of this information on the market. Note that investors might be advantaged relative to firms in assessing certain components of risk, which I do not consider in the model. For instance, they may better understand macroeconomic trends or demand factors that influence the firm’s risk (Bond et al. (2012)). Plausibly, firms may attempt to learn this information from their prices should it be relevant to their decision making. I leave an analysis of this case to future research.⁹

Nature of the disclosure

The disclosure policy I consider is implicitly one in which the firm’s disclosure is verifiable (i.e., it cannot be biased) and cannot strategically be withheld. This focus is consistent with a setting where a firm is required by a regulation to provide risk information, e.g., financial-reporting requirements. In contrast, Lassak (2021) and Schneemeier (2021) study feedback-effects models that are better suited towards studying voluntary disclosure of risk information. They find that firms may voluntarily disclose information that raises investors’ risk perceptions in order to increase investors’ incentives to acquire information. Relatedly, Petrov and Chen (2021) study a model in which feedback influences a manager’s decision to bias a disclosure. They find that, when managerial bias raises investor uncertainty, information acquisition rises; this, in turn, amplifies managers’ incentives to bias.

Moreover, rather than derive the optimal disclosure policy from a regulator’s point of view, I instead simply compare market outcomes under the policies of risk disclosure and nondisclosure. The reason is that, as we will see, risk information can create a trade-off between a decline in the welfare of liquidity or noise traders and an increase in productive efficiency. There is no natural means to compare these two effects without taking a strong stand on the regulator’s objective function. This comparison is also useful in terms of offering empirical predictions on the relationship between the amount of risk information a firm provides to the market and market outcomes; see Section 5 for a summary of these predictions.

Investor learning technology

The technology I employ for investor learning – perfect learning with some probability, at a quadratic cost – is a useful but unnecessary simplification. As we will see in the next section, it serves as a useful benchmark because it implies that the disclosure policy has no impact on the expected amount of information that the investor acquires. This enables the model to illustrate that risk disclosure can influence informed traders’ profits and real efficiency without influencing the on-average amount of information acquired by investors. In the internet appendix, I illustrate that the main results in the paper are robust to alternative means of modeling investor learning.¹⁰

Investment decision

I focus on a binary investment in the benchmark model, which simplifies the exposition of a number of results. While I refer to this as the decision over whether to liquidate a project, the results apply equally to the case in which the firm chooses whether to adopt a new project, presuming the firm has information on the new project’s scope/risk.¹¹ Moreover, the main results are qualitatively similar in the case of a continuous investment decision; see the internet appendix for an analysis of this case.

2.3 Investment choice

When the manager makes the investment decision, they use the information contained in the price $\tilde {P}$. The manager’s decision rule conditional on their information set $\left \{\tilde {P},\tilde {s}\right \}$ is:

$$ \underset{I\left( P,s\right) \in \left\{ 0,1\right\} }{\arg \max}E\left[ u_{m}\left( I\left( P,s\right) \tilde{x}\right) |\tilde{P}=P,\tilde{s}=s \right] \text{.} $$

The solution to the manager’s optimization problem involves a threshold probability, $T\left (\mu ,\tilde {s}\right ) \in \left (0,1\right )$, such that they liquidate the project when theprobability that the investment is profitable conditional on the information they learn from price, $\Pr \left (\tilde {\omega }=1|\tilde {P}\right )$, is below $T\left (\mu ,\tilde {s}\right )$. The next lemma characterizes $T\left (\mu ,\tilde {s}\right )$ assuming that a manager who is indifferent between continuing and liquidating their investment chooses to continue the investment.

Lemma 1

The manager continues the investment when their perceived probability that the investment is profitable, $\Pr \left (\tilde {\omega }=1|\tilde {P}\right )$, exceeds a threshold $T\left (\mu ,\tilde {s}\right ) \in \left (0,1\right )$, and liquidates the investment otherwise, where:

$$ T\left( \mu ,\tilde{s}\right) =\frac{E\left[ u_{m}\left( \mu -\tilde{V} \right)|\tilde{s}\right] }{E\left[ u_{m}\left( \mu -\tilde{V}\right) -u_{m}\left( \mu +\tilde{V}\right) |\tilde{s}\right] }\text{.} $$

Furthermore,

• (i) The threshold HCode $T\left (\mu ,\tilde {s}\right )$ decreases in the investment’s ex ante expected payoff μ.

• (ii) There exists a value $\hat {s}\in S\cup \infty$ such that the manager liquidates the investment should they receive no information from price if and only if $\tilde {s}>\hat {s}$.

Result (i) in the lemma simply states that the manager is more willing to continue the project when it is, in expectation, more profitable. Result (ii) plays an important role in the analyses that follow. It states that the manager liquidates the project when they hold their prior belief regarding the probability that the investment is profitable if and only if their risk signal $\tilde {s}$ falls above a threshold $\hat {s}$. Note this threshold $\hat {s}$ may take on the maximum value in the support of $\tilde {s}$ when the support is bounded and $\infty$ when it is not, which is simply to say that the manager may never liquidate the project when they hold their prior belief regarding $\tilde {\omega }$. In particular, this holds when the manager is risk neutral because the project is, on average, profitable.

2.4 Financial market

I next assess the equilibrium in the financial market. This requires considering how the manager’s investment decision depends upon the information that they glean from price. The manager’s ability to learn from price creates a “feedback effect” whereby the trading strategy of the investor is a function of their conjecture regarding the manager’s investment decision, which itself depends upon the behavior of the investor. The next lemma characterizes the resulting equilibria.

Lemma 2

• (i) Suppose q > 0 and that the firm either refrains from disclosure or discloses a risk signal $\tilde {s}\leq \hat {s}$. Then, there exists an equilibrium in the financial market in which the investor submits a demand order of 1 when they learn $\tilde {\omega }=1$, a demand order of − 1 when they learn $\tilde {\omega }=0$, and a demand order of 0 when they do not receive a signal. The firm’s price P as a function of the order flow $\tilde {O}$ and disclosure $\tilde {\Delta }$ satisfies:

  $$ \begin{array}{@{}rcl@{}} P\left( \tilde{O}=2,\tilde{\Delta}\right) &=&\mu +E\left( \tilde{V}|\tilde{ {\Delta}}\right) \\ P\left( \tilde{O}\in \left\{ -1,0,1\right\} ,\tilde{\Delta}\right) &=&\mu \Pr \left( \tilde{s}\leq \hat{s}|\tilde{\Delta}\right) \\ P\left( \tilde{O}=-2,\tilde{\Delta}\right) &=&0\text{.} \end{array} $$

  (1)

  This equilibrium is the unique equilibrium in which the investor trades (i.e., submits a non-zero order with positive probability).

• (ii) Suppose that either (a) q = 0 or (b) q > 0 and the firm discloses a risk signal $\tilde {s}>\hat {s}$. Then, in the unique equilibrium, the investor does not trade.

The first part of the lemma states that when q > 0 and the firm either refrains from disclosure or discloses $\tilde {s}\leq \hat {s}$, there exists an equilibrium in which the investor trades. In this case, there also exists a no-trade equilibrium; I focus on the equilibrium with trade when it exists.¹² In this equilibrium, the investor buys upon observing $\tilde {\omega }=1$, sells upon observing $\tilde {\omega }=0$, and does not trade when they do not learn. To understand the equilibrium price function, note that order flows $\tilde {O}=$ 2 and $\tilde {O}=-2$ perfectly reveal that the investor learned $\tilde {\omega }=1$ ($\tilde {\omega }=0$) to the market maker. In contrast, order flows $\tilde {O}\in \left \{ -1,0,1\right \}$ are completely uninformative. Since the price takes on distinct values in each of these cases, order flow and price contain the same information, and thus the manager’s and market maker’s beliefs are aligned.

When $\tilde {O}=2$, the manager realizes the trader has learned $\tilde { \omega }=1$ and continues the project, leading to a price of $\mu +E\left (\tilde {V}|\tilde {s}\right )$. In contrast, when $\tilde {O}=-2$, independent of $\tilde {s}$, the manager realizes the trader has learned $\tilde {\omega }=0$ and liquidates the project, leading to a price of 0. When the order flow is uninformative ($\tilde {O}\in \left \{ -1,0,1\right \}$), whether the manager liquidates the project depends upon the risk signal $\tilde {s}$ they observe. Specifically, when $\tilde {s}\leq \hat {s}$, they do not liquidate the project, and thus the expected firm value equals μ. On the other hand, when $\tilde {s}>\hat {s}$, they liquidate the project, and the firm’s value is 0. Thus, the market maker sets price equal to $\mu \Pr \left (\tilde {s} \leq \hat {s}|\tilde {\Delta }\right )$. Note that by trading on their information, the investor earns positive expected profits only when both (1) their information is not revealed and (2) the manager does not liquidate the investment.

The second part of the lemma states that if the investor does not acquire information (q = 0), they do not trade in the unique equilibrium. This is also the only equilibrium when the firm discloses $\tilde {s}>\hat {s}$. Intuitively, when $\tilde {s}>\hat {s}$, the only case in which the manager would continue the project is when the investor acquires positive information and this information is impounded into price. However, this implies that the investor is never able to profit: given any realized order flow, either the manager liquidates the project or their information is revealed.

The next corollary summarizes the investor’s expected profits should they learn $\tilde {\omega }$ under the assumption that the equilibrium with trade is played when it exists, which I refer to as ${\Pi } \left (\tilde {\Delta }\right )$; this will play a critical role in determining the investor’s information acquisition decision.

Corollary 1

Given the disclosure $\tilde {\Delta }$, conditional on successfully acquiring information, the investor earns positive expected profits equal to:

$$ {\Pi} \left( \tilde{\Delta}\right) =\frac{1}{2}\Pr \left( \tilde{s}\leq \hat{s} |\tilde{\Delta}\right) E\left( \tilde{V}|\tilde{s}\leq \hat{s},\tilde{\Delta} \right) . $$

(2)

Moreover, the investor’s expected profits conditional on successfully acquiring information are identical under the policies of risk disclosure and nondisclosure: HCode $E\left [ {\Pi } \left (\tilde {s}\right ) \right ] =E\left [ {\Pi } \left (ND\right ) \right ]$.

The first term in the investor’s expected profit, $\frac {1}{2}\Pr \left (\tilde {s}\leq \hat {s}|\tilde {\Delta }\right )$, captures the joint probability that noise trade moves against the investor and the manager continues the investment. The second term, $E\left (\tilde {V}|\tilde {s}\leq \hat {s},\tilde {\Delta }\right )$, reflects the quantity that the investor expects to earn when these two events occur. This term is equal to the expected difference between the true value of the investment and the firm’s price conditional on a risk signal that leads the manager to continue the project. Notice the disclosure $\tilde {\Delta }$ affects both components of the investor’s expected profit. Intuitively, when the firm discloses its risk, it informs the investor of whether $\tilde {s}\leq \hat {s}$, that is, whether the manager will liquidate the project given an uninformative order flow. Furthermore, it informs them of their expected profits conditional upon $\tilde {s}\leq \hat {s}$. When $\tilde {\Delta }$ is uninformative, the investor’s expected profit depends upon their prior regarding the likelihood that $\tilde {s}\leq \hat {s}$ and their prior expectation of $\tilde {V}$ given that $\tilde {s}\leq \hat {s}$.

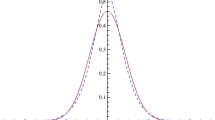
Figure 1 depicts the investor’s expected profits as a function of $\tilde {s}$ under the two disclosure policies. The investor’s expected profit is clearly unrelated to $\tilde {s}$ under the policy of nondisclosure. Under a policy of risk disclosure, the investor’s expected profit increases in $\tilde {s}$ up until $\hat {s}$. However, beyond $\hat {s}$, the investor’s expected profit drops to zero, reflecting the fact that, for $\tilde {s}>\hat {s}$, the manager liquidates the project when $\tilde {O}=0$.

Corollary 1 further states that risk disclosure has no impact on the investor’s expected profits if they learn $\tilde {\omega }$: $E\left [ {\Pi } \left (\tilde {s}\right ) \right ]=E\left [{\Pi } \left (ND\right ) \right ]$. That is, risk information has no direct effect on the investor’s ability to profit should they become informed. This contrasts with existing models of complementary disclosure that consider disclosure concerning expected future cash flows. In these models, disclosure enhances informed investors’ ability to profit even when their information endowment is taken as exogenous (e.g., Kim and Verrecchia (1994), Boot and Thakor (2001), and Cheynel and Levine (2020)).

2.5 Risk information, investor learning, and liquidity

This section compares the investor’s equilibrium level of information acquisition under the policies of risk disclosure and nondisclosure and studies the effect of risk disclosure on the profits to the investor and the losses to liquidity traders. I focus on the case in which the trader’s choice of q is always interior. A necessary and sufficient condition for this to hold is $k\in \left (\frac {1}{2}\max \limits _{\tilde {s}\leq \hat {s}}E\left (\tilde {V}|\tilde {s}=s\right ) ,\infty \right )$, which states that k exceeds the maximum profits expected by the investor over all possible realizations of the risk signal $\tilde {s}$. The following proposition summarizes the main results.

Proposition 1

The investor chooses $q\left (\tilde {\Delta } \right ) =\frac {1}{k}{\Pi } \left (\tilde {\Delta }\right )$. Moreover,

• (i) The expected amount of information acquired by the investor is identical under the policies of risk disclosure and nondisclosure: $E\left [ q\left (\tilde {s}\right ) \right ] =q\left (ND\right )$.

• (ii) The expected profits earned by the investor and the losses suffered by liquidity traders under a policy of risk disclosure exceed those under a policy of nondisclosure.

The proposition states that the investor’s information acquisition choice $q\left (\tilde {\Delta }\right )$ is proportional to the amount of profit they expect to acquire should they successfully acquire information, ${\Pi } \left (\tilde {\Delta }\right )$. Consequently, $q\left (\tilde {\Delta }\right )$ exhibits the same relationship with the disclosure $\tilde {\Delta }$ as the relationship between ${\Pi } \left (\tilde {\Delta }\right )$ and $\tilde {\Delta }$ depicted in Fig. 1. Furthermore, the expected amount of information acquired by the investor is the same whether or not the firm discloses its risk; i.e., $E\left [ q\left (\tilde {s}\right ) \right ] =q\left (ND\right )$. This feature of the model is specific to the quadratic cost function; under more general convex cost functions, risk disclosure would also influence the expected amount of information acquired, though the direction would depend upon the precise shape of the cost function. Nevertheless, this result is useful for two reasons. First, it indicates that, unlike disclosure regarding the mean, there is no definitive connection between risk disclosure and information acquisition. Second, it demonstrates that, in contrast to the existing literature, the subsequent results regarding the effects of disclosure on liquidity and real efficiency do not stem from a relationship between disclosure and the expected amount of information acquisition.

Fig. 1

This figure depicts the expected profits earned by the informed investor when they successfully acquire information as a function of the risk signal $\tilde {s}$ under the policies of risk disclosure and nondisclosure

The proposition further states that, despite the fact that disclosure does not impact the informed trader’s expected information acquisition, it nonetheless increases their ex ante expected trading profits. Intuitively, risk information enables the investor to attune their information acquisition to the profitability of this acquisition. This increase in the investor’s expected profits comes at the expense of liquidity traders and in this sense can be viewed as a reduction in liquidity. The appendix further shows that, when the manager is risk neutral, the increase in the trader’s expected profits that risk disclosure creates is proportional to $Var\left [E\left (\tilde {V}|\tilde {s}\right ) \right ]$. Hence, a more informative risk disclosure has a larger impact on the trader’s profits.

Note that the model cannot speak to how liquidity traders’ losses affect the firm’s cost of capital. However, it is straightforward to extrapolate the results to frameworks suited to answering this question. For instance, in Diamond and Verrecchia (1991), the firm internalizes the losses to liquidity traders at the time of raising capital, as traders buying into the firm may anticipate future liquidity shocks and price protect themselves. Thus, in this setting, one might expect a commitment to risk disclosure to increase the firm’s cost of capital.

While the results in this proposition will serve as a foundation for the remainder of the paper, they do not rely upon the feedback channel embedded in the model. As they are driven entirely by the decision-usefulness of risk information to informed traders, they would also hold in a simpler setting in which the firm’s investment decision is taken as given, and in other micro-structure frameworks, including the strategic-trading model of Kyle (1985).¹³ As a final point, note that this analysis is framed in a single-firm model with a convex cost function to acquiring information. Alternatively, we might view investors’ information acquisition choice as a decision regarding how to allocate a fixed amount of resources in each time period across a selection of firms (Van Nieuwerburgh and Veldkamp (2010)). In this case, an analogous result to Proposition 1 will arise because risk disclosure informs investors of which firms to learn about as opposed to whether to learn about a specific firm in any given time period.

Figure 2 depicts, as a function of the underlying parameters, the impact of risk disclosure on liquidity in the case in which (1) the manager has CARA utility, and (2)$\tilde {V}=m_{V}+\tilde {s}+\tilde { \varepsilon }$ where $\tilde {s}$ and $\tilde {\varepsilon }$ are independent and gamma distributed, and m_V > 0 is chosen to ensure that the manager always liquidates the project when $\tilde {\omega }=0$. The figure shows that an increase in managerial risk aversion or a reduction in the investment’s profitability reduces the impact of risk disclosure on liquidity, as this increases the probability that the investment is liquidated given an unrevealing order flow. On the other hand, the effect of the expected variance on liquidity is non-monotonic; intuitively, as risk has a second-order impact on the manager’s utility, an increase in the expected variance (as captured by the mean of $\tilde {V}$) initially has only a small effect on the probability that the manager liquidates the investment, but ultimately has a large effect on this probability.

Fig. 2

This figure depicts the investor’s trading profits, which represents a notion of illiquidity, in the cases of risk disclosure and nondisclosure when (1) the manager has CARA utility; (2) $\tilde {V}=m_{V}+ \tilde {s}+\tilde {\protect \varepsilon }$ where $\tilde {s}$ and $\tilde {\protect \varepsilon }$ are independent and gamma distributed, and m_V is chosen to ensure that the manager always liquidates the project when $\tilde {\protect \omega }=0$

3 Risk information and the investment decision

While the results in the prior section may suggest that risk information has a detrimental impact on the market, they are driven purely by the fact that this information improves the ability of investors to profit by acquiring private information. Moreover, while private information in the marketplace can cause undesirable wealth transfers across investors, it is often also thought to have beneficial real effects on firm value. Note, however, that the analysis in the prior section also suggests that risk information does not impact on the average amount of private information in the market, which leaves open the question of whether it has a real effect on firm value.

I next show that despite the fact that risk information does not affect the on-average amount of private information in the market, it can influence both investment efficiency and the likelihood that the firm liquidates its project. I evaluate investment efficiency in terms of the firm’s expected profits, which is consistent with the investment’s risk being idiosyncratic. ¹⁴ I first consider the case in which the manager is risk neutral and acts to maximize the firm’s expected profits, and then consider the case in which the manager is risk averse. In the latter case, the manager’s incentives are not perfectly aligned with maximizing the firm’s value, which may arise when the manager’s compensation schedule exposes them to idiosyncratic firm risk.

3.1 Risk-neutral manager

The next result establishes that, when the manager is risk neutral, risk disclosure enhances investment efficiency and has no impact on the likelihood that the manager liquidates the project.

Proposition 2

Suppose the manager is risk neutral. Then,

• (i) The firm’s expected value in the case of risk disclosure less that in the case of non-disclosure equals $\frac {1}{8k}Var\left [ E\left (\tilde {V}|\tilde {s}\right ) \right ] >0$.

• (ii) The probability that the manager liquidates the investment does not differ across the policies of risk disclosure and nondisclosure.

Result (i) of the proposition establishes that risk disclosure enhances investment efficiency. This result rests upon two observations. First, when the manager is risk neutral, they continue the project given an uninformative price independent of their risk signal $\tilde {s}$. Thus, Proposition 1 implies that risk disclosure causes the investor’s information acquisition to increase monotonically in $\tilde {s}$. Second, the manager’s liquidation decision has a greater impact on the firm’s expected value when the investment’s expected risk, as captured by $\tilde {s}$, is higher. Intuitively, a riskier project has both a greater upside and downside. Thus, it is more valuable to the firm that its manager makes the correct investment decision, obtaining the investment’s upside and avoiding its downside.

Taken together, these two results imply that risk disclosure causes the investor’s information acquisition to rise precisely when information is of greater use to the firm, which increases the firm’s expected value. Note that the positive effect of risk information on investment efficiency is proportional to the variance of the expectation of $\tilde {V}$ given $\tilde {s}$, $Var\left [ E\left (\tilde {V}|\tilde {s}\right ) \right ]$. This implies that risk disclosure has a larger positive impact on the firm’s value when this disclosure is more informative in the sense that it causes expected posterior beliefs over the investment’s risk, $E\left (\tilde {V}|\tilde {s} \right )$, to vary to a greater extent.

Result (ii) of the proposition establishes that risk information has no effect on the likelihood that the firm liquidates the project. Intuitively, a risk-neutral manager liquidates the project if and only if the price reveals that $\tilde {\omega }=0$. This occurs when the investor learns $\tilde {\omega }=0$ and noise trade moves in the same direction as the investor’s trade. Risk disclosure has no impact on the probability of this event since it has no impact on the expected amount of information acquisition.

3.2 Risk-averse manager

The following proposition summarizes the impact of risk disclosure on the firm’s expected profit and the likelihood the manager liquidates the project when the manager is risk averse.

Proposition 3

Suppose the manager is strictly risk averse. Then,

• (i) The firm’s expected value in the case of risk disclosure less that in the case of nondisclosure may be either positive or negative.

• (ii) Risk disclosure increases the probability that the manager liquidates its investment.

To understand part (i) of the proposition, recall from Proposition 1 that risk disclosure induces a positive relationship between the investor’s information acquisition and firm risk for low risk signals, but causes the investor’s information acquisition to drop to zero when the risk signal grows sufficiently high ($\tilde {s}>\hat {s}$). This implies that risk disclosure has two offsetting effects on the firm’s expected profits: (i) for moderate risk signals such that the manager continues the project given an uninformative price ($\tilde {s}\leq \hat {s}$), it attunes the incentives of the investor to acquire information with the manager’s demand for information, and (ii) it causes the investor to stop acquiring information when the risk is high ($\tilde {s}>\hat {s}$) and the manager has a strong need for information. In general, it is ambiguous which of these two effects dominates.

The proposition further states that risk disclosure unambiguously increases the likelihood that the firm liquidates the project. Intuitively, risk disclosure causes investors to neglect to acquire information precisely when the manager liquidates their investment given an uninformative price ($\tilde {s}>\hat {s}$). That is, risk disclosure reduces the information available to the manager exactly when information could prevent them from liquidating the project. This result suggests that, beyond influencing the firm’s expected value, risk disclosure also negatively influences the firm’s expected risk: when the firm reduces investment, from an ex ante point of view, the firm’s risk declines.

To provide intuition for the drivers of whether risk disclosure increases investment efficiency, consider the case in which the manager has CARA utility with risk aversion parameter ρ ($u_{m}\left (x\right ) =\frac { 1-\exp \left (-\rho x\right ) }{\rho }$). Furthermore, assume that the distribution of $\tilde {V}$ is binary, taking on values in $\left \{ \bar {V} -\delta ,\bar {V}+\delta \right \}$ with equal probabilities, and that the disclosure reveals $\tilde {V}$ perfectly: $\tilde {s}=\tilde {V}$. The following corollary states conditions on the profitability of the project, managerial risk aversion, and the distribution of $\tilde {V}$ that ensure that risk disclosure increases the firm’s expected value.

Corollary 2

Fixing the remaining parameters of the model, there exist thresholds μ^T, ρ^T, and $\bar {V}^{T}$ such that risk disclosure increases the firm’s expected value if and only if μ ≥ μ^T, ρ ≤ ρ^T, or $\bar {V}\leq \bar {V}^{T}$.

This corollary holds because risk disclosure improves the firm’s expected value when the manager is unlikely to liquidate the project. In this case, the high-risk region of the distribution of $\tilde {s}$ on which the investor reduces their information acquisition to zero occurs with a small probability. Liquidation is unlikely when the project is expected to be highly profitable, the manager is not excessively risk averse, or the project’s outcome is relatively certain.

4 Extensions

4.1 Investor risk aversion

The analysis to this point assumes that the investor is risk neutral. This assumption approximates a setting in which there are a large number of traders who acquire information regarding the firm, each of whom takes only a small stake in its stock (as in, e.g., Dow et al. (2017)). In this case, the firm’s risk disclosure affects information acquisition only through its impact on the expected profits to acquiring information. In this section, I consider the case in which the investor is risk averse, such that the firm’s risk disclosure also affects the risk to acquiring and trading on private information. This case applies to settings in which there are a few large players in the market who invest a significant amount of capital based on their information acquisition choices.

Assume now the investor has CARA utility with risk aversion parameter α: $u_{I}\left (x\right ) =\frac {1-\exp \left (-\alpha x\right ) }{ \alpha }$.¹⁵ Moreover, to introduce risk to trading, assume now that the investor receives an imperfect signal $\tilde {\psi }$ regarding $\tilde {\omega }$ with the following conditional distribution:

$$ \Pr \left( \tilde{\psi}=1|\tilde{\omega}=1\right) =\Pr \left( \tilde{\psi}=0| \tilde{\omega}=0\right) =\gamma \text{,} $$

where $\gamma \in \left (\frac {1}{2},1\right )$. In order to focus on the effect of investor risk aversion, I assume the manager is risk neutral in their project selection and that the risk disclosure is perfect ($\tilde {s}= \tilde {V}$). Moreover, I assume that $\gamma >\frac {1}{2}\left (\frac {\mu }{ \inf \upsilon }+1\right )$, which ensures that, given a negative signal from price, the manager liquidates the project for any $\tilde {s}\in S$. I continue to assume the market maker sets price equal to the expected value of the firm, which may raise the question of why the market maker is risk neutral while the investor is risk averse. This set of assumptions is intended to capture a setting consisting of a large competitive fringe of traders who take the other side of a smaller number of sophisticated investors’ trades (as in, e.g., Hirshleifer et al. (1994)).

The nature of the manager’s investment decision follows precisely as in the main model. The key change in the analysis arises in the financial market. In particular, the investor must take on risk in order to profit from their information by taking a long or short position in the firm’s stock in order to camouflage their orders with those of noise traders.¹⁶ As a result, for a disclosed risk that is sufficiently large, the investor’s risk aversion may overrule their desire for profits, leading them to abstain from trading. The next lemma summarizes the equilibrium in the trading stage for any given disclosure policy and fixed q > 0.

Lemma 3

Suppose q > 0. There exists a threshold that is a function of the disclosure $\tilde {\Delta }$, $\tau \left (\tilde {\Delta }\right )$, such that, for $\alpha >\tau \left (\tilde {\Delta }\right )$, in the unique equilibrium, the investor does not trade. For $\alpha \leq \tau \left (\tilde {\Delta }\right )$, there exists an equilibrium in which the investor submits a demand order of 1 given $\tilde {\psi }=1$, a demand order of − 1 given $\tilde {\psi }=0$, and a demand order of 0 when they do not receive a signal. Prices in this equilibrium satisfy:

$$ \begin{array}{@{}rcl@{}} P\left( \tilde{O}=2,\tilde{\Delta}\right) &=&\mu +\left( 2\gamma -1\right) E\left( \tilde{V}|\tilde{\Delta}\right) \\ P\left( \tilde{O}\in \left\{ -1,0,1\right\} ,\tilde{\Delta}\right) &=&\mu \\ P\left( \tilde{O}=-2,\tilde{\Delta}\right) &=&0\text{.} \end{array} $$

Under a policy of risk disclosure, $\tau \left (\tilde {\Delta }\right )$ decreases in the disclosed risk $\tilde {\Delta }$.

The lemma states that there is a threshold level of risk aversion, $\tau \left (\tilde {\Delta }\right )$, such that there exists an equilibrium in which the investor trades as in Lemma 2 when $\alpha \leq \tau \left (\tilde {\Delta }\right )$. As in the previous sections, I assume that this equilibrium is played when it exists. When $\alpha >\tau \left (\tilde {\Delta }\right )$, the unique equilibrium is for the trader to abstain from trading altogether. Intuitively, for α sufficiently large, the potential downside to trading on an inaccurate signal outweighs the upside to trading on an accurate one.

The next proposition establishes that the impact of risk disclosure on investor learning is similar to the case in which the manager is risk averse. To distinguish from the previous section, I now refer to the investor’s equilibrium information acquisition as $q^{RA}\left (\tilde {\Delta }\right )$.

Proposition 4

Under a policy of risk disclosure, the investor’s information acquisition $q^{RA}\left (\tilde {V}\right )$ is single-peaked in $\tilde {V}$. Moreover, $q^{RA}\left (\tilde {V}\right )$ is positive for $\alpha \leq \tau \left (\tilde {V}\right )$ and zero for $\alpha >\tau \left (\tilde {V}\right )$, where $\tau \left (\tilde {V}\right )$ is the threshold defined in Lemma 3.

The proposition states that the investor’s information acquisition $q^{RD}\left (\tilde {V}\right )$ initially increases but ultimately decreases in $\tilde {V}$. Intuitively, for low levels of $\tilde {V}$, the investor’s taste for higher expected profits dominates their distaste for additional risk, while, for high levels of $\tilde {V}$, the investor’s distaste for risk takes over. For $\tilde {V}$ sufficiently large, the investor acquires no information as the unique equilibrium in the financial market involves no trade.

Note that a revealed-preference argument implies that the investor is better off under a policy of risk disclosure. Specifically, under the policy of risk disclosure, the investor has the option, but chooses not, to deviate to $q^{RA}\left (ND\right )$, in which case they would achieve the same expected utility as in the case of nondisclosure. However, unlike in the case in which the investor is risk neutral, it need not be the case that the expected losses suffered by the noise trader decline under a policy of risk disclosure. The reason is that, while the informed investor achieves higher expected utility, under certain parameterizations of the model, this is attained by decreasing the risk they endure as opposed to increasing the expected profits they earn. Finally, as risk disclosure again leads to an inverse-U-shaped relationship between information acquisition and firm risk, its influence on investment efficiency is ambiguous.

4.2 Asymmetric risk

In the baseline analysis, the firm’s risk is symmetric; i.e., positive and negative outcomes were equally likely (formally, $\Pr \left (\tilde {\omega }=1\right ) =$ $\frac {1}{2}$). As a result, the firm’s risk $\tilde {V}$ and the disclosure about this risk do not impact expected firm cash flows. However, many risks faced by firms, and disclosures about such risks, are not symmetric, in that they may alter firms’ expected cash flows. For example, firms may be subject to adverse events such as lawsuits, data-security breaches, and changes in the competitive environment. Moreover, firms frequently disclose such risks in press releases, 8-Ks, and section 1A of the 10-K. Such downside risks not only raise cash flow risk but also lower expected cash flows. In other cases, heightened risk disclosure may be associated with an increase in expected cash flows. For instance, riskier investments may be less competitive and thus more profitable on average. Thus, disclosing that a new project is riskier may signal that it is likely to be more profitable.

I next extend the model to consider such asymmetric risks by allowing the ex ante probability that the project is successful to be arbitrary; i.e., $\Pr \left (\tilde {\omega }=1 \right )=p \in (0,1)$. In this case, a higher risk disclosure $\tilde {s}$ always raises expected firm risk, but may either increase or decrease expected cash flows. To see this, notice that the project’s expected cash flows given $\tilde {s}=s$ are:

$$ E\left( \tilde{x}|\tilde{s}=s \right) = \mu+(2p-1)*E\left( \tilde{V}|\tilde{s}=s \right). $$

Hence, an increase in s raises (lowers) expected firm cash flows when $p>\frac {1}{2}$ ($p<\frac {1}{2}$). Thus, this generalization of the model enables it to capture both downside risk disclosure and the potential for a positive correlation between investment risk and return.¹⁷

The next proposition establishes that the qualitative features of the equilibrium, as well as the detrimental impact of risk disclosure on liquidity, largely carry over to this case. Intuitively, regardless of the disclosure’s impact on expected cash flows, it continues to inform traders of the profits available to investigating the firm. The one exception is that the manager’s desire to invest given an uninformative order flow may no longer decline in the risk signal s when $p > \frac {1}{2}$. The reason is that, in this case, a higher risk signal also raises the expected payoff to the investment.

Proposition 5

There is a unique equilibrium in which the investor trades. This equilibrium is characterized as follows:

• The manager invests when the price reveals $\tilde {\omega }=1$ or when the price is uninformative and $\tilde {s} \in S_{I} \subseteq S$.

• If the firm either refrains from disclosure or discloses $\tilde {s} \in S_{I}$, the investor submits a demand order of 1 when they learn $\tilde {\omega }=1$, a demand order of − 1 when they learn $\tilde {\omega }=0$, and a demand order of 0 when they do not receive a signal. The firm’s price P as a function of the order flow $\tilde {O}$ and disclosure $\tilde {\Delta }$ satisfies:

  $$ \begin{array}{@{}rcl@{}} P\left( \tilde{O}=2,\tilde{\Delta}\right) &=& \mu +E\left( \tilde{V} | \tilde{\Delta} \right) \\ P\left( \tilde{O}\in \left\{ -1,0,1\right\} ,\tilde{\Delta}\right) &=& \Pr\left( \tilde{s} \in S_{I} | \tilde{\Delta} \right) \left[ \mu +\left( 2p-1 \right) E\left( \tilde{V} |\tilde{\Delta}, \tilde{s} \in S_{I} \right) \right] \\ P\left( \tilde{O}=-2,\tilde{\Delta}\right) &=& 0. \end{array} $$

• If the firm discloses $\tilde {s}\notin S_{I}$, the investor does not trade and the firm’s price equals 0.

Moreover, in this equilibrium, the expected profits earned by the investor and the losses suffered by liquidity traders under a policy of risk disclosure exceed those under a policy of nondisclosure.

I next study risk disclosure’s impact on expected firm profits via the feedback channel. To focus on the impact of asymmetric risk, I again study the case in which the manager is risk neutral. The next corollary shows that, when the correlation between project risk and return is positive, risk disclosure enhances feedback and raises investment efficiency. On the other hand, disclosure concerning downside risks need not enhance feedback.

Corollary 3

Suppose that the manager is risk neutral. Then,

• (i) Risk disclosure increases the firm’s expected profits when $p\ge \frac {1}{2}$.

• (ii) Risk disclosure has an ambiguous impact on the firm’s expected profits when $p<\frac {1}{2}$.

This result stems from how heightened risk influences the manager’s incentives to invest given an uninformative price. When $p> \frac {1}{2}$, a higher risk signal encourages investment because it raises expected cash flows. Consequently, it encourages the investor to acquire information when $\tilde {s}$ is higher. As this is again when the manager benefits the most from learning, risk disclosure enhances feedback in this case. On the other hand, for $p< \frac {1}{2}$, a greater risk signal discourages investment. This can cause the investor to refrain from acquiring information when it is most valuable to the manager, dampening feedback.

5 Empirical implications

5.1 Applications

In order to highlight applications of the model, in this section, I review the empirical literature that documents risk information in firms’ financial disclosures. I then discuss the model’s empirical predictions in the next section. The empirical literature finds risk information in four types of financial disclosures: the financial statements, other components of the 10-K, forecasts, and disclosures of material events. I summarize the literature on each of these categories below.

• 1. Financial statements. Prior work shows that lines items on the balance sheet related to asset growth and accruals provide risk information to markets that influences firms’ discount rates (Penman and Zhu (2014), Hou et al. (2015), and Penman and Yehuda (2019)). The income statement also appears to provide risk information. Earnings-based risk-factor estimates outperform return-basedestimates at predicting future risk-factor exposures and explaining firms’ risk premia (Cohen et al. (2009)). Moreover, the level and extremity of earnings induce changes in option-implied metrics of future volatility (Neururer et al. (2016) and Smith and So (2022)). Kim and Zhang (2014) further show that an opacity metric derived from the income statement and balance sheet relates to option-implied tail risk.

• 2. Other components of the 10-K. Empirical work shows that sections 1A and 7A in the 10-K, which are explicitly labeled as risk disclosures, are related to market-based metrics of firm risk. Previous studies applying textual analysis techniques show that the qualitative risk information provided in section 1A is correlated with future volatility and firms’ discount rates (e.g., Loughran and McDonald (2011), Bao and Datta (2014), Campbell et al. (2014), and Hope et al. (2016)). Moreover, prior work shows that the sensitivities to currency, interest, and commodity factors discussed in section 7A reflect firms’ future factor exposures (Linsmeier et al. (2002) and Thornton and Welker (2004)). Prior literature also studies the sensitivity disclosures required by oil and gas companies and finds that they predict market reactions to future shifts in commodity prices and bid-ask spreads (Rajgopal (1999) and Badia et al. (2020)).

• 3. Managerial forecasts. Empirical evidence suggests that managers’ forecasts contain information on firm risk. Jayaraman and Wu (2020) show that capex forecasts can stimulate information acquisition and generate informational feedback effects. These forecasts likely influence investors’ perceptions of risk by adjusting their beliefs regarding future investment scale. Baginski et al. (1993) show that when managers provide wider range forecasts, investors disagree more and place less weight on earnings, suggesting they are left with a greater perception of firm risk.

• 4. Disclosures of material events. Disclosures of potential mergers or acquisitions may also indicate novel risks that are worthy of investor attention (Luo (2005)). Note that other disclosures of material events, such as those in form 8-Ks that discuss issues including changes in corporate governance practices, acquisition or disposition of assets, equity sales, creation of debt, loan defaults, and contingent liabilities, also likely influence investors’ perception of firm risk.

5.2 Predictions

The model offers a number of predictions regarding the relationship between the risk component of firms’ financial disclosures, subsequent liquidity, and investment efficiency. I first summarize the predictions for firms whose managers are aligned with investors in that they are willing to endure idiosyncratic risk in order to improve expected firm value.

A core feature and prediction of the model is that, following disclosures that heighten risk perceptions, information acquisition rises; as a result, informed trade rises and market depth declines. This feature is consistent with existing empirical literature that studies risk information. For example, Badia et al. (2020) document reductions in spreads following disclosures by oil and gas companies that suggest their reserve values are uncertain.¹⁸ Furthermore, the model predicts that managers place more weight on price following such disclosures, as they have a greater demand for information and more private information is impounded into prices. This prediction is consistent with the findings in Jayaraman and Wu (2020), who show that following capex forecasts that suggest higher levels of investment and thus higher risk, managers adjust their investment according to stock-price movements.

Next, the model yields untested predictions regarding the ex ante relationship between the amount and quality of risk information that a firm provides, market liquidity, and investment efficiency. First, it predicts that higher-quality risk information leads to reduced market depth, defined as the expected losses suffered by a trader who takes a position without having information. This finding speaks to the relationship between disclosure quality and the extent of informed trade, for which prior empirical research documents mixed evidence. For instance, Leuz and Verrecchia (2000) document a negative relationship and Lee et al. (1993) a positive relationship between accounting quality and bid-ask spreads. The model predicts that when shifts in disclosure quality tilt towards risk information, they are more likely to complement, as opposed to substitute, private information acquisition. Additionally, the model predicts that firms that provide higher-quality risk information acquire more useful information from prices and, as a result, make more efficient investment decisions. The magnitude of this effect depends upon the extent to which investors are able to acquire information that is relevant to a firm’s decisions.

The model’s predictions are more nuanced when the firm’s manager is excessively averse to idiosyncratic risk. Corollary 1 demonstrates that the relationship between the disclosed level of risk and market depth in this case is no longer monotonically increasing, but is instead inverse U-shaped. Moreover, Proposition 3 and Corollary 2 show that higher-quality risk information may reduce investment efficiency in this case. Specifically, risk information reduces investment efficiency when the manager is inclined to liquidate (or, more generally, downsize) their investment, such as when this investment is highly risky or only marginally profitable. Finally, Proposition 3 predicts that, in this case, higher-quality risk information leads to a greater likelihood that the firm liquidates its investment and thus to lower firm risk. Sections 4.1 and 4.2 further show that risk disclosure may reduce investment efficiency when (i) investors hold highly concentrated positions in a stock or (ii) the disclosure concerns a downside risk such as a lawsuit.

6 Conclusion

In this article, I analyze how public risk information affects the ability of sophisticated investors to profit from private information regarding the firm’s value and the resultant impacts on liquidity and real efficiency. I find that risk disclosure reduces liquidity by enabling these investors to acquire more information when it is more lucrative to do so. I then demonstrate that risk disclosure influences the ability of a manager to use their firm’s stock price as a source of information when making investment decisions. I find that risk information tends to improve investment efficiency, though it can have a deleterious effect on investment efficiency should the firm’s investments be only marginally profitable or should the firm’s manager be excessively averse to idiosyncratic risk.

My findings highlight the importance of tailoring specific models to address the unique features of the different types of information disclosed by firms. Much of the theoretical literature models disclosure in a reduced-form fashion, whereby a disclosure equals the firm’s fundamental value plus a stochastic error term. While this approach is a convenient way to capture information releases, it is unlikely to capture the full effects of all types of disclosures. Note that in my analysis, I ignore any strategic incentives that firms may have to manipulate or withhold risk information. In the model, firms may have an incentive to manipulate their risk information upwards in order to incentivize investors to acquire more private information, thereby increasing the information content of stock prices. A productive avenue for future research may be to explore the equilibrium that arises when managers trade off incentivizing private information acquisition and reducing risk premia when making risk-disclosure decisions. Alternatively, one might consider the impact of risk disclosure on informed trade in option markets and the ability of managers to learn information on the second moment from option prices.

Appendix A: Proofs

I first prove the claim in the main text that if s₁ > s₂, then $\tilde {x}|\tilde {s}=s_{1}$ is a mean-preserving spread of $\tilde {x}|\tilde {s}=s_{2}$. Since $\tilde {s}$ does not impact the mean of $\tilde {x}$, it is sufficient to show that $\tilde {x}|\tilde {s}=s_{2}$ second-order stochastic dominates $\tilde {x}|\tilde {s}=s_{1}$, i.e.,

$$ \forall T \in \mathcal{R} \text{, }{\int}_{-\infty }^{T }F_{x|s}\left( t|\tilde{s}=s_{2}\right) dt<{\int}_{-\infty }^{T }F_{x|s}\left( t|\tilde{s}=s_{1}\right) dt\text{.} $$

Applying the law of total probability and the fact that $\tilde {x}$ is conditionally independent of $\tilde {s}$ given $\tilde {V}$, we have:

$$ \begin{array}{@{}rcl@{}} {\int}_{-\infty }^{T }F_{x|s}\left( t|\tilde{s}=s\right) dt &=&{\int}_{-\infty }^{T }{\int}_{\upsilon }F_{x|s,V}\left( t|\tilde{s}=s,\tilde{V}=v\right) f_{V|s}\left( v|\tilde{s}=s\right) dvdt \\ &=&{\int}_{-\infty }^{T }{\int}_{\upsilon }F_{x|V}\left( t|\tilde{V}=v\right) f_{V|s}\left( v|\tilde{s}=s\right) dvdt \\ &=& {\int}_{\upsilon }\left[ {\int}_{-\infty }^{T }F_{x|V}\left( t|\tilde{V}=v\right) dt\right] f_{V|s}\left( v|\tilde{s}=s\right) dv. \end{array} $$

Now, applying the distribution of $\tilde {x}$, we have:

$$ \begin{array}{@{}rcl@{}} &&{\int}_{\upsilon }\left[ {\int}_{-\infty }^{T }F_{x|V}\left( t|\tilde{V} =v\right) dt\right] f_{V|s}\left( v|\tilde{s}=s\right) dv \\ &=&{\int}_{\upsilon }\left[ {\int}_{-\infty }^{T }\frac{\mathbf{1}\left( t\ge-v\right) +\mathbf{1}\left( t\ge v\right) }{2}dt\right] f_{V|s}\left( v| \tilde{s}=s\right) dv \\ &=&{\int}_{\upsilon }\left( \frac{\max \left\{ T +v,0\right\} +\max \left\{T -v,0\right\} }{2}\right) f_{V|s}\left( v|\tilde{s}=s\right) dv \\ &=& E \left[ \frac{\max \left\{ T +\tilde{V},0\right\} +\max \left\{T -\tilde{V},0\right\} }{2} \mid \tilde{s}=s\right]. \end{array} $$

Given that this is the expectation of an increasing function of $\tilde {V}$, by the definition of first-order stochastic dominance, it increases in s. This completes the proof.

Proof of Lemma 1

The manager continues the project if and only their expected utility from doing so is non-negative:

$$ \Pr \left( \tilde{\omega}=1|\tilde{P},\tilde{s}\right) E\left[ u_{m}\left( \mu +\tilde{V}\right) |\tilde{s}\right] +\Pr \left( \tilde{\omega}=0|\tilde{P },\tilde{s}\right) E\left[ u_{m}\left( \mu -\tilde{V}\right) |\tilde{s} \right] \geq 0\text{.} $$

(3)

This inequality reduces to $\Pr \left (\tilde {\omega }=1|\tilde {P},\tilde {s} \right ) \geq T\left (\mu ,\tilde {s}\right ) \equiv \frac {E\left [ u_{m}\left (\mu -\tilde {V}\right ) |\tilde {s}\right ] }{E\left [ u_{m}\left (\mu -\tilde {V} \right ) -u_{m}\left (\mu +\tilde {V}\right ) |\tilde {s}\right ] }<1$. Define

$H\left (\mu ,\tilde {s}\right )$ $\equiv E\left [ u_{m}\left (\mu +\tilde {V} \right ) |\tilde {s}\right ]$ and $L\left (\mu ,\tilde {s}\right ) \equiv E\left [ u_{m}\left (\mu -\tilde {V}\right ) |\tilde {s}\right ]$, so that $T\left (\mu , \tilde {s}\right ) =\frac {L\left (\mu ,\tilde {s}\right ) }{L\left (\mu ,\tilde {s }\right ) -H\left (\mu ,\tilde {s}\right ) }$. Note that, since $u_{m}\left (\cdot \right )$ is increasing and $\tilde {s}$ orders $\tilde {V}$ in the sense of first-order stochastic dominance, $\frac {\partial }{\partial \tilde { s}}H\left (\mu ,\tilde {s}\right ) >0$ and $\frac {\partial }{\partial \tilde {s} }L\left (\mu ,\tilde {s}\right ) <0$. Furthermore, using the assumption that ∀s ∈ S, $E\left [ u_{m}\left (\mu -\tilde {V}\right ) |\tilde {s}=s \right ] <0$, note that $T\left (\mu ,\tilde {s}\right ) >0$.

Result (i):

We have:

$$ \begin{array}{@{}rcl@{}} &&\frac{\partial T\left( \mu ,\tilde{s}\right) }{\partial \mu }=\frac{\frac{ \partial L\left( \mu ,\tilde{s}\right) }{\partial \mu }\left( L\left( \mu , \tilde{s}\right) -H\left( \mu ,\tilde{s}\right) \right) -L\left( \mu ,\tilde{ s}\right) \left( \frac{\partial L\left( \mu ,\tilde{s}\right) }{\partial \mu }-\frac{\partial H\left( \mu ,\tilde{s}\right) }{\partial \mu }\right) }{ \left( L\left( \mu ,\tilde{s}\right) -H\left( \mu ,\tilde{s}\right) \right)^{2}} \\ &=&\frac{\frac{\partial H\left( \mu ,\tilde{s}\right) }{\partial \mu } L\left( \mu ,\tilde{s}\right) -\frac{\partial L\left( \mu ,\tilde{s}\right) }{\partial \mu }H\left( \mu ,\tilde{s}\right) }{\left( L\left( \mu ,\tilde{s} \right) -H\left( \mu ,\tilde{s}\right) \right)^{2}}. \end{array} $$

Since $u_{m}\left (\cdot \right )$ is increasing, $\frac {\partial L\left (\mu ,\tilde {s}\right ) }{\partial \mu }>\frac {\partial H\left (\mu ,\tilde {s} \right ) }{\partial \mu }>0$, and, since $u_{m}\left (0\right ) =0$, $H\left (\mu ,\tilde {s}\right ) >0>L\left (\mu ,\tilde {s}\right )$. Therefore, the above expression is negative.

Result (ii):

To prove this result, it is sufficient to show that:

$$ T\left( \mu ,s^{\ast }\right) =\frac{1}{2}\implies \left[ \frac{\partial T\left( \mu ,s\right) }{\partial s}\right]_{s=s^{\ast }}>0. $$

(4)

To see why this is sufficient, recall that, by assumption, with positive probability, the manager invests when they believe $\Pr \left (\tilde {\omega }=1\right )=\frac {1}{2}$; i.e., for some s ∈ S, $T\left (\mu ,s\right ) \leq \frac {1}{2}$. Hence, if $T\left (\mu ,s\right ) -\frac {1}{2}$ is increasing in s whenever it crosses zero, then it must be the case that either: (i) $\exists \hat {s}\in S$ such that $T\left (\mu ,s\right ) >\frac {1}{2}$ if and only if $s>\hat {s},$ or (ii) $T\left (\mu ,s\right ) <\frac {1}{2}$ for all s ∈ S (i.e., $\hat {s}=\infty$).

Now, to show that statement (4) holds, note that:

$$ \begin{array}{@{}rcl@{}} T\left( \mu ,s^{\ast }\right) =\frac{1}{2}&\Leftrightarrow & \frac{ L\left( \mu ,s^{\ast }\right) }{L\left( \mu ,s^{\ast }\right) -H\left( \mu ,s^{\ast }\right) }=\frac{1}{2} \\ &\Leftrightarrow &L\left( \mu ,s^{\ast }\right) +H\left( \mu ,s^{\ast }\right) =0\text{.} \end{array} $$

(5)

Next, we have:

$$ \frac{\partial T\left( \mu ,\tilde{s}\right) }{\partial \tilde{s}}=\frac{ \frac{\partial H\left( \mu ,\tilde{s}\right) }{\partial \tilde{s}}L\left( \mu ,\tilde{s}\right) -\frac{\partial L\left( \mu ,\tilde{s}\right) }{ \partial \tilde{s}}H\left( \mu ,\tilde{s}\right) }{\left( L\left( \mu , \tilde{s}\right) -H\left( \mu ,\tilde{s}\right) \right)^{2}}\text{.} $$

To sign this expression, notice that, since $u_{m}^{\prime \prime }\left (\cdot \right ) <0$, $\frac {\partial }{\partial \tilde {V}}\left (u_{m}\left (\mu +\tilde {V}\right )+u_{m}\right .$ $\left .\left (\mu -\tilde {V}\right ) \right ) <0$. Now, applying first-order stochastic dominance,

$$ \frac{\partial }{\partial \tilde{s}}E\left( u_{m}\left( \mu +\tilde{V} \right) +u_{m}\left( \mu -\tilde{V}\right) |\tilde{s}\right) <0\implies 0< \frac{\partial H\left( \mu ,\tilde{s}\right) }{\partial \tilde{s}}<-\frac{ \partial L\left( \mu ,\tilde{s}\right) }{\partial \tilde{s}}\text{.} $$

Therefore, applying expression (5),

$$ \left[ \frac{\partial T\left( \mu ,s\right) }{\partial s}\right]_{s=s^{\ast }}>-\left[\frac{\partial L\left( \mu ,s\right) }{\partial s}\right]_{s=s^{\ast}}\frac{ L\left( \mu ,s^{\ast}\right) +H\left( \mu ,s^{\ast}\right) }{\left( L\left( \mu ,s^{\ast}\right) -H\left( \mu ,s^{\ast}\right) \right)^{2}}=0 \text{.} $$

□

Proof of Lemma 2

Result (i) I demonstrate the existence of the equilibrium discussed in the lemma and then show that the only other equilibrium is one in which the investor never trades. Given the investor’s strategy, the posterior beliefs of the market maker are:

$$ \begin{array}{@{}rcl@{}} \Pr \left( \tilde{\omega}=1|\tilde{O}=z,\tilde{\Delta}\right) &=&\frac{1}{2} \text{ for }z\in \left\{ -1,0,1\right\} \text{;} \\ \Pr \left( \tilde{\omega}=1|\tilde{O}=-2,\tilde{\Delta}\right) &=&0\text{;} \\ \Pr \left( \tilde{\omega}=1|\tilde{O}=2,\tilde{\Delta}\right) &=&1\text{.} \end{array} $$

Moreover, given the prices conjectured in this equilibrium, price and order flow contain the same information such that the manager’s beliefs are the same as the market maker’s beliefs. Now, as $0<T\left (\mu ,\tilde {s}\right ) <1$, the manager continues (liquidates) the project given $\tilde {O}=-2$ ($\tilde {O}=2$). Calculating the stock’s expected value given the manager’s strategy, we arrive at the price function in the lemma. It is easily verified that the investor does no better from a deviation from their strategy independent of $\tilde {\Delta }$. I next show via a series of remarks that the only other equilibrium is one in which the informed trader never trades.

Remark 1

There do not exist equilibria in which (a) the investor buys when observing $\tilde {\omega }=1$ but does not sell when observing $\tilde {\omega } =0$ or (b) sells when observing $\tilde {\omega }=0$ but does not buy when observing $\tilde {\omega }=1$.

Proof

I argue that there is no equilibrium of type (a); a similar argument shows there is not equilibrium of type (b). In such an equilibrium, order flows $\tilde {O}\in \left \{ 0,2\right \}$ arise only when $\tilde {\omega }=1$ and order flows $\tilde {O}\in \left \{ -1,1\right \}$ arise when the investor learns $\tilde {\omega }=0$ or is uninformed. Thus, the investor and market maker’s beliefs are the same when the investor purchases, implying they earn zero expected profits. Given the assumption that the investor prefers not to trade if they do not acquire positive profits from doing so, this is not an equilibrium. □

Remark 2

There do not exist equilibria in which the investor buys when observing $\tilde {\omega }=1$ and sells when observing $\tilde {\omega }=0$ and in which prices take a form other than in expression (3).

Proof

Note that, by Bayes’ rule, in any equilibrium in which the investor follows the strategy in the remark and the market maker and manager have the same information, price takes the form in expression (3). Thus, in any other equilibrium in which the investor follows this strategy, it must be that two distinct order flows $o_{1},o_{2}\in \left \{ -2,0,2\right \}$ lead to the same price, such that the manager’s information is coarser than that of the market maker. In any such equilibrium, the manager must liquidate the project given the order flows o₁ and o₂. The reason is that if the manager took the project, the market maker would price the order flows o₁ and o₂ differently. Now, suppose o₁ = 2 and o₂ = − 2, in which case the associated price leaves the manager with their prior. Note that this is not an equilibrium when the firm discloses its risk and $\tilde {s}\leq \hat {s }$, or the manager does not disclose their risk, as, in either case, the manager continues the project with positive probability. Next, suppose o₁ = 0 and o₂ = 2. In this case, if the manager liquidates the project, the investor who purchases earns no profits and thus prefers to deviate to not trading. The same argument implies that it cannot be that o₁ = 0 and o₂ = − 2. □

Remark 3

There exists an equilibrium in which the informed trader never trades.

Proof

If the informed trader does not trade, then $\tilde {O}\in \left \{ -1,1\right \}$ is uninformative. If the investor were to take a position, it would lead to one of the order flows $\tilde {O}\in \left \{ -2,0,2\right \}$, which are all off the equilibrium path. Consider off-equilibrium-path beliefs given $\tilde {O}\in \left \{ -2,0,2\right \}$, $\lambda \left (\tilde { {\Delta }},\tilde {O}\right )$, that satisfy, for any $\tilde {\Delta }$, $\tilde {s }$, and $\tilde {O}\in \left \{ -2,0,2\right \}$, $T\left (\mu ,\tilde {s} \right ) >\lambda \left (\tilde {\Delta },\tilde {O}\right )$. Then, the manager never invests given $\tilde {O}\in \left \{ -2,0,2\right \}$. Naturally, this implies that the trader cannot earn profits by deviating from their strategy of not trading, confirming that this is an equilibrium. □

Result (ii) Note when q = 0, the investor has no private information; thus, in any equilibrium, their beliefs align with the market maker’s. This implies that there is no equilibrium in which they trade. When $\tilde {s}>\hat {s}$, there is no equilibrium in which the investor buys (sells) when observing $\tilde {\omega }=1$ ($\tilde {\omega }=0$), as the manager liquidates the project when $\tilde {O}=0$. Moreover, an argument similar to the one in Remark 1 implies that there does not exist an equilibrium in which the investor buys but does not sell or vice versa. □

Proof of Corollary 1

Note that the investor and market maker have the same beliefs regarding the firm’s value whenever $\tilde {O}=2$ or $\tilde {O}=-2.$ Hence, the investor only earns profits in expectation when $\tilde {O}=0$. Upon performing the calculation, in the case of nondisclosure, conditional on learning, the investor is left with an expected trading profit of:

$$ \begin{array}{@{}rcl@{}} {\Pi} \left( ND\right) &=&\frac{1}{4}\ast \left[ \Pr \left( \tilde{s}\leq \hat{s}\right) \left( \mu +E\left( \tilde{V}|\tilde{s}\leq \hat{s}\right) -\mu \Pr \left( \tilde{s}\leq \hat{s}\right) \right) \right. \\ &&+\Pr \left( \tilde{s}\leq \hat{s}\right) \left( \mu \Pr \left( \tilde{s} \leq \hat{s}\right) -\mu +E\left( \tilde{V}|\tilde{s}\leq \hat{s}\right) \right) \\ &&\left. +\Pr \left( \tilde{s}>\hat{s}\right) \left( -\mu \Pr \left( \tilde{s }\leq \hat{s}\right) \right) +\Pr \left( \tilde{s}>\hat{s}\right) \left( \mu \Pr \left( \tilde{s}\leq \hat{s}\right) \right) \right] \\ &=&\frac{\Pr \left( \tilde{s}\leq \hat{s}\right) E\left( \tilde{V}|\tilde{s} \leq \hat{s}\right) }{2}\text{,} \end{array} $$

and, in the case of risk disclosure, the investor is left with an expected trading profit of:

$$ {\Pi} \left( \tilde{s}\right) =\frac{\mathbf{1}\left( \tilde{s}\leq \hat{s} \right) E\left( \tilde{V}|\tilde{s}\right) }{2}\text{.} $$

Note that in both cases, we may write ${\Pi } \left (\tilde {\Delta }\right ) =\frac {1}{ 2}\Pr \left (\tilde {s}\leq \hat {s}|\tilde {\Delta }\right ) E\left (\tilde {V}| \tilde {s}\leq \hat {s},\tilde {\Delta }\right )$. □

Proof of Proposition 1

Consider first the optimal strictly positive information acquisition choice. In the case of nondisclosure, the investor solves:

$$ q\left( \tilde{\Delta}\right) =\arg \max_{q}q{\Pi} \left( \tilde{\Delta} \right) -\frac{1}{2}kq^{2}=\frac{\Pi \left( \tilde{\Delta}\right) }{k}\text{. } $$

(6)

Note that, for $\Pr \left (\tilde {s}\leq \hat {s}|\tilde {\Delta }\right ) >0$, the profits resulting from setting $q\left (\tilde {\Delta }\right )$ to equal expression (6) are strictly positive and, thus, exceed those given the decision to set $q\left (\tilde {\Delta }\right ) =0$.

Result (i) Let the notation ${\int \limits } dF_{s}$ denote Riemann-Stieltjes integral with respect to the distribution of $\tilde {s}$. That is, ${\int \limits } dF_{s}={\int \limits } f_{s}\left (t\right ) dt$ when $\tilde {s}$ is continuously distributed with PDF $f_{s}\left (\cdot \right ) ,$ and ${\int \limits } dF_{s}=\sum p_{s}\left (t\right )$ when $\tilde {s}$ is discretely distributed with PGF $p_{s}\left (\cdot \right )$. We have that:

$$ \begin{array}{@{}rcl@{}} E\left[ q\left( \tilde{s}\right) \right] &=&E\left[ \frac{\mathbf{1}\left( \tilde{s}\leq \hat{s}\right) E\left( \tilde{V}|\tilde{s}\right) }{2k}\right] \\ &=&\frac{{\int}_{\tilde{s}\leq \hat{s}}dF_{s}}{2k}\frac{{\int}_{\tilde{s}\leq \hat{s}}E\left( \tilde{V}|\tilde{s}\right) dF_{s}}{{\int}_{\tilde{s}\leq \hat{s }}dF_{s}} \\ &=&\frac{\Pr \left( \tilde{s}\leq \hat{s}\right) E\left( \tilde{V}|\tilde{s} \leq \hat{s}\right) }{2k}=q\left( ND\right) \text{.} \end{array} $$

Result (ii) Substituting, the investor’s expected profits in the case of nondisclosure are

$\frac {1}{8k}\left [ \Pr \left (\tilde {s}\leq \hat {s}\right ) E\left (\tilde {V} |\tilde {s}\leq \hat {s}\right ) \right ]^{2}$, while in the case of disclosure their profits are $\frac {1}{8k}E\left [ \mathbf {1}\left (\tilde {s}\leq \hat {s} \right ) E\left (\tilde {V}|\tilde {s}\right )^{2}\right ]$. Now, note that:

$$ \begin{array}{@{}rcl@{}} \Pr \left( \tilde{s}\leq \hat{s}\right) E\left( \tilde{V}|\tilde{s}\leq \hat{ s}\right) &=&E\left[ \mathbf{1}\left( \tilde{s}\leq \hat{s}\right) \tilde{V} \right] \\ &=&E\left[ E\left( \mathbf{1}\left( \tilde{s}\leq \hat{s}\right) \tilde{V}| \tilde{s}\right) \right] \\ &=&E\left[ \mathbf{1}\left( \tilde{s}\leq \hat{s}\right) E\left( \tilde{V}| \tilde{s}\right) \right] \text{.} \end{array} $$

Therefore, the investor’s expected profit net of costs given risk disclosure less that given nondisclosure equals:

$$ \frac{E\left\{ \left[ \mathbf{1}\left( \tilde{s}\leq \hat{s}\right) E\left( \tilde{V}|\tilde{s}\right) \right]^{2}\right\} }{8k}-\frac{E\left[ \mathbf{1 }\left( \tilde{s}\leq \hat{s}\right) E\left( \tilde{V}|\tilde{s}\right) \right]^{2}}{8k}=\frac{1}{8k}Var\left[ \mathbf{1}\left( \tilde{s}\leq \hat{s }\right) E\left( \tilde{V}|\tilde{s}\right) \right] >0\text{.} $$

Since expected information acquisition is the same under the two policies, a similar calculation implies that the investor’s revenues (profits plus acquisition costs) given risk disclosure less those given nondisclosure equal $\frac {1}{4k}Var\left [ \mathbf {1}\left (\tilde {s}\leq \hat {s}\right ) E\left (\tilde {V}|\tilde {s}\right ) \right ]$. Given that revenues to the investor equal the losses to the noise trader, we have that the noise trader suffers greater losses in the case of risk disclosure. □

Proof of Propositions 2 and 3

I begin by proving the results on risk disclosure’s impact on expected profits. I derive expressions for the firm’s profits in the general case when the manager is risk averse and then consider the special case in which the manager is risk neutral.

Result (i) Let $\tilde {\pi }_{RD}$ ($\tilde {\pi }_{ND}$) denote the firm’s realized profits under a policy of risk disclosure (nondisclosure). Then, we have that:

$$ \begin{array}{@{}rcl@{}} E\left( \tilde{\pi}_{RD}|\tilde{s}\right) &=&{\sum}_{o=-2}^{2}\Pr \left( \tilde{O}=o|\tilde{s}\right) E\left[ I\left( \tilde{P},\tilde{s}\right) \ast \tilde{x}|\tilde{O}=o,\tilde{s}\right] \\ &=&\mathbf{1}\left( \tilde{s}\leq \hat{s}\right) \left( 1-\frac{q\left( \tilde{s}\right) }{2}\right) \mu +\frac{q\left( \tilde{s}\right) }{4}\left( \mu +E\left( \tilde{V}|\tilde{s}\right) \right) \\ &=&\mathbf{1}\left( \tilde{s}\leq \hat{s}\right) \left[ \mu -\frac{E\left( \tilde{V}|\tilde{s}\right) }{8k}\left( \mu -E\left( \tilde{V}|\tilde{s} \right) \right) \right] \text{.} \end{array} $$

Taking the expected value of this expression yields:

$$ \begin{array}{@{}rcl@{}} E\left( \tilde{\pi}_{RD}\right) &=&\Pr \left( \tilde{s}\leq \hat{s}\right) \mu -\frac{1}{8k}E\left[ \mathbf{1}\left( \tilde{s}\leq \hat{s}\right) E\left( \tilde{V}|\tilde{s}\right) \left( \mu -E\left( \tilde{V}|\tilde{s} \right) \right) \right] \\ &=&\Pr \left( \tilde{s}\leq \hat{s}\right) \mu -\frac{\mu }{8k}\Pr \left( \tilde{s}\leq \hat{s}\right) E\left( \tilde{V}|\tilde{s}\leq \hat{s}\right) + \frac{1}{8k}E\left[ \mathbf{1}\left( \tilde{s}\leq \hat{s}\right) E\left( \tilde{V}|\tilde{s}\right)^{2}\right] \text{.} \end{array} $$

Performing the analogous calculation in the case of nondisclosure yields:

$$ \begin{array}{@{}rcl@{}} E\left( \tilde{\pi}_{ND}|\tilde{s}\right) &=&\mathbf{1}\left( \tilde{s}\leq \hat{s}\right) \left( 1-\frac{q\left( ND\right) }{2}\right) \mu +\frac{ q\left( ND\right) }{4}\left( \mu +E\left( \tilde{V}|\tilde{s}\right) \right) \\ &=&\mathbf{1}\left( \tilde{s}\leq \hat{s}\right) \left( 1-\frac{E\left( \tilde{V}|\tilde{s}\leq \hat{s}\right) \Pr \left( \tilde{s}\leq \hat{s} \right) }{4k}\right) \mu +\frac{E\left( \tilde{V}|\tilde{s}\leq \hat{s} \right) \Pr \left( \tilde{s}\leq \hat{s}\right) }{8k}\left( \mu +E\left( \tilde{V}|\tilde{s}\right) \right) \text{.} \end{array} $$

Taking the expected value of this expression, we have:

$$ E\left( \tilde{\pi}_{ND}\right) =\Pr \left( \tilde{s}\leq \hat{s}\right) \mu +\frac{\mu}{8k} \Pr \left( \tilde{s} \leq \hat{s}\right) \left( 1-2\Pr \left( \tilde{s}\leq \hat{s}\right) \right)E\left( \tilde{V}|\tilde{s}\leq \hat{s}\right) +\frac{1}{8k} \Pr \left( \tilde{s}\leq \hat{s}\right) E\left( \tilde{V}|\tilde{s}\leq \hat{s}\right) E\left( \tilde{V}\right) \text{. } $$

Therefore, we have that:

$$ \begin{array}{@{}rcl@{}} E\left( \tilde{\pi}_{ND}-\tilde{\pi}_{RD}\right) &=&\frac{\mu }{8k} \Pr \left( \tilde{s}\leq \hat{s} \right) \left( 1-2\Pr \left( \tilde{s}\leq \hat{s}\right) \right) E\left( \tilde{V}|\tilde{s}\leq \hat{s}\right) \\ &&+\frac{1}{8k}\Pr \left( \tilde{s}\leq \hat{s}\right) E\left( \tilde{V}|\tilde{s}\leq \hat{s}\right) E\left( \tilde{ V}\right) \\ &&+\frac{\mu }{8k}\Pr \left( \tilde{s}\leq \hat{s}\right)E\left( \tilde{V}|\tilde{s}\leq \hat{s}\right) -\frac{1}{4k}E\left[ \mathbf{1}\left( \tilde{s} \leq \hat{s}\right) E\left( \tilde{V}|\tilde{s}\right)^{2}\right] \\ &=&\frac{\mu }{8k} \Pr \left( \tilde{s}\leq \hat{s}\right) \left( 1-\Pr \left( \tilde{s}\leq \hat{s} \right) \right) E\left( \tilde{V}|\tilde{s}\leq \hat{s}\right) \\ &&+\frac{\Pr \left( \tilde{s}\leq \hat{s}\right) }{8k}\left[ E\left( \tilde{V }|\tilde{s}\leq \hat{s}\right) E\left( \tilde{V}\right) -E\left[ \mathbf{1} \left( \tilde{s}\leq \hat{s}\right) E\left( \tilde{V}|\tilde{s}\right)^{2} \right] \right] \text{.} \end{array} $$

(7)

Note that when the manager is risk neutral, the event $\tilde {s}\leq \hat {s}$ occurs with probability one, such that this equals:

$$ \frac{1}{8k}\left\{ E\left( \tilde{V}\right)^{2}-E\left[ E\left( \tilde{V}| \tilde{s}\right)^{2}\right] \right\} =-\frac{Var\left[ E\left( \tilde{V}| \tilde{s}\right) \right] }{8k}<0\text{.} $$

When the manager is risk averse, the proof of the next corollary presents two cases, one in which this is positive and one in which this is negative, which demonstrates that it is ambiguous.

Result (ii) Let ${\Lambda }_{RD}\left (\tilde {s}\right )$ $\left ({\Lambda }_{ND}\left (\tilde {s}\right ) \right )$ denote the probability that the manager continues the investment under a policy of risk disclosure (nondisclosure) for a given signal $\tilde {s}$. In the case of risk disclosure, we have that:

$$ \begin{array}{@{}rcl@{}} E\left( {\Lambda}_{RD}\left( \tilde{s}\right) \right) &=&{\int}_{\tilde{s}\leq \hat{s}}{\Lambda}_{RD}\left( s\right) dF_{s}+{\int}_{\tilde{s}>\hat{s}}{\Lambda}_{RD}\left( s\right) dF_{s} \\ &=&{\int}_{\tilde{s}\leq \hat{s}}\Pr \left( \tilde{O}>-2|\tilde{s}\right) dF_{s}+{\int}_{\tilde{s}>\hat{s}}\Pr \left( \tilde{O}=2|\tilde{s}\right) dF_{s} \\ &=&{\int}_{\tilde{s}\leq \hat{s}}\left( 1-\frac{\mathbf{1}\left( \tilde{s}\leq \hat{s}\right) E\left( \tilde{V}|\tilde{s}\right) }{8k}\right) dF_{s}\text{,} \end{array} $$

where I used the fact that the unique equilibrium when $\tilde {s}>\hat {s}$ is one without trade, such that $\Pr \left (\tilde {O}=2|\tilde {s}\right ) =0$. This expression may be rewritten as follows:

$$ \begin{array}{@{}rcl@{}} {\int}_{\tilde{s}\leq \hat{s}}\left( 1-\frac{\mathbf{1}\left( \tilde{s}\leq \hat{s}\right) E\left( \tilde{V}|\tilde{s}\right) }{8k}\right) dF_{s} &=&\Pr \left( \tilde{s}\leq \hat{s}\right) -\frac{{\int}_{\tilde{s}\leq \hat{s}}dF_{s} }{8k}\frac{{\int}_{\tilde{s}\leq \hat{s}}E\left( \tilde{V}|\tilde{s}\right) dF_{s}}{{\int}_{\tilde{s}\leq \hat{s}}dF_{s}} \\ &=&\Pr \left( \tilde{s}\leq \hat{s}\right) \left( 1-\frac{E\left[ E\left( \tilde{V}|\tilde{s}\right) |\tilde{s}\leq \hat{s}\right] }{8k}\right) \\ &=&\Pr \left( \tilde{s}\leq \hat{s}\right) \left( 1-\frac{E\left( \tilde{V}| \tilde{s}\leq \hat{s}\right) }{8k}\right) \text{.} \end{array} $$

Next, we have that:

$$ \begin{array}{@{}rcl@{}} E\left( {\Lambda}_{ND}\left( \tilde{s}\right) \right) &=&{\int}_{\tilde{s}\leq \hat{s}}{\Lambda}_{ND}\left( s\right) dF_{s}+{\int}_{\tilde{s}>\hat{s}}{\Lambda}_{ND}\left( s\right) dF_{s} \\ &=&{\int}_{\tilde{s}\leq \hat{s}}\Pr \left( \tilde{O}>-2|\tilde{s}\right) dF_{s}+{\int}_{\tilde{s}>\hat{s}}\Pr \left( \tilde{O}=2|\tilde{s}\right) dF_{s} \\ &=&{\int}_{\tilde{s}\leq \hat{s}}\left( 1-\frac{\Pr \left( \tilde{s}\leq \hat{s }\right) E\left( \tilde{V}|\tilde{s}\leq \hat{s}\right) }{8k}\right) dF_{s}+{\int}_{\tilde{s}>\hat{s}}\frac{\Pr \left( \tilde{s}\leq \hat{s}\right) E\left( \tilde{V}|\tilde{s}\leq \hat{s}\right) }{8k}dF_{s} \\ &=&\Pr \left( \tilde{s}\leq \hat{s}\right) -\frac{\Pr \left( \tilde{s}\leq \hat{s}\right)^{2}E\left( \tilde{V}|\tilde{s}\leq \hat{s}\right) }{8k}+ \frac{\left( 1-\Pr \left( \tilde{s}\leq \hat{s}\right) \right) \Pr \left( \tilde{s}\leq \hat{s}\right) E\left( \tilde{V}|\tilde{s}\leq \hat{s}\right) }{8k}\text{.} \end{array} $$

Therefore, we have that:

$$ E\left( {\Lambda}_{ND}\left( \tilde{s}\right) -{\Lambda}_{RD}\left( \tilde{s} \right) \right) =\frac{\Pr \left( \tilde{s}\leq \hat{s}\right) \left( 1-\Pr \left( \tilde{s}\leq \hat{s}\right) \right) E\left( \tilde{V}|\tilde{s}\leq \hat{s}\right) }{4k}\geq 0\text{.} $$

This is strictly positive if and only if $\Pr \left (\tilde {s}\leq \hat {s} \right ) <1$, i.e., if and only if the manager is risk averse, which completes the proof. □

Proof of Corollary 2

To begin, I show that risk disclosure enhances investment efficiency if and only if $T\left (\mu ,\bar {V}+\delta \right ) \leq \frac {1}{2}$. If $T\left (\mu ,\bar {V}+\delta \right ) \leq \frac {1}{2}$; then, substituting into expression (7), we have that:

$$ E\left( \tilde{\pi}_{ND}-\tilde{\pi}_{RD}\right) =-\frac{Var\left( \tilde{V} \right) }{8k}<0\text{.} $$

Next, suppose $T\left (\mu ,\bar {V}+\delta \right ) >\frac {1}{2}$. Then, again substituting into expression (7),

$$ E\left( \tilde{\pi}_{ND}-\tilde{\pi}_{RD}\right) =\frac{\left( \mu + \bar{V}+\delta \right) \left( \bar{V}-\delta \right) }{32k}>0\text{.} $$

I next show that the conditions stated in parts (i)-(iii) determine whether $T\left (\mu ,\bar {V}+\delta \right ) \leq \frac {1}{2}$. Note that, given the assumed form of the manager’s utility,

$$ T\left( \mu ,\bar{V}+\delta \right) =\frac{1-\exp \left( -\rho \left( \mu - \bar{V}-\delta \right) \right) }{1-\exp \left( -\rho \left( \mu -\bar{V} -\delta \right) \right) -1+\exp \left( -\rho \left( \mu +\bar{V}+\delta \right) \right) }\text{.} $$

I now show this single crosses $\frac {1}{2}$ in ρ; the results for μ and $\bar {V}$ follow similarly. Note:

$$ \begin{array}{@{}rcl@{}} &&\frac{\partial }{\partial \rho }\left[ \frac{1-\exp \left( -\rho \left( \mu -\bar{V}-\delta \right) \right) }{1-\exp \left( -\rho \left( \mu -\bar{V} -\delta \right) \right) -1+\exp \left( -\rho \left( \mu +\bar{V}+\delta \right) \right) }\right] \\ &\propto &\left( \mu +\bar{V}+\delta \right) \left[ \exp \left( -\rho \left( \mu +\bar{V}+\delta \right) \right) -\exp \left( -2\mu \rho \right) \right] -\left( \mu -\bar{V}-\delta \right) \left[ \exp \left( -\rho \left( \mu - \bar{V}-\delta \right) \right) -\exp \left( -2\mu \rho \right) \right] \text{ .} \end{array} $$

By the assumption that the investment is unprofitable when $\tilde {\omega }=0$ , $\mu -\bar {V}-\delta <0$, and thus this is positive. Now, using the fact $\lim _{t\rightarrow 0}\frac {1-\exp \left (-tz\right ) }{t}=z$, note:

$$ \begin{array}{@{}rcl@{}} \lim_{\rho \rightarrow 0}\frac{\frac{1-\exp \left( -\rho \left( \mu -\bar{V} -\delta \right) \right) }{\rho }}{\frac{1-\exp \left( -\rho \left( \mu -\bar{ V}-\delta \right) \right) -\left( 1-\exp \left( -\rho \left( \mu +\bar{V} +\delta \right) \right) \right) }{\rho }} &=&\frac{1}{2}\frac{\bar{V}+\delta -\mu }{\bar{V}+\delta }<\frac{1}{2}\text{;} \\ \lim_{\rho \rightarrow \infty }\frac{\frac{1-\exp \left( -\rho \left( \mu - \bar{V}-\delta \right) \right) }{\rho }}{\frac{1-\exp \left( -\rho \left( \mu -\bar{V}-\delta \right) \right) -1+\exp \left( -\rho \left( \mu +\bar{V} +\delta \right) \right) }{\rho }} &=&1\text{.} \end{array} $$

The result now follows by the intermediate value theorem. □

Proof of Lemma 3

To prove the lemma, I examine under what conditions the equilibrium in which the investor buys when they observe $\tilde {\psi }=1$, sells when they observe $\tilde {\psi }=0$, and does not trade when they do not learn exists (a similar argument to the one used in the proof of Lemma 2 can be used to show that the only other equilibrium is one in which the investor does not trade). In such an equilibrium, the prices articulated in the lemma follow by Bayes’ rule. I demonstrate that there exists a threshold $\tau \left (\tilde {\Delta }\right ) >0$ such that investor has no profitable deviation from their strategy precisely when $\alpha <\tau \left (\tilde { {\Delta }}\right )$. Let $\tilde {n}$ denote the noise trader’s order. Note that for a disclosed risk of $\tilde {V}$, the investor’s utility from purchasing when they observe $\tilde {\psi }=1$ is equal to:

$$ \begin{array}{@{}rcl@{}} &&\frac{1}{\alpha }E\left[ 1-\exp \left( -\alpha \left( \tilde{x}-P\left( \tilde{O}=\tilde{n}+1,\tilde{V}\right) \right) \right) |\tilde{s}=1\right] \\ &\propto &1-\frac{1}{2}\gamma \left[ \exp \left( -\alpha \tilde{V}\right) +\exp \left( -2\alpha \left( 1-\gamma \right) \tilde{V}\right) \right] - \frac{1}{2}\left( 1-\gamma \right) \left[ \exp \left( \alpha \tilde{V} \right) +\exp \left( 2\alpha \gamma \tilde{V}\right) \right] \text{,} \end{array} $$

(8)

and the investor’s utility from selling when they observe $\tilde {\psi }=0$ is equal to:

$$ \begin{array}{@{}rcl@{}} &&\frac{1}{\alpha }E\left[ 1-\exp \left( -\alpha \left( \tilde{x}-P\left( \tilde{O}=\tilde{n}-1,\tilde{V}\right) \right) \right) |\tilde{s}=0\right] \\ &\propto &1-\frac{1}{2}\gamma \exp \left( -\alpha \tilde{V}\right) -\frac{1}{ 2}\gamma \exp \left( 0\right) -\frac{1}{2}\left( 1-\gamma \right) \exp \left( \alpha \tilde{V}\right) -\frac{1}{2}\left( 1-\gamma \right) \exp \left( 0\right) \\ &=&\frac{1}{2}-\frac{1}{2}\gamma \exp \left( -\alpha \tilde{V}\right) -\frac{ 1}{2}\left( 1-\gamma \right) \exp \left( \alpha V\right) \text{.} \end{array} $$

Note that the difference between the investor’s utility from buying given $\tilde {\psi }=1$ less their utility from selling given $\tilde {\psi }=0$ is strictly negative:

$$ \begin{array}{@{}rcl@{}} &&\frac{1}{\alpha }\left\{ 1-\frac{1}{2}\gamma \left[ \exp \left( -\alpha \tilde{V}\right) +\exp \left( -2\alpha \left( 1-\gamma \right) \tilde{V} \right) \right] -\frac{1}{2}\left( 1-\gamma \right) \left[ \exp \left( \alpha \tilde{V}\right) +\exp \left( 2\alpha \gamma \tilde{V}\right) \right] \right\} \\ &&-\left[ \frac{1}{2}-\frac{1}{2}\gamma \exp \left( -\alpha \tilde{V}\right) -\frac{1}{2}\left( 1-\gamma \right) \exp \left( \alpha \tilde{V}\right) \right] \\ &\propto &\frac{1}{2}-\frac{1}{2}\gamma \exp \left( -2\alpha \left( 1-\gamma \right) \tilde{V}\right) -\frac{1}{2}\left( 1-\gamma \right) \exp \left( 2\alpha \gamma \tilde{V}\right) \text{.} \end{array} $$

By the concavity of the exponential, this is less than $\frac {1}{2}-\frac {1}{ 2}\exp \left (-2\alpha \gamma \right .$ $\left .\left (1-\gamma \right ) \tilde {V}+2\alpha \gamma \left (1-\gamma \right ) \tilde {V}\right ) =0$. Hence, the investor will deviate from buying to not trading when they learn $\tilde {\psi }=1$ more willingly than they deviate from selling to not trading when they learn $\tilde {\psi }=0$. Thus, we must show that there exists a threshold $\tau \left (\tilde {\Delta }\right )$ such that the investor is willing to deviate from purchasing given $\tilde {\psi }=1$ if and only if $\alpha >\tau \left (\tilde {\Delta }\right )$. In order to see this, the derivative of expression (8) with respect to α when expression (8) equals zero is proportional to:

$$ 2-2\left( 1-\gamma \right) \exp \left( \alpha V\right) -\left( 1-\gamma \right) \left( 1+2\gamma \right) \exp \left( 2\alpha \gamma V\right) +\gamma \left( 1-2\gamma \right) \exp \left( -2\alpha V\left( 1-\gamma \right) \right) \text{.} $$

Applying the fact that $\gamma >\frac {1}{2}$, this is negative. Thus, the investor’s expected utility from buying given $\tilde {\psi }=1$ single-crosses zero from above. □

Proof of Proposition 4

Let ${\Pi }^{RA}\left (\tilde {V}\right )$ denote the investor’s expected utility conditional on learning $\tilde {\omega }$ given the disclosure $\tilde {V}$. It is easily verified that the investor chooses $q\left (\tilde {V} \right ) ={\max \limits } \left \{ \frac {{\Pi }^{RA}\left (\tilde {V}\right ) }{k},0\right \}$. Note that for $\alpha \geq \tau \left (\tilde {V}\right )$, since the unique equilibrium involves no trading, $q\left (\tilde {V}\right ) ={u_{I}^{E}}\left (\tilde {V}\right ) =0$. Moreover, since the investor prefers to trade when $\alpha <\tau \left (\tilde {\Delta }\right )$, $q\left (\tilde {V}\right ) ={\Pi }^{RA}\left (\tilde {V}\right ) >0$. To complete the proof, I show that ${\Pi }^{RA}\left (\tilde {V}\right )$ is initially increasing and ultimately decreasing in $\tilde {V}$. Applying the results from Lemma 3 , we have:

$$ \begin{array}{@{}rcl@{}} {\Pi}^{RA}\left( \tilde{V}\right) &=&\frac{3}{4}-\frac{1}{2}\gamma \exp \left( -\alpha \tilde{V}\right) -\frac{1}{2}\left( 1-\gamma \right) \exp \left( \alpha \tilde{V}\right) \\ &&-\frac{1}{2}\gamma \exp \left( -2\alpha \left( 1-\gamma \right) \tilde{V} \right) -\frac{1}{2}\left( 1-\gamma \right) \exp \left( 2\alpha \gamma \tilde{V}\right) \text{.} \end{array} $$

Differentiating with respect to $\tilde {V}$ yields:

$$ \frac{\partial {\Pi}^{RA}\left( \tilde{V}\right) }{\partial \tilde{V}}\propto -\left( 1-\gamma \right) \exp \left( \alpha \tilde{V}\right) +\gamma \exp \left( -\alpha \tilde{V}\right) +2\gamma \left( 1-\gamma \right) \exp \left( -2\alpha \left( 1-\gamma \right) \tilde{V}\right) +2\gamma \left( \gamma -1\right) \exp \left( 2\alpha \gamma \tilde{V}\right) \text{.} $$

As $\tilde {V}\rightarrow 0$, this equals $\alpha \left (2\gamma -1\right ) >0$. Next, note that upon taking the second derivative, we find the function is concave:

$$ \begin{array}{@{}rcl@{}} \frac{\partial^{2}{\Pi}^{RA}\left( \tilde{V}\right) }{\partial \tilde{V}^{2}} &=&-\frac{1}{2}\frac{\alpha^{2}}{\exp \left( -\alpha \tilde{V}\right) } \left[ \gamma \left( \exp \left( -2\alpha \tilde{V}\right) -1\right) +1 \right] \\ &&-2\alpha^{2}\gamma \left( 1-\gamma \right) \left[ \left( 1-\gamma \right) \exp \left( -2\alpha \left( 1-\gamma \right) \tilde{V}\right) +\gamma \exp \left( 2\alpha \gamma \tilde{V}\right) \right] \\ &<&-\frac{1}{2}\frac{\alpha^{2}}{\exp \left( -\alpha \tilde{V}\right) } \left( 1-\gamma \right) -2\alpha^{2}\gamma \left( 1-\gamma \right) \left[ \left( 1-\gamma \right) \exp \left( -2\alpha \left( 1-\gamma \right) \tilde{V }\right) +\gamma \exp \left( 2\alpha \gamma \tilde{V}\right) \right] <0\text{ .} \end{array} $$

Finally, it is easily checked that ${\Pi }^{RA}\left (\tilde {V}\right ) \rightarrow -\infty$ as $\tilde {V}\rightarrow \infty$. □

Proof of Proposition 5

Note that the manager invests if and only if:

$$ \Pr \left( \tilde{\omega}=1|\tilde{P},\tilde{s}\right) E\left[ u_{m}\left( \mu +\tilde{V}\right) |\tilde{s}\right] +\Pr \left( \tilde{\omega}=0|\tilde{P },\tilde{s}\right) E\left[ u_{m}\left( \mu -\tilde{V}\right) |\tilde{s} \right] \geq 0\text{.} $$

Clearly, the manager invests (does not invest) when the price reveals $\tilde {\omega }=1$ ($\tilde {\omega }=0$). Let $S_{I}\subseteq S$ denote the values of $\tilde {s}$ that lead the manager to invest when $\Pr \left (\tilde {\omega }=1|\tilde {P},\tilde {s}\right ) =p$. Then, the same arguments in the proof of Lemma 2 can be applied to verify that the investor’s trading behavior must take the form stated in the proposition. Now, given the investor’s trading behavior, order flows of 2 and − 2 are again perfectly revealing, leading to prices of $\mu +E\left (\tilde {V}|\tilde {\Delta }\right )$ and 0, respectively. Furthermore, recalculating the expected value of the firm given an uninformative order flow, we arrive at:

$$ P\left( \tilde{O}\in \left\{ -1,0,1\right\} ,\tilde{\Delta}\right) =\Pr \left( \tilde{s}\in S_{I}|\tilde{\Delta}\right) \left[\mu +\left( 2p-1\right) E\left( \tilde{V}|\tilde{\Delta},\tilde{s}\in S_{I}\right) \right] \text{.} $$

The informed trader’s expected profits given $\tilde {\Delta }$ thus equal:

$$ \begin{array}{@{}rcl@{}} {\Pi} \left( \tilde{\Delta} \right)&=&\frac{p}{2}\Pr \left( \tilde{s}\in S_{I}|\tilde{\Delta}\right) \left( 1-\left( 2p-1\right) \right) E\left( \tilde{V}|\tilde{\Delta},\tilde{s}\in S_{I}\right) \\ && +\frac{1-p}{2}\Pr \left( \tilde{s}\in S_{I}|\tilde{\Delta}\right) \left( \left( 2p-1\right) +1\right) E\left( \tilde{V}|\tilde{\Delta},\tilde{s}\in S_{I}\right) \\ &=&2p\left( 1-p\right) \Pr \left( \tilde{s}\in S_{I}|\tilde{\Delta}\right) E\left( \tilde{V}|\tilde{\Delta},\tilde{s}\in S_{I}\right) \text{.} \end{array} $$

As the investor’s optimization problem is unchanged from the baseline model, we again have $q\left (\tilde {\Delta }\right )=k^{-1} {\Pi }\left (\tilde {\Delta }\right )$. Hence, conditional on $\tilde {\Delta }$, the investor’s ex ante expected profits are:

$$ \begin{array}{@{}rcl@{}} q\left( \tilde{\Delta}\right){\Pi}\left( \tilde{\Delta}\right)-\frac{k}{2}q\left( \tilde{\Delta}\right)^{2} &=&\frac{2}{k}\left( p\left( 1-p\right) \Pr \left( \tilde{s}\in S_{I}|\tilde{\Delta}\right) E\left( \tilde{V}|\tilde{\Delta},\tilde{s}\in S_{I}\right) \right)^{2}\text{.} \end{array} $$

Taking the difference between these profits under the policy of risk disclosure and the policy of no risk disclosure, we arrive at:

$$ \frac{2p^{2}\left( 1-p\right)^{2}}{k}Var\left[ \mathbf{1}\left( \tilde{s} \in S_{I}\right) E\left( \tilde{V}|\tilde{s}\right) \right] >0\text{.} $$

(9)

□

Proof of Corollary 3

When the manager is risk neutral, they invest given an uninformative price if and only if:

$$ \begin{array}{@{}rcl@{}} 0 \leq p\left( \mu +E\left( \tilde{V}|\tilde{s}\right) \right) +\left( 1-p\right) \left( \mu -E\left( \tilde{V}|\tilde{s}\right) \right) &\Leftrightarrow & 0 \leq \mu +\left( 2p-1\right) E\left( \tilde{V}|\tilde{s}\right) . \end{array} $$

(10)

I break the analysis into the cases in which $p \geq \frac {1}{2}$ and in which $p < \frac {1}{2}$, which correspond to parts (i) and (ii) of the corollary.

Case 1::

$p\geq \frac {1}{2}$. Note that in this case, expression Eq. 10 reveals that the manager always continues the investment when the price is uninformative. Hence, $q\left (\tilde {\Delta } \right )=\frac {2 p\left (1-p\right )}{k} E\left (\tilde {V}|\tilde {\Delta }\right )$, and expected firm profits reduce as follows:

$$ \begin{array}{@{}rcl@{}} E\left( \tilde{\pi}_{RD}|\tilde{s}\right) &=&\left( 1-\frac{q\left( \tilde{s }\right) }{2}\right) \left( \mu +\left( 2p-1\right) E\left( \tilde{V}|\tilde{ s}\right) \right) +\frac{pq\left( \tilde{s}\right) }{2}\left( \mu +E\left( \tilde{V}|\tilde{s}\right) \right) \\ &=&\mu +\left( 2p-1\right) E\left( \tilde{V}|\tilde{s}\right) - \frac{ p\left( 1-p\right)^{2} E\left( \tilde{V}|\tilde{s}\right) }{k} \left( \mu -E\left( \tilde{V}|\tilde{s}\right) \right) \text{.} \end{array} $$

Similarly, we have:

$$ \begin{array}{@{}rcl@{}} E\left( \tilde{\pi}_{ND}|\tilde{s}\right) &=&\left( 1-\frac{1}{k}E\left( \tilde{V}\right) p\left( 1-p\right) \right) \left( \mu +\left( 2p-1\right) E\left( \tilde{V}|\tilde{s}\right) \right) +\frac{1}{k}E\left( \tilde{V} \right) p^{2}\left( 1-p\right) \left( \mu +E\left( \tilde{V}|\tilde{s} \right) \right) \\ &=&\mu +\left( 2p-1\right) E\left( \tilde{V}|\tilde{s}\right) -\frac{ p\left( 1-p\right)^{2} E\left( \tilde{V}\right)}{k}\left( \mu -E\left( \tilde{V}| \tilde{s}\right) \right) \text{.} \end{array} $$

Taking the difference yields:

$$ E\left( \tilde{\pi}_{RD}-\tilde{\pi}_{ND}|\tilde{s}\right) =\frac{p\left( 1-p\right)^{2}\left( \mu -E\left( \tilde{V}|\tilde{s}\right) \right) \left( E\left( \tilde{V}\right) -E\left( \tilde{V}|\tilde{s}\right) \right) }{k} \text{.} $$

Thus, we have:

$$ \begin{array}{@{}rcl@{}} E\left( \tilde{\pi}_{RD}-\tilde{\pi}_{ND}\right) &=&\frac{p\left( 1-p\right)^{2}}{k} E\left[ E\left( \tilde{V}|\tilde{s}\right)^{2}-E\left( \tilde{V}\right) E\left( \tilde{V}|\tilde{s}\right) \right] \\ &=&\frac{p\left( 1-p\right)^{2}}{k} Var\left[ E\left( \tilde{V}|\tilde{s}\right) \right] >0\text{,} \end{array} $$

which completes the proof of part (i) of the corollary.

Case 2::

$p<\frac {1}{2}$. To show that risk disclosure’s impact on expected profits is ambiguous in this case, I construct cases in which it is positive and negative. To see that this impact may be positive, note that the firm’s expected profits are continuous in p for p in a neighborhood of $p=\frac {1}{2}$ (assuming that the manager is not indifferent between investing and not investing when $p=\frac {1}{2}$). Thus, since the baseline model demonstrates that risk disclosure increases expected firm profits when $p=\frac {1}{2}$, it also does so for p less than but sufficiently close to $\frac {1}{2}$. I next construct an example in which risk disclosure reduces expected firm profits. Suppose that $\tilde {V}\in \left \{ V_{L},V_{H}\right \}$ equal probabilities, where V_H > V_L. Given that $p<\frac {1}{2}$, inequality Eq. 10 can be rewritten as:

$$ p \ge -\frac{1}{2}\frac{\mu}{E\left( \tilde{V} | \tilde{s}\right)}+\frac{1}{2}. $$

Thus, given any prior p such that $p\in \left (-\frac {1}{2}\frac {\mu }{V_{L}}+\frac {1}{2},-\frac {1}{2}\frac {\mu }{V_{H}}+\frac {1}{2}\right )$, the manager liquidates the project when the price is uninformative if and only if $\tilde {V}=V_{H}$. Thus, we have that:

$$ q\left( \tilde{\Delta}\right) =\frac{2 p\left( 1-p\right) }{k} \ast \Pr \left( \tilde{V}=V_{L}|\tilde{\Delta} \right) \ast V_{L}. $$

Hence, the manager’s expected profits given risk disclosure equal:

$$ \begin{array}{@{}rcl@{}} E\left( \tilde{\pi}_{RD}|\tilde{V}\right) &=& \begin{cases} \left( 1-\frac{q\left( V_{L}\right) }{2}\right) \left( \mu +\left( 2p-1\right) V_{L}\right) +\frac{pq\left( V_{L}\right) }{2}\left( \mu +V_{L}\right) & \text{ if }\tilde{V}=V_{L} \\ 0 & \text{ if }\tilde{V}=V_{H} \end{cases} \\ &=& \begin{cases} \left( 1-\frac{V_{L}p\left( 1-p\right) }{k}\right) \left( \mu +\left( 2p-1\right) V_{L}\right) +\frac{V_{L}p^{2}\left( 1-p\right) }{k}\left( \mu +V_{L}\right) & \text{ if }\tilde{V}=V_{L} \\ 0 & \text{ if }\tilde{V}=V_{H} \end{cases} \text{,} \end{array} $$

and given nondisclosure equal:

$$ E\left( \tilde{\pi}_{ND}|\tilde{V}\right) = \begin{cases} \left( 1-\frac{V_{L}p\left( 1-p\right) }{2k}\right) \left( \mu +\left( 2p-1\right) V_{L}\right) +\frac{V_{L}p^{2}\left( 1-p\right) }{2k}\left( \mu +V_{L}\right) & \text{ if }\tilde{V}=V_{L} \\ \frac{V_{L}p^{2}\left( 1-p\right) }{2k}\left( \mu +V_{H}\right) & \text{ if } \tilde{V}=V_{H} \end{cases} \text{.} $$

Substituting and simplifying yields:

$$ \begin{array}{@{}rcl@{}} E\left( \tilde{\pi}_{ND}-\tilde{\pi}_{RD}\right) &=&\frac{1}{2}\left[ \frac{V_{L}p\left( 1-p\right) }{2k}\left( \mu +\left( 2p-1\right) V_{L}\right) +\frac{V_{L}p^{2}\left( 1-p\right) }{2k}\left( V_{H}-V_{L}\right) \right] >0. \end{array} $$

□