Abstract
This study examines how a strategic tax auditor affects a multinational firm’s transfer pricing in a tax compliance game. Our model uses a divisionalized firm, in both a low-tax and a high-tax country, that decides to implement a transfer-pricing regime with either one or two sets of books. After observing its unit costs, the firm reports a compliant or noncompliant tax transfer price. In a regime with one set of books, the single transfer price coordinates the quantity decision and determines the tax payments. In a regime with two sets, different transfer prices serve those tasks. In contrast to previous studies, our analysis incorporates a strategic tax auditor, who observes the tax transfer price and decides whether to audit the firm. Real-world regulations suggest larger penalties for detected noncompliance under a two-sets-of-books transfer-pricing regime. Our analysis identifies the mixed strategy equilibria and examines how variations in the tax regulation—the tax rate difference and the penalty difference—affect the firm’s tax aggressiveness. We show that a firm acts less tax aggressively with a higher tax rate difference. Additionally, the model predicts that the firm either increases or decreases the probability of keeping one set of books for a smaller penalty difference.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Transfer prices are necessary for computing divisional profits in a multinational firm whenever its divisions engage in intra-firm trade. As multinationals can use divisional profit for managerial performance evaluation, transfer pricing affects internal decisions. Moreover, divisional profits determine a multinational’s tax liability in its different countries. Research shows that multinationals keep either two sets of books (TSB) or one set of books (OSB).Footnote 1 The TSB transfer-pricing regime uses an internal transfer price that coordinates the quantity decision and a tax transfer price that determines the tax liability, respectively. Thus TSB allow the multinational to optimize the tax liability and the internal decisions. In contrast, the OSB transfer-pricing regime uses the same transfer price for those tasks and thus limits the multinational’s flexibility to optimize both tasks.
To reduce their tax liability, multinationals often use tax transfer prices to shift profit from high- to low-tax countries (e.g. Blouin et al. 2018; Clausing 2003; De Simone et al. 2017; Jacob 1996). The tax transfer prices might not comply with tax regulation. As profit shifting deprives tax authorities of a large amount of tax income, the authorities have their auditors rigorously examine multinationals’ transfer pricing for noncompliance (OECD, 2015).Footnote 2 However, as tax authorities are resource constrained (e.g., Hoopes et al. 2012), tax auditors cannot scrutinize each multinational’s transfer pricing. Instead, the auditors seek to effectively deploy their available resources (OECD 2015, p. 9); that is, they strategically decide whether to audit an multinational’s transfer pricing.
When a tax auditor challenges the tax transfer price, many multinationals fear negative consequences from keeping TSB instead of OSB.Footnote 3 Although the international transfer-pricing literature acknowledges these different consequences, the specific transfer-pricing regime choice of the multinational while it is considering the possibility of a tax audit remains largely unexplored. This omission is problematic, because it restricts scholars’ and tax regulators’ understanding of multinationals’ profit-shifting incentives. In this study, we examine how a strategic tax auditor affects a multinational’s transfer-pricing regime in a tax compliance game.
We study an multinational with an upstream division in a low-tax country and a downstream division in a high-tax country. The upstream division produces an intermediate product and transfers it to the downstream division. Our model comprises three decision-making stages. In the first stage, the multinational decides whether to implement an OSB or a TSB transfer-pricing regime (implementation decision). In the second, after experiencing operating conditions (i.e., high or low unit costs of the intermediate product), the multinational determines the transfer price(s). The multinational chooses a compliant or a noncompliant tax transfer price (compliance decision). In the third stage, a strategic tax auditor observes the tax transfer price and decides whether to conduct an audit, a decision that factors in the audit costs.
During an audit, the tax auditor evaluates the multinational’s transfer pricing. With OSB, the tax transfer price follows the management view,Footnote 4 thereby exhibiting economic substance. In contrast, the use of an internal transfer price different from the tax transfer price under TSB may undermine the economic substance of the tax transfer price (Cools & Emmanuel, 2006; Narayanan & Smith, 2010).Footnote 5 The lack of economic substance indicates that the multinational’s primary objective for keeping TSB is tax minimization.
Many countries reduce the penalty for detected noncompliance when the multinational shows economic substance, whereas they increase the penalty if the the primary objective is tax minimization. For example, in Spain, a tax auditor can reduce or eliminate the penalty when the multinational keeps OSB (KPMG 2012, p. 202). Australia levies a penalty of 25%, which decreases to 10% when the multinational demonstrates economic substance and increases to 50% when the tax auditor shows that the dominant purpose is tax minimization (EY, 2012). In New Zealand, the penalties vary between 20% and 150% (EY, 2012), with the applied rate depending on the degree of intent to avoid tax payments in the multinational’s gross negligence. In Hong Kong, the tax auditor scales the penalty upward or downward according to the nature of the omission and the amount of understatement of profits (EY, 2012). In sum, these real-world regulations suggest higher penalty factors for detected noncompliance as a negative consequence of keeping TSB. We incorporate this penalty difference into our model.
In our analysis, the multinational faces a trade-off between flexibility and the level of penalties. With TSB, it uses the internal transfer price to affect the downstream division’s quantity decision. In contrast, the tax transfer price under OSB limits the multinational’s possibilities of affecting the quantity decision; that is, the multinational is less flexible. Beyond flexibility, the multinational also considers the level of penalties. With low unit costs, the multinational (hereafter “low-cost multinational”) has an incentive to mimic a multinational with high unit costs (hereafter “high-cost multinational”) and to use a noncompliant tax transfer price. If the tax auditor detects a noncompliant tax transfer price, the penalty under TSB is higher than under OSB. In other words, with the use of TSB, higher flexibility goes hand in hand with higher penalties.
After identifying the mixed strategy equilibria, we find that the penalty difference determines the first-stage implementation decision about using OSB or TSB. For a large penalty difference between OSB and TSB, the advantage of OSB is high. In this case, the multinational never implements TSB as a pure strategy but instead randomizes between OSB and TSB. While the low-cost multinational may benefit from the lower level of penalties under OSB, this advantage is irrelevant for the high-cost multinational, which always acts compliantly. Consequently, the multinational never implements OSB as a pure strategy. If the advantage of OSB is small, an equilibrium exists in which the multinational always implements TSB, due to its greater flexibility.
The second-stage decision is a choice between compliance and noncompliance. We find that, when an OSB regime is in place, a low-cost multinational always reports noncompliantly. The low-cost multinational’s compliance decision under a TSB regime depends on the level of the tax auditor’s audit costs. For low audit costs, the tax auditor wants to conduct audits more frequently. Thus, ceteris paribus, the probability of detecting noncompliance increases: anticipating the higher detection probability, the low-cost multinational reports compliantly with a higher probability.
Using the equilibrium strategies, we derive empirically testable predictions for tax aggressiveness. As various definitions of tax aggressiveness exist (Hanlon and Heitzman, 2010), in our model, we define tax aggressiveness as noncompliant reporting under either TSB or OSB. We consider noncompliant reporting under TSB a more tax-aggressive transfer pricing than that under OSB. Our findings show that a higher tax rate difference between the countries decreases the multinational’s tax aggressiveness. Because profit shifting is especially beneficial for a high tax rate difference, less tax aggressiveness appears counterintuitive. Our finding, however, is due to the presence of the strategic tax auditor. Given that a high tax rate difference causes high penalties for detected noncompliance, the tax auditor has strong incentives for conducting an audit. The multinational anticipates the stronger audit incentives and counteracts them by less tax-aggressive transfer pricing.
In addition, our model predicts that the multinational either increases or decreases the probability of keeping OSB for a smaller penalty difference. The multinational’s choice in the first stage depends on its compliance decision in the second stage. Because a smaller penalty difference results in a smaller OSB advantage, an increasing probability of an multinational’s keeping OSB for a decreasing penalty difference might appear surprising at first glance. The finding stems from the presence of the strategic tax auditor, who incorporates a higher penalty for detected noncompliance under OSB and the multinational’s incentives for switching toward more TSB in his or her audit decision, thereby increasing audit incentives. For an intermediate level of audit costs, the multinational counteracts the stronger audit incentives by using more OSB in the first stage, because the OSB advantage still remains.
For our main analysis, we assume that the multinational chooses the transfer-pricing regime before observing the operating conditions. In the short term, because of implementation, user training, and other organizational issues, the multinational does not revise the transfer-pricing regime according to operating conditions (Martini et al. 2012). Nevertheless, for comparison, we also study a model in which the multinational chooses the transfer-pricing regime after observing the operating conditions. Our analysis shows that our findings persist in the model with the alternative timing.Footnote 6
Our model builds on the cost-based transfer pricing setting established by Baldenius et al. (2004) while introducing the following adaptations. (1) The multinational chooses to keep either OSB or TSB. (2) The multinational can either incur high or low unit costs, so that the low-cost multinational has an incentive to choose a noncompliant tax transfer price. (3) The tax auditor strategically decides whether to audit the multinational. These adaptations allow us to study the multinational’s implementation and compliance decision when the multinational considers a potential tax audit.
Our paper contributes to the vast literature studying international tax transfer pricing that incorporates internal decision-making.Footnote 7 Research typically takes the transfer-pricing regime as given; that is, either OSB or TSB is in place (Baldenius et al. 2004; Choe and Hyde, 2007; Hyde & Choe, 2005; Narayanan & Smith, 2010). An exception is Nielsen and Raimondos-Møller (2012), who investigate whether OSB or TSB is preferable under certain circumstances. However, they do not consider the presence of a strategic tax auditor. In contrast, rather than assuming the dominance of a specific transfer-pricing regime, we endogenize the multinational’s implementation decision.
Our paper adds to the international tax transfer-pricing literature on tax audits. Kant (1988), Smith (2002), Hyde and Choe (2005), and Choe and Hyde (2007) study the impact of a penalty for noncompliance on multinational’s transfer prices. However, they neither examine the presence of a strategic tax auditor nor consider whether the multinational keeps OSB or TSB.
Our paper also contributes to the strategic coordination literature that examines the benefits that multinationals accrue from keeping OSB. Schjelderup and Sorgard (1997), Arya and Mittendorf (2008), and Dürr and Göx (2011) illustrate that, under imperfect competition, multinationals gain benefits from keeping OSB. In their studies, OSB serves as a commitment device for softening competition in external markets. While this strand of the literature assumes that the competitors observe the multinational’s transfer-pricing regime, we do not make a similar assumption for the tax auditor. Instead, and in line with previous research (Bärsch et al. 2019; Davis, 1994; Tang, 1993),Footnote 8 we assume that the tax auditor observes the multinational’s transfer-pricing regime during a tax audit. We complement the strategic coordination literature by showing that the multinational keeps OSB as part of the equilibrium strategy in response to the presence of a strategic tax auditor.
The paper proceeds as follows. Section 2 describes the model. Section 3 presents the multinational’s internal and tax transfer prices. Section 4 identifies and describes the mixed strategy equilibria. Section 5 depicts comparative statics. Section 6 shows that our main findings do not depend on the timing of the game. Section 7 concludes.
2 Model description
We study a multinational operating an upstream division in a low-tax country and a downstream division in a high-tax country, where transfer prices evaluate intra-firm trade. In the low-tax country, an income tax rate t prevails, whereas the high-tax country taxes income at a rate t + h, with 0 ≤ t, h ≤ 1 and t + h ≤ 1. The parameter h captures the tax rate difference between the countries. We assume taxation in terms of the separate entity approach and that each division has additional income, so that the divisional after-tax income is always positive.
In the first stage, the multinational chooses whether to implement an OSB or a TSB transfer-pricing regime (implementation decision). With OSB, the multinational uses a single transfer price to evaluate the intra-firm trade internally and to calculate the tax liability; that is, the internal transfer price pi equals the tax transfer price pr. For TSB, the multinational decouples its transfer-pricing decisions and uses two different transfer prices; that is, pi≠pr.
The upstream division makes an intermediate product that is transformed into the final product by the downstream division, which faces monopolistic market conditions for the final product. No external market for the intermediate product exists. The upstream division faces either high unit costs cH with probability β or low unit costs cL with probability 1 − β for producing the intermediate product, where 0 < β < 1 and 0 ≤ cL < cH. While the probability β is common knowledge, only the multinational observes the cost realization after the implementation decision. We label the multinational with low (high) unit costs as a low-cost (high-cost) multinational.
In the second stage, after the realization of the unit costs, the multinational sets the tax transfer price using a cost-plus method, which comports with the OECD transfer pricing guidelines and the monopolistic setting. Under this transfer pricing method, unit costs plus an appropriate markup fulfill the arm’s length principle. Thus the upper bound for the tax transfer price of a low-cost multinational is given by \(\underline {p_{r}}=c_{L}+m_{L}\), where mL ≥ 0 captures the accepted markup. The appropriate markup for the high-cost multinational is mH, yielding an upper bound \(\overline {p_{r}}=c_{H}+m_{H}\). We assume mH and mL such that \(\overline {p_{r}}>\underline {p_{r}}\). For convenient notation, we assume that the lower bound of the arm’s length range is prL (prH) for the low-cost (high-cost) multinational, where \(0\leq p_{rL} \leq p_{rH} < \underline {p_{r}} < \overline {p_{r}}\) holds. Thus the arm’s length ranges are \(\left [p_{rL},\underline {p_{r}}\right ]\) and \(\left [p_{rH},\overline {p_{r}}\right ]\) for the low-cost and high-cost multinational, respectively. The multinational chooses either a compliant tax transfer price or a noncompliant tax transfer price that does not belong to the cost-specific arm’s length range (compliance decision). In addition, with TSB, the multinational determines the internal transfer price.
The multinational evaluates the downstream division on the basis of pre-tax divisional profit πD,Footnote 9 so that the downstream division uses the internal transfer price for the quantity decision. Without loss of generality, the downstream division’s costs for transforming the intermediate product into the final product are equal to zero. Due to monopolistic market conditions, the revenue function for the final product is \(R(q)=\left (a-\frac {1}{2} q\right )q\), where q denotes the quantity. Thus the downstream division determines the quantity according to
In the third stage, the tax auditor observes the tax transfer price and decides to conduct an audit. The tax auditor is located in the high-tax country, that is, the home country of the downstream division.Footnote 10 We assume that the tax auditor maximizes the additional income that he or she generates for the tax authority while facing personal audit costs Ka if he or she conducts an audit.
In line with empirical findings (Cools et al. 2008; Cools & Slagmulder, 2009) and the extensive documentation requirements imposed on multinationals, we assume that, if a tax audit occurs, the tax auditor observes the realized unit costs, the transfer-pricing regime (i.e., OSB or TSB), and, for TSB, the internal transfer price.
If noncompliance is detected, the tax auditor enforces a compliant transfer price, where \(\underline {p_{r}}\) (\(\overline {p_{r}}\)) is the enforced transfer price for a low-cost (high-cost) multinational. The tax auditor asks the multinational to pay the previously unpaid taxes, which are the difference between the tax payment that the tax auditor determines using the enforced transfer price pa and the tax transfer price pr. Moreover, the tax auditor levies an additional penalty, captured by a linear penalty factor δ ∈{δOSB,δTSB} applied to the previously unpaid taxes (Yitzhaki, 1974).Footnote 11 In line with real-world regulations (EY 2003, 2012; KPMG 2012), we assume 1 ≤ δOSB < δTSB. Thus, depending on its transfer-pricing regime, the multinational faces the following payment.
Hereafter, we refer to S as the penalty.Footnote 12 Thus the tax auditor’s payoff is as follows.
After the third stage, the multinational obtains the following global after-tax profit:
with \(c\in \left \{c_{L},c_{H}\right \}\). The multinational maximizes its global after-tax profit and incorporates tax savings due to the tax rate difference and the possibly resulting penalty.
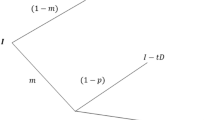
Figure 1 shows the timing of the game.
3 Internal and tax transfer prices
This section shows that the multinational reports \(p_{r} \in \{\underline {p_{r}}, \overline {p_{r}}\}\) if the reservation price a is sufficiently large. Furthermore, it demonstrates how the internal transfer price pi is adjusted for tax payments and tax audit risk.
The multinational may choose an arbitrary tax transfer price pr > 0. A tax transfer price \(p_{r} >\overline {p_{r}}\) is evidence of noncompliance for the tax auditor, even without a tax audit. Because obvious noncompliance with tax regulation is beyond dispute, we assume that the tax auditor punishes obvious noncompliance without facing substantial audit costs. Thus neither the high-cost nor the low-cost multinational reports \(p_{r} > \overline {p_{r}}\).
The high-cost multinational minimizes the tax payment with a tax transfer price \(\overline {p_{r}}\). Therefore the high-cost multinational uses \(\overline {p_{r}}\) with TSB. The high-cost multinational using OSB considers a trade-off between tax savings and quantity distortion. Given q = a − pr, the optimal tax transfer price fulfills
rearranging yields
Despite the trade-off, for a sufficiently large reservation price a, the multinational chooses \(\overline {p_{r}}\) as the tax transfer price—unit costs plus markup. When choosing the quantity, the downstream division considers both the tax transfer price and the reservation price. By internalizing the markup as costs, the downstream division distorts the quantity downward (standard double marginalization problem). Because the downstream division internalizes the reservation price as the multinational does, the negative quantity distortion is constant in a (see Eq. 5). As a large reservation price results in a large quantity, which in turn causes a high marginal benefit from the tax savings, a large a makes the tax savings more important than the quantity distortion. Consequently, the multinational seeks a high tax transfer price and thus implements \(\overline {p_{r}}\).
The low-cost multinational may choose a noncompliant tax transfer price; that is, \(p_{r}>\underline {p_{r}}\). As the tax auditor anticipates that a high-cost multinational will always report \(\overline {p_{r}}\), reporting a tax transfer price in the range \((\underline {p_{r}},\overline {p_{r}})\) immediately identifies the low-cost multinational as noncompliant. Therefore the noncompliant low-cost multinational chooses \(p_{r} = \overline {p_{r}}\) for both OSB (for sufficiently high a) and TSB. If, instead, the low-cost multinational decides not to mimic the high-cost multinational and reports compliantly, to minimize the tax payment, the low-cost multinational uses the highest compliant arm’s length price \(\underline {p_{r}}\) under TSB. Likewise, as with the high-cost multinational, a sufficiently large reservation price ensures that \(\underline {p_{r}}\) is optimal for a compliant low-cost multinational that keeps OSB. Lemma 1 summarizes:
Lemma 1
Assume a sufficiently large reservation price a.
-
1.
A high-cost multinational reports the compliant tax transfer price \(p_{r} = \overline {p_{r}}\) for TSB and OSB.
-
2.
A noncompliant low-cost multinational reports \(p_{r} = \overline {p_{r}}\) for TSB and OSB.
-
3.
A compliant low-cost multinational reports \(p_{r} = \underline {p_{r}}\) for TSB and OSB.
Proof
See Appendix. □
With TSB, to maximize global after-tax profits, the multinational additionally determines an internal transfer price. The compliant multinational uses tax-adjusted unit costs as the internal transfer price (see Baldenius et al. 2004). This transfer price induces the downstream division to make the optimal quantity decision. In the noncompliance case, the low-cost multinational also considers the costs following a potential tax audit. Thus when the low-cost multinational considers a strategic tax auditor, the noncompliant low-cost multinational uses tax- and audit-adjusted unit costs to induce the optimal quantity decision. Lemma 2 summarizes:
Lemma 2
Given that the multinational has installed a TSB regime in the first stage, and the tax auditor audits with probability η, the multinational determines the internal transfer price as follows.
A noncompliant low-cost multinational adopts tax- and audit-adjusted unit costs as internal transfer price piL1:
In case of compliance, the high- and low-cost multinationals adopt tax-adjusted unit costs cH and cL as internal transfer prices piH and piL2, respectively:
and
Proof
See Appendix. □
The game tree in Fig. 2 displays those strategies (for the multinational and the tax auditor) that are not dominated by another strategy. The tax auditor never audits a tax transfer price \(p_{r} = \underline {p_{r}}\) because \(p_{r} = \underline {p_{r}}\) indicates a compliant low-cost multinational.
Game tree without dominated strategies [The multinational (MNF) implements TSB with probablility τ and OSB with probability 1 − τ. After observing the unit costs, the low-cost MNF chooses \(\overline {p_{r}}\) \(\left (\underline {p_{r}}\right )\) with probability λj \(\left (1-\lambda _{j}\right )\), \(j\in \left \{TSB,OSB\right \}\). The tax auditor (TA) conducts an audit with probability‘η]
4 Transfer pricing regimes and compliance
Our model is a tax compliance game, with the audit decision depending on the tax transfer price. Pure strategy equilibria exist for extremely high or low audit costs in combination with low or high penalties for a detected noncompliance. In such cases, the multinational selects TSB or OSB in the first stage and then either always or never chooses a compliant tax transfer price in the second stage. The tax auditor either never or always audits the multinational. Given that pure strategy equilibria cannot explain why compliance and noncompliance and nontrivial tax audit strategies appear simultaneously in reality, we concentrate our analysis on mixed strategy equilibria.
In our model, randomization may appear at three stages. First, the multinational may randomize between TSB and OSB. We denote the corresponding implementation probability of TSB (OSB) by τ (1 − τ). Second, after observing the unit costs, the low-cost multinational chooses the noncompliant tax transfer price \(\overline {p_{r}}\) with probability λj, \(j\in \left \{TSB,OSB\right \}\), and the compliant tax transfer price \(\underline {p_{r}}\) with probability 1 − λj. We refer to λj as the noncompliance probability. Third, after observing the tax transfer price \(\overline {p_{r}}\), the tax auditor decides whether to audit the multinational (probability η) or not (probability 1 − η).
The strategies τ, λTSB, λOSB, and η constitute an equilibrium if the following conditions hold.
-
1.
First Stage: Implementation
$$ \tau\in \arg\max_{\acute{\tau}} E_{t=0}\left[{\varPi}\left( \acute{\tau},\lambda_{TSB},\lambda_{OSB},\eta\right)\right] $$ -
2.
Second Stage: Compliance
$$ \lambda_{TSB}\in \arg\max_{\acute{\lambda}_{TSB}} E_{t=2}\left[\left.{\varPi}\left( \acute{\lambda}_{TSB},\eta\right)\right|\text{TSB}\right] \text{~and} $$$$ \lambda_{OSB}\in \arg\max_{\acute{\lambda}_{OSB}} E_{t=2}\left[\left.{\varPi}\left( \acute{\lambda}_{OSB},\eta\right)\right|\text{OSB}\right] $$ -
3.
Third Stage: Audit
$$ \eta\in \arg\max_{\acute{\eta}} E_{t=4}\left[\left.{\varPi}^{TA}\left( \tau,\lambda_{TSB},\lambda_{OSB},\acute{\eta}\right)\right| p_{r}=\overline{p_{r}}\right] $$
In a mixed strategy equilibrium, each player—in our model, the multinational and the tax auditor—has to be indifferent between all the pure strategies that the player plays with positive probability. The multinational’s strategy comprises the implementation decision in the first stage and the compliance decision in the second. Randomization in both stages requires indifference between OSB and TSB and between compliance and noncompliance. The tax auditor, however, has only the audit probability for inducing indifference. Therefore the multinational randomizes at either the implementation or the compliance stage.Footnote 13 Proposition 1 exhibits the mixed strategy equilibria of our model.
Proposition 1
Assume a sufficiently large reservation price a. The following three mixed-strategy equilibria exist.
-
1.
Equilibrium I: For \(\delta _{OSB} \geq \overline {\delta }_{OSB}\) and Ka < Ka2(ηI), the multinational always implements TSB. After the realization of the unit costs, the high-cost multinational reports the compliant tax transfer price \(\overline {p_{r}}\) and the low-cost multinational reports the noncompliant tax transfer price \(\overline {p_{r}}\) (compliant tax transfer price \(\underline {p_{r}}\)) with probability λTSB,I (1 − λTSB,I). The tax auditor audits \(\overline {p_{r}}\) with audit probability ηI.
-
2.
Equilibrium II: For Ka < Ka1(δOSB), the multinational implements TSB (OSB) with probability τII (1 − τII). After the realization of the unit costs, the high-cost multinational reports the compliant tax transfer price \(\overline {p_{r}}\) and the low-cost multinational reports the compliant tax transfer price \(\underline {p_{r}}\) under TSB and the noncompliant tax transfer price \(\overline {p_{r}}\) under OSB. The tax auditor audits \(\overline {p_{r}}\) with probability ηII.
-
3.
Equilibrium III: For \(K_{a1}(\delta _{OSB}) < K_{a} < K_{a2}\left (\eta _{III}\right )\), the multinational chooses TSB (OSB) with probability τIII (1 − τIII). After the realization of the unit costs, the high-cost multinational reports the compliant tax transfer price \(\overline {p_{r}}\) and the low-cost multinational chooses the noncompliant tax transfer price \(\overline {p_{r}}\) under TSB and under OSB. The tax auditor audits \(\overline {p_{r}}\) with probability ηIII.
Proof
All proofs, equilibrium probabilities, and thresholds appear in the Appendix. □
Figure 3 depicts the findings of Proposition 1 and shows that the equilibrium in our model is unique if the penalty factor δOSB is sufficiently low. For a fixed penalty factor δTSB, a low penalty factor δOSB corresponds to a large penalty difference. In such a case, the multinational randomizes between TSB and OSB. After the realization of the unit costs, the high-cost multinational always reports compliantly while the audit costs determine the compliance decision of the low-cost multinational under TSB. In other words, both TSB and OSB can be part of the equilibrium strategy.
Equilibrium areas depending on Ka and δOSB. Area I shows equilibrium I, where the multinational always implements TSB. After the realization of the unit costs, the low-cost multinational randomizes between compliant and noncompliant reporting. Area II shows equilibrium II, where the multinational implements TSB with probability τII and OSB with probability 1 − τII. After the realization of the unit costs, the low-cost multinational reports compliantly (noncompliantly) under TSB (OSB). Area III shows equilibrium III, where the multinational implements TSB (OSB) with probability τIII (1 − τIII). After the realization of the unit costs, the low-cost multinational always reports noncompliantly. Values: a = 10,000, cH = 100, cL = 60, t = 0.2, h = 0.1, β = 0.8, \(\overline {p_{r}} = 120\), \(\underline {p_{r}} = 70\), δTSB = 1.2
This finding comports with both empirical and anecdotal evidence from Klassen et al. (2017) and Springsteel (1999). We observe that the equilibrium—where the multinational randomizes between OSB and TSB in the first stage and the low-cost (high-cost) multinational always reports a noncompliant (compliant) tax transfer price (equilibrium III)—appears if δOSB is low and Ka is high. This finding is intuitive: a low penalty factor, under OSB together with high audit costs, implies weak audit incentives. Therefore the low-cost multinational chooses TSB with noncompliance instead of TSB with compliance. For a small penalty difference, the deterministic implementation of TSB and random compliance (equilibrium I) coexists with equilibria II and III.
The deterministic implementation of TSB (equilibrium I) is an equilibrium strategy for a small penalty difference. The intuition for this finding is as follows: with the deterministic implementation of TSB, the quantity is optimal, and the low-cost multinational randomizes between compliance and noncompliance. For a small penalty difference, the disadvantage of TSB is small. In contrast, for a large penalty difference, the multinational prefers to deviate to OSB in the first stage so that the deterministic implementation of TSB does not occur.
When the multinational randomizes between TSB and OSB in the first stage, the high-cost multinational always chooses compliance in the second stage, and the low-cost multinational conditions its compliance decision in the second stage on the audit costs. This randomization occurs in equilibria II and III. In the case of low audit costs, the multinational expects frequent tax audits. In the second stage, the low-cost multinational thus chooses OSB with the noncompliant tax transfer price \(\overline {p_{r}}\) or TSB with the compliant tax transfer price \(\underline {p_{r}}\). With the noncompliant use of OSB, the low-cost multinational realizes tax savings. The compliant use of TSB minimizes tax payments within the legal boundaries and yields the optimal quantity decision. With high audit costs, tax audits are infrequent, and, for the low-cost multinational, reporting the noncompliant tax transfer price dominates in the second stage. While OSB implies lower penalties if noncompliance is detected for the low-cost multinational, both types of the multinational benefit from separating internal and tax transfer prices under TSB. Consequently, neither OSB nor TSB dominates in the first stage.
Furthermore, Proposition 1 shows that we do not observe an equilibrium in which the low-cost multinational reports a compliant tax transfer price under OSB because, given the quantity distortion under OSB, any equilibrium with OSB and a compliant tax transfer price as part of a mixed strategy implies a strictly lower payoff for the low-cost multinational than with TSB and compliance.
5 Effects of increases in tax rate difference and penalties
Equipped with the equilibrium strategies of both the multinational and the tax auditor, we analyze how variations in the tax regulation affect the multinational’s decisions on quantity, compliance, and the implementation of transfer-pricing regimes. The regulatory parameters of interest are the tax rate difference and the penalty factors for detected noncompliance.
5.1 Tax rate difference
For each equilibrium determined in Section 4, Proposition 2 shows how the internal transfer price and the noncompliance or implementation probability change with an increase in the tax rate difference h.Footnote 14
Proposition 2
Assume a sufficiently large reservation price a. An increase in the tax rate difference h
-
1.
decreases the internal transfer price under TSB in all equilibria;
-
2.
decreases the probability of a noncompliant tax transfer price in equilibrium I (λTSB,I);
-
3.
increases the probability of using TSB in equilibrium II (τII), where the low-cost multinational uses a compliant tax transfer price with TSB;
-
4.
decreases the probability of using TSB in equilibrium III (τIII), where the low-cost multinational uses a noncompliant tax transfer price with TSB.
Proof
See Appendix. □
Proposition 2, part 1, states that the multinational boosts the quantity for a higher tax rate difference whenever the multinational uses TSB. A higher tax rate difference increases the multinational’s profit-shifting benefits. With TSB the tax transfer price is already set to optimally exploit the tax rate difference. Thus the multinational exploits the increasing tax rate difference by selling a larger quantity. Because the low-cost noncompliant multinational that implements TSB uses tax- and audit-adjusted unit costs as the internal transfer price (see Lemma 2), the low-cost noncompliant multinational additionally incorporates the tax auditor’s reaction to a higher tax rate difference. Nevertheless, we show that the low-cost noncompliant multinational also lowers the internal transfer price for an increasing tax rate difference.
The noncompliance and implementation results in Proposition 2, parts 2 to 4, have an instructive interpretation in terms of tax aggressiveness. In our model, we define tax aggressiveness as noncompliant reporting under either TSB or OSB. We consider noncompliant reporting under TSB more tax aggressive transfer pricing than noncompliant reporting under OSB. An increasing tax rate difference implies less frequent noncompliance in equilibria I and II, and a shift from TSB with noncompliance to less tax aggressive OSB with noncompliance in equilibrium III for the low-cost multinational. As better profit-shifting opportunities induce less tax-aggressive decisions by the multinational, this result appears counterintuitive.
The appealing intuition that a higher tax rate difference induces more tax aggressiveness due to more beneficial profit-shifting holds true when no tax audit is considered. For example, Baldenius et al. (2004, p. 600) show that the incremental gain of TSB is relatively large for a high tax rate difference. However, with a strategic tax auditor, the multinational also considers potential penalties and audit incentives. In this case, as the penalty depends on the previously unpaid taxes, an increasing tax rate difference directly increases the penalty for detected noncompliance. Additionally, in a setting with TSB, an increasing tax rate difference leads to a larger quantity, which also increases the penalty for detected noncompliance. Therefore the tax auditor obtains a higher income when he or she detects noncompliance in a tax audit; that is, a higher penalty implies stronger audit incentives for the tax auditor. In equilibrium, to counteract the stronger audit incentives, the multinational reports less tax aggressively.
Our findings comport with the empirical finding of Chan and Chow (1997), who show that high tax rate differences are not crucial for inducing noncompliant transfer prices. Their work demonstrates that the tax auditor is aware of an multinational’s profit shifting incentives. Thus, accounting for the strategic interaction with the tax auditor, the multinational is less tax aggressive with an increasing tax rate difference. Furthermore, our result is consistent with the finding of Hoopes et al. (2012) that a stricter tax enforcement is associated with less tax aggressiveness.
5.2 Penalty factors
For each equilibrium determined in Section 4, Proposition 3 shows how the internal transfer price and the noncompliance or implementation probability react to changes in the penalty factors for detected noncompliance under OSB and TSB.
Proposition 3
Assume a sufficiently large reservation price a. An increase in the penalty factor for detected noncompliance under OSB (TSB), δOSB (δTSB) has the following effects.
-
1.
Neither δOSB nor δTSB affects the internal transfer prices in equilibria I and II or the internal transfer price of the high-cost multinational in equilibrium III. In equilibrium III, the internal transfer price of the low-cost multinational under TSB increases (decreases) in δOSB (δTSB).
-
2.
An increasing δOSB (δTSB) does not affect (decreases) the probability that the low-cost multinational chooses a noncompliant tax transfer price λTSB,I in equilibrium I.
-
3.
An increasing δOSB (δTSB) increases (does not affect) the probability of using TSB τII in equilibrium II, where the low-cost multinational uses a compliant tax transfer price.
-
4.
The probability of using TSB τIII in equilibrium III, where the low-cost multinational uses a noncompliant tax transfer price, decreases in δOSB for \(K_{a} \in (K_{a1},{K_{a}^{c}})\)Footnote 15 and increases in δOSB for \(K_{a} \in ({K_{a}^{c}}, K_{a2}(\eta _{III}))\). The probability τIII decreases in δTSB.
Proof
See Appendix. □
We start with the intuition for Proposition 3, part 1. Because penalty factors are irrelevant when the multinational reports compliantly, penalty factors do not affect the internal transfer price with TSB and compliance in equilibria I, II, or III. When the low-cost multinational keeps TSB with noncompliance in equilibrium I, the audit probability is such that the expected penalty equals the tax savings that the low-cost multinational obtains through noncompliance. Consequently, for the low-cost multinational, the internal transfer prices with TSB and compliance or noncompliance are equal in equilibrium I and neither δOSB nor δTSB affects the internal transfer price with TSB and noncompliance.
When the low-cost multinational keeps TSB with noncompliance in equilibrium III, the penalty factors influence the internal transfer price via the audit adjustment. First, we consider the effect of δOSB. The penalty factor δOSB affects the audit adjustment only via the audit probability ηIII. We show that ηIII increases in δOSB, and thus the internal transfer price increases in δOSB. The intuition is as follows. TSB with noncompliance becomes more attractive to the low-cost multinational when δOSB increases. The tax auditor counters with a higher audit probability because TSB with noncompliance implies a higher penalty than for OSB with noncompliance.
Second, we consider the effect of δTSB. The penalty factor δTSB affects the audit adjustment both directly and via the audit probability ηIII. The direct effect increases the audit adjustment and, in turn, the internal transfer price. Because ηIII decreases in δTSB, the effect via the audit probability works in the opposite direction. The intuition is as follows. An increase in δTSB makes TSB with noncompliance less attractive for the low-cost multinational and induces the tax auditor to audit less frequently. Our results show that the decrease in the audit probability overcompensates for the direct effect; thus, in equilibrium III, the internal transfer price of the low-cost multinational decreases with δTSB.
Part 2 of Proposition 3 is intuitive: because a higher penalty for a detected noncompliance under TSB decreases the benefit of using a noncompliant tax transfer price with TSB, the low-cost multinational reduces the noncompliance probability λTSB,I.
As the low-cost multinational reports the compliant tax transfer price under TSB in equilibrium II, changes in the TSB penalty factor δTSB do not affect the implementation probability for TSB. An increasing penalty factor δOSB reduces the attractiveness of OSB and, in an intuitively appealing way, induces the multinational to shift from OSB to TSB in equilibrium II (see Proposition 3, part 3).
An increase in the penalty factor δOSB ambiguously affects the implementation probability in equilibrium III, where the low-cost multinational uses a noncompliant tax transfer price under both the TSB and OSB transfer-pricing regimes. Proposition 3, part 4, states that the multinational implements TSB less frequently for an intermediate level of audit costs; that is, \(K_{a}\in (K_{a1},{K_{a}^{c}})\) with \({K_{a}^{c}}<K_{a2}(\eta _{III})\), when δOSB increases. In this case, ceteris paribus the low-cost multinational has a stronger incentive to implement the more tax-aggressive TSB with noncompliance. The tax auditor anticipates the multinational’s incentive while deciding whether to audit the multinational. Additionally, the higher penalty factor directly increases the tax auditor’s audit incentives. As an advantage of OSB still remains, the multinational reacts to the tax auditor’s stronger audit incentives by increasing the probability of keeping OSB for an intermediate level of audit costs. For audit costs above \({K_{a}^{c}}\), the tax auditor’s audit incentives are sufficiently weak so that the low-cost multinational’s incentive to switch towards more tax-aggressiveness by keeping TSB hardly affects the audit decision. Therefore a higher penalty for detected noncompliance under OSB induces the multinational to refrain from the use of OSB.
In equilibrium III, an increase in the penalty factor δTSB makes TSB with noncompliance less attractive for the low-cost multinational, and thus, before the realization of the unit costs, the multinational implements OSB more frequently.
In sum, either an increasing penalty factor δOSB or a decreasing penalty factor δTSB cause a smaller penalty difference. Proposition 3 states that a decreasing penalty difference ambiguously affects the implementation of the transfer-pricing regime: for intermediate audit costs and a smaller penalty difference caused by an increase of δOSB, the probability of OSB increases, if TSB with noncompliance of the low-cost multinational is the alternative action in equilibrium, that is, in equilibrium III. In all other cases of equilibrium III and in equilibrium II, the probability of OSB decreases for a smaller penalty difference.
Our findings relate to those of Klassen et al. (2017), who find that the enforcement level does not affect multinationals’ transfer-pricing focus if the focus is either “tax minimization” or “lack of disputes.” In our model, we interpret (1) the enforcement level as the size of the penalty factors for detected noncompliance under OSB or TSB, (2) “tax minimization” as a noncompliant tax transfer price for the low-cost multinational, and (3) the “lack of disputes” as a compliant tax transfer price. We show that the penalty factors affect the implementation decision, which is exogenous in Klassen et al. (2017). For exogenous implementation decisions, where OSB and TSB coexist, the compliance decisions and thus the transfer-pricing focuses are deterministic. Put differently, the penalty factors do not affect multinationals’ compliance. By considering both decisions, we show in Proposition 3 that larger penalty factors can influence multinationals’ implementation decisions, thereby affecting their compliance and thus the transfer-pricing focus.
6 Alternative sequence of events
Thus far in this paper, the multinational has chosen its transfer-pricing regime, OSB or TSB, before knowing its unit costs. This timing assumes that it does not continually revise its decision to implement OSB or TSB to adjust for changes in the short-term operating conditions, such as unit costs. Nevertheless, multinationals may reconsider their decisions. For example, a new executive team might revise the previous team’s decisions, or changes in tax regulation might induce an multinational to adjust its accounting system. Thus the multinational might be able to choose its transfer-pricing regime after observing the unit costs. This section discusses the potential impact of this alternative sequence of events on our findings.Footnote 16
The model with the alternative sequence of events qualitatively yields the same results as those in Propositions 1, 2, and 3. All three mixed-strategy equilibria still occur for the low-cost multinational, and no further mixed-strategy equilibria appear. Because the low-cost multinational still trades off flexibility and the level of penalties, this finding is intuitive. For the high-cost multinational, no advantage of OSB exists. Consequently, when the high-cost multinational chooses its transfer-pricing regime after observing the realized unit costs, it always implements TSB. As the tax auditor cannot observe the multinational’s unit costs prior to an audit, he or she audits the high tax transfer price with positive probability.
In contrast to the model with the previous timing of the game, only the low-cost multinational adapts its implementation decision as response to a varying tax rate difference or changes in the penalty factors for OSB and TSB. Nevertheless, in the model with the previous timing of the game, the low-cost multinational’s incentives cause the comparative static results, meaning that the results qualitatively carry over to the model with the alternative sequence of events. The low-cost multinational becomes less tax aggressive in response to a higher tax rate difference. Additionally, for an intermediate level of audit costs, the low-cost multinational keeps OSB more frequently when the penalty factor for OSB increases. In sum, our results show that the timing of the game is immaterial for obtaining our main findings.
7 Conclusion
This paper examines how a strategic tax auditor affects a multinational’s transfer-pricing regime choice—TSB or OSB—and compliance decision in a tax compliance game. The multinational faces a trade-off between flexibility and the level of penalties. Our analysis identifies the mixed strategy equilibria and shows that the level of the tax auditor’s audit costs and the penalty factors for detected noncompliance determine the multinational’s equilibrium behavior. Specifically, our findings illustrate that OSB is part of the multinational’s equilibrium strategy whenever the penalty difference is large. Put differently, strategic considerations in a tax compliance game are a potential reason for multinationals to implement OSB.
Our analysis shows that a higher tax rate difference reduces multinationals’ tax aggressiveness. This result stems from the presence of the strategic tax auditor. A high tax rate difference in particular yields a high tax-savings potential for the multinational, allowing it to benefit from shifting profits to the low-tax country. At the same time, a high tax rate difference corresponds to a high penalty for detected noncompliance. The tax auditor incorporates the penalty into the audit decision, making the audit incentives strong. To counteract the stronger audit incentives, the multinational increasingly refrains from tax aggressiveness.
Furthermore, our analysis illustrates that, for an intermediate level of audit costs, the multinational increases the probability of keeping OSB when the penalty advantage for detected noncompliance under OSB decreases. Specifically, the OSB advantage decreases for an increasing OSB penalty factor. Thus the multinational’s incentives for keeping noncompliant TSB increase. As with the tax rate difference finding, because the penalty for detected noncompliance under OSB increases, the tax auditor’s incentives increase. The stronger audit incentives greatly diminish the multinational’s incentives for keeping noncompliant TSB. Therefore the multinational increases the probability of keeping OSB.
Our paper adds to the literature on international transfer pricing by enhancing the theoretical understanding of how a strategic tax auditor and tax regulation—in the form of the tax rate difference and the penalty factors for noncompliant reporting—affect a multinational’s transfer-pricing decisions and resulting tax aggressiveness. A promising extension of our research would be to investigate how the presence of a strategic tax auditor affects a multinational’s decisions in more general intra-firm relationships. For example, in a setting where the divisions decide on upfront investments to either enhance revenues or decrease unit costs, the transfer-pricing regime affects both the investment incentives and the compliance decision. Consequently, the tax auditor’s incentives potentially affect the divisions’ investment decisions.
Notes
While previous studies discuss the fear of negative consequences, they assume the transfer-pricing regime is exogenous (e.g., Baldenius et al. 2004; Halperin and Srinidhi1991; Johnson 2006; Narayanan & Smith 2010; Nielsen & Raimondos-Møller 2012; Reineke & Weiskirchner-Merten 2021; Shunko et al. 2014; Smith 2002).
Alignment with the management view enhances the multinational’s defensibility of its transfer pricing (EY, 2003).
Martini (2015) notes that unrelated firms would not use two different prices for an inter-firm trade. Therefore a tax auditor may doubt the economic substance of an multinational’s keeping TSB.
Section 6 analyzes an alternative sequence of events.
Sansing (2014) provides a comprehensive overview of international transfer prices and their functions.
In Germany, e.g., a firm must provide all documents related to a specific transaction to the tax auditor, even if these documents do not relate to tax accounts (§90 AO).
Other studies assume that the divisions maximize their after-tax profits. This assumption is also ad hoc in the transfer pricing setting. Baldenius et al. (2004) explicitly highlight this fact. For further discussion of the advantages of pre-tax versus after-tax profit maximization for divisional performance measurement, see Nielsen and Raimondos-Møller (2012).
We do not consider tax audits in the low-tax country, which anticipates the multinational’s incentives to shift profits to it, so that profit shifting does not deprive it of tax income. Therefore the low-tax country cannot generate additional tax income by auditing the multinational’s transfer pricing.
While we assume that the tax auditor enforces the upper bound of the arm’s length range, in some countries (e.g., the U.S.), the enforced transfer price is the median of the arm’s length range. By enforcing the median instead of the upper bound, the tax auditor additionally punishes a noncompliant multinational. If a country enforces the median of the arm’s length range, we assume that this additional punishment is included in the penalty factor δ.
A transfer-pricing adjustment by the tax auditor in the high-tax country leads to double taxation. We assume that the low-tax country does not pay any refunds that may result from double taxation agreements.
We do not consider knife-edge cases where the multinational randomizes at both stages.
Alternative possibilities for modeling the tax rate difference exist. Nevertheless, because all results hold for the entire range of t and h, our specification is without loss of generality when we conduct comparative statics with respect to h.
See Appendix for the threshold \({K_{a}^{c}}\).
All formal claims and proofs for the alternative sequence of events are in the internet Appendix. The internet appendix is available at https://ssrn.com/abstract=3904634.
References
Arya, A., & Mittendorf, B. (2008). Pricing internal trade to get a leg up on external rivals. Journal of Economics & Management Strategy, 17(3), 709–731.
Baldenius, T., Melumad, N.D., & Reichelstein, S. (2004). Integrating managerial and tax objectives in transfer pricing. The Accounting Review, 79(3), 591–615.
Bärsch, S.E., Heckemeyer, J.H., & Olbert, M. (2019). Transfer pricing and the decision-making authority of the tax function in multinational companies. Working paper. https://doi.org/10.2139/ssrn.3271267.
Blouin, J.L., Robinson, L.A., & Seidman, J.K. (2018). Conflicting transfer pricing incentives and the role of coordination. Contemporary Accounting Research, 35(1), 87–116.
Chan, K.H., & Chow, L. (1997). An empirical study of tax audits in China on international transfer pricing. Journal of Accounting and Economics, 23(1), 83–112.
Choe, C., & Hyde, C.E. (2007). Multinational transfer pricing, tax arbitrage and the arm’s length principle. Economic Record, 83(263), 398–404.
Clausing, K.A. (2003). Tax-motivated transfer pricing and US intrafirm trade prices. Journal of Public Economics, 87(9), 2207–2223.
Cools, M., & Emmanuel, C. (2006). Transfer pricing: The implications of fiscal compliance. In C.S. Chapman, A.G. Hopwood, & M.D. Shields (Eds.). Handbook of management accounting research (pp. Vol. 2, 573–585).
Cools, M., & Slagmulder, R. (2009). Tax-compliant transfer pricing and responsibility accounting. Journal of Management Accounting Research, 21, 151–178.
Cools, M., Emmanuel, C., & Jorissen, A. (2008). Management control in the transfer pricing tax compliant multinational enterprise. Accounting, Organizations and Society, 33(6), 603–628.
Davis, H.T. Jr (1994). Transfer prices in the real world—10 steps companies should take before it’s too late. The CPA Journal, 64(10), 82.
De Simone, L., Klassen, K.J., & Seidman, J.K. (2017). Unprofitable affiliates and income shifting behavior. The Accounting Review, 92(3), 113–136.
Dürr, O.M., & Göx, R.F. (2011). Strategic incentives for keeping one set of books in international transfer pricing. Journal of Economics & Management Strategy, 20(1), 269–298.
EY. (2003). Transfer pricing 2003 global survey.
EY. (2012). Transfer pricing global reference guide.
EY. (2013). Global transfer pricing survey.
EY. (2019). Transfer pricing and international tax survey.
Halperin, R.M., & Srinidhi, B. (1991). US income tax transfer-pricing rules and resource allocation: The case of decentralized multinational firms. The Accounting Review, 66(1), 141–157.
Hanlon, M., & Heitzman, S. (2010). A review of tax research. Journal of Accounting and Economics, 50(2/3), 127–178.
Hoopes, J.L., Mescall, D., & Pittman, J.A. (2012). Do IRS audits deter corporate tax avoidance? The Accounting Review, 87(5), 1603–1639.
Hyde, C.E., & Choe, C. (2005). Keeping two sets of books: The relationship between tax and incentive transfer prices. Journal of Economics & Management Strategy, 14(1), 165–186.
Jacob, J. (1996). Taxes and transfer pricing: Income shifting and the volume of intrafirm transfers. Journal of Accounting Research, 34(2), 301–312.
Johnson, N.B. (2006). Divisional performance measurement and transfer pricing for intangible assets. Review of Accounting Studies, 11(2-3), 339–365.
Kant, C. (1988). Endogenous transfer pricing and the effects of uncertain regulation. Journal of International Economics, 24(1–2), 147–157.
Klassen, K.J., Lisowsky, P., & Mescall, D. (2017). Transfer pricing: Strategies, practices, and tax minimization. Contemporary Accounting Research, 34(1), 455–493.
KPMG. (2012). Global transfer pricing review.
Martini, J.T. (2015). The optimal focus of transfer prices: pre-tax profitability versus tax minimization. Review of Accounting Studies, 20(2), 866–898.
Martini, J.T., Niemann, R., & Simons, D. (2012). Transfer pricing or formula apportionment? Tax-induced distortions of multinationals’ investment and production decisions. Contemporary Accounting Research, 29(4), 1060–1086.
Narayanan, V.G., & Smith, M. (2010). Impact of competition and taxes on responsibility center organization and transfer prices. Contemporary Accounting Research, 17(3), 497–529.
Nielsen, S.B., & Raimondos-Møller, P. (2012). Multiple roles of transfer prices: one vs. two books. In W. Schön K.A. Konrad (Eds.) Fundamentals of international transfer pricing in law and economics (pp. 25–46).
OECD. (2015). OECD/G20 base erosion and profit shifting project—transfer pricing documentation and country-by-country reporting, action 13—2015 final report.
Reineke, R., & Weiskirchner-Merten, K. (2021). Transfer pricing and location of intangibles–spillover and tax avoidance through profit shifting. Journal of Management Accounting Research, 33(1), 129–148.
Sansing, R. (2014). International transfer pricing. Foundations and Trends in Accounting, 9(1), 1–57.
Schjelderup, G., & Sorgard, L. (1997). Transfer pricing as a strategic device for decentralized multinationals. International Tax and Public Finance, 4 (3), 277–290.
Shunko, M., Debo, L., & Gavirneni, S. (2014). Transfer pricing and sourcing strategies for multinational firms. Production and Operations Management, 23(12), 2043–2057.
Smith, M. (2002). Tax and incentive trade-offs in multinational transfer pricing. Journal of Accounting, Auditing & Finance, 17(3), 209–236.
Springsteel, I. (1999). Separate but unequal. When tax-based transfer prices fall short, a second managerial system helps some companies measure internal profits better. CFO, 15(8), 89–92.
Tang, R.Y. (1993). Transfer pricing in the 1990s: tax and management perspectives. Praeger Pub Text.
Yitzhaki, S. (1974). Income tax evasion: A theoretical analysis. Journal of Public Economics, 3(2), 201–202.
Acknowledgements
We thank Eva Eberhartinger, Christian Hofmann (discussant), Clemens Löffler, Zoltán Novotny-Farkas, Thomas Pfeiffer, Christian Riegler, Georg Schneider, Caren Sureth-Sloane (discussant), and participants in the annual VHB tax group meeting 2020 and the EAA Virtual Congress 2021 for helpful comments. We are grateful to Harald Amberger, Oliver Dürr (discussant), Michael Ebert, Joachim Gassen, Ulrich Schäfer, Andreas Scholze, Robert Ullmann, and Alfred Wagenhofer, and participants in the ARFA-Workshop 2017, the EAA Annual Congress 2017, the Annual VHB Conference 2017, and the Accounting Research Workshop 2017 for helpful comments on an earlier version of this paper. We are also grateful to Stefan Reichelstein (the editor) and two anonymous reviewers for their constructive suggestions. This paper is a substantially revised version of an earlier draft, which was coauthored by Marcel Haak, whose contribution we gratefully acknowledge.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
1.1 Proof of Lemma 1
Figure 4 depicts the multinational’s possible strategies.
Note that \(p_{r}>\overline {p_{r}}\) is an unambiguous signal of tax evasion (punished without audit costs) so that the multinational never chooses \(p_{r}>\overline {p_{r}}\).
For \(p_{r}\leq \overline {p_{r}}\), a high-cost multinational is compliant. To minimize its tax payments, the high-cost multinational keeping TSB sets \(p_{r}=\overline {p_{r}}\).
Under OSB, a high-cost multinational maximizes its expected profit determining a transfer price:
for sufficiently large a so that a high-cost multinational keeping OSB chooses \(p_{r}=\overline {p_{r}}\).
A noncompliant low-cost multinational keeping TSB that reports a \(p_{r}\in \left (\underline {p_{r}}, \overline {p_{r}}\right )\) reveals itself as a noncompliant low-cost multinational. By choosing \(p_{r}=\overline {p_{r}}\), a low-cost multinational mimics a high-cost one. Thus a noncompliant low-cost multinational keeping TSB sets \(p_{r}=\overline {p_{r}}\).
A noncompliant low-cost multinational keeping OSB chooses a transfer price \(\underline {p_{r}}< p_{r}\leq \overline {p_{r}}\). A noncompliant low-cost multinational maximizes its expected profit by determining a transfer price, where the tax auditor audits with probability η:
\(\left .\frac {d^{2} {\varPi }}{d {p_{r}^{2}}}\right |_{q=a-p_{r}}\) is negative for \(\delta _{OSB}<\frac {1-t+h}{2\eta (t+h)}\). Thus, for a \(\delta _{OSB}>\frac {1-t+h}{2\eta (t+h)}\), the first-order condition (FOC) determines a local minimum, and the multinational prefers a corner solution, that is, \(p_{r}\in \left \{\underline {p_{r}},\overline {p_{r}}\right \}\). With \(p_{r}=\underline {p_{r}}\), the multinational is compliant. Thus a noncompliant low-cost multinational keeping OSB sets \(p_{r}=\overline {p_{r}}\) for \(\delta _{OSB}>\frac {1-t+h}{2\eta (t+h)}\). For \(\delta _{OSB}<\frac {1-t+h}{2\eta (t+h)}\) the FOC determines a local maximum. For a sufficiently large a, the multinational’s FOC determines a \(p_{r}>\overline {p_{r}}\) so that a noncompliant low-cost multinational keeping OSB sets \(p_{r}=\overline {p_{r}}\) for \(\delta _{OSB}<\frac {1-t+h}{2\eta (t+h)}\).
A compliant low-cost multinational keeping TSB minimizes its tax payments by choosing \(p_{r}=\underline {p_{r}}\).
Under OSB a compliant low-cost multinational maximizes its expected profit determining a transfer price:
for sufficiently large a. Thus a compliant low-cost multinational keeping OSB chooses \(p_{r}=\underline {p_{r}}\).
1.2 Proof of Lemma 2
Note that TSB allows the multinational to disentangle its internal from its tax transfer price. The multinational’s profit with unit costs cj and j = H,L is as follows.
The noncompliant low-cost multinational considers the consequences resulting from a tax transfer price \(\overline {p_{r}}\) in a tax audit:
Thus the FOC for pi determines a local maximum:
The FOC for a compliant multinational reduces to
Thus the FOC for pi determines a local maximum for the compliant high-cost multinational:
Thus the FOC for pi determines a local maximum for the compliant low-cost multinational:
1.3 Proof of Proposition 1
We examine each equilibrium. We identify the tax auditor’s audit and the multinational’s randomization probability. In addition, we determine the parameter constellations for Ka and δOSB so that the identified probabilities constitute an equilibrium in mixed strategies.
1.3.1 Proof of equilibrium I
With TSB in place, the low-cost multinational randomizes between compliance and noncompliance if and only if the expected profits from both strategies are the same; that is, \(\eta {\varPi }_{3}^{}+ (1-\eta ) {\varPi }_{4}^{}={\varPi }_{5}^{} \):
The tax auditor incurs costs for conducting an audit. Thus the tax auditor audits with probability
The multinational wants to deviate to OSB with \(\overline {p_{r}}\) in t = 0 when \(\overline {\delta }_{OSB}\leq \delta _{OSB}\). The following equation determines \(\overline {\delta }_{OSB}\):
When the tax auditor observes a high tax transfer price, he or she is indifferent between audit and no audit if \( \beta {\varPi }_{1}^{TA}+ (1-\beta )\lambda _{TSB}{\varPi }_{3}^{TA}=0 \)
λTSB,I is smaller than 1 if and only if Ka < Ka2(ηI), where
In sum, for \(\delta _{OSB} \geq \overline {\delta }_{OSB}\) and Ka < Ka2(ηI), the multinational always implements TSB. After the realization of the unit costs, the high-cost multinational reports the compliant tax transfer price \(\overline {p_{r}}\) and the low-cost multinational reports the noncompliant (compliant) tax transfer price \(\overline {p_{r}}\) (\(\underline {p_{r}}\)) with probability λTSB,I (1 − λTSB,I). The tax auditor audits \(\overline {p_{r}}\) with audit probability ηI.
1.3.2 Proof of equilibrium II
The multinational randomizes the strategies OSB and TSB if
for sufficiently large a.
ηII is always smaller than 1 because:
π6 < π1, and for a sufficiently large prohibitive price a, \({\varPi }_{9}^{} > {\varPi }_{5}^{}>0\) holds true.
The low-cost multinational might have an incentive to deviate to TSB with the noncompliant tax transfer price \(\overline {p_{r}}\). This deviation occurs if and only if
For a sufficiently large a, the term \(\left [h-\eta _{II}\delta _{TSB}(t+h)\right ]\) becomes negative so that \(a\left [h-\eta _{II}\delta _{TSB}(t+h)\right ]\) is negative. Therefore the low-cost multinational does not want to deviate to noncompliant TSB.
When the tax auditor observes a high tax transfer price, he or she is indifferent between audit and no audit if:
τII is positive if and only if Ka ≤ Ka1(δOSB) with
In sum, for Ka < Ka1(δOSB), the multinational implements TSB (OSB) with probability τII (1 − τII). After the realization of the unit costs, the high-cost multinational reports the compliant tax transfer price \(\overline {p_{r}}\) and the low-cost multinational reports the compliant tax transfer price \(\underline {p_{r}}\) under TSB and the noncompliant tax transfer price \(\overline {p_{r}}\) under OSB. The tax auditor audits \(\overline {p_{r}}\) with probability ηII. __
1.3.3 Proof of equilibrium III
The multinational randomizes the strategies OSB and TSB if
where
For sufficiently large a, B < 0 and B2 − C > 0. Thus the multinational is indifferent between OSB and TSB for
For a sufficiently large a, ηIII is smaller than 1.
The multinational might have an incentive to deviate to TSB and then choose the compliant tax transfer price \(\underline {p_{r}}\) in the case of low unit costs. This deviation occurs if and only if
For a sufficiently large a, the term \(\left [\eta _{III}\delta _{OSB}(t+h)-h\right ]\) becomes negative so that \(a\left [\eta _{III}\delta _{OSB}(t+h)-h\right ]\) is negative. Therefore the low-cost multinational never deviates to TSB with a compliant tax transfer price.
When the tax auditor observes a high tax transfer price, he or she wants to randomize between conducting and not conducting an audit if:
τIII is positive and smaller than 1 if and only if Ka1(δOSB) < Ka < Ka2(ηIII), where Ka1 is defined in Eq. 11 and
In sum, for \(K_{a1}(\delta _{OSB}) < K_{a} < K_{a2}\left (\eta _{III}\right )\), the multinational chooses TSB (OSB) with probability τIII (1 − τIII). After the realization of the unit costs, the high-cost multinational reports the compliant tax transfer price \(\overline {p_{r}}\) and the low-cost multinational chooses the noncompliant tax transfer price \(\overline {p_{r}}\) under TSB and under OSB. The tax auditor audits \(\overline {p_{r}}\) with probability ηIII. __
1.4 Proof of Proposition 2
An increasing tax rate difference
-
1.
decreases the internal transfer price (see Lemma 2) under TSB in all equilibria:
$$ \begin{array}{@{}rcl@{}} &&\frac{d p_{iH}}{d h}=(-1)\frac{1}{(1-t-h)^{2}}\left[(1-t)m_{H}\right]<0,\\ &&\frac{d p_{iL2}}{d h}=(-1)\frac{1}{(1-t-h)^{2}}\left[(1-t)m_{L}\right]<0,\\ &&\frac{d p_{iL1}\left( \eta_{I}\right)}{d h}=(-1)\frac{1}{(1-t-h)^{2}}\left[(1-t)m_{L}\right]<0,\\ &&\frac{d p_{iL1}\left( \eta_{III}\right)}{d h}=\frac{(1-t)}{(1-\beta) (1-h-t)^{2}}\cdot\\ &&\left[-a (\beta -1) (c_{L}-\overline{p_{r}}) (\delta_{OSB}-\delta_{TSB}) (h+t-1)\right.\\ &&+\overline{p_{r}} (\overline{p_{r}}-c_{L}) (\delta_{OSB}-\delta_{TSB}) (h+t-1)\\ &&+\beta (c_{H} \delta_{TSB}(1-t)(c_{H}-2\overline{p_{r}}) +\overline{p_{r}} (c_{L} (\delta_{OSB}-\delta_{TSB}) (h+t-1)\\ &&\left.\left.\left.+\overline{p_{r}} (\delta_{TSB} h-\delta_{OSB}(h+t-1))\right)\right)\right]\cdot\\ &&\left[(a (\delta_{TSB}-\delta_{OSB}) (1-h-t)+c_{L} \delta_{TSB} (t-1)\right.\\ &&+\overline{p_{r}} (\delta_{TSB} h-\delta_{OSB} (h+t-1)))^{2}\\ &&\left.+\frac{\delta_{TSB}^{2} (t-1)^{2} \left( \beta (c_{H}-c_{L}) (c_{H}+c_{L}-2 \overline{p_{r}})+(c_{L}-\overline{p_{r}})^{2}\right)}{\beta -1}\right]^{-\frac{1}{2}} \end{array} $$\(\frac {d p_{iL1}\left (\eta _{III}\right )}{d h}\) is negative for sufficiently high a.
-
2.
decreases the probability of a noncompliant tax transfer price in equilibrium I (see Proposition 1):
$$ \begin{array}{@{}rcl@{}} \frac{\partial \lambda_{TSB,I}}{\partial h} = \frac{(-1)}{(t+h)^{2}} \frac{K_{a}}{(1-\beta)\delta_{TSB}(a-p_{iL1})(\overline{p_{r}}-\underline{p_{r}})}<0, \\ \frac{\partial \lambda_{TSB,I}}{\partial p_{iL1}}=\frac{K_{a} (a-p_{iL1})^{2}}{(1-\beta)(t+h)\delta_{TSB}(\overline{p_{r}}-\underline{p_{r}})}>0. \end{array} $$Therefore
$$ \frac{d\lambda_{TSB,I}}{d h}=\underbrace{\frac{\partial \lambda_{TSB,I}}{\partial h}}_{<0}+\underbrace{\frac{\partial \lambda_{TSB,I}}{\partial p_{iL1}}}_{>0}\underbrace{\frac{d p_{iL1}}{d h}}_{<0}<0. $$ -
3.
increases the probability of using TSB in equilibrium II (see Proposition 1):
$$ \frac{d\tau_{II}}{d h}=\frac{K_{a}}{(1-\beta)(t+h)^{2}(a-\overline{p_{r}})\delta_{OSB}(\overline{p_{r}}-\underline{p_{r}})}>0. $$ -
4.
decreases the probability of using TSB in equilibrium III (see Proposition 1):
$$ \begin{array}{@{}rcl@{}} \frac{\partial \tau_{III}}{\partial h}\!&=&\!(-1)\frac{K_{a}}{(1 - \beta)(t + h)^{2}(\overline{p_{r}} - \underline{p_{r}})\left[\delta_{TSB}(a - p_{iL1}) - \delta_{OSB}(a - \overline{p_{r}})\right]} <0.\\ \frac{\partial \tau_{III}}{\partial p_{iL1}}\!&=&\!\delta_{TSB}\left[\delta_{TSB}(a - p_{iL1}) - \delta_{OSB}(a - \overline{p_{r}})\right]^{-2} \left[(1 - \beta)(t + h)(\overline{p_{r}} - \underline{p_{r}})\right]^{-1}\cdot \\ &&\underbrace{\left[K_{a}-\delta_{OSB}(a-\overline{p_{r}})(1-\beta)(t+h)(\overline{p_{r}}-\underline{p_{r}})\right]}_{>0 \text{ for } K_{a}>K_{a1}} >0. \end{array} $$In sum,
$$ \frac{d\tau_{III}}{d h}=\underbrace{\frac{\partial \tau_{III}}{\partial h}}_{<0}+\underbrace{\frac{\partial \tau_{III}}{\partial p_{iL1}}}_{>0}\underbrace{\frac{d p_{iL1}}{d h}}_{<0}<0. $$
1.5 Proof of Proposition 3
An increase in δOSB or δTSB affects
-
1.
the internal transfer prices (see Lemma 2) as follows:
$$ \begin{array}{@{}rcl@{}} \frac{d p_{iH}}{d \delta_{OSB}}&=&0, \frac{d p_{iH}}{d \delta_{TSB}}=0, \frac{d p_{iL2}}{d \delta_{OSB}}=0, \frac{d p_{iL2}}{d \delta_{TSB}}=0, \\ \frac{d p_{iL1}(\eta_{I})}{d \delta_{OSB}}&=&0, \frac{d p_{iL1}(\eta_{I})}{d \delta_{TSB}}=0, \\ \frac{\partial p_{iL1}\left( \eta_{III}\right)}{\partial \delta_{OSB}}&=&0, \frac{\partial p_{iL1}\left( \eta_{III}\right)}{\partial \eta_{III}}=\frac{t+h}{1-t-h}\delta_{TSB}(\overline{p_{r}}-\underline{p_{r}})>0, \\ \frac{d\eta_{III}}{d\delta_{OSB}}&=&\frac{(1-t-h)(a-\overline{p_{r}})}{\delta_{TSB}(\overline{p_{r}}-\underline{p_{r}})(t+h)}\frac{\eta_{III}}{\sqrt{B^{2}-C}}>0, \end{array} $$In sum,
$$ \begin{array}{@{}rcl@{}} &&\!\!\!\!\!\frac{d p_{iL1}\left( \eta_{III}\right)}{d \delta_{OSB}}=\underbrace{\frac{\partial p_{iL1}\left( \eta_{III}\right)}{\partial \delta_{OSB}}}_{=0}+\underbrace{\frac{\partial p_{iL1}\left( \eta_{III}\right)}{\partial \eta_{III}}}_{>0}\underbrace{\frac{d \eta_{III}}{d \delta_{OSB}}}_{>0}>0. \\ &&\!\!\!\!\!\frac{\partial p_{iL1}\left( \eta_{III}\right)}{\partial \delta_{TSB}}=\frac{t+h}{1-t-h}\eta_{III}(\overline{p_{r}}-\underline{p_{r}})>0, \\ &&\!\!\!\!\!\frac{d\eta_{III}}{d\delta_{TSB}}=\frac{1}{\sqrt{B^{2}-C}}\left[\frac{1}{2} \frac{(-2)(1-t)^{2}}{(1-\beta)\delta_{TSB}^{3}(\overline{p_{r}}-\underline{p_{r}})^{2}(t+h)^{2}}\right.\\ &&\!\!\!\!\!\times\left[\beta(c_{H}-c_{L})(c_{H}+c_{L}-2\overline{p_{r}})+(c_{L}-\overline{p_{r}})^{2}\right] \\ &&\!\!\!\!\!\left.+\frac{\eta_{\mathit{III}}\left[a(1 - t - h)(\delta_{\mathit{TSB}} - 2\delta_{\mathit{OSB}}) - c_{L}\delta_{\mathit{TSB}}(1 - t) + \overline{p_{r}}h\delta_{\mathit{TSB}} + 2\overline{p_{r}}\delta_{\mathit{OSB}}(1 - t - h)\!\right]}{\delta_{TSB}^{3}(\overline{p_{r}}-\underline{p_{r}})(t+h)}\right]\\&&\!\!\!\!\!<0, \end{array} $$for sufficiently large a. In sum,
$$ \frac{d p_{iL1}\left( \eta_{III}\right)}{d \delta_{TSB}}=\underbrace{\frac{\partial p_{iL1}\left( \eta_{III}\right)}{\partial \delta_{TSB}}}_{>0}+\underbrace{\frac{\partial p_{iL1}\left( \eta_{III}\right)}{\partial \eta_{III}}}_{>0}\underbrace{\frac{d \eta_{III}}{d \delta_{TSB}}}_{<0}, $$where \(\frac {d p_{iL1}\left (\eta _{III}\right )}{d \delta _{TSB}}\) is negative for sufficiently large a.
-
2.
the probability that the low-cost multinational chooses a noncompliant tax transfer price λTSB,I in equilibrium I (see Proposition 1) as follows.
$$ \frac{d \lambda_{TSB,I}}{d\delta_{OSB}}=0, \frac{d \lambda_{TSB,I}}{d\delta_{TSB}}=\frac{-K_{a}}{(1-\beta)(t+h)\delta_{TSB}^{2}(\overline{p_{r}}-\underline{p_{r}})(a-p_{iL1})}<0. $$ -
3.
the probability of using TSB τII in equilibrium II (see Proposition 1) as follows:
$$ \frac{d \tau_{II}}{d \delta_{OSB}}=\frac{K_{a}}{(1-\beta)(t+h)(a-\overline{p_{r}})\delta_{OSB}^{2}(\overline{p_{r}}-\underline{p_{r}})}>0, \frac{d \tau_{II}}{d \delta_{TSB}}=0. $$ -
4.
the probability of using TSB τIII in equilibrium III (see Proposition 1) as follows.
$$ \begin{array}{@{}rcl@{}} \frac{d \tau_{III}}{d \delta_{OSB}}=\frac{a-\overline{p_{r}}}{(1-\beta)(t+h)(\overline{p_{r}}-\underline{p_{r}})(\delta_{TSB}(a-p_{iL1})-\delta_{OSB}(a-\overline{p_{r}}))^{2}}\cdot \\ \left[K_{a}\left( 1+\frac{\eta_{III}}{\sqrt{B^{2}-C}}\right)-K_{a2}(\eta_{III})\left( 1+\frac{\eta_{III}}{\sqrt{B^{2}-C}}\frac{\delta_{OSB}(a-\overline{p_{r}})}{\delta_{TSB}(a-p_{iL1})}\right)\right]. \end{array} $$\(\frac {d \tau _{III}}{d \delta _{OSB}}\) is monotonically increasing in Ka, negative for Ka = Ka1 and positive for Ka = Ka2(ηIII). Thus a \({K_{a}^{c}}\in (K_{a1},K_{a2}(\eta _{III}))\) exists so that \(\frac {d \tau _{III}}{d \delta _{OSB}}\) equals zero. Therefore \(\frac {d \tau _{III}}{d \delta _{OSB}}\) is negative (positive) for \(K_{a}\in (K_{a1},{K_{a}^{c}})\) (\(K_{a}\in ({K_{a}^{c}},K_{a2}(\eta _{III}))\)).
$$ \frac{\partial \tau_{III}}{\partial \delta_{TSB}}=\frac{(K_{a1}-K_{a})(a-p_{iL1})}{(1-\beta)(t+h)(\overline{p_{r}}-\underline{p_{r}})\left[\delta_{TSB}(a-p_{iL1})-\delta_{OSB}(a-\overline{p_{r}})\right]^{2}}, $$which is negative because equilibrium III occurs for Ka ≥ Ka1. As shown in the Proof of Proposition 2, \(\frac {\partial \tau _{III}}{\partial p_{iL1}}>0\). In sum, for sufficiently large a,
$$ \frac{d\tau_{III}}{d \delta_{TSB}}=\underbrace{\frac{\partial \tau_{III}}{\partial \delta_{TSB}}}_{<0}+\underbrace{\frac{\partial \tau_{III}}{\partial p_{iL1}}}_{>0}\underbrace{\frac{d p_{iL1}}{d \delta_{TSB}}}_{<0}<0. $$
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Reineke, R., Weiskirchner-Merten, K. & Wielenberg, S. When do firms use one set of books in an international tax compliance game?. Rev Account Stud 28, 1856–1885 (2023). https://doi.org/10.1007/s11142-021-09667-9
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11142-021-09667-9