Abstract
We define quality as characteristics that investors should be willing to pay a higher price for. Theoretically, we provide a tractable valuation model that shows how stock prices should increase in their quality characteristics: profitability, growth, and safety. Empirically, we find that high-quality stocks do have higher prices on average but not by a large margin. Perhaps because of this puzzlingly modest impact of quality on price, high-quality stocks have high risk-adjusted returns. Indeed, a quality-minus-junk (QMJ) factor that goes long high-quality stocks and shorts low-quality stocks earns significant risk-adjusted returns in the United States and across 24 countries. The price of quality varies over time, reaching a low during the internet bubble, and a low price of quality predicts a high future return of QMJ. Analysts’ price targets and earnings forecasts imply systematic quality-related errors in return and earnings expectations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
When did our field stop being “asset pricing” and become “asset expected returning?” … Market-to-book ratios should be our left-hand variable, the thing we are trying to explain, not a sorting characteristic for expected returns.
– John Cochrane, Presidential Address, American Finance Association, 2011
1 Introduction
The asset pricing literature in accounting and financial economics studies the drivers of returns, but, while linked, the economic consequences of market efficiency ultimately depend on prices, not returns, as emphasized by Summer (1986) and Cochrane (2011). Do the highest quality firms command the highest price so that these firms can finance their operations and invest?
To address this question, we define quality as characteristics that investors should be willing to pay a higher price for, everything else equal, and study the price of quality, theoretically and empirically. We show that investors pay more for firms with higher quality characteristics. However, the explanatory power of quality for prices is limited, presenting a puzzle for asset pricing. This puzzle for asset prices is analogous to the old puzzle of the low R2 of asset returns presented by Roll (1984, 1988). Consistent with the limited pricing of quality, high-quality stocks have delivered high risk-adjusted returns while low-quality junk stocks have delivered negative risk-adjusted returns. Hence, a quality-minus-junk (QMJ) portfolio that invests long quality stocks and shorts junk stocks produces high risk-adjusted returns. Further, we find that the price of quality (the marginal amount extra investors pay for higher quality characteristics) has varied over time, as the market has sometimes put a larger or smaller price premium on quality stocks versus junk stocks. For instance, the price of quality was particularly low during the internet bubble. Since prices and returns are linked, the price of quality predicts the future return to the QMJ factor. Lastly, we consider analyst forecast and broader asset pricing applications.
To apply our general definition of quality, we must identify stock characteristics that should command a higher price. For this, we derive a dynamic asset pricing model with time-varying growth, profitability, and risk. We show closed form how price-to-book ratios increase linearly in each of these quality characteristics. To get some intuition before we present the general model, we can rewrite Gordon’s growth model to express a stock’s price-to-book value (P/B) as followsFootnote 1:
We scale prices by book values to make them more stationary over time and in the cross section. For instance, a food company with 10,000 restaurants likely has a price and book value that are 10 times that of another food company with only 1000 restaurants, but it is more interesting to consider which firm has the larger price-to-book (or, in this example, price per restaurant).
The three key right-hand side variables form the basis for our definition of quality.Footnote 2
-
i.
Profitability. Profitability is the profits per unit of book value. All else equal, more profitable companies should command a higher stock price. We measure profits in several ways, including gross profits, margins, earnings, accruals, and cash flows and focus on each stock’s average rank across these metrics.
-
ii.
Growth. Investors should also pay a higher price for stocks with growing profits. We measure growth as the prior five-year growth in each of our profitability measures.
-
iii.
Safety. Investors should also pay, all-else-equal, a higher price for a stock with a lower required return, that is, a safer stock. What should enter into required return is still a very contentious part of the literature. We do not attempt to resolve those issues here, but rather consider both return-based measures of safety (e.g., market beta) and fundamental-based measures of safety (low volatility of profitability, low leverage, and low credit risk).
While Gordon’s growth model assumes that all variables are constant over time, it is central to our empirical analysis that price-to-book ratios and quality characteristics vary across stocks and across time. Our general model allows such time variation, showing how prices increase with quality in a dynamic setting.
For the market to rationally put a price on these quality characteristics, they need to be measured in advance and predict future quality characteristics, that is, they need to be persistent. We show that this is indeed the case; profitable, growing, and safe stocks continue on average to display these characteristics over the following 5 or 10 yrs.
We test the pricing of quality over a long sample of U.S. stocks from 1957 to 2016 and a broad sample of stocks from 24 developed markets from 1989 to 2016. To evaluate the pricing of quality, we first run cross-sectional regressions of price-to-book on each stock’s overall quality score. Both in the long and broad sample, we find that higher quality is significantly associated with higher prices. However, the explanatory power of quality on price is limited, as the average R2 is only about 10% in both samples. When we also control for the firm’s size, the past 12-month stock returns, controls suggested by Pástor and Veronesi (2003), and include industry-, country-, and firm-fixed effects, the cross-sectional R2 increases to a maximum of, respectively, 49 and 43%, still leaving unexplained a large fraction of the cross-sectional distribution of prices. Interestingly, larger firms are more expensive, controlling for quality, the analogue of the size effect on returns (Banz 1981; Asness et al. 2018).
We also regress the price-to-book on the three quality measures separately and in a multivariate regression. Each of the quality components has a positive marginal price, accounting for all the control variables, and having all quality measures separately modestly increases the R2. Lastly, we consider the price of quality in different subsamples, finding a positive price of quality across industries and size deciles, with a somewhat larger price of quality for large stocks relative to small ones.
There could be several reasons for the limited explanatory power of quality on prices. (a) Market prices are based on superior quality characteristics than the ones we consider (e.g., an omitted variable). (b) The quality characteristics are correlated with risk factors not captured in our risk adjustments (so while the quality measure alone might command a higher price-to-book, the risk increase we fail to capture could imply an offsetting lower one). Or (c) market prices fail to fully reflect these characteristics for reasons linked to behavioral finance or constraints.
These three hypotheses have different implications for the return of quality sorted stocks. The first does not necessarily predict that the stocks that we classify as high quality have high risk-adjusted returns. The second predicts that high-quality stocks should have low returns during distress periods or other times of high marginal utility. And the third predicts that high-quality stocks do have high risk-adjusted returns.
To examine these potential explanations, we first consider the returns of high- versus low-quality stocks. We sort stocks into 10 deciles based on their quality scores and consider the value-weighted return in each portfolio. We find that high-quality stocks have significantly higher excess returns than junk stocks. The difference in their risk-adjusted returns (i.e., four-factor alphas) is even larger since high-quality stocks tend to have lower market, size, value and momentum exposures than junk stocks.
We then construct a QMJ factor with a methodology that follows that of Fama and French (1993) and Asness and Frazzini (2013). The factor is long the top 30% high-quality stocks and short the bottom 30% junk stocks within the universe of large stocks and similarly within the universe of small stocks. This QMJ factor (as well as its large-cap only and small-cap only components) delivers positive returns in 23 out of 24 countries that we study and highly significant risk-adjusted returns in our long and broad samples. QMJ portfolios have negative market, value, and size exposures, positive alpha, relatively small residual risk, and QMJ returns are high during market downturns, presenting a challenge to risk-based explanations relying on covariance with market crises. Rather than exhibiting crash risk, if anything, QMJ exhibits a mild positive convexity, that is, it benefits from flight to quality during crises. In other words, the evidence challenges hypotheses (a) and (b) above, while appearing more consistent with (c).
To test (c) more directly, we examine equity analysts’ forecasts as reflected in their “target prices,” that is, the expected stock price 1 yr into the future using the methodology of Brav et al. (2005). Analysts’ target prices (scaled by book value) are higher for high-quality stocks, consistent with a positive price of quality. However, analysts’ implied return expectations (target price divided by current actual price) are lower for high-quality stocks than junk stocks, presenting a systematic error, relative to the realized returns. In other words, analysts appear to have higher target prices for high-quality stocks but not high enough on average, consistent with (c). Looking at earnings forecast errors, we find consistent results: analysts are indeed too optimistic about junk stocks (i.e., forecasted earnings are above realized earnings, on average) and much more so than about quality stocks.
To further test the link between the price and return to quality, it is interesting to exploit the time-variation in the price of quality. In particular, each month, we estimate the current price of quality as the cross-sectional regression coefficient of price-to-book on quality. The time series of these cross-sectional regression coefficients reflects how the pricing of quality varies over time. Intuitively, the price of quality reached its lowest level in February 2000, during the height of the internet bubble. The price of quality was also relatively low leading into the 1987 crash and leading into the global financial crisis of 2007–2009. Following each of these three dramatic events, the price of quality increased, reaching highs in late 1990 (first gulf war), in late 2002 (after the Enron and WorldCom scandals), and in early 2009 (at the height of the banking crisis). Prices and returns are naturally connected, and we show that the price of quality negatively predicts the future return on QMJ. Said differently, a higher price of quality is associated with a lower return on high-quality stocks, consistent with the theory (c) that a low price of quality means that the market is inefficient in incorporating quality into prices.
We note that the QMJ strategy of buying profitable, safe, growing stocks while shorting unprofitable, risky, shrinking stocks is very different from the standard value strategy, high minus low (HML) – in fact, the two are negatively correlated. QMJ is buying and selling based on quality characteristics, irrespective of stock prices, while HML is buying based on stock prices, irrespective of quality. Naturally, the two concepts can be combined, which we call quality at a reasonable price (QARP).Footnote 3 This concept goes back at least to Graham and Dodd (1934), who stated that “investment must always consider the price as well as the quality of the security.” Naturally, value investing is improved by QARP, consistent with the finding in the accounting literature that information from financial statements can improve value investing (e.g., Frankel and Lee 1998; Piotroski 2000).
Our paper relates to a large literature. A number of papers study return-based anomalies. It has been documented that stocks with high profitability outperform (Novy-Marx 2012, 2013), stocks that repurchase tend to do well (Baker and Wurgler 2002; Pontiff and Woodgate 2008; McLean et al. 2009), low beta is associated with high alpha for stocks, bonds, credit, and futures (Black et al. 1972; Frazzini and Pedersen 2014), firms with low leverage have high alpha (George and Hwang 2010; Penman et al. 2007), firms with high credit risk tend to underperform (Altman 1968; Ohlson 1980; Campbell et al. 2008), growing firms outperform firms with poor growth (Mohanram 2005), and firms with high accruals are more likely to suffer subsequent earnings disappointments and their stocks tend to underperform peers with low accruals (Sloan 1996; Richardson et al. 2005). While these papers are very different and appear disconnected, our framework illustrates a unifying theme, namely that all these effects are about the outperformance of high-quality stocks, and we link returns and prices.
Our paper also relates to the literature that considers how the price-to-book predicts future returns and future fundamentals, based on the present-value relationship. Campbell and Shiller (1988) consider the overall market, and their dividend growth variable can be interpreted an as aggregate quality variable. Vuolteenaho (2002); Cohen et al. (2003, 2009); and Fama and French (2006) consider individual stocks. Cohen et al. (2003) decompose the cross-sectional variance of firms’ book-to-market ratios across book-to-market portfolios, and Cohen et al. (2009) consider how cash-flow betas affect price levels and long-run returns. See also the overview by Cochrane (2011) and references therein.
In summary, we complement the literature by showing (i) the theoretical price of quality in a dynamic model; (ii) how quality affects price multiples and how much of the cross-sectional variation of price multiples can be explained by quality; (iii) that the price of quality varies over time and predicts the future return on quality factors; (iv) that quality stocks earn higher returns and yet appear safer, not riskier, than junk stocks, benefitting from flight to quality; and (v) that analysts’ target prices and earnings forecast errors imply systematic quality-related errors in return and earnings expectations.
The rest of the paper is organized as follows. Section 1 presents our model. Section 2 presents our data and quality measures, showing that ex ante quality forecasts future quality (i.e., quality is sticky, as would be necessary for it to affect prices). Section 3 analyzes the price of quality. Section 4 tests different potential explanations for the limited explanatory power of quality for price. Section 5 further asset pricing applications. Section 6 concludes. The Appendix contains a number of additional results and robustness checks.
2 The price of quality: dynamic model
2.1 A dynamic model of firm quality: time-varying profits, growth, and risk
We consider a firm in an economy with pricing kernel Mt. The pricing kernel is given by \( \frac{M_{t+1}}{M_t}=\frac{1}{1+{r}^f}\left(1+{e}_{t+1}^M\right) \), where rf is the risk-free rate and \( {e}_{t+1}^M \) is the zero-mean innovation to the pricing kernel. For example, if the Capital Asset Pricing Model (CAPM) holds then \( {\varepsilon}_{t+1}^M \) is linked to the return on the market portfolio, \( {r}_{t+1}^{MKT} \). More specifically, the CAPM pricing kernel is \( {e}_{t+1}^M=-{\lambda}_t\left(\frac{r_{t+1}^{MKT}-{E}_t\left({r}_{t+1}^{MKT}\right)}{\sigma_t^2\left({r}_{t+1}^{MKT}\right)}\right) \), where \( {\lambda}_t={E}_t\left({r}_{t+1}^{MKT}\right)-{r}^f \) is the market risk premium.
The value of the firm is the present value of all future dividends, dt:
We rewrite the valuation equation in terms of the book value Bt and earnings (or net income) NIt by using the clean surplus relation, Bt = Bt − 1 + NIt − dt:
where the so-called residual income, RIt + s = NIt + s − rfBt + s − 1, is the net income in excess of the cost of book capital.Footnote 4 We assume that the firm keeps all financial assets in risk-free securities, which implies that dividend policy and capital structure do not affect residual income.Footnote 5 Therefore we can specify an exogenous process for the residual income (which depends on the firm’s free cash flows from operations). Residual income consists of two components:
where et captures “sustainable residual income” (that is, “sustainable earnings” adjusted for the cost of book capital) and at captures “transitory residual income shocks.” As defined precisely below, sustainable residual income is characterized by the fact that it predicts future residual income and may grow over time, whereas transitory shocks are temporary profits or losses that do not affect the long-term earnings of the firm. Specifically, sustainable residual income et is expected to grow by gt such that
The zero-mean income innovation \( {\varepsilon}_t^e \) has a risk premium πt due to covariation with the pricing kernel, \( {\pi}_t=- co{v}_t\left({\varepsilon}_{t+1}^e,{\varepsilon}_{t+1}^M\right) \). We use the negative covariation such that a high risk premium corresponds to a higher required return. Under the CAPM, the risk premium is the cash flow’s standard market beta multiplied by the market risk premium λt, that is,
The growth gt and risk premium πt are time-varying:
where \( \overline{g} \) and \( \overline{\pi} \) are the long-run means, φg and φπ indicate the persistence of the processes, and \( {\varepsilon}_{t+1}^g \) and \( {\varepsilon}_{t+1}^{\pi } \) are zero-mean shocks that are uncorrelated to \( {\varepsilon}_{t+1}^M \).
The transitory residual income shock follows a moving average process and for simplicity we only consider a single lag:
We see that \( {\varepsilon}_t^a \) captures zero-mean random shocks to residual income, and θ measures dependence on past shocks. The transitory income does not grow over time, and a positive shock is even expected to be partly reversed in the next period if θ > 0. For example, aggressive accounting accruals can lead to such reversals in earnings.Footnote 6
2.2 Valuation: the price of quality
To compute the fundamental value, we first compute the conditional expectation of the sustainable residual income et + 1 for the next period:
We can iterate this result to show that the value of sustainable income τ periods into the future is
Based on this result, we can next compute the fundamental value as the sum of the book value and all future discounted residual incomesFootnote 7:
where the valuation coefficients are \( v=\frac{1+{r}_f}{r_f^2}\left(\overline{g}-\overline{\pi}\right) \), \( {v}^e=\frac{1}{r_f} \), \( {v}^g=\frac{\varphi_g\left(1+{r}_f\right)}{r_f\left(1+{r}_f-{\varphi}_g\right)} \), \( {v}^{\pi }=\frac{\varphi_{\pi}\left(1+{r}_f\right)}{r_f\left(1+{r}_f-{\varphi}_{\pi}\right)} \), and \( {v}^a=\frac{\theta }{1+{r}_f} \). The fundamental value can be written as a fraction of book value Bt:
This specification motivates our empirical work. In particular, we see that the ratio of fundamental value to book value increases in the current residual earnings adjusted for accruals divided by book (which we call profitability),Footnote 8 it increases in the growth of sustainable profits, and it increases in safety (i.e., it decreases in market risk πt). Further, we see that the valuation is linear in these values.
3 Data, quality measures, and preliminary analysis
3.1 Data sources
The data is collected from a variety of sources. Our sample consists of 54,616 stocks covering 24 countries between June 1957 and December 2016. The 24 markets in our sample correspond to union of all countries belonging to the MSCI World Developed Index over our sample period. We report summary statistics in Table 10 in the Appendix. Stock returns and accounting data are from the union of the Center for Research on Security Prices (CRSP) pricing database, the Compustat North America Fundamentals Annual, Fundamentals Quarterly and Security Daily databases, the Compustat Global Fundamentals Annual, Fundamentals Quarterly, and Security Daily databases. All returns are in U.S. dollars. They do not include any currency hedging, and they are measured as excess returns above the U.S. Treasury bill rate.Footnote 9 We follow the standard convention (Fama and French (1992) and align accounting variables at the end of the firm’s fiscal year ending anywhere in calendar year t-1 to June of calendar year t. We focus on a long sample of U.S. stocks and a broad sample of global stocks.
Our long sample of U.S. data includes all available common stocks on the merged CRSP/Compustat North America data.Footnote 10 Our default primary source for pricing information is Compustat, supplemented with CRSP over the earlier period when Compustat pricing data is not available. Table 10 in the Appendix reports details on the data sources for each period. The first available date for our regressions and return tests is June 1957.Footnote 11
Our broad sample includes all available common stocks on the union of the CRSP, the Compustat North America and the Compustat Global database for 24 developed markets. We assign individual issues to the corresponding market based on the location of the primary exchange. For companies traded in multiple markets, we use the primary trading vehicle identified by Compustat. The first available date for our regressions and return test is June 1989. Table 10 reports date coverage of the individual markets.
Target prices are from the Thomson Reuters I/B/E/S global database, which contains the projected price level forecasted by analysts within a specific time horizon. For our analysis, we use the monthly mean and median consensus target prices. I/B/E/S computes consensus prices are over a 12-month time horizon. Earnings forecast errors are also from Thomson Reuters. Every month, we compute the actual EPS earnings for the next fiscal year minus the I/B/E/S consensus forecasts, deflated by the stock price.
3.2 Quality score
To avoid data mining, we base our measures on our theoretical model implemented using standard off-the-shelf empirical measures to compute three composite quality measures: profitability, growth, and safety. We then average these three quality components to compute a single overall quality score. Our results are qualitatively robust to the specific choices of factors.
The theory suggests that profitability should be measured as the “sustainable” part of profits in relation to book value, adjusted for accruals, which we implement empirically by averaging several measures of profitability to reduce noise (hopefully leaving the more sustainable part) and avoiding focusing on a particular measure. Our empirical exercise is focused on cross-sectional comparisons of firms sorted by their overall quality scores as well as the three quality components. When comparing firms’ profitability, note that there is no difference between comparing their residual-income-to-book versus net-income-to-book, since these only differ by the common risk-free rate, RIt/Bt − 1 = NIt/Bt − 1 − rf.
Second, theory suggests that growth should be the increase in sustainable profits in relation to book values. Since profits are noisy, we use a five-year window to focus on sustainable growth, and, again based on our model, accruals are not included in the growth measure. When computing growth measures, using residual income, rather than net income, does matter.Footnote 12 Further, to account for issuance, we consider all variables on a per-share basis. That is, we compute the value to a buy-and-hold investor who does not participate in issuances.Footnote 13
More specifically, our quality measures are constructed as follows (details are in the Appendix). We measure profitability as gross profits over assets (GPOA), return on equity (ROE), return on assets (ROA), cash flow over assets (CFOA), gross margin (GMAR), and the fraction of earnings composed of cash (i.e., minus accruals, ACC). To put each measure on equal footing and combine them, each month we convert each variable into ranks and standardize to obtain a z-score. More formally, let x be the variable of interest and r be the vector of ranks, ri = rank (xi). Then the z-score of the ranks of x is given by z(x) = zx = (r − μr)/σr, where μr and σr are the cross-sectional mean and standard deviation of r. Our Profitabiliy score is the average of the individual z-scores:
Similarly, we measure growth as the five-year growth in residual per-share profitability measures (excluding accruals), averaged across five measures. Letting Δ denote the five-year change in each measure of residual income per share, divided by the lagged denominator (e.g., assets per share), we have:
Further, we define safe securities as companies with low beta (BAB), low leverage (LEV), low bankruptcy risk (O-Score and Z-Score), and low ROE volatility (EVOL):
Finally, we combine the three measures into a single quality score:
To construct our composite quality measure as well as the individual subcomponents, we use all available information: if a particular measure is missing due lack of data availability, we simply average the remaining ones. We also consider a number of robustness tests, for example, using raw values rather than the ranks.
3.3 Portfolios
Our portfolio analysis relies on two sets of test factors: quality-sorted portfolios and quality-minus-junk factors (hereafter, QMJ factors). For both, we form one set of portfolios in each country and compute global portfolios by weighting each country’s portfolio by the country’s total (lagged) market capitalization.
To form quality-sorted portfolios, at the end of each calendar month, we assign stocks in each country to 10 quality-sorted portfolios. U.S. sorts are based on NYSE breakpoints. Portfolios are value-weighted, refreshed every calendar month, and rebalanced every calendar month to maintain value weights.
The QMJ portfolio construction follows Fama and French (1993) and Asness and Frazzini (2013). QMJ factors are constructed as the intersection of six value-weighted portfolios formed on size and quality. At the end of each calendar month, we assign stocks to two size-sorted portfolios, based on their market capitalization. For U.S. securities, the size breakpoint is the median NYSE market equity. For other markets, the size breakpoint is the 80th percentile by country.Footnote 14 We use conditional sorts, first sorting on size and then on quality. Portfolios are value-weighted, refreshed every calendar month, and rebalanced every calendar month to maintain value weights. The QMJ factor return is the average return on the two high-quality portfolios minus the average return on the two low-quality (junk) portfolios:
Portfolios based on profitability, growth and safety are constructed in a similar manner. We compute alphas with respect to a domestic and a global four-factor model. The explanatory variables are the market (MKT), size (small-minus-big, SMB), book-to-market (high-minus-low, HML), and momentum (up-minus-down, UMD) portfolios. We report a more detailed description in the Appendix.Footnote 15 In some of our tests, we also use the Fama and French (2015) five-factor model, based on the market factor (MKT), size (small-minus-big, SMB), book-to-market (high-minus-low, HML), profitability (robust-minus-weak, RMW), and an investment factor (conservative-minus-aggressive, CMA).Footnote 16
3.4 Ex ante quality forecasts fundamentals
We start by showing that a stock’s quality is persistent. That is, by selecting companies that were profitable, growing, and safe in the recent past, we succeed in selecting companies that display these characteristics in the future. This step is important when we turn to the central analysis of whether the high-quality firms command higher prices since, in a forward-looking rational market, prices should be related to future quality characteristics. Of course, predictability of quality is perfectly consistent with an efficient market—market efficiency says only that, since prices should reflect quality, stock returns should be unpredictable (or only predictable due to risk premia), not that quality itself should be unpredictable.
Table 1 analyzes the predictability of quality as follows. Each month, we sort stocks into 10 portfolios by their quality scores (as defined in Section 2). The table reports the value-weighted average of our quality measures across stocks in each of the portfolios. The table shows these average quality scores both at the time of the portfolio formation (time t) and in the subsequent 10 yrs (t + 120 months). The standard errors are adjusted for heteroskedasticity and autocorrelation with a lag length of 5 yrs (Newey and West (1987)). By construction, the quality scores vary monotonically across portfolios at the time of portfolio formation, so the interesting part of the table is the future quality scores. Table 1 shows that, on average, high-quality firms today remain high-quality firms five and 10 yrs into the future (conditional on survival) and we can reject the null hypothesis of no difference in each of quality characteristics up to 10 yrs. Table 11 in the Appendix reports additional results: we sort firms separately using each component of our quality score (profitability, growth, and safety) and report the spread in each variable up to 10 yrs, yielding similarly consistent results.
To summarize, quality is a persistent characteristic such that high quality today predicts future high quality. For both the U.S. long and global sample, profitability is the most persistent, and, while still surprisingly stable, growth and safety are the least persistent.
4 The price of quality
Given that future quality can be forecasted, we now turn to the central question of how quality affects prices: do high-quality stocks command higher prices than low-quality ones?
4.1 The price of quality in the United States and globally
To address this question, we run a cross-sectional regression of each stock i’s log market-to-book (MB) ratio on its overall quality score, \( {Quality}_t^i \) (defined in Section 2). Specifically, we let \( {P}_t^i=\mathit{\log}{(MB)}_t^i \) and run the regression:
Market-to-book is defined as book equity divided by the current market equity of the firm in June of year t. This regression tests whether high quality is associated with high prices in the cross section. Using ranked z-scores as our explanatory variable limits the effect of outliers and implies that the regression coefficient b has a simple interpretation: b measures the percentage increase (log changes) in market-to-book associated to a one standard deviation increase in our quality score.Footnote 17 We include several control variables motivated by theory as discussed below.
Panel A of Table 2 reports results of Fama and MacBeth (1973) regressions of prices on quality. In June of each year, we regress scaled prices on quality measures, and we report time series averages of the cross-sectional slope estimates. Standard errors are adjusted for heteroskedasticity and autocorrelation (Newey and West 1987) with a lag length of 5 yrs. We run the regression with and without industry-, country-, or firm-fixed effects, as indicated.
We see that the price of quality b is generally positive and highly statistically significant: high-quality firms do command higher (scaled) prices. Indeed, the price of quality is positive both in the U.S. and global samples and across specifications with controls and fixed effects. The univariate estimated price of quality in the long domestic (broad global) sample is 0.22 (0.17). This coefficient implied that a one standard deviation change in a stock’s quality score is associated (in the cross section) with a 22% (17%) increase in its price-to-book.
While theory does not provide specific guidance on what the R2 should be, the explanatory power of quality on price appears limited. Quality alone explains only about 9% of the cross-sectional variation in prices in both our U.S. and global sample.
We also include several controls. With the exception of dummy variables, we measure each of these controls as the z-score of their cross-sectional rank for consistency and ease of interpretation of the coefficients. First, we control for size, motivated by the theory that large stocks are more liquid and have less liquidity risk than small firms and thus higher prices and lower required returns (Amihud and Mendelson 1986; Pástor and Stambaugh 2003; Acharya and Pedersen 2005). Consistent with this theory, we see that larger firms do have higher prices, controlling for quality. This result is the analogue of the size effect on returns (Banz 1981; also Berk 1995), expressed in terms of prices. That is, big firms, even for the same quality, are more expensive, possibly leading to the return effect observed by Banz.
Motivated by the theory of learning about profitability by Pástor and Veronesi (2003), we also control for age, profit uncertainty, and a dividend payer dummy, as defined as in their paper. Firm age is the cumulative number of years since the firm’s IPO. Profit uncertainty is the standard deviation of the residuals of an AR(1) model for each firm’s ROE, using the longest continuous series of a firm’s valid annual ROE up to June of each year. Dividend payer is a dummy equal to one if the firm paid any dividends over the prior year. Consistent with Pástor and Veronesi (2003), we find that prices are lower for firms that pay dividends, decrease in age, and increase in profit uncertainly, especially for firms that pay no dividends.
We also control for past stock returns. Including past returns is necessary since our sample include firms with fiscal year-ends up to 11 months apart. (Accounting variables at the end of the firm’s fiscal year ending anywhere in calendar year t-1 are aligned to June of calendar year t.) A positive coefficient on past returns simply reflects that high recent returns raise current prices while the book value has not had time to adjust. Consistent with this observation, Table 2 shows that, ceteris paribus, stocks with higher stock returns tend to have higher scaled prices.
Finally, we also consider industry-, country-, and firm-fixed effects. We see that the R2 increases markedly with these controls. Nevertheless, the coefficient on quality is relatively immune to the inclusion of these controls, and its statistical significance actually increases. The maximum R2 across all these specifications is 49%, leaving the majority of cross-sectional variation on prices unexplained.
4.2 The price of quality sub-components
Panel B of Table 2 considers cross-sectional regressions on each separate quality score, univariately and multivariately:
We see that prices of profitability, growth and safety are positive throughout, controlling for each other and our other control variables and fixed effects. In other words, high-quality stocks tend to have relatively higher prices than low-quality stocks. The maximum R2 reaches 48% in the United States and 42% in the global sample, still leaving a large part of the cross section of prices unexplained.
4.3 The price of quality across subsets of stocks
The Appendix contains further robustness tests. Table 12 reports results from monthly regressions, where market-to-book follows the convention of Asness and Frazzini (2013), defined as book equity divided by the current market equity of the firm each month. Figure 6 report results by industry. This figure plots t-statistics of the quality coefficients from annual Fama-Macbeth regressions within 71 GICS industries, using our full set of controls. All the results tell a consistent story: high-quality firms tend to command higher prices.
Table 12 also reports the price of quality by size decile. In particular, we run regression (8) for each subsample of stocks sorted by size. We see that the results are consistent across size groups, both in the United States and globally. Also note that the average R2 rises across decile size, reaching 72% (56%) for U.S. (global) firms in the top size deciles. Although for the median firm the vast majority of cross-sectional variation on prices remains unexplained, over the largest firms, quality does explain a significant amount of cross-sectional dispersion in (scaled) prices.
To summarize, our results are consistent with the hypothesis that high-quality firms command higher (scaled) prices. However, the explanatory power of quality is limited, leaving a large amount of variation in prices unexplained. Our results appear robust to specification and not driven by effects related to small stocks or by a particular industry or geography.
5 Understanding the price of quality: the return of quality stocks
We would like to shed light on our finding that quality explains prices only to a limited extent: is this finding because (a) the market uses superior quality measures (and, if we observed these measures, they would strongly relate to prices) or, in some cases, reverse causality; (b) quality is linked to risk in a way not captured by our safety measure; or (c) limited market efficiency. Explanation (c) implies that high-quality stocks have higher risk-adjusted returns than low-quality stocks, as market prices fail to fully reflect the quality characteristics. Explanation (b) implies a univariate relation between quality and future returns, which is reduced or eliminated by an effective risk model. And explanation (a) means that the relation between our measured quality and ex post returns is attenuated, noisy, or potentially biased—in the simplest form, this explanation means that quality should be unrelated to risk-adjusted returns. Hence, to try to explain the limited relation between price and quality, we need to analyze the future returns of quality stocks.Footnote 18
5.1 The returns of quality-sorted portfolios
Table 3 reports the returns of stocks sorted into 10 deciles based on their quality score. The table reports both excess returns over T-bills and alphas with respect to the CAPM one-factor model; the Fama and French (1993) three-factor model, which includes the size factor SMB and the value factor HML, in addition to the market factor MKT; and the four-factor model, which includes the momentum factor UMD (Jegadeesh and Titman 1993; Asness 1994; Carhart 1997). Specifically, these alphas are the intercepts from the following regression with the first one, three, or four right-hand-side variables included:
We see that excess returns increase almost monotonically in quality such that high-quality stocks outperform low-quality stocks. The right-most column reports the return difference between the highest and lowest deciles and the associated t-statistic, showing that high-quality stocks earn higher average returns than low quality stocks (42 and 52 basis points per month depending on the sample), and we can reject the null hypothesis of no difference in average returns (t-statistics of 2.56 and 2.49).
When we control for market risk and other factor exposures, the outperformance in the alpha of high-quality stocks and their statistical significance is in fact even larger. This higher outperformance arises because high-quality stocks actually have lower market exposures and lower exposures to other factors than low-quality stocks. In other words, as measured by the CAPM or a three- and four-factor model, high-quality stocks are safer (have lower factor loadings) than low-quality stocks. Adjusting by the CAPM alone materially strengthens our results, as higher-quality stocks are, partly by construction, lower beta stocks. Across our three risk models in our long U.S. sample, a portfolio that is long high-quality stocks and short low-quality stocks earns average abnormal returns ranging from 64 to 105 basis points per month with associated t-statistics ranging between 4.26 and 9.31. In our broad global sample, we obtain similar results with abnormal returns between 71 to 99 basis points and t-statistics between 4.05 and 6.67.
Our results are thus consistent with explanation (c) discussed above but do not appear to support the simplest versions of explanations (a) and (b). Indeed, a simple risk explanation (b) is inconsistent with our finding that high-quality stocks have lower factor exposures than junk stocks, but we study risk in more detail by considering the performance of the QMJ factor.
5.2 Quality minus junk
In this section, we examine the returns of our QMJ factors. As described in Section 2 (Eq. 7), QMJ is long the average of the Small Quality and Big Quality portfolios and short the average of the Small Junk and Big Junk portfolios. We also construct long/short factors based on each separate quality component using the same method. Hence, in addition to QMJ, we have quality factors based on profitability, safety, and growth.
Table 13 reports the correlations between the different quality components. The table reports the correlation both for the excess returns and for the abnormal returns relative to a four-factor model (i.e., the correlations of the regression residuals). We see that all of the pairwise correlations among the quality components are positive. The average pairwise correlation among the quality components is 0.67 in the United States and 0.64 in the global sample and 0.59 and 0.57 for abnormal returns in the two samples. Hence, while the quality components measure different firm characteristics that investors should be willing to pay for, firms that are high quality in one respect tend to also be high quality in others. This did not have to be. Each of these variables, we argue, is a quality measure investors should pay for at the margin, but the measures did not have to be related to one another. While theory is no guide here, we think these significant positive correlations lend support to our practical decision to combine these three thematic sets of measures as one quality variable.
Table 4 reports the performance of each of our quality factors in the United States (panel A) and globally (panel B). Specifically, the table reports the average excess returns and the alphas with respect to the CAPM, three-, and four-factor models. We see that each quality factor delivers a statistically significant positive excess return and alpha with respect to the CAPM, three-, and four-factor models in the U.S. sample and significant four-factor alphas in the global sample as well (the three- and four-factor results are quite similar as momentum, or UMD, does not change much). The overall QMJ factor tends to be the strongest of the three, with highly significant alphas in the United States and global samples. The abnormal returns are large in magnitude and highly statistically significant. In our U.S. long sample, a QMJ portfolio that is long high-quality stocks and short junk stocks delivers CAPM, three-, and four-factor abnormal returns of 39, 51, and 60 basis points per month (with corresponding t-statistics of 5.43, 8.90, and 9.95). Similarly, in our global broad sample, the QMJ factor earns abnormal returns of 51, 61 and 61 basis points per month (with corresponding t-statistics of 5.76, 8.75, and 8.07).
Panels A and B of Table 4 also report the risk-factor loadings for the four-factor model. We see that the QMJ factor (with the exception of the UMD loading in the global sample) has significant negative factor exposures, that is, according to four-factor model, quality stocks are in general safer than junk stocks yet surprisingly earn higher (not lower) average returns. QMJ has a significantly negative market and size exposures. That is, QMJ is long low-beta and large stocks, while being short high-beta small ones. As would be expected, the safety factor has the most negative market exposure, though only growth attains a zero or small positive market beta. The other quality composites also show negative beta. The value exposure of QMJ is negative in the United States and globally. This negative value loading is expected since high-quality stocks have high prices while the value factor HML is long cheap stocks. The loadings on UMD tend to be smaller in magnitude and statistically insignificant in some the specifications. The loadings are consistent across quality sub-components, with profitability, safety, and growth all having negative market, SMB, and HML loadings in the U.S. and global samples.
Figure 1 and Table 16 report the performance of the QMJ factor across countries. Remarkably, the QMJ factor delivers positive returns and alphas in all but one of the 24 countries that we study, displaying a strikingly consistent pattern (with the only small negative in our sample being in New Zealand, one of the smallest countries in market capitalization and number of stocks). Furthermore four-factors alphas are statistically significant in 18 out of 24 countries, despite the fact that many individual countries have a small cross section of securities and a short time series.
QMJ: 4-Factor Adjusted Information Ratios. This figure plots four-factor adjusted information ratios of quality minus junk (QMJ) factors. At the end of each calendar month, stocks are assigned to two size-sorted portfolios based on their market capitalization. For U.S. securities, the size breakpoint is the median NYSE market equity. For other markets, the size breakpoint is the 80th percentile by country. We use conditional sorts, first sorting on size, then on quality. Portfolios are value-weighted, refreshed every calendar month, and rebalanced every calendar month to maintain value weights. The QMJ factor return is the average return on the two high-quality portfolios minus the average return on the two low-quality (junk) portfolios. We form one set of portfolios in each country and compute global portfolios by weighting each country’s portfolio by the country’s total (lagged) market capitalization. Information ratios are equal to the intercept of a time-series regression of monthly excess return divided by the standard deviation of the estimated residuals. The explanatory variables are the monthly returns of the market (MKT), size (SMB), book-to-market (HML), and momentum (UMD) portfolios from Appendix 2. Returns are in U.S. dollars, do not include currency hedging, and excess returns are over the U.S. Treasury bill rate. Information ratios are annualized
Fig. 2 shows the performance of the QMJ factor over time in the U.S. and global samples. Specifically, Fig. 2 shows the cumulative sum of QMJ’s four-factor risk-adjusted returns (the sum of the monthly in-sample regression alpha plus the regression error), illustrating that QMJ factor has consistently delivered positive risk-adjusted returns over time with no particular subsample driving our results. Figs. 7 and 8 in the Appendix plot, respectively, the raw excess returns over time (i.e., without risk adjustments) and the four-factor alphas by year.
QMJ: Cumulative Four-Factor Alphas. This figure shows four-factor adjusted cumulative returns of quality minus junk (QMJ) factors. At the end of each calendar month, stocks are assigned to two size-sorted portfolios based on their market capitalization. For U.S. securities, the size breakpoint is the median NYSE market equity. For other markets, the size breakpoint is the 80th percentile by country. We use conditional sorts, first sorting on size, then on quality. Portfolios are value-weighted, refreshed every calendar month, and rebalanced every calendar month to maintain value weights. The QMJ factor return is the average return on the two high-quality portfolios minus the average return on the two low-quality (junk) portfolios. We form one set of portfolios in each country and compute global portfolios by weighting each country’s portfolio by the country’s total (lagged) market capitalization. Panel A reports results from our Long Sample of domestic stocks. The sample period runs from June 1957 to December 2016. Panel B reports results from our Broad Sample of global stocks. The sample period runs from June 1989 to December 2016. Alpha is the intercept in a time-series regression of monthly excess return. The explanatory variables are the monthly returns of the market, (MKT), size (SMB), book-to-market (HML), and momentum (UMD) portfolios from Appendix 2. Returns are in U.S. dollars, do not include currency hedging, and excess returns are over the U.S. Treasury bill rate. We plot the cumulative abnormal returns (alpha plus regression residual) from the time-series regression
5.3 Robustness of QMJ performance
Table 5 reports the performance of our quality factors using alternative risk-adjustments. Specifically, we report alphas relative to the five-factor model of Fama and French (2015) and the six-factor model augmented with the (UMD) momentum portfolio.Footnote 19 While using this six-factor adjustment reduces the magnitude of the abnormal returns, the results are consistent with prior ones: QMJ portfolios earn significant returns, controlling for the five- or six-factor models. We note that QMJ portfolios have large positive loading on the RMW factor based on gross profit over assets (GPOA), which is not surprising given that GPOA is a component out our profitability composite. Nevertheless, alphas are positive, ranging from 16 to 38 basis points per month, and most of them are significant. Said differently, RMW is a quality factor, so we are measuring the return of quality broadly defined, controlling for a narrow quality measure and other factors.
Furthermore, factor loadings to the market, size, and value remain negative, indicating that high-quality stocks are safer than junk stocks in terms of these risk exposures (while CMA, RMW, and UMD have less clear interpretations as risk).
We report a series of additional results and robustness checks in the Appendix. Table 14 reports returns for the individual components (small quality, big quality, small junk, big junk) of the QMJ factors. In Table 15, we split the sample in 20-year subsamples and report QMJ returns by size (10 size-sorted based on NYSE-breakpoints). Figure 9 report results for large- and small-cap stocks within each country. Table 17 reports QMJ abnormal returns controlling for the four-factor model augmented with the betting against beta (BAB) factor of Frazzini and Pedersen (2014). Table 18 reports QMJ abnormal returns controlling for the six-factor model plus BAB. Finally, Fig. 10 reports results by industry using 71 global GICS industries. We form a QMJ portfolio within each industry and report four-factor adjusted information ratios.
All the results point in the same direction with consistency across size, time periods, countries, and construction methodology: QMJ portfolios that are long high-quality stocks and short junk stocks earn large and significant abnormal returns, relative to variety of factor models, ranging from one- to seven-factor models. Furthermore, quality stocks do not appear riskier (as defined by model loadings); if anything, they appear safer than junk stocks and, as a result, earn abnormal returns that are larger than their excess returns.
The return evidence on the QMJ factors could be consistent with both mispricing (quality stocks are underpriced and junk stocks are overpriced) or risk (quality stocks underperform junk stocks in bad states of the world) that is not fully captured by the factor models considered above. Although a full explanation of the driver of quality returns is beyond the scope of this paper, we can nonetheless provide some stylized facts that either explanation should generate to fit the available evidence.
5.4 The risk of quality stocks
We have already noted that the evidence does not point toward compensation for risk measured by the host of factor models considered above. The evidence also does not point toward compensation for tail risk as seen in Table 6. We compute the return of the QMJ factors during recessions and expansions, during severe bear and bull markets (defined as total market returns in the past 12 months below −25% or above +25%), during periods of high and low market volatility (measured as the one-month standard deviation of daily returns of the CRSP-value weighted index or the MSCI-World index and splitting the sample in the 30% top and bottom periods), and during periods of a large increase or drop in aggregate volatility (again splitting the sample into the 30% top and bottom periods in terms of the one-month change in volatility). We find no evidence of compensation for tail risk. If anything, the evidence again points toward high-quality stocks being safer than junk stocks: quality appears to hedge (as opposed being correlated to) periods of market distress.
To study further the risk of QMJ, Fig. 3 plots the performance of QMJ against the return on the market. The negative beta of QMJ is clearly visible by the downward sloping relation of the excess return of QMJ and the market. Further, the relatively tight fit around the curve shows the limited residual risk, implying a strong and consistent historical performance of QMJ during down periods for the market. QMJ also performs well in extreme down markets; in fact, the estimated second-order polynomial shown in the graph has a positive (but insignificant) quadratic term, meaning that the fitted curve bends upward in the extreme. This mild concavity is mostly driven by the returns to the profitability subcomponent of quality. The quadratic term is marginally significant (t-statistic of 2.4) for the profitability factor in our long sample. The strong return in extreme down markets is consistent with a flight to quality (or at least to profitability). That is, in down markets, investors may exhibit flight to quality in the sense that prices of unprofitable stocks drop more than the prices of profitable stocks, even adjusting for their betas. The strong performance of QMJ in down markets is robust to considering longer periods such as down-market quarters or down-market years (not shown for brevity).
QMJ: Flight to Quality. This figure shows monthly returns and four-factor alpha of quality minus junk (QMJ) factors. At the end of each calendar month, stocks are assigned to two size-sorted portfolios based on their market capitalization. For U.S. securities, the size breakpoint is the median NYSE market equity. For other markets, the size breakpoint is the 80th percentile by country. We use conditional sorts, first sorting on size, then on quality. Portfolios are value-weighted, refreshed every calendar month, and rebalanced every calendar month to maintain value weights. The QMJ factor return is the average return on the two high-quality portfolios minus the average return on the two low-quality (junk) portfolios. We form one set of portfolios in each country and compute global portfolios by weighting each country’s portfolio by the country’s total (lagged) market capitalization. Panel A reports results from our Long Sample of domestic stocks. The sample period runs from June 1957 to December 2016. Panel B reports results from our Broad Sample of global stocks. The sample period runs from June 1989 to December 2016. Alpha is the intercept in a time-series regression of monthly excess return. The explanatory variables are the monthly returns of the market (MKT), size (SMB), book-to-market (HML), and momentum (UMD) portfolios from Appendix 2. Returns are in U.S. doolars, do not include currency hedging, and excess returns are over the U.S. Treasury bill rate. We plot monthly excess returns and alphas on the y-axes and market excess returns on the x-axes. Market returns indices are either the CRSP-value weighted index (U.S.) or the MSCI-World index (global)
The alphas also reveal a similar pattern of mild flight to quality. At the very least, quality stocks, even after adjustment for their factor loadings, do not appear to perform poorly in periods of extreme market distress; if anything, they tend to deliver higher returns at those times.
Overall, our findings present serious challenges for the risk-based theories (explanation (b) above). Using a variety of factor models ranging from the CAPM to a seven-factor model as our risk adjustment, we show that QMJ factors earn significant abnormal returns. Looking at factor exposures and performance during distressed market conditions, quality stocks appear safer, not riskier, than junk stocks. Of course, alternative risk-based explanations are always possible; such explanations will have to generate these patterns to match the empirical evidence.
5.5 Market (in)efficiency: analysts’ expectations of the price of quality
To test whether the limited explanatory power of quality on price could be driven at least partly by limited efficiency (theory (c) above), we consider the expectations of equity analysts using the methodology of Brav et al. (2005). We consider each analyst’s target price, that is, the expected price 1 yr into the future. As seen in Table 7, target prices scaled by book values are higher for high-quality stocks. In other words, analyst forecasts appear consistent with the idea that high-quality stocks deserve higher prices.
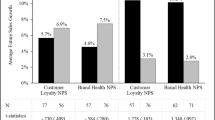
Next, Table 7 and Fig. 4 consider the implied return expectations, computed as the ratio of the target price to the current price minus 1. We see that analysts have lower return expectations for higher-quality stocks than junk stocks. In other words, analyst expectations are inconsistent with the high ex-post realized returns of high-quality stocks.
Expected Returns versus Return Expectations. This figure plots realized returns and return expectations based on I/B/E/S target prices for quality-sorted portfolios. Portfolio P1 contains the stocks with the lowest quality scores, and P10 those with the highest quality scores. Each calendar month, stocks in each country are ranked in ascending order on the basis of their quality score. The ranked stocks are assigned to one of 10 portfolios, where U.S. sorts are based on NYSE breakpoints. For each portfolio, each month we compute the weighted-average target price (scaled by book equity) using the I/B/E/S mean and median consensus for each stock. We report time-series averages of each variable. The implied expected return is given by the ratio of target prices to current prices minus 1. For the global sample, we form one set of portfolios in each country and compute global portfolios by weighting each country’s portfolio by the country’s total (lagged) market capitalization. The sample period of our I/B/E/S target price data runs from March 1999 to December 2016
Analysts’ implied return expectations could reflect that the required return of high-quality stocks is lower than that of junk stocks (because quality stocks are viewed as safer). If so, quality stocks should realize lower returns than junk stocks, or, said differently, quality stocks should have a larger price premium. However, since quality stocks actually realize high risk-adjusted returns, our findings reflect erroneous analyst expectations consistent with theory (c) for our finding that the price of quality is too limited.Footnote 20
Table 7 presents further evidence of analyst bias, which could help explain our results on the price of quality. In particular, we find that analysts are too optimistic about junk stocks on average and much more so than about quality stocks. Further, the dispersion of analyst forecasts is much larger for junk stocks.
As further evidence consistent with the idea of mispricing and limited arbitrage, we show in Table 19 in the Appendix that short-sellers more frequently short junk stocks, relative to quality stocks, and shorting costs are higher for junk stocks.Footnote 21
If the limited price of quality is partly driven by limited market efficiency, then how far off the mark are market prices? This is an important question, but a precise answer is beyond the scope of this paper. To get a sense of magnitudes, we can consider the event-time cumulative five-year abnormal return of QMJ.Footnote 22 Buying quality and shorting junk for 5 yrs earns a cumulative four-factor alpha of 20.85% on average in our U.S. sample (22.04% in the global sample). The cumulative abnormal return can be interpreted as an average underpricing of 10.72% among high-quality stocks and overpricing of 10.72% of junk stocks across the two samples. Of course, this could reflect that some quality stocks are more underpriced while others are less underpriced or even overpriced.
5.6 Linking prices and returns: the price of quality predicts QMJ
We next consider more directly the link between the price of quality and the future returns of QMJ. The theory of limited market efficiency (explanation (c) above) implies that a higher price of quality predicts lower future returns to quality. In other words, when market prices incorporate quality to a larger extent, then the expected return to buying quality is lower. In contrast, theories (a) and (b) do not have clear predictions for the time-variation of risk-adjusted returns.
We first consider how the price of quality varies over time. To study this, Fig. 5 shows the time series of the price of quality, that is, the time series of the Fama-MacBeth regression coefficients that we estimate above in Eq. 8. Specifically, we plot the monthly coefficients from Table 12, columns (1) and (7). We see that the price of quality varies significantly over time. As one might expect, the price of quality is low during the height of the internet bubble in early 2000 and has other large swings during periods consistent with the economics intuition as discussed in the introduction. Figure 11 in the Appendix plots the time series of cross-sectional coefficients for the quality sub-components.
Cross-Sectional Regressions Coefficient, the Price of Quality. This figure plots coefficients from monthly cross-sectional regressions. The dependent variable is the log of a firm’s market-to-book ratio in month t. The explanatory variable is the quality score in month t. We plot the time series of the cross-sectional coefficients
The intuitive pattern of the price of quality suggests that the variation is not just driven by noise. To explore further the variation in the price of quality, it is interesting to link prices and subsequent returns in the time series. Specifically, if this time variation is not due to mis-measurement noise, then a high price of quality should predict low subsequent returns of QMJ. Table 8 provides evidence of such predictability. This table reports the regression coefficients of time-series regressions of future QMJ returns on the ex ante price of quality:
Said simply, QMJt → t + k is the return of QMJ over the future k months, bt − 1 is the lagged price of quality (the variable of interest), and QMJt − 12, t − 1 controls for past returns. Let us describe each of these variables in detail.
We run the regression in two ways: using the excess returns of the QMJ factor on the left-hand side (“Ret-Rf”) and using the alpha of the QMJ factor on the left-hand side (“Alpha”). The future excess return on the raw QMJ factor is computed simply by cumulating returns, \( QM{J}_{t\to t+k}={\prod \limits}_{j=0}^k\left(1+ QM{J}_{t+j}+{r}_{t+j}^f\right)-{\prod \limits}_t\left(1+{r}_{t+j}^f\right) \). To compute the alphas, we regress QMJ on the contemporaneous returns of the market, size, value, and momentum factors and compute the alpha as the regression residual plus the intercept (i.e., as the return of QMJ with its factor exposures hedged out). We then cumulate these alphas \( QM{J}_{t\to t+k}={\prod \limits}_{j=0}^k\left(1+{\alpha}_{t+j}+{r}_{t+j}^f\right)-{\prod \limits}_t\left(1+{r}_{t+j}^f\right) \) and use them on the left-hand side of (11). We consider alphas to ensure that the predictability of the price of quality on QMJ is not driven by any potential predictability of other factors.
The price of quality, bt − 1, is the lagged Fama-MacBeth regression coefficient from Eq. (8) that gives the connection between price and quality at each time. Specifically, the price of quality is estimated from the monthly regressions reported in Table 14, columns (1) and (7). We are interested in testing the hypothesis that a high lagged price of quality predicts lower subsequent returns, that is, bt − 1 < 0.
Last, QMJt − 12, t − 1 is defined as the portfolio-weighted average of the past one-year returns of the stocks in the QMJ portfolio. This captures standard momentum effects, again to ensure that the predictability of the price of quality is a novel finding.
Table 8 reports only the regression coefficient for the variable of interest, bt − 1, the ex ante price of quality. We run overlapping forecasting regressions predicting returns from 1 mo up to 5 yrs. We adjust standard errors for heteroskedasticity and autocorrelation (Newey and West 1987) with a lag length of 5 yrs.
Table 8 shows that a high price of quality indeed predicts lower future returns on QMJ. In our U.S. long sample shown in Panel A, all the coefficients have the expected negative sign, and we can reject the null hypothesis of no predictability in all but one specification. Predictability rises with the forecasting horizon, indicating slowly changing expected returns. The results for our shorter global sample in Panel B are noisier, but we see that all of the statistically significant coefficients are negative as expected. The bottom rows of Table 8 similarly test whether the price of the separate quality characteristics predict the returns of the corresponding long/short factors. While these results are noisier, the estimates tend to be negative, as conjectured.
To summarize, the results in Table 8 are consistent with the hypothesis that the variation of the price of quality is not pure noise but rather reflects changes in the market pricing of quality characteristics, generating variation in QMJ returns.
6 Further asset pricing applications
6.1 Quality at a reasonable price
It is interesting to consider what is the fair price of quality? That is, if we suppose that a stock’s fundamental value V is a multiple of its quality, V = m Quality, then what is the fair value of m? Relatedly, if the market pays a price for quality different from m, then what is the best way to buy cheap quality stocks?
To answer these questions, we construct a long-short portfolio that we call quality at a reasonable price (QARP) as follows. Using the same factor construction as for QMJ, we construct a long-short portfolio based on the signal \( n\ {Quality}_t^i-z\left({P}_t^i\right) \) for various choices of n. That is, QARP is based on a stock’s quality times n, minus its price-to-book (normalized as a z-score). We should get the highest risk-adjusted return if we let n = m, that is, if we base the signal on the quality multiple that corresponds to the true fundamental value. Indeed, in this case, the portfolio is long the highest-alpha securities and short the lowest-alpha securities.Footnote 23
While m is generally unobservable, as we do not know true fundamental values, we can proceed by relying on the fact that we have normalized quality and prices based on the cross-section. Specifically, if the highest-quality stocks were the most expensive, then the quality and price ranks would line up, corresponding to m = 1. When we construct QARP empirically, we do find that the alpha is highest for n close to 1 both in the United States and globally (as seen in Fig. 12 in the Appendix, which plots the monthly alpha of QARP as function of n).
Another way to consider QARP is to simply form a portfolio of quality (QMJ) and value (HML). The combination of QMJ and HML that has the highest Sharpe ratio puts a weight of about 63% on QMJ (and hence the remaining 37% on HML) in the United States and about 62% weight on QMJ globally.
The Sharpe ratio of QARP (whether constructed based on combining signals or combining factor returns) is naturally higher than either quality or value alone, about 0.7 in the United States and 0.9 globally. QARP performs well, as quality strategies complement value by helping an investor avoid the “value trap,” that is, buying securities that look cheap but deserve to be cheap. Instead, QARP buys securities that are cheap, relative to their quality. Our evidence suggests that the return to QARP is above the equity risk premium, which seems to challenge rational risk-based models.
6.2 QMJ on the right-hand-side of a factor model
We have seen that QMJ is an intuitive and powerful factor that has significant alpha, relative to a series of standard factor models. It is also interesting to switch things around and put QMJ on the right-hand-side to see how it affects the alphas and interpretation of the standard factors. More broadly, QMJ is a useful factor to add to the toolbox of global factors, for example, when researchers need to test whether new phenomena are driven by quality.
Table 9 reports the results of regressing each of the SMB, HML, and UMD on the other standard factors, with and without QMJ on the right-hand-side. Let us first consider SMB, that is, the size effect. SMB has a modest, but significant, excess return in our U.S. and global samples. In both, SMB has a small and insignificant alpha when controlling for the other standard factors (the market, HML, and UMD). The size effect is not present in our sample, but controlling for QMJ completely changes this conclusion. SMB has a very large negative exposure to QMJ. Clearly, small stocks are junky. This finding is intuitive, as small stocks could, for instance, be young firms that are yet to be profitable and are more volatile. Moreover, controlling for QMJ, the size effect becomes large and highly significant in both samples. The size effect is alive and well when we account for quality as small stocks outperform large stocks when we compare firms of similar quality (and market beta, value, and momentum exposures). This finding in return space is the analog of the strong size effect for prices that we documented in Table 2. Asness et al. (2018) further analyze the size effect when controlling for quality.
Table 9 further shows that HML has a negative loading on QMJ. This is also intuitive, as cheap stocks (with high book-to-market) are naturally lower quality than expensive stocks. This negative loading implies that controlling for QMJ increases the alpha of HML, strengthening the value effect.
The Appendix contains further tests. Indeed, Tables 20, 21, and 22 analyze different combinations of size (SMB), value (HML), momentum (UMD), investments (CMA), profitability (RMW), and betting against beta (BAB). The results show, for instance, that controlling for quality eliminates the alpha of RMW.
To summarize, quality stocks, despite earning on average higher returns, appear safer, not riskier, than junk stocks in terms of their market, size, and value exposures. As a result, these factors’ alphas increase when we control for quality, since they, too, load negative on QMJ. At the same time, quality can explain other factors, such as RMW, and possibly other factors related to quality or mispricing.
6.3 QMJ: alternative definition based on profitability, growth, safety and payout
Table 23 in the Appendix reports returns of QMJ factors that include an explicit payout component. All our results are robust to this alternative specification. The relevance of payout for asset prices is discussed in footnotes 2 and 12.
7 Conclusion
We define a quality security as one that has characteristics that should command a higher (scaled) price. We present a dynamic valuation model, which shows how stock prices should increase in their quality characteristics, profitability, growth, and safety. We create empirical counterparts of each quality sub-component and quality in general, which are robust and inclusive from across the literature, testing the hypothesis that high-quality firms have higher scaled prices.
Consistent with the theory, we find that high-quality firms do exhibit higher prices, on average. However, the explanatory power of quality on prices is low, leaving the majority of cross-sectional dispersion in scaled prices unexplained. As a result, high quality firms exhibit high risk-adjusted returns. A quality-minus-junk (QMJ) factor that goes long high-quality stocks and shorts low-quality stocks earns significant risk-adjusted returns with an information ratio above 1 (i.e., a Sharpe ratio above 1 after hedging its other factor exposures) in the United States and globally across 24 countries.
Our results are consistent with quality stocks being underpriced and junk stocks overpriced or, alternatively, with quality stocks being riskier than junk stocks. However, while one can never rule out a risk explanation for the high return of quality stocks, we are unable to identify this risk; in anything, we find evidence of the opposite. We show that quality stocks are low beta, and, rather than exhibiting crash risk, they, if anything, benefit from flight to quality, that is, they have a tendency to perform well during periods of extreme market distress. These findings present a challenge for risk-based explanations. To test the mispricing hypothesis, we consider analysts’ expectations. Analysts’ expectations are consistent with the idea that high-quality stocks deserve higher prices. However, analysts expect high-quality stocks to deliver lower returns than junk stocks, contrary to the ex post realized returns. Analysts’ earnings forecasts also suggest errors in expectations that vary systematically with quality. This evidence of systematic analyst errors is consistent with the mispricing hypothesis that the price of quality is too low.
Finally, we show that the price of quality varies over time, generating a time-varying expected return on quality-minus-junk portfolios: a low price of quality predicts a high future return of quality stocks relative to junk stocks.
In summary, we document strong and consistent abnormal returns to quality and do so in a far more inclusive and complete setting than prior papers simultaneously using all quality components implied by our theoretical model. We also tie these results to the cross section and time series of the pricing of quality in novel ways. Our results present an important puzzle for asset pricing: we cannot tie the returns of quality to risk or, in a highly related finding, demonstrate that prices cross-sectionally vary “enough” with quality measures. At this point the returns to quality must be either an anomaly, data mining (incredibly robust data mining, including across countries, size, and periods, and out-of-sample, relative to the first draft of the paper) or the results of a still-to-be-identified risk factor.
Notes
We rewrite the Gordon model simply as \( \frac{P}{B}=\frac{1}{B}\frac{\mathrm{dividend}}{\mathrm{required}\hbox{-} \mathrm{return}-\mathrm{growth}}=\frac{\mathrm{profit}/B\times \mathrm{dividend}/\mathrm{profit}}{\mathrm{required}\hbox{-} \mathrm{return}-\mathrm{growth}} \).
In our more sophisticated dynamic model, payout only comes in implicitly through its effect on residual income, and, based on that model, we focus on residual income (rather than net income) and not explicitly on payout (as we did in an earlier version of this paper). Of course, the timing of dividend payouts does not matter in a frictionless economy in which Modigliani-Miller holds, but a company is more valuable if it can achieve the same stream of profits over its lifetime with a larger payout (since the present value of dividends is higher). Further, the payout (fraction of profits paid out to shareholders) can be seen as a measure of shareholder friendliness if management’s agency problems are diminished when free cash flows are reduced through higher dividends (Jensen (1986)).
Our definition of QARP is a generalization of the so-called growth at a reasonable price (GARP) strategy.
Residual income is often defined as NIt − kBt − 1 where k is the required return on equity, but one should use the risk-free rate rf when the valuation equation is written with a pricing kernel Mt (rather than a required return in the denominator). This can be seen using a simple calculation based on inserting the clean surplus relation into the valuation equation, or see the derivation in appendix and Feltham and Ohlson (1999).
To see this result, suppose first that the firm lowers dividends by 1 at time t, puts the money in risk-free securities, and increases the dividend by (1 + rf)τ at time t + τ. Then, at any time t + s < t + τ, the net income NIt + s increases by the interest income rf(1 + rf)s − 1, and the book value Bt + s − 1 increases by (1 + rf)s − 1, leaving the residual income unchanged. Second, suppose that the firm takes a loan of and invests the money in the risk-free asset at time t. Then, at any time t + s, the income from the risk-free asset cancels the interest payment on the loan, again leaving residual income unchanged. Other changes of dividend policy and capital structure can be seen as combinations of such actions.
Accrual accounting is a method to measure profits at the time when an economic activity happens, rather than when cash is paid or received. Accruals can be used to make reported earnings capture true profits better than pure cash-based measures, but accruals can also be used to artificially boost earnings. For example, see Richardson et al. (2005), who find that “less reliable accruals lead to lower earnings persistence.”
We are using the standard results that \( {\sum \limits}_{\tau =1}^{\infty }{z}^{\tau }=\frac{1}{1-z} \) and \( {\sum \limits}_{\tau =1}^{\infty}\tau {z}^{\tau }=\frac{z}{{\left(1-z\right)}^2} \).
Note that there may be two reasons to adjust for transitory earnings shocks. First, if θ > 0, then va > 0, leading to the adjustment shown in the valuation equation. Second, if we start with net income NIt, then sustainable earnings et is net income adjusted transitory shocks (and cost of capital), et= NIt − at − rfBt − 1.
We include delisting returns when available. If a firm is delisted but the delisting return is missing and the delisting is performance related, we follow Shumway (1997) and assume a − 30% delisting return.
Common stocks are identified by a CRSP share code (SHRCD) of 10 or 11 or by a Compustat issue code (TPCI) of 0. We also drop stocks traded on over-the-counter (OTC) exchanges.
Our tests require at least a five-year history as some of our variables are five-year growth measures.
Growth in residual income increases in the growth in net income and decreases in asset growth, all else equal:
\( \frac{R{I}_t-R{I}_{t-5}}{B_{t-5}}=\frac{N{I}_t-N{I}_{t-5}}{B_{t-5}}-{r}^f\frac{B_{t-1}-{B}_{t-6}}{B_{t-5}}. \)
For example, consider two firms that are equally profitable in terms of NIt and NIt − 5 and have the same starting book value Bt − 5. Further, suppose that firm X pays out all of the profits to shareholders such that its book value stays constant, Bt = Bt − 5, while firm Y keeps all profits in the firm such that its book value increases Bt >> Bt − 5. Then it is more impressive that firm X can deliver the same NI today, since firm Y should have generated some net income from the retained earnings.
The appendix considers a version of QMJ where payout is as a separate factor.
In our sample, the 80th size percentile by country corresponds approximately to NYSE breakpoints.
The data can be downloaded at https://www.aqr.com/library/data-sets.
The data can be downloaded at http://mba.tuck.dartmouth.edu/pages/faculty/ken.french/data_library.html
Using the z-score of the market-to-book on the left hand side as opposed to logs or computing ordinal z-scores by dropping the rank step from the z-score construction does not significally impact any of the results. For brevity, we do not report these additional results.
Table A2 Panel C shows the results of regressing future quality on the current price-to-book as well as a number of control variables. The small positive coefficient shows that market prices do have some predictive power for future quality, consistent with a rational explanation. However, we still need to consider future risk-adjusted returns to fully test the rational theory.
The explanatory variables are the returns of the market (MKT), size (SMB), book-to-market (HML), profitability (RMW), and investment (CMA) portfolios from Fama and French (2015) and the momentum (UMD) portfolio. All the portfolios are from Ken’s French data library. The shorter sample period (July 1963 to December 2016 for the U.S. sample and November 1990 to December 2016 for the global sample) is due to the slightly shorter availability of the data on Ken’s French data library, relative to our sample.
Analysts tend to self-select to cover stocks for which they have relatively optimistic expectations (McNichols and O’Brien 1997) and this overrepresentation of optimistic analysts leads to an upward bias of their forecasts, which could be especially strong for junk stocks that have greater fundamental uncertainty (and hence greater potential dispersion in analyst beliefs). For further analysis of errors in analysts’ target prices and associated mispricing of stocks, see Dechow and You (2017).
We compute the k-month event-time abnormal return αk as the intercept in a regression:
$$ {r}_t^k={\alpha}^k+{\beta}^{MKT}{MKT}_t+{\beta}^{SMB}{SMB}_t+{\beta}^{HML}{HML}_t+{\beta}^{UMD}{UMD}_t+{\varepsilon}_t, $$where \( {r}_t^k={\sum}_i{w}_{i,t-k}{r}_{i,t} \) is excess return in month t of a calendar-time portfolio formed in month t − k. The event-time cumulative abnormal return CAR is given by \( CAR={\sum}_k{\alpha}^k \).
For simplicity consider a two-period model so that the fundamental value is the expected payoff at time 2 discounted at the required return, \( V=\frac{E\left({P}_2\right)}{1+k} \), where k is the required return. The alpha of the security, that is, the expected excess return above the required return is then
$$ \alpha =E\left(\frac{P_2}{P_1}\right)-1-k=\frac{V-{P}_1}{P_1}\left(1+k\right). $$Naturally, the alpha depends on the difference between the fundamental value V and the price P1. Since our measures of quality and price are based on z-scores, we simply subtract the two (rather than dividing by price as above).
Quarterly data is unavailable for countries in our global sample.
References
Acharya, V., & Pedersen, L. H. (2005). Asset pricing with liquidity risk. Journal of Financial Economics, 77, 375–410.
Altman, E. I. (1968). Financial ratios, discriminant analysis and the prediction of corporate bankruptcy. The Journal of Finance, 23(4), 589–609.
Amihud, Y., & Mendelson, H. (1986). Asset pricing and the bid-ask spread. Journal of Financial Economics, 17(2), 223–249.
Ang, A., Hodrick, R., Xing, Y., & Zhang, X. (2006). The cross-section of volatility and expected returns. Journal of Finance, 61, 259–299.
Asness, C., (1994). Variables that explain stock returns. Ph.D. Dissertation, University of Chicago.
Asness, C., & Frazzini, A. (2013). The devil in HML’s detail. Journal of Portfolio Management, 39, 49–68.
Asness, C., Frazzini, A., Israel, R., Moskowitz, T. J., & Pedersen, L. H. (2018). Size matters, if you control your junk. Journal of Financial Economics, 129(3), 479–509.
Baker, M., & Wurgler, J. (2002). Market timing and capital structure. Journal of Finance, 57, 1–32.
Banz, R. W. (1981). The relationship between return and market value of common stocks. Journal of Financial Economics, 9, 3–18.
Berk, J. B. (1995). A critique of size-related anomalies. The Review of Financial Studies, 8(2), 275–286.
Black, F., Jensen, M. C., & Scholes, M. (1972). The capital asset pricing model: Some empirical tests. In M. C. Jensen (Ed.), Studies in the theory of capital markets (pp. 79–121). New York: Praeger.
Brav, A., Lehavy, R., & Michaely, R. (2005). Using expectations to test asset pricing models. Financial Management, 34(3), 31–64.
Campbell, J. Y., & Shiller, R. J. (1988). The dividend-price ratio and expectations of future dividends and discount factors. Review of Financial Studies, 1, 195–228.
Campbell, J. Y., Hilscher, J., & Szilagyi, J. (2008). In search of distress risk. Journal of Finance, 63, 2899–2939.
Carhart, M. M. (1997). On persistence in mutual fund performance. The Journal of Finance, 52(1), 57–82.
Cochrane, J. (2011). Presidential address: Discount rates. The Journal of Finance, 66(4), 1047–1108.
Cohen, R. B., Polk, C., & Vuolteenaho, T. (2003). The value spread. The Journal of Finance, 58, 609–642.
Cohen, R. B., Polk, C., & Vuolteenaho, T. (2009). The price is (almost) right. The Journal of Finance, 64, 2739–2782.
Daniel, K., & Titman, S. (2006). Market reaction to tangible and intangible information. Journal of Finance, 61, 1605–1643.
Dechow, P., & You, H. (2017). Determinants of errors in analysts’ target price implied returns. Working paper, University of Southern California.
Duffie, D., Garleanu, N., & Pedersen, L. H. (2002). Securities lending, shorting, and pricing. Journal of Financial Economics, 66, 307–339.
Fama, E. F., & French, K. R. (1992). The cross-section of expected stock returns. The Journal of Finance, 47(2), 427–465.
Fama, E. F., & French, K. R. (1993). Common risk factors in the returns on stocks and bonds. Journal of Financial Economics, 33, 3–56.
Fama, E. F., & French, K. R. (2006). Profitability, investment and average returns. Journal of Financial Economics, 82, 461–518.
Fama, E. F., & French, K. R. (2015). A five-factor asset pricing model. Journal of Financial Economics, 116, 1–22.
Fama, E. F., & MacBeth, J. D. (1973). Risk, return, and equilibrium: Empirical tests. The Journal of Political Economy, 81, 607–636.
Feltham, G. A., & Ohlson, J. A. (1999). Residual earnings valuation with risk and stochastic interest rates. The Accounting Review, 74(2), 165–183.
Frankel, R., & Lee, C. (1998). Accounting valuation, market expectation, and cross-sectional stock returns. Journal of Accounting and Economics, 25, 283–319.
Frazzini, A., & Pedersen, L. H. (2014). Betting against beta. Journal of Financial Economics, 111(1), 1–25.
George, T. J., & Hwang, C. Y. (2010). A resolution of the distress risk and leverage puzzles in the cross section of stock returns. Journal of Financial Economics, 96, 56–79.
Graham, B., & Dodd, D. L. (1934). Security analysis. New York: McGraw-Hill.
Jegadeesh, N., & Titman, S. (1993). Returns to buying winners and selling losers: Implications for stock market efficiency. The Journal of Finance, 48(1), 65–91.
Jensen, M. C. (1986). Agency costs of free cash flow, corporate finance, and takeovers. The American Economic Review, 76(2), 323–329.
McLean, D., Pontiff, J., & Watanabe, A. (2009). Share issuance and cross-sectional returns: International evidence. Journal of Financial Economics, 94, 1–17.
McNichols, M., & O’Brien, P. C. (1997). Self-selection and analyst coverage. Journal of Accounting Research, 35, 167–199.
Mohanram, P. (2005). Separating winners from losers among low book-to-market stocks using financial statement analysis. Review of Accounting Studies, 10, 133–170.
Newey, W. K., & West, K. D. (1987). A simple, positive semi-definite, heteroskedasticity and autocorrelation consistent covariance matrix. Econometrica, 55(3), 703–708.
Novy-Marx, R. (2012). Quality investing. Working paper, Rochester.
Novy-Marx, R. (2013). The other side of value: The gross profitability premium. Journal of Financial Economics, 108(1), 1–28.
Ohlson, J. A. (1980). Financial ratios and the probabilistic prediction of bankruptcy. Journal of Accounting Research, 18(1), 109–131.
Pástor, L., & Stambaugh, R. F. (2003). Liquidity risk and expected stock returns. Journal of Political Economy, 111(3), 642–685.
Pástor, L., & Veronesi, P. (2003). Stock valuation and learning about profitability. The Journal of Finance, 58(5), 1749–1790.
Penman, S., Richardson, S., & Tuna, I. (2007). The book-to-price effect in stock returns: Accounting for leverage. Journal of Accounting Research, 45(2), 427–467.
Piotroski, J. D. (2000). Value investing: The use of historical financial statement information to separate winners from losers. Journal of Accounting Research, 38, 1–41.
Pontiff, J., & Woodgate, W. (2008). Share issuance and cross-sectional returns. Journal of Finance, 63, 921–945.
Richardson, S., Sloan, R. G., Soliman, M., & Tuna, I. (2005). Accrual reliability, earnings persistence and stock prices. Journal of Accounting and Economics, 39(3), 437–485.
Roll, R. (1984). Orange juice and weather. American Economic Review, 74(5), 861–880.
Roll, R. (1988). R2. Journal of Finance, 43, 541–566.
Shleifer, A., & Vishny, R. W. (1997). The limits of arbitrage. The Journal of Finance, 52(1), 35–55.
Shumway, T. (1997). "The delisting bias in CRSP data." The Journal of Finance 52.1, 327–340.
Sloan, R. G. (1996). Do stock prices reflect information in accruals and cash flows about future earnings? The Accounting Review, 71, 289–315.
Summer, L. H. (1986). Does the stock market rationally reflect fundamental values? The Journal of Finance, 41(3), 591–601.
Vuolteenaho, T. (2002). What drives firm-level stock returns? The Journal of Finance, 57(1), 233–264.
Acknowledgements
We thank Richard Sloan (the editor), Peter Ove Christensen, Antti Ilmanen, Ronen Israel, Johnny Kang, Charles Lee, John Liew, Toby Moskowitz, Per Olsson, Thomas Plenborg, Scott Richardson, Richard Thaler, and Tuomo Vuolteenaho for helpful comments as well as seminar participants at Harvard University, Harvard Business School; University of Bocconi; and conference participants in the NBER Asset Pricing Meeting 2013, the NBER Behavioral Economics Meeting 2013, and the SIFR Institute of Financial Research Conference on Re-Thinking Beta. AQR Capital Management is a global investment management firm, which may or may not apply similar investment techniques or methods of analysis as described herein. The views expressed here are those of the authors and not necessarily those of AQR.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
ESM 1
(XLSX 860 kb)
Appendix 1
Appendix 1
1.1 Variable definitions
In this section, we report details of each variable used on our quality score. Our variables’ definitions are based on Altman (1968); Ohlson (1980); Ang et al. (2006); Daniel and Titman (2006); Penman et al. (2007); Campbell et al. (2008); Novy-Marx (2012); Frazzini and Pedersen (2014); and Asness and Frazzini (2013). Variable names correspond to CRSP and Compustat data items, and we omit the time subscript t for contemporaneous variables. Finally, unless specified, Compustat data items refer to annual items, and time subscripts refer to years. To compute the z-score of a variable x at time t, we rank x cross-sectionally in ascending order
The cross-sectional ranks are rescaled to have a zero cross-sectional mean and a cross-sectional standard deviation of one:
Profitability
We compute a profitability z-score by averaging z-scores of various measures of profitability. For cross-sectional comparisons, we get the same result whether we use our measures of profitability or residual profitability since these measures only differ by the common risk-free rate (but this is not true when we consider growth below).
Specifically, we consider gross profits over assets (GPOA), return on equity (ROE), return on assets (ROA), cash flow over assets (CFOA), gross margin (GMAR), and low accruals (ACC):
GPOA is equal to revenue minus costs of goods sold divided by total assets (REVT − COGS)/AT. ROE is net income divided by book-equity IB/BE. ROA is net income divided by total assets IB/AT. CFOA is net income plus depreciation minus changes in working capital and capital expenditures divided by total assets: (NB + DP − ΔWC − CAPX)/AT. GMAR is revenue minus costs of goods sold divided by total sales: (REVT − COGS)/SALE. ACC is depreciation minus changes in working capital −(ΔWC − DP)/AT. Working capital WC is defined as current assets minus current liabilities minus cash and short-term instruments plus short-term debt and income taxes payable ACT − LCT − CHE + DLC + TXP. Book equity BE is defined as shareholders’ equity minus preferred stock. To obtain shareholders’ equity, we use stockholders’ equity (SEQ), but if it is not available, we use the sum of common equity (CEQ) and preferred stock (PSTK). If both SEQ and CEQ are unavailable, we proxy shareholders’ equity by total assets (AT) minus the sum of total liability (LT) and minority interest (MIB). To obtain book equity (BE), we subtract from shareholders’ equity the preferred stock value (PSTKRV, PSTKL, or PSTK depending on availability).
Growth
We compute a growth z-score by averaging z-scores of various measures of five-year growth in residual profits:
First, we compute growth in residual gross profits over assets [(gpt − rfatt − 1) − (gpt − 5 − rfatt − 6)]/att − 5, where GP = REVT − COGS and lowercase indicates quantities per share. For example, for any accounting measure X, we let x ≡ X/S, using the split-adjusted number of shares outstanding S. Similarly, we compute five-year growth in residual return on equity [(ibt − rfbet − 1) − (ibt − 5 − rfbet − 6)]/bet − 5, five-year growth in residual return over assets [(ibt − rfat − 1) − (ibt − 5 − rfat − 6)]/at − 5, five-year growth in residual cash flow over assets [(cft − rfat − 1) − (cft − 5 − rfat − 6)]/att − 5 where CF = IB + DP − ΔWC − CAPX, and five-year growth in gross margin (gpt − gpt − 5)/salet − 5.
Safety
We compute a safety z-score by averaging z-scores of low beta (BAB), low leverage (LEV), low bankruptcy risk (Ohlson’s O and Altman’s Z), and low earnings volatility (EVOL):
BAB is equal to minus market beta –β. Betas are estimated as in Frazzini and Pedersen (2014) based on the product of the rolling one-year daily standard deviation and the rolling five-year three-day correlations. For correlations, we use three-day returns to account for nonsynchronous trading and a longer horizon because correlations are more stable than volatilities. LEV is minus total debt (the sum of long-term debt, short-term debt, minority interest, and preferred stock) over total assets −(DLTT + DLC + MIBT + PSTK)/AT. We compute Ohlson’s O-Score as
where ADJASSET is adjusted total assets equal to total assets plus 10% of the difference between book equity and market equity AT + .1 ∗ (ME − BE). CPI is the consumer price index. TLTA is equal to book value of debt (DLC + DLTT) divided by ADJASSET. WCTA is current assets minus current liabilities scaled by adjusted assets (ACT − LCT)/ADJASSET . CLCA is current liabilities divided by current assets LCT/ACT. OENEG is a dummy equal to 1 if total liabilities exceed total assets 1(LT > AT) . NITA is net income over assets IB/AT. FUTL is pre-tax income over total liabilities PT/LT. INTWO is a dummy equal to one if net income is negative for the current and prior fiscal year 1(MAX{IBt, IBt − 1} < 0). CHIN is changes in net income, defined as (IBt − IBt − 1)/(|IB|t + |IBt − 1|). Altman’s Z-Score is a weighted average of working capital, retained earnings, earnings before interest and taxes, market equity, and sales, all over total assets:
EVOL is the standard deviation of quarterly ROE over the past 60 quarters. We require at least 12 nonmissing quarters. If quarterly data is unavailable we use the standard deviation of annual ROE over the past 5 yrs, and we require five nonmissing fiscal years.Footnote 24
Quality
We combine the three measures into a single quality score:
Payout
We also compute QMJ factors that include an explicit payout component. We compute a payout z-score by averaging z-scores of net equity issuance (EISS), net debt issuance (DISS), and total net payout over profits (NPOP):
EISS is minus one-year percentage change in split-adjusted number of shares − log(SHROUT _ ADJt/SHROUT _ ADJt − 1 ), where SHROUT _ ADJ is split-adjusted shares outstanding. DISS is minus one-year percentage change in total debt − log(TOTDt/TOTDt − 1), where TOTD is the sum of long-term debt, short-term debt, minority interest, and preferred stock, DLTT + DLC + MIBT + PSTK. NPOP is equal the sum of total net payout (net income minus changes in book equity IB − ΔBE) over the past 5 yrs divided by total profits (RETV − COGS) over the past 5 yrs.
Quality (alternative definition including payout)
We combine the four measures into a single quality score:
1.2 Global factor returns
In this section, we report details of the construction of the market (MKT), size (SMB), book-to-market (HML), and momentum (UMD) portfolios used on the analysis. The data can be downloaded at https://www.aqr.com/library/data-sets/quality-minus-junk-factors-monthly. The portfolio construction follows Fama and French (1993) and Asness and Frazzini (2013). We form one set of portfolios in each country and compute global factor portfolios by weighting each country’s portfolio by the country’s total (lagged) market capitalization. The market factor MKT is the value-weighted return on all available stocks minus the one-month Treasury bill rate. The size, value, and momentum factors are constructed using six value-weighted portfolios formed on size (market value of equity ME) and book-to-market (book equity divided by the most recent market equity BE/ME) and one-year return (return over the prior 12 months, skipping the most recent month). At the end of each calendar month, stocks are assigned to two size-sorted portfolios based on their market capitalization. For U.S. securities, the size breakpoint is the median NYSE market equity. For our international sample, the size breakpoint is the 80th percentile by country. We use conditional sorts, first sorting on size, then on the second variable. Portfolios are value-weighted, refreshed every calendar month, and rebalanced every calendar month to maintain value weights. The size factor SMB is the average return on the three small portfolios minus the average return on the three big portfolios:
The value factors HML is the average return on the two value portfolios minus the average return on the two growth portfolios:
The momentum factor UMD is the average return on the two high return portfolios minus the average return on the two low return portfolios:
Portfolio returns are in U.S. dollars and do not include any currency hedging. Excess returns are over the U.S. Treasury bill rate.
Cross Sectional Regressions Coefficient t-statistics by Industry. This figure plots coefficients from annual Fama-Macbeth regressions within 71 GICS industries. The dependent variable is the log of a firm’s market-to-book ratio in June of each calendar year (date t). The explanatory variables are the quality scores on date t and a series of controls. “Firm size” is the log of the firm’s market capitalization; “one-year return” is the firm’s stock return over the prior year. “Firm age” is the cumulative number of years since the firm’s IPO. “Uncertainty about mean profitability” (Pástor and Veronesi 2003) is the standard deviation of the residuals of an AR(1) model for each firm’s ROE, using the longest continuous series of a firm’s valid annual ROE up to date t. We require a minimum of 5 yrs of nonmissing ROEs. “Dividend payer” is a dummy equal to one if the firm paid any dividends over the prior year. With the exception of the “Dividend payer” dummy, all explanatory variables at time t are ranked cross-sectionally and rescaled to have a zero cross-sectional mean and a cross-sectional standard deviation of one. We plot t-statistics of the quality regression coefficient
QMJ: Cumulative Returns. This figure shows cumulative returns of quality minus junk (QMJ) factors. At the end of each calendar month, stocks are assigned to two size-sorted portfolios based on their market capitalization. For U.S. securities, the size breakpoint is the median NYSE market equity. For other markets, the size breakpoint is the 80th percentile by country. We use conditional sorts, first sorting on size, then on quality. Portfolios are value-weighted, refreshed every calendar month, and rebalanced every calendar month to maintain value weights. The QMJ factor return is the average return on the two high-quality portfolios minus the average return on the two low-quality (junk) portfolios. We form one set of portfolios in each country and compute global portfolios by weighting each country’s portfolio by the country’s total (lagged) market capitalization. Panel A reports results from our Long Sample of domestic stocks. The sample period runs from June 1957 to December 2016. Panel B reports results from our Broad Sample of global stocks. The sample period runs from June 1989 to December 2016. Returns are in U.S. dollars, do not include currency hedging, and excess returns are over the U.S. Treasury bill rate
QMJ: 4-Factor Alphas by Year. This figure plots four-factor adjusted information ratios of quality minus junk (QMJ) factors. For U.S. securities, the size breakpoint is the median NYSE market equity. For other markets, the size breakpoint is the 80th percentile by country. Information ratios are equal to the intercept of a time-series regression of monthly excess return divided by the standard deviation of the estimated residuals. The explanatory variables are the monthly returns of the market (MKT), size (SMB), book-to-market (HML), and momentum (UMD) portfolios from Fig. 7. Returns are in U.S. dollars, do not include currency hedging, and excess returns are over the U.S. Treasury bill rate. We run a separate regression by year. Alphas are annualized
QMJ: Four-Factor Adjusted Information Ratios by Size. This figure plots four-factor adjusted information ratios of quality minus junk (QMJ) factors. For U.S. securities, the size breakpoint is the median NYSE market equity. For other markets, the size breakpoint is the 80th percentile by country. Information ratios are equal to the intercept of a time-series regression of monthly excess return divided by the standard deviation of the estimated residuals. The explanatory variables are the monthly returns of the market (MKT), size (SMB), book-to-market (HML), and momentum (UMD) portfolios from Fig. 7. Returns are in U.S. dollars, do not include currency hedging, and excess returns are over the U.S. Treasury bill rate. Information ratios are annualized
QMJ: Four-Factor Adjusted Information Ratios by Industry. This figure plots four-factor adjusted information ratios of quality minus junk (QMJ) factor within 71 GICS industries. Information ratios are equal to the intercept of a time-series regression of monthly excess return divided by the standard deviation of the estimated residuals. The explanatory variables are the monthly returns of the market (MKT), size (SMB), book-to-market (HML), and momentum (UMD) portfolios from Fig. 7. Returns are in U.S. dollars, do not include currency hedging, and excess returns are over the U.S. Treasury bill rate. Information ratios are annualized
Cross-Sectional Regressions Coefficient, the Price of Quality. This figure plots coefficients from monthly cross-sectional regressions. The dependent variable is the log of a firm’s market-to-book ratio in in month t. The explanatory variables are the quality scores in month t. We plot the time series of the cross-sectional coefficients
Quality at a Reasonable Price (QARP). This figure plots monthly returns of quality at a reasonable price (QARP) factors. QARP factors are constructed as the intersection of six value-weighted portfolios formed on size and price adjusted quality \( n\ {Quality}_t^i-\mathrm{z}\left({\mathrm{P}}_t^i\right) \), where \( \mathrm{z}\left({\mathrm{P}}_t^i\right) \) is the z-score of a firm’s market-to-book and n a constant. At the end of each calendar month, stocks are assigned to two size-sorted portfolios based on their market capitalization. For U.S. securities, the size breakpoint is the median NYSE market equity. For other markets, the size breakpoint is the 80th percentile by country. We use conditional sorts, first sorting on size, then on quality. Portfolios are value-weighted, refreshed every calendar month, and rebalanced every calendar month to maintain value weights. The QARP factor return is the average return on the two high-quality portfolios minus the average return on the two low-quality (junk) portfolios. We form one set of portfolios in each country and compute global portfolios by weighting each country’s portfolio by the country’s total (lagged) market capitalization. The figure reports results from our Long Sample of domestic stocks and from our Broad Sample of global stocks. The long sample period runs from July 1963 to December 2016. The broad sample period runs from June 1990 to December 2016. Returns are in U.S. dollars, do not include currency hedging, and excess returns are over the U.S. Treasury bill rate. Alpha is the intercept in a time-series regression of monthly excess return. The explanatory variables are the returns of the market (MKT) portfolios from Fig. 7. The figures plot the monthly alpha as function of n
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Asness, C.S., Frazzini, A. & Pedersen, L.H. Quality minus junk. Rev Account Stud 24, 34–112 (2019). https://doi.org/10.1007/s11142-018-9470-2
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11142-018-9470-2