Abstract
We examine whether fundamental measures of volatility are incremental to market-based measures of volatility in (i) predicting bankruptcies (out of sample), (ii) explaining cross-sectional variation in credit spreads, and (iii) explaining future credit excess returns. Our fundamental measures of volatility include (i) historical volatility in profitability, margins, turnover, operating income growth, and sales growth; (ii) dispersion in analyst forecasts of future earnings; and (iii) quantile regression forecasts of the interquartile range of the distribution of profitability. We find robust evidence that these fundamental measures of volatility improve out-of-sample forecasts of bankruptcy and help explain cross-sectional variation in credit spreads. This suggests that an analysis of credit risk can be enhanced with a detailed analysis of fundamental information. As a test case of the benefit of volatility forecasting, we document an improved ability to forecast future credit excess returns, particularly when using fundamental measures of volatility.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Fixed income markets are enormous. As of Dec. 31, 2016 over $45 trillion of investment grade bonds were included in the Barclays/Bloomberg Global Aggregate Index (AGG). Out of the AGG, roughly $10 trillion represents bonds issued by investment grade-rated companies from developed markets. In addition, there is about $1.5 trillion of corporate bonds outstanding that have been issued by high yield-rated companies from developed markets. Together, investment-grade and high-yield corporate credits comprise a very large market, and to date, little research has explored the role of fundamental analysis in the context of credit markets.
The key risk in credit markets is default. Investors who are long credit claims are exposed to the risk that the issuer will default before making all of the contractual payments required by the credit instrument. The workhorse model in understanding how the risk of default links to security prices in credit markets is the work of Merton (1974). In this structural model, volatility is arguably the most important primitive variable for determining default risk. While there are many variants of structural models, a theme is that a firm will default if its asset value is below a default threshold at some future point. Thus structural models provide a framework to quantify the probability that a firm will have an insufficient asset value to satisfy its debt commitments. A firm’s closeness to the default threshold is a function of both (i) the expected difference between asset values and debt commitments and (ii) volatility. For a given asset value and capital structure today, higher expected volatility implies a greater probability that future asset values will not cover debt commitments (i.e., a greater chance of default).Footnote 1
Our objective is to conduct a comprehensive empirical analysis of the usefulness of market-based and fundamental-based measures of volatility from the perspective of a credit investor. The FASB recognizes the potential usefulness of fundamental information contained in general purpose financial reports for both equity and debt investors. We focus on the latter group. While there is a rich literature examining how accounting data can be used to help forecast corporate bankruptcy and default (e.g., Beaver 1966; Altman 1968; Ohlson 1980; Beaver et al. 2005; Bharath and Shumway 2008; Campbell et al. 2008; Correia et al. 2012), there is scant analysis of how fundamental measures of risk can be used to improve credit-related investment decisions. Most of these studies use a mix of fundamental and market-based variables to predict bankruptcy, but a theme in this research is the central importance of market-based measures of volatility. A recent notable exception is the work of Konstantinidi and Pope (2016), who document that quantile-based forecasts of the risks embedded in accounting rates of return can help explain credit ratings and spreads. Our focus is on whether information from the accounting system could be additive to market-based measures of volatility in helping investors in the credit markets quantify default risk and how that risk is priced. While it is clear that measuring asset volatility is key for credit markets, it is ultimately an empirical question as to whether and how measures of asset volatility derived from financial statement data can be additive to market-based measures of asset volatility. At a minimum, the information contained in historical volatility of fundamentals (e.g., accounting rates of return) differs from market-based measures. Financial statements are prepared under modified historical cost accounting (not full mark to market). Penman (2016) suggests that the unconditional conservatism built into financial reporting creates the possibility of risk to be reflected in the outputs of that system. It is volatility in these outputs that we examine.
We source our market-based measures of asset volatility from traded security prices in secondary markets. We derive several measures of historical asset volatility, ranging from a simple deleveraging of historical equity volatility to a complete measure that uses historical equity and credit return volatilities and historical return correlations (e.g., Schaefer and Strebulaev 2008). We also combine forward-looking market information using the implied volatility from at-the-money put and call options. Our fundamental-based measures of volatility are obtained from the primary financial statements and are designed to capture fundamental volatility in unlevered profitability. We use a wide range of fundamental volatility measures, including (i) historical volatility in profitability, margins, turnover, operating income growth, and sales growth; (ii) dispersion in analyst forecasts of future earnings; and (iii) quantile regression forecasts of the interquartile range of the distribution of profitability (e.g., Konstantinidi and Pope 2016).
Our empirical analysis is comprised of three main sections. First, we examine the relative importance of market- and fundamental-based measures of asset volatility to forecast (out-of-sample) bankruptcy and default. For a large sample of U.S. firms from 1989 to 2012 using traditional discrete-hazard modelling and classification and regression trees (CART) methodology, which allows for nonlinear and interactive associations between probability of default and different explanatory variables, we find that combining information about volatility from market and fundamental sources improves forecasts of corporate bankruptcy. Our bankruptcy prediction models are superior to the standard models in at least two respects. First, we demonstrate improvement in out-of-sample classification accuracy, which is typically not reported (e.g., Altman 1968; Ohlson 1980; Bharath and Shumway 2008; Campbell et al. 2008). Second, we show that combining multiple measures of volatility generates superior forecasts, relative to prevailing bankruptcy forecasting models (e.g., Campbell et al. 2008).
Second, we assess the relative importance of market- and fundamental-based measures of asset volatility to explain cross-sectional variation in credit spreads. Assuming markets are reasonably efficient with respect to the usefulness of market- and fundamental-based measures of volatility in forecasting (out-of-sample) bankruptcies, these measures should also help explain variation in credit spreads. Using traditional unconstrained linear regression analysis and CART, which allows for various nonlinear and interactive effects, we find that combining market- and fundamental-based volatility estimates improves explanatory power of cross-sectional credit spreads, although the market-based measures appear to dominate fundamental measures. This analysis is robust to a broad cross-section of corporate bond spreads from 1992 to 2012 as well as CDS spreads from 2004 to 2012. We extend this analysis by using market- and fundamental-based measures of asset volatility within the structural model of Merton (1974). This constrained use of asset volatility significantly improves our ability to explain cross-sectional variation in credit spreads. This is because the relation between leverage and asset volatility and default risk and hence credit spreads is inherently nonlinear. For the constrained analysis, we continue to find robust evidence that combining market- and fundamental-based volatility estimates improves explanatory power of cross-sectional credit spreads, but again the market-based measures appear to dominate.
Third, we explore the relative importance of market- and fundamental-based measures of asset volatility to forecast future credit excess returns. We undertake this analysis given the somewhat surprising result from our first two sets of analyses. In the first set of empirical tests, we find that both market- and fundamental-based measures of asset volatility are important to forecast bankruptcy, but in our second set of analyses, market-based measures tend to dominate. This raises the possibility that credit markets are not paying enough attention to fundamental-based measures. Using the regression framework from Correia et al. (2012), we assess whether measures of credit risk mispricing (the difference between observed credit spreads and modelled credit spreads using either market- or fundamental-based measures of asset volatility) help predict credit excess returns. If the market is not paying enough attention to fundamental measures of asset volatility, we would expect to see measures of credit risk mispricing based on fundamental asset volatility better predict credit excess returns. Using a large sample of corporate bonds from 1996 to 2012, we find results consistent with this hypothesis.
Overall, our paper fits into the broad default forecasting literature and the more recent literature linking fundamental analysis to asset pricing attributes from the credit market (both spreads and returns). The paper also relates, more broadly to the risk ratings (e.g., Liu et al. 2007) and to the credit ratings literatures (e.g., Kraft 2014). Our results speak to the relevance of fundamental analysis from the perspective of a credit investor. While our focus is on measuring asset volatility using fundamental information, there are additional aspects of financial statement information that also matter from the perspective of a credit investor, including measuring different aspects of leverage: on and off balance sheet financial leverage as well as operating leverage. Given the growing size and importance of credit markets globally, we hope that future research can continue to explore the relevance of financial statement information for credit valuation.
The rest of the paper is structured as follows. Section 2 describes our sample selection and research design. Section 3 presents our empirical analysis and robustness tests, and section 4 concludes.
2 Sample and research design
2.1 Secondary credit market data
Our analysis is based on a comprehensive panel of U.S. corporate bond data, which includes all the constituents of (i) Barclays U.S. Corporate Investment Grade Index and (ii) Barclays U.S. High Yield Index. The data includes monthly returns and bond characteristics from September 1988 to February 2013. We exclude financial firms with SIC codes between 6000 and 6999.
2.2 Representative bond
Given that corporate issuers often issue multiple bonds and that our analysis is directed at measuring asset volatility of the issuer, we need to select a representative bond for each issuer. To do this, we follow the criteria of Haesen et al. (2013). We repeat this exercise every month for our sample period. The criteria used for identifying the representative bond are selected so as to create a sample of liquid and cross-sectionally comparable bonds. Specifically, we select representative bonds on the basis of (i) seniority, (ii) maturity, (iii) age, and (iv) size.
First, we filter bonds by seniority. Because most companies issue the majority of their bonds as senior debt, we select only bonds corresponding to the largest rating of the issuer. To do this, we first compute the amount of bonds outstanding for each rating category for a given issuer. We then keep only those bonds that belong to the rating category that contains the largest fraction of debt outstanding. These bond tends to have the same rating as the issuer. Second, we then filter based on maturity. If the issuer has bonds with time to maturity between 5 and 15 years, we remove all other bonds for that issuer from the sample. If not, we keep all bonds in the sample. Third, we then filter based on time since issuance. If the issuer has any bonds that are at most two years old, we remove all other bonds for that issuer. If not, we keep all bonds from that issuer in the sample. Finally, we filter based on size. Of the remaining bonds, we pick the one with the largest amount outstanding.Footnote 2
Our resulting sample includes 121,300 unique bond-month observations, corresponding to 5362 bonds issued by 1504 unique firms. Table 1 Panel A shows the industry composition of the sample, using Barclays Capital’s industry definitions. Approximately 35% of the sample firms are consumer products firms. Capital goods firms and basic industry make up another 20% of the sample. Sample bonds have an average option-adjusted spread (OAS) of 3.31% over the sample period and an average option adjusted duration of 5.16 years (Table 1, Panel B). Appendix I defines these variables as well as other variables used in the paper in more detail.
2.3 Measures of asset volatility
2.3.1 Historical market data
We calculate historical equity volatility using the annualized standard deviation of CRSP realized daily stock returns over the past 252 days, σE. We combine historical credit and equity market data to obtain our first measure of asset volatility, \( {\upsigma}_{\mathrm{A}}^{\upomega} \):
where ω is the ratio of the market value of the firm’s equity to the total firm value, σ D is the annualized standard deviation of total monthly bond returns, and ρ D, E is an estimate of the historical correlation between equity and bond returns. Note that, while our selection of a representative bond can change each month for a given issuer, our correlation and volatility measures hold a given bond fixed when looking back in time.
Table 1 Panel B presents descriptive statistics for the variables used to compute asset volatility. Sample firms have an average market leverage of approximately 36% (1–0.6348) and exhibit an average correlation between equity and debt returns ρD, E of 0.2194.
2.3.2 Forward-looking market data
We obtain Black-Scholes implied volatility estimates for at-the-money 91-day options from the OptionMetrics Ivy DB standardized database.Footnote 3 We average the implied volatility for a 91-day put and call option. Based on this implied equity volatility, σI, we compute \( {\upsigma}_{\mathrm{AI}}^{\upomega} \), using the approach in (1). Option implied volatility has been shown to have incremental power with respect to historical volatility in explaining time-series and cross-sectional variation in credit spreads (Cremers et al. 2008b; Cao et al. 2010).
2.3.3 Fundamental data
Following Penman (2014), we use return on net operating assets (RNOA) as the measure of unlevered (or enterprise) profitability. For each quarter, we compute RNOA as operating income (OIADPQ) to average net operating assets (NOA) during the quarter.
We construct a simple fundamental volatility measure, σF, based on the historical volatility of quarterly RNOA, which we then average across fiscal quarters to remove the effects of seasonality. Specifically, we compute σF as:
where Std k (RNOA itk ) is the standard deviation of RNOA for quarter k calculated over the previous 20 quarters, requiring a minimum of 10 quarters of data. We annualize σ F , by multiplying the average standard deviation by \( \sqrt{4} \).
Our second fundamental volatility measure, σIQR, is based on an estimate of the interquartile range of the distribution of profitability, which is obtained using a quantile regression approach (Konstantinidi and Pope 2016). This approach, which is described in detail in Appendix III, has the advantage of not requiring time series data for computation as it relies only on cross-sectional fundamental characteristics.
Our third fundamental volatility measure is based on the dispersion of analysts’ earnings forecasts. The dispersion of analysts’ earnings forecasts may be regarded as a proxy for future earnings (fundamental) uncertainty. We obtain the standard deviations of analyst EPS forecasts for the following two fiscal years (\( {\upsigma}_{{\mathrm{FEPS}}_1} \), \( {\upsigma}_{{\mathrm{FEPS}}_2} \)) from the IBES Summary database and compute a weighted average standard deviation as follows:
where α is the number of months to the end of the current fiscal year divided by 12.
Based on the Dupont decomposition of profitability into profit margin and asset turnover, we further compute the volatility of operating margins (the ratio of operating income to sales) and asset turnover (the ratio of sales to total assets). Similarly to σF, these volatilities, σMARGIN and σTURNOVER, represent an average of quarter-specific volatilities. We calculate two additional fundamental volatility measures, the volatility of operating income growth (σOI GROWTH) and the volatility of sales growth (σSALES GROWTH). Operating income (sales) growth is defined as the percentage change in operating income (sales), relative to the same quarter of the previous year.
2.3.4 Correlations across volatility measures
Table 1 Panel C reports descriptive statistics for the different volatility measures. We winsorize all volatility measures at the 1st and 99th percentile values of their respective distributions. These measures exhibit differences in scale. We discuss how we deal with differences in scale when using different measures of asset volatility to derive implied credit spreads in section 3.2.2.
Panel D of Table 1 reports the average monthly pairwise correlations across volatility measures. Historical equity volatility, σE, is highly correlated with implied volatility, σI, (0.8814 (0.9005) Pearson (Spearman) correlation). The Pearson (Spearman) correlation between these equity volatility measures and debt volatility, σD, ranges between 0.4329 and 0.4878 (0.3064 and 0.3377), respectively. As a result, the correlations between weighted asset volatilities and the corresponding equity volatility measures are, on average, lower than 0.75. The Pearson (Spearman) correlations among the different fundamental volatility measures range from −0.0670 to 0.6717 (−0.2007 to 0.6161) and average 0.2152 (0.2237). Pairwise Pearson (Spearman) correlations between fundamental- and market-based asset volatility measures (\( {\upsigma}_{\mathrm{A}}^{\upomega},{\upsigma}_{\mathrm{A}\mathrm{I}}^{\upomega}\ \Big) \) average 0.2042 (0.2317).
2.4 Bankruptcy data and distance to default
We estimate the probability of bankruptcy based on a large sample of Chapter 7 and Chapter 11 bankruptcies filed between 1980 and the end of 2012. We combine bankruptcy data from four main sources: Beaver et al. (2012)Footnote 4; the New Generation Research bankruptcy database (bankruptcydata.com); Mergent FISD; and the UCLA-Lo Pucki bankruptcy database.
We use a discrete time-hazard model and include three types of observations in the estimation: nonbankrupt firms, years before bankruptcy for bankrupt firms, and bankruptcy years (Shumway 2001). Our dependent variable equals 1 if a firm files for bankruptcy within one year of the end of the month and zero otherwise. We keep the first bankruptcy filing and remove from the sample all months after this filing.
Following Correia et al. (2012), we use quarterly financial data to compute the default barrier and update market data on a monthly basis to obtain monthly estimates of the probabilities of bankruptcy. Market variables are measured at the end of each month, and accounting variables are based on the most recent quarterly information reported before the end of the month. We winsorize all independent variables at 1% and 99%. We ensure that all independent variables are observable before the declaration of bankruptcy. Furthermore, to ensure that prediction is made out of sample and to avoid a potential bias of ex post over-fitting the data, we estimate coefficients using an expanding window approach. We convert the different scores into probabilities as follows: Prob = escore/1 + escore. All of the models are nonlinear transformations of various fundamental and market data.
The primary regression model for estimating bankruptcy over the next 12 months is as follows:
\( \ln \left(\frac{V_{it}}{X_{it}}\right) \) is a measure of dollar distance to default barrier (akin to an inverse measure of leverage). We compute V it as the sum of the market value of the firm’s equity and the book value of debt. We compute our default barrier, X it , as the sum of short-term debt (DLCQ) and half of long-term debt (DLTTQ) as reported at the most recent fiscal quarter (e.g., Bharath and Shumway 2008). Exret it is the excess equity return over the value-weighted market return over the previous 12 months. ln(E it ) is the logarithm of the market value of equity measured at the start of the forecasting month. P 5, it is an estimate of the 5th percentile of the distribution of RNOA. It is calculated as described in Appendix III, using the quantile regressions employed by Konstantinidi and Pope (2016). P 5, it is a measure of left-tail risk in profitability. Skew it is an estimate of the skewness of the distribution of RNOA. Following Konstantinidi and Pope (2016), we estimate skewness as \( \frac{\left({P}_{75}-{P}_{50}\right)-\left({P}_{50}-{P}_{25}\right)}{IQR} \), where IQR is the interquartile range (P 75 − P 25). Accordingly, Skew it ranges between −1 and 1 and is zero when the distribution of RNOA is symmetric within the interquartile range. Kurt it is an estimate of the kurtosis of the distribution of RNOA, estimated following Konstantinidi and Pope (2016) as \( \frac{\left({P}_{87.5}-{P}_{62.5}\right)+\left({P}_{37.5}-{P}_{12.5}\right)}{IQR} \). σ k, it is the respective measure of asset volatility as defined in section 2.3. The choice of independent variables is based on the Merton model of credit spreads to which we add a measure of left-tail risk. We estimate equation (4) using various combinations of our measures of asset volatility over different samples to assess the relative importance of market-based and fundamental-based measures of asset volatility in the context of forecasting bankruptcy.
Our priors for equation (4) are as follows. (i) \( \ln \left(\frac{{\mathrm{V}}_{\mathrm{it}}}{{\mathrm{X}}_{\mathrm{it}}}\right) \) is expected to be negatively associated with bankruptcy likelihood (the further the market value of assets is from the default barrier the lower the likelihood of hitting that barrier in the next 12 months). (ii) Exretit is expected to be negatively associated with bankruptcy likelihood (assuming there is information content in security prices, decreases in security prices should be associated with increased bankruptcy likelihood). (iii) ln(Eit) is expected to be negatively associated with bankruptcy likelihood (large firms offer better diversification and better realizations of asset values in the event of default). (iv) P 5, it is expected to be negatively associated with bankruptcy likelihood (the higher the 5th percentile of the RNOA distribution, the lower the probability that asset value will fall below the book value of debt). (v) Skew it is expected to be negatively associated with bankruptcy likelihood (the more negatively skewed the distribution of earnings, the higher the likelihood the asset value will fall below the book value of debt). (vi) Kurt it is expected to be positively associated with bankruptcy likelihood (higher kurtosis indicates that the density of the tails of the distribution is higher than what would be expected under a normal distribution). (vii) σk, it is expected to be positively associated with bankruptcy likelihood (the greater the volatility of the asset value the greater the chance of passing through the default barrier).
In an alternative specification, we also control for the level of option-adjusted spreads (OAS it ) as a market based measure of credit risk. To the extent that credit market participants incorporate fundamental volatility in assessing credit risk, OAS it could subsume the fundamental volatility measures.
2.5 Credit spreads
Given that a measure of asset volatility is useful in forecasting bankruptcy and under the assumption that security prices in the secondary credit market are reasonably efficient, we also test how different combinations of measures of asset volatility can explain cross-sectional variation in credit spreads. We view the analysis of credit spreads as supporting evidence for assessing the information content of fundamental- and market-based measures of asset volatility.
We do this via two approaches. First, we estimate an unconstrained cross-sectional regression where we include multiple measures of determinants of credit spreads in a linear model. Second, we estimate a constrained cross-sectional regression where we combine our various measures of asset volatility into measures of distance to default, which are in turn mapped to an implied credit spread following the approach of Crouhy et al. (2000); Kealhofer (2003); and Arora et al. (2005). A benefit of the constrained approach is that it combines the dollar distance to default, \( \ln \left(\frac{{\mathrm{V}}_{\mathrm{it}}}{{\mathrm{X}}_{\mathrm{it}}}\right) \), with measures of asset volatility, σk, it, to better identify closeness to the default threshold. An unconstrained regression cannot capture the inherent nonlinear relations between leverage, asset volatility, defaults (bankruptcy), and credit spreads.
For the unconstrained approach, we estimate the following regression model.
OASit is the option-adjusted spread for the respective bond as reported in the Barclays Index. An intercept is not reported as we include time fixed effects. In addition to the determinants of bankruptcy, i.e., \( \ln \left(\frac{{\mathrm{V}}_{\mathrm{it}}}{{\mathrm{X}}_{\mathrm{it}}}\right) \), Exretit, ln(Eit), P5, it , Skew it , Kurt it , and σk, it, which are all issuer-level determinants of credit risk, we also include issue-specific determinants of credit risk and liquidity that will influence the level of credit spreads. Specifically, our additional controls include (i) Ratingit, the issue-specific rating (higher rated issues are expected to have higher credit spreads, given that we code ratings to be increasing in risk), (ii) Ageit, the time since issuance in years (liquidity is decreasing for progressively off-the-run securities, so we expect credit spreads to be increasing in time since issuance), and (iii) Durationit, the option-adjusted duration of the issue (for the vast majority of corporate issuers the credit term structure is upward sloping so we expect credit spreads to increase with duration; see Helwege and Turner 1999).
For the constrained approach, we then estimate the following regression model.
\( {\mathrm{CS}}_{\upsigma_{\mathrm{k},\mathrm{it}}} \) is the theoretical credit spread for the kth measure of asset volatility. The estimation of theoretical credit spreads entails six main steps (which are described in detail in Appendix II). (1) We standardize each asset volatility measure and match its moments to the moments of weighted historical asset volatility, \( {\sigma}_A^{\omega } \). (2) We construct estimates of distance to default, based on each asset volatility measure. (3) We empirically map each distance-to-default measure to our bankruptcy data, using a discrete time hazard model to generate a forecast of physical bankruptcy probability (see equation (A.1) of Appendix II).Footnote 5 (4) We compute a cumulative physical bankruptcy probability by cumulating default probabilities over the duration of the bond. (5) We convert each cumulative physical probability measure into a risk-neutral measure, by adding a risk-premium (see equation (A.2) of Appendix II). (6) Based on this risk-neutral measure and the expected recovery rate (which is assumed to be constant), we calculate theoretical credit spread as in equation (A.3).
We obtain a different theoretical credit spread for each asset volatility measure. We estimate two additional credit spreads, \( {\mathrm{CS}}_{\upsigma_{\mathrm{AVG}}} \)and \( {\mathrm{CS}}_{{\mathrm{PROB}}_{\mathrm{AVG}}} \), based on the combination of our seven fundamental volatility measures (i.e., σF, σIQR, σFEPS, σMARGIN, σTURNOVER, σOI GROWTH, σSALES GROWTH). \( {\mathrm{CS}}_{\upsigma_{\mathrm{AVG}}} \) and \( {\mathrm{CS}}_{{\mathrm{PROB}}_{\mathrm{AVG}}} \) differ in the way in which the different volatilities are combined. To obtain \( {\mathrm{CS}}_{\upsigma_{\mathrm{AVG}}} \), we take the average of the seven fundamental volatility measures after step (1) above (i.e., after matching their respective moments to \( {\upsigma}_{\mathrm{A}}^{\omega } \)). We then follow steps (2) to (6), using this average as a measure of fundamental volatility. In contrast, to calculate \( {\mathrm{CS}}_{{\mathrm{PROB}}_{\mathrm{AVG}}} \), we first follow steps (1) to (3) to obtain estimates of the physical default probabilities corresponding to each of the seven fundamental volatility measures. We then take the average of these physical default probabilities and follow steps (4) to (6) based on this average. The average monthly correlation between \( {\mathrm{CS}}_{\upsigma_{\mathrm{AVG}}} \) and \( {\mathrm{CS}}_{{\mathrm{PROB}}_{\mathrm{AVG}}} \) is above 0.9 (Table 1 Panel E).
\( {\mathrm{CS}}_{\upsigma_{\mathrm{AVG}}} \) and \( {\mathrm{CS}}_{{\mathrm{PROB}}_{\mathrm{AVG}}} \) exhibit an average Pearson (Spearman) correlation with market-based credit spreads (\( {\mathrm{CS}}_{\upsigma_{\mathrm{A}}^{\upomega}},{\mathrm{CS}}_{\upsigma_{\mathrm{A}\mathrm{I}}^{\upomega}} \)) of 0.7740 (0.5938) and an average Pearson (Spearman) correlation of 0.7172 (0.6165) with observed credit spreads. The high correlation with OAS suggests that our structured use of leverage and asset volatility as outlined in Appendix II is an effective way to aggregate market and fundamental information for credit valuation purposes.
Theoretical spreads based on historical security data or option-implied volatility exhibit a higher correlation with observed spreads than theoretical spreads based on fundamental accounting data. In particular, OAS exhibits an average Pearson (Spearman) correlation with market-based spreads (\( {\mathrm{CS}}_{\upsigma_{\mathrm{A}}^{\upomega}},{\mathrm{CS}}_{\upsigma_{\mathrm{A}\mathrm{I}}^{\upomega}} \)) of 0.7664 (0.6946) and an average Pearson (Spearman) correlation with accounting-based spreads (\( {\mathrm{CS}}_{\upsigma_{\mathrm{AVG}}} \), \( {\mathrm{CS}}_{{\mathrm{PROB}}_{\mathrm{AVG}}} \)) of 0.7172 (0.6165). Also note that \( {\mathrm{CS}}_{\upsigma_{\mathrm{AVG}}} \) and \( {\mathrm{CS}}_{{\mathrm{PROB}}_{\mathrm{AVG}}} \)exhibit stronger correlations with OAS than \( {\mathrm{CS}}_{\upsigma_{\mathrm{F}}} \). (The Pearson (Spearman) correlation between \( {\mathrm{CS}}_{\upsigma_{\mathrm{F}}} \) and OAS is 0.6288 (0.5781)). This suggests that there is value to conducting a deeper financial statement analysis and combining different fundamental volatility measures.
3 Results
3.1 Bankruptcy forecasting
Table 2 reports the estimation results of regression equation (4). The sample size used for the basis of estimating equation (4) is 81,802 bond-month observations (in specifications with σI the sample is reduced to 61,132 observations, as σI is only available from 1996 onward). The sample is further reduced in specifications that include σFEPS and hence require availability of IBES data.
Across all specifications, we find expected relations for our primary determinants: bankruptcy likelihood is decreasing in (i) distance to default barrier, \( \ln \left(\frac{{\mathrm{V}}_{\mathrm{it}}}{{\mathrm{X}}_{\mathrm{it}}}\right) \), (ii) recent equity returns, Exretit, and (iii) firm size, ln(Eit). The coefficients on P5, it, Skew it , and Kurt it are insignificant across most specifications. To assess the relative importance of our different measures of asset volatility, we first examine each measure individually after controlling for the same-issuer-level determinants of bankruptcy. Across models (1) to (6) in Table 2, we find that all of the measures of asset volatility are significantly positively associated with the probability of bankruptcy.
To provide a sense of the relative economic significance across the different measures of asset volatility, we report in Panel B of Table 2 the marginal effects for each explanatory variable. Specifically, we hold each explanatory variable at its average value and report the change in probability of bankruptcy for a one standard deviation change in the respective explanatory variable, relative to the full sample unconditional probability of bankruptcy. For example, column (1) in Panel B of Table 2 states that the marginal effect of σE is 0.0110. This means that a one standard deviation change in σE is associated with a 1.1% increase in bankruptcy probability, relative to the full sample unconditional probability of bankruptcy (0.80%). Comparing marginal effects across explanatory variables reveals that the distance to default barrier is the most economically important explanatory variable. Individually, the most important measure of asset volatility is σI (marginal effect of 0.0531 is the largest in the first 6 columns of Panel B of Table 2).
Models (7) to (14) in Panel A combine different measures of asset volatility. We do not include σE and σI in the same specification due to multi-collinearity (Panel D of Table 1 shows that σE and σI have a parametric correlation of 0.8814). In model (7), we start with issuer-level determinants (\( \ln \left(\frac{{\mathrm{V}}_{\mathrm{it}}}{{\mathrm{X}}_{\mathrm{it}}}\right) \), Exretit, ln(Eit), P 5, it , Skew it , and Kurt it ) and σE. We then add a measure of volatility from the credit markets, σD. Combining market-based measures of asset volatility from the equity and credit markets is superior to examining equity market information alone. (The pseudo-R2 marginally increases from 39.22% in model (1) to 39.84% in model (7) and from 28.52% in model (2) to 28.53% in model (11).) However, the coefficient on σD is not statistically significant when σD is combined with σ I in model (11). In model (8), when we add our first measure of fundamental volatility, σF, we find that both σD and σF are significantly associated with bankruptcy but σE is not. When σF is added to σI and σD in model (12), σI and σF are significant but σD is not. Using the interquartile range of the RNOA distribution and the dispersion of analyst forecasts as measures of fundamental volatility in models (9) and (13) and in models (10) and (14), respectively, we find similar results: combining measures of volatility from market and fundamental sources improves explanatory power of bankruptcy prediction models. While we do not run a horse-race between the fundamental volatility measures, we believe this could be an interesting avenue for future research. In an untabulated robustness analysis, we document further that our fundamental volatility measures also improve upon the explanatory power of a bankruptcy prediction model that includes Merton-based volatility and leverage measures (e.g., Bharath and Shumway 2008). This approach takes equity prices, equity volatility, and current leverage as given and then solves iteratively for asset value and asset volatility that price equity as a call option on the asset value of the firm.
In Panel C, we add a control for the spread level, OAS. We find that OAS subsumes σE and σD, which both cease to be significant in models (1) and (3). Fundamental volatility measures remain significant, both when included by themselves (models (4) to (6)) and when combined with σE, σI and σD (models (8) to (10) and (12) to (14)). Interestingly, the marginal effects reported in panel D of Table 2 reveal that, after controlling for credit spreads, the difference in the relative importance of market-based and fundamental-based measures is more muted. For example, in models (12) to (14) σF, σIQR and σFEPS have similar importance to the market-based measures. The fact that σF, σIQR and σFEPS remain significant, after controlling for OAS could be consistent with the market not paying enough attention to fundamental measures of asset volatility.
In Table 3, we start with a model that includes σI, σD, and σF, in column (1).Footnote 6 We then replace σF by the volatility of operating profit margins, σMARGIN, and the volatility of asset turnover, σTURNOVER, in the spirit of the Dupont profitability decomposition. The Pearson (Spearman) correlation between σMARGIN and σTURNOVER volatility is 0.0087 (−0.1665) (Table 1 Panel C). When we include both σMARGIN and σTURNOVER in equation (4), we find that σTURNOVER is marginally significant but σMARGIN is not (column (2)). We obtain similar results when we control for OAS in column (5)). The volatility of operating income growth σOI GROWTH is significant in both specifications (columns (3) and (6)). In unreported analysis, we find similar results with the volatility of sales growth, σSALES GROWTH, but due to its high correlation with σOI GROWTH we do not report these results separately.
One limitation with the traditional discrete hazard model analysis is that it cannot capture nonlinearities and interactions that are likely among the independent variables. As an alternative methodological approach, we analyze our default data using the classification and regression trees methodology developed by Breiman et al. (1984).Footnote 7 Frydman et al. (1985) apply this technique to the prediction of financial distress and document that it outperforms discriminant analysis in out-of-sample tests. The data is recursively split into more homogeneous subsets, using the Gini rule to choose the optimal split at each node of the tree. Based on this approach, we generate a maximal tree and a set of sub-trees. We then use tenfold cross validation to estimate the area under the receiver operating characteristic curve (i.e., AUC) for the different sub-trees and retain the minimal cost tree. The resulting tree structure allows for nonlinear and interactive associations between probability of default and the different explanatory variables, alleviating the concern that documented results are simply due to method variance.
To focus on the relative importance of accounting- and market-based measures of asset volatility, we first apply this technique to a basic set of bankruptcy determinants, i.e., \( \ln \left(\frac{{\mathrm{V}}_{\mathrm{it}}}{{\mathrm{X}}_{\mathrm{it}}}\right) \), Exretit, ln(Eit), P5, it , Skew it , Kurt it and a representative market-based measure of asset volatility that combines information from implied equity option data and debt market volatility, \( {\upsigma}_{\mathrm{AI}}^{\upomega} \). The CART estimation does not pose the same multicollinearity issues as the discrete hazard model estimation reported in Tables 2 and 3, and therefore we can include all asset volatility measures simultaneously in the model. We thus augment the set of bankruptcy predictors with our seven fundamental volatility measures: σF, σIQR, σFEPS, σMARGIN, σTURNOVER, σOI GROWTH, σSALES GROWTH.
Panel A of Table 4 reports summary statistics for the predictive ability of the resulting trees. Column (1) serves as the benchmark case where no fundamental-based measures of asset volatility are included. Comparing columns (1) and (2), it is clear that the test-sample (out-of-sample) AUC improves with the inclusion of fundamental-based measures of asset volatility. Note that the test-sample AUC for the augmented model is 0.9337, while the test-sample AUC for the basic model that only includes market volatility is 0.9215. We use bootstrap resampling to test the statistical significance of improvement in AUC. In particular, we construct 100 bootstrap samples and apply CART to each of these samples, thus building 100 different trees for each set of variables. We then compute the difference between the AUC of each of the augmented models and the AUC of the basic model. The 5th percentile of this difference is positive for the augmented model (column (2)), indicating that the improvement in the AUC achieved by incorporating the fundamental volatility measures is statistically significant at conventional levels. The relative cost (the simple sum of type I and type II classification errors) is also reduced by the inclusion of fundamental asset volatility measures. In the base model the relative cost is 0.1716. However, the inclusion of accounting based measures of asset volatility lowers the relative cost measure to 0.1374. The inclusion of OAS in the model (column (3)) does not significantly increase the AUC, with respect to the model that includes fundamental volatility information, and, in contrast, increases the relative cost.
To further understand the economic significance of fundamental-based measures of asset volatility, we compute importance scores for each of the variables in the model (Panel B of Table 4). These scores attempt to measure how much work a variable does in a particular tree. They are calculated as the sum of the improvement that can be attributed to that variable at each node of the tree, weighted by the number of observations passing through that node (i.e., splits lower in the tree with only a smaller fraction of data passing through receive lower scores). For example, suppose that there are N observations in a given tree node (the parent node, t) and that variable s is chosen to split those N observations into two child nodes (t L and t R ). Variable s, together with all the other variables used to recursively split the sample data in the tree, is called a primary splitter. The improvement attributed to variable s in that specific node t is simply ∆R(s, t) = R(t) − R(t L ) − R(t H ), with \( R(t)=\frac{1}{N}\sum \limits_{x_n\in t}{\left({y}_n-\overline{y}(t)\right)}^2 \), and effectively reflects a change in the sum of square errors as a result of the split. To compute the variable importance score for variable s, we thus (1) identify all the nodes t in which variable s is used as a splitter, (2) compute the split improvement (∆R(s, t)) for all of these nodes, (3) adjust the split improvement to take into account the percentage of the sample flowing through each node, (4) add all the resulting improvement scores to compute the raw variable importance of variable s, and (5) rank and scale all raw variable importance scores, such that the variable with highest importance receives a score of 100. Following Breiman et al. (1984), we also examine the role that each variable plays as a surrogate. A surrogate is simply a substitute for a primary splitter at a certain node. The surrogate divides the data in a similar way to the primary splitter and may thus be used to replace the primary splitter when the primary splitter is missing. Our total variable importance score considers the role of each variable both as a primary splitter and as a surrogate. It is estimated following the approach described above, except that we now identify all the nodes where CART selects the variable either as a primary splitter or a surrogate and add all the corresponding improvement scores.
Leverage is the most important variable in models (1) and (3). Furthermore, the importance scores of fundamental-based measures of asset volatility are higher than those of market-based volatility measures, both considering just the role of each variable as primary splitter and its combined role as primary splitter and surrogate. When OAS is included in the model (model (3)) it becomes the second highest importance variable (after leverage). While OAS is assigned a total variable importance score of 94.35 in model (3), it has no importance as a primary splitter. This is in contrast with leverage, which has a total variable importance of 100 and a variable importance as a primary splitter of 100. This suggests that, while OAS is not directly used in the prediction tree, it plays an important role as a surrogate, i.e., it could replace leverage and other predictors if they were missing. Most importantly, the variable importance of the fundamental volatility measures remains high when OAS is added to the model, ranging from 7.63 to 43.90, compared to the 2.34 variable importance of \( {\upsigma}_{\mathrm{AI}}^{\upomega} \).
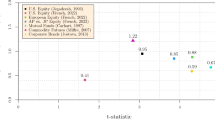
Variable importance scores capture the role played by a variable in a specific tree, and CART trees may be sensitive to the training data. This issue is partially addressed by the fact that we use cross-validation to build test samples and choose the optimal tree. To further circumvent this potential issue and assess the stability of our variable importance scores, we build 100 bootstrap samples and compute variable importance scores for each of these samples. Figure 1 plots the distribution (specifically, the minimum, 25th percentile, median, 75th percentile and maximum) of these scores. Note that the ranking of the variables in each of the panels of Fig. 1 may not exactly correspond to the ranking of the variables in Table 4, Panel B. This is because the ranking in Fig. 1 is based on the median importance of the variable in the 100 trees built using the bootstrap samples, whereas the importance scores reported in Table 4, Panel B are based on the tree built using our original data. Both Figure 1 and Table 4 highlight the importance of fundamental asset volatility for predicting defaults out of sample, when compared to both \( {\upsigma}_{\mathrm{AI}}^{\upomega} \) and the basic set of bankruptcy determinants.
Variable importance: bankruptcy prediction. Panels A, B, and C of this figure present the distribution of the variable importance scores of the models reported in Table 4, columns (1), (2), and (3), respectively. We form 100 bootstrap samples and estimate the minimum cost tree for each of these samples. We report the minimum, 25th percentile, median, 75th percentile, and maximum of the variable importance scores for each variable
3.2 Cross-sectional variation in credit spreads
3.2.1 Unconstrained analysis
Having established the information content of our candidate measures of asset volatility for bankruptcy prediction, we now turn to assess the information content of the same measures for secondary credit market prices. As discussed in section 2.5, under the assumption that security prices in the secondary credit market are reasonably efficient, we expect to see that the determinants of bankruptcy prediction models should also be able to explain cross-sectional variation in credit spreads.
Table 5 reports estimates of equation (5). This is our unconstrained analysis of how and whether different measures of asset volatility have information content for security prices. We include month fixed effects to control for macroeconomic factors, and as such we do not report an intercept. As discussed in section 2.5, we include additional issue specific measures (Ratingit, Ageit, and Durationit) to help control for other known determinants of credit spreads. Of course, we may be controlling for characteristics that subsume volatility by including these determinants, especially Ratingit. For example, the rating agencies may be using algorithms to assess credit risk that span fundamental and market data sources, and as such included rating categories might subsume the ability of this data to explain cross-sectional variation in credit spreads. In unreported analysis, we find that our inferences of the combined information content of market- and accounting-based information to measure asset volatility are unaffected by the inclusion of Ratingit.
Across all models estimated in Table 5, we find expected relations for our primary determinants. Credit spreads are consistently decreasing in (i) distance to default barrier, \( \ln \left(\frac{{\mathrm{V}}_{\mathrm{it}}}{{\mathrm{X}}_{\mathrm{it}}}\right) \), and (ii) firm size, ln(Eit). Credit spreads are consistently increasing in (i) credit rating (scaled to take higher values for higher yielding issues), Ratingit, and (ii) time since issuance, Ageit. Recent excess equity returns, Exretit, is usually negative across different models but is not consistently significant at conventional levels. Option-adjusted duration, Durationit, is usually negatively associated with credit spreads. P5, it and Skewit exhibit negative coefficients across most models but are often not significant at conventional levels. Conversely, Kurtit exhibits positive but often insignificant coefficients across most models.
Models (1) to (6) in Table 5 examine each of our measures of asset volatility separately. Individually, each is significantly positively associated with credit spreads. To provide a sense of their relative economic significance, we also report in Panel B of Table 5 the marginal effects for each explanatory variable. Similar to the marginal effects reported in Table 2, we report the change in credit spreads for a one standard deviation change for the respective explanatory variable, relative to the full-sample unconditional-mean credit spread. Individually, the most important measure of asset volatility is σE. (Marginal effect of 0.7736 is the largest in the first 6 columns of Panel B of Table 5.)
Models (7) to (14) in Table 5 combine different measures of asset volatility. As in Table 2, we do not include σE and σI in the same specification due to multi-collinearity concerns. In models (7) and (11), we add a measure of volatility from the credit markets, σD, to σE and σI, respectively. Consistent with the results in Table 2, combining market-based measures of asset volatility from the equity and credit markets is superior to examining equity-market information alone. (The R2 increases from 52.5% in model (1) to 57.7% in model (7) and from 65.9% in model (2) to 70.4% in model (11).) When we add our measures of fundamental volatility, σF, σIQR and σFEPS, to the model that includes σE and σD (i.e., model (7)), we find that the three measures are significantly associated with credit spreads. In terms of relative economic significance in model (8), σD is 1.47 times as large as that for σE, and σF is only 8% as large as that for σE. Similarly, in model (9), σD is 1.48 times as large as that for σE, and σIQR is 16% as large as that for σE. Finally, in model (10), σD is 1.46 times as large as that for σE, and σFEPS is 27% as large as that for σE. When σF, σIQR, and σFEPS are added to a model that includes σI and σD, σIQR remains statistically significant, but σF and σFEPS become insignificant.
In Table 6, we start with a model that includes σI, σD, and σF. We then replace σF by σMARGIN and σTURNOVER, based on the Dupont decomposition, and examine the incremental explanatory power of these variables. Neither σMARGIN nor σTURNOVER are statistically significant. In column (3), we instead replace σF by σOI GROWTH, which, contrary to expectation, has a negative and significant coefficient. In columns (4) to (6), we remove Rating from the model, as credit rating agencies may take into account fundamental volatility and specifically σOI GROWTH in assigning credit ratings. In fact, the correlation between Rating and σOI GROWTH (untabulated) is 0.5246. The coefficient on σOI GROWTH remains negative but insignificant.
In Table 7, we report the results from a CART regression analysis of OAS. Column (1) of Panel A presents the base model, which includes a market-based measure of asset volatility \( {\upsigma}_{\mathrm{AI}}^{\omega } \). Column (2) adds the fundamental volatility measures to the base model. As in the CART bankruptcy prediction analysis in Table 4, we can add all fundamental volatility measures simultaneously, as multicollinearity does not raise estimation concerns. The inclusion of fundamental volatility measures increases the test sample (i.e., out of sample) R2 from 0.7455 to 0.7796. This increase is significant at the 5% level. The R2 of the model further increases to 0.7859 as Rating is included.
Panel B reports the variable importance scores. Consistent with the analysis in Table 5, the average variable importance of fundamental volatility measures (12.94 in model (2) an 12.55 in model (3)) is considerably lower than the variable importance of the market-based measure, \( {\upsigma}_{\mathrm{AI}}^{\omega } \) (55.53 in model (2) and 46.78 in model (3)). Figure 2 plots the distribution of variable importance across the 100 bootstrapped samples. It confirms that fundamental volatility measures have much lower variable importance scores than market-based volatility measures. This is in stark contrast to the findings of the bankruptcy-prediction CART analysis reported in Figure 1, where \( {\upsigma}_{\mathrm{AI}}^{\omega } \) was the variable with the lowest importance.
Variable importance: credit spreads (unconstrained). Panels A, B, and C of this figure present the distribution of the variable importance scores of the models reported in Table 7, columns (1), (2), and (3), respectively. We form 100 bootstrap samples and estimate the minimum cost tree for each of these samples. We report the minimum, 25th percentile, median, 75th percentile, and maximum of the variable importance scores for each variable
Given the similarity in relative importance of market- and fundamental-based measures of volatility for the purposes of forecasting bankruptcy (out of sample) reported in Tables 2, 3 and 4 and the difference in relative importance of market- and fundamental-based measures of volatility for the purposes of explaining cross-sectional variation in credit spreads in Tables 5, 6 and 7 (with market-based measures seeming to be more important), this raises the possibility the market is not paying sufficient attention to the fundamental-based measures. We return to this issue in section 3.3.
3.2.2 Constrained analysis
We now assess the relative information content of the different measures of volatility in a constrained specification. As described in Appendix II and equation (A.1), we combine our measures of asset volatility with dollar distance to default (\( \ln \left(\frac{{\mathrm{V}}_{\mathrm{it}}}{{\mathrm{X}}_{\mathrm{it}}}\right) \)) to identify a distance to default barrier in standard deviation units. We then calibrate the various distance to default measures to an expected physical default probability, which is converted to an implied spread as per equations (A.2) and (A.3). We thus generate k different theoretical spreads where the difference is attributable to the use of different measures of asset volatility. This approach is arguably superior to the unconstrained analysis discussed in section 3.2.1, because of the inherent nonlinearity between leverage, asset volatility, defaults (bankruptcy), and credit spreads. Two firms could have the same dollar distance to default but different levels of asset volatility. It is the ratio of these two measures that matters for determining physical bankruptcy probability, not the two measures separately.
An empirical challenge that we face is combining different measures of volatility that vary in scale (see Panel C of Table 1). To handle these differences in scale when we combine measures of asset volatility, we first standardize each accounting-based measure and rescale them such that they have the same mean and standard deviation as the market-based measures of asset volatility to which they will be combined with. As a result of this process, we end up with seven different measures of theoretical spreads. We have four market-based theoretical spreads: (i) \( {\mathrm{CS}}_{\upsigma_{\mathrm{E}}} \), which is based only on historical equity volatility; (ii) \( {\mathrm{CS}}_{\upsigma_{\mathrm{I}}} \), which is based on only implied equity volatility; (iii) \( {\mathrm{CS}}_{\upsigma_{\mathrm{A}}^{\upomega}} \), which is based on a weighted combination of historical equity volatility and historical credit volatility; and (iv) \( {\mathrm{CS}}_{\upsigma_{\mathrm{AI}}^{\upomega}} \), which is based on a weighted combination of implied equity volatility and historical credit volatility. We have three accounting-based theoretical spreads: (i) \( {\mathrm{CS}}_{\upsigma_{\mathrm{F}}} \), which is based on historical volatility of RNOA; (ii) \( {\mathrm{CS}}_{\upsigma_{\mathrm{AVG}}} \), which is based on the average of the different fundamental volatility measures; and (iii) \( {\mathrm{CS}}_{{\mathrm{PROB}}_{\mathrm{AVG}}} \), which is based on the average of the default probabilities based on the different fundamental volatility measures. The distinction between \( {\mathrm{CS}}_{\upsigma_{\mathrm{AVG}}} \) and \( {\mathrm{CS}}_{{\mathrm{PROB}}_{\mathrm{AVG}}} \)is described in more detail in Section 2.5.
Table 8 reports regression results of equation (6). We retain the same set of controls and explanatory variables to allow comparability of explanatory power between equations (5) and (6). We include a set of month fixed effects and as such do not report a regression intercept. Model (1) shows that theoretical spreads based on a simple measure of historical equity volatility can explain 65% of the variation in credit spreads, and the regression coefficient on \( {\mathrm{CS}}_{\upsigma_{\mathrm{E}}}^{\mathrm{BASE}} \) is 0.629. A regression coefficient that is less than one may suggest that our measure of theoretical credit spread is larger than the actual market spread. This is not the case, as our regression model includes an intercept (via time fixed effects). In unreported analysis, if we exclude fixed effects and other control variables, we find that the regression coefficient on \( {\mathrm{CS}}_{\upsigma_{\mathrm{E}}}^{\mathrm{BASE}} \) is statistically greater than 1, consistent with the well-known result that some structural models tend to under forecast credit spreads (e.g., Eom et al. 2004; Huang and Huang 2012).
Before assessing the incremental improvement in explanatory power from alternative measures of asset volatility, we first use our secondary credit market data to apply a haircut to the book value of debt used as an approximation for the market value of assets. While fixed and floating rate debt is usually issued at par, changes in the credit risk of the issuer over time will create situations where the market value of debt differs from its book value. Thus our estimate of market value of assets may be too high (low) for issuers whose credit quality has worsened (improved) since debt issuance. A direct consequence is that any implied spread will be too low (high). To help mitigate this error, we take a fraction of the book value of debt as our approximation for the market value of debt using the change in the spread from when the representative bond first appears in our data set to the current period. Specifically, we multiply the book value of debt by \( \frac{1}{{\left(1+\Delta \mathrm{OAS}\right)}^{\mathrm{Duration}}} \). Thus our estimate of the market value of debt adjusts the reported book value by the change in credit spreads, ∆OAS, measured from when the representative bond was first recorded in the Barclays bond dataset to the current period. For coupon bearing debt, this simply allows market value of debt to fall (rise) as credit spreads increase (decrease). Model (2) of Table 8 shows that, once we incorporate this haircut, we observe a noticeable change in explanatory power. The R2 in model (2) increases to 70.9% from 65.0% for model (1).
Models (3) to (11) in Table 8 consider various combinations of our theoretical spreads. Models (6) to (11) add the three different fundamental credit spread measures. Across the three measures (models (9) to (11)), we see evidence of the joint role of market- and fundamental-based measures of asset volatility. In fact, fundamental-based credit spreads are statistically significant across all specifications.
The last four rows of Table 8 contain summary information based on estimating the unconstrained regression equation (5) for the same sample of 51,546 bond-months. The sample we use in Table 8 is smaller than that in Table 5, as we require an initial out-of-sample period to empirically calibrate our distance to default to a physical bankruptcy probability. Across all of the models in Table 8, we see that the constrained regression specification results in a statistically and economically significant increase in the ability to explain cross-sectional variation in spread levels. (Vuong 1989 Z-statistics reject the null hypothesis that the unconstrained regression, i.e. equation (5), has the same explanatory power as the constrained regression, i.e. equation (6), for a constant sample of 51,546 bond-months.) The regression specifications are identical, except for how we combine leverage and volatility. The constrained specification combines leverage and volatility consistent with the Merton model, and this generates a significant improvement in explanatory power.
Table 9 presents the results from a CART regression analysis of OAS, where we include theoretical credit spreads, as opposed to the raw volatility measures. Column (1) presents the base model, which includes \( {\mathrm{CS}}_{\upsigma_{\mathrm{AI}}^{\upomega}} \). When we add the fundamental credit spreads measures to the base model, \( {\mathrm{CS}}_{\upsigma_{\mathrm{F}}} \), \( {\mathrm{CS}}_{\upsigma_{\mathrm{IQR}}} \), \( {\mathrm{CS}}_{\upsigma_{\mathrm{FEPS}}} \), \( {\mathrm{CS}}_{\upsigma_{\mathrm{MARGIN}}} \), \( {\mathrm{CS}}_{\upsigma_{\mathrm{TURNOVER}}} \), \( {\mathrm{CS}}_{\upsigma_{\mathrm{OI}\ \mathrm{GROWTH}}} \) and \( {\mathrm{CS}}_{\upsigma_{\mathrm{SALES}\ \mathrm{GROWTH}}} \), in column (2) the test sample R2 increases from 0.7713 to 0.7950. This increase is significant at the 5% level. The R2 of the model further increases to 82.12 when Rating is added.
The variable with highest variable importance across all models is the market-based credit spread, \( {\mathrm{CS}}_{\upsigma_{\mathrm{AI}}^{\upomega}} \) (Panel B). The variable importance of fundamental theoretical credit spreads ranges from 1.33 (\( {\mathrm{CS}}_{\upsigma_{\mathrm{FEPS}}} \)) to 94.33 (\( {\mathrm{CS}}_{\upsigma_{\mathrm{OI}\ \mathrm{GROWTH}}} \)) and averages 59.16 when rating is not included. When rating is included, the variable importance of fundamental theoretical credit spreads slightly decreases to an average of 56.35. Fundamental credit spreads play a less prominent role as primary splitters. (Their average importance as primary splitters is 8.13 (7.34) in the model that includes (doesn’t include) credit rating.) Variables that are highly correlated with primary splitters are most likely to be selected as successful surrogates. Therefore the difference between the total variable importance of fundamental credit spreads and their importance as primary splitters is consistent with their relatively high correlation with \( {\mathrm{CS}}_{\upsigma_{\mathrm{AI}}^{\upomega}} \). Figure 3 illustrates the distribution of variable importance scores for the 100 bootstrapped samples. It clearly illustrates a striking difference between the importance scores of theoretical spreads and the remaining independent variables. In fact, with the exception of \( {\mathrm{CS}}_{\upsigma_{\mathrm{FEPS}}} \), theoretical credit spreads display importance scores that are significantly higher than the remaining variables in the model.
Variable Importance: Credit Spreads (Constrained). Panels A, B, and C of this figure present the distribution of the variable importance scores of the models reported in Table 9, columns (1), (2), and (3), respectively. We form 100 bootstrap samples and estimate the minimum cost tree for each of these samples. We report the minimum, 25th percentile, median, 75th percentile and maximum of the variable importance scores for each variable
3.3 Return prediction
The empirical analysis in section 3.1 showed the similarity in relative importance of market- and fundamental-based measures of volatility for the purposes of forecasting bankruptcy (out of sample). The empirical analysis in section 3.2 showed that, while market and fundamental-based measures were both useful for explaining cross-sectional variation in credit spreads, there was a clear difference in their relative importance (with market-based measures seeming to be more important). As noted in section 3.2, this raises the possibility the market is not paying sufficient attention to fundamental-based measures of asset volatility. We now explore this directly.
We first need to define a measure of mispricing by comparing the difference between the actual credit spread in the secondary markets with our theoretical credit spreads. If it is the case that our measures of theoretical credit spreads contain superior forecasts of default than that implicit in the actual credit spread, then we would expect the actual credit spread to converge toward the theoretical credit spread. Alternatively, the difference between actual and theoretical credit spreads should be positively associated with future credit excess returns. We build two measures to capture the percentage deviation of credit spreads from their theoretical levels. We denote these measures as CRV Market and CRV Fundamental . CRV Market is computed as \( \mathit{\ln}\left(\frac{OAS}{{\mathrm{CS}}_{\upsigma_{\mathrm{AI}}^{\omega }}}\right) \) and CRV Fundamental as \( \mathit{\ln}\left(\frac{OAS}{{\mathrm{CS}}_{{\mathrm{PROB}}_{\mathrm{AVG}}}}\right) \). CRV Fundamental is designed to take into account all fundamental volatility measures. In untabulated robustness tests, we run our analysis with an alternative CRV Fundamental measure defined as \( \mathit{\ln}\left(\frac{OAS}{{\mathrm{CS}}_{\upsigma_{\mathrm{AVG}}}}\right) \). The two CRV Fundamental measures exhibit a Pearson (Spearman) correlation of 0.9790 (0.9787) and, unsurprisingly, produce similar results. To the extent that the credit market has not fully incorporated fundamental volatility information and will do so with a lag, there should be a positive association between CRV Fundamental and future credit returns.
We conduct standard cross-sectional return predictability regressions and examine whether CRV accounting can forecast returns (over and above CRV market). Specifically, we run the following cross-sectional regression model using the Fama and Macbeth (1973) approach as described by Correia et al. (2012).
RET i, t + k is the credit return for month t + k. MOMS it is the equity return for issuer i for the most recent month (i.e., the month prior to the start of the credit return accumulation period). MOML it is an exponentially weighted (three-month half-life) cumulative return over the 11 months prior to the computation of MOMS it . We use an exponential weighting, instead of equal weighting, because we are interested in capturing the delayed response of credit markets to recent information in equity markets. BTM it is book-to-price computed as the ratio of book value of equity (Compustat mnemonic CEQ from the recent fiscal quarter, relative to market capitalization corresponding to that fiscal period’s end date). SIZE it is the log of market capitalization at the start of the credit return accumulation period. E/P it is the earnings-to-price ratio calculated as the ratio of net income (NIQ) from the recent four fiscal quarters, relative to market capitalization corresponding to that fiscal period’s end date. BETA it is the equity market beta, estimated from a rolling regression of 60 months of data requiring at least 36 months of nonmissing return data.
We estimate this regression k times every month, with k reflecting the number of months into the future we are forecasting. The relevant test is whether β CRV Fundamental, t =0, and finding β CRV Fundamental, t > 0 is consistent with actual credit spreads reverting to theoretical credit spreads. We expect to see a positive relation between credit returns and MOMS it , MOML it , E/P it , BETA it , and BTM it and a negative relation between credit returns and SIZE it .
We report the results from the estimation of equation (7) using risk- and value-weighted least squares in Table 10 Panels A and B, respectively. In Panel A, the weight of each observation is as defined as − ln(OAS it ), which naturally places less weight on riskier firms. In Panel B, the weight is defined as the amount outstanding of that bond as a percentage of the total amount outstanding for all the bonds in the sample.
The Pearson (Spearman) correlation between CRV Fundamental, it and CRV Market, it (untabulated) is 0.364 (0.373). Across both weighting schemes (risk and value) and return horizons (k = 1,…,6), we find a positive and significant coefficient on CRV Fundamental, it . The coefficient on CRV Market, it is positive and significant, when the variable is included by itself (unreported), but insignificant when CRV Fundamental, it is added to the model. MOMS and MOML exhibit positive and significant coefficients for shorter return horizons but insignificant ones for longer return horizons. Consistent with our priors, fundamental-based measures of asset volatility help forecast bankruptcy but have a more moderate role in explaining credit spreads, suggesting that the market is not fully appreciating the information content of financial statement information when forming views on expected default.
3.4 Extensions and robustness tests
3.4.1 CDS data
In Table 11, we report regression estimates of a modified version of equation (5) (Panel A) and equation (6) (Panel B) where we use credit spreads from CDS contracts rather than bonds. As with our previous spread level regressions, we include a set of month fixed effects and as such do not report a regression intercept. A benefit of this approach is that the CDS credit spread is a cleaner representation of credit risk, but a disadvantage is the shorter period for which this data is available (2004 to 2012 only). Because we are examining cross-sectional variation in five-year CDS spreads, CDS5Yit, we no longer need to control for issue specific characteristics such as Ageit and Durationit. All five-year CDS contracts have the same seniority, the same time since issuance (we only examine on-the-run contracts), and the same tenor (five years). Thus we estimate the following models.
Our sample size decreases from 75,548 bond-months examined in Table 5 to 27,564 CDS-months examined in Table 11 Panel A and from 51,546 in Table 8 to 19,005 in Table 11, Panel B. Despite the smaller sample size, we find similar results with this alternative sample. Models (1) to (5) examine the different volatility measures one at a time. All variables are positive and coefficient, with the exception of σFEPS, whose coefficient is positive but not significant. σF and σIQR remain significant when added to a model that also includes σE and σD, but σF ceases to be significant when σE is replaced by σI.
Panel B presents the results from the constrained analysis. Models (1) to (3) show that theoretical spreads based on equity market information can explain up to 49% of the cross-sectional variation in credit spreads. Models (4) and (5) show that combining measures of asset volatility generates theoretical spreads that can explain a greater fraction of the cross-sectional variation in credit spreads. (The R2 increases to 54% for model (5).) Strikingly, our measure of theoretical spread using fundamental volatility alone, and specifically, \( {\mathrm{CS}}_{\upsigma_{\mathrm{F}}} \), \( {\mathrm{CS}}_{\upsigma_{\mathrm{AVG}}} \) and \( {\mathrm{CS}}_{{\mathrm{PROB}}_{\mathrm{AVG}}} \), can explain from 45.7 to 50.0% of the cross-sectional variation in credit spreads (see models (6) to (8)). Finally, including both market- and accounting-based measures of asset volatility yields theoretical spreads that can explain even more of the cross-sectional variation in credit spreads: a maximum R2 of 55.2% across models (9) to (11). Similar to the analysis in Table 8, at the bottom of Panel B of Table 11, we also report the R2 of the equivalent unconstrained regression on the CDS sample (equation (7)). Across all specifications, with the exception of model (1), we see statistically significant increases in explanatory power when we constrain asset volatility and leverage, consistent with the Merton model, as compared to including these variables linearly and independently. In other words, the Vuong test rejects the null hypotheses that the constrained and unconstrained models have similar R2.
3.4.2 Alternative specifications
Research has examined the relative importance of fundamental- and market-based variables to predict defaults (e.g., Altman 1968; Beaver et al. 2005; Bharath and Shumway 2008; Campbell et al. 2008) and explain cross-sectional variation in credit spreads (e.g., Das et al. 2009). While our focus is on the relative usefulness of fundamental- and market-based measures of volatility within a structural model framework, we also examine the relative usefulness of fundamental- and market-based variables in a reduced form analysis similar to this past research. It is important to remember a key result from Table 8, which showed a marked improvement in explanatory power of cross-sectional credit spread regressions when measures of leverage and volatility are combined in a manner consistent with the structural models. Thus we view the analysis in this section as a robustness analysis and not the focus of the paper.
In untabulated analysis, we expand the bankruptcy forecasting model to control for average accounting profitability over the previous four quarters, cash holdings, market-to-book ratio, and price, following Campbell et al. (2008). We choose not to include these variables in our main specification, which only includes (albeit linearly) the main determinants of probability of default as per the Merton model. Specifically, we add the following variables to the analysis reported in Table 2 (variables are defined and labelled consistently with Campbell et al. 2008): (i) NIMTAAVG, a geometrically weighted average level of net income scaled by market value of total assets, which places higher weight on more recent quarters; (ii) CASHMTA, cash and short-term investments scaled by the market value of assets; (iii) MB, the market-to-book ratio; and (iv) PRICE, the natural logarithm of the firm’s stock price. The sample size does not change significantly as a result of the inclusion of these additional control variables. Our measures of fundamental volatility continue to be significant, both when included individually and together with implied volatility and debt volatility.
We also re-estimate the unconstrained and constrained credit-spread regressions adding the control variables of Campbell and Taksler (2003). In particular, we control for operating income and long-term debt to total assets. Consistent with our main analysis, we continue to find that σ F is significant both when included individually and when considered incrementally to debt volatility and historical equity volatility. In the constrained analysis, all credit spreads based on fundamental volatility remain both individually and incrementally significant.
We further repeat the analysis in Table 2 (bankruptcy prediction) and Table 5 (credit spreads regression: (1) including the skewness and kurtosis of equity returns, (2) including the average skewness and kurtosis of quarterly RNOA, (3) replacing P 5 by the level of RNOA (we cannot control for both variables simultaneously in the regression because they display high correlations), and (4) replacing P 5 by a loss indicator. Our inferences are unaffected by these alternative specifications.
4 Conclusion
We examine whether and how fundamental measures of volatility are incremental to market-based measures of volatility in (i) predicting bankruptcies (out of sample), (ii) explaining cross-sectional variation in credit spreads, and (iii) explaining future credit excess returns. For a large sample of U.S. firms, we find that a variety of fundamental-based measures of asset volatility help forecast bankruptcies and, to a lesser extent, help explain cross-sectional variation in credit spreads. Our finding of similar relative importance of market-based and fundamental-based measures to forecast bankruptcy but a dominance of market-based measures to explain credit spread suggests that the market is not fully incorporating fundamental-based measures of asset volatility into credit spreads. Our predictive analysis of future credit excess returns confirms these priors.
Our paper is a comprehensive analysis of many measures of asset volatility, using a variety of econometric methods to show the importance of detailed fundamental analysis from the perspective of a credit investor. Credit markets are very large – as of December 2016, there were over $12 trillion of outstanding corporate debt from companies in the developed world. This is a huge asset class and one that has been relatively unexplored to date. The information that we use is taken directly from general purpose research reports, and the financial reporting system underlying these statements has an objective of providing relevant, reliable information not only to equity investors but also to credit investors. We hope that future research can extend our analysis to focus on other important—and measurable—aspects of default risk. Notable examples would include improved measures of financial leverage (on- and off-balance-sheet contractual commitments) and operating leverage (e.g., Penman 2014).
Notes
For example, Basic Energy Services, Inc. has two bonds in the Barclays Capital bond sample with return information for October 2009, one with rating BA3 and another with rating CAA1. We first compute the fraction of debt outstanding for each rating. In this case, half of the debt is rated BA3, and the other half CAA1, as the bonds have the same amount outstanding of $225,000. Therefore both bonds are kept in the sample after the first step. The second selection step is based on years to maturity. The first bond has 4.75 years to maturity, and the second bond 6.46. We drop the first bond as time to maturity is lower than five, and therefore the second bond is selected as the representative bond. Viacom Inc. has five bonds in the sample in December 2012, all with the same rating of BAA1. Two of these bonds have time to maturity between 5 and 15 years. Therefore we remove the remaining three bonds from the sample. Both bonds were issued at the same time. They are both 1.36 years old. Therefore we select the representative bond based on amount outstanding. Similar bond selection criteria are used by Correia et al. (2012) and Cascino (2017).
The standardized implied volatilities are calculated by OptionMetrics using linear interpolation from their Volatility Surface file.
Beaver et al. (2012) combine the bankruptcy database from Beaver et al. (2005), which was derived from multiple sources including CRSP, Compustat, Bankruptcy.com, Capital Changes Reporter, and a list provided by Shumway with a list of bankruptcy firms provided by Chava and Jarrow and used by Chava and Jarrow (2004).
We estimate this model using expanding windows to ensure that all observation used in the estimation is available at time t.
We keep the sample constant across columns (1) to (3) and (4) to (6).
We use the Salford Predictive Modeler software suit, developed by Salford Systems, to perform the CART analysis.
References
Altman, E. (1968). Financial ratios, discriminant analysis and the prediction of corporate bankruptcy. The Journal of Finance, 23(4), 589–609.
Arora, N., Bohn, J., & Zhu, F. (2005). Reduced form vs. structural models of credit risk: a case study of 3 models. Journal of Investment Management, 3(4), 43–67.
Beaver, W. H. (1966). Financial ratios as predictors of bankruptcy. Journal of Accounting Research, 4, 71–111.
Beaver, W. H., Correia, M., & McNichols, M. (2012). Do differences in financial reporting attributes impair the predictive ability of financial ratios for bankruptcy. Review of Accounting Studies, 17(4), 969–1010.
Beaver, W. H., McNichols, M., & Rhie, J. (2005). Have financial statements become less informative? Evidence from the ability of financial ratios to predict bankruptcy. Review of Accounting Studies, 10, 93–122.
Bharath, S., & Shumway, T. (2008). Forecasting default with the Merton distance to default model. Review of Financial Studies, 21, 1339–1369.
Breiman, L., Friedman, J., Olshen, R.A., & Stone, C. J. (1984). Classification and regression trees. Boca Raton: CRC Press.
Bruche, M., & Gonzales-Aguado, C. (2010). Recovery rates, default probabilities, and the credit cycle. Journal of Banking and Finance, 34(4), 754–764.
Campbell, J., Hilscher, J., & Szilagyi, J. (2008). In search of distress risk. The Journal of Finance, 63(6), 2899–2939.
Campbell, J., & Taksler, G. (2003). Equity volatility and corporate bond yields. The Journal of Finance, 58(6), 2321–2349.
Cao, C., Yu, F., & Zhong, Z. (2010). The information content of option-implied volatility for credit default swap valuation. Journal of Financial Markets, 13, 321–343.
Cascino, S. (2017). Stock bond return co-movement and accounting information. Journal of Business Finance & Accounting, 44(7-8), 1036–1072.
Chava, S., & Jarrow, R. (2004). Bankruptcy prediction with industry effects. Review of Finance, 8, 537–569.
Correia, M., Richardson, S., & Tuna, I. (2012). Value Investing in Credit Markets. Review of Accounting Studies, 17(3), 572–609.
Cremers, K. J. M., Driessen, J., & Maenhout, P. (2008a). Explaining the level of credit spreads: option-implied jump risk premia in a firm value model. Review of Financial Studies, 21(5), 2209–2242.
Cremers, M., Driessen, J., Maenhout, P., & Weinbaum, D. (2008b). Individual stock-option prices and credit spreads. Journal of Banking & Finance, 32(12), 2706–2715.
Crouhy, M., Galai, D., & Mark, R. (2000). A comparative analysis of current credit risk models. Journal of Banking & Finance, 24, 59–117.
Das, S., Hanouna, P., & Sarin, A. (2009). Accounting-based versus market-based cross-sectional models of CDS spreads. Journal of Banking & Finance, 33, 719–730.
Eom, Y., Helwege, J., & Huang, J. (2004). Structural models of corporate bond pricing: an empirical analysis. Review of Financial Studies, 17(2), 499–544.
Fama, E., & French, K. (2000). Forecasting profitability and earnings. Journal of Business, 72, 161–175.
Fama, E., & Macbeth, J. (1973). Risk, return and equilibrium: empirical tests. Journal of Political Economy, 81(3), 3–56.
Feldhutter, P., & Schaefer, S. (2013). The credit spread puzzle – myth or reality? Working paper, London Business School. http://papers.ssrn.com/sol3/papers.cfm?abstract_id=2363081
Frydman, H., Altman, E., & Kao, D. (1985). Introducing recursive partitioning for financial classification: the case of financial distress. Journal of Finance, 40(1), 269–291.
Haesen D., P. Howeling, & Van Zundert, V. (2013). Residual Equity Momentum for Corporate Bonds. Working Paper. http://papers.ssrn.com/sol3/papers.cfm?abstract_id=2131032
Helwege, J., & Turner, C. M. (1999). The slope of the credit yield curve for speculative grade issuers. Journal of Finance, 54(5), 1869–1884.
Hou, K., Van Dijk, M. A., & Zhang, Y. (2012). The Implied Cost of Capital: A New Approach. Journal of Accounting and Economics, 53(3), 504–526.
Huang, J., & Huang, M. (2012). How much of the corporate-treasury yield spread is due to credit risk? Review of Asset Pricing Studies, 2(2), 153–202.
Kealhofer, S. (2003). Quantifying Credit Risk II: Debt Valuation. Financial Analysts Journal, May/June: 78–92.
Konstantinidi, T., & Pope, P. (2016). Forecasting Risk in Earnings. Contemporary Accounting Research, 33(2), 487–525.
Kraft, P. (2014). Rating agency adjustments to GAAP financial statements and their effect on ratings and credit spreads. The Accounting Review, 90(2), 641–674.
Liu, D., Markov, S., & Tamayo, A. (2007). What makes a stock risky? Evidence from sell-side analysts’ risk ratings. Journal of Accounting Research, 45(3), 629–665.
Lok, S., & Richardson, S. (2011). Credit markets and financial information. Review of Accounting Studies, 16, 487–500.
Merton, R. (1974). On the pricing of corporate debt: The risk structure of interest rates. Journal of Finance, 29, 449–470.
Ohlson, J. (1980). Financial ratios and the probabilistic prediction of bankruptcy. Journal of Accounting Research, 18(1), 109–131.
Penman, S. H. (1991). An Evaluation of Accounting Rate-of-Return. Journal of Accounting, Auditing and Finance Spring, 233–255.
Penman, S. H. (2014). Financial statement analysis and security valuation (5th ed.). New York: McGraw-Hill International Edition.
Penman, S. H. (2016). Valuation: accounting for risk and the expected return. Abacus, 52(1), 106–130.
Richardson, S. A., Sloan, R. G., Soliman, M. T., & Tuna, I. (2006). The implications of accounting distortions and growth for accruals and profitability. The Accounting Review, 81(3), 713–743.
Schaefer, S., & Strebulaev, I. (2008). Structural models of credit risk are useful: evidence from hedge ratios on corporate bonds. Journal of Financial Economics, 90(1), 1–19.
Shumway, T. (2001). Forecasting bankruptcy more accurately: A simple hazard model. Journal of Business, 74, 101–124.
Sloan, R. G. (1996). Do stock prices fully reflect information in accruals and cash flows about future earnings? The Accounting Review, 81(3), 289–315.
Vuong, Q. H. (1989). Likelihood ratio-tests for model selection and non-nested hypotheses. Econometrica, 57(2), 307–333.
Zhang, B. Y., Zhou, H., & Zhu, H. (2009). Explaining credit default swap spreads with the equity volatility and jump risks of individual firms. Review of Financial Studies, 22(12), 5099–5131.
Acknowledgements
We are grateful to Arne Staal and Philippe Vannerem at Barclays Capital for providing us access to the Barclays Capital bond dataset. We also thank Korcan Ak (discussant), Cliff Asness, Max Bruche, John Campbell, Joachim Gassen, John Hand, Jens Hilscher, Ronen Israel, Anya Kleymenova, Sonia Konstantinidi, David Lando, Lasse Pedersen, Carolin Pflueger, Robert Resutek (discussant), Tjomme Rusticus, Frank Zhang, and seminar participants at the American Accounting Association Annual Meeting, Cass Business School, Copenhagen Business School, European Accounting Association Annual Meeting, FARS Annual Meeting, Humboldt University, London Business School, LUBRAFIN and University of Porto for helpful discussion and comments. AQR Capital Management LLC invests in, among other strategies, securities studied in this paper. The views and opinions expressed herein are those of the authors and do not necessarily reflect the views of AQR Capital Management LLC (“AQR”), its affiliates, or its employees. This information does not constitute an offer or solicitation of an offer, or any advice or recommendation, by AQR, to purchase any securities or other financial instruments, and may not be construed as such. The views expressed here are those of the authors alone and not necessarily those of BlackRock, its officers, or directors. The paper is intended to stimulate further research and is not a recommendation to trade particular securities or any investment strategy.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix I: Variable definitions
Appendix II: Theoretical credit spreads
In this appendix, we describe the calculation of theoretical credit spreads. We first combine our measures of the dollar distance to default, \( \ln \left(\frac{{\mathrm{V}}_{\mathrm{it}}}{{\mathrm{X}}_{\mathrm{it}}}\right) \), and the respective measures of asset volatility, σk, it, to construct a measure of expected distance to default. The expected distance to default measure also includes a drift term \( \left({\upmu}_{\mathrm{it}}-{\updelta}_{\mathrm{it}}-\frac{\upsigma_{\mathrm{A},\mathrm{it}}^2}{2}\right)\mathrm{t} \). μ it is defined as rf, it + βRP it , where rf, it is the one-year swap rate, RP it is the market risk premium, which we set equal to 4%, and β is the asset beta of the firm, the coefficient from a rolling regression of the firm’s monthly asset returns over the previous 24 months on the average asset returns, requiring at least 12 months of available data. Following Feldhutter and Schaefer (2013), the payout ratio, δ, is calculated as the sum of interest payments to debtholders over the previous four quarters (based on INTNY), the dividend payments to equityholders (the product of the annual dividend DVI and the number of shares outstanding CSHOC) and purchases of common and preferred stock over the previous four quarters (based on PRSTKCY), scaled by the firm’s total assets (E + STD + LTD). This distance to default is then empirically mapped to our bankruptcy data using a discrete-time hazard model to generate a forecast of physical bankruptcy probability, labelled as \( \mathrm{E}\left({\mathrm{PD}}_{\mathrm{it}}^{\mathrm{k}}\right) \). We estimate this physical bankruptcy probability for each of our asset volatility measures, according to equation (A.1) below:
We next convert each physical bankruptcy probability into a risk-neutral measure, following the approach described by Kealhofer (2003) and Arora et al. (2005). We first compute the cumulative physical bankruptcy probability, \( {\mathrm{CPD}}_{\mathrm{it}}^{\mathrm{k}} \), from \( \mathrm{E}\left({\mathrm{PD}}_{\mathrm{it}}^{\mathrm{k}}\right) \) by cumulating survival probabilities over the relevant number of periods. In particular, \( {\mathrm{CPD}}_{\mathrm{it}}^{\mathrm{k}}=1-{\left(1-\mathrm{E}\left({\mathrm{PD}}_{\mathrm{it}}^{\mathrm{k}}\right)\right)}^{\mathrm{T}} \). We then convert this cumulative physical bankruptcy probability, \( {\mathrm{CPD}}_{\mathrm{it}}^{\mathrm{k}} \), to a cumulative risk-neutral bankruptcy probability, \( {\mathrm{CQDF}}_{\mathrm{it}}^{\mathrm{k}} \). We use a normal distribution to convert physical probabilities of bankruptcy to risk-neutral probabilities, following the approach of Crouhy et al. (2000); Kealhofer (2003); and Arora et al. (2005):
The cumulative physical bankruptcy probability is first converted into a point in the cumulative normal distribution. A risk premium is then added. The risk premium is the product of (i) the issuer’s sensitivity to the market price of risk, as measured by the correlation between the underlying issuer-level asset returns and the market index return, \( \sqrt{{\mathrm{r}}_{\mathrm{it}}^2} \); (ii) the market price of risk (i.e., the market Sharpe ratio, measured by λ); and (iii) the duration of the credit risk exposure, T. The risk modified physical bankruptcy probability is then mapped back to risk neutral space. We set the market Sharpe ratio, λ, equal to 0.5, consistent with the values observed by Kealhofer (2003). We set \( \sqrt{{\mathrm{r}}_{\mathrm{it}}^2} \) equal to the correlation between monthly firm stock returns and monthly market returns using a rolling 60-month window. We impose a floor (ceiling) on the estimated correlation at 0.1 (0.7). Finally, we estimate implied (or theoretical) credit spreads as follows:
Rit is expected recovery rate conditional on bankruptcy, which we set equal to 0.4 for all firms. While we assume Rit to be a constant, recovery rates may exhibit systematic time-variation (Bruche and Gonzales-Aguado 2010). While this could affect the gap between theoretical and observed credit spreads, we have no reason to believe it will present a concern to our analysis, given that we do not examine this gap directly.
Appendix III: Quantile regression approach
In this appendix, we describe the quantile regression approach discussed in Section 2.4. We use this approach to estimate the quantiles and conditional moments of the RNOA distribution. For each year t, we estimate the following equation using quarterly data from 1963 to t:
Our model resembles the one of Hou et al. (2012), with the exception that we forecast return on net operating assets (RNOA), instead of return on equity (ROE), and therefore do not include leverage as an explanatory variable and scale all variables by the average balance of net operating assets (NOA), rather than by the average balance of book equity. All variables used in the estimation are described in Appendix I. We compute these variables at the end of each quarter, using the most recent four quarters of data.
In unreported analyses, we find the expected relations between our included explanatory variables and future profitability. Specifically, the median quantile regression generates the following results: (i) \( {\upbeta}_1^{50} \) is 0.94 consistent with mean reversion in accounting rates of return (e.g., Penman 1991; Fama and French 2000); (ii) \( {\upbeta}_2^{50} \) is −0.01 consistent with loss makers having lower levels of future profitability (e.g., Hou et al. 2012); (iii) \( {\upbeta}_3^{50} \) is −0.14 consistent with faster mean reversion in profitability for loss making firms (e.g., Beaver et al. 2012); (iv) \( {\upbeta}_4^{50} \) is −0.02 consistent with the well-documented negative relation between accruals and future firm performance (e.g., Sloan 1996; Richardson et al. 2006); (v) \( {\upbeta}_5^{50} \) is 0.02 consistent with dividend-paying firms having higher levels of future profitability (e.g., Hou et al. 2012); and (vi) \( {\upbeta}_6^{50} \) is 0.26 also consistent with firms with higher dividend payout having higher levels of profitability (e.g., Hou et al. 2012).
We combine the values of the independent variables in year t with the vector of coefficients, \( {\upbeta}_{\mathrm{t}}^{\mathrm{q}} \)=\( {\upbeta}_{0\mathrm{t}}^{\mathrm{q}},\dots, {\upbeta}_{6\mathrm{t}}^{\mathrm{q}} \), to obtain out-of-sample estimates of the percentiles for the year t + 1. In particular, we obtain a vector of coefficient estimates, \( \widehat{\upbeta_{\mathrm{t}}^{\mathrm{q}}} \), for each percentile and sample quarter. Based on this vector, we estimate the expected value of each of the 100 percentiles as \( \widehat{\mathrm{E}\left({\mathrm{q}}_{\mathrm{it}+1}|{\mathrm{X}}_{\mathrm{it}}\right)}=\widehat{\upbeta_{\mathrm{t}}^{\mathrm{q}}}{\mathrm{X}}_{\mathrm{it}} \), where Xit includes RNOAit, LOSSit, LOSSit × RNOAit, ACCit, PAYERit, PAYOUTit.
For purposes of estimation of the vector of coefficient estimates, we delete extreme observations of dependent and independent variables. In particular, we delete all observations with |RNOAit|>2, |RNOAit − 1|>2, |ACCit − 1|>2, |PAYOUTit − 1|>1, |PAYOUTit − 1|<0. We retain all values of these variables, irrespective of extreme values, when we generate the expected quantile values.
Our measure of left-tail fundamental risk is the predicted value of the 5th percentile, \( {\mathrm{P}}_5=\widehat{\mathrm{E}\left({5}_{\mathrm{it}+1}|{\mathrm{X}}_{\mathrm{it}}\right)} \). We also include in our analysis a measure of skewness (Skew) and kurtosis (Kurt) of the distribution, defined as Skew=((P 75 − P 50) − (P 50 − P 25))/IQR, and Kurt=((P 87.5 − P 62.5) − (P 37.5 − P 12.5))/IQR, where IQR=P 75 − P 25 and \( {\mathrm{P}}_q=\widehat{\mathrm{E}\left({\mathrm{Q}}_{\mathrm{it}+1}|{\mathrm{X}}_{\mathrm{it}}\right)} \).
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Correia, M., Kang, J. & Richardson, S. Asset volatility. Rev Account Stud 23, 37–94 (2018). https://doi.org/10.1007/s11142-017-9431-1
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11142-017-9431-1