On effective irrationality exponents of cubic irrationals

Abstract

We provide an upper bound for the effective irrationality exponents of cubic algebraics x with the minimal polynomial $x^3 - tx^2 - a$. In particular, we show that it becomes non-trivial, i.e. better than the classical bound of Liouville, in the case $|t| > 19.71 a^{4/3}$. Moreover, under the condition $|t| > 86.58 a^{4/3}$, we provide an explicit lower bound for the expression ||qx|| for all large $q\in \mathbb {Z}$. These results are based on the recently discovered continued fractions of cubic irrationals and improve the currently best-known bounds of Wakabayashi.

1 Introduction

The irrationality exponent $\lambda (x)$ of an irrational real number x is defined as the supremum of real numbers $\lambda$ such that the inequality

$$\begin{aligned} \left| x - \frac{p}{q}\right| < q^{-\lambda } \end{aligned}$$

(1)

has infinitely many rational solutions p/q. It follows from the classical Dirichlet theorem that for all $x\in \mathbb {R}\setminus \mathbb {Q}$, $\lambda (x)\geqslant 2$. On the other hand, Khintchine’s theorem implies that almost all $x\in \mathbb {R}$ with respect to the Lebesgue measure satisfy $\lambda (x) = 2$. In the first half of the 20th century, there was substantial interest in estimating the irrationality exponent of real algebraic numbers. It culminated in 1955 with the work of Roth [8], who established the best possible result, i.e. that for any algebraic $x\in \mathbb {R}\setminus \mathbb {Q}$, $\lambda (x) = 2$. Unfortunately, that result is ineffective, i.e. for $\lambda >2$ it does not allow us to find all rational p/q that satisfy (1). Therefore, for example, it can not be used to solve the Thue equations

$$\begin{aligned} F(p,q) = c \end{aligned}$$

in integer p, q, where $F\in \mathbb {Z}[x,y]$ is a homogeneous polynomial of degree $d\geqslant 3$ and c is some integer parameter. Since then, many mathematicians have worked on effective results regarding the irrationality exponents of algebraic numbers.

Given $x\in \mathbb {R}\setminus \mathbb {Q}$, by the effective irrationality exponent of x we define a positive real number $\lambda _{eff}(x)$ such that for all $\lambda >\lambda _{eff}(x)$ there exists an effectively computable $Q>0$ such that all rational solutions of the inequality (1) in reduced form satisfy $q\leqslant Q$.

All known upper bounds on $\lambda _{eff} (x)$ for algebraic real x are much weaker than in Roth’s theorem. First of all, the classical theorem of Liouville states that $\lambda _{eff}(x) \leqslant d$ where d is the degree of x. Therefore any non-trivial bound on $\lambda _{eff}(x)$ should be strictly smaller than d. One of the notable improvements of Liouville’s bound is based on Feldman’s refinement of the theory of linear forms in logarithms [6]. Its advantage is that it gives $\lambda _{eff}(x)<d$ for all algebraic numbers. However, the difference between $\lambda _{eff}(x)$ and d is usually extremely small. For state-of-the-art results regarding this approach, we refer to the book of Bugeaud [5]. For other notable achievements on this problem, we refer to [3, 4] and the references therein.

In this paper, we focus on the case of cubic irrationals. Multiplying by some integer number and shifting by another rational number, we can always guarantee that the minimal polynomial of the resulting cubic x is $x^3 + px + q$ for some $p,q\in \mathbb {Z}$. Notice also that such a transformation does not change the (effective) irrationality exponent of x. The first general result about $\lambda _{eff}(x)$ for these specific values x was achieved by Bombieri, van der Poorten and Vaaler [4] in 1996. They showed that under the conditions $|p|>e^{1000}$ and $|p|\geqslant q^2$, one has

$$\begin{aligned} \lambda _{eff}(x)\leqslant \frac{2\log (|p|^3)|}{\log (|p|^3/q^2)} + \frac{14}{(\log (|p|^3/q^2))^{1/3}}. \end{aligned}$$

Later, Wakabayashi [9] improved that bound for real cubic x that have the smallest absolute value among all real roots of $x^3+px+q$. For those values x, he showed that $\lambda _{eff}(x)\leqslant \lambda _w(p,q)$. It becomes non-trivial (i.e. smaller than 3) under the condition

$$\begin{aligned} |p|>2^{2/3}3^4|q|^{8/3} \left( 1+\frac{1}{390|q|^3}\right) ^{2/3} \end{aligned}$$

(2)

and for large p and q it asymptotically behaves like $\lambda _w(p,q)\sim 2 + (4\log |q| + 9.364)/(3\log |p|)$.

In this paper we investigate what estimates on $\lambda _{eff}(x)$ can be achieved with help of the convergents of the recently discovered continued fractions [1] of cubic irrationals with the minimal polynomial $x^3 - tx^2 - a\in \mathbb {Z}[x]$. There it was shown [1, Lemma 18] that, as soon as $|t|^3> 12 a>0$, the real root of this equation with the largest absolute value admits the continued fraction

$$\begin{aligned} x = \mathop {\textbf{K}}\left[ \begin{array}{l} \\ \!\!t \end{array} \overline{\begin{array}{llll}3(12k+1)(3k+1)a &{}3(12k+5)(3k+2)a &{}3(12k+7)(6k+5)a &{} 3(12k-1)(6k+1)a\\ (2i+1)t^2&{}(2i+1)t&{}2(2i+1)t^2&{}(2i+1)t\!\! \end{array}\hspace{-1.5ex}}\;\; \right] . \end{aligned}$$

Here i is the index of the corresponding partial quotient and $k = \big [\frac{i}{4}\big ]$.

The resulting upper bounds on $\lambda _{eff}(x)$ (see Theorems 3 and 4 in the next section) depend on prime factorisations of a and t but in any case they are better than those in [9]. Here we provide simplified versions of Theorems 3 and 4 that are not as powerful but are much easier to grasp. Also, to simplify the expressions in (3) and (4), we only provide the asymptotic behaviour of $\lambda _{eff}(x)$. For full and completely explicit bounds we refer to Theorems 3 and 4.

Theorem 1

Let x be the real root with the largest absolute value of the irreducible cubic polynomial $x^3-tx^2-a$. If $a,t\in \mathbb {Z}$ satisfy $|t|^3 > 12|a|$ then the effective Diophantine exponent of x satisfies

$$\begin{aligned} \lambda _{eff}(x)\leqslant 2 + \frac{5.609 + 2\log |a|}{3\log |t|} + O_a(1/\log ^2 |t|). \end{aligned}$$

(3)

This bound becomes non-trivial, i.e. less than 3, if $|t|>19.71|a|^{4/3}$.

In this paper we are able to provide the explicit upper bound on ||qx|| for slightly bigger values $\lambda$ than $\lambda _{eff}(x)$ from Theorem 1:

Theorem 2

Let x, a and t satisfy the same conditions as in Theorem 1. Then there exist explicitly computable constants $\tau = \tau (a,t)$, $q_0 = q_0(a,t)$ and $\lambda = \lambda (a,t)$ with

$$\begin{aligned} \lambda = 1 + \frac{8.574 + 2\log |a|}{3\log |t|} + O_a(1/\log ^2 |t|) \end{aligned}$$

(4)

such that for all $q\in \mathbb {Z}$ with $q\geqslant q_0$ one has

$$\begin{aligned} ||qx|| > \tau q^{-\lambda } \log (8|t| q)^{-\lambda - 1/2}. \end{aligned}$$

The formulae for $\tau , q_0$ and $\lambda$ are provided in (8) and Theorem 3. For $|t|>86.58 a^{4/3}$ the value of $\lambda$ becomes smaller than 2, i.e. better than in Liouville’s theorem.

Notice that by considering the particular case $t=-p$ and $a = -q^2$ and changing the vaiable $y = \frac{q}{x}$, one transforms the minimal polynomial of x from Theorems 1 and 2 to $y^3 + py + q$. That is the equation considered in [4, 9]. Theorem 1 implies that

$$\begin{aligned} \lambda _{eff}(y) \leqslant 2 + \frac{5.609 + 4\log |q|}{3\log |p|} + O_a(1/\log ^2 |p|) \end{aligned}$$

which is better than the value $\lambda _w(p,q)$ from Wakabayashi’s result.

2 Preliminaries and main results

Consider the real root of the equation $x^3 - tx^2 - a=0$ that has the largest absolute value among other roots of the same equation. Notice that $a\ne 0$ because otherwise x is not cubic. Also, by replacing x with $-x$ if needed, we can guarantee that $a>0$.

Next, by the standard CF transformations (see [1, Lemma 1]), we can cancel some common divisors of t and 3a from the continued fraction of x. Let $g_1:= \gcd (t^2, 3a)$ and $g_2:=\gcd (t, 3a/g_1)$. For convenience, we denote $t^2 = g_1t_2$, $t = g_2t_1$ and $3a = g_1g_2a^*$. We divide the following partial quotients of x by $g_1$: $\beta _1,a_1,\beta _2$; $\beta _3, a_3,\beta _4$; ..., $\beta _{2k-1},a_{2k-1},\beta _{2k}$,.... After that we divide the following partial quotients by $g_2$: $\beta _0, a_0, \beta _1$; $\beta _2,a_2,\beta _3$; ...; $\beta _{2k}, a_{2k}, \beta _{2k+1}$,...The resulting continued fraction has the same limit x as the initial one. To make $\beta _0$ integer, we consider the number $x/g_2$ instead of x. Its continued fraction is then

$$\begin{aligned} \mathop {\textbf{K}}\left[ \begin{array}{l} \\ \!\!t_1 \end{array} \begin{array}{llll}(12k+1)(3k+1)a^*&{}(12k+5)(3k+2)a^*&{}(12k+7)(6k+5)a^*&{} (12k-1)(6k+1)a^*\\ (2i+1)t_2&{}(2i+1)t_1&{}2(2i+1)t_2&{}(2i+1)t_1\!\! \end{array}\hspace{-1.5ex}\;\; \cdots \right] \nonumber \\ \end{aligned}$$

(5)

We define the following notions:

$$\begin{aligned} c_6 = c_6(t_1,t_2,a^*):= & {} \left\{ \begin{array}{ll} \displaystyle \frac{\sqrt{64t_1t_2 + 270a^*}}{2^{7/4}ec_1}&{}\text{ if } \; t>0\\ \displaystyle \frac{\sqrt{64|t_1t_2| - 54a^*}}{2^{7/4}ec_1}&{}\text{ if } \; t<0, \end{array}\right. \end{aligned}$$

(6)

$$\begin{aligned} c_7 = c_7(t_1,t_2,a^*):= & {} \left\{ \begin{array}{ll} \displaystyle \frac{2^{7/4}ec_1(16t_1t_2+9a^*)}{9a^*\sqrt{64t_1t_2 + 270a^*}}&{}\text{ if } \; t>0\\ \displaystyle \frac{2^{23/4}ec_1(|t_1t_2|-3a^*)}{9a^*\sqrt{64|t_1t_2| - 54a^*}}&{}\text{ if } \; t<0, \end{array}\right. \end{aligned}$$

(7)

where $c_1 = c_1(a^*)$ is defined in (13). Next,

$$\begin{aligned} \tau = \tau (t_1,t_2,a^*):= \frac{g_2\cdot (\log c_7)^{1/2}}{8c_6^8(8|t_1|)^{\frac{\log c_6}{\log c_7}}};\quad q_0 = q_0(t_1,t_2,a^*):= \frac{c_7^4}{8|t_1|}. \end{aligned}$$

(8)

The main result of this paper is

Theorem 3

Let x be the real root of the irreducible cubic polynomial $x^3-tx^2-a=0$ that has the largest absolute value. If $t_1t_2>12a^*$ then for all integer $q\geqslant q_0$ one has

$$\begin{aligned} ||qx|| > \tau q^{-\lambda } \log (8|t_1| q)^{-\lambda -1/2} \end{aligned}$$

where $\lambda = \frac{\log c_6}{\log c_7}$ and all the other parameters $t_1, t_2, a^*, q_0, c_6$ and $c_7$ are defined above in (6), (7) and (8). In particular, $\lambda _{eff}(x) \leqslant \lambda +1$.

As shown in Sect. 5, the constant $c_1$ can be replaced by a bigger constant $c_2$ defined in (14). But in that case, writing such an explicit inequality as in Theorem 3 is much harder (but theoretically possible). We do not provide it in the exact form here but only state the following result. Let $c_6^*$ and $c_7^*$ be defined in the same way as $c_6$ and $c_7$ but with the constant $c_2$ instead of $c_1$.

Theorem 4

Under the same conditions as in Theorem 3, The effective irrationality exponent of x satisfies

$$\begin{aligned} \lambda _{eff} (x)\leqslant \lambda ^*:= \frac{\log c_6^*}{\log c_7^*}+1. \end{aligned}$$

3 Deriving Theorems 1 and 2

In this section, we prove Theorems 1 and 2, given that the corresponding Theorems 3 and 4 are satisfied. We start with Theorem 3. It implies that $\lambda \leqslant \frac{\log c_6}{\log c_7}$. Equations (6), (7) then imply that

$$\begin{aligned} \log c_6= & {} \frac{1}{2} (\log 64 + \log |t_1t_2|) - \log (2^{7/4} ec_1) + O_a(|t_1t_2|^{-1});\\ \log c_7= & {} \log (2^{7/4}ec_1)+\log 16 - \log (9a^*) -\frac{1}{2}\log 64 +\frac{1}{2}\log |t_1t_2| + O_a(|t_1t_2|^{-1}). \end{aligned}$$

Then one computes

$$\begin{aligned} \frac{\log c_6}{\log c_7} - 1 = \frac{4\log 3 -3\log 2-4-4\log c_1 +2\log a^*}{\log |t_1t_2|} + O_a(1/\log ^2|t_1t_2|). \end{aligned}$$

(9)

Notice that by the definition of $t_1$ and $t_2$, $\log |t_1t_2| = 3\log |t| + O_a(1)$. From the definition (13) we see that $c_1$ and in turn the upper bound on $\lambda$ depend on the prime factorisation of $a^*$. If $3\not \mid a^*$ we always get $c_1> 0.0924$ and also $a^* \leqslant a$. All of that combined together, gives

$$\begin{aligned} \lambda \leqslant \frac{7.842 + 2\log a}{3\log |t|} + O_a(1/\log ^2|t|). \end{aligned}$$

In the case $3\mid a^*$, the lower bound for $c_1$ is better: $c_1> 0.1333$. On the other hand, the upper bound on $a^*$ is weaker: $a^*\leqslant 3a$. These two adjustments together give the first claim (4) of Theorem 2.

To show the second claim of Theorem 2, we notice that Theorem 3 provides a nontrivial lower bound for ||qx|| as soon as $\frac{\log c_6}{\log c_7}$ is strictly less that 2 or in other words, $c_6<c_7^2$. In view of (6) and (7), for $t>0$ this is equivalent to

$$\begin{aligned}{} & {} \frac{\sqrt{64t_1t_2+270a^*}}{2^{7/4} ec_1}< \frac{2^{7/2}e^2c_1^2(16t_1t_2+9a^*)^2}{81a^{*2}(64t_1t_2+270a^*)}\\{} & {} \Longleftrightarrow \qquad a^{*2}(64t_1t_2 + 270a^*)^{3/2} < \frac{2^{21/4}e^3c_1^3}{81}(16t_1t_2+9a^*)^2. \end{aligned}$$

Define the parameter u such that $16t_1t_2 = ua^{*4}-9a^*$. Also for convenience define $\tau := \frac{2^{21/4}e^3c_1^3}{81}$. Then the last inequality can be rewritten as

$$\begin{aligned} a^{*2}(4ua^{*4} + 234 a^*)^{3/2}< \tau u^2a^{*8} \quad \Longleftrightarrow \quad 4ua^{*3} + 234 < \tau ^{2/3}u^{4/3} a^{*3}. \end{aligned}$$

Notice that for $u\geqslant \left( \frac{4}{\tau ^{2/3}} + \frac{234}{64a^{*3}}\tau ^{4/3}\right) ^3$ one has

$$\begin{aligned} \tau ^{2/3}u^{4/3}a^{*3}\geqslant \left( 4 + \frac{234}{64a^{*3}}\tau ^2\right) \cdot ua^{*3} \geqslant 4ua^{*3} + \frac{234\tau ^2}{64a^{*3}}\cdot \frac{4^3}{\tau ^2}a^{*3} = 4ua^{*3} + 234 \end{aligned}$$

and the condition $c_6 < c_7^2$ is satisfied.

Recall that $t_1t_2 = t^3/(g_1g_2)$ and $a^* = 3a/(g_1g_2)$. Therefore, $16t_1t_2 > ua^{*4} - 9a^*$ is equivalent to $16t^3 > \frac{81}{(g_1g_2)^3}ua^4-27a$.

If $3\not \mid a^*$ then we get $c_1> 0.0924$ which in turn implies $\tau > 0.00744$ and

$$\begin{aligned} \left( \frac{4}{\tau ^{2/3}} + \frac{234}{64a^{*3}}\tau ^{4/3}\right) ^3\leqslant 104.97^3. \end{aligned}$$

On the other hand, we have $g_1g_2\geqslant 3$.

Finally, we get that for $t>0$ the non-trivial bound on $\lambda _{eff}(x)$ is always achieved if $t > \frac{104.97}{3}\cdot \left( \frac{81}{16}\right) ^{1/3}a^{4/3}\approx 60.08 a^{4/3}$. However, for many pairs a and t it is satisfied under essentially weaker conditions.

In the case $3\mid a^*$ we get $c_1> 0.13329$, thus $\tau > 0.0223$ and

$$\begin{aligned} \left( \frac{4}{\tau ^{2/3}} + \frac{234}{64a^{*3}}\tau ^{4/3}\right) ^3\leqslant 50.42^3. \end{aligned}$$

Then the non-trivial bound is achieved if $t> 50.42\cdot \left( \frac{81}{16}\right) ^{1/3}a^{4/3}\approx 86.57 a^{4/3}$.

The case $t<0$ is dealt analogously. The condition $c_6<c_7^2$ is equivalent to

$$\begin{aligned}{} & {} \frac{\sqrt{64|t_1t_2|-54a^*}}{2^{7/4}ec_1}< \frac{2^{7/2}e^2c_1^2(16|t_1t_2|-48a^*)^2}{81a^{*2}(64|t_1t_2|-54a^*)}\\{} & {} \quad \Longleftrightarrow \qquad a^{*2}(64|t_1t_2| - 54a^*)^{3/2} < \tau (16|t_1t_2|-48a^*)^2. \end{aligned}$$

Define u such that $16|t_1t_2| = ua^{*4} + 48a^*$. Then the last inequality can be rewritten as

$$\begin{aligned} 4ua^{*3} + 138 < \tau ^{2/3}u^{4/3}a^{*3}. \end{aligned}$$

One can check that the last inequality is satisfied for $u\geqslant \left( \frac{4}{\tau ^{2/3}} + \frac{138 \tau ^{4/3}}{64a^{*3}}\right) ^3$. As in the case of positive t, the right hand side is always smaller than $104.93^3$ in the case $3\not \mid a^*$ and is smaller than $50.42^3$ in the case $3\mid a^*$. Therefore for $3\not \mid a^*$ the condition $c_6<c_7^2$ is always satisfied if $|t|^3> \frac{104.93^3\cdot 81}{3^3\cdot 16} a^4 + 9a$ which follows from $|t| >60.06 a^{4/3}$. For $3\mid a^*$, similar computations give us $|t|^3 > \frac{50.42^3\cdot 81}{16} a^4 + 9a$ which follows from $|t|> 86.58a^{4/3}$. We now exhaust all possible cases for t and a, hence the second claim and in turn the whole proof of Theorem 2 is now complete.

To verify Theorem 1. one can repeat the same analysis as above for Theorem 4. In that case, the constant $c_1$ in the computations should be replaced by $c_2$ which is defined in (14). If $3\not \mid a^*$ it always satisfies $c_2\geqslant 0.1939$ and the inequality (9) becomes

$$\begin{aligned} \lambda ^* \leqslant 2 + \frac{4.877 + 2\log a}{3\log |t|} + O_a(1/\log ^2|t|). \end{aligned}$$

Next, we compute that $\tau \geqslant 0.0688$ and then

$$\begin{aligned} \left( \frac{4}{\tau ^{2/3}} + \frac{234}{64a^{*3}}\tau ^{4/3}\right) ^3\leqslant 23.93^3. \end{aligned}$$

If $3\mid a^*$, we have $c_2\geqslant 0.2797$ and $a^*\leqslant 3a$. Then (9) becomes (3). We also verify that $\tau \geqslant 0.206$ and

$$\begin{aligned} \left( \frac{4}{\tau ^{2/3}} + \frac{234}{64a^{*3}}\tau ^{4/3}\right) ^3\leqslant 11.47^3. \end{aligned}$$

Finally, for the case $3\not \mid a^*$, the condition $c_6<c_7^2$ is always satisfied if $|t|^3 > \frac{23.93^3\cdot 81}{3^3\cdot 16}a^4 + 9a$ which follows from $|t|>13.72 a^{4/3}$. For the case $3\mid a^*$ similar calculations give $|t|> 19.71 a^{4/3}$.

4 Nice, convenient and perfect continued fractions

Definition 1

Let x be a continued fraction given by

$$\begin{aligned} x = \mathop {\textbf{K}}\left[ \begin{array}{ccc} \beta _0&{}\beta _1&{}\beta _2\\ a_0&{}a_1&{}a_2 \end{array} \cdots \right] ;\quad \beta _i, a_i\in \mathbb {Z},\; \forall i\in \mathbb {Z}_{\geqslant 0}. \end{aligned}$$

For given positive integers k, r with $-1\leqslant r\leqslant k$ we define

$$\begin{aligned} \gamma _{k,r}:= \prod _{\begin{array}{c} i=k-r\\ 2\mid (i-k+r) \end{array}}^{k+r} \beta _i, \quad \gamma _{k,-1}:=1. \end{aligned}$$

We say that x is d-nice at index k where $d,k\in \mathbb {N}$ if $d\mid a_k$ and for all positive integer $r\leqslant k$ one has $a_{k-r}\beta _{k+r}\gamma _{k,r-2}\equiv -a_{k+r}\gamma _{k,r-1}$ (mod d). We call x (d, r)-perfect at index k, where $0\leqslant r\leqslant k$ if it is d-nice at index k and $\beta _{k-r}\equiv \beta _{k+r+1}\equiv 0$ (mod d).

We say that x is eventually d-nice at index k from position $k_0$ if the same conditions as above are satisfied for all $0\leqslant r\leqslant k-k_0$. In this paper the value $k_0$ will often be a fixed absolute constant. If there is no confusion about its value we will omit it in the text.

Let $p_n/q_n$ be the n’th convergent of x. Define the following matrices

$$\begin{aligned} S_n:= \left( \begin{array}{cc} p_{n}&{}q_{n}\\ p_{n-1}&{}q_{n-1} \end{array}\right) ;\qquad C_n:=\left( \begin{array}{cc} a_{n}&{}\beta _{n}\\ 1&{}0 \end{array}\right) . \end{aligned}$$

From the theory of continued fractions we know that $S_n = C_nC_{n-1}\cdots C_0$. To make this product shorter, we use the usual notation but in the descending order: $S_n = \prod _{i=n}^0 C_i$.

Lemma 1

Let the continued fraction x be eventually d-nice at index k from the position $k_0$. Then for all $0\leqslant r\leqslant k-k_0$ one has

$$\begin{aligned} \prod _{i=k+r}^{k-r} C_i \equiv \left( \begin{array}{cc} 0&{} \gamma _{k,r}\\ \gamma _{k,r-1}&{}0 \end{array}\right) \;\;(\textrm{mod}\; d). \end{aligned}$$

Moreover, if x is (d, r)-perfect at index k then $\prod _{i=k+r+1}^{k-r} C_i \equiv \textbf{0}$ (mod d).

Proof

We prove this by induction on r. For $r=0$ the statement is straightforward. Suppose that the statement is true for r and verify it for $r+1$.

$$\begin{aligned} \begin{array}{rl} \displaystyle \prod _{i=k+r+1}^{k-r-1} C_i &{}\equiv \left( \begin{array}{cc} a_{k+r+1}&{}\beta _{k+r+1}\\ 1&{}0 \end{array}\right) \left( \begin{array}{cc} 0&{} \gamma _{k,r}\\ \gamma _{k,r-1}&{}0 \end{array}\right) \left( \begin{array}{cc} a_{k-r-1}&{}\beta _{k-r-1}\\ 1&{}0 \end{array}\right) \\ &{}\equiv \left( \begin{array}{cc} a_{k-r-1}\beta _{k+r+1}\gamma _{k,r-1} + a_{k+r+1}\gamma _{k,r}&{} \beta _{k-r-1}\beta _{k+r+1}\gamma _{k,r-1}\\ \gamma _{k,r}&{}0 \end{array}\right) \;\;(\textrm{mod}\; d). \end{array} \end{aligned}$$

By the conditions of d-nice CF at index k, the last matrix is congruent to $\left( \begin{array}{cc} 0&{} \gamma _{k,r+1}\\ \gamma _{k,r}&{}0 \end{array}\right)$.

If x is (d, r)-perfect at index k then $\gamma _{k,r}\equiv 0$ (mod d) and we have

$$\begin{aligned} \prod _{i=k+r+1}^{k-r} C_i \equiv \left( \begin{array}{cc} a_{k+r+1}&{}0\\ 1&{}0 \end{array}\right) \left( \begin{array}{cc} 0&{} \gamma _{k,r}\\ \gamma _{k,r-1}&{}0 \end{array}\right) \equiv \textbf{0}\;\;(\textrm{mod}\; d). \end{aligned}$$

Another two properties of d-nice continued fractions that easily follow from the definition are

• Let $d_1,d_2$ be two coprime positive integer numbers. If a continued fraction is eventually $d_1$-nice and eventually $d_2$-nice at the same index k for the same position $k_0$ then it is eventually $d_1d_2$-nice at index k.

• If a continued fraction is eventually d-nice at index k then it is also eventually e-nice at the same index from the same position for all positive integer divisors e of d.

Definition 2

We say that the continued fraction x is (eventually) d-convenient at index k if there exists a sequence $(c_r)_{0\leqslant r\leqslant \lfloor k/2\rfloor }$ of residues modulo m such that for all nonnegative integers $r\leqslant k$ (resp. $r\leqslant k-k_0$) one has

• $\beta _{k+r+1}\equiv c_{\lfloor \frac{r}{2}\rfloor }\beta _{k-r}$ (mod d);

• if r is odd then $a_{k+r}\equiv -c_{\lfloor \frac{r}{2}\rfloor } a_{k-r}$ (mod d);

• if r is even then $a_{k+r}\equiv -a_{k-r}$ (mod d).

Lemma 2

Let $d>2$. Then any eventually d-convenient continued fraction at index k is also eventually d-nice. For $d=2$, any d-convenient continued fraction at index k such that $a_k\equiv 0$ (mod d) is also d-nice.

Proof

First of all, for $d>2$ and $r=0$ the condition $a_{k+r}\equiv -a_{k-r}$ (mod d) implies that $a_k\equiv 0$ (mod d), which is the first condition of d-nice CF.

Secondly, one can check that the first condition of d-convenient CF implies that for odd r, $\gamma _{k,r} \equiv c_{\lfloor \frac{r}{2}\rfloor }\gamma _{k,r-1}\beta _{k-r}\equiv \gamma _{k,r-1}\beta _{k+r+1}$ (mod d). Then we get

$$\begin{aligned} a_{k-r-1}\beta _{k+r+1}\gamma _{k,r-1}\equiv a_{k-r-1}\gamma _{k,r}\equiv -a_{k+r+1}\gamma _{k,r}\;(\textrm{mod}\; d) \end{aligned}$$

and the second condition of d-nice CF is verified.

Thirdly, for even r we get $c_{r/2}\gamma _{k,r}\equiv c_{r/2}\gamma _{k,r-1}\beta _{k-r}\equiv \gamma _{k,r-1}\beta _{k+r+1}$ (mod d) and therefore

$$\begin{aligned} a_{k-r-1}\beta _{k+r+1}\gamma _{k,r-1}\equiv c_{r/2}a_{k-r-1}\gamma _{k,r}\equiv -a_{k+r+1}\gamma _{k,r}\;(\textrm{mod}\; d). \end{aligned}$$

Again, the second condition of d-nice CF is satisfied.

5 Divisibility of entries of $S_n$

Lemma 3

Let $k\in \mathbb {N}$, $k\geqslant 2$ and d be any integer divisor of $2k+1$. The continued fraction (5) is eventually d-convenient at index k from the position 2. Additionally, the same statement is true for $k\equiv 3$ (mod 4) and $d=2$.

In the further discussion we will always deal with eventually d-convenient or d-nice continued fractions from the position 2. Therefore, to make the description shorter, we will omit the words ‘eventually’ and ‘from the position 2’ and call the continued fraction (5) d-convenient or d-nice.

Proof

We will check the conditions of d-convenient continued fraction separately for each of the cases, depending on k modulo 4.

Case $k=4m+1$. Then $m\equiv -\frac{3}{8}$ (mod d) and we use (5) to compute

$$\begin{aligned}{} & {} a_{k+4r}\equiv 8rt_2,\\{} & {} \beta _{k+4r}= a^*(12m+1+12r)(3m+1+3r)\equiv \frac{a^*}{16}(24r-7)(24r-1)\;(\textrm{mod}\; d);\\{} & {} a_{k+4r+1}\equiv (8r+2)t_1,\quad \beta _{k+4r+1}\equiv \frac{a^*}{16}(24r+1)(24r+7)\;(\textrm{mod}\; d);\\{} & {} a_{k+4r+2}\equiv 2(8r+4)t_2,\quad \beta _{k+4r+2}\equiv \frac{a^*}{8}(24r+5)(24r+11)\;(\textrm{mod}\; d);\\{} & {} a_{k+4r-1}\equiv (8r-2)t_1,\quad \beta _{k+4r-1}\equiv \frac{a^*}{8}(24r-11)(24r-5)\;(\textrm{mod}\; d). \end{aligned}$$

The conditions of d-convenient continued fraction at index k can now be easily checked where $c_r$ is the constant 1 sequence.

We proceed the same way in all other cases.

Case $k=4m+2$. Then $m\equiv -\frac{5}{8}$ (mod d) and

$$\begin{aligned}{} & {} a_{k+4r}\equiv 8rt_1,\quad \beta _{k+4r}\equiv \frac{a^*}{16}(24r-5)(24r+1)\;(\textrm{mod}\; d);\\{} & {} a_{k+4r+1}\equiv 2(8r+2)t_2,\quad \beta _{k+4r+1}\equiv \frac{a^*}{8}(24r-1)(24r+5)\;(\textrm{mod}\; d);\\{} & {} a_{k+4r+2}\equiv (8r+4)t_1,\quad \beta _{k+4r+2}\equiv \frac{a^*}{8}(24r+7)(24r+13)\;(\textrm{mod}\; d);\\{} & {} a_{k+4r-1}\equiv (8r-2)t_2,\quad \beta _{k+4r-1}\equiv \frac{a^*}{16}(24r-13)(24r-7)\;(\textrm{mod}\; d). \end{aligned}$$

One can easily check that for $s\equiv 0,1$ (mod 4), $\beta _{k+s+1} \equiv 2\beta _{k-s}$ (mod d) and for $s\equiv 2,3$ (mod 4), $\beta _{k+s+1}\equiv 2^{-1} \beta _{k-s}$ (mod d). Also, for $s\equiv 1$ (mod 4), $a_{k+s} \equiv 2a_{k-s}$ (mod d) and for $s\equiv 3$ (mod 4), $a_{k+s} \equiv 2^{-1}a_{k-s}$ (mod d). Hence, the conditions of d-convenient CF are verified, where the sequence $c_s$ is periodic with the period $2, 2^{-1}$.

Case $k=4\,m+3$, $d\ne 2$. Then $m\equiv -\frac{7}{8}$ (mod d) and

$$\begin{aligned}{} & {} a_{k+4r}\equiv 16rt_2,\quad \beta _{k+4r}\equiv \frac{a^*}{8}(24r-7)(24r-1)\;(\textrm{mod}\; d);\\{} & {} a_{k+4r+1}\equiv (8r+2)t_1,\quad \beta _{k+4r+1}\equiv \frac{a^*}{8}(24r+1)(24r+7)\;(\textrm{mod}\; d);\\{} & {} a_{k+4r+2}\equiv (8r+4)t_2,\quad \beta _{k+4r+2}\equiv \frac{a^*}{16}(24r+5)(24r+11)\;(\textrm{mod}\; d);\\{} & {} a_{k+4r-1}\equiv (8r-2)t_1,\quad \beta _{k+4r-1}\equiv \frac{a^*}{16}(24r-11)(24r-5)\;(\textrm{mod}\; d). \end{aligned}$$

One can then check the conditions of d-convenient CF at index k for the constant 1 sequence $c_r$.

Case $k=4\,m+3$, $d=2$. in this case one can easily see that $a_{k+4r}\equiv 0$ (mod 2), $a_{k+4r+1}\equiv a_{k+4r+3}\equiv t_1$ (mod 2), $a_{k+4r+2}\equiv t_2$ (mod 2); $\beta _{k+4r}\equiv \beta _{k+4r+1}\equiv a^*$ (mod 2) and $\beta _{k+4r+2}\equiv \beta _{k+4r-1}$ (mod 2). Therefore, the CF is 2-convenient at index k with the constant 1 sequence $c_r$.

Case $k=4m$. Then $m\equiv -\frac{1}{8}$ (mod d) and

$$\begin{aligned}{} & {} a_{k+4r}\equiv 8rt_1,\quad \beta _{k+4r}\equiv \frac{a^*}{8}(24r-5)(24r+1)\;(\textrm{mod}\; d);\\{} & {} a_{k+4r+1}\equiv (8r+2)t_2,\quad \beta _{k+4r+1}\equiv \frac{a^*}{16}(24r-1)(24r+5)\;(\textrm{mod}\; d);\\{} & {} a_{k+4r+2}\equiv (8r+4)t_1,\quad \beta _{k+4r+2}\equiv \frac{a^*}{16}(24r+7)(24r+13)\;(\textrm{mod}\; d);\\{} & {} a_{k+4r-1}\equiv 2(8r-2)t_2,\quad \beta _{k+4r-1}\equiv \frac{a^*}{8}(24r-13)(24r-7)\;(\textrm{mod}\; d). \end{aligned}$$

One can then check the conditions of d-convenient CF with the periodic sequence $c_r$ with the period $2^{-1},2$.

Lemmata 2 and 3 show that x is d-nice at each index $k\geqslant 2$ for appropriately chosen d. As the next step, we show that for almost every prime p, it is also (p, t)-perfect at infinitely many carefully chosen indices k and t. This fact will allow us to show that all the entries of $C_kC_{k-1}\cdots C_1$ are multiples of some big power of p.

First of all, let’s consider the case $p>2$ and $p\mid a^*$. Let $s\in \mathbb {N}$ be such that $p^s|| a^*$. Consider $q = p^l$ for some $1\leqslant l\leqslant s$. If we write $q=2m+1$ then we have $q\mid \alpha _k$ for $k=m + rq = \frac{(2r+1)q - 1}{2}$ where $r\in \mathbb {Z}_{\geqslant 0}$. One can easily see that for any such value of k, x is (q, 0)-perfect at index k. In view of Lemma 1, we can then split the product $S_k$ into $\left\lfloor \frac{2k+q-1}{2q}\right\rfloor$ groups such that all entries of the resulting product matrix in each group are multiples of q. Finally, we combine this information for $q^l$ for all $1\leqslant l\leqslant s$ and derive that all entries of the product $\prod _{i=k}^2 C_i$ are divisible by

$$\begin{aligned} p^{\;\sum \limits _{i=1}^s \left\lfloor \frac{2k+p^i-1}{2p^i}\right\rfloor }. \end{aligned}$$

Next, consider the case $p=2$ and $p\mid a^*$. We have $p\mid a_k$ for all $k\equiv 3$ (mod 4) and one can easily see that for all such k, x is (p, 0) perfect at index k. Then the analogous application of Lemma 1 as in the previous case implies that all entries of $\prod _{i=k}^2 C_i$ are divisible by $2^{\lfloor k/4\rfloor }.$

For the case $p=2$, $p\not \mid a^*$ the result is slightly weaker. From (5) one can verify that $\beta _{8\,m+2}\equiv \beta _{8\,m+5}\equiv 0$ (mod 2) for all $m\in \mathbb {Z}_{\geqslant 0}$ and therefore x is (2, 1)-perfect at indices $8m+3$. Then Lemma 1 then implies that all entries of $\prod _{i=k}^2 C_i$ are divisible by $2^{\lfloor (k+3)/8\rfloor }.$

Finally, in the next lemma we consider the remaining case of $p\in \mathbb {N}$ that do not divide $a^*$.

Lemma 4

Let $p\in \mathbb {N}$ be such that $\gcd (p,6)=1$. Then for all $k\in \mathbb {Z}$ all the entries of the product of matrices $\prod _{i=k}^2 C_i$ are divisible by

$$\begin{aligned} p^{\left\lfloor \frac{3k + p-2}{3p}\right\rfloor }. \end{aligned}$$

Proof

We prove by routinely considering all the cases, depending on p modulo 12.

Case $p = 12m+1$. Then with help of (5) one can verify that for all $r\in \mathbb {Z}_{\geqslant 0}$,

$$\begin{aligned} \begin{array}{rl} 0&{}\equiv \beta _{4(m+rp)+1}\equiv \beta _{4(2m+rp)}\equiv \beta _{4(4m+rp)+1}\\ &{}\equiv \beta _{4(5m+rp)+2}\equiv \beta _{4(7m+rp)+3}\equiv \beta _{4(8m+rp)+2}\\ &{}\equiv \beta _{4(10m+rp)+3}\equiv \beta _{4(11m+rp)+4}\;(\textrm{mod}\; p) \end{array} \end{aligned}$$

and $0\equiv a_{6m+rp}$ (mod p). In view of Lemma 3, we then derive that x is $(p,2m-1)$-perfect at indices $k = 6m+2rp$ for all $r\in \mathbb {Z}_{\geqslant 0}$ and is (p, 2m)-perfect at indices $k = 6\,m+(2r+1)p$. Lemma 1 then implies that all the entries of the following products of matrices are divisible by p:

$$\begin{aligned} \prod _{i=8m+2rp}^{4m+2rp+1} C_i,\qquad \prod _{i=20m+2rp+2}^{16m+4rp+1} C_i. \end{aligned}$$

Finally, one can easily check that for $k = (n+1)p - \frac{p-1}{3}$, the product $\prod _{i=k}^2 C_i$ contains $n+1$ blocks of the above form. Therefore all its entries are divisible by $p^{n+1}$.

The other cases are done analogously.

Case $p=12m+5$. One verifies that for all $r\in \mathbb {Z}_{\geqslant 0}$,

$$\begin{aligned} \begin{array}{rl} 0&{}\equiv \beta _{4(m+rp)+2}\equiv \beta _{4(2m+rp)+3}\equiv \beta _{4(4m+rp)+6}\equiv \beta _{4(5m+rp)+9}\\ &{}\equiv \beta _{4(7m+rp)+12}\equiv \beta _{4(8m+rp)+13}\\ &{}\equiv \beta _{4(10m+rp)+16}\equiv \beta _{4(11m+rp)+19}\;(\textrm{mod}\; p) \end{array} \end{aligned}$$

and $0\equiv a_{6m+rp+2}$ (mod p). Then Lemma 3 implies that x is (p, 2m)-perfect at indices $k=6m+2rp$ for all $r\in \mathbb {Z}$ and is $(p,2m-1)$-perfect at indices $k=6m+(2r+1)p$. Lemma 1 then implies that all the entries of the following products are divisible by p:

$$\begin{aligned} \prod _{i=8m+2rp+3}^{4m+2rp+2} C_i,\qquad \prod _{i=20m+2rp+9}^{16m+4rp+6} C_i. \end{aligned}$$

For $k\geqslant (n+1)p-\frac{p-2}{3}$ one can easily check that the product $\prod _{i=k}^2 C_i$ contains $n+1$ blocks of the above form. Therefore all its entries are divisible by $p^{n+1}$.

Case $p=12m+7$. Then for all $r\in \mathbb {Z}_{\geqslant 0}$,

$$\begin{aligned} \begin{array}{rl} 0&{}\equiv \beta _{4(m+rp)+3}\equiv \beta _{4(2m+rp)+4}\equiv \beta _{4(4m+rp)+9}\equiv \beta _{4(5m+rp)+12}\\ &{}\equiv \beta _{4(7m+rp)+17}\equiv \beta _{4(8m+rp)+18}\\ &{}\equiv \beta _{4(10m+rp)+23}\equiv \beta _{4(11m+rp)+26}\;(\textrm{mod}\; p) \end{array} \end{aligned}$$

and $0\equiv a_{6m+rp+3}$ (mod p). Lemmata 3 and 1 imply that all the entries of the following products are divisible by p:

$$\begin{aligned} \prod _{i=8m+2rp+4}^{4m+2rp+3} C_i,\qquad \prod _{i=20m+2rp+12}^{16m+4rp+9} C_i. \end{aligned}$$

For $k\geqslant (n+1)p-\frac{p-1}{3}$ one can easily check that the product $\prod _{i=k}^2 C_i$ contains $n+1$ blocks of the above form. Therefore all its entries are divisible by $p^{n+1}$.

Case $p=12m+11$. Then for all $r\in \mathbb {Z}_{\geqslant 0}$,

$$\begin{aligned} \begin{array}{rl} 0&{}\equiv \beta _{4(m+rp)+4}\equiv \beta _{4(2m+rp)+7}\equiv \beta _{4(4m+rp)+14}\equiv \beta _{4(5m+rp)+19}\\ &{}\equiv \beta _{4(7m+rp)+26}\equiv \beta _{4(8m+rp)+29}\\ &{}\equiv \beta _{4(10m+rp)+36}\equiv \beta _{4(11m+rp)+41}\;(\textrm{mod}\; p) \end{array} \end{aligned}$$

and $0\equiv a_{6m+rp+5}$ (mod p). Lemmata 3 and 1 imply that all the entries of the following products are divisible by p:

$$\begin{aligned} \prod _{i=8m+2rp+7}^{4m+2rp+4} C_i,\qquad \prod _{i=20m+2rp+19}^{16m+4rp+14} C_i. \end{aligned}$$

For $k\geqslant (n+1)p-\frac{p-2}{3}$ one can easily check that the product $\prod _{i=k}^2 C_i$ contains $n+1$ blocks of the above form. Therefore all its entries are divisible by $p^{n+1}$.

In all four cases we have that for $k\geqslant (n+1)p - \frac{p-2}{3}$ all the entries of $\prod _{i=k}^2 C_i$ are divisible by $p^{n+1}$. Writing it in terms of k we get that this power of p is

$$\begin{aligned} \left\lfloor \frac{k+\frac{p-2}{3}}{p}\right\rfloor = \left\lfloor \frac{3k + p - 2}{3p}\right\rfloor . \end{aligned}$$

We combine all the divisibility properties of $\prod _{i=n}^1 C_i$ together and get the following

Proposition 1

Let the prime factorisation of $a^*$ be $a^* = 2^{\sigma _0}p_1^{\sigma _1}p_2^{\sigma _2}\cdots p_d^{\sigma _d}$ where $\sigma _0$ can be equal to zero while the other powers $\sigma _i$ are strictly positive. Define $\mathbb {P}_1:= \{p_1, \ldots , p_d\}$, $\mathbb {P}_2:= \mathbb {P}\setminus (\mathbb {P}_1\cup \{2,3\})$. If $2\mid a^*$ then

$$\begin{aligned} \gcd (p_n,q_n) \geqslant 2^{\big \lfloor \frac{n}{4}\big \rfloor }\prod _{p_i\in \mathbb {P}_1} p_i^{\;\sum \limits _{j=1}^{\sigma _i} \left\lfloor \frac{2n+p^j-1}{2p^j}\right\rfloor } \cdot \prod _{p\in \mathbb {P}_2} p^{\big \lfloor \frac{3n+p-2}{3p}\big \rfloor }. \end{aligned}$$

(10)

If $2\not \mid a^*$ then

$$\begin{aligned} \gcd (p_n,q_n) \geqslant 2^{\big \lfloor \frac{n+3}{8}\big \rfloor }\prod _{p_i\in \mathbb {P}_1} p_i^{\;\sum \limits _{j=1}^{\sigma _i} \left\lfloor \frac{2n+p^j-1}{2p^j}\right\rfloor } \cdot \prod _{p\in \mathbb {P}_2} p^{\big \lfloor \frac{3n+p-2}{3p}\big \rfloor }. \end{aligned}$$

(11)

We now provide simpler lower bounds for (10) and (11) and then provide slightly better ones that, after some effort, can still be made effective for large enough n. Observe that $\big \lfloor \frac{2n+ p^j-1}{2p^j}\big \rfloor \geqslant \big \lfloor \frac{n}{p^j}\big \rfloor$ and $\big \lfloor \frac{3n+ p-2}{3p}\big \rfloor \geqslant \big \lfloor \frac{n}{p}\big \rfloor$. For convenience, if $3\not \mid a^*$ we still add 3 to the set $\mathbb {P}_1$ by setting $p_{d+1}:=3, \sigma _{d+1}:=0$. Then

$$\begin{aligned}{} & {} 2^{\sum _{i=1}^\infty \frac{n}{2^i}}\cdot \prod _{p_j\in \mathbb {P}_1} p_j^{\sum _{i=1}^{\sigma _j}\big \lfloor \frac{n}{p_j^i}\big \rfloor } \cdot \prod _{p\in \mathbb {P}_2} p^{\big \lfloor \frac{n}{p}\big \rfloor }\cdot \prod _{p_j\in \mathbb {P}_1} p_j^{\sum _{i=\sigma _j+1}^\infty \frac{n}{p_j^i}} \cdot \prod _{p\in \mathbb {P}_2}p^{\sum _{i=2}^\infty \frac{n}{p^i}} \geqslant n!\\{} & {} \quad \geqslant \sqrt{2\pi n} \left( \frac{n}{e}\right) ^n. \end{aligned}$$

The last inequality implies that

$$\begin{aligned} \gcd (p_n,q_n)\geqslant \sqrt{2\pi n}(c_1n)^n \end{aligned}$$

(12)

where $c_1=c_1(a^*)$ is defined as

$$\begin{aligned} c_1 = \left\{ \begin{array}{ll} 2^{-3/4} \exp \left( -1-\sum _{p_j\in \mathbb {P}_1} \frac{\ln p_j}{p_j^{\sigma _j}(p_j-1)} - \sum _{p\in \mathbb {P}_2} \frac{\ln p}{p(p-1)}\right) &{} \text{ if } \; 2\mid a^*;\\ 2^{-7/8} \exp \left( -1-\sum _{p_j\in \mathbb {P}_1} \frac{\ln p_j}{p_j^{\sigma _j}(p_j-1)} - \sum _{p\in \mathbb {P}_2} \frac{\ln p}{p(p-1)}\right) &{} \text{ if } \; 2\not \mid a^*. \end{array}\right. \end{aligned}$$

(13)

The parameter $c_1$ reaches its minimal value in the case $\mathbb {P}_1 = \{3\}$ with $\sigma _1 = 0$. Then $c_1\approx 0.0924$. However, if $a^* = 3$ then $c_1\approx 0.13329$. In general, more squares of small prime numbers divide $a^*$, bigger is the value of $c_1$.

We can provide a better asymptotic lower estimate on $\gcd (p_n,q_n)$ for large enough n. The exact condition on n can be effectively computed, however the computations will not be nice. Consider a prime $p\in \mathbb {P}_2$. The term $p^{\big \lfloor \frac{3n+p-2}{3p}\big \rfloor }$ has an extra power of p compared to $p^{\lfloor n/p\rfloor }$ if for some integer k,

$$\begin{aligned} \frac{n}{p}<k\leqslant \frac{3n+p-2}{3p}\qquad \Longleftrightarrow \qquad \frac{n}{k}< p\leqslant \frac{3n-2}{3k-1}. \end{aligned}$$

We also have $\prod _{p\in \mathbb {P}_1} p\asymp 1$ where the implied constants only depend on $a^*$ but not on n. Define the set

$$\begin{aligned} K:= \bigcup _{k=1}^n \left( \frac{n}{k}, \frac{3n-2}{3k-1}\right] \end{aligned}$$

Then $\gcd (p_n,q_n)\geqslant T \cdot \sqrt{2\pi n}(c_1n)^n$ where

$$\begin{aligned} T \asymp \prod _{p\in \mathbb {P}\cap K} p = \exp \left( \sum _{p\in K\cap \mathbb {P}} \ln p\right) = \exp \left( \sum _{k=1}^n \left( \theta \left( \frac{3n-2}{3k-1}\right) - \theta \left( \frac{n}{k}\right) \right) \right) , \end{aligned}$$

where $\theta (x)$ is the first Chebyshev function. It is well known (see [7] for example) that for large enough x, $|\theta (x) - x|< \frac{x}{2\ln x}$. Therefore for $y>x$ one has $\theta (y)-\theta (x)\geqslant y-x - \frac{y}{\ln y}$. This implies

$$\begin{aligned} \sum _{k=1}^{\sqrt{\ln n}} \left( \theta \left( \frac{3n-2}{3k-1}\right) - \theta \left( \frac{n}{k}\right) \right)\geqslant & {} \sum _{k=1}^{\sqrt{\ln n}} \frac{n-2k}{k(3k-1)}\ -\ O\left( \frac{n}{\sqrt{\ln n}}\right) \\= & {} n\sum _{k=1}^{\sqrt{\ln n}} \frac{1}{k(3k-1)}\ -\ O\left( \frac{n}{\sqrt{\ln n}}\right) . \end{aligned}$$

For any $\varepsilon >0$ and for large enough n, the last expression can be made bigger that $\tau (1 - \varepsilon )n$ where $\tau := \sum _{k=1}^\infty \frac{1}{k(3k-1)}\approx 0.74102$. Therefore $T \gg e^{\tau (1 -\varepsilon )n} = \gamma ^{n(1-\varepsilon )}$ where $\gamma = e^\tau$. Finally, we get

$$\begin{aligned} \gcd (p_n,q_n)\gg ((c_2-\delta ) n)^n,\quad \text{ where } c_2 = c_1\cdot \gamma , \end{aligned}$$

(14)

$\delta$ can be made arbitrarily small and the implied constant in the inequality only depends on $a^*$ and $\delta$ but not on n. For the case $a^* = 1$, when the constant $c_1$ is minimal possible, we get $c_2 \approx 0.1939$. Respectively, for $a^*=6$, $c_2 \approx 0.2797$.

6 Lower and upper bounds on the denominators $q_n$.

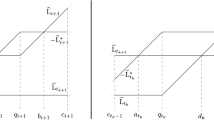
In this section we will get upper and lower bounds of the denominators $q_n$, compared to $q_{n-1}$. Since the recurrent formulae between $q_n, q_{n-1}$ and $q_{n-2}$ depend on n modulo 4, it makes sense to compare $q_{4k}$ and $q_{4k+4}$.

We adapt some notation from [1]. Denote

$$\begin{aligned} T_{4k}:= \left( \begin{array}{cc} p_{4k}&{}q_{4k}\\ p_{4k-4}&{}q_{4k-4} \end{array}\right) \end{aligned}$$

Then [1, (69) and (70)] one has

$$\begin{aligned} T_{4k+4} = \left( \begin{array}{cc} a_{k11}&{}a_{k12}\\ 1&{}0 \end{array} \right) S_{4k} \end{aligned}$$

(15)

where $a_{k11}$ and $a_{k12}$ are the corresponding indices of $C_{4k+4}C_{4k+3}C_{4k+2}C_{4k+1}$. In view of (5), one computes

$$\begin{aligned}{} & {} \begin{array}{rl} a_{k11} = 2(8k+3)(8k+5)(8k+7)(8k+9)(t_1t_2)^2 &{}+ 6(8k+5)(8k+7)(36k^2+55k+16)a^*t_1t_2\\ &{}+ (12k+5)(12k+11)(3k+2)(6k+7)a^{*2} \end{array};\\{} & {} a_{k12} = 2(12k+1)(3k+1)(8k+7)a^*t_1((8k+5)(8k+9)t_1t_2 + 2(36k^2+63k+25)a^*).\nonumber \end{aligned}$$

(16)

To make the notation shorter, we write $a_{k12} = 2(12k+1)(3k+1)(8k+7)a^*t_1 p(k)$ where p(k) is a polynomial of k with parameters $t_1t_2$ and $a^*$.

Then an easy adaptation of the proof of [1, Lemma 16] gives

Lemma 5

Let $a^*\in \mathbb {N}$ and $t_1,t_2\in \mathbb {Z}$ satisfy $12a^*\leqslant |t_1t_2|$. Then $q_{4k+4}$ and $q_{4k}$ satisfy the relation

$$\begin{aligned} |q_{4k+4}| > (8k+3)(8k+5)(8k+7)(8k+9) (t_1t_2+2a^*)^2 |q_{4k}|. \end{aligned}$$

(17)

Now we will provide an opposite inequality between the denominators $q_{4k+4}$ and $q_{4k}$. Three consecutive denominators of this form are related by the equation [1, (72)]:

$$\begin{aligned} q_{4k+4} = a_{k11}q_{4k} + (dq_{4k-4}-b_{k21}q_{4k})\frac{a_{k12}}{b_{k22}}, \end{aligned}$$

(18)

where $b_{k21}/d$ and $b_{k22}/d$ are the corresponding entries of $C_{4k-2}^{-1}C_{4k-1}^{-1}C_{4k}^{-1}$, i.e.

$$\begin{aligned} d= & {} -(12k-7)(12k-5)(12k-1)(3k-1)(6k-1)(6k+1)a^{*3},\\ b_{k21}= & {} -(12k-5)(6k-1)a^* - 2(8k-3)(8k-1)t_1t_2,\nonumber \\ b_{k22}= & {} 2(8k-1)t_1((8k-3)(8k+1)t_1t_2+2(36k^2-9k-2)a^*) \nonumber \\=: & {} 2(8k-1)t_1p(k-1).\nonumber \end{aligned}$$

(19)

Lemma 6

Let $a^*$, $t_1, t_2$ be the same as in Lemma 5. Then $q_{4k+4}$ and $q_{4k}$ satisfy the following relations:

$$\begin{aligned} |q_{4k+4}|\leqslant & {} 2(8k+3)(8k+5)(8k+7)(8k+9)\left( t_1t_2+\frac{135}{32}a^*\right) ^2|q_{4k}|,\quad \text{ if } \; t_1t_2>0, \end{aligned}$$

(20)

$$\begin{aligned} |q_{4k+4}|\leqslant & {} 2(8k+3)(8k+5)(8k+7)(8k+9)\left( t_1t_2 + \frac{27}{32} a^*\right) ^2|q_{4k}|,\quad \text{ if } \; t_1t_2<0.\nonumber \\ \end{aligned}$$

(21)

Proof

First, we estimate the terms in (18). Since $|t_1t_2|\geqslant 12a^*$, we get for all $k\geqslant 1$ that $\frac{1}{12}(12k-5)(6k-1)(12a^*) < (8k-3)(8k-1)(12a^*) \leqslant (8k-3)(8k-1)|t_1t_2|$. Therefore

$$\begin{aligned} |b_{k21}|\leqslant 3(8k-3)(8k-1)|t_1t_2|. \end{aligned}$$

(22)

Next, by Lemma 5 we have

$$\begin{aligned} |dq_{4k-4}|\leqslant \frac{(12k-7)(12k-5)(12k-1)(3k-1)(6k-1)(6k+1)a^{*3}}{(8k-5)(8k-3)(8k-1)(8k+1)(t_1t_2+2a^*)^2} q_{4k}. \end{aligned}$$

Since $|t_1t_2 + 2a^*|\geqslant 10a^*$ and $12a^* \leqslant |t_1t_2|$, one can verify that

$$\begin{aligned} |dq_{4k-4}| < (8k-3)(8k-1) |t_1t_2 q_{4k}|. \end{aligned}$$

(23)

Next, we have $(8k+5)(8k+9)|t_1t_2| > 12(36k^2+63k+25)a^*$, therefore we always have

$$\begin{aligned} \frac{|p(k)|}{(8k+5)(8k+9)|t_1t_2|}\in \left\{ \begin{array}{ll} \left[ 1,\frac{7}{6} \right] &{}\text{ if } \; t_1t_2\geqslant 0;\\ \left[ \frac{5}{6}, 1\right] &{} \text{ if } \; t_1t_2<0. \end{array}\right. \end{aligned}$$

The last inequality in turn implies that for $k\geqslant 1$ the ratio $a_{k12}/b_{k22}$ is always positive and satisfies

$$\begin{aligned} \frac{a_{k12}}{b_{k12}} \leqslant \frac{6(12k+1)(3k+1)(8k+7)a^*}{8k-1}. \end{aligned}$$

(24)

Assume that $t_1t_2\geqslant 0$. In that case, the last inequality together with (22) and (23) imply that

$$\begin{aligned} \left| (dq_{4k-4}-b_{k21}q_{4k})\frac{a_{k12}}{b_{k22}}\right| \leqslant 24 (8k-3)(8k+7)(12k+1)(3k+1) a^*t_1t_2 q_{4k}. \end{aligned}$$

One can check that for all $k\geqslant 1$,

$$\begin{aligned} \frac{6(8k+5)(8k+7)(36k^2+55k+16) + 24 (8k-3)(8k+7)(12k+1)(3k+1)}{2(8k+3)(8k+5)(8k+7)(8k+9)} <\frac{135}{16}\nonumber \\ \end{aligned}$$

(25)

and

$$\begin{aligned} \frac{81}{256}<\frac{(12k+5)(12k+11)(3k+2)(6k+7)}{2(8k+3)(8k+5)(8k+7)(8k+9)} \leqslant \frac{23}{66} < 1. \end{aligned}$$

(26)

These bounds together with the formula (16) and equation (18) imply the inequality (20) for $k\geqslant 1$. Finally, this bound can be easily verified for $k=0$ from the equation $q_4 = a_{011}q_0 + a_{012} q_{-1}$ and $q_{-1} = 0$.

Consider the case $t_1<0$. One can check that for all $k\geqslant 1$,

$$\begin{aligned} \frac{321}{187}\geqslant \frac{6(8k+5)(8k+7)(36k^2+55k+16)}{2(8k+3)(8k+5)(8k+7)(8k+9)} \geqslant \frac{27}{16}. \end{aligned}$$

(27)

This together with the condition $|t_1t_2|>12a^{*2}$ imply that $a_{k11}>0$ and $q_{4k}$ and $q_{4k+4}$ share the same sign for all $k\in \mathbb {N}$. Next, since $(12k-5)(6k-1)a^* < (8k-3)(8k-1)|t_1t_2|$, we have that $b_{k21}>0$ and then in view of (23) and $\frac{a_{k12}}{b_{k22}}>0$, the term $(dq_{4k-4}-b_{k21}q_{4k})\frac{a_{k12}}{b_{k22}}$ has the opposite sign compared to $a_{k11}q_{4k}$. That all implies that $|q_{4k+4}|\leqslant |a_{k11} q_{4k}|$. Finally, the inequalities (26) together with (27) establish the bound (21).

Lemma 6 immediately implies that for $t_1t_2>0$,

$$\begin{aligned} |q_{4k}|\leqslant 2^k \left( t_1t_2 + \frac{135}{32}a^*\right) ^{2k}(8k+1)!! \leqslant 16k \left( 8\cdot 2^{1/4}e^{-1}\sqrt{t_1t_2 + \frac{135}{32}a^*}\right) ^{4k} k^{4k}. \end{aligned}$$

The case of $t_1t_2<0$ can be dealt with in a similar way. Finally, we get the estimate

$$\begin{aligned} |q_{4k}| \leqslant 16 k c_3^{4k} k^{4k}, \end{aligned}$$

(28)

where

$$\begin{aligned} c_3 = c_3(t_1,t_2,a^*) = \left\{ \begin{array}{ll} 8\cdot 2^{1/4}e^{-1}\sqrt{t_1t_2 + \frac{135}{32}a^*}&{}\text{ if } \; t_1t_2>0\\ 8\cdot 2^{1/4}e^{-1}\sqrt{|t_1t_2| - \frac{27}{32}a^*}&{}\text{ if } \; t_1t_2<0. \end{array}\right. \end{aligned}$$

Lemma 7

Under the same conditions on $a^*, t_1,t_2$ as in the previous lemma, one has

$$\begin{aligned}{} & {} |q_{4k+4}|\geqslant 2(8k+3)(8k+5)(8k+7)(8k+9)\left( t_1t_2+\frac{9}{16}a^*\right) ^2|q_{4k}|,\quad \text{ if } \; t_1t_2>0, \end{aligned}$$

(29)

$$\begin{aligned}{} & {} |q_{4k+4}|\geqslant 2(8k+3)(8k+5)(8k+7)(8k+9)\left( t_1t_2 + 3 a^*\right) ^2|q_{4k}|,\quad \text{ if } \; t_1t_2<0.\nonumber \\ \end{aligned}$$

(30)

Proof

If $t_1t_2>0$ we have $q_{4k+4} > a_{k11}q_{4k}$. Then the lower bound in (26) together with the lower bound in (27) imply the bound (29).

Now assume that $t_1t_2<0$. Then, as we have shown in the proof of Lemma 6, $b_{k21}>0$ and $dq_{4k-4}$ and $b_{k21}q_{4k}$ have the opposite signs. This together with $\frac{a_{k12}}{b_{k22}}>0$, the inequality (24) and $0<b_{k21}\leqslant 2(8k-3)(8k-1)|t_1t_2|$ in turn imply that

$$\begin{aligned} |q_{4k+4}|\geqslant & {} |a_{k11}q_{4k}| - \frac{b_{k21}a_{k12}}{b_{k22}}|q_{4k}|\\\geqslant & {} (a_{k11} + 12(8k-3)(12k+1)(3k+1)(8k+7)a^*t_1t_2)|q_{4k}| \end{aligned}$$

We need to show that the expression

$$\begin{aligned}{} & {} a_{k11}+ 12(8k-3)(12k+1)(3k+1)(8k+7)a^*t_1t_2 \\{} & {} \quad - 2(8k+3)(8k+5)(8k+7)(8k+9)\left( t_1t_2 + 3 a^*\right) ^2 \end{aligned}$$

is always positive. Notice that after substituting (16) into it and expanding the brackets, the term with $(t_1t_2)^2$ disappears. The term for $a^*t_1t_2$ then equals

$$\begin{aligned} -6(8k+7)(160k^3+1532k^2+1063k+196)a^*t_1t_2 \end{aligned}$$

and the term for $a^{*2}$ is

$$\begin{aligned} -(71136 k^4 + 212976 k^3 + 227970 k^2 + 102633 k + 16240) \end{aligned}$$

(we made these computations with Wolfram Mathematika). Finally, one can check that in the case $|t_1t_2|> 12a^*$, the absolute value of the first term is always bigger than that of the second term and therefore the whole expression is positive.

Remark. By performing neater computations, one can make the coefficient 3 in $(t_1t_2+3a^*)^2$ slightly smaller. However we decide not to further complicate already tedious calculations.

Analogously to (28), one can find simpler lower bounds for $|q_{4k}|$. With help of the known inequality $(8k+1)!!\geqslant 8k(8k/e)^{2k}$, Lemma 7 infers

$$\begin{aligned} |q_{4k}|\geqslant 8 k c_4^{4k} k^{4k}, \end{aligned}$$

(31)

where

$$\begin{aligned} c_4 = c_4(t_1,t_2,a^*) = \left\{ \begin{array}{ll} 8\cdot 2^{1/4}e^{-1}\sqrt{t_1t_2 + \frac{9}{16}a^*}&{}\text{ if } \; t_1t_2>0\\ 8\cdot 2^{1/4}e^{-1}\sqrt{|t_1t_2| - 3a^*}&{}\text{ if } \; t_1t_2<0. \end{array}\right. \end{aligned}$$

7 Distance between x and the convergents

From [1, Lemma 17] we know that, under the condition $12a^*\leqslant |t_1t_2|$, one has

$$\begin{aligned} \left| x - \frac{p_{4k}}{q_{4k}}\right| < 2 \left| \frac{p_{4k}}{q_{4k}} - \frac{p_{4k+4}}{q_{4k+4}}\right| . \end{aligned}$$

In order to estimate the right hand side, we use the matrix equation [1, (72)]:

$$\begin{aligned} T_{k+1} = \left( \begin{array}{cc} a_{k11} - a_{k12} \frac{b_{k21}}{b_{k22}}&{}\frac{da_{k12}}{b_{k22}}\\ 1&{}0 \end{array}\right) T_k. \end{aligned}$$

Notice that the values of d in fact depends on k (see the formula (19)). to emphasize this dependence, in this section we write d(k) for it. Then the above equation gives the following formula:

$$\begin{aligned} \left| \frac{p_{4k}}{q_{4k}} - \frac{p_{4k+4}}{q_{4k+4}}\right| = \frac{\left| \prod _{i=1}^k \frac{d(i)a_{i12}}{b_{i22}}\right| \cdot |p_0q_4-q_0p_4|}{q_{4k}q_{4k+4}}. \end{aligned}$$

We first compute its product term:

$$\begin{aligned}{} & {} \left| \prod _{i=1}^k \frac{d(i)a_{i12}}{b_{i22}}\right| \\{} & {} \quad = \prod _{i=1}^k \frac{2(12i-7)(12i-5)(12i-1)(3i-1)(6i-1)(6i+1)(12i+1)(3i+1)(8i+7)a^{*4}|t_1p(i)|}{2(8i-1)|t_1p(i-1)|}\\{} & {} \quad = \frac{(8k+7)|p(k)|}{7|p(0)|}\cdot \frac{(3k+1)(6k+1)(12k+1)a^{*4k}(12k)!}{2^{6k}3^{4k}(4k)!} \\{} & {} \quad \leqslant \frac{\sqrt{3}(3k+1)(6k+1)(12k+1)(8k+7)|p(k)|}{7|p(0)|}\cdot \left( \frac{12^2k^2a^*}{2\sqrt{2}e^2}\right) ^{4k}. \end{aligned}$$

Next, from (15) for $k=0$ we get that $|p_0q_4-p_4q_0| = 14a^*t_1|p(0)|$. Finally, we unite all these bounds together with the lower bounds (29), (30) and (31) for $|q_{4k}|$ to get

$$\begin{aligned} \left| x - \frac{p_{4k}}{q_{4k}}\right| \leqslant \frac{2\sqrt{3}(3k+1)(6k+1)(12k+1)(8k+7)|t_1a^*p(k)|}{2(8k+3)(8k+5)(8k+7)(8k+9)(|t_1t_2|-3a^*)^2\cdot 64k^2}\cdot \left( \frac{12^2a^*}{2\sqrt{2}e^2c_4^2}\right) ^{4k} \end{aligned}$$

To simplify the right hand side, notice that $\frac{(3k+1)(6k+1)(12k+1)}{(8k+3)(8k+5)(8k+9)} < \frac{27}{64}$. Next, since $|t_1t_2|\geqslant 12a^*$, one has $|p(k)| = |(8k+5)(8k+9)t_1t_2 + 2(36k^2+63k+25)a^*|\leqslant 2(8k+5)(8k+9)|t_1t_2|$ which for all $k\geqslant 1$ is smaller than $442k^2|t_1t_2|$. Finally, $(|t_1t_2|-3a^*)^2 \geqslant \frac{9}{16} (t_1t_2)^2$. Collecting all of these inequalities together gives,

$$\begin{aligned} \left| x - \frac{p_{4k}}{q_{4k}}\right| \leqslant \frac{\sqrt{3}\cdot 27\cdot 442|t_1^2t_2a^*|}{64\cdot (9/16)\cdot 64 (t_1t_2)^2}\cdot \left( \frac{72a^*}{\sqrt{2}e^2c_4^2}\right) ^{4k} \leqslant |t_1| c_5^{4k}, \end{aligned}$$

(32)

where

$$\begin{aligned} c_5 = \left\{ \begin{array}{ll} \frac{9a^*}{(16t_1t_2 + 9a^*)}&{}\text{ if } \; t_1t_2>0\\ \frac{9a^*}{16(|t_1t_2| - 3a^*)}&{}\text{ if } \; t_1t_2<0. \end{array}\right. \end{aligned}$$

8 Estimating the irrationality exponent

In this section we establish Theorems 3 and 4. Consider $p_k^*:=p_{4k}/\gcd (p_{4k}, q_{4k})$ and $q_k^*:=q_{4k}/\gcd (p_{4k}, q_{4k})$. Definitely, they are both integers and (28) together with (12) imply

$$\begin{aligned} |q^*_k|\leqslant 4\sqrt{\frac{2k}{\pi }} \left( \frac{c_3}{4c_1}\right) ^{4k} =: 4\sqrt{\frac{2k}{\pi }}\cdot c_6^{4k}. \end{aligned}$$

(33)

For arbitrary $\delta >0$ and large enough k, one can use the inequality (14) to get

$$\begin{aligned} |q^*_k|\ll 16k\left( \frac{c_3}{4(c_2-\delta )}\right) ^{4k} \ll \left( \frac{c_3}{4c_2} + \delta _1\right) ^{4k} =: (c^*_6+\delta _1)^{4k} \end{aligned}$$

(34)

where $\delta _1>0$ can be made arbitrarily close to zero for large enough k. Denote the upper bound for $b^*_k$ by Q(k, t, a).

Next, we combine the last two inequalities with (32) and get

$$\begin{aligned} ||q_k^*x||\leqslant |t_1| c_5^{4k}\cdot 4\sqrt{\frac{2k}{\pi }}\left( \frac{c_3}{4c_1}\right) ^{4k} \leqslant 4|t_1|\sqrt{k}\left( \frac{c_3c_5}{4c_1}\right) ^{4k} =: 4|t_1|\sqrt{k} c_7^{-4k} \end{aligned}$$

(35)

or

$$\begin{aligned} ||q_k^*x||\ll \left( \frac{4c_2}{c_3c_5}-\delta _2\right) ^{-4k} =: (c_7^* - \delta _2)^{-4k} \end{aligned}$$

(36)

where $\delta _2$ can be made arbitrarily small and k is large enough, depending on $\delta _2$. Denote the upper bound of $||q^*_kx||$ by R(k, t, a).

Consider an arbitrary $q \geqslant \frac{1}{2R(1,t,a)}= q_0$. We now impose the condition $c_7 > e^{1/4}$. In this case, by examining the derivative of $\sqrt{k}c_7^{-4k}$, one can check that it strictly decreases for $k\geqslant 1$. Therefore, there exists a unique $k\geqslant 2$ such that $R(k,t,a)< \frac{1}{2q}\leqslant R(k-1,t,a)$. Let $p\in \mathbb {Z}$ be such that $||qx|| = |qx-p|$. Since two vectors $(p_k^*, q_k^*)$ and $(p_{k+1}^*, q_{k+1}^*)$ are linearly independent, at least one of them must be linearly independent with (p, q). Suppose that is $(p_k^*, q_k^*)$. Then we estimate the absolute value of the following determinant:

$$\begin{aligned} 1\leqslant \left| \begin{array}{cc} q&{}q_k^*\\ p&{}p_k^* \end{array}\right| \leqslant \left| \begin{array}{cc} q&{}q_k^*\\ p-qx&{} p_k^* - q_k^*x \end{array}\right| \leqslant q R(k,t,a) + ||qx||Q(k,t,a). \end{aligned}$$

Since $qR(k,t,a) < \frac{1}{2}$, we must have $||qx|| \geqslant (2Q(k,t,a))^{-1}$. Analogously, if (p, q) is linearly independent with $(p_{k+1}^*, q_{k+1}^*)$, we have $||qx||\geqslant (2Q(k+1,t,a))^{-1}$. The latter lower bound is weaker. Now, we need to rewrite the right hand side of the inequality in terms of q rather than k.

Since $\frac{1}{2q}\leqslant R(k-1,t,a)$, we have that

$$\begin{aligned} \frac{c_7^{4(k-1)}}{8|t_1| \sqrt{k-1}} \leqslant q\quad \Longrightarrow \quad k-1\leqslant \frac{\log (8|t_1|q)+\log \log (8|t_1|q)}{4\log c_7}. \end{aligned}$$

The last implication can be justified by standard techniques on working with logarithms, see [1, (40)].

Finally, substitute the last lower bound for k in $||qx||\geqslant (2Q(k+1,t,a))^{-1}$ and get

$$\begin{aligned} ||qx||\geqslant & {} \frac{\sqrt{\pi }}{8\sqrt{2(k+1)} c_6^{4(k+1)}} \\\geqslant & {} \frac{2\sqrt{\pi } (\log c_7)^{1/2}}{8\sqrt{6}c_6^8 (\log (8|t_1| q) + \log \log (8|t_1|q))^{1/2}\cdot (8|t_1|q)^{\frac{\log c_6}{\log c_7}} (\log (8|t_1| q))^{\frac{\log c_6}{\log c_7}}}.\\\geqslant & {} \frac{(\log c_7)^{1/2}}{8c_6^8(8|t_1|)^{\frac{\log c_6}{\log c_7}}}\cdot q^{-\frac{\log c_6}{\log c_7}} (\log (8|t_1| q))^{-\frac{\log c_6}{\log c_7} - \frac{1}{2}} = \frac{\tau }{g_2}q^{-\lambda }(\log (8|t_1|q))^{-\lambda -\frac{1}{2}}. \end{aligned}$$

To finish the proof of Theorem 3, we recall, that for convenience, we in fact worked with the number $x/g_2$ rather than x, i.e. the inequality above is for $||qx/g_2||$. Hence one needs to multiply both sides by $g_2$.

Regarding Theorem 4, we use inequalities (34) and (36). in this case the computations are much easier and we get for any $\delta _3>0$ and large enough integer q that

$$\begin{aligned} ||qx|| \geqslant q^{-\frac{\log c_6^*}{\log c_7^*} - \delta _3} \end{aligned}$$

or in other words $\lambda _{eff}(x)\leqslant \frac{\log c_6^*}{\log c_7^*}$. That completes the proof of Theorem 4.