Abstract
We construct a q-analogue of the truncated version of symmetric multiple zeta values, which satisfies the double shuffle relation. Using it, we define a q-analogue of symmetric multiple zeta values and see that it satisfies many of the same relations as symmetric multiple zeta values, which are the reversal relation and a part of the double shuffle relation and the Ohno-type relation.
Similar content being viewed by others
References
Bachmann, H., van-Ittersum, J-W.: Partitions, multiple zeta values and the \(q\)-bracket, preprint, arXiv:2203.09165, https://doi.org/10.48550/arXiv.2203.09165.
Bachmann, H., Kühn, U.: A dimension conjecture for \(q\)-analogues of multiple zeta values, in Periods in quantum field theory and arithmetic, pp. 237–258, Springer Proceedings in Mathematics Statistics 314, Springer (2020)
Cartier, P.: On the double zeta values. In: Galois-Teichmüller theory and arithmetic geometry, pp. 91–119, Advanced Studies in Pure Mathematics, 63, Mathematical Society of Japan, Tokyo (2012)
Castillo-Medina, J., Ebrahimi-Fard, K., Manchon, D.: Unfolding the double shuffle structure of \(q\)-multiple zeta values. Bull. Aust. Math. Soc. 91(3), 368–388 (2015)
Hoffman, E.: The algebra of multiple harmonic series. J. Algebra 194(2), 477–495 (1997)
Ihara, K., Kaneko, M., Zagier, D.: Derivation and double shuffle relations for multiple zeta values. Compos. Math. 142(2), 307–338 (2006)
Jarossay, D.: Adjoint cyclotomic multiple zeta values and cyclotomic multiple harmonic values, preprint (2019), arXiv:1412.5099v5
Kaneko, M.: An introduction to classical and finite multiple zeta values, Publications mathématiques de Besançon. Algébre et théorie des nombres. 2019/1, 103–129, Publicationes Mathematicae Besançon Algébre Théorie Nr., 2019/1, Presses Univ. Franche-Comté, Besançon, (2020)
Ono, M., Seki, S. and Yamamoto, S.: Truncated \(t\)-adic symmetric multiple zeta values and double shuffle relations, Res. Number Theory 7 (2021), no. 1, Paper No. 15, 28 pp, https://doi.org/10.1007/s40993-021-00241-5.
Oyama, K.: Ohno-type relation for finite multiple zeta values. Kyushu J. Math. 72(2), 277–285 (2018)
Reutenauer, C.: Free Lie Algebras. Oxford Science Publications, Oxford (1993)
Takeyama, Y.: The algebra of a \(q\)-analogue of multiple harmonic series. Symmetry Integrability Geom. 9, 15 (2013). https://doi.org/10.3842/SIGMA.2013.061
Zagier, D.: Evaluation of the multiple zeta values \(\zeta (2, \ldots, 2, 3, 2, \ldots, 2)\). Ann. Math. 175(2), 977–1000 (2012)
Zhao, J.: Multiple Zeta Functions, Multiple Polylogarithms and Their Special Values. World Scientific Publishing Co. Pte. Ltd, Hackensack (2016)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work was supported by JSPS KAKENHI Grant Number 22K03243.
Appendices
Appendix A. Proof of Proposition 3.4
Lemma A.1
Suppose that \(\alpha \ge 0\) and \(\max {(1, \alpha )}\le \beta \le 2\alpha +1\). Then the function \(f(x)=x^{\alpha }(1-x)/(1-x^{\beta })\) is non-decreasing on the interval [0, 1).
Proof
If \(\beta =1\), the statement is trivial. We assume that \(\beta >1\). From the assumption we see that \(\alpha \ge (\beta -1)/2>0\). Set
Since \(g(0)=\alpha >0\) and \(g(1)=0\), it suffices to show that \(g'(x)<0\) on the interval (0, 1). Set
Then we see that \(h(1)=0\) and, from the assumption,
for \(0<x<1\). Therefore we see that \(h(x)<0\), and hence \(g'(x)<0\), on the interval (0, 1). \(\square \)
Corollary A.2
Under the assumption in Lemma A.1, it holds that
for \(0<x<1\).
Proof
It is because \(f(x) \rightarrow 1/\beta \) as \(x \rightarrow 1\). \(\square \)
Proposition A.3
Suppose that \(0<q<1\). Set
Then, for any non-negative integer \(\alpha _{1}, \ldots , \alpha _{r}, \beta _{1}, \ldots , \beta _{r}\), it holds that
Proof
From Corollary A.2, we see that
for any \(n \ge 1\). Therefore, it holds that
Set \(l_{j}=n_{j}-n_{j-1}\) for \(1\le j \le r\). Then the right-hand side is dominated by \(B_{q}(\alpha _{1}, \ldots , \alpha _{r}; \beta _{1}, \ldots , \beta _{r})\) since \(0<q<1\). \(\square \)
Proposition A.4
Suppose that \(0<q<1\) and \(\alpha _{1}, \ldots , \alpha _{r}, \beta _{1}, \ldots , \beta _{r}\) are non-negative integers. Then it holds that
Moreover, if \(\alpha _{s} \ge 1\) and \(\beta _{t}\ge 1\) for some \(1\le s\le t \le r\), then we have
Proof
For a non-negative integer \(\alpha \), we define
We have
Hence \(\varphi _{\alpha }(x)=O(-\log {(1-x)})\) as \(x \rightarrow 1-0\) for any \(\alpha \ge 0\). If \(\alpha \ge 1\), we see that
for \(0\le x \le 1\). Hence \(\tilde{\varphi }_{\alpha }(x)=(1-x)\,O(-\log {(1-x)})\) as \(x \rightarrow 1-0\) for any \(\alpha \ge 1\).
Since \(\beta _{j}\ge 0\) for \(1\le j \le r\), we see that
Hence we have (A.1). Now assume further that \(\alpha _{s} \ge 1\) and \(\beta _{t}\ge 1\) for some \(1\le s\le t \le r\). If \(s=t\), it holds that
Hence we obtain (A.2) if \(s=t\). If \(s<t\), we see that
since \(\beta _{t} \ge 1\). Thus we get (A.2) in the case where \(s<t\) either. \(\square \)
Proof of Proposition 3.4
From Lemma A.1 and the monotone convergence theorem, we see that \(Z_{q}(g_{\textbf{k}}) \rightarrow \zeta (\textbf{k})\) as \(q \rightarrow 1\) for any admissible index \(\textbf{k}\). Suppose that w is an element of \(\widehat{{\mathfrak {H}}^{0}}\) of the form (3.2). Proposition A.3 and (A.1) imply that \(Z_{q}(w)=O((-\log {(1-q)})^{r})\) as \(q \rightarrow 1\). Hence \(Z_{q}(\hbar w)\rightarrow 0\) in the limit as \(q \rightarrow 1\). If \(w \in {\mathfrak {n}}_{0}\), then there exist s and t such that \(\alpha _{s}\ge 1, \beta _{t}\ge 1\) and \(1\le s\le t \le r\). Then Proposition A.3 and (A.2) imply that \(Z_{q}(w)\rightarrow 0\) in the limit as \(q \rightarrow 1\). Thus we see that \(\lim _{q\rightarrow 1}Z_{q}(w)=0\) for any \(w \in {\mathfrak {n}}\). \(\square \)
Remark A.5
For a polynomial P(x) and a positive integer n, we set \((\partial P)(n)=P(n)-P(n-1)\). We also set \((\partial P)(0)=P(0)\). Then it holds that
where we set \(m_{0}=0\) and \(P_{k}(x)=\left( {\begin{array}{c}x\\ k\end{array}}\right) \) for \(k \ge 1\). In [1], Bachmann and van-Ittersum discuss the asymptotics as \(q \rightarrow 1\) of infinite sums of the following form:
where \(d_{j}\) and \(k_{j} \, (1\le j \le k)\) are non-negative integers and \(\{f_{k}(x)\}_{k=0}^{\infty }\) is a family of polynomials such that \(\textrm{deg}f_{k}(x)=k\) for \(k \ge 0\) and \(f_{k}(0)=0\) for \(k\ge 1\).
Appendix B. Proofs
1.1 B.1. Formulas of shuffle product
Proposition B.1
Suppose that U(X) and V(X) belong to the ideal \(X {\mathcal {C}}[b][[X]]\) of the formal power series ring \({\mathcal {C}}[b][[X]]\) generated by X. Then it holds that

for any \(w, w' \in {\mathfrak {H}}\).
Proof
Set

Using \((1-U(X)a)^{-1}=1+(1-U(X)a)^{-1}U(X)a\), we see that

Since all the coefficients of U(X) and V(Y) are polynomials in b, the fourth term of the right-hand side is equal to

Using \((1-U(X)a)^{-1}=1+(1-U(X)a)^{-1}U(X)a\) again, we see that it is equal to

Thus we get the desired equality. \(\square \)
Proposition B.2
Suppose that \(U(X) \in X{\mathcal {C}}[b][[X]]\). Then it holds that

for any \(w, w' \in {\mathfrak {H}}\).
Proof
Set \(V(Y)=Y\) in Proposition B.1, differentiate both sides with respect to Y and set \(Y=0\). Then we get the desired equality. \(\square \)
Proof of Lemma 3.10
From Proposition B.1 and Proposition B.2, we see that

Using (3.9), we get the desired equality. \(\square \)
Corollary B.3
For \(U(X) \in X {\mathcal {C}}[b][[X]]\), we define the map \(\rho _{U(X)}: {\mathfrak {H}} \rightarrow {\mathfrak {H}}[[X]]\) by

Then the map \(\rho _{U(X)}\) is a \({\mathcal {C}}\)-algebra homomorphism with respect to the concatenation product on \({\mathfrak {H}}\), and we have
Proof
Set \(w=1\) and U(X) to bU(X) in Proposition B.2. Then we see that
From the definition of \(\rho _{U(X)}\), we also see that
Since \(\rho _{U(X)}(1)=1\), we have (B.1) and see that \(\rho _{U(X)}\) is an algebra homomorphism. \(\square \)
1.2 B.2. Generating function of \(E_{1^{m}}\)
Here we calculate the generating function
Recall that
Note that R(X) belongs to \(X {\mathcal {C}}[b][[X]]\).
Proposition B.4
It holds that

Proof
The power series  is the unique solution of the differential equation
is the unique solution of the differential equation  satisfying \(\Psi (0)=1\). Since the right-hand side with \(X=0\) is equal to one, it suffices to show that
satisfying \(\Psi (0)=1\). Since the right-hand side with \(X=0\) is equal to one, it suffices to show that

The right-hand side is equal to \(\rho _{R(X)}(g_{1})(1-R(X)g_{1})^{-1}\). Hence (B.1) implies that

since  . \(\square \)
. \(\square \)
Proposition B.5
It holds that
Proof
Note that \(g_{1}\) and \(\hbar b\) are commutative with respect to the shuffle product  . From the definition of \(E_{1^{m}}\), we see that
. From the definition of \(E_{1^{m}}\), we see that

Using
and (B.2), we see that

\(\square \)
Corollary B.6
For any index \(\textbf{k}\), it holds that  modulo \(\hbar {\mathfrak {e}}\). Moreover, if \(\textbf{k}\) (resp. \(\overline{\textbf{k}}\)) is admissible, then
modulo \(\hbar {\mathfrak {e}}\). Moreover, if \(\textbf{k}\) (resp. \(\overline{\textbf{k}}\)) is admissible, then  belongs to \(\hbar \sum _{j\ge 2}e_{j}{\mathfrak {e}}\) (resp. \(\hbar \sum _{j\ge 2}{\mathfrak {e}}e_{j}\)).
belongs to \(\hbar \sum _{j\ge 2}e_{j}{\mathfrak {e}}\) (resp. \(\hbar \sum _{j\ge 2}{\mathfrak {e}}e_{j}\)).
Proof
For \(k \ge 2\), using (3.1), we see that

Next we calculate  using Proposition B.5. Since
using Proposition B.5. Since  and
and  , it holds that
, it holds that

We have
Thus we see that  . Hence
. Hence

for \(m \ge 0\). Therefore, for an index \(\textbf{k}\) of the form (5.1), we have

and it implies the statement. \(\square \)
1.3 B.3. Proof of Proposition 5.4
Note that
because \((e_{1}-g_{1})a=\hbar g_{1}\) and \(g_{k}a=g_{k+1}\) for \(k \ge 1\).
We define the \({\mathcal {C}}\)-trilinear map  by
by

for \(w, w' \in {\mathcal {C}}\langle A \rangle \) and \(u_{1}, \ldots , u_{r} \in A\). It suffices to show that  belongs to \({\mathfrak {H}}^{0}\) for any admissible index \(\textbf{m}, \textbf{m}'\) and \(r \ge 0\).
belongs to \({\mathfrak {H}}^{0}\) for any admissible index \(\textbf{m}, \textbf{m}'\) and \(r \ge 0\).
Lemma B.7
For any \(w, w' \in {\mathcal {C}}\langle A \rangle \), it holds that

Proof
Decompose \((1-R(X)g_{1})^{-1}=1+(1-R(X)g_{1})^{-1}R(X)g_{1}\). Then we obtain

From the definition of  , we see that the second term in the right-hand side is equal to
, we see that the second term in the right-hand side is equal to

Hence, it holds that

Since  , we see that the right-hand side above is equal to
, we see that the right-hand side above is equal to

Therefore, by replacing \(w'\) with \((1-g_{1}R(X))^{-1}w'\), we obtain

Since  and
and  , it holds that
, it holds that

Now the desired equality (B.7) follows from (B.4). \(\square \)
Since \(R(X)+R(-X)+\hbar b\, R(X)R(-X)=0\), from Proposition B.1, we see that the right-hand side of (B.7) is equal to

Now set \(w=E_{\textbf{m}}\) and \(w'=E_{\overline{\textbf{m}'}}\) with admissible indices \(\textbf{m}\) and \(\textbf{m}'\). We have  modulo \(\hbar \widehat{{\mathfrak {H}}^{0}}\) because of Proposition 3.3, Corollary B.6 and \(E_{\textbf{m}} \in \widehat{{\mathfrak {H}}^{0}}\). From the definition of the shuffle product and (B.6), we see that
modulo \(\hbar \widehat{{\mathfrak {H}}^{0}}\) because of Proposition 3.3, Corollary B.6 and \(E_{\textbf{m}} \in \widehat{{\mathfrak {H}}^{0}}\). From the definition of the shuffle product and (B.6), we see that  belongs to \({\mathfrak {H}}^{0}\), hence so does the first term of (B.8) with \(w=E_{\textbf{m}}\) and \(w'=E_{\overline{\textbf{m}'}}\). Since \(\textbf{m}\) and \(\textbf{m}'\) are admissible, we can write \(E_{\textbf{m}}=ua\) and
belongs to \({\mathfrak {H}}^{0}\), hence so does the first term of (B.8) with \(w=E_{\textbf{m}}\) and \(w'=E_{\overline{\textbf{m}'}}\). Since \(\textbf{m}\) and \(\textbf{m}'\) are admissible, we can write \(E_{\textbf{m}}=ua\) and  with some \(u, v \in \widehat{{\mathfrak {H}}^{0}}\) because of (B.3). Then, from Proposition B.2, the second term of (B.8) is equal to
with some \(u, v \in \widehat{{\mathfrak {H}}^{0}}\) because of (B.3). Then, from Proposition B.2, the second term of (B.8) is equal to

which belongs to \({\mathfrak {H}}^{0}[[X]]\) because of (B.6). Similarly, the third term of (B.8) also belongs to \({\mathfrak {H}}^{0}[[X]]\). Thus we find that  belongs to \({\mathfrak {H}}^{0}[[X]]\), and this completes the proof of Proposition 5.4.
belongs to \({\mathfrak {H}}^{0}[[X]]\), and this completes the proof of Proposition 5.4.
1.4 B.4 Proof of Lemma 5.9
We use the map \(\rho _{R(X)}\) and \(\rho _{X}\) defined in Corollary B.3 with \(U(X)=R(X)\) and \(U(X)=X\), respectively. Let \(w \in {\mathfrak {H}}\). Since \(\rho _{R(X)}\) is a \({\mathcal {C}}\)-algebra homomorphism and \(\rho _{R(X)}(g_{1})=(1-R(X)g_{1})^{-1}e^{\hbar b X}g_{1}\), we have

Similarly, we have

Note that \({\mathfrak {n}}\) is a two-sided ideal of \(\widehat{{\mathfrak {H}}^{0}}\) with respect to the concatenation product. Hence, to prove Lemma 5.9, it suffices to show that
modulo \({\mathfrak {n}}[[X]]\) for any non-empty admissible index \(\textbf{k}\).
First we calculate \(\rho _{R(X)}(g_{\textbf{k}})\). For \(k \ge 1\), we have
modulo \(\hbar \, \widehat{{\mathfrak {H}}^{0}}[[X]]\). Moreover,
modulo \({\mathfrak {n}}_{0}[[X]]\). Therefore, it holds that
modulo \({\mathfrak {n}}[[X]]\) for \(k \ge 1\). If \(k \ge 2\), each coefficient of the formal power series \(g_{1}( (1-g_{1}X)^{-1} a)^{k-1}\) belongs to \(\sum _{j \ge 2}{\mathcal {C}}\langle A \rangle g_{j}\). For any \(w \in {\mathcal {C}}\langle A \rangle \) and \(j\ge 2\), we see that \((\hbar b) w g_{j}=(e_{1}-g_{1})wg_{j} \in {\mathfrak {n}}\). Therefore, if \(\textbf{k}=(k_{1}, \ldots , k_{r})\) is a non-empty admissible index, it holds that
modulo \({\mathfrak {n}}[[X]]\), where \(\prod _{1\le i \le r}^{\curvearrowright }A_{i}=A_{1}\cdots A_{r}\) denotes the ordered product.
Next we calculate \(\rho _{X}(E_{\textbf{k}})\). For \(k \ge 1\), we have
modulo \(\hbar \,\widehat{{\mathfrak {H}}^{0}}[[X]]\). Note that
which belongs to \({\mathfrak {n}}[[X]]\). Since \({\mathfrak {n}}a\subset {\mathfrak {n}}\), it holds that
modulo \({\mathfrak {n}}[[X]]\) for \(k \ge 2\). Now we set \(\textbf{k}=(k_{1}, \ldots , k_{r})\) and \(\textbf{k}'=(k_{1}, \ldots , k_{r-1})\). Since \(\textbf{k}\) is admissible, it holds that \(\rho _{X}(E_{\textbf{k}})=\rho _{X}(E_{\textbf{k}'})\rho _{X}(e_{k_{r}})\), and each coefficient of \(\rho _{X}(e_{k_{r}})\) belongs to \(\sum _{j \ge 2}{\mathcal {C}}\langle A \rangle g_{j}\) because of (B.9). Therefore, we may calculate \(\rho _{X}(E_{\textbf{k}'})\) modulo \(({\mathcal {C}}\langle A \rangle (e_{1}-g_{1}) {\mathcal {C}}\langle A \rangle )[[X]]\). Then we see that
modulo \(({\mathcal {C}}\langle A \rangle (e_{1}-g_{1}) {\mathcal {C}}\langle A \rangle )[[X]]\), and hence
for \(m \ge 0\). As a result we find that
modulo \({\mathfrak {n}}[[X]]\). This completes the proof of Lemma 5.9.
1.5 B.5. Proof of Proposition 6.4
We set
For \(w, w' \in {\mathfrak {H}}\), we set \(\Xi (w, w')\)

where \(E_{1}=(e_{1}+g_{1})/2\). Note that \(\Xi (w, w')\) is symmetric with respect to w and \(w'\), and

We also set

Proposition B.8
Set
It holds that

for any \(w, w' \in {\mathfrak {H}}\).
Proof
Set

Since \(E_{1}=\hbar b/2+ba\), we have

We calculate the second term of the right-hand side by using Proposition B.2 and
Then we obtain
By changing \(w \leftrightarrow w'\) and \(Y_{1} \leftrightarrow Y_{2}\), we obtain a similar formula for  . Thus we get
. Thus we get
where
From Proposition B.1 and (B.11), we see that

Using (B.11) we see that
Because \(R(Y_{j})(1+Y_{j}g_{1}E(Y_{j}))=Y_{j}E(Y_{j})\), we have
Thus we get the desired formula. \(\square \)
Lemma B.9
For any \(w, w' \in {\mathfrak {H}}\), the following formulas hold.


Proof
Note that \(e^{0}(X)=e(X)a\) and  for any \(w, w' \in {\mathfrak {H}}\). Hence
for any \(w, w' \in {\mathfrak {H}}\). Hence

Since \(e(X)=e_{1}+e(X)aX\), we see that

Therefore we have

since \(e_{1}(1-aX)^{-1}=e(X)\). Thus we get (B.12).
Next we prove (B.13). Using \(e^{0}(X)=e(X)a\) and Proposition B.2, we see that

The second term of the right-hand side is equal to

because of (B.14). Thus we get (B.13). \(\square \)
Proposition B.10
For any \(w, w' \in {\mathfrak {H}}\), it holds that

Proof
We denote the left-hand side by J(X, Y). We see that

using (B.12) and (B.13). It implies the desired equality. \(\square \)
Proposition B.11
For any \(w, w' \in {\mathfrak {H}}\), it holds that

Proof
Since \(e^{0}(X)=(e(X)-e_{1})/X\), we have

Calculate  using Proposition B.1, and we see that
using Proposition B.1, and we see that

Now the desired equality follows from (B.10) and (B.14). \(\square \)
Now we prove Proposition 6.4. For a subset \({\mathfrak {a}}\) of \({\mathfrak {H}}\) and a formal power series \(f(X_{1}, \ldots , X_{n}) \in {\mathfrak {H}}[[X_{1}, \ldots , X_{n}]]\), we say that \(f(X_{1}, \ldots , X_{n})\) belongs to \({\mathfrak {a}}\) if all the coefficients of \(f(X_{1}, \ldots , X_{n})\) belong to \({\mathfrak {a}}\). We show that
-
(i)
\(\Xi (w, w')\) belongs to \({\mathfrak {e}}\),
-
(ii)
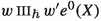 and
and 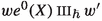 belong to \({\mathfrak {e}}\),
belong to \({\mathfrak {e}}\), -
(iii)
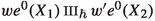 belongs to \({\mathfrak {e}}^{0}\)
belongs to \({\mathfrak {e}}^{0}\)
for any \(w, w' \in {\mathfrak {e}}\). Proposition 6.4 follows from (ii) and (iii). The third property (iii) follows from (i) and (ii) because of Proposition B.11 and (B.12). Hence it suffices to prove (i) and (ii). Note that the \({\mathcal {C}}\)-module \({\mathfrak {e}}\) is generated by the coefficients of the formal power series
with \(r \ge 0\). Hence we may assume that \(w=C_{r}\) and \(w'=C_{s}'\) for some \(r, s\ge 0\), where the prime symbol indicates that \(w'\) contains a different family of variables from w. We proceed the proof of (i) and (ii) by induction on \(r+s\).
First we consider the case of \(r=0\). From Proposition B.8, we see that \(\Xi (E(Y_{1}), E(Y_{2}))=E(Y_{1}, Y_{2})\) belongs to \({\mathfrak {e}}\), and it implies that  also belongs to \({\mathfrak {e}}\) because of Proposition B.10. Hence (i) and (ii) are true in the case of \(r=s=0\). Now we consider the case where \(r=0\) and \(s \ge 1\). Set \(w=C_{0}=E(Y_{1})\) and \(w'=C_{s}'=C_{s-1}'e^{0}(X_{2})E(Y_{2})\). Proposition B.8 and Proposition B.10 imply that
also belongs to \({\mathfrak {e}}\) because of Proposition B.10. Hence (i) and (ii) are true in the case of \(r=s=0\). Now we consider the case where \(r=0\) and \(s \ge 1\). Set \(w=C_{0}=E(Y_{1})\) and \(w'=C_{s}'=C_{s-1}'e^{0}(X_{2})E(Y_{2})\). Proposition B.8 and Proposition B.10 imply that

From Lemma B.9 and the induction hypothesis, we see that \(\partial (C_{0}, C_{s-1}'e^{0}(X_{2}))\) and \(\Lambda _{Y_{1}}(1, C_{s-1}'e^{0}(X_{2}))\) belong to \({\mathfrak {e}}^{0}\). Hence \(\Xi (C_{0}, C_{s}')\) belongs to \({\mathfrak {e}}\), and it implies that  belongs to \({\mathfrak {e}}\). Moreover, since
belongs to \({\mathfrak {e}}\). Moreover, since  belongs to \({\mathfrak {e}}^{0}\) because of the induction hypothesis (iii), we see that
belongs to \({\mathfrak {e}}^{0}\) because of the induction hypothesis (iii), we see that  belongs to \({\mathfrak {e}}\). Thus we obtain (i), (ii) with \(w=C_{0}\) and \(w'=C_{s}'\) for any \(s\ge 0\). Since \(\Xi (w, w')\) is symmetric with respect to w and \(w'\), they are also true in the case where \(w=C_{r}\) with \(r \ge 0\) and \(w'=C_{0}'\).
belongs to \({\mathfrak {e}}\). Thus we obtain (i), (ii) with \(w=C_{0}\) and \(w'=C_{s}'\) for any \(s\ge 0\). Since \(\Xi (w, w')\) is symmetric with respect to w and \(w'\), they are also true in the case where \(w=C_{r}\) with \(r \ge 0\) and \(w'=C_{0}'\).
Next we consider the case where \(r, s\ge 1\). Set \(w=C_{r}=C_{r-1}e^{0}(X_{1})E(Y_{1})\) and \(w'=C_{s}'=C_{s-1}' e^{0}(X_{2})E(Y_{2})\). From Propositions B.8, B.10 and (B.13), we see that

and

From (B.13) and the induction hypothesis, we see that \(\partial (C_{r}, C_{s-1}' e^{0}(X_{2})), \partial (C_{s}', C_{r-1} e^{0}(X_{1}))\) and  belong to \({\mathfrak {e}}^{0}\). Hence \(\Xi (C_{r}, C_{s}')\) belongs to \({\mathfrak {e}}\). The induction hypothesis says that
belong to \({\mathfrak {e}}^{0}\). Hence \(\Xi (C_{r}, C_{s}')\) belongs to \({\mathfrak {e}}\). The induction hypothesis says that  , and hence
, and hence  belongs to \({\mathfrak {e}}\). Similarly we find that
belongs to \({\mathfrak {e}}\). Similarly we find that  belongs to \({\mathfrak {e}}\). Therefore (i) and (ii) hold for \(w=C_{r}\) and \(w'=C_{s}\), and this completes the proof of Proposition 6.4.
belongs to \({\mathfrak {e}}\). Therefore (i) and (ii) hold for \(w=C_{r}\) and \(w'=C_{s}\), and this completes the proof of Proposition 6.4.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Takeyama, Y. A q-analogue of symmetric multiple zeta value. Ramanujan J 63, 209–252 (2024). https://doi.org/10.1007/s11139-023-00755-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11139-023-00755-9




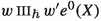 and
and 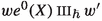 belong to
belong to 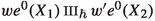 belongs to
belongs to