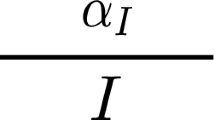Additive functions in short intervals, gaps and a conjecture of Erdős

Abstract

With the aim of treating the local behaviour of additive functions, we develop analogues of the Matomäki–Radziwiłł theorem that allow us to approximate the average of a general additive function over a typical short interval in terms of a corresponding long average. As part of this treatment, we use a variant of the Matomäki–Radziwiłł theorem for divisor-bounded multiplicative functions recently proven in Mangerel (Divisor-bounded multiplicative functions in short intervals. arXiv: 2108.11401). We consider two sets of applications of these methods. Our first application shows that for an additive function ${\varvec{g:}} \mathbb {N} \rightarrow \mathbb {C}$ any non-trivial savings in the size of the average gap $|{\varvec{g}}{} {\textbf {(}}{\varvec{n}}{} {\textbf {)}}-{\varvec{g}}{} {\textbf {(}}{\varvec{n}}-{\textbf {1}}{} {\textbf {)}} |$ implies that ${\varvec{g}}$ must have a small first centred moment i.e. the discrepancy of ${\varvec{g}}{} {\textbf {(}}{\varvec{n}}{} {\textbf {)}}$ from its mean is small on average. We also obtain a variant of such a result for the second moment of the gaps. This complements results of Elliott and of Hildebrand. As a second application, we make partial progress on an old question of Erdős relating to characterizing constant multiples of ${{\textbf {log}}} \,{\varvec{n}}$ as the only almost everywhere increasing additive functions. We show that if an additive function is almost everywhere non-decreasing then it is almost everywhere well approximated by a constant times a logarithm. We also show that if the set $\{{\varvec{n}} \in \mathbb {N} : {\varvec{g}}{} {\textbf {(}}{\varvec{n}}{} {\textbf {)}} < {\varvec{g}}{} {\textbf {(}}{\varvec{n}}-{\textbf {1}}{} {\textbf {)}}\}$ is sufficiently sparse, and if ${\varvec{g}}$ is not extremely large too often on the primes (in a precise sense), then ${\varvec{g}}$ is identically equal to a constant times a logarithm.

1 Introduction

An arithmetic function $g: \mathbb {N} \rightarrow \mathbb {C}$ is called additive if, whenever $n,m \in \mathbb {N}$ are coprime, $g(nm) = g(n)+g(m)$; it is said to be completely additive if the coprimality condition on n, m can be ignored. Additive functions are objects of classical study in analytic and probabilistic number theory, their study being enriched by a close relationship with the probabilistic theory of random walks.

Much is understood about the global behaviour of general additive functions. For instance, the orders of magnitude of all of the centred moments

$$\begin{aligned} \frac{1}{X}\sum _{n \le X} \left|g(n)-\frac{1}{X}\sum _{n \le X} g(n)\right|^k, \quad k >0, \end{aligned}$$

have been computed by Hildebrand [1]. When $k = 2$, the slightly weaker but generally sharp Turán–Kubilius inequality (see Lemma 3.2) gives an upper bound, uniform in g, of the form

$$\begin{aligned} \frac{1}{X}\sum _{n \le X} \left|g(n)-\frac{1}{X}\sum _{n \le X} g(n)\right|^2 \ll B_g(X)^2, \end{aligned}$$

(1)

where we have denoted by $B_g(X)^2$ the approximate variance defined via

$$\begin{aligned} B_g(X) := \left( \sum _{p^k \le X} \frac{|g(p^k) |^2}{p^k}\right) ^{1/2}. \end{aligned}$$

When g is real-valued one can determine necessary and sufficient conditions according to which the distribution functions $F_X(z) := \frac{1}{X}|\{n \le X : g(n) \le z\} |$ converge to a distribution function F as $X \rightarrow \infty$; this is the content of the Erdős–Wintner theorem [2]. Under certain conditions the corresponding distribution functions (with suitable normalizations) converge to a Gaussian, a fundamental result of Erdős and Kac [3].

Much less is understood regarding the local behaviour of additive functions i.e. the simultaneous behaviour of g at neighbouring integers. Questions of interest from this perspective include

• (i) the distribution of $\{g(n)\}_n$ in typical short intervals $[x,x+H]$, where $x \in [X,2X]$ and $H = H(X)$ grows slowly,

• (ii) the distribution of the sequence of gaps $|g(n)-g(n-1) |$ between consecutive values and

• (iii) the distribution of tuples $(g(n+1),\ldots ,g(n+k))$, for $k \ge 2$.

Pervasive within this scope are questions surrounding the characterization of those additive functions g whose local behaviour is rigid in some sense, such questions are discussed in Sect. 1.2.

The purpose of this paper is to consider questions of a local nature about general additive functions.

1.1 Matomäki–Radziwiłł type theorems for additive functions

The study of additive functions is intimately connected with that of multiplicative functions i.e. arithmetic functions $f: \mathbb {N} \rightarrow \mathbb {C}$ such that $f(nm) = f(n)f(m)$ whenever $(n,m) = 1$. The mean-value theory of bounded multiplicative functions, which provides tools for the analysis of the global behaviour of multiplicative functions, was developed in the ’60s and ’70s in the seminal works of Wirsing [4] and Halász [5].

In contrast, the study of the local behaviour of multiplicative functions has long been the source of intractable problems. An important example of this is Chowla’s conjecture [6]. This conjecture states, among other things, that for any $k \ge 2$ and any tuple $\varvec{\epsilon } \in \{-1,+1\}^k$, the set

$$\begin{aligned} \{n \le X: \lambda (n+1) = \epsilon _1,\ldots ,\lambda (n+k) = \epsilon _k\} \end{aligned}$$

has $(2^{-k}+o(1)) X$ elements, where $\lambda$ is the Liouville¹ function. In other terms, the sequence of tuples $(\lambda (n+1),\ldots ,\lambda (n+k))$ equidistributes among the tuples of signs in $\{-1,+1\}^k$. The depth of this conjecture is revealed upon observing that when $k = 1$, this corresponds to the statement that $\lambda (n)$ takes value $+1$ and $-1$ with asymptotically equal probability 1/2. This was shown by Landau [7] to be equivalent to the prime number theorem.

Problems of this type have recently garnered significant interest, thanks to the celebrated theorems of Matomäki and Radziwiłł [8]. Broadly speaking, their results show that averages of a bounded multiplicative function in typical short intervals are well approximated by a corresponding long average. In a strong sense, this suggests that the local behaviour of many multiplicative functions is determined by their global behaviour. The simplest version of their theorems to state is as follows.

Theorem

(Matomäki–Radziwiłł [8]) Let $f: \mathbb {N} \rightarrow [-1,1]$ be multiplicative. Let $10 \le h \le X/100$. Then

$$\begin{aligned} \frac{2}{X}\sum _{X/2< n \le X} \left|\frac{1}{h} \sum _{n-h< m \le n} f(m) - \frac{2}{X}\sum _{X/2 < m \le X} f(m)\right|^2 \ll \frac{\log \log h}{\log h} + (\log X)^{-1/50}. \end{aligned}$$

This result, its natural extensions to complex-valued functions [9], and further improvements, extensions and variants (e.g. [10]) have had profound impacts not only in analytic number theory, but equally in combinatorics and dynamics. For instance, Tao [11] used this result to develop technology in order to obtain estimates for the logarithmically-averaged binary correlation sums

$$\begin{aligned} \frac{1}{\log X}\sum _{n \le X} \frac{f(n)f(n+h)}{n}, \text { for multiplicative functions } f: \mathbb {N} \rightarrow \mathbb {C}, |f(n) |\le 1. \end{aligned}$$

This was essential in his proof of the Erdős discrepancy problem [12], and also enabled him to obtain a logarithmic density analogue of the case $k = 2$ of Chowla’s conjecture. It has also been pivotal in the various developments towards Sarnak’s conjecture on the disjointness of the Liouville function from zero entropy dynamical systems (see [13] for a survey).

Our first main result establishes an $\ell ^1$-averaged comparison theorem for short and long averages of additive functions, inspired by the theorem of Matomäki and Radziwiłł.

Theorem 1.1

Let $g: \mathbb {N} \rightarrow \mathbb {C}$ be an additive function. Let $10 \le h \le X/100$ be an integer.² Then

$$\begin{aligned}&\frac{2}{X}\sum _{\tfrac{X}{2}< n \le X} \left|\frac{1}{h} \sum _{n-h< m \le n} g(m) - \frac{2}{X}\sum _{\tfrac{X}{2} < m \le X} g(m) \right|\\&\quad \quad \quad \quad \quad \quad \quad \quad \ll \left( \sqrt{\frac{\log \log h}{\log h}} + (\log X)^{-\tfrac{1}{800}}\right) B_g(X). \end{aligned}$$

Remark 1.2

Theorem 1.1 should be compared to the “trivial bound” arising from applying the triangle inequality, the Cauchy–Schwarz inequality and (1) (which is valid for dyadic long averages as well) to obtain

$$\begin{aligned}&\frac{2}{X}\sum _{X/2< n \le X} \left|\frac{1}{h} \sum _{n-h< m \le n} g(m) - \frac{2}{X}\sum _{X/2< m \le X} g(m) \right|\\&\quad \le \frac{2}{X}\sum _{X/2-h< m \le X} \left|g(m) - \frac{2}{X}\sum _{X/2< n \le X} g(n)\right|\\&\quad \ll \left( \frac{1}{X}\sum _{m \le X}\left|g(m)-\frac{2}{X}\sum _{X/2 < n \le X} g(n)\right|^2\right) ^{\frac{1}{2}} \\&\quad \ll B_g(X). \end{aligned}$$

In contrast, Theorem 1.1 gives the non-trivial bound $o(B_g(X))$ whenever $h = h(X) \rightarrow \infty$ as $X \rightarrow \infty$.

To get a more precise additive function analogue of the Matomäki–Radziwiłł theorem, one would hope to obtain a mean square (or $\ell ^2$) version of Theorem 1.1. We are limited in this matter by the possibility of very large values of g. Specifically, if $\vert g(p) \vert /B_g(X)$ can get very large for many primes $p \le X$, it is possible for the $\ell ^2$ average to be dominated by a sparse set (i.e. the multiples of these p), wherein the discrepancy between the long and short sums is not small. We will thus work with a specific collection of additive functions in order to preclude such pathological behaviour.

To describe this collection we introduce the following notations. Given $\varepsilon > 0$ and an additive function g, we define³

$$\begin{aligned} F_g(\varepsilon ) := \limsup _{X \rightarrow \infty } \frac{1}{B_g(X)^2} \sum _{\begin{array}{c} p \le X \\ |g(p) |> \varepsilon ^{-1} B_g(X) \end{array}} \frac{|g(p) |^2}{p}. \end{aligned}$$

Roughly speaking, $F_g(\varepsilon )$ measures the contribution to $B_g(X)^2$ from prime values g(p) of very large absolute value.

Clearly, $0 \le F_g(\varepsilon ) \le 1$ for all $\varepsilon > 0$ and additive functions g. We will concern ourselves with functions g such that $F_g(\varepsilon ) \rightarrow 0$ as $\varepsilon \rightarrow 0^+$, a condition that is satisfied by many additive functions. When g is bounded on the primes e.g. when $g(n) = \Omega (n)$, the number of prime factors of n counted with multiplicity, it is clear that $F_g(\varepsilon ) = 0$ whenever $\varepsilon$ is sufficiently small. For a different example, taking $g = c\log$ for some $c \in \mathbb {C}$ we find $B_g(X) \sim \frac{|c |}{\sqrt{2}}\log X$, so that $|g(p) |\le (\sqrt{2} + o(1)) B_g(X)$ for all primes p and hence $F_g(\varepsilon ) = 0$ for all $\varepsilon < 1/2$, say.

Definition 1.3

We define the collection $\mathcal {A}$ to be the set of those additive functions $g : \mathbb {N} \rightarrow \mathbb {C}$ such that

• (a) $B_g(X) \rightarrow \infty$, and

• (b) $B_g(X)$ is dominated by the prime values $|g(p) |$, in the sense that

  $$\begin{aligned} \limsup _{X \rightarrow \infty } \frac{1}{B_g(X)^2} \sum _{\begin{array}{c} p^k \le X \\ k \ge 2 \end{array}} \frac{|g(p^k) |^2}{p^k} = 0. \end{aligned}$$

We shall see below (see Lemma 3.6a)) that $\mathcal {A}$ contains all completely additive and all strongly additive⁴ functions g with $B_g(X) \rightarrow \infty$. Within $\mathcal {A}$ we define

$$\begin{aligned} \mathcal {A}_s := \{g \in \mathcal {A} : \lim _{\varepsilon \rightarrow 0^+} F_g(\varepsilon ) = 0\}. \end{aligned}$$

(2)

Thus, among other examples, $\Omega (n), \omega (n) := \sum _{p\mid n} 1$ and, for any $c \in \mathbb {C}$, $c\log$ all belong to $\mathcal {A}_s$. We show in general that whenever $g \in \mathcal {A}_s$, we may obtain an $\ell ^2$ analogue of Theorem 1.1.

Theorem 1.4

Let $g: \mathbb {N} \rightarrow \mathbb {C}$ be an additive function in $\mathcal {A}_s$. Let $10 \le h \le X/100$ be an integer with $h = h(X) \rightarrow \infty$. Then

$$\begin{aligned} \frac{2}{X}\sum _{X/2< n \le X} \left|\frac{1}{h} \sum _{n-h< m \le n} g(m) - \frac{2}{X}\sum _{X/2 < m \le X} g(m) \right|^2 = o(B_g(X)^2). \end{aligned}$$

Our proof of Theorem 1.4 relies on a variant of the Matomäki–Radziwiłł theorem that applies to a large collection of divisor-bounded multiplicative functions, proven in the recent paper [14]. See Theorem 5.3 for a statement relevant to the current circumstances.

Remark 1.5

The rate of decay in this result depends implicitly on the rate at which $F_g(\varepsilon ) \rightarrow 0$ as $\varepsilon \rightarrow 0^+$, and on the size of the contribution to $B_g(X)$ from the prime power values of g. We have therefore chosen to state the theorem in this qualitative form for the sake of simplicity.

It deserves mention that the application of the Matomäki–Radziwiłł method, which will be used in this paper, to the study of specific additive functions is not entirely new. Goudout [15, 16] applied this technique to derive distributional information about $\omega (n)$ in typical short intervals; for example, he proved in [15] that the Erdős–Kac theorem holds in short intervals $(x-h,x]$ for almost all $x \in [X/2,X]$, as long as $h = h(X) \rightarrow \infty$. The specific novelty of Theorems 1.1 and 1.4 lie in their generality, and it is this aspect which will be used in the applications to follow.

1.2 Applications: gaps and rigidity problems for additive functions

Given $c \in \mathbb {C}$, the arithmetic function $n \mapsto c \log n$ is completely additive. In contrast to a typical additive function g, whose values g(n) depend on the prime factorization of n which might vary wildly from one integer to the next, $c\log$ varies slowly and smoothly, with very small gaps

$$\begin{aligned} c\log (n+1)-c\log n = O(1/n)\quad \text { for all } n \in \mathbb {N}. \end{aligned}$$

In the seminal paper [17], Erdős studied various characterization problems for real- and complex-valued additive functions relating to their local behaviour, and in so doing found several characterizations of the logarithm as an additive function. Among a number of results, he showed that if either

• (a) $g(n+1) \ge g(n)$ for all $n \in \mathbb {N}$, or

• (b) $g(n+1)-g(n) = o(1)$ as $n \rightarrow \infty$,

then there exists $c \in \mathbb {R}$ such that $g(n) = c\log n$ for all $n \ge 1$.

Moreover, Erdős and later authors posited that these hypotheses could be relaxed. Kátai [18] and independently Wirsing [19] weakened assumption (b), and proved the above result under the averaged assumption

$$\begin{aligned} \lim _{X \rightarrow \infty } \frac{1}{X} \sum _{n \le X} |g(n+1)-g(n) |= 0. \end{aligned}$$

Hildebrand [20] showed the stronger conjecture of Erdős that if $g(n_k+1)-g(n_k) \rightarrow 0$ on a set $\{n_k\}_k$ of density⁵ 1 then $g = c \log$; this, of course, is an almost sure version of (b).

In a different direction, Wirsing [21] showed that for completely additive functions g, (b) may be weakened to $g(n+1)-g(n) = o(\log n)$ as $n \rightarrow \infty$, and this is best possible.

A number of these results were strengthened and generalized by Elliott [22, Ch. 11], in particular to handle functions g with small gaps $|g(an+b)-g(An+B) |$, for independent linear forms $n \mapsto an+b$ and $n \mapsto An+B$ (i.e. such that $aB - Ab \ne 0$).

Characterization problems of these kinds for both additive and multiplicative functions have continued to garner interest more recently. In [23], Klurman proved a long-standing conjecture of Kátai, showing that if a unimodular multiplicative function $f: \mathbb {N} \rightarrow S^1$ has gaps satisfying $|f(n+1)-f(n) |\rightarrow 0$ on average then there is a $t \in \mathbb {R}$ such that $f(n) = n^{it}$ for all n. In a later work, Klurman and the author [24] proved a conjecture of Chudakov from the ’50s characterizing completely multiplicative functions having uniformly bounded partial sums. See Kátai’s survey paper [25] for numerous prior works in this direction for both additive and multiplicative functions.

While these multiplicative results have consequences for additive functions, they are typically limited by the fact that if g is a real-valued additive function then the multiplicative function $e^{2\pi i g}$ is only sensitive to the values $g(n) \pmod {1}$. In particular, considerations about e.g. the monotone behaviour of g cannot be directly addressed by appealing to corresponding results for multiplicative functions.

1.2.1 Erdős’ conjecture for almost everywhere monotone additive functions

One still open problem stated in [17] concerns the almost sure variant of problem (a) above. For convenience, given an additive function $g: \mathbb {N} \rightarrow \mathbb {R}$ we set $g(0) := 0$ and define the set of decrease of g:

$$\begin{aligned} \mathcal {B} := \{n \in \mathbb {N} : g(n) < g(n-1)\}, \quad \quad \mathcal {B}(X) := \mathcal {B} \cap [1,X]. \end{aligned}$$

Conjecture 1.6

[17] Let $g: \mathbb {N} \rightarrow \mathbb {R}$ be an additive function, such that

$$\begin{aligned} |\mathcal {B}(X) |= o(X) \text { as }X \rightarrow \infty . \end{aligned}$$

(3)

Then there exists $c \in \mathbb {R}$ such that $g(n) = c\log n$ for all $n \in \mathbb {N}$.

Thus, if g is non-decreasing except on a set of integers of natural density 0 then it is conjectured that g must be a constant times a logarithm.

Condition (3) is necessary, as for any $\varepsilon > 0$ one can construct a function g, not a constant multiple of $\log n$, which is monotone except on a set of density at most $\varepsilon$. Indeed, picking a prime $p_0 > 1/\varepsilon$ and defining $g = g_{p_0}$ to be the completely additive function defined at primes by

$$\begin{aligned} g_{p_0}(p) := {\left\{ \begin{array}{ll} \log p &{}: \ p \ne p_0 \\ p_0 &{}: \ p = p_0,\end{array}\right. } \end{aligned}$$

one finds that $g_{p_0}(n) = \log n$ if and only if $p_0 \not \mid n$, and that $\mathcal {B} = \{mp_0 + 1: m \in \mathbb {N}\}$. It is easily checked that the density $d\mathcal {B}$ of $\mathcal {B}$ satisfies $0< d\mathcal {B} = 1/p_0 < \varepsilon$.

As a consequence of our results on short interval averages of additive functions, we will prove the following partial result towards Erdős’ conjecture.

Corollary 1.7

Let $g: \mathbb {N} \rightarrow \mathbb {R}$ be a completely additive function that satisfies

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0^+} F_g(\varepsilon ) = \lim _{\varepsilon \rightarrow 0^+} \limsup _{X \rightarrow \infty } \frac{1}{B_g(X)^2} \sum _{\begin{array}{c} p \le X \\ |g(p) |> \varepsilon ^{-1}B_g(X) \end{array}} \frac{g(p)^2}{p} = 0. \end{aligned}$$

(4)

Assume furthermore that there is a $\delta > 0$ such that

$$\begin{aligned} |\mathcal {B}(X) |\ll X/(\log X)^{2+\delta }. \end{aligned}$$

Then there is a constant $c \in \mathbb {R}$ such that $g(n) = c\log n$ for all $n \in \mathbb {N}$.

The above corollary reflects the fact that the main difficulties involved in fully resolving Conjecture 1.6 are

• (i) the possible lack of sparseness of $\mathcal {B}$ beyond $|\mathcal {B}(X) |= o(X)$, and

• (ii) the possibility of very large values $|g(p) |$.

More generally, we show that any function $g \in \mathcal {A}_s$ that satisfies $|\mathcal {B}(X) |= o(X)$ is close to a constant multiple of a logarithm at prime powers.

Theorem 1.8

Let $g:\mathbb {N} \rightarrow \mathbb {R}$ be an additive function belonging to $\mathcal {A}_s$, and suppose $|\mathcal {B}(X) |= o(X)$. Let $X \ge 10$ be large. Then there is $\lambda = \lambda (X)$ with $|\lambda (X) |\ll B_g(X)/\log X$ such that

$$\begin{aligned} \sum _{p^k \le X} \frac{|g(p^k)-\lambda (X)\log p^k |^2}{p^k} = o\left( \sum _{p^k \le X} \frac{g(p^k)^2}{p^k}\right) \text { as } X \rightarrow \infty . \end{aligned}$$

Moreover, $\lambda$ is slowly varying as a function of X in the sense that for every fixed $0 < u \le 1$,

$$\begin{aligned} \lambda (X^u) = \lambda (X) + o\left( \frac{B_g(X)}{\log X}\right) . \end{aligned}$$

Finally, using a result of Elliott [26], we will prove the following approximate version of Erdős’ conjecture under weaker conditions than in Corollary 1.7.

Theorem 1.9

Let $g: \mathbb {N} \rightarrow \mathbb {R}$ be an additive function, such that $|\mathcal {B}(X) |= o(X)$. Then there are parameters $\lambda = \lambda (X)$ and $\eta = \eta (X)$ such that for all but o(X) integers $n \le X$,

$$\begin{aligned} g(n) = \lambda \log n - \eta + o(B_g(X)). \end{aligned}$$

(5)

The functions $\lambda ,\eta$ are slowly varying in the sense that for any $u \in (0,1)$ fixed,

$$\begin{aligned} \lambda (X^u) = \lambda (X) + o\left( \frac{B_g(X)}{\log X}\right) , \quad \quad \eta (X^u) = \eta (X) + o(B_g(X)). \end{aligned}$$

Remark 1.10

Note that if we knew (5) held for all three of $n,m,nm \in [1,X]$ then we could deduce that

$$\begin{aligned} \lambda \log (nm) - 2\eta + o(B_g(X))= & {} g(n) + g(m) = g(nm) \\= & {} \lambda \log (nm) - \eta + o(B_g(X)), \end{aligned}$$

and thus that $\eta = o(B_g(X))$. As such, (5) would be valid with $\eta \equiv 0$. Unfortunately, we are not able to confirm this unconditionally.

1.2.2 On Elliott’s property of gaps

Gap statistics provide an important example of local properties of a sequence. Obviously, an additive function g whose values g(n) are globally close to g’s mean value must have small gaps $|g(n+1) - g(n) |$. Conversely, it was observed by Elliott that the growth of the gaps between consecutive values of g also control the typical discrepancy of g(n) from its mean.

More precisely, given an additive function $g: \mathbb {N} \rightarrow \mathbb {C}$ and $X \ge 2$, define

$$\begin{aligned} A_g(X) := \sum _{p^k \le X} \frac{g(p^k)}{p^k}\left( 1-\frac{1}{p}\right) . \end{aligned}$$

(6)

It is well known (see e.g. Lemma 3.1) that as $X \rightarrow \infty$, $A_g(X)$ is the asymptotic mean value of $\{g(n)\}_{n \le X}$. Elliott showed the following estimate relating the average deviations $\vert g(n)-A_g(X) \vert$ to the average gaps $\vert g(n)-g(n-1) \vert$.

Theorem

[22, Thm. 10.1] There is an absolute constant⁶$c > 0$ such that for any additive function $g: \mathbb {N} \rightarrow \mathbb {C}$ one has

$$\begin{aligned} \frac{1}{X} \sum _{n \le X} |g(n) - A_g(X) |^2 \ll \sup _{X \le y \le X^c} \frac{1}{y} \sum _{n \le y} |g(n)-g(n-1) |^2. \end{aligned}$$

Elliott’s result shows that if g has exceedingly small gaps on average, even at scales that grow polynomially in X, then g must globally be very close to its mean.

The drawback of this result is that it is in principle possible for the upper bound to be trivial even if the gaps $|g(n) - g(n-1) |$, $n \le X$, are $o(B_g(X))$ on average, as long as the average savings over $n \le X^c$ is not large enough to offset the difference in size between $B_g(X)$ and $B_g(X^c)$.

In Sect. 6, we obtain two results that complement Elliott’s. The first shows that for any additive function g, any savings in the $\ell ^1$-averaged moment of $|g(n)-g(n-1) |$ provides a savings over the trivial bound for the first centred moment. The second, which holds whenever $g \in \mathcal {A}_s$, gives the same type of information as the first but in an $\ell ^2$ sense.

Theorem 1.11

Let $g: \mathbb {N} \rightarrow \mathbb {C}$ be an additive function.

• (a) The following are equivalent:

  $$\begin{aligned}&\frac{1}{X} \sum _{n \le X} |g(n)-g(n-1) |= o(B_g(X)),&\frac{1}{X} \sum _{n\le X} |g(n) - A_g(X) |= o(B_g(X)). \end{aligned}$$

• (b) Assume furthermore that $g \in \mathcal {A}_s$. Then the following are equivalent:

  $$\begin{aligned}&\frac{1}{X} \sum _{n \le X} |g(n)-g(n-1) |^2 = o(B_g(X)^2), \\&\frac{1}{X} \sum _{n \le X} |g(n) - A_g(X) |^2 = o(B_g(X)^2). \end{aligned}$$

See Proposition 6.1, where an explicit dependence between the rates of decay of the gap average and the first centred moment in Theorem 1.11(a) is given as a consequence of Theorem 1.1.

As a corollary of Theorem 1.11(b) and a second moment estimate of Ruzsa (see Lemma 3.3), we will deduce the following.

Corollary 1.12

Let $g \in \mathcal {A}_s$ be an additive function. Assume that

$$\begin{aligned} \frac{1}{X}\sum _{n \le X} \vert g(n)-g(n-1) \vert ^2 = o(B_g(X)^2). \end{aligned}$$

Then there is a function $\lambda = \lambda (X)$ such that as $X \rightarrow \infty$,

$$\begin{aligned} \sum _{p^k \le X} \frac{\vert g(p^k) - \lambda \log p^k\vert ^2}{p^k} = o(B_g(X)^2). \end{aligned}$$

Remark 1.13

Even in the weak sense of Theorem 1.11 and even when g takes bounded values at primes, it can be seen that having small gaps on average is a very special property. As a simple example, $g = \omega$, for which $B_{\omega }(X)^2 \sim \log \log X$, satisfies

$$\begin{aligned} \frac{1}{X}\sum _{n \le X} |\omega (n)-\omega (n-1) |^2 \gg \log \log X, \end{aligned}$$

since by a bivariate version of the Erdős–Kac theorem (see e.g. [28]) one can find a positive proportion of integers $n \in [X/2,X]$ such that, simultaneously,

$$\begin{aligned} \frac{\omega (n)-\log \log X}{\sqrt{\log \log X}} \ge 2, \quad \quad \frac{\omega (n-1) - \log \log X}{\sqrt{\log \log X}} \le 1. \end{aligned}$$

In fact, as Corollary 1.12 shows, if $g \in \mathcal {A}_s$ has a small $\ell ^2$ average gap then g must behave like $\lambda (X) \log$ on average over prime powers $p^k \le X$.

2 Proof ideas

In this section, we will explain the principal ideas that inform the proofs of our main theorems.

2.1 On the Matomäki–Radziwiłł type theorems

In Theorems 1.1 and 1.4 , our objective is to estimate the averaged deviations

$$\begin{aligned} \frac{2}{X}\sum _{X/2< n \le X} \left|\frac{1}{h}\sum _{n-h< m \le n} g(m) - \frac{2}{X}\sum _{X/2 < m \le X} g(m) \right|^k, \end{aligned}$$

(7)

where $k \in \{1,2\}$, and $10 \le h \le X/10$ with $h \in \mathbb {Z}$. Though our result applies to any complex-valued additive function g, by considering first $\text {Re}(g)$ and $\text {Im}(g)$ separately it is always possible to restrict to $g(n) \in \mathbb {R}$ for all n, which we shall assume henceforth.

The key idea underlying the results for both $k = 1,2$ involves the fact that for $n \in \mathbb {N}$ and $z \in \mathbb {C} \backslash \{0\}$ the function⁷$n \mapsto z^{g(n)}$ is multiplicative in the n-aspect and analytic in the z-aspect. In the case of Theorem 1.1, for $t \in \mathbb {R}$ the corresponding function $G_t(n) := e^{2\pi i t g(n)}$ takes values on the unit circle $S^1$. Moreover, by replacing $G_t(n)$ by its constant (in n) multiple ${\tilde{G}}_t(n) := e^{2\pi i t(g(n)-A_g(X))}$ (see (6) for the definition of $A_g$), we see that for $r = 1,2$,

$$\begin{aligned} \frac{\mathrm{d}^r}{\mathrm{d}t^r} \left( \frac{1}{h}\sum _{n-h< m \le n} {\tilde{G}}_t(m)\right) \bigg \vert _{t = 0} = (2\pi i)^r \frac{1}{h}\sum _{n-h < m \le n} (g(m) - A_g(X))^r. \end{aligned}$$

Taylor expanding ${\tilde{G}}_t(m) = G_t(m)e^{-2\pi i t A_g(X)}$ to second order around $t = 0$ for each m leads to

$$\begin{aligned}&\frac{1}{h}\sum _{n-h< m \le n} G_t(m)\nonumber \\&\quad =e^{2\pi i tA_g(X)}\left( 1 + \frac{2\pi i t}{h} \sum _{n-h< m \le n} (g(m)-A_g(X))\right) \nonumber \\&\qquad + (2\pi i)^2 e^{2\pi i tA_g(X)}\int _0^t \left( \frac{1}{h}\sum _{n-h < m \le n} (g(m)-A_g(X))^2{\tilde{G}}_u(m)\right) u \,\mathrm{d}u. \end{aligned}$$

(8)

As the sum of $g(m)-A_g(X)$ over a medium-length interval $(n-h^{*},n]$, where $h^{*} = X/(\log X)^c$ for a small constant $c > 0$, is well approximated by the sum over [X/2, X] (see Lemma 4.1), it suffices to compare the short averages over $(n-h,n]$ to those over $(n-h^{*},n]$. Using the Turán–Kubilius inequality to treat the integral error term in (8), the above allows us to approximate, for t close to 0, the average in (7) with $k = 1$ by the corresponding average

$$\begin{aligned} \frac{2}{X}\sum _{X/2< n \le X} \left|\frac{1}{h}\sum _{n-h< m \le n} G_t(m) - \frac{1}{h^{*}}\sum _{n-h^{*} < m \le n} G_t(m) \right|, \end{aligned}$$

where now our summands are, crucially, values of a bounded multiplicative function. After passing to the mean square by the Cauchy–Schwarz inequality, we may estimate these averages using the work of Matomäki and Radziwiłł [10] (and their joint work with Tao [8]), along with some additional ideas from pretentious number theory relating to the possible correlations of $G_t(n)$ with the so-called Archimedean characters $n^{i\lambda }$ for $\lambda \in \mathbb {R}$.

The above strategy fails to work in the case $k = 2$ for the important reason that the integral error term in (8), when squared and then averaged over n, cannot be controlled by an $\ell ^2$ moment of $g(n)-A_g(X)$, but rather only by an $\ell ^4$ moment. This can be far larger than $B_g(X)^4$, especially if g takes irregularly large values on prime powers.

In place of the Taylor approximation argument given above, we instead use Cauchy’s integral formula to obtain an expression for short averages of g without an error term, namely⁸ for $\rho \in (0,1)$,

$$\begin{aligned} \frac{1}{h}\sum _{n-h< m \le n} g(m)&= \frac{\mathrm{d}}{\mathrm{d}z}\left( \frac{1}{h}\sum _{n-h< m \le n} z^{g(m)} \right) \bigg \vert _{z = 1} \\&= \frac{1}{2\pi i} \int _{\vert z-1 \vert = \rho } \left( \frac{1}{h}\sum _{n-h<m \le n} z^{g(m)}\right) \frac{\mathrm{d}z}{(z-1)^2}. \end{aligned}$$

Though this manoeuvre has eliminated the problematic error term and still introduced multiplicative functions into the game, it has also introduced a different issue in that the path of integration⁹ intersects the region $\vert z \vert > 1$. Any point in that region yields a function $n\mapsto z^{g(n)}$ that is unbounded whenever g takes unbounded, positive values, say.

While this issue prevents us from obtaining an $\ell ^2$ result for arbitrary additive functions g, we may still succeed if we impose restrictions on the growth of g. Indeed, as shown in [14], the work of Matomäki and Radziwiłł can be generalized to cover certain collections of unbounded multiplicative functions of controlled growth. This includes most natural multiplicative functions f that are uniformly bounded on the primes and not too large on average at prime powers. Assuming the hypothesis $g \in \mathcal {A}_s$ and modifying g on a small set of prime powers, it can be shown that the resulting multiplicative function $z^{g(n)/B_g(X)}$ satisfies the necessary hypotheses for the generalization of the Matomäki–Radziwiłł theorem in [14] to be applicable, which is crucial to the proof of Theorem 1.4.

2.2 On gaps between consecutive values of additive functions

Theorem 1.11 establishes that for suitable additive functions g, having a small kth moment of gaps is equivalent to having a small kth centred moment, for $k \in \{1,2\}$. Since the proof follows similar lines in each of the cases $k = 1,2$, we will confine ourselves mainly to explaining the case $k = 1$ here.

By the triangle inequality,

$$\begin{aligned} \frac{1}{X}\sum _{n \le X} \vert g(n)-g(n-1) \vert \le \frac{1}{X}\sum _{n \le X} (\vert g(n)-A_g(X) \vert + \vert g(n-1)-A_g(X) \vert ), \end{aligned}$$

which implies that if the first centred moment is $o(B_g(X))$ then the average gap is also $o(B_g(X))$.

The converse is more delicate. The main idea here is to note that if $h = h(X)$ is slowly growing then as $h < n \le X$ varies the average gap $\vert g(n)-g(n-1) \vert$ controls the size of typical differences between g(n) and its length h averages:

$$\begin{aligned} g(n)-\frac{1}{h}\sum _{n-h < m \le n} g(m) = \sum _{0 \le j \le h-2} \left( 1-\frac{j+1}{h}\right) (g(n-j)-g(n-j-1)).\nonumber \\ \end{aligned}$$

(9)

Thus, if we assume that g has gaps $\vert g(n)-g(n-1) \vert$ of size $o(B_g(X))$ on average, then (by selecting h growing sufficiently slowly) the left-hand side of (9) will also typically be small. Now, Theorem 1.1 allows us to conclude that for almost all $n \in [X,2X]$,

$$\begin{aligned} \left|g(n) - \frac{1}{h}\sum _{n-h< m \le n} g(m) \right|&= \left|g(n)-\frac{2}{X}\sum _{X/2 < n\le X} g(n) \right|+ o(B_g(X)) \\&= \vert g(n) - A_g(X) \vert + o(B_g(X)), \end{aligned}$$

and in this way we deduce that $\vert g(n)-A_g(X) \vert$ is also $o(B_g(X))$ on average.

The corresponding result comparing the 2nd moments is analogous, but relies on our Theorem 1.4 instead of Theorem 1.1. For this reason, we must assume that $g \in \mathcal {A}_s$ in Theorem 1.11(b).

2.3 On the Erdős monotonicity problem

Our application to Erdős’ problem, Conjecture 1.6, was the original motivation for this paper. The connection between our short interval average results and this conjecture arose from the observation that if g is a real-valued additive function that is non-decreasing outside of a set $\mathcal {B}$ of density 0, then the average of the gaps of $\{g(n)\}_n$ is nearly a telescoping sum, that is

$$\begin{aligned} \frac{1}{X}\sum _{n \le X} \vert g(n)-g(n-1) \vert&= \frac{1}{X}\sum _{n \le X} (g(n)-g(n-1)) + \frac{2}{X}\sum _{n \in \mathcal {B}(X)} (g(n-1)-g(n)) \nonumber \\&= \frac{g(\lfloor X\rfloor )}{X} + \frac{2}{X}\sum _{n \in \mathcal {B}(X)} (g(n-1)-g(n)), \end{aligned}$$

(10)

since $g(0) = 0$ by definition. It can be shown (see Lemma 3.5) that $\vert g(\lfloor X \rfloor ) \vert /X = o(B_g(X))$; via the Cauchy–Schwarz inequality, the sparseness of $\mathcal {B}$ results in the second expression also being $o(B_g(X))$. By Theorem 1.11(a), which, as just discussed, is a consequence of Theorem 1.1, the first centred moment thus also satisfies $\tfrac{1}{X}\sum _{n \le X} \vert g(n)-A_g(X) \vert = o(B_g(X))$.

A classical second moment estimate of Ruzsa (see Lemma 3.3) shows that if, instead, we could obtain savings over $O(B_g(X)^2)$ for the second centred moment $\tfrac{1}{X}\sum _{n \le X} \vert g(n)-A_g(X) \vert ^2$, then we could conclude the existence of a slowly-varying function $\lambda = \lambda (X)$ such that $g_{\lambda } = g-\lambda \log$ takes smaller values on average over prime powers than g does. That is, $\lambda \log n$ approximates g(n) in a precise sense. Achieving such savings in the second centred moment is the objective of the proof of Theorem 1.8.

In analogy to the treatment of the first moment of the gaps in (10), the bulk of the work towards Theorem 1.8 involves obtaining savings over $B_g(X)^2$ on sparsely-supported $\ell ^2$ sums of the shape

$$\begin{aligned} \frac{1}{X}\sum _{n \in \mathcal {S}(X)} \vert g(n)-A_g(X) \vert ^2, \end{aligned}$$

where $\mathcal {S} \subset \mathbb {N}$ and $\mathcal {S}(X) := \mathcal {S} \cap [1,X]$ satisfies $\vert \mathcal {S}(X)\vert = o(X)$, as $X \rightarrow \infty$. Having no recourse to Hölder’s inequality for savings in $\ell ^2$, we instead use the large sieve (see Proposition 7.1), together with some ideas due to Elliott, to show that either this sparse average is $o(B_g(X)^2)$, or else $\mathcal {S}$ contains many multiples of a sparse set of primes p where $\vert g(p) \vert$ is extremely large (in a precise sense). As $g \in \mathcal {A}_s$, this latter set is provably empty, and consequently we obtain the required savings. It would be interesting to understand whether a similar conclusion could be obtained under weaker conditions on g.

The slow variation of $\lambda$ i.e. $\lambda (X^u) = (1+o(1)) \lambda (X)$ for fixed $0 < u \le 1$ is a key property that we exploit in the proof of Corollary 1.7. Though we do not need to directly invoke the general theory of slowly-varying functions due to Karamata (see e.g. [29, Ch. 1]), his representation theorem informs our proof that $\lambda$ is slowly growing in X i.e. $\lambda (X) \in [(\log X)^{-\varepsilon }, (\log X)^{\varepsilon }]$ for any $\varepsilon > 0$ (see Lemma 8.6). Given that, provably, $B_g(X) \asymp \lambda (X) \log X$ here, we find that $B_g(X) = (\log X)^{1+o(1)}$. For reference, as noted above we have $B_g(X) \sim \frac{\vert c \vert }{\sqrt{2}} \log X$ whenever $g = c \log$.

Corollary 1.7 follows readily from this conclusion, since if $\vert \mathcal {B}(X) \vert \ll X/(\log X)^{2+\delta }$ for some $\delta > 0$, then by Cauchy–Schwarz we have

$$\begin{aligned} \frac{1}{X}\sum _{n \in \mathcal {B}(X)} \vert g(n)-g(n-1) \vert \ll \left( \frac{\vert \mathcal {B}(X) \vert }{X}\right) ^{1/2} B_g(X) = o(1). \end{aligned}$$

Since $g(\lfloor X \rfloor )/X = o(B_g(X)/(\log X)^2) = o(1)$, the right-hand side in (10) is thus o(1), and so the Kátai–Wirsing theorem mentioned in the introduction (see also Theorem 3.7 for a statement) implies that $g = c\log$ exactly, for some $c \in \mathbb {R}$. Without this additional sparseness assumption on $\mathcal {B}$, however, it is not clear how to proceed further. It would be interesting to obtain the bound $\tfrac{1}{X}\sum _{n \le X} \vert g(n)-g(n-1) \vert = o(1)$, even assuming $g \in \mathcal {A}_s$, under weaker hypotheses on the rate of decay of $\vert \mathcal {B}(X) \vert /X$, or perhaps assuming to begin with that $B_g(X) = (\log X)^{1+o(1)}$.

3 Auxiliary lemmas

In this section, we record several results that will be used repeatedly in the sequel. For the convenience of the reader, we recall that for an additive function $g: \mathbb {N} \rightarrow \mathbb {C}$ and $X \ge 2$,

$$\begin{aligned} A_g(X) := \sum _{p^k \le X} \frac{g(p^k)}{p^k}\left( 1-\frac{1}{p}\right) , \quad B_g(X)^2 := \sum _{p^k \le X} \frac{ \vert g(p^k) \vert ^2}{p^k}. \end{aligned}$$

Lemma 3.1

Let $g: \mathbb {N} \rightarrow \mathbb {C}$ be additive. Then for any $Y \ge 3$,

$$\begin{aligned} \frac{1}{Y}\sum _{n \le Y} g(n) = A_g(Y) + O\left( \frac{B_g(Y)}{\sqrt{\log Y}}\right) . \end{aligned}$$

Proof

As $g(n) = \sum _{p^k \Vert n} g(p^k)$, we have

$$\begin{aligned} \frac{1}{Y}\sum _{n \le Y} g(n) - A_g(Y)&= \frac{1}{Y} \sum _{p^k \le Y}g(p^k) \sum _{\begin{array}{c} n \le Y \\ p^k \Vert n \end{array}} 1 - \sum _{p^k \le Y} \frac{g(p^k)}{p^k}\left( 1-\frac{1}{p}\right) \\&= \sum _{p^k \le Y} g(p^k)\left( Y^{-1}\left( \left\lfloor \frac{Y}{p^k} \right\rfloor - \left\lfloor \frac{Y}{p^{k+1}}\right\rfloor \right) - \frac{1}{p^k}(1-1/p)\right) \\&\ll \frac{1}{Y}\sum _{p^k \le Y} |g(p^k) |\le Y^{-1/2} \sum _{p^k \le Y} |g(p^k) |p^{-k/2} \\&\ll B_g(Y) (\pi (Y)/Y)^{1/2} \ll \frac{B_g(Y)}{\sqrt{\log Y}}, \end{aligned}$$

using the Cauchy–Schwarz inequality and Chebyshev’s estimate $\pi (Y) \ll Y/\log Y$ in the last two steps. $\square$

Lemma 3.2

(Turán–Kubilius Inequality) Let $X \ge 3$. Uniformly over all additive functions $g: \mathbb {N} \rightarrow \mathbb {C}$,

$$\begin{aligned} \frac{1}{X}\sum _{n\le X} |g(n) - A_g(X) |^2 \ll B_g(X)^2. \end{aligned}$$

Proof

This is e.g. [22, Lem. 1.5] (taking $\sigma = 0$). $\square$

The following estimate due to Ruzsa, which sharpens the Turán–Kubilius inequality, gives an order of magnitude estimate for the second centred moment of a general additive function.

Lemma 3.3

[30] Let $g: \mathbb {N} \rightarrow \mathbb {C}$ be an additive function. Then

$$\begin{aligned} \frac{1}{X} \sum _{n \le X} |g(n) - A_g(X) |^2 \asymp \min _{\lambda \in \mathbb {R}} (B_{g_{\lambda }}(X)^2 + \vert \lambda \vert ^2) \asymp B_{g_{\lambda _0}}(X)^2 + \vert \lambda _0\vert ^2, \end{aligned}$$

where for $\lambda \in \mathbb {R}$ and $n \in \mathbb {N}$ we set $g_{\lambda }(n) := g(n)-\lambda \log n$, and $\lambda _0 = \lambda _0(X)$ is given by

$$\begin{aligned} \lambda _0(X) := \frac{2}{(\log X)^2} \sum _{p \le X} \frac{g(p)\log p}{p}. \end{aligned}$$

Lemma 3.4

Let $g: \mathbb {N} \rightarrow \mathbb {C}$ be additive, and let $z \ge y \ge 2$. Then

$$\begin{aligned} A_g(y) = A_g(z) + O\left( B_g(z)\sqrt{\log \big (\tfrac{\log z}{\log y}\big )}\right) . \end{aligned}$$

In particular, if $y \in (z/2,z]$ then

$$\begin{aligned} A_g(y) = A_g(z) + O\left( \frac{B_g(z)}{\sqrt{\log z}}\right) . \end{aligned}$$

Proof

By Mertens’ theorem,

$$\begin{aligned} |A_g(z)-A_g(y) |\le \sum _{y< p^k \le z} \frac{|g(p^k) |}{p^k} \le B_g(z)\left( \sum _{y < p^k \le z} \frac{1}{p^k}\right) ^{1/2} \ll B_g(z)\sqrt{\log (\tfrac{\log z}{\log y})}. \end{aligned}$$

The second claim follows immediately from this. $\square$

Lemma 3.5

Let $X\ge 3$ and let $n \in (X/2,X]$. Then $\frac{|g(n) |}{n} \ll \frac{B_g(X)\log X}{\sqrt{X}}$.

Proof

Observe that whenever $p^k \le X$ we have $\vert g(p^k) \vert /p^{k/2} \le B_g(X)$. It follows from the triangle inequality and the bound $\omega (n) \ll \log n$ for all $n \ge 2$ that

$$\begin{aligned} \frac{|g(n) |}{n} \le \frac{\omega (n)}{n} \max _{p^k ||n} |g(p^k) |\le \frac{\omega (n)}{\sqrt{n}} \max _{p^k ||n} \frac{|g(p^k) |}{p^{k/2}} \ll \frac{\log X}{\sqrt{X}} B_g(X), \end{aligned}$$

as claimed. $\square$

Working within the collection $\mathcal {A}$ (see Definition 1.3), the following properties will be useful.

Lemma 3.6

(a) Let $g: \mathbb {N} \rightarrow \mathbb {C}$ be an additive function satisfying $B_g(X) \rightarrow \infty$. If g is either completely or strongly additive then $g \in \mathcal {A}$.

(b) Let $g \in \mathcal {A}$. Then there is a strongly additive function $g^{*}$ such that $g(p) = g^{*}(p)$ for all primes p, and $B_{g-g^{*}}(X) = o(B_g(X))$ as $X \rightarrow \infty$.

Proof

(a) Let g be either strongly or completely additive. We put $\theta _g := 1$ if g is completely additive, and $\theta _g := 0$ otherwise. Then $g(p^k) = k^{\theta _g}g(p)$ for any prime power $p^k$, and thus

$$\begin{aligned} \sum _{\begin{array}{c} p^k \le X \\ k \ge 2 \end{array}} \frac{|g(p^k) |^2}{p^k} \le \sum _{p \le X} \frac{|g(p) |^2}{p} \sum _{k \ge 2} \frac{k^{2\theta _g}}{p^{k-1}} \ll \sum _{p \le X} \frac{|g(p) |^2}{p^2}. \end{aligned}$$

Since $B_g(X) \rightarrow \infty$, choosing $M = M(X)$ tending to infinity arbitrarily slowly we see that

$$\begin{aligned} \sum _{p \le X} \frac{|g(p) |^2}{p^2}\le & {} \sum _{p \le M} \frac{|g(p) |^2}{p} + \frac{1}{M} \sum _{M < p \le X} \frac{|g(p) |^2}{p} \\\le & {} B_g(M)^2 + \frac{B_g(X)^2}{M} = o(B_g(X)^2). \end{aligned}$$

It follows that $g \in \mathcal {A}$, as required.

(b) We define $g^{*}$ to be an additive function defined by $g^{*}(p^k) := g(p)$ for all primes p and $k \ge 1$. Thus, $g^{*}$ is strongly additive. Moreover, if $(g-g^{*})(p^k) \ne 0$ then $k \ge 2$, for any p. By assumption and part (a), $g,g^{*} \in \mathcal {A}$, and thus

$$\begin{aligned} \sum _{\begin{array}{c} p^k \le X \\ k \ge 2 \end{array}} \frac{|h(p^k) |^2}{p^k} \ll \sum _{p \le X} \frac{|h(p^k) |^2}{p^2} = o(B_g(X)^2) \end{aligned}$$

for both $h = g$ and $h = g^{*}$. By the Cauchy–Schwarz inequality,

$$\begin{aligned} B_{g-g^{*}}(X)^2 \ll \sum _{\begin{array}{c} p^k \le X \\ k \ge 2 \end{array}} \frac{|g(p^k) |^2}{p^k} + \sum _{\begin{array}{c} p^k \le X \\ k \ge 2 \end{array}} \frac{|g^{*}(p^k) |^2}{p^k} = o(B_g(X)^2), \end{aligned}$$

as required. $\square$

Finally, we record the characterization result of Kátai and Wirsing, mentioned in the introduction.

Theorem 3.7

[18, 21] Let $g: \mathbb {N} \rightarrow \mathbb {C}$ be an additive function such that as $X \rightarrow \infty$,

$$\begin{aligned} \frac{1}{X}\sum _{n \le X} |g(n)-g(n-1) |= o(1). \end{aligned}$$

Then there is $c \in \mathbb {C}$ such that $g(n) = c\log n$ for all $n \in \mathbb {N}$.

4 The Matomäki–Radziwiłł theorem for additive functions: $\ell ^1$ variant

In this section, we prove Theorem 1.1.

We begin with the following simple observation, amounting to the fact that the mean value of an additive function changes little when passing from a long interval of length $\asymp X$ to a medium-sized one of length $X/(\log X)^{c}$, for $c > 0$ sufficiently small.

Lemma 4.1

Let $g: \mathbb {N} \rightarrow \mathbb {C}$ be additive and let X be large. Let $X/2 < x \le X$, and let $X/(\log X)^{1/3} \le h \le X/3$. Then

$$\begin{aligned} \frac{2}{X} \sum _{X/2 < n \le X} g(n) = \frac{1}{h} \sum _{x-h \le n \le x} g(n) + O\left( \frac{B_g(X)}{(\log X)^{1/6}}\right) . \end{aligned}$$

Proof

Applying Lemma 3.1 with $Y = X/2,X,x-h$ and x, we obtain

$$\begin{aligned}&\frac{2}{X}\sum _{X/2< n \le X} g(n) = 2A_g(X) - A_g(X/2) + O\left( \frac{B_g(X)}{\sqrt{\log X}}\right) \\&\frac{1}{h}\sum _{x-h < n \le x} g(n) = \frac{x}{h}A_g(x) - \left( \frac{x}{h}-1\right) A_g(x-h) + O\left( \frac{XB_g(X)}{h\sqrt{\log X}}\right) . \end{aligned}$$

Since $h \ge X/(\log X)^{1/3}$, the error term in the second line is $\ll \frac{B_g(X)}{(\log X)^{1/6}}$. By Lemma 3.4,

$$\begin{aligned} 2A_g(X)-A_g(X/2) = A_g(X) + O(|A_g(X)-A_g(X/2) |) = A_g(X) + O\left( \frac{B_g(X)}{\sqrt{\log X}}\right) \end{aligned}$$

for the main term in the first equation, and also

$$\begin{aligned} \frac{x}{h} |A_g(x)-A_g(x-h) |\ll (\log X)^{1/3} \cdot \frac{B_g(x)}{\sqrt{\log x}} \ll \frac{B_g(X)}{(\log X)^{1/6}}, \end{aligned}$$

so that by a second application of Lemma 3.4,

$$\begin{aligned} \frac{x}{h}A_g(x) - \left( \frac{x}{h}-1\right) A_g(x-h)&= A_g(x) + O\left( \frac{x}{h}|A_g(x)-A_g(x-h) |\right) \\&= A_g(X) + O\left( \frac{B_g(X)}{(\log X)^{1/6}}\right) . \end{aligned}$$

Combining these estimates, we may conclude that

$$\begin{aligned} \left|\frac{2}{X}\sum _{X/2< n \le X} g(n)-\frac{1}{h} \sum _{x-h < n \le x} g(n)\right|\ll \frac{B_g(X)}{(\log X)^{1/6}}, \end{aligned}$$

as claimed. $\square$

In light of the above lemma, to prove Theorem 1.1 it suffices to prove the following: if $h' = X/(\log X)^{1/3}$ and $10 \le h \le h'$ then

$$\begin{aligned}&\frac{2}{X}\sum _{X/2<m \le X}\left|\frac{1}{h}\sum _{m-h< n \le m} g(n)-\frac{1}{h'} \sum _{m-h' < n \le m} g(n)\right|\\&\quad \ll B_g(X) \left( \sqrt{\frac{\log \log h}{\log h}} + (\log X)^{-1/800}\right) . \end{aligned}$$

Splitting $g = \text {Re}(g) + i \text {Im}(g)$, and noting that both $\text {Re}(g)$ and $\text {Im}(g)$ are real-valued additive functions, we may assume that g is itself real-valued, after which the general case will follow by the triangle inequality.

Let $10 \le h \le X/3$, with X large. Following [8], fix $\eta \in (0,1/12)$, parameters $Q_1 = h$, $P_1 = (\log h)^{40/\eta }$, and define further parameters $P_j,Q_j$ by

$$\begin{aligned} P_j := \exp \left( j^{4j} (\log Q_1)^{j-1}\log P_1\right) , \quad Q_j := \exp \left( j^{4j+2} (\log Q_1)^j\right) , \end{aligned}$$

for all $j \le J$, where J is chosen maximally subject to $Q_J \le \exp (\sqrt{\log X})$. We then define

$$\begin{aligned} \mathcal {S} = \mathcal {S}_{X,P_1,Q_1} := \{n \le X : \omega _{[P_j,Q_j]}(n) \ge 1 \text { for all }1 \le j \le J\}, \end{aligned}$$

where for any set $S \subset \mathbb {N}$ we write $\omega _S(n) := \sum _{p \mid n} 1_S(p)$.

The following key step in the proof of Theorem 1.1 allows us to pass from comparing averages of the additive g to averages of a corresponding multiplicative function, supported on $\mathcal {S}$.

Lemma 4.2

Let $g: \mathbb {N} \rightarrow \mathbb {R}$ be an additive function. Let $10 \le h \le h'$, where $h' := \frac{X}{(\log X)^{1/3}}$ and $h \in \mathbb {Z}$, and $(\log X)^{-1/6}< t < 1$. Then

$$\begin{aligned}&\frac{2}{X}\sum _{X/2< m \le X} \left|\frac{1}{h'} \sum _{\begin{array}{c} m-h'< n \le m \end{array}} g(n) - \frac{1}{h} \sum _{\begin{array}{c} m-h< n \le m \end{array}} g(n)\right|\\&\ll \frac{B_g(X)}{t}\cdot \frac{1}{X} \int _{X/2}^X \left|\frac{1}{h'} \sum _{\begin{array}{c} x-h'< n \le x \\ n \in \mathcal {S} \end{array}} e(t{\tilde{g}}(n;X)) - \frac{1}{h} \sum _{\begin{array}{c} x-h < n \le x\\ n \in \mathcal {S} \end{array}} e(t{\tilde{g}}(n;X)) \right|\mathrm{d}x \\&\quad + B_g(X)\left( t + \frac{\log \log h}{t\log h}\right) , \end{aligned}$$

where ${\tilde{g}}(n;X) := B_g(X)^{-1}(g(n) - A_g(X))$ for all $n \in \mathbb {N}$.

Proof

In view of Lemma 3.5, at the cost of an error term of size $\max _{X/2<n \le X} |g(n) |/h' \ll B_g(X)X^{-1/4}$, we may assume that both $h,h' \in \mathbb {Z}$ (else replace $h'$ by $\left\lfloor h'\right\rfloor$). Given $u \in [0,1]$, $x \in [X/2,X] \cap \mathbb {Z}$ and an integer $1 \le H \le h'$, define

$$\begin{aligned} S_{H}(u;x) := \frac{1}{H}\sum _{\begin{array}{c} x-H < n \le x \end{array}} e(u{\tilde{g}}(n;X)), \end{aligned}$$

which is clearly an analytic function of u. Fix $x \in [X/2,X] \cap \mathbb {Z}$, and observe that $S_{h'}(0;x) = 1 = S_h(0;x)$. By Taylor expansion in t,

$$\begin{aligned} S_{h'}(t;x)-S_h(t;x) = t(S_{h'}'(0;x)-S_h'(0;x)) + \int _0^t (S_{h'}''(u;x)-S_h''(u;x)) u \,\mathrm{d}u,\nonumber \\ \end{aligned}$$

(11)

wherein we have

$$\begin{aligned}&S_{h'}'(0;x) - S_h'(0;x) \end{aligned}$$

(12)

$$\begin{aligned}&= \frac{2\pi i}{B_g(X)} \left( \frac{1}{h'} \sum _{\begin{array}{c} x-h'< n \le x \end{array}} (g(n)-A_g(X)) - \frac{1}{h} \sum _{\begin{array}{c} x-h< n \le x \end{array}}(g(n)-A_g(X))\right) \nonumber \\&= \frac{2\pi i}{B_g(X)} \left( \frac{1}{h'} \sum _{\begin{array}{c} x-h'< n \le x \end{array}} g(n) - \frac{1}{h} \sum _{\begin{array}{c} x-h < n \le x \end{array}} g(n)\right) . \end{aligned}$$

(13)

By inserting the expression (13) into (11), rearranging the latter and then taking absolute values and averaging over $x \in [X/2,X] \cap \mathbb {Z}$, we find

$$\begin{aligned}&\frac{2}{X}\sum _{X/2<m \le X} \left|\frac{1}{h'}\sum _{\begin{array}{c} m-h'< n \le m \end{array}} g(n) - \frac{1}{h} \sum _{\begin{array}{c} m-h< n \le m \end{array}} g(n)\right|\\&\ll B_g(X) t^{-1} \cdot \frac{1}{X} \sum _{X/2<m\le X} \left|\frac{1}{h'} \sum _{\begin{array}{c} m-h'< n \le m \end{array}} e(t{\tilde{g}}(n;X)) - \frac{1}{h} \sum _{\begin{array}{c} m-h< n \le m \end{array}} e(t{\tilde{g}}(n;X))\right|\\&\quad + B_g(X) t^{-1}\cdot \frac{t^2 }{X} \sum _{X/2< m \le X}\max _{0 \le u \le t} |\frac{1}{h'} \sum _{\begin{array}{c} m-h'< n \le m \end{array}} {\tilde{g}}(n;X)^2 e(u{\tilde{g}}(n;X)) \\&\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad - \frac{1}{h} \sum _{\begin{array}{c} m-h < n \le m \end{array}} {\tilde{g}}(n;X)^2 e(u{\tilde{g}}(n;X))|. \end{aligned}$$

Since g is real-valued by assumption, $|e(u{\tilde{g}}(n;X)) |= 1$ for all n. Thus, applying the triangle inequality and Lemma 3.2, we may bound the last expression above by

$$\begin{aligned}&\ll t B_g(X) \frac{1}{X} \sum _{X/2< m \le X} \sum _{H \in \{h,h'\}} \frac{1}{H} \sum _{m-H< n \le m} \left( \frac{g(n)-A_g(X)}{B_g(X)}\right) ^2 \\&\ll tB_g(X) \cdot \frac{1}{X} \sum _{X/2-h'< n \le X} \left( \frac{g(n)-A_g(X)}{B_g(X)}\right) ^2 \cdot \sum _{H \in \{h,h'\}} \frac{1}{H}\sum _{X/2 < m \le X} 1_{[n,n+H]}(m) \\&\ll tB_g(X). \end{aligned}$$

We now split

$$\begin{aligned} S_H(t;x)&= \frac{1}{H}\sum _{\begin{array}{c} x-H< n \le x \\ n\in \mathcal {S} \end{array}} e(t{\tilde{g}}(n;X)) + \frac{1}{H}\sum _{\begin{array}{c} x-H < n \le x \\ n\notin \mathcal {S} \end{array}} e(t{\tilde{g}}(n;X)) \\&=: S_H^{(\mathcal {S})}(t;x) + S_H^{(\mathcal {S}^c)}(t;x), \end{aligned}$$

with $H\in \{h,h'\}$. By the triangle inequality, we have

$$\begin{aligned} \frac{2}{X}\sum _{X/2< x \le X} |S_H^{(\mathcal {S}^c)}(t;x) |\le \frac{1}{HX}\sum _{X/2< x \le X} |\mathcal {S}^c \cap (x-H,x] |\le \frac{1}{X}\sum _{X/3 < n \le X}1_{\mathcal {S}^c}(n). \end{aligned}$$

Since $P_J \le \exp (\sqrt{\log X})$, the union bound and the fundamental lemma of the sieve (see [31, Remark after Lem. 6.3]) yield

$$\begin{aligned} |\mathcal {S}^c \cap [X/3,X] |&\ll X\sum _{1 \le j \le J}\prod _{P_j \le p \le Q_j} \left( 1-\frac{1}{p}\right) \ll X\sum _{1 \le j \le J}\frac{\log P_j}{\log Q_j} \nonumber \\&= X\frac{\log P_1}{\log Q_1} \sum _{1\le j \le J} \frac{1}{j^2} \ll X\frac{\log \log h}{\log h}. \end{aligned}$$

(14)

We thus find by the triangle inequality that

$$\begin{aligned} \frac{2}{X}\sum _{X/2< n \le X} \left|S_h(t;n) - S_{h'}(t;n)\right|\ll \frac{2}{X}\sum _{X/2 < n \le X} \left|S_h^{(\mathcal {S})}(t;n) - S_{h'}^{(\mathcal {S})}(t;n)\right|+ \frac{\log \log h}{\log h}. \end{aligned}$$

Finally, if $n \in [X/2,X] \cap \mathbb {Z}$ and $x \in [n,n+1)$ then $S_H^{(\mathcal {S})}(t;x) = S_H^{(\mathcal {S})}(t; n) + O(1/H)$, and thus

$$\begin{aligned} \frac{2}{X}\sum _{X/2 < n \le X} |S_h^{(\mathcal {S})}(t;n) - S_{h'}^{(\mathcal {S})}(t;n) |\le \frac{2}{X}\int _{X/2}^X |S_h^{(\mathcal {S})}(t;x) - S_{h'}^{(\mathcal {S})}(t;x) |\mathrm{d}x + O(1/h). \end{aligned}$$

Combined with the preceding estimates, we obtain

$$\begin{aligned}&\frac{2}{X}\sum _{X/2< m \le X} \left|\frac{1}{h'}\sum _{\begin{array}{c} m-h'< n \le m \end{array}} g(n) - \frac{1}{h} \sum _{\begin{array}{c} m-h < n \le m \end{array}} g(n)\right|\\&\ll t^{-1} B_g(X)\left( \frac{2}{X}\int _{X/2}^X \left|S_h^{(\mathcal {S})}(t;x) - S_{h'}^{(\mathcal {S})}(t;x)\right|\mathrm{d}x + \frac{\log \log h}{\log h}\right) + tB_g(X), \end{aligned}$$

which implies the claim. $\square$

Define the multiplicative function

$$\begin{aligned} G_{t,X}(n) := e(tg(n)/B_g(X)) = e(t {\tilde{g}}(n;X)) e(tA_g(X)/B_g(X)). \end{aligned}$$

In light of Lemma 4.2, the proof of Theorem 1.1 essentially boils down to the following comparison result for short- and medium-length interval averages of $G_{t,X}$.

Lemma 4.3

Let $g: \mathbb {N} \rightarrow \mathbb {R}$ be an additive function. Let $X \ge 3$ be large, $(\log X)^{-1/6} < t \le 1/100$ be small and let $10 \le h_1 \le h_2$ where $h_2 = X/(\log X)^{1/3}$. Then

$$\begin{aligned}&\frac{2}{X}\int _{X/2}^{X} \left|\frac{1}{h_1}\sum _{\begin{array}{c} x-h_1< n \le x \\ n \in \mathcal {S} \end{array}} G_{t,X}(n) - \frac{1}{h_2}\sum _{\begin{array}{c} x-h_2 < n \le x \\ n \in \mathcal {S} \end{array}} G_{t,X}(n) \right|\mathrm{d}x \end{aligned}$$

(15)

$$\begin{aligned}&\quad \ll B_g(X)\left( \frac{\log \log h_1}{\log h_1} + (\log X)^{-1/400}\right) . \end{aligned}$$

(16)

To prove Lemma 4.3 we will appeal to some ideas from pretentious analytic number theory. Let $\mathbb {U} := \{z \in \mathbb {C} : |z |\le 1\}$. In what follows, given multiplicative functions $f,g: \mathbb {N} \rightarrow \mathbb {U}$ and parameters $1 \le T \le X$, we introduce the pretentious distance of Granville and Soundararajan:

$$\begin{aligned} \mathbb {D}(f,g; X)^2&:= \sum _{p \le X} \frac{1-\text {Re}(f(p){\overline{g}}(p))}{p},\\ M_f(X;T)&:= \min _{|\lambda |\le T} \mathbb {D}(f,n^{i\lambda }; X)^2. \end{aligned}$$

For multiplicative functions f, g, h taking values in $\mathbb {U}$, it is well known (see e.g. [32, Lem 3.1]) that $\mathbb {D}$ satisfies the triangle inequality

$$\begin{aligned} \mathbb {D}(f,h;X) \le \mathbb {D}(f,g;X) + \mathbb {D}(g,h;X). \end{aligned}$$

(17)

For each $t \in [0,1]$, select $\lambda _{t,X} \in [-X,X]$ such that $M_{G_{t,X}}(X;X) = \mathbb {D}(G_{t,X},n^{i\lambda _{t,X}}; X)^2$ (if there are multiple such minimizers, pick any one of them).

Lemma 4.4

Let $0 < t \le 1/100$ be sufficiently small. Then either

• (i) $M_{G_{t,X}}(X;X) \ge \frac{1}{25}\log \log X$, or else

• (ii) $|\lambda _{t,X}|= O(1)$.

Proof

Assume (i) fails. Then by assumption, $\mathbb {D}(G_{t,X}, n^{i\lambda _{t,X}};X)^2 \le \frac{1}{25} \log \log X$. We claim that there is also ${\tilde{\lambda }}_{t,X} = O(1)$ such that

$$\begin{aligned} \mathbb {D}(G_{t,X}, n^{i{\tilde{\lambda }}_{t,X}};X) \ll 1. \end{aligned}$$

(18)

To see that this is sufficient to prove (ii), we apply (17) to obtain

$$\begin{aligned} \mathbb {D}(n^{i\lambda _{t,X}},n^{i{\tilde{\lambda }}_{t,X}};X) \le O(1)+\frac{1}{5}\sqrt{\log \log X} \le \sqrt{0.3 \log \log X} \end{aligned}$$

for large enough X. Now, if $|\lambda _{t,X} - {\tilde{\lambda }}_{t,X}|\ge 100$ then as $|\lambda _{t,X}|, |{\tilde{\lambda }}_{t,X}|\le X$ the Vinogradov–Korobov zero-free region for $\zeta$ (see e.g. [9, (1.12)]) gives

$$\begin{aligned} \mathbb {D}(n^{i\lambda _{t,X}}, n^{i{\tilde{\lambda }}_{t,X}}; X)^2&= \log \log X - \log |\zeta (1+1/\log X + i(\lambda _{t,X} - {\tilde{\lambda }}_{t,X}))|+ O(1)\\&\ge 0.33 \log \log X, \end{aligned}$$

which is a contradiction. It follows that

$$\begin{aligned} |\lambda _{t,X}|\le |{\tilde{\lambda }}_{t,X}|+ 100 = O(1), \end{aligned}$$

as required.

It thus remains to prove that (18) holds. By Lemma 3.2, we obtain

$$\begin{aligned} |\{n \le X : |{\tilde{g}}(n;X) |> t^{-1/2} \} |\le t\sum _{n \le X} {\tilde{g}}(n;X)^2 \ll tX. \end{aligned}$$

It follows from Taylor expansion that

$$\begin{aligned} \sum _{n \le X} e(t{\tilde{g}}(n;X)) = \sum _{n \le X}\left( 1+O(\sqrt{t})\right) + O(tX) = (1+O(\sqrt{t}))X. \end{aligned}$$

On the other hand, by Halász’ theorem in the form of Granville and Soundararajan [33, Thm. 1],

$$\begin{aligned} \left|\sum _{n \le X} e(t{\tilde{g}}(n;X))\right|= \left|\sum _{n \le X} G_{t,X}(n)\right|\ll M_{G_{t,X}}(X; U)e^{-M_{G_{t,X}}(X; U)} X + \frac{X}{U}, \end{aligned}$$

where $1 \le U \le \log X$ is a parameter of our choice. If U is a suitably large absolute constant and t is sufficiently small in an absolute sense, we obtain $M_{G_{t,X}}(X; U) \ll 1$, and therefore there is a ${\tilde{\lambda }}_{t,X} \in [-U,U]$ (thus of size O(1)) such that

$$\begin{aligned} \mathbb {D}(G_{t,X},n^{i{\tilde{\lambda }}_{t,X}};X) \ll 1, \end{aligned}$$

as claimed. $\square$

Proof of Lemma 4.3

Set $\varepsilon = (\log X)^{-1/100}$. If $M_{G_{t,X}}(X;X) \ge 4\log (1/\varepsilon )$ then by the triangle inequality, Cauchy–Schwarz and [9, Theorem A.2], the LHS of (15) is

$$\begin{aligned}&\ll \sum _{j = 1,2} \left( \frac{1}{X}\int _{X/2}^{X} \left|\frac{1}{h_j}\sum _{\begin{array}{c} x-h_j < n \le x \\ n \in \mathcal {S} \end{array}} G_{t,X}(n) \right|^2 \mathrm{d}x\right) ^{1/2} \\&\ll \exp \left( -\frac{1}{2}M_{G_{t,X}}(X;X)\right) M_{G_{t,X}}(X;X)^{1/2} + \frac{(\log h_1)^{1/6}}{P_1^{1/12-\eta /2}} + (\log X)^{-1/200} \\&\ll \varepsilon ^2 (\log (1/\varepsilon ))^{1/2} + (\log h_1)^{-1} +(\log X)^{-1/200} \\&\ll (\log h_1)^{-1} +(\log X)^{-1/200}. \end{aligned}$$

Next, assume that $M_{G_{t,X}}(X;X) < 4\log (1/\varepsilon )$. For $\lambda \in \mathbb {R}$ and $h \ge 1$ define

$$\begin{aligned} I(x;\lambda , h) := h^{-1} \int _{x-h}^x u^{i\lambda } \mathrm{d}u. \end{aligned}$$

By Lemma 4.4 we have $\lambda _{t,X} = O(1)$, so that with $h \in \{h_1,h_2\}$,

$$\begin{aligned} I(x;\lambda _{t,X},h)&= x^{i\lambda _{t,X}} \left( \frac{1-(1-h/x)^{1+i\lambda _{t,X}}}{(1+i\lambda _{t,X})h/x}\right) = x^{i\lambda _{t,X}} \left( 1+O\left( |\lambda _{t,X}|\frac{h}{X}\right) \right) \\&= x^{i\lambda _{t,X}}\left( 1+O\left( \frac{h}{X}\right) \right) , \end{aligned}$$

and thus for each $x \in [X/2,X]$ and $j = 1,2$,

$$\begin{aligned}&x^{i\lambda _{t,X}} \frac{2}{X} \sum _{\begin{array}{c} X/2< n \le X \\ n \in \mathcal {S} \end{array}} G_{t,X}(n)n^{-i\lambda _{t,X}} \nonumber \\&\quad = I(x;\lambda _{t,X},h_j) \cdot \frac{2}{X}\sum _{\begin{array}{c} X/2 < n \le X \\ n \in \mathcal {S} \end{array}} G_{t,X}(n)n^{-i\lambda _{t,X}} + O\big (\tfrac{h_j}{X}\big ). \end{aligned}$$

(19)

Reinstating the $n \notin \mathcal {S}$ and using the arguments surrounding (14), we also note that

$$\begin{aligned}&\frac{2}{X}\int _{X/2}^X \left|\frac{1}{h_j} \sum _{\begin{array}{c} x-h_j< n \le x \\ n \in \mathcal {S} \end{array}} G_{t,X}(n) - x^{i\lambda _{t,X}} \frac{2}{X} \sum _{\begin{array}{c} X/2< n \le X \\ n \in \mathcal {S} \end{array}} G_{t,X}(n)n^{-i\lambda _{t,X}}\right|\mathrm{d}x \\&\quad \ll \frac{2}{X}\int _{X/2}^X \left|\frac{1}{h_j} \sum _{\begin{array}{c} x-h_j< n \le x \end{array}} G_{t,X}(n) - x^{i\lambda _{t,X}} \frac{2}{X} \sum _{\begin{array}{c} X/2 < n \le X \end{array}} G_{t,X}(n)n^{-i\lambda _{t,X}}\right|\mathrm{d}x \\&\quad + \frac{\log \log h_1}{\log h_1}. \end{aligned}$$

Adding and subtracting the expression on the LHS of (19) inside the absolute values bars in (15), we obtain the upper bound

$$\begin{aligned} \ll \mathcal {T}_1 + \mathcal {T}_2 + \frac{h_2}{X}, \end{aligned}$$

where we have set

$$\begin{aligned} \mathcal {T}_j := \frac{2}{X}\int _{X/2}^{X} \left|I(x;\lambda _{t,X}, h_j) \frac{2}{X}\sum _{\begin{array}{c} X/2< n \le X \\ n \in \mathcal {S} \end{array}} G_{t,X}(n)n^{-i\lambda _{t,X}} - \frac{1}{h_j}\sum _{\begin{array}{c} x-h_j < n \le x \\ n \in \mathcal {S} \end{array}} G_{t,X}(n) \right|. \end{aligned}$$

If $j = 2$ then as just noted we also have

$$\begin{aligned} \mathcal {T}_2&\ll \frac{1}{X}\int _{X/2}^X \left|\frac{1}{h_2} \sum _{\begin{array}{c} x-h_2< n \le x \end{array}} G_{t,X}(n) - I(x;\lambda _{t,X}, h_2)\frac{2}{X} \sum _{\begin{array}{c} X/2 < n \le X \end{array}} G_{t,X}(n)n^{-\lambda _{t,X}} \right|\mathrm{d}x \\&\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad + \frac{\log \log h_1}{\log h_1}, \end{aligned}$$

and so by Cauchy–Schwarz and [34, Theorem 1.6] (taking $Q = 1$ and $\varepsilon = (\log X)^{-1/200}$ there), we have

$$\begin{aligned} \mathcal {T}_2&\ll \left( \frac{2}{X}\int _{X/2}^{X} \left|I(x;\lambda _{t,X}, h_2) \frac{2}{X}\sum _{\begin{array}{c} X/2< n \le X \end{array}} G_{t,X}(n)n^{-i\lambda _{t,X}} - \frac{1}{h_2}\sum _{\begin{array}{c} x-h_2 < n \le x \end{array}} G_{t,X}(n) \right|^2 dx\right) ^{\frac{1}{2}} \\&\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad + \frac{\log \log h_1}{\log h_1} \\&\ll (\log X)^{-1/400} + \frac{\log \log h_1}{\log h_1}. \end{aligned}$$

In the same way, when $h_1 > \sqrt{X}$ we obtain the same bound $\mathcal {T}_1 \ll (\log X)^{-1/400} + \frac{\log \log h_1}{\log h_1}$ as well.

Thus, assume that $10 \le h_1 \le \sqrt{X}$. Combining Cauchy–Schwarz with [10, Theorem 9.2(ii)] (taking $\delta = (\log h_1)^{1/3}P_1^{-1/6+\eta }$, $\nu _1 = 1/20$ and $\nu _2 = 1/12$, there), we then get

$$\begin{aligned} \mathcal {T}_1 \ll \left( \frac{(\log h_1)^{4/3}}{P_1^{1/12-\eta }} + (\log X)^{-1/200}\right) ^{1/2} \ll (\log h_1)^{-1} + (\log X)^{-1/400}. \end{aligned}$$

Combining these estimates, we obtain that the LHS of (15) is

$$\begin{aligned} \ll (\log h_1)^{-1} + (\log X)^{-1/400}+\frac{\log \log h_1}{\log h_1} + \frac{h_2}{X} \ll (\log X)^{-1/400} + \frac{\log \log h_1}{\log h_1}, \end{aligned}$$

as claimed. $\square$

Proof of Theorem 1.1

Set $h_1 := h$ and $h_2 := X/(\log X)^{1/3}$. As mentioned, we may assume that g is real-valued (otherwise the result follows for complex-valued g by applying the theorem to $\text {Re}(g)$ and $\text {Im}(g)$ and applying the triangle inequality). By Lemma 4.1, we have

$$\begin{aligned}&\frac{2}{X}\sum _{X/2< m \le X} \left|\frac{1}{h_1}\sum _{m-h_1< n \le m} g(n) - \frac{2}{X}\sum _{X/2<n \le X} g(n) \right|\nonumber \\&\ll \frac{2}{X}\sum _{X/2< m \le X} \left|\frac{1}{h_1}\sum _{m-h_1< n \le m} g(n) - \frac{1}{h_2}\sum _{m-h_2 < n \le m} g(n)\right|+ \frac{B_g(X)}{(\log X)^{1/6}}. \end{aligned}$$

(20)

By Lemma 4.2, the latter is

$$\begin{aligned} \ll \frac{B_g(X)}{t} \cdot \frac{1}{X}\int _{X/2}^X |S_{h_1}^{(\mathcal {S})}(t;x) - S_{h_2}^{(\mathcal {S})}(t;x) |\mathrm{d}x \nonumber \\ \quad + B_g(X) \left( t+\frac{\log \log h}{t\log h} + (\log X)^{-\tfrac{1}{6}}\right) . \end{aligned}$$

(21)

Observe next that for any $x \in [X/2,X]$ and $t \in (0,1)$,

$$\begin{aligned}&S_{h_1}^{(\mathcal {S})}(t;x) - S_{h_2}^{(\mathcal {S})}(t;x) = \frac{1}{h_1} \sum _{\begin{array}{c} x-h_1< n \le x \\ n \in \mathcal {S} \end{array}} e(t{\tilde{g}}(n;X)) - \frac{1}{h_2} \sum _{\begin{array}{c} x-h_2< n \le x \\ n \in \mathcal {S} \end{array}} e(t{\tilde{g}}(n;X)) \\&\quad = e(-t\tfrac{A_g(X)}{B_g(X)}) \cdot \left( \frac{1}{h_1} \sum _{\begin{array}{c} x-h_1< n \le x \\ n \in \mathcal {S} \end{array}} G_{t,X}(n) - \frac{1}{h_2} \sum _{\begin{array}{c} x-h_2 < n \le x \\ n \in \mathcal {S} \end{array}} G_{t,X}(n)\right) . \end{aligned}$$

Taking $t := \max \big \{\sqrt{\frac{\log \log h_1}{\log h_1}}, (\log X)^{-1/800}\big \}$, Theorem 1.1 now follows on combining this last expression with Lemma 4.3 and inserting the resulting bound into (21) . $\square$

5 The Matomäki–Radziwiłł theorem for additive functions: $\ell ^2$ variant

In this section, we will prove Theorem 1.4.

Let $g \in \mathcal {A}_s$, so that $B_g(X) \rightarrow \infty$, and the conditions

$$\begin{aligned} \lim _{\delta \rightarrow 0^+} F_g(\delta ) = \lim _{\delta \rightarrow 0^+} \limsup _{X \rightarrow \infty } \frac{1}{B_g(X)^2} \sum _{\begin{array}{c} p \le X \\ |g(p) |> \delta ^{-1} B_g(X) \end{array}} \frac{|g(p) |^2}{p}&= 0 , \end{aligned}$$

(22)

$$\begin{aligned} \limsup _{X \rightarrow \infty } \frac{1}{B_g(X)^2} \sum _{\begin{array}{c} p^k \le X \\ k \ge 2 \end{array}} \frac{|g(p^k) |^2}{p^k}&= 0. \end{aligned}$$

(23)

both hold. We seek to show that

$$\begin{aligned} \Delta _g(X,h) := \frac{2}{X}\sum _{X/2< n \le X} \left|\frac{1}{h} \sum _{n-h< m \le n} g(m) - \frac{2}{X}\sum _{X/2 < m \le X} g(m)\right|^2 = o(B_g(X)^2),\nonumber \\ \end{aligned}$$

(24)

whenever $10 \le h \le X/10$ is an integer that satisfies $h = h(X) \rightarrow \infty$ as $X \rightarrow \infty$.

We begin by making the following convenient reduction.

Lemma 5.1

Suppose that Theorem 1.4 holds for any non-negative, strongly additive function $g \in \mathcal {A}_s$. Then Theorem 1.4 holds for any $g \in \mathcal {A}_s$.

Proof

By splitting $g = \text {Re}(g) + i\text {Im}(g)$, and separately decomposing

$$\begin{aligned} \text {Re}(g) = \text {Re}(g)^+ - \text {Re}(g)^-, \quad \quad \text {Im}(g) = \text {Im}(g)^+ - \text {Im}(g)^-, \end{aligned}$$

where, for an additive function h we define the non-negative additive functions $h^{\pm }$ on prime powers via

$$\begin{aligned} h^+(p^k) := \max \{h(p^k),0\}, \quad h^-(p^k) := \max \{0,-h(p^k)\}, \end{aligned}$$

the Cauchy–Schwarz inequality implies that if (24) holds for non-negative g satisfying (22) and (23) then it holds for all additive g satisfying those conditions.

Therefore, we may assume that g is non-negative. Now, by Lemma 3.6, we can find a strongly additive function $g^{*}$, satisfying $g(p) = g^{*}(p)$ for all p, such that upon setting $G := g-g^{*}$ we have $B_{G}(X) = o(B_g(X))$. If we write, for a non-negative additive function h,

$$\begin{aligned} {\tilde{F}}_h(\delta ;X) := \frac{1}{B_h(X)^2} \sum _{\begin{array}{c} p \le X \\ h(p) > \delta ^{-1} B_h(X) \end{array}} \frac{h(p)^2}{p} \end{aligned}$$

then we see that when X is large enough,

$$\begin{aligned} {\tilde{F}}_{g^{*}}(\delta /2;X) \le 2{\tilde{F}}_g(\delta ;X) \le 4{\tilde{F}}_{g^{*}}(2\delta ;X). \end{aligned}$$

Taking limsups as $X \rightarrow \infty$ in these inequalities, it follows that $g^{*}$ satisfies (22) whenever g does; that $g^{*}$ also satisfies (23) is an immediate consequence of Lemma 3.6. Moreover, we see by the Cauchy–Schwarz inequality and Lemma 3.2 that

$$\begin{aligned}&\frac{2}{X}\sum _{X/2<n \le X} \left|\frac{1}{h}\sum _{n-h< m \le n} (G(m)-A_G(X))\right|^2 \\&\quad \le \frac{1}{Xh} \sum _{X/2< n \le X} \sum _{n-h< m \le n} |G(m)-A_G(X) |^2 \\&\quad \ll \frac{1}{X} \sum _{X/3 < m \le X} |G(m)-A_G(X)|^2 \ll B_G(X)^2 = o(B_g(X)^2). \end{aligned}$$

Using the estimate $\frac{2}{X}\sum _{X/2 < n \le X} G(n) = A_G(X) + o(B_g(X))$ by Lemmas 3.1 and 3.4 (as in the proof of Lemma 4.1), we see that

$$\begin{aligned} \Delta _g(X,h) \ll \Delta _{g^{*}}(X,h) + \Delta _{G}(X,h) = \Delta _{g^{*}}(X,h) + o(B_g(X)), \end{aligned}$$

so that if (24) holds for strongly additive $g^{*} \in \mathcal {A}_s$ then it also holds for all $g \in \mathcal {A}_s$. This completes the proof. $\square$

Until further notice we may thus assume that g is non-negative and strongly additive. For a fixed small parameter $\varepsilon > 0$, let $\delta \in (0,1/100)$ be chosen such that $F_g(\delta ) < \varepsilon$. Let X be a scale chosen sufficiently large so that

$$\begin{aligned} \sum _{\begin{array}{c} p \le X \\ g(p) > \delta ^{-1} B_g(X) \end{array}} \frac{ g(p)^2}{p}&\le 2F_g(\delta ) B_g(X)^2 < 2\varepsilon B_g(X)^2, \end{aligned}$$

(25)

$$\begin{aligned} \sum _{\begin{array}{c} p^k \le X \\ k \ge 2 \end{array}} \frac{ g(p^k) ^2}{p^k}&= \sum _{\begin{array}{c} p^k \le X \\ k \ge 2 \end{array}} \frac{ g(p) ^2}{p^k} < \varepsilon B_g(X)^2. \end{aligned}$$

(26)

With these data, define

$$\begin{aligned} \mathcal {C} = \mathcal {C}(X,\delta ) := \{p \le X : g(p) \le \delta ^{-1}B_g(X)\}. \end{aligned}$$

We decompose g as

$$\begin{aligned} g = g_{\mathcal {C}} + g_{\mathcal {P} \backslash \mathcal {C}}, \end{aligned}$$

where $g_{\mathcal {C}}$ and $g_{\mathcal {P} \backslash \mathcal {C}}$ are strongly additive functions defined at primes by

$$\begin{aligned} g_{\mathcal {C}}(p) := {\left\{ \begin{array}{ll} g(p) &{}\text { if }p \in \mathcal {C} \\ 0 &{}\text { if }p \notin \mathcal {C}.\end{array}\right. } \quad \quad g_{\mathcal {P}\backslash \mathcal {C}}(p) := {\left\{ \begin{array}{ll} 0 &{}\text { if }p \in \mathcal {C} \\ g(p) &{}\text { if }p \notin \mathcal {C}.\end{array}\right. } \end{aligned}$$

We will consider the mean-squared errors

$$\begin{aligned} \frac{2}{X}\sum _{X/2< n \le X} \left|\frac{1}{h} \sum _{n-h<m\le n} g_{\mathcal {A}}(m) - \frac{2}{X}\sum _{X/2 < m\le X} g_{\mathcal {A}}(m)\right|^2 \end{aligned}$$

for $\mathcal {A} \in \{\mathcal {C},\mathcal {P}\backslash \mathcal {C}\}$, separately. The fact that $g \in \mathcal {A}_s$ means, in particular, that $g_{\mathcal {P} \backslash \mathcal {C}}$ contributes little to $\Delta _g(X,h)$.

Lemma 5.2

Let $g \in \mathcal {A}_s$ be a non-negative, strongly additive function. Assume that X and $\delta$ are chosen such that (25) and (26) both hold. Then we have

$$\begin{aligned} \Delta _g(X,h) \ll \Delta _{g_{\mathcal {C}}}(X,h) + \varepsilon B_g(X)^2, \end{aligned}$$

where $\mathcal {C} = \mathcal {C}(X,\delta )$.

Proof

Arguing as in the proof of Lemma 5.1, we obtain from (25) and (26) that

$$\begin{aligned} \Delta _{g_{\mathcal {P} \backslash \mathcal {C}}}(X,h) \ll B_{g_{\mathcal {P} \backslash \mathcal {C}}}(X)^2 < 3\varepsilon B_g(X)^2. \end{aligned}$$

Thus, by the Cauchy–Schwarz inequality, we obtain

$$\begin{aligned} \Delta _g(X,h) \ll \Delta _{g_{\mathcal {C}}}(X,h) + \Delta _{g_{\mathcal {P}\backslash \mathcal {C}}}(X,h) \ll \Delta _{g_{\mathcal {C}}}(X,h) + \varepsilon B_g(X)^2, \end{aligned}$$

as claimed. $\square$

In analogy to the work of the previous section, we will reduce the estimation of $\Delta _{g_{\mathcal {C}}}(X)$ to that of the variance of short- and long-interval averages of certain multiplicative functions determined by $g_{\mathcal {C}}$. These are defined as follows.

Fix $r \in (0,\delta ^{2}]$. Given $z \in \mathbb {C}$ satisfying $|z-1 |= r$, define

$$\begin{aligned} F_{z}(n) := z^{g_{\mathcal {C}}(n)/B_g(X)} \text { for all } n \in \mathbb {N}. \end{aligned}$$

Since $g_{\mathcal {C}}$ is strongly additive and satisfies $0 \le g_{\mathcal {C}}(p) \le \delta ^{-1} B_g(X)$ for all $p \le X$, we have

$$\begin{aligned} |F_{z}(p^k) |= |F_z(p) |\le (1+\delta ^2)^{\delta ^{-1}} \le 2 \end{aligned}$$

(27)

for all $p^k \le X$, and thus also

$$\begin{aligned} |F_{z}(n) |\le \left( \max _{p\mid n} |F_{z}(p) |\right) ^{\omega (n)} \le 2^{\omega (n)} \le d(n), \end{aligned}$$

(28)

where d(n) is the divisor function. Furthermore, as $\delta \in (0,1/100)$, for any $2 \le u \le v \le X$ we get

$$\begin{aligned} \sum _{u< p \le v} \frac{|F_z(p) |}{p} \ge (1-\delta ^2)^{\delta ^{-1}} \sum _{u< p \le v} \frac{1}{p} \ge 0.98 \sum _{u < p \le v} \frac{1}{p}. \end{aligned}$$

(29)

Our treatment of short sums of $g_{\mathcal {C}}$ will entail an analysis of corresponding short sums of $F_z$, for z lying in a small neighbourhood of 1. In preparation to apply a relevant result from the recent paper [14], we introduce some further notation. Given a multiplicative function $f: \mathbb {N} \rightarrow \mathbb {C}$ set

$$\begin{aligned} H(f;X) := \prod _{p \le X} \left( 1+\frac{( |f(p) |-1)^2}{p}\right) , \quad \quad \mathcal {P}_f(X) := \prod _{p \le X} \left( 1+ \frac{|f(p) |-1}{p}\right) . \end{aligned}$$

We also define the following variant of the pretentious distance:

$$\begin{aligned} \rho (f,n^{it};X)^2 := \sum _{p \le X} \frac{|f(p)|- \text {Re}(f(p)p^{-it})}{p}. \end{aligned}$$

We let $t_0 = t_0(f,X)$ denote a real number $t \in [-X,X]$ that minimizes $t \mapsto \rho (f,n^{it};X)^2$.

Theorem 5.3

[14, Thm. 2.1] Let $0 < A \le 2$, and let X be large. Let $f: \mathbb {N} \rightarrow \mathbb {C}$ be a multiplicative function that satisfies

• (i) $|f(n) |\le d(n)$ for all $n \le X$, and in particular $|f(p) |\le 2$ for all $p \le X$,

• (ii) for any $2 \le u \le v \le X$,

  $$\begin{aligned} \sum _{u< p \le v} \frac{|f(p) |}{p} \ge A \sum _{u < p \le v} \frac{1}{p} - O\left( \frac{1}{\log u}\right) . \end{aligned}$$

Let $10 \le h_0 \le X/(10H(f;X))$, and put $h_1 := h_0 H(f;X)$ and $t_0 = t_0(f,X)$. Then there are constants $c_1,c_2 \in (0,1/3)$, depending only on A, such that if $X/(\log X)^{c_1} < h_2 \le X$,

$$\begin{aligned}&\frac{2}{X}\int _{X/2}^X \left|\frac{1}{h_1}\sum _{x-h_1< n \le x} f(n) - \frac{1}{h_1}\int _{x-h_1}^x u^{it_0} \mathrm{d}u \cdot \frac{1}{h_2}\sum _{x-h_2 < n \le x} f(n)n^{-it_0}\right|^2 \mathrm{d}x\\&\quad \ll _A \left( \left( \frac{\log \log h_0}{\log h_0}\right) ^A + \left( \frac{\log \log X}{(\log X)^{c_2}}\right) ^{\min \{1,A\}} \right) \mathcal {P}_f(X)^2. \end{aligned}$$

Let $c_1 \in (0,1/3)$ be the constant from Theorem 5.3, applied with $A = 0.98$. By Lemma 4.1, if $h_2 = \left\lceil X/(\log X)^{c_1}\right\rceil$ then for any $x \in (X/2,X]$

$$\begin{aligned} \frac{1}{h_2}\sum _{x-h_2< n \le x} g_{\mathcal {C}}(n) = \frac{2}{X} \sum _{X/2<n \le X} g_{\mathcal {C}}(n) + O\left( \frac{B_g(X)}{(\log X)^{1/6}}\right) . \end{aligned}$$

(30)

In view of Lemma 5.2, in order to prove Theorem 1.4 it suffices to show that as $X \rightarrow \infty$,

$$\begin{aligned} \Delta _{g_{\mathcal {C}}}(X;h_1,h_2)&:= \frac{2}{X}\sum _{X/2< n \le X} \left|\frac{1}{h_1}\sum _{n-h_1<m \le x} g_{\mathcal {C}}(m) - \frac{1}{h_2} \sum _{n-h_2< m \le n} g_{\mathcal {C}}(m)\right|^2 \\&= o(B_g(X)^2), \end{aligned}$$

where $h_1 = h$ and $h_2 = \left\lceil X/(\log X)^{c_1} \right\rceil$.

Using Theorem 5.3, we will prove the following.

Corollary 5.4

Let $10 \le h_1 \le X/10$ be an integer and $h_2 := \lceil X/(\log X)^{c_1}\rceil$ as above. Then there is a constant $\gamma > 0$ such that

$$\begin{aligned} \Delta _{g_{\mathcal {C}}}(X;h_1,h_2) \ll \delta ^{-4}\left( \left( \frac{\log \log h}{\log h}\right) ^{0.98} + (\log X)^{-\gamma }\right) B_g(X)^2. \end{aligned}$$

The conditions (i) and (ii) of Theorem 5.3 were verified for $f = F_z$ in (27), (28) and (29) (with $A = 0.98$), and it remains to elucidate information about $t_0(F_z,X)$, $H(F_z;X)$ and the size of the Euler product $\mathcal {P}_{F_z}(X)$. This is provided by the following lemma.

Lemma 5.5

Fix $r \in (0,\delta ^2]$ and let $z \in \mathbb {C}$ satisfy $|z-1 |= r$. Then

• (a) $t_0(F_z,X) \ll 1/\log X$,

• (b) $H(F_z;X) \asymp 1$ and

• (c) $\mathcal {P}_{F_z}(X)^2 \ll \prod _{p \le X} \left( 1+\frac{|F_z(p) |^2 -1}{p}\right)$.

Proof

(a) Applying [14, (7)] with $A = 0.98$, $B = 2$ and $C = 1$ (which is a straightforward consequence of [10, Lem. 5.1(i)]), we see that if $(\log X) |t_0(F_z;X) |\ge D$ for a suitably large constant $D > 0$ then by minimality of $t_0$,

$$\begin{aligned} \rho (F_z,1;X)^2 \ge \sigma \min \{\log \log X, 3\log (|t_0(F_z;X)|\log X + 1)\} + O(1) \ge 100, \end{aligned}$$

say, where $\sigma > 0$ is an absolute constant.

To obtain a contradiction, observe next that for any $z = re(\theta )$ with $\theta \in [0,1]$, we have already shown that $\vert F_z(p) \vert \le 2$ for $\delta \in (0,1/100)$. Thus, writing $F_z(p) = \vert F_z(p) \vert e(\theta g_{\mathcal {C}}(p)/B_g(X))$ and applying the inequality $0 \le 1-\cos x \le x^2/2$ for all $x \ge 0$, we find

$$\begin{aligned} \rho (F_z,1;X)^2= & {} \sum _{\begin{array}{c} p \le X \end{array}} \vert F_z(p) \vert \frac{1-\cos (2\pi \theta g_{\mathcal {C}}(p)/B_g(X))}{p} \\\le & {} \frac{4\pi ^2}{B_g(X)^2} \sum _{p \le X} \frac{g(p)^2}{p} \le 4\pi ^2. \end{aligned}$$

This contradiction implies that $\vert t_0(F_z;X) \vert \log X \le D$ for some constant D, and the claim follows.

(b) By Taylor expansion, $|z |^{g_{\mathcal {C}}(p)/B_g(X)} = 1 + O(\delta g(p)/B_g(X))$, and thus

$$\begin{aligned} H(F_z;X)\ll & {} \exp \left( \sum _{p \le X} \frac{(|z |^{g_{\mathcal {C}}(p)/B_g(X)}-1)^2}{p}\right) \\= & {} \exp \left( O\left( \frac{\delta ^2}{B_g(X)^2}\sum _{p \le X} \frac{g(p)^2}{p}\right) \right) \ll 1. \end{aligned}$$

The corresponding lower bound is trivial from the definition of $H(F_z;X)$.

(c) Since $\vert F_z(p) \vert \le 2$ for all $p \le X$, we have the upper bounds

$$\begin{aligned} \mathcal {P}_{F_z}(X)^2 \ll \prod _{p \le X} \left( 1+\frac{2(|F_z(p) |-1)}{p}\right) \le \prod _{p \le X} \left( 1+\frac{|F_z(p) |^2-1}{p}\right) , \end{aligned}$$

the latter of which arises from $(\vert F_z(p) \vert - 1)^2 \ge 0$ for all p. $\square$

Lemma 5.6

Let g be non-negative and strongly additive. Let $r \in (0,\delta ^2]$, and set $h_1 = h$ and $h_2 = \lceil X/(\log X)^{c_1}\rceil$ as above. Then there is $z_0 \in \mathbb {C}$ with $|z_0-1 |= r$ such that as $X \rightarrow \infty$,

$$\begin{aligned}&\Delta _{g_{\mathcal {C}}}(X;h_1,h_2) \\&\ll \frac{B_g(X)^2}{r^2} |z_0 |^{-2\frac{A_g(X)}{B_g(X)}} \\&\quad \cdot \frac{2}{X} \sum _{X/2< n \le X} \left|\frac{1}{h_1} \sum _{n-h_1< m \le n} F_{z_0}(m) - I(n;t_0,h_1) \cdot \frac{1}{h_2}\sum _{n-h_2 < m \le n} F_{z_0}(m)m^{-it_0}\right|^2\\&\quad +\frac{B_g(X)^2}{r^2} (\log X)^{-c_1+o(1)}, \end{aligned}$$

where $t_0 = t_0(F_{z_0},X)$ and $I(x; t,h) := \frac{1}{h} \int _{x-h}^x u^{it} \mathrm{d}u$ as in the previous section.

Proof

For each $n \in (X/2,X]$, $z \in \mathbb {C}$ and $j = 1,2$, define the maps

$$\begin{aligned} \phi _n(z;h_j) := \frac{1}{h_j}\sum _{n-h_j < m \le n} z^{(g_{\mathcal {C}}(m)-A_{g_{\mathcal {C}}}(X))/B_g(X)}, \end{aligned}$$

which are analytic in z. Note that

$$\begin{aligned} \frac{1}{h_j} \sum _{n-h_j < m \le n} \left( \frac{g_{\mathcal {C}}(m)-A_{g_{\mathcal {C}}}(X)}{B_g(X)}\right) = \frac{\mathrm{d}}{\mathrm{d}z}\phi _n(z;h_j) \Big |_{z = 1}. \end{aligned}$$

Recall that $h_1,h_2 \in \mathbb {Z}$. Thus, by Cauchy’s integral formula we have

$$\begin{aligned}&\frac{1}{h_1}\sum _{n-h_1< m \le n} g_{\mathcal {C}}(m) - \frac{1}{h_2} \sum _{n-h_2<m \le n} g_{\mathcal {C}}(m) \\&\quad = \frac{1}{h_1}\sum _{n-h_1< m \le n} (g_{\mathcal {C}}(m)-A_{g_{\mathcal {C}}}(X)) - \frac{1}{h_2} \sum _{n-h_2 <m \le n} (g_{\mathcal {C}}(m)-A_{g_{\mathcal {C}}}(X)) \\&\quad = \frac{B_g(X)}{2\pi i} \int _{|z-1 |= r} (\phi _n(z;h_1) - \phi _n(z;h_2))\frac{\mathrm{d}z}{(z-1)^2}. \end{aligned}$$

By Cauchy–Schwarz and the definition of $F_{z}$, we obtain

$$\begin{aligned}&\Delta _{g_{\mathcal {C}}}(X;h_1,h_2) \ll \frac{B_g(X)^2}{r^2} \max _{|z-1 |= r} \frac{2}{X} \sum _{X/2< n \le X} \left|\phi _n(z;h_1) - \phi _n(z;h_2)\right|^2 \\&= \frac{B_g(X)^2}{r^2} |z_0 |^{-2\frac{A_{g_{\mathcal {C}}}(X)}{B_g(X)}} \frac{2}{X} \sum _{X/2<n \le X} \left|\frac{1}{h_1} \sum _{n-h_1< m \le n} F_{z_0}(m) - \frac{1}{h_2} \sum _{n-h_2 < m \le n} F_{z_0}(m) \right|^2, \end{aligned}$$

for some $z_0 \in \mathbb {C}$ with $|z_0-1 |= r$. To complete the proof, note that by Taylor expansion and Lemma 5.5(a),

$$\begin{aligned} \frac{1}{h_1}\int _{n-h_1}^n u^{it_0} \mathrm{d}u = n^{it_0} \frac{1-(1-h_1/n)^{1+it_0}}{(1+it_0)h_1/n} = n^{it_0} + O(h_1/X), \end{aligned}$$

and also

$$\begin{aligned} m^{-it_0} = n^{-it_0} + O(|t_0 |\log (n/m)) = n^{-it_0} + O(h_2/X) \end{aligned}$$

uniformly in $n-h_2 < m \le n$. It follows that

$$\begin{aligned} \frac{1}{h_2}\sum _{n-h_2< m \le n} F_{z_0}(m)&= I(n;t_0,h_1)\cdot \frac{1}{h_2}\sum _{n-h_2< m \le n} F_{z_0}(m) m^{-it_0} \\&+ O\left( \frac{1}{X}\sum _{n-h_2 < m \le n} |F_{z_0}(m) |\right) . \end{aligned}$$

The error term is, by Shiu’s theorem [35, Thm. 1] and the Cauchy–Schwarz inequality,

$$\begin{aligned} \ll \frac{h_2}{X} \exp \left( \sum _{p \le X} \frac{|F_{z_0}(p) |-1}{p}\right)\ll & {} \frac{h_2}{X} \exp \left( \frac{2r}{B_g(X)}\sum _{p \le X} \frac{g(p)}{p}\right) \\\ll & {} \frac{h_2}{X} \exp \left( 2\sqrt{\log \log X}\right) , \end{aligned}$$

which suffices to prove the claim. $\square$

We are now in a position to apply Theorem 5.3 in order to prove Corollary 5.4.

Proof of Corollary 5.4

Let $z_0$ be chosen as in Lemma 5.6. Since $h_1,h_2 \in \mathbb {Z}$ we may replace the discrete average in Lemma 5.6 by an integral average at the cost of an error term of size

$$\begin{aligned}&\ll \frac{B_g(X)^2}{r^2}\max _{x \in [X/2,X]} \left( \vert I(x;t_0,h_1) - I(\lfloor x \rfloor ;t_0, h_1) \vert \cdot \frac{1}{h_2} \sum _{\left\lfloor x \right\rfloor - h_2 < n \le \left\lfloor x \right\rfloor } |F_{z_0}(n) |\right) ^2 \\&\ll \frac{B_g(X)^2}{h_1^2r^2} |z_0 |^{-2\frac{A_{g_{\mathcal {C}}}(X)}{B_g(X)}} \mathcal {P}_{F_{z_0}}(X)^2, \end{aligned}$$

again by Shiu’s bound [35, Thm. 1]. Using the data from Lemma 5.5, Theorem 5.3 therefore yields

$$\begin{aligned} \Delta _{g_{\mathcal {C}}}(X;h_1,h_2)&\ll \frac{B_g(X)^2}{\delta ^{4}} \left( \left( \frac{\log \log h_1}{\log h_1}\right) ^{0.98} + \left( \frac{\log \log X}{(\log X)^{c_2}}\right) ^{0.98}\right) \end{aligned}$$

(31)

$$\begin{aligned}&\quad \cdot |z_0 |^{-2\frac{A_{g_{\mathcal {C}}}(X)}{B_g(X)}} \prod _{p \le X} \left( 1+\frac{|F_{z_0}(p) |^2 - 1}{p}\right) . \end{aligned}$$

(32)

As g is strongly additive,

$$\begin{aligned} A_{g_{\mathcal {C}}}(X) = \sum _{p \le X} \frac{g_{\mathcal {C}}(p)}{p} + O\left( \sum _{p \le X} \frac{g(p)}{p^2}\right) = \sum _{p \le X} \frac{g_{\mathcal {C}}(p)}{p} + O(B_g(X)), \end{aligned}$$

the bound in the error term arising from the Cauchy–Schwarz inequality. Now put $\rho := \log |z_0 |\in (-10\delta ^2,10\delta ^2)$, say. Using the estimates $\log (1+x) = x + O(x^2)$ and $|e^x-1-x |\le \tfrac{1}{2}|x |^2$ for $|x |\le 1/2$, the factors in (32) can be estimated as

$$\begin{aligned}&\ll \exp \left( \sum _{p \le X} \left( -\frac{2\rho }{p}\frac{g_{\mathcal {C}}(p)}{B_g(X)} + \log \left( 1+\frac{e^{2\rho g_{\mathcal {C}}(p)/B_g(X)} - 1}{p}\right) \right) \right) \\&\ll \exp \left( \sum _{p \le X} \frac{1}{p}\left( e^{2\rho g_{\mathcal {C}}(p)/B_g(X)} - 1 - 2\rho \frac{g_{\mathcal {C}}(p)}{B_g(X)}\right) \right) \\&\le \exp \left( \frac{2\rho ^2}{B_g(X)^2}\sum _{p \le X} \frac{g_{\mathcal {C}}(p)^2}{p}\right) \ll 1. \end{aligned}$$

The claimed bound now follows with any $0< \gamma < 0.98 c_2$ (changing the implicit constant as needed). $\square$

Proof of Theorem 1.4

Let $g \in \mathcal {A}_s$. By Lemma 5.1 we may assume that g is non-negative and strongly additive. Let $\varepsilon > 0$ and pick $\delta >0$ and $X_0 = X_0(\delta )$ such that if $X \ge X_0$ then (25) and (26) both hold, and also define $\mathcal {C}$ as above. Set also $h_1 = h$ and $h_2 := \left\lceil \frac{X}{(\log X)^{c_1}}\right\rceil$ as above. Combining Lemma 5.2 and (30), we have

$$\begin{aligned} \Delta _g(X,h) \ll \Delta _{g_{\mathcal {C}}}(X,h) + \varepsilon B_g(X)^2 \ll \Delta _{g_{\mathcal {C}}}(X;h_1,h_2) + \left( \varepsilon + (\log X)^{-1/6}\right) B_g(X)^2. \end{aligned}$$

Applying Corollary 5.4 in this estimate, we find that there is a $\gamma \in (0,1/6)$ for which

$$\begin{aligned} \Delta _g(X,h) \ll \left( \varepsilon + \delta ^{-4}\left( \left( \frac{\log \log h}{\log h}\right) ^{0.98} + (\log X)^{-\gamma }\right) \right) B_g(X)^2. \end{aligned}$$

Selecting $h \ge \exp \left( \delta ^{-5} \varepsilon ^{-2}\log (1/(\delta \varepsilon ))\right)$, picking $X_0$ larger if necessary, we deduce that $\Delta _g(X,h) \ll \varepsilon B_g(X)$. Since $\varepsilon$ was arbitrary, we deduce that $\Delta _g(X,h) = o(B_g(X))$, as claimed. $\square$

6 Gaps and moments

In this section, we will prove Theorem 1.11.

6.1 Small gaps and small first moments are equivalent: proof of Theorem 1.11(a)

We start by proving the following quantitative $\ell ^1$ gap result.

Proposition 6.1

Let $0< \varepsilon < 1/3$ and let X be large. Let $g: \mathbb {N} \rightarrow \mathbb {C}$ be an additive function. Assume that

$$\begin{aligned} \frac{1}{Y} \sum _{n \le Y} |g(n)-g(n-1) |\ll \varepsilon B_g(X) \end{aligned}$$

(33)

for all $X/\log X < Y \le X$. Then we have

$$\begin{aligned} \frac{1}{X} \sum _{n \le X} |g(n) - A_g(X) |\ll \left( \sqrt{\frac{\log \log (1/\varepsilon )}{\log (1/\varepsilon )}} + (\log X)^{-1/800}\right) B_g(X). \end{aligned}$$

Proof

Let $h = \left\lfloor \min \{X/(2\log X), \varepsilon ^{-1/2}\} \right\rfloor$, and let $X/\log X < Y \le X$. By the triangle inequality and (33), for any $1 \le m \le h$ we obtain

$$\begin{aligned} \frac{1}{Y} \sum _{h< n \le Y} |g(n)-g(n-m) |&\le \frac{1}{Y} \sum _{0 \le j \le m-1} \sum _{j < n \le Y} |g(n-j)-g(n-j-1) |\\&\ll \frac{h}{Y} \sum _{1 \le n \le Y} |g(n)-g(n-1) |\ll \varepsilon ^{1/2}B_g(X). \end{aligned}$$

Averaging over $1 \le m \le h$ and then applying the triangle inequality once again, we obtain

$$\begin{aligned}&\frac{1}{Y} \sum _{Y/2< n \le Y} \left|g(n)-\frac{1}{h} \sum _{1 \le m \le h} g(n-m)\right|\\&\quad \le \frac{1}{Y} \sum _{h < n \le Y} \left|g(n)-\frac{1}{h} \sum _{1 \le m \le h} g(n-m)\right|\ll h^{-1}B_g(X). \end{aligned}$$

Applying Theorem 1.1, we deduce from this that

$$\begin{aligned} \frac{1}{Y} \sum _{Y/2<n \le Y} \left|g(n)-\frac{2}{Y}\sum _{Y/2 < m \le Y} g(m)\right|\ll B_g(X)\left( \sqrt{\frac{\log \log h}{\log h}} + (\log X)^{-1/800}\right) . \end{aligned}$$

Now, for each such Y, Lemmas 3.1 and 3.4 combine to yield

$$\begin{aligned} \frac{2}{Y}\sum _{Y/2 < m \le Y} g(m)= & {} 2A_g(Y)-A_g(Y/2) + O\left( \frac{B_g(Y)}{\sqrt{\log Y}}\right) \\= & {} A_g(X) + O\left( B_g(X)\sqrt{\frac{\log \log X}{\log X}}\right) , \end{aligned}$$

and thus combining this estimate into the previous expression and summing over all dyadic subintervals of $[X/\log X,X]$, we obtain

$$\begin{aligned} \frac{1}{X} \sum _{\tfrac{X}{\log X}< n \le X} \vert g(n)-A_g(X) \vert&\le \sum _{\tfrac{X}{\log X}< Y = X/2^j \le X} \frac{Y}{2X} \cdot \frac{2}{Y} \sum _{Y/2 < n \le Y} \vert g(n)-A_g(X) \vert \\&\ll B_g(X) \left( \sqrt{\frac{\log \log h}{\log h}} + (\log X)^{-1/800}\right) . \end{aligned}$$

Applying Lemma 3.2 and the Cauchy–Schwarz inequality on $[1,X/\log X]$, we obtain

$$\begin{aligned} \frac{1}{X}\sum _{1 \le n \le \tfrac{X}{\log X}} \vert g(n)-A_g(X) \vert \le \frac{1}{\sqrt{\log X}}\left( \frac{1}{X}\sum _{n \le X} \vert g(n)-A_g(X) \vert ^2\right) ^{\frac{1}{2}} \ll \frac{B_g(X)}{\sqrt{\log X}}. \end{aligned}$$

The latter two estimates together imply the claim. $\square$

Proof of Theorem 1.11(a)

By the triangle inequality, we see that if

$$\begin{aligned} \frac{1}{X}\sum _{n \le X} |g(n) - A_g(X) |= o(B_g(X)) \end{aligned}$$

then, consequently,

$$\begin{aligned} \frac{1}{X}\sum _{n \le X} |g(n)-g(n-1) |\le & {} \frac{1}{X}\sum _{n \le X} |g(n) - A_g(X) |+ \frac{1}{X}\sum _{m \le X-1} |g(m)-A_g(X) |\\= & {} o(B_g(X)). \end{aligned}$$

The converse implication follows immediately from Proposition 6.1. $\square$

6.2 A gap theorem for the second moment

In parallel to the results of the previous subsection, we will apply Theorem 1.4 to prove the following result.

Proposition 6.2

Let $g \in \mathcal {A}_s$ Then for any integer $10 \le h \le \tfrac{X}{10\log X}$ we have

$$\begin{aligned} \frac{1}{X}\sum _{n \le X} |g(n) - A_g(X) |^2 \ll \frac{h^2}{X}\sum _{n \le X} |g(n)-g(n-1) |^2 + o_{h \rightarrow \infty }(B_g(X)^2). \end{aligned}$$

Proof

Given our assumptions about g, we may apply Theorem 1.4 to obtain

$$\begin{aligned} \sum _{Y/2< n \le Y} \left|\frac{1}{h}\sum _{n-h< m \le n} g(m) - \frac{2}{Y} \sum _{Y/2 < m \le Y} g(m)\right|^2 = o_{h \rightarrow \infty }(YB_g(X)^2), \end{aligned}$$

for any $X/\log X < Y \le X$. Applying Lemmas 3.1 and 3.4, we deduce that

$$\begin{aligned}&\frac{1}{X} \sum _{Y/2< n \le Y} |g(n)-A_g(Y) |^2\\&\quad \ll \frac{1}{X} \sum _{Y/2< n \le Y} \left|g(n) - \frac{1}{h} \sum _{n-h < m \le n} g(m)\right|^2 + o_{h \rightarrow \infty }\left( \frac{Y}{X}B_g(X)^2\right) . \end{aligned}$$

By telescoping,

$$\begin{aligned} g(n) - \frac{1}{h} \sum _{n-h < m \le n} g(m)&= \frac{1}{h} \sum _{0 \le j \le h-1} (g(n)-g(n-j)) \\&= \sum _{0 \le j \le h-2} \left( 1-\frac{j+1}{h}\right) (g(n-j)-g(n-j-1)). \end{aligned}$$

Squaring both sides and applying Cauchy–Schwarz, we obtain

$$\begin{aligned}&\frac{1}{X} \sum _{Y/2< n \le Y} \left|g(n)-\frac{1}{h}\sum _{n-h< m \le n} g(m)\right|^2 \\&\quad \ll \frac{h}{X} \sum _{0\le j \le h-2} \sum _{Y/2< n \le Y} (g(n-j)-g(n-j-1))^2 \\&\quad \le \frac{h^2}{X} \sum _{\frac{Y}{2}-h< n \le Y < n \le Y} (g(n)-g(n-1))^2. \end{aligned}$$

Combined with the previous estimates, we obtain

$$\begin{aligned}&\frac{1}{X} \sum _{Y/2< n \le Y} |g(n)-A_g(Y) |^2 \\&\quad \ll \frac{h^2}{X} \sum _{\frac{Y}{2}-h < n \le Y} |g(n)-g(n-1) |^2 + o_{h \rightarrow \infty }\left( \frac{Y}{X}B_g(X)^2\right) . \end{aligned}$$

By Lemma 3.4, for each $X/\log X < Y \le X$ we have

$$\begin{aligned} \vert A_g(X)-A_g(Y) \vert \ll B_g(X) \sqrt{\frac{\log \log X}{\log X}}, \end{aligned}$$

so that, summing over dyadic subintervals of $[X/\log X,X]$ and noting that by our assumption $h \le X/(10\log X)$ at most two dyadic intervals contain any point of

$$\begin{aligned} \bigcup _{\tfrac{X}{\log X} < Y = X/2^j \le X} [Y/2-h,Y], \end{aligned}$$

we find

$$\begin{aligned}&\frac{1}{X} \sum _{\tfrac{X}{\log X}< n \le X} \vert g(n)-A_g(X) \vert ^2 \\&\quad \ll \sum _{\tfrac{X}{\log X}< Y = X/2^j \le X} \frac{1}{X} \sum _{Y/2< n \le Y} \left( \vert g(n)-A_g(Y)|^2 + B_g(X)^2 \cdot \frac{\log \log X}{\log X}\right) \\&\quad \ll \frac{h^2}{X} \sum _{\tfrac{X}{4\log X} < n \le X} \vert g(n)-g(n-1) \vert ^2 + o_{h \rightarrow \infty }(B_g(X)^2). \end{aligned}$$

Applying Lemma 3.2 trivially to the segment $[1,X/\log X]$ gives

$$\begin{aligned} \frac{1}{X}\sum _{n \le \tfrac{X}{\log X}} \vert g(n)-A_g(X) \vert ^2 \ll \frac{B_g(X)^2}{\log X}, \end{aligned}$$

so combining these two estimates implies the claim. $\square$

Proof of Theorem 1.11(b)

To obtain the theorem, we note first the trivial estimate

$$\begin{aligned} \frac{1}{X}\sum _{n \le X} |g(n)-g(n-1) |^2&\ll \frac{1}{X}\sum _{n \le X} |g(n) - A_g(X) |^2 + \frac{1}{X}\sum _{m \le X-1} |g(m)-A_g(X) |^2 \\&\ll \frac{1}{X}\sum _{n \le X} |g(n) - A_g(X) |^2, \end{aligned}$$

so that if the RHS is $o(B_g(X)^2)$ then so is the LHS.

Conversely, suppose that

$$\begin{aligned} \frac{1}{X} \sum _{n \le X} |g(n)-g(n-1) |^2 \le \xi (X)B_g(X)^2, \end{aligned}$$

for some function $\xi (Y) \rightarrow 0$ as $Y \rightarrow \infty$. Set $h := \lfloor \xi (X)^{-1/3}\rfloor .$ By Proposition 6.2,

$$\begin{aligned} \frac{1}{X} \sum _{n \le X} |g(n) - A_g(X) |^2 \ll \xi (X)^{-2/3} \cdot \xi (X) B_g(X)^2 + o(B_g(X)^2) = o(B_g(X)^2) \end{aligned}$$

as $X \rightarrow \infty$, as required. $\square$

Proof of Corollary 1.12

Let $g \in \mathcal {A}_s$ and suppose that

$$\begin{aligned} \frac{1}{X}\sum _{n \le X} \vert g(n) - g(n-1) \vert ^2 = o(B_g(X)^2). \end{aligned}$$

By Theorem 1.11(b), we obtain that

$$\begin{aligned} \frac{1}{X}\sum _{n \le X} \vert g(n)-A_g(X) \vert ^2 = o(B_g(X)^2). \end{aligned}$$

Now, by Lemma 3.3, this implies that there is $\lambda = \lambda (X) \in \mathbb {R}$ such that

$$\begin{aligned} B_{g_{\lambda }}(X)^2 + \vert \lambda \vert ^2 = o(B_g(X)^2), \end{aligned}$$

where $g_{\lambda } = g-\lambda \log$. Since the left-hand side is $\ge B_{g_{\lambda }}(X)^2$, the claim follows immediately. $\square$

7 Erdős’ almost everywhere monotonicity problem

Let $g: \mathbb {N} \rightarrow \mathbb {R}$ be additive. For convenience, set $g(0) := 0$, and recall the definitions

$$\begin{aligned} \mathcal {B} := \{n \in \mathbb {N} : g(n) < g(n-1)\}, \quad \quad \mathcal {B}(X) := \mathcal {B} \cap [1,X]. \end{aligned}$$

In this and the following section, we will study functions g such that $|\mathcal {B}(X) |= o(X)$.

7.1 The second moment along sparse subsets

To prove Theorem 1.8 we will eventually need control over a sparsely-supported sum such as

$$\begin{aligned} \frac{1}{X} \sum _{n \in \mathcal {B}(X)} |g(n) - A_g(X) |^2, \end{aligned}$$

with the objective of obtaining savings over the trivial bound $O(B_g(X)^2)$ from Lemma 3.2. The purpose of this subsection is to determine sufficient conditions in order to achieve a non-trivial estimate of this kind.

Given a set of positive integers $\mathcal {S}$, a positive real number $X \ge 1$ and a prime power $p^k \le X$, write $\mathcal {S}(X) := \mathcal {S} \cap [1,X]$ and $\mathcal {S}_{p^k}(X) := \{n \in \mathcal {S}(X) : p^k \mid n\}$.

Proposition 7.1

Let $g: \mathbb {N} \rightarrow \mathbb {C}$ be an additive function belonging to $\mathcal {A}$. Let $\mathcal {S}$ be a set of integers with $|\mathcal {S}(X) |= o(X)$, and let $\varepsilon \in (0,1)$ satisfy the conditions

$$\begin{aligned} |\mathcal {S}(X)|< \tfrac{\varepsilon }{2}X, \quad \quad \sum _{\begin{array}{c} p^k \le X \\ k \ge 2 \end{array}} \frac{|g(p) |^2 + |g(p^k) |^2}{p^k} < \varepsilon B_g(X)^2. \end{aligned}$$

Then the following bound holds:

$$\begin{aligned} \frac{1}{X}\sum _{n \in \mathcal {S}(X)} |g(n) - A_g(X) |^2 \ll&B_g(X)^2\left( \varepsilon + \varepsilon ^{-1} \left( \frac{|\mathcal {S}(X)|}{X}\right) ^{1/2}\right) \\&+ \sum _{\begin{array}{c} p \le X \\ |\mathcal {S}_p(X)|> \varepsilon X/p \end{array}} \frac{|g(p) |^2}{p}. \end{aligned}$$

Moreover, we have

$$\begin{aligned} \sum _{\begin{array}{c} p \le X \\ |\mathcal {S}_p(X)|> \varepsilon X/p \end{array}} \frac{1}{p} \ll \varepsilon ^{-2} \frac{|\mathcal {S}(X)|}{X}. \end{aligned}$$

(34)

Remark 7.2

Proposition 7.1 states that if the bulk of the contribution to the variance of g(n) occurs along a sparse subset $\mathcal {S}(X) \subseteq [1,X]$ then $B_g(X)$ is dominated by primes p of which $\mathcal {S}(X)$ has many multiples $\le X$. For sufficiently small primes p this is ruled out by the sparseness of $\mathcal {S}(X)$, but it may occur for large enough primes.

Our proof will proceed by applying variants of the large sieve and Turán–Kubilius inequalities. The first of these is due to Elliott.

Lemma 7.3

(Elliott’s Dual Turán–Kubilius Inequality) Let $\{a(n)\}_n \subset \mathbb {C}$ be a sequence and let $X \ge 2$. Then

$$\begin{aligned} \sum _{p \le X} p\left|\sum _{\begin{array}{c} n \le X \\ p\mid n \end{array}} a(n) - \frac{1}{p} \sum _{n \le X} a(n)\right|^2 \ll X \sum _{n\le X} |a(n)|^2. \end{aligned}$$

Proof

This is [22, Lemma 5.2] (taking $\sigma = 0$ there). $\square$

A variant of the latter result, for divisibility by products of two large primes, is as follows.

Lemma 7.4

(Variant of Dual Turán–Kubilius) Let $\{a(n)\}_n \subset \mathbb {C}$. Then

$$\begin{aligned} \sum _{\begin{array}{c} X^{1/4} < p,q \le X \\ p \ne q \end{array}} pq\left|\sum _{\begin{array}{c} n \le X \\ pq\mid n \end{array}} a(n) - \frac{1}{pq} \sum _{n \le X} a(n)\right|^2 \ll X \sum _{n \le X} |a(n)|^2. \end{aligned}$$

Proof

By including the factor pq into the square, we observe that this establishes an $\ell ^2 \rightarrow \ell ^2$ operator norm for the matrix with entries

$$\begin{aligned} M = \left( (pq)^{1/2}1_{pq\mid n} - (pq)^{-1/2}\right) _{\begin{array}{c} X^{1/4} < p,q \le X, p\ne q \\ n \le X \end{array}}. \end{aligned}$$

Thus, by the duality principle [31, Sec. 7.1] it suffices to show that for any sequence $\{b(p,q)\}_{p,q \text { prime}} \subset \mathbb {C}$ we have

$$\begin{aligned} \sum _{n \le X} \left|\sum _{\begin{array}{c} X^{1/4}< p,q \le X \\ p \ne q \end{array}} \frac{b(p,q)}{pq} (pq1_{pq\mid n} - 1)\right|^2 \ll X\sum _{\begin{array}{c} X^{1/4} < p,q \le X \\ p \ne q \end{array}} \frac{|b(p,q)|^2}{pq}. \end{aligned}$$

(35)

Expanding the square on the LHS and swapping orders of summation, we obtain

$$\begin{aligned} \sum _{\begin{array}{c} X^{1/4} < p_1,p_2,q_1,q_2 \le X \\ p_j \ne q_j \\ j = 1,2 \end{array}}&\frac{b(p_1,q_1){\overline{b}}(p_2,q_2)}{p_1q_1p_2q_2} \\&\cdot \sum _{n \le X}\left( p_1q_1p_2q_2 1_{p_1q_1\mid n}1_{p_2q_2\mid n} - p_1q_11_{p_1q_1\mid n} - p_2q_21_{p_2q_2\mid n} + 1\right) . \end{aligned}$$

Fix the quadruple $(p_1,q_1,p_2,q_2)$ for the moment, and consider the inner sum over $n \le X$. If $(p_1q_1,p_2q_2) = 1$ then as $p_1q_1p_2q_2 > X$ the sum is

$$\begin{aligned} \ll p_1q_1\left\lfloor \frac{X}{p_1q_1}\right\rfloor + p_2q_2 \left\lfloor \frac{X}{p_2q_2} \right\rfloor + X \ll X. \end{aligned}$$

If $(p_1q_1, p_2q_2) = p_1$ (so that $q_1 \ne q_2)$, say, then the sum is

$$\begin{aligned} \ll p_1^2q_1q_2 \left\lfloor \frac{X}{p_1q_1q_2} \right\rfloor + p_1q_1\left\lfloor \frac{X}{p_1q_1}\right\rfloor + p_2q_2 \left\lfloor \frac{X}{p_2q_2} \right\rfloor + X \ll p_1 X. \end{aligned}$$

By symmetry, the analogous result holds if $(p_1q_1,p_2q_2) = q_1$. Finally, if $p_1q_1 = p_2q_2$ then similarly the bound is $\ll p_1q_1 X$. We thus obtain from these cases that the LHS in (35) is bounded above by

$$\begin{aligned}&\ll X \sum _{\begin{array}{c} X^{1/4}< p_1,q_1,p_2,q_2 \le X \\ p_1 \ne q_1, p_2 \ne q_2 \\ (p_1q_1,p_2q_2) = 1 \end{array}} \frac{|b(p_1,q_1)||b(p_2,q_2)|}{p_1p_2q_1q_2} \\&\quad + \sum _{\begin{array}{c} X^{1/4}< p,q,r \le X \\ p \ne q, p \ne r, q \ne r \end{array}} \frac{|b(p,q)|(|b(p,r)|+ |b(r,q)|) }{pqr} \\&\quad + X\sum _{\begin{array}{c} X^{1/4} < p,q \le X \\ p \ne q \end{array}} \frac{|b(p,q)|( |b(p,q)|+ |b(q,p)|)}{pq}. \end{aligned}$$

By the AM–GM inequality we simply have $2|b(p,q)||b(p',q')|\le |b(p,q)|^2 + |b(p',q')|^2$ for any pairs of primes p, q and $p',q'$, so invoking Mertens’ theorem and symmetry the above expressions are

$$\begin{aligned} \ll X \sum _{\begin{array}{c} X^{1/4} < p,q \le X \\ p \ne q \end{array}} \frac{|b(p,q)|^2}{pq}, \end{aligned}$$

and the claim follows. $\square$

Proof of Proposition 7.1

Let $g \in \mathcal {A}$, and let $g^{*}$ be the strongly additive function equal to g at primes, provided by Lemma 3.6. Applying Lemma 3.2, then following the proof of Lemma 3.6, we find

$$\begin{aligned} \frac{1}{X}\sum _{n \in \mathcal {S}(X)} |(g-g^{*}) - A_{g-g^{*}}(X)|^2\ll & {} B_{g-g^{*}}(X)^2 \\\ll & {} \sum _{\begin{array}{c} p^k \le X \\ k \ge 2 \end{array}} \frac{|g(p) |^2 + |g(p^k) |^2}{p^k} \ll \varepsilon B_g(X)^2, \end{aligned}$$

by assumption. It follows that

$$\begin{aligned} \frac{1}{X}\sum _{n \in \mathcal {S}(X)} |g(n) - A_g(X) |^2 \ll \varepsilon B_g(X)^2 + \frac{1}{X}\sum _{n \in \mathcal {S}(X)} |g^{*}(n)-A_{g^{*}}(X)|^2, \end{aligned}$$

so replacing g by $g^{*}$, we may assume in what follows that g is strongly additive.

Fix $z = X^{1/4}$ and split $g = g_{\le z} + g_{>z}$, where $g_{\le z}$ is the strongly additive function defined by $g_{\le z}(p^k) := g(p)1_{p \le z}$ at primes powers $p^k$. By Cauchy–Schwarz, we seek to estimate

$$\begin{aligned} \frac{1}{X} \sum _{n \in \mathcal {S}(X)} |g_{\le z}(n) - A_{g_{\le z}}(X)|^2 + \frac{1}{X} \sum _{n \in \mathcal {S}(X)} |g_{> z} (n) - A_{g_{ > z}}(X)|^2. \end{aligned}$$

(36)

We begin with the first expression. Writing

$$\begin{aligned} g_{\le z}(n)-A_{g_{\le z}}(X)&= \sum _{p \le z} g(p)\sum _{1 \le k \le \log X/\log p} \left( 1_{p^k||n} - p^{-k}(1-1/p)\right) \nonumber \\&= \sum _{p \le z} g(p)(1_{p\mid n}-1/p) + O(X^{-1} \sum _{p \le z} |g(p) |) \end{aligned}$$

(37)

for each $n \le X$ and expanding the square, the first sum in (36) is

$$\begin{aligned}&= \frac{1}{X}\sum _{n \in \mathcal {S}(X)}\sum _{\begin{array}{c} p,q \le z \\ p \ne q \end{array}} \frac{g(p)\overline{g(q)}|}{pq} (p1_{p\mid n} - 1)(q1_{q\mid n} - 1)\\&\quad + O\left( \sum _{p \le z} \frac{|g(p) |^2}{p^{2}} \frac{1}{X} \sum _{n \in \mathcal {S}(X)} (p1_{p\mid n} - 1)^2\right) \\&\quad + O(B_g(z)^2X^{-1}(z\pi (z))^{1/2}) \\&=: O + D + O(B_g(X)^2X^{-3/4}). \end{aligned}$$

Consider the off-diagonal term O. Observe that for any two distinct primes p and q, the Chinese remainder theorem implies that

where the asterisked sum is over reduced residues modulo pq. Note that for any two distinct products $p_1q_1$ and $p_2q_2$ the gap between fractions with these denominators satisfies

$$\begin{aligned} \left|\frac{c_1}{p_1q_1} - \frac{c_2}{p_2q_2}\right|\ge \frac{1}{p_1q_1p_2q_2} \ge \frac{1}{z^4} = \frac{1}{X}, \end{aligned}$$

and the number of pairs yielding the same product pq is $\le 2$. Using this expression in O, applying the Cauchy–Schwarz inequality twice followed by the large sieve inequality [31, Lem. 7.11], we obtain

Expanding $g_{>z}(n) - A_{g>z}(X)$ in a similar way as in (37), then inserting this and the previous estimate into (36) we obtain the upper bound,

$$\begin{aligned}&\ll \frac{1}{X}\sum _{p \le z} \frac{|g(p) |^2}{p^2}\sum _{n \in \mathcal {S}(X)} |p1_{p\mid n}-1|^2 + \frac{1}{X} \sum _{n \in \mathcal {S}(X)} \left|\sum _{X^{1/4}< p \le X} \frac{g(p)}{p}(p1_{p\mid n}-1)\right|^2 \nonumber \\&\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad + \left( \frac{|\mathcal {S}(X)|}{X}\right) ^{1/2} B_g(X)^2 \nonumber \\&\ll \left|\sum _{\begin{array}{c} X^{1/4} < p,q \le X \\ p \ne q \end{array}} \frac{ g(p)\overline{g(q)} }{pq} \frac{1}{X}\sum _{n \in \mathcal {S}(X)}(p1_{p\mid n}-1)(q1_{q\mid n}-1)\right| \nonumber \\&\quad + \sum _{p \le X} \frac{|g(p) |^2}{p^2}\frac{1}{X}\sum _{n \in \mathcal {S}(X)}|p1_{p\mid n}-1 |^2 + \left( \frac{|\mathcal {S}(X)|}{X}\right) ^{1/2} B_g(X)^2. \end{aligned}$$

(38)

Denote by T the expression in (38), so that

$$\begin{aligned} T&= \sum _{\begin{array}{c} X^{1/4}< p,q \le X \\ p \ne q \end{array}} \frac{ g(p)\overline{g(q)} }{pq} \left( \frac{pq}{X}|\mathcal {S}_{pq}(X)|- \frac{p}{X} |\mathcal {S}_p(X)|- \frac{q}{X} |\mathcal {S}_q(X)|+ \frac{|\mathcal {S}(X)|}{X}\right) \\&=: \sum _{\begin{array}{c} X^{1/4} < p,q \le X \\ p \ne q \end{array}} \frac{ g(p)\overline{g(q)} }{pq} T_{p,q}(X), \end{aligned}$$

say. We split the pairs of primes $X^{1/4} < p,q \le X$, $p \ne q$ in the support of T as follows. Given a squarefree integer d, call $E_d(\varepsilon )$ the condition $\frac{d}{X}|\mathcal {S}_d(X)|\le \varepsilon$, and let $L_d(\varepsilon )$ be the converse condition $\frac{d}{X}|\mathcal {S}_d(X)|> \varepsilon$. If, simultaneously, the three conditions $E_{pq}(\varepsilon ),E_p(\varepsilon )$ and $E_q(\varepsilon )$ all hold, then as $|\mathcal {S}(X)|/X < \varepsilon$ we have $T_{p,q}(X) \ll \varepsilon$; otherwise, we trivially have $T_{p,q}(X) \ll 1$. We thus find by the Cauchy–Schwarz inequality that

$$\begin{aligned} T&\ll \varepsilon \sum _{\begin{array}{c} X^{1/4}< p,q \le X \\ p \ne q \end{array}} \frac{|g(p)g(q)|}{pq} + \sum _{\begin{array}{c} X^{1/4}< p,q \le X \\ p \ne q \\ L_p(\varepsilon ), L_q(\varepsilon ) \text { or } L_{pq}(\varepsilon ) \\ \text {holds} \end{array}} \frac{|g(p)g(q)|}{pq} \nonumber \\&\ll B_g(X)^2 \left( \varepsilon \sum _{X^{1/4}< p \le X} \frac{1}{p} + \left( \sum _{\begin{array}{c} X^{1/4} < p,q \le X \\ p \ne q \\ L_p(\varepsilon ), L_q(\varepsilon ) \text { or } L_{pq}(\varepsilon )\\ \text {holds} \end{array}} \frac{1}{pq}\right) ^{1/2}\right) . \end{aligned}$$

(39)

Now suppose $L_d(\varepsilon )$ holds for some $d\ge 2$. As $\varepsilon > 2 \frac{|\mathcal {S}(X)|}{X}$ we have

$$\begin{aligned} \frac{1}{d} = \frac{4d}{(\varepsilon X)^2} \left( \frac{\varepsilon X}{2d}\right) ^2 < \frac{4d}{(\varepsilon X)^2} \left( |\mathcal {S}_d(X)|- \frac{|\mathcal {S}(X)|}{d}\right) ^2. \end{aligned}$$

Using this with $d = p$ for each $X^{1/4} < p \le X$, and applying Lemma 7.3, we get

$$\begin{aligned} \sum _{\begin{array}{c} X^{1/4} < p \le X \\ L_p(\varepsilon ) \text { holds} \end{array}} \frac{1}{p} \ll \frac{1}{(\varepsilon X)^{2}} \sum _{p \le X} p \left|\sum _{\begin{array}{c} n \le X \\ p \mid n \end{array}} 1_{\mathcal {S}}(n) - \frac{1}{p} \sum _{n \le X} 1_{\mathcal {S}}(n)\right|^2 \ll \varepsilon ^{-2} \frac{|\mathcal {S}(X)|}{X}; \end{aligned}$$

this, by the way, establishes (34). Similarly, by Lemma 7.4 we get

$$\begin{aligned} \sum _{\begin{array}{c} X^{1/4}< p,q \le X \\ p \ne q \\ L_{pq}(\varepsilon ) \text { holds} \end{array}} \frac{1}{pq}\ll & {} \frac{1}{(\varepsilon X)^{2}} \sum _{\begin{array}{c} X^{1/4} < p,q \le X \\ p\ne q \end{array}} pq \left|\sum _{\begin{array}{c} n \le X \\ pq\mid n \end{array}} 1_{\mathcal {S}}(n) - \frac{1}{pq} \sum _{n \le X} 1_{\mathcal {S}}(n)\right|^2 \\\ll & {} \varepsilon ^{-2} \frac{|\mathcal {S}(X)|}{X}. \end{aligned}$$

Combining these estimates in (39) shows that

$$\begin{aligned} T \ll B_g(X)^2 \left( \varepsilon + \varepsilon ^{-1} \left( \frac{|\mathcal {S}(X)|}{X}\right) ^{1/2}\right) . \end{aligned}$$

Thus, putting $\delta (X) := \varepsilon + \varepsilon ^{-1} \left( \frac{|\mathcal {S}(X)|}{X}\right) ^{1/2}$, we finally conclude that

$$\begin{aligned}&\frac{1}{X} \sum _{n \in \mathcal {S}(X)} |g(n) - A_g(X) |^2\\&\quad \ll \sum _{p \le X} \frac{|g(p) |^2}{p^2} \frac{1}{X}\sum _{n \in \mathcal {S}(X)}|p1_{p\mid n}-1 |^2 + \delta (X)B_g(X)^2 \\&\quad = \sum _{p \le X} \frac{|g(p) |^2}{p} \left( \frac{(p-2)|\mathcal {S}_p(X)|}{X} + \frac{|\mathcal {S}(X)|}{pX}\right) + \delta (X) B_g(X)^2\\&\quad \ll \sum _{\begin{array}{c} p \le X \\ |\mathcal {S}_p(X)|> \varepsilon X/p \end{array}} \frac{|g(p) |^2}{p} + B_g(X)^2\left( \varepsilon + \frac{|\mathcal {S}(X)|}{X}\right) + \delta (X) B_g(X)^2\\&\quad \ll \sum _{\begin{array}{c} p \le X \\ |\mathcal {S}_p(X)|> \varepsilon X/p \end{array}} \frac{|g(p) |^2}{p} + \delta (X) B_g(X)^2, \end{aligned}$$

and the claim follows. $\square$

Corollary 7.5

Let $g: \mathbb {N} \rightarrow \mathbb {R}$ be an additive function in $\mathcal {A}_s$. Let $\mathcal {S} \subset \mathbb {N}$ be a set with $|\mathcal {S}(X)|= o(X)$. Then for any fixed $j \in \mathbb {Z}$,

$$\begin{aligned} \frac{1}{X} \sum _{n+j \in \mathcal {S}(X)} |g(n) - A_g(X) |^2 = o(B_g(X)^2). \end{aligned}$$

Proof

By appealing to Proposition 7.1, we will show that for any $\varepsilon > 0$ there is $X_0(\varepsilon )$ such that if $X \ge X_0(\varepsilon )$ then

$$\begin{aligned} \frac{1}{X}\sum _{n+j \in \mathcal {S}(X)} \vert g(n)-A_g(X) \vert ^2 \ll \varepsilon B_g(X)^2, \end{aligned}$$

for any fixed $j \in \mathbb {Z}$.

First, note that as $B_g(X) \rightarrow \infty$, if $X \ge X_0(\varepsilon )$ then

$$\begin{aligned} \sum _{\begin{array}{c} p^k \le X \\ k \ge 2 \end{array}} \frac{g(p)^2}{p^k} \ll \sum _{p \le X} \frac{g(p)^2}{p^2} \le B_g(\log X)^2 + \frac{1}{\log X} \sum _{\log X < p \le X} \frac{g(p)^2}{p} \le \frac{1}{2}\varepsilon B_g(X)^2. \end{aligned}$$

Taking X larger if necessary, we may combine this with (23) to deduce that

$$\begin{aligned} \sum _{\begin{array}{c} p^k \le X \\ k \ge 2 \end{array}} \frac{g(p)^2 + g(p^k)^2}{p^k} \le \varepsilon B_g(x)^2. \end{aligned}$$

Next, for any fixed $j \in \mathbb {Z}$ we have $|(\mathcal {S}-j)(X)|\le |\mathcal {S}(X)|+ j = o(X)$ as $X \rightarrow \infty$, and so for X taken even larger if needed we have $\vert (\mathcal {S}-j)(X) \vert /X< \varepsilon ^4 < \varepsilon /2$, for $\varepsilon$ sufficiently small. We claim that

$$\begin{aligned} \sum _{\begin{array}{c} p \le X \\ |(\mathcal {S}-j)_p(X)|> \varepsilon X/p \end{array}} \frac{g(p)^2}{p} \ll \varepsilon B_g(X)^2 \end{aligned}$$

(40)

for sufficiently large X. Assuming this, Proposition 7.1 will imply that

$$\begin{aligned} \frac{1}{X}\sum _{n + j \in \mathcal {S}(X)} \vert g(n)-A_g(X) \vert ^2 \ll B_g(X)^2 \left( \varepsilon + \varepsilon ^{-1}(\varepsilon ^4)^{1/2}\right) + \varepsilon B_g(X)^2 \ll \varepsilon B_g(X)^2, \end{aligned}$$

as required.

We may split the sum in (40) according to whether or not $|g(p) |> \delta ^{-1}B_g(X)$, where $\delta = \delta (\varepsilon ) > 0$ is to be chosen. In light of (34), we obtain

$$\begin{aligned} \sum _{\begin{array}{c} p \le X \\ |(\mathcal {S}-j)_p(X)|> \varepsilon X/p \\ |g(p) |\le \delta ^{-1} B_g(X) \end{array}} \frac{g(p)^2}{p} \le \delta ^{-2} B_g(X)^2 \sum _{\begin{array}{c} p \le X \\ |(\mathcal {S}-j)_p(X)|> \varepsilon X/p \end{array}} \frac{1}{p} \ll (\varepsilon \delta )^{-2} \frac{|\mathcal {S}(X)|}{X} B_g(X)^2, \end{aligned}$$

so that this is $\ll \varepsilon B_g(X)^2$ if $X \ge X_0(\varepsilon )$.

On the other hand, by our assumption (22),

$$\begin{aligned} \sum _{\begin{array}{c} p \le X \\ |(\mathcal {S}-j)_p(X)|> \varepsilon X/p \\ |g(p) |> \delta ^{-1} B_g(X) \end{array}} \frac{g(p)^2}{p} \le \sum _{\begin{array}{c} p \le X \\ |g(p) |> \delta ^{-1} B_g(X) \end{array}} \frac{g(p)^2}{p} \le 2F_g(\delta )B_g(X)^2, \end{aligned}$$

provided $X \ge X_0(\delta )$. For $\delta = \delta (\varepsilon )$ sufficiently small we can make this $\ll \varepsilon B_g(X)^2$ whenever $X\ge X_0(\varepsilon )$ (with $X_0(\varepsilon )$ taken larger if necessary). The claim now follows. $\square$

We are now able to prove the first part of Theorem 1.8, namely that there is a parameter $\lambda = \lambda (X) \ll \tfrac{B_g(X)}{\log X}$ such that

$$\begin{aligned} \sum _{p^k \le X} \frac{|g(p^k)-\lambda (X)\log p^k |^2}{p^k} = o(B_g(X)^2). \end{aligned}$$

The proof of the slow variation condition $\lambda (X^u) = \lambda (X) + o(\tfrac{B_g(X)}{\log X})$, for $0 < u \le 1$ fixed, is postponed to the next section.

Proof of Theorem 1.8: Part I

In light of Lemma 3.3, we begin by showing that

$$\begin{aligned} \frac{1}{X} \sum _{n \le X} |g(n) - A_g(X) |^2 = o(B_g(X)^2). \end{aligned}$$

(41)

By Lemma 3.4, when $X/\log X < Y \le X$ we have

$$\begin{aligned} |A_g(X)-A_g(Y)|\ll B_g(X) \sqrt{\frac{\log \log X}{\log X}}, \end{aligned}$$

so that upon dyadically decomposing the range $[X/\log X,X]$ and applying Lemma 3.2 to the range $[1,X/\log X]$ in the sum on the LHS of (41), we get

$$\begin{aligned}&\le \frac{1}{X}\sum _{n \le \tfrac{X}{\log X}} |g(n) - A_g(X) |^2 + \sum _{1 \le 2^j \le \log X} 2^{-j} \cdot \frac{2^j}{X}\sum _{X/2^{j+1}< n \le X/2^j} |g(n) - A_g(X) |^2 \\&= \sum _{1 \le 2^j \le \log X} 2^{-j} \cdot \frac{2^j}{X}\sum _{X/2^{j+1} < n \le X/2^j} |g(n) - A_g(X/2^j) |^2 + O\left( \frac{B_g(X)^2 \log \log X}{\log X}\right) . \end{aligned}$$

It thus suffices to show that, uniformly over $1 \le 2^j \le 2\log X$,

$$\begin{aligned} \frac{2^{j}}{X} \sum _{X/2^{j+1} < n \le X/2^j} |g(n)-A_g(X/2^j)|^2 = o(B_g(X)^2). \end{aligned}$$

Fix $1 \le 2^k \le 2\log X$, set $Y_k := X/2^k$ and introduce a parameter $1 \le R \le (\log X)^{1/2}$, which will eventually be chosen as slowly growing as a function of X. Let

$$\begin{aligned} \mathcal {B}_R := \bigcup _{|i |\le R} (\mathcal {B}+i), \quad \quad \mathcal {G}_R(Y_k) := [Y_k/2,Y_k] \backslash \mathcal {B}_R, \quad \quad \mathcal {B}_R(Y_k) := \mathcal {B}_R \cap [Y_k/2,Y_k]. \end{aligned}$$

We observe that if $n \in \mathcal {G}_R(Y_k)$ then we have

$$\begin{aligned} g(n-R) \le g(n-R+1) \le \cdots \le g(n) \le g(n+1) \le \cdots \le g(n+R). \end{aligned}$$

We divide $\mathcal {G}_R(Y_k)$ further into the sets

$$\begin{aligned} \mathcal {G}_R^+(Y_k) := \{n \in \mathcal {G}_R(Y_k) : g(n) \ge A_g(Y_k)\}, \quad \mathcal {G}_R^-(Y_k) := \{n \in \mathcal {G}_R(Y_k) : g(n) < A_g(Y_k)\}. \end{aligned}$$

Suppose $n \in \mathcal {G}_R^+(Y_k)$. Since

$$\begin{aligned} 0 \le g(n)-A_g(Y_k) \le \frac{1}{R} \sum _{1 \le j \le R} g(n+j) - A_g(Y_k), \end{aligned}$$

we deduce from the monotonicity of the map $y \mapsto y^2$ for $y \ge 0$ that (shifting $n \mapsto n+R =: n'$)

$$\begin{aligned}&\frac{2}{Y_k}\sum _{\begin{array}{c} n \in \mathcal {G}_R^+(Y_k) \\ n+R \le Y_k \end{array}} |g(n)-A_g(Y_k)|^2 \\&\le \frac{2}{Y_k}\sum _{\begin{array}{c} n'-R \in \mathcal {G}_R^+(Y_k) \\ n' \le Y_k \end{array}} \left|\frac{1}{R} \sum _{n'-R< m \le n'} g(m) - \frac{2}{Y_k}\sum _{Y_k/2 < m \le Y_k} g(m)\right|^2 + O\left( \frac{B_g(X)^2}{\log X}\right) , \end{aligned}$$

where the error term comes from replacing $A_g(Y_k)$ by the sum over $[Y_k/2,Y_k]$ by applying Lemma 3.4. Similarly, if $n \in \mathcal {G}_R^-(Y_k)$ then

$$\begin{aligned} 0 \le A_g(Y_k) - g(n) \le A_g(Y_k) - \frac{1}{R} \sum _{0 \le j \le R-1} g(n-j), \end{aligned}$$

and so by the same argument we obtain

$$\begin{aligned}&\frac{2}{Y_k} \sum _{\begin{array}{c} n \in \mathcal {G}_R^-(Y_k) \\ n-R \ge Y_k/2 \end{array}} |g(n)-A_g(Y_k)|^2 \\&\quad \le \frac{2}{Y_k} \sum _{\begin{array}{c} n \in \mathcal {G}_R^-(Y_k) \\ n-R \ge Y_k/2 \end{array}} \left|\frac{1}{R}\sum _{n-R< m \le n} g(m) - \frac{2}{Y_k}\sum _{Y_k/2 < m \le Y_k} g(m)\right|^2 \\&\qquad + O\left( \frac{B_g(X)^2}{\log X}\right) . \end{aligned}$$

The above sums cover all elements of $\mathcal {G}_R(Y_k)$ besides those in $[Y_k/2,Y_k/2 + R) \cup (Y_k-R,Y_k]$. To deal with these, we define

$$\begin{aligned} \mathcal {S} := \bigcup _{\begin{array}{c} j \in \mathbb {Z} \\ 0 < 2^j \le X \end{array}} [X/2^j-R,X/2^j+R] \cap \mathbb {N}, \quad \quad \mathcal {S}(Z) := \mathcal {S} \cap [1,Z] \end{aligned}$$

for $Z \ge 1$. We see that $|\mathcal {S}(Z)|\ll R \log Z = o(Z)$, and $\mathcal {S}$ contains $[Y_k/2,Y_k/2 + R] \cup [Y_k-R,Y_k]$ for each k. By Corollary 7.5 (taking $j = 0$ there), we thus obtain

$$\begin{aligned} \frac{1}{Y_k}\sum _{\begin{array}{c} n \in \mathcal {G}_R(Y_k) \cap \mathcal {S}(Y_k) \end{array}} |g(n)-A_g(Y_k)|^2 = o(B_g(X)^2) \end{aligned}$$

uniformly over all $X/\log X < Y_k \le X$, provided X is large enough in terms of R. Combining the foregoing estimates and using positivity, we find that

$$\begin{aligned}&\frac{2}{Y_k}\sum _{n \in \mathcal {G}_R(Y_k)} |g(n)-A_g(Y_k)|^2 \\&\quad \ll \frac{1}{Y_k}\sum _{Y_k/2< n \le Y_k} \left|\frac{1}{R} \sum _{n-R< m \le n} g(m) - \frac{2}{Y}\sum _{Y_k/2 < m \le Y_k} g(m)\right|^2 + o(B_g(X)^2). \end{aligned}$$

By Theorem 1.4, this gives $o_{R \rightarrow \infty }(B_g(X)^2)$, uniformly over $X/\log X < Y_k \le X$.

It remains to estimate the contribution from $n \in \mathcal {B}_R(Y_k)$. By the union bound, we have

$$\begin{aligned} \frac{2}{Y_k} \sum _{n \in \mathcal {B}_R(Y_k)} |g(n)-A_g(Y_k)|^2 \le R\max _{|i |\le R} \frac{2}{Y_k}\sum _{\begin{array}{c} Y_k/2 < n \le Y_k \\ n +i \in \mathcal {B} \end{array}} |g(n)-A_g(Y_k)|^2. \end{aligned}$$

By Corollary 7.5, the above expression is $o(B_g(X))$, again provided X is sufficiently large in terms of R.

To conclude, for any $\varepsilon > 0$ we can find R large enough in terms of $\varepsilon$ and $X_0$ sufficiently large in terms of $\varepsilon$ and R such that if $X \ge X_0$ then

$$\begin{aligned} \frac{2}{Y_k} \sum _{Y_k/2 < n \le Y_k} |g(n)-A_g(Y_k)|^2 \ll \varepsilon B_g(X)^2 \end{aligned}$$

uniformly in $X/\log X < Y_k = X/2^k \le X$, and (41) follows.

Now, applying Lemma 3.3, we deduce that

$$\begin{aligned} B_{g_{\lambda _0}}(X)^2 + \lambda _0(X)^2&= \sum _{p^k \le X} \frac{\vert g(p^k)-\lambda _0(X) \log p^k \vert ^2}{p^k} + \lambda _0(X)^2 \\&\ll \frac{1}{X}\sum _{n \le X} |g(n) - A_g(X) |^2 = o(B_g(X)^2), \end{aligned}$$

where we recall that $g_{\lambda _0}(n) = g(n)-\lambda _0 \log n$ for all $n \ge 1$, and

$$\begin{aligned} \lambda _0(X) := \frac{2}{(\log X)^2} \sum _{p \le X} \frac{g(p)\log p}{p}. \end{aligned}$$

(42)

Note that by Cauchy–Schwarz and the prime number theorem,

$$\begin{aligned} \lambda _0(X)^2 \ll \frac{1}{(\log X)^2} \left( \sum _{p\le X} \frac{g(p)^2}{p}\right) \left( \frac{1}{(\log X)^2}\sum _{p \le X} \frac{(\log p)^2}{p}\right) \ll \frac{B_g(X)^2}{(\log X)^2}. \end{aligned}$$

Thus, $\vert \lambda _0(X) \vert \ll B_g(X)/\log X$, and $B_{g_{\lambda _0}}(X)^2 = o(B_g(X)^2)$, as wanted. We will verify that $\lambda _0(X)$ is slowly varying in the next section (immediately following the proof of Proposition 8.1). $\square$

8 Rigidity properties for almost everywhere monotone functions

We continue to assume that g is almost everywhere monotone in the sense of the previous section. Theorem 1.8 claims that an additive function $g \in \mathcal {A}$ is well approximated by a constant times a logarithm, assuming g(p) is not frequently much larger than $B_g(X)$ for $p \le X$. In this section, we will complete the proof of this theorem, along with those of Corollary 1.7 and Theorem 1.7, all of which are consequences of the almost everywhere monotonicity property. A key input in this direction is Proposition 8.1, which is a structure theorem for the asymptotic mean value $A_g(X)$.

8.1 The structure of $A_g(X)$

The first main result of this section is the following.

Proposition 8.1

Let $g:\mathbb {N} \rightarrow \mathbb {R}$ be an additive function satisfying $B_g(X) \rightarrow \infty$ as $X \rightarrow \infty$. Assume that $\mathcal {B} := \{n \in \mathbb {N} : g(n) < g(n-1)\}$ satisfies $\vert \mathcal {B}(X) \vert := \vert \mathcal {B} \cap [1,X] \vert = o(X)$ as $X \rightarrow \infty$. Then for each X sufficiently large there is $\lambda = \lambda (X) \in \mathbb {R}$ such that for any $\frac{\log \log X}{\sqrt{\log X}} < \delta \le 1/4$,

$$\begin{aligned} \sum _{X^{\delta } < p^k \le X} \frac{1}{p^k}|A_g(X)-A_g(X/p^k) - \lambda \log p^k |= o(B_g(X)(\log (1/\delta ))^{1/2}), \end{aligned}$$

(43)

and also

$$\begin{aligned} \sum _{X^{\delta } < p^k \le X} \frac{\vert g(p^k)-\lambda \log p^k \vert }{p^k} = o(B_g(X) (\log (1/\delta ))^{1/2}). \end{aligned}$$

(44)

Furthermore, $A_g(X)$ and $\lambda (X)$ satisfy the following properties:

• (i) $\lambda (X) \ll B_g(X)/\log X$,

• (ii) for X sufficiently large and any $X^{\delta } < t_1 \le t_2 \le X$,

  $$\begin{aligned} A_g(t_2) = A_g(t_1) + \lambda (X)\log (t_1/t_2) + o((\log (1/\delta )^{1/2}B_g(X)), \end{aligned}$$

• (iii) for every $u \in (\delta ,1]$ we have

  $$\begin{aligned} \lambda (X) = \lambda (X^u) + o\left( (\log (1/\delta )^{1/2} \delta ^{-1} \frac{B_g(X)}{\log X}\right) . \end{aligned}$$

Remark 8.2

It would be desirable to determine $A_g(t)$ directly as a function of t in some range, say $X^{\delta } < t \le X$. Proposition 8.1 provides the approximation $A_g(t) = A_g(X^{\delta }) + (1-\delta u) \lambda (X) \log t + o(B_g(X))$, where $u := \log X/\log t$, but this still contains a reference to a second value $A_g(X^{\delta })$. We might iterate this argument to obtain (using the slow variation of $\lambda$) a further approximation in terms of $A_g(X^{\delta ^2})$, $A_g(X^{\delta ^3})$, and so forth, but without further data about g (say, $A_g(X^{1/1000}) = o(B_g(X))$) it is not obvious that this argument yields an asymptotic formula for $A_g(t)$ alone.

To prove this proposition we will require a few lemmas.

Lemma 8.3

Let $g: \mathbb {N} \rightarrow \mathbb {C}$ be an additive function satisfying $B_g(X) \rightarrow \infty$ as $X \rightarrow \infty$. Let $\alpha \in (1,2)$ and $\frac{\log \log X}{\sqrt{\log X}} < \delta \le 1/4$. Then

$$\begin{aligned}&\sum _{X^{\delta } < p^k \le X} \frac{1}{p^k}|g(p^k)-A_g(X)+A_g(X/p^k)|\\&\ll _{\alpha } (\log (1/\delta ))^{1/2}\left( \frac{1}{X}\sum _{n \le X} |g(n) - A_g(X) |^{\alpha }\right) ^{1/\alpha } + \frac{B_g(X)}{(\log X)^{1/4}}. \end{aligned}$$

Proof

We will estimate the quantity

$$\begin{aligned} {\mathscr {M}} := \frac{1}{X}\sum _{X^{\delta } < p^k \le X} \left|\sum _{\begin{array}{c} n \le X \\ p^k||n \end{array}} g(n) - \frac{1}{p^k}\left( 1-\frac{1}{p}\right) \sum _{\begin{array}{c} n \le X \end{array}} g(n)\right|\end{aligned}$$

in two different ways.

First, we will obtain a lower bound for ${\mathscr {M}}$ as follows. Given $2 \le Y \le X$ observe that for any fixed prime p

$$\begin{aligned} S_p(Y)&:= \sum _{\begin{array}{c} m \le Y \\ p \not \mid m \end{array}} g(m) = \sum _{m \le Y} g(m) - \sum _{j \ge 1} \sum _{\begin{array}{c} r \le Y/p^j \\ p \not \mid r \end{array}} (g(r) + g(p^j)) \\&= \sum _{m \le Y} g(m)-\sum _{m \le Y/p} g(m) + \sum _{j \ge 1}\sum _{\begin{array}{c} r \le Y/p^j \\ p \not \mid r \end{array}} (g(p^{j-1})-g(p^j)) \\&= Y\left( 1-\frac{1}{p}\right) A_g(Y) + \frac{Y}{p} (A_g(Y)-A_g(Y/p)) \\&\quad + \sum _{j \ge 1} (g(p^{j-1})-g(p^j))\left( \left\lfloor \frac{Y}{p^j}\right\rfloor - \left\lfloor \frac{Y}{p^{j+1}}\right\rfloor \right) + O\left( \frac{YB_g(Y)}{\sqrt{\log Y}}\right) , \end{aligned}$$

where the last equality arises from Lemma 3.1.

Using this estimate with $Y =X/p^k$ for $p^k \le X$, we obtain

$$\begin{aligned} \sum _{\begin{array}{c} n \le X \\ p^k||n \end{array}} g(n)&= \sum _{\begin{array}{c} mp^k\le X \\ p \not \mid m \end{array}} g(mp^k) = g(p^k)\left( \left\lfloor \frac{X}{p^k}\right\rfloor - \left\lfloor \frac{X}{p^{k+1}}\right\rfloor \right) + S_p(X/p^k) \\&= \frac{X}{p^k}\left( 1-\frac{1}{p}\right) \left( g(p^k)+ A_g(X/p^k)\right) \\&\quad + O\left( \frac{X}{p^{k+1}} \vert A_g(X/p^k) - A_g(X/p^{k+1}) \vert \right) \\&\quad + O\left( \vert g(p^k) \vert + X \sum _{\begin{array}{c} j \ge 1 \\ p^j \le X/p^k \end{array}} \frac{\vert g(p^{j-1})\vert + \vert g(p^j)\vert }{p^{k+j}} + \frac{XB_g(X/p^k)}{p^k\sqrt{\log (2X/p^k)}}\right) , \end{aligned}$$

noting that the third error term is 0 unless $p^k \le X/2$. Similarly, again by Lemma 3.1 we have

$$\begin{aligned} \frac{1}{p^k}\left( 1-\frac{1}{p}\right) \sum _{\begin{array}{c} n \le X \end{array}} g(n) = \frac{X}{p^k}\left( 1-\frac{1}{p}\right) \left( A_g(X) + O\left( \frac{B_g(X)}{\sqrt{\log X}}\right) \right) . \end{aligned}$$

We thus deduce that

$$\begin{aligned} {\mathscr {M}}&= \sum _{X^{\delta } < p^k \le X} \frac{1}{p^k}\left( 1-\frac{1}{p}\right) \left|g(p^k) + A_g(X/p^k) - A_g(X)\right|+ O\left( \mathcal {R}(X)\right) \end{aligned}$$

(45)

$$\begin{aligned}&\ge \frac{1}{2}\sum _{X^{\delta } < p^k \le X} \frac{1}{p^k} \left|g(p^k) + A_g(X/p^k) - A_g(X)\right|+ O\left( \mathcal {R}(X) \right) , \end{aligned}$$

(46)

where we have set

$$\begin{aligned} \mathcal {R}(X)&:=\sum _{X^{\delta }< p^k \le X} \frac{1}{p^k} \left( 1+\sum _{\begin{array}{c} j \ge 1 \\ p^j \le X/p^k \end{array}} \frac{|g(p^j)|}{p^j}\right) + \sum _{\begin{array}{c} X^{\delta }< p^k \le X/2 \end{array}} \frac{B_g(X)}{p^k\sqrt{\log (X/p^k)}} \\&\quad + \frac{1}{X}\sum _{p^k \le X} |g(p^k) |+ \sum _{X^{\delta } < p^k \le X} \frac{1}{p^{k+1}}\vert A_g(X/p^k)-A_g(X/p^{k+1})\vert \\&=: \mathcal {R}_1(X) + \mathcal {R}_2(X) + \mathcal {R}_3(X) + \mathcal {R}_4(X). \end{aligned}$$

As in the proof of Lemma 3.1,

$$\begin{aligned} \mathcal {R}_3(X) \le \frac{1}{\sqrt{X}} \sum _{p^k \le X} \frac{|g(p^k) |}{p^{k/2}} \le \left( \frac{\pi (X)}{X}\right) ^{1/2} B_g(X) \ll \frac{B_g(X)}{\sqrt{\log X}}. \end{aligned}$$

Next, we may upper bound $\mathcal {R}_2(X)$ as

$$\begin{aligned} \mathcal {R}_2(X)&\le B_g(X)\left( \frac{1}{(\log X)^{1/4}} \sum _{\begin{array}{c} X^{\delta }< p^k \le Xe^{-\sqrt{\log X}} \end{array}} \frac{1}{p^k} + \sum _{Xe^{-\sqrt{\log X}} < p^k \le \tfrac{X}{2}} \frac{1}{p^k}\right) \\&\ll \frac{B_g(X)}{(\log X)^{1/4}}. \end{aligned}$$

To treat $\mathcal {R}_1(X)$, we use $|g(p^j)|/p^j \le B_g(p^j)p^{-j/2}$ to get

$$\begin{aligned}&\sum _{X^{\delta }< p^k \le X} \sum _{\begin{array}{c} j \ge 1 \\ p^j \le X/p^k \end{array}} \frac{|g(p^j)|}{p^{j+k}} \le B_g(X) \sum _{X^{\delta }< p^k \le X} \sum _{ \begin{array}{c} j \ge 1 \\ p^j \le X/p^k \end{array}} p^{-(k+j/2)} \\&\quad \ll B_g(X) \left( X^{-\delta } \sum _{\begin{array}{c} X^{\delta }< p^k \le X \\ k \ge 2/\delta \end{array}} 1 + \sum _{\begin{array}{c} X^{\delta } < p^k \le X \\ p> X^{\delta ^2/2} \end{array}} p^{-k} \sum _{\begin{array}{c} j \ge 1 \\ p^j \le X/p^k \end{array}} \frac{1}{p^{j/2}}\right) \\&\quad \ll B_g(X)\left( X^{-\delta /2} + \sum _{p > X^{\delta ^2/2}} p^{-3/2}\right) \ll B_g(X) X^{-\delta ^2/4}. \end{aligned}$$

Furthermore, we have

$$\begin{aligned} \sum _{X^{\delta } < p^k \le X} \frac{1}{p^{k+1}} \le \sum _{1 \le k \le \log X} \sum _{\max \{2,X^{\delta /k}\} \le p \le X^{1/k}} \frac{1}{p^{k+1}} \ll \sum _{1 \le k \le \log X} k X^{-\delta } \ll \frac{(\log X)^2}{ X^{\delta }}.\nonumber \\ \end{aligned}$$

(47)

Since $B_g(X) \gg 1$ these last two bounds combine to give

$$\begin{aligned} \mathcal {R}_1(X) \ll B_g(X)X^{-\delta ^2/4}. \end{aligned}$$

Finally, to bound $\mathcal {R}_4(X)$ we use Lemma 3.4 to obtain

$$\begin{aligned} \vert A_g(X/p^k)-A_g(X/p^{k+1}) \vert \ll B_g(X/p^k) (\log \log X)^{1/2} \le B_g(X) (\log \log X)^{1/2} \end{aligned}$$

uniformly over $p^k \le X$, and thus using (47) we find

$$\begin{aligned} \mathcal {R}_4(X) \ll B_g(X)(\log \log X)^{1/2} \sum _{X^{\delta } < p^k \le X} \frac{1}{p^{k+1}} \ll B_g(X) \frac{(\log X)^3}{X^{\delta }}. \end{aligned}$$

Combining the estimates for $\mathcal {R}_j(X)$, $1 \le j \le 4$, in view of the range of $\delta$ we finally obtain

$$\begin{aligned} \mathcal {R}(X) \ll B_g(X)/(\log X)^{1/4} \end{aligned}$$

in (45). Thus,

$$\begin{aligned} \sum _{X^{\delta } < p^k \le X} \frac{1}{p^k} |g(p^k)+A_g(X/p^k) - A_g(X)|\le 2 {\mathscr {M}} + O(B_g(X)/(\log X)^{1/4}). \end{aligned}$$

Next, we execute the second estimation of ${\mathscr {M}}$. If $p^k \in (X^{\delta },X]$ define

$$\begin{aligned} \Delta _{g}(X;p^k) := \frac{p^k}{X}\left|\sum _{\begin{array}{c} n \le X \\ p^k ||n \end{array}} g(n) - \frac{1}{p^k}\left( 1-\frac{1}{p}\right) \sum _{\begin{array}{c} n \le X \end{array}} g(n)\right|. \end{aligned}$$

Set $g'(n) := g(n) -A_g(X)$ for $n \le X$, and note that

$$\begin{aligned} \Delta _g(X;p^k) = \Delta _{g'}(X;p^k) + O\left( \frac{p^k}{X}|A_g(X)|\right) . \end{aligned}$$

Thus, as $\vert A_g(X) \vert \le B_g(X)\sqrt{\log \log X}$ by Lemma 3.4, we find

$$\begin{aligned} {\mathscr {M}}&= \sum _{X^{\delta }< p^k \le X} \frac{1}{p^k}\Delta _{g'}(X;p^k)+ O\left( \frac{|A_g(X)|\pi (X)}{X}\right) \nonumber \\&= \sum _{X^{\delta }< p^k \le X} \frac{1}{p^k}\Delta _{g'}(X;p^k) + O\left( \frac{B_g(X) \sqrt{\log \log X}}{\log X}\right) . \end{aligned}$$

(48)

Recall that $\alpha \in (1,2)$. Let us now partition the set of prime powers $X^{\delta } < p^k \le X$ into the sets

$$\begin{aligned} \mathcal {P}_1&:= \left\{ X^{\delta }< p^k \le X : \Delta _{g'}(X;p^k) > \left( \frac{1}{X}\sum _{n \le X}|g'(n)|^{\alpha }\right) ^{1/\alpha }\right\} \\ \mathcal {P}_2&:= \left\{ X^{\delta } < p^k \le X : \Delta _{g'}(X;p^k) \le \left( \frac{1}{X}\sum _{n \le X}|g'(n)|^{\alpha }\right) ^{1/\alpha }\right\} . \end{aligned}$$

Note that by Mertens’ theorem,

$$\begin{aligned} \sum _{X^{\delta }< p^k \le X} \frac{1}{p^k}&\le \sum _{X^{\delta }< p \le X} \frac{1}{p} + X^{-\delta } \sum _{\begin{array}{c} X^{\delta }< p^k \le X \\ k \ge 2/\delta \end{array}} 1 + \sum _{\begin{array}{c} X^{\delta } < p^k \le X \\ 2 \le k \le 2/\delta \\ p > X^{\delta ^2/2} \end{array}} \frac{1}{p^k} \nonumber \\&\ll \log (1/\delta )\left( 1+\delta ^{-1}X^{-\delta ^2/2}\right) + X^{-\delta /2} \ll \log (1/\delta ). \end{aligned}$$

(49)

Using this and Hölder’s inequality, we obtain

$$\begin{aligned}&\sum _{X^{\delta }< p^k \le X} p^{-k} \Delta _{g'}(X;p^k) \\&\quad \ll _{\alpha } \left( \log \left( 1/\delta \right) \right) ^{1-\frac{1}{\alpha }}\left( \sum _{\begin{array}{c} X^{\delta }< p^k \le X \\ p^k \in \mathcal {P}_1 \end{array}} p^{-k} \Delta _{g'}(X;p^k)^{\alpha }\right) ^{\frac{1}{\alpha }} \\&\qquad + (\log (1/\delta ))^{\frac{1}{2}} \left( \sum _{\begin{array}{c} X^{\delta } < p^k \le X \\ p^k \in \mathcal {P}_2 \end{array}} p^{-k} \Delta _{g'}(X;p^k)^{2}\right) ^{\frac{1}{2}}. \end{aligned}$$

By Theorem 3.1 of [36] this is bounded by

$$\begin{aligned} \ll (\log (1/\delta ))^{\frac{1}{2}}\left( \frac{1}{X} \sum _{n \le X}|g'(n)|^{\alpha }\right) ^{\frac{1}{\alpha }}. \end{aligned}$$

Combining this with (45) and (48) completes the proof of the lemma. $\square$

Next, we show that, in an $\ell ^1$ sense, $g(p^k)$ is well approximated by $\lambda \log p^k$ on average over the prime powers $X^{\delta } < p^k \le X$, for some function $\lambda = \lambda (X)$. This will be the $\lambda$ that appears in the statement of Proposition 8.1.

Lemma 8.4

There is a parameter $\lambda =\lambda (X) \in \mathbb {R}$ such that the following holds. For any $\alpha \in (1,2)$,

$$\begin{aligned} \sum _{X^{\delta }<p^k \le X} \frac{1}{p^k}|g(p^k)-\lambda \log p^k |\ll _{\alpha } (\log (1/\delta ))^{1/2}\left( \frac{1}{X}\sum _{n \le X} |g(n) - A_g(X) |^{\alpha }\right) ^{1/\alpha }. \end{aligned}$$

Proof

By [1, Théorème 1], there are $\lambda = \lambda (X)$ and $c = c(X)$ (both depending on g but independent of $\alpha$) such that

$$\begin{aligned} \left( \frac{1}{X}\sum _{n \le X} |g(n) - A_g(X) |^{\alpha }\right) ^{\alpha } \gg _{\alpha } \left( \sum _{p^k \le X} \frac{|g_{\lambda ,c}''(p^k)|^{\alpha }}{p^k}\right) ^{1/\alpha } + \left( \sum _{p^k \le X} \frac{|g_{\lambda ,c}'(p^k)|^2}{p^k}\right) ^{1/2}. \end{aligned}$$

(50)

Here, writing $g_{\lambda }(n) = g(n)-\lambda \log (n)$, we have set

$$\begin{aligned} g_{\lambda ,c}'(p^k) := {\left\{ \begin{array}{ll} g_{\lambda }(p^k) &{}\text { if } |g_{\lambda }(p^k)|\le c, \\ 0 &{}\text { otherwise;} \end{array}\right. } \quad \quad g_{\lambda ,c}''(p^k) := {\left\{ \begin{array}{ll} 0 &{}\text { if } |g_{\lambda }(p^k)|\le c, \\ g_{\lambda }(p^k) &{}\text { otherwise.} \end{array}\right. } \end{aligned}$$

Since $g_{\lambda }(p^k) = g_{\lambda ,c}'(p^k) + g_{\lambda ,c}''(p^k)$ for each $p^k$, by Hölder’s inequality and (49) once again,

$$\begin{aligned} \sum _{X^{\delta }< p^k \le X} \frac{|g_{\lambda }(p^k)|}{p^k}&\ll _{\alpha } (\log (1/\delta ))^{1-1/\alpha }\left( \sum _{X^{\delta }< p^k \le X} \frac{|g_{\lambda ,c}''(p^k)|^{\alpha }}{p^k}\right) ^{1/\alpha } \\&\qquad + (\log (1/\delta ))^{1/2}\left( \sum _{X^{\delta } < p^k \le X} \frac{|g_{\lambda ,c}'(p^k)|^2}{p^k}\right) ^{1/2}. \end{aligned}$$

The result now follows upon combining this last estimate with (50) and using positivity. $\square$

To make use of the previous two lemmas we establish the following upper bound for moments of order $\alpha \in [1,2)$ that crucially uses the almost-everywhere monotonicity property of g.

Lemma 8.5

Assume that $\mathcal {B} := \{n \in \mathbb {N} : g(n) < g(n-1)\}$ satisfies $\vert \mathcal {B}(X) \vert = o(X)$, where $\mathcal {B}(X) = \mathcal {B} \cap [1,X]$. Then for any $\alpha \in [1,2)$,

$$\begin{aligned} \frac{1}{X} \sum _{n \le X} |g(n) - A_g(X) |^{\alpha } \ll \left( \frac{\log \log (1/r(X))}{\log (1/r(X))} + (\log X)^{-\tfrac{1}{800}} \right) ^{2-\alpha } B_g(X)^{\alpha }, \end{aligned}$$

where $r(X) := \max _{\tfrac{X}{\log X} < Y \le X} \left( \left( \frac{|\mathcal {B}(Y) |}{Y}\right) ^{1/2} + \frac{\log Y}{\sqrt{Y}}\right)$.

Proof

By Hölder’s inequality, for any $\alpha \in (1,2)$ we have

$$\begin{aligned} \frac{1}{X}\sum _{n \le X} |g(n) - A_g(X) |^{\alpha } \le \left( \frac{1}{X}\sum _{n \le X}|g(n) - A_g(X) |\right) ^{2-\alpha } \cdot \left( \frac{1}{X}\sum _{n \le X} |g(n) - A_g(X) |^2\right) ^{\alpha -1}, \end{aligned}$$

an inequality that is vacuously also true when $\alpha = 1$. Applying Lemma 3.2 to the second bracketed expression, we obtain the upper bound

$$\begin{aligned} \ll B_g(X)^{2\alpha -2} \left( \frac{1}{X}\sum _{n \le X} |g(n) - A_g(X) |\right) ^{2-\alpha }. \end{aligned}$$

Next, we show that for all $X/\log X < Y \le X$ we get

$$\begin{aligned} \frac{1}{Y}\sum _{n \le Y}|g(n)-g(n-1) |\ll \left( \left( \frac{|\mathcal {B}(Y) |}{Y}\right) ^{1/2} + \frac{\log Y}{\sqrt{Y}} \right) B_g(Y) \le r(X) B_g(X). \end{aligned}$$

(51)

This will imply the claim of the lemma, since by Proposition 6.1 the latter bound gives

$$\begin{aligned} \frac{1}{X}\sum _{n \le X} |g(n) - A_g(X) |\ll \left( \frac{\log \log (1/r(X))}{\log (1/r(X))} + (\log X)^{-\tfrac{1}{800}}\right) B_g(X). \end{aligned}$$

To prove (51), we note that for all $1 \le n \le Y$,

$$\begin{aligned} |g(n)-g(n-1) |= g(n)-g(n-1) + 2|g(n)-g(n-1) |1_{n \in \mathcal {B}(Y)}. \end{aligned}$$

It follows from this and telescoping that

$$\begin{aligned} \frac{1}{Y}\sum _{n \le Y} |g(n)-g(n-1) |= \frac{g(\left\lfloor Y\right\rfloor )}{Y} + \frac{2}{Y}\sum _{n \in \mathcal {B}(Y)} |g(n)-g(n-1) |. \end{aligned}$$

By Lemma 3.5, $g(\left\lfloor Y \right\rfloor )/Y \ll B_g(Y)(\log Y)Y^{-1/2}$. Owing to Lemma 3.2 and the triangle and Cauchy–Schwarz inequalities, we also obtain

$$\begin{aligned} \frac{1}{Y}\sum _{n \in \mathcal {B}(Y)}|g(n)-g(n-1) |&\le 2\left( \frac{|\mathcal {B}(Y) |}{Y}\right) ^{1/2} \left( \frac{1}{Y} \sum _{n \le Y} |g(n) - A_g(Y) |^2\right) ^{1/2} \\&\ll \left( \frac{|\mathcal {B}(Y) |}{Y}\right) ^{1/2}B_g(Y). \end{aligned}$$

This implies (51), and completes the proof of the lemma. $\square$

Proof of Proposition 8.1

We begin with the proof of (44). Set $\alpha = 3/2$, say. Combining Lemmas 8.4 and 8.5, there is a $\lambda = \lambda (X) \in \mathbb {R}$ such that

$$\begin{aligned} \sum _{X^{\delta } < p^k \le X} \frac{\vert g(p^k)-\lambda \log p^k \vert }{p^k}&\ll (\log (1/\delta ))^{1/2} \left( \frac{1}{X}\sum _{n \le X} \vert g(n)-A_g(X) \vert ^{3/2}\right) ^{2/3} \nonumber \\&= o((\log (1/\delta ))^{1/2} B_g(X)). \end{aligned}$$

(52)

We use this to obtain (43). Indeed, this time combining Lemmas 8.3 and 8.5 , we get

$$\begin{aligned}&\sum _{X^{\delta } < p^k \le X} \frac{\vert g(p^k)-A_g(X)+A_g(X/p^k) \vert }{p^k} \\&\quad \ll (\log (1/\delta ))^{1/2} \left( \frac{1}{X}\sum _{n \le X} \vert g(n)-A_g(X) \vert ^{3/2}\right) ^{2/3} + \frac{B_g(X)}{(\log X)^{1/4}} \\&\quad = o((\log (1/\delta ))^{1/2} B_g(X)). \end{aligned}$$

Combining this with (52) and applying the triangle inequality in the form

$$\begin{aligned} \vert A_g(X)-A_g(X/p^k)-\lambda \log p^k \vert \le \vert g(p^k) - A_g(X) + A_g(X/p^k) \vert + \vert g(p^k)-\lambda \log p^k \vert \end{aligned}$$

for each $X^{\delta } < p^k \le X$, we quickly deduce (43).

Next, we proceed to the proofs of properties (i)–(iii).

(i) By the triangle inequality and positivity, we obtain

$$\begin{aligned} \vert \lambda (X)\vert \sum _{X^{1/4}< p \le X^{1/2}} \frac{\log p}{p}&\le \sum _{X^{1/4}< p \le X} \frac{|A_g(X)-A_g(X/p)-\lambda (X)\log p |}{p} \nonumber \\&\quad + \sum _{X^{1/4} < p \le X^{1/2}} \frac{|A_g(X)-A_g(X/p)|}{p}. \end{aligned}$$

(53)

By Mertens’ theorem,

$$\begin{aligned}&\sum _{X^{1/4} < p \le X^{1/2}} \frac{\log p}{p} = \frac{1}{4}\log X+ O\left( \frac{1}{\log X}\right) \gg \log X, \end{aligned}$$

and by the Cauchy–Schwarz inequality we have, for $X^{1/4} \le p \le X^{1/2}$,

$$\begin{aligned}&|A_g(X)-A_g(X/p)|\ll B_g(X) \left( \sum _{X/p \le q^k \le X} \frac{1}{q^k}\right) ^{1/2} \ll B_g(X)\left( \frac{\log p}{\log X}\right) ^{1/2}. \end{aligned}$$

Using the above, (43), the prime number theorem and partial summation in (53), we find that

$$\begin{aligned} \vert \lambda (X) \vert \log X \ll o(B_g(X)) + \frac{B_g(X)}{\sqrt{\log X}} \sum _{p \le X^{1/2}} \frac{(\log p)^{1/2}}{p} \ll B_g(X), \end{aligned}$$

and (i) follows immediately.

(ii) We observe, using (i) and (44) that if $X^{\delta } < t_1 \le t_2 \le X$,

$$\begin{aligned}&\left|A_g(t_2)-A_g(t_1) - \lambda (X) \log (t_2/t_1)\right|\\&= \left|\sum _{t_1< p^k \le t_2} \left( 1-\frac{1}{p}\right) \frac{g(p^k)-\lambda (X) \log p^k}{p^k}\right|\\&\quad + O\left( \lambda (X) \left( \frac{1}{\delta \log X} + \sum _{t_1< p^k \le t_2} \frac{\log p^k}{p^{k+1}} \right) \right) \\&\le \sum _{X^{\delta } < p^k \le X} \frac{|g(p^k)-\lambda (X)\log p^k |}{p^k} + O\left( B_g(X) \left( \frac{1}{\delta (\log X)^2} + \frac{(\log X)^3}{x^{\delta }}\right) \right) \\&= o((\log (1/\delta )^{1/2}B_g(X)), \end{aligned}$$

where in the penultimate line the second error term is estimated similarly to (47). This proves the required estimate.

(iii) Applying (ii) with $(t_1,t_2) = (X^y,X^z)$, where, in sequence, $(y,z) = (u,1)$, $(y,z) = (uv,1)$ and $(y,z) = (uv,u)$ for any $v \in (\delta /u,1/2]$ and $u \in (\delta ,1]$, we get

$$\begin{aligned} A_g(X) - A_g(X^u)&= (1-u) \lambda (X)\log X + o((\log (1/\delta )^{1/2}B_g(X)) \\ A_g(X)-A_g(X^{uv})&= (1-uv)\lambda (X)\log X + o((\log (1/\delta )^{1/2}B_g(X)) \\ A_g(X^u) - A_g(X^{uv})&= (u-uv) \lambda (X^u) \log X + o((\log (1/\delta )^{1/2}B_g(X^u)). \end{aligned}$$

We subtract the second equation from the first and combine the result with the third equation. Using $B_g(X^u) \le B_g(X)$ we conclude that

$$\begin{aligned} u(1-v) \lambda (X)\log X = u(1-v)\lambda (X^u)\log X + o((\log (1/\delta )^{1/2}B_g(X)). \end{aligned}$$

Since $1-v \ge 1/2$ and $u > \delta$, the claim follows immediately upon rearranging (with a potentially larger implicit constant in the error term). $\square$

Proof of Theorem 1.8: Part II

The work at the end of Sect. 7 implies that

$$\begin{aligned} \sum _{p^k \le X} \frac{|g(p^k)-\lambda _0(X)\log p^k |^2}{p^k} = B_{g_{\lambda _0}}(X)^2 = o(B_g(X)^2), \end{aligned}$$

(54)

where $\lambda _0$ is as in (42). Now, by Proposition 8.1 we have

$$\begin{aligned} \sum _{X^{1/2} < p^k \le X} \frac{|g(p^k)-\lambda (X) \log p^k |}{p^k} = o(B_g(X)), \end{aligned}$$

(55)

where $\lambda (X)$ satisfies

$$\begin{aligned} \lambda (X) = \lambda (X^u) + o(\tfrac{B_g(X)}{\log X}), \quad 0 < u \le 1 \text { fixed.} \end{aligned}$$

Thus, by (54) and (55), Cauchy–Schwarz and Mertens’ theorem, whenever $Y = X^u$ with $0 < u \le 1$ fixed we have

$$\begin{aligned} |\lambda (Y)-\lambda _0(Y)|\log Y&\ll |\lambda (Y)-\lambda _0(Y)|\sum _{Y^{1/2} < p \le Y} \frac{\log p}{p} \end{aligned}$$

(56)

$$\begin{aligned}&\le \sum _{Y^{1/2}< p \le Y} \frac{|g(p)-\lambda _0(Y)\log p |}{p} \nonumber \\&\quad + \sum _{Y^{1/2}< p \le Y} \frac{|g(p)-\lambda (Y)\log p |}{p} \nonumber \\&\le B_{g_{\lambda _0}}(Y) \left( \sum _{Y^{1/2} < p \le Y} \frac{1}{p}\right) ^{1/2} + o(B_g(Y)) = o(B_g(X)). \end{aligned}$$

(57)

We thus deduce that $\lambda (X^u) = \lambda _0(X^u) + o(B_g(X)/\log X)$ for all $0 < u \le 1$ fixed, and therefore also that

$$\begin{aligned} \lambda _0(X^u) = \lambda (X^u) + o\left( \frac{B_g(X)}{\log X}\right) = \lambda (X) + o\left( \frac{B_g(X)}{\log X}\right) = \lambda _0(X) + o\left( \frac{B_g(X)}{\log X}\right) , \end{aligned}$$

and the second claim of Theorem 1.8 is proved. $\square$

8.2 Growth of $B_g(X)$ and the proof of Corollary 1.7

In this subsection we prove Corollary 1.7. The key step will be to show that if there is a $\lambda (X)$ such that $B_{g_{\lambda }}(X) = o(B_g(X))$ (which follows from Theorem 1.8) then $B_g(X)$ grows roughly like $\log X$.

We begin by showing that this is the case assuming in addition that $\lambda (X)$ is fairly large (this assumption is subsequently removed in Lemma 8.7).

Until further notice, assume that $B_g(X) \gg 1$ as X gets large.

Lemma 8.6

Assume that there is a $C > 0$ such that $\lambda (X) \ge C B_g(X)/\log X$ for all X sufficiently large in the conclusion of Proposition 8.1. Then for any $\varepsilon > 0$, $(\log X)^{1-\varepsilon } \ll _{\varepsilon } B_g(X) \ll _{\varepsilon } (\log X)^{1+\varepsilon }$.

Proof

By Proposition 8.1 and our assumption $\lambda (X) \gg B_g(X)/\log X$,

$$\begin{aligned} \lambda (X) = \lambda (X^u) + o(B_g(X)/\log X) = \lambda (X^u) + o(\lambda (X)) \end{aligned}$$

(58)

whenever $0 < u \le 1$ is fixed. This implies in particular that $\lambda (X) \ll \lambda (X^u)$. Setting $Y := X^u$ and $v := 1/u \ge 1$, we see also that

$$\begin{aligned} \lambda (Y^v) = \lambda (Y) + o(\lambda (Y^v)) = \lambda (Y) + o(\lambda (Y^{uv})) =\lambda (Y) + o(\lambda (Y)). \end{aligned}$$

Thus, (58) holds for all fixed $u \ge 1$ as well, and thus for all fixed $u > 0$. We thus deduce that for each $u > 0$ fixed and $\varepsilon > 0$ there is $X_0(\varepsilon ,u)$ such that if $X\ge X_0(\varepsilon ,u)$,

$$\begin{aligned} \left|\frac{\lambda (X^u)}{\lambda (X)} - 1\right|< \varepsilon . \end{aligned}$$

Set $u = 1/2$, put $X_0 = X_0(\varepsilon ,1/2)$ and for each $k \ge 1$ define $X_k := X_0^{2^k}$. Let K be large. Then

$$\begin{aligned} \frac{\lambda (X_0)}{\lambda (X_K)} = \prod _{1 \le k \le K} \frac{\lambda (X_{k-1})}{\lambda (X_k)} \in [(1-\varepsilon )^K, (1+\varepsilon )^K]. \end{aligned}$$

As $K \le 2\log \log X_K$ for large enough K and $X_0$, we find

$$\begin{aligned} |\lambda (X_K)|&\le |\lambda (X_0)|\exp \left( -K\log (1-\varepsilon )\right) \ll _{\varepsilon } \exp \left( 4\varepsilon \log \log X_K\right) = (\log X_K)^{4\varepsilon }, \\ |\lambda (X_K)|&\ge |\lambda (X_0)|\exp \left( -K\log (1+\varepsilon )\right) \gg _{\varepsilon } \exp \left( -4\varepsilon \log \log X_K\right) = (\log X_K)^{-4\varepsilon }. \end{aligned}$$

Thus, we have $B_g(X_K) \ll |\lambda (X_K) |(\log X_K) \ll _{\varepsilon } (\log X_K)^{1+4\varepsilon }$ by assumption, and by Proposition 8.1(i) we have $B_g(X_K) \gg |\lambda (X_K)|\log X_K \gg _{\varepsilon } (\log X_k)^{1-4\varepsilon }$.

Since $\log X_K \asymp \log X_{K+1}$, by monotonicity of $B_g$ we also have

$$\begin{aligned} B_g(X) \le B_g(X_{K+1}) \ll _{\varepsilon } (\log X_{K+1})^{1+4\varepsilon } \ll _{\varepsilon } (\log X_K)^{1+4\varepsilon } \le (\log X)^{1+4\varepsilon } \end{aligned}$$

for any $X_K< X < X_{K+1}$. Similarly, we obtain $B_g(X) \gg _{\varepsilon } (\log X)^{1-4\varepsilon }$ on the same interval. Since $\varepsilon > 0$ was arbitrary, the claim now follows. $\square$

Lemma 8.7

Assume $B_{g_{\nu }}(X) = o(B_g(X))$ for some $\nu = \nu (X)$ that satisfies $|\nu |\ll B_g(X)/\log X$. Then for any $\varepsilon > 0$, $(\log X)^{1-\varepsilon } \ll _{\varepsilon } B_g(X) \ll _{\varepsilon } (\log X)^{1+\varepsilon }$.

Proof

By Cauchy–Schwarz, we have

$$\begin{aligned} B_g(X)^2 = \sum _{p^k \le X} \frac{|g(p^k) |^2}{p^k}&\le 2\left( \nu (X)^2 \sum _{p^k \le X} \frac{(\log p^k)^2}{p^k} + \sum _{p^k \le X} \frac{|g_{\nu }(p^k)|^2}{p^k}\right) \\&= 2\nu (X)^2 (\log X)^2 + o(B_g(X)^2). \end{aligned}$$

It follows that $|\nu (X)|\ge \frac{1}{4}B_g(X)/\log X$ when X is sufficiently large. The conclusion follows from Lemma 8.6, provided we can show that $\lambda (X) = \nu (X) + o(B_g(X)/\log X)$ for all large X, where $\lambda (X)$ is the function from the conclusion of Proposition 8.1. But this can be verified by the same argument as that which leads to (57), so the claim follows. $\square$

Proof of Corollary 1.7

Suppose $g: \mathbb {N} \rightarrow \mathbb {R}$ is a completely additive function that satisfies

$$\begin{aligned} F_g(\varepsilon ) \rightarrow 0 \text { as } \varepsilon \rightarrow 0^+, \text { and } |\mathcal {B}(X) |\le \frac{X}{(\log X)^{2+\eta }}, \text { for some } \eta > 0. \end{aligned}$$

Suppose first that $B_g(X) \rightarrow \infty$, so that $g \in \mathcal {A}_s$. By Theorem 1.8 there is a parameter $\lambda _0(X)$ with $|\lambda _0(X)|\ll B_g(X)/\log X$, such that $B_{g_{\lambda _0}}(X) = o(B_g(X))$, as $X \rightarrow \infty$. By Lemma 8.7, we deduce that $B_g(X) \ll _{\varepsilon } (\log X)^{1+\varepsilon }$. Now, applying (51), we obtain

$$\begin{aligned} \frac{1}{X}\sum _{n \le X} |g(n)-g(n-1) |&\ll B_g(X) \left( \left( \frac{|\mathcal {B}(X) |}{X}\right) ^{\frac{1}{2}} + \frac{\log X}{\sqrt{X}}\right) \\&\ll _{\eta } (\log X)^{1+\frac{\eta }{3}} \cdot (\log X)^{-\frac{1}{2}(2+\eta )} \ll (\log X)^{-\frac{\eta }{6}}. \end{aligned}$$

By Theorem 3.7, we deduce that there is a constant $c\in \mathbb {R}$ such that $g(n) = c\log n$ for all n, as required.

If, instead, $B_g(X) \ll 1$ then we again deduce (even if $g \notin \mathcal {A}_s$) from (51) that

$$\begin{aligned} \frac{1}{X}\sum _{n \le X} |g(n)-g(n-1) |= o(B_g(X)) = o(1), \end{aligned}$$

and so the claim follows (necessarily with $c = 0$) by Theorem 3.7. $\square$

8.3 Proof of Theorem 1.9

To prove Theorem 1.9 we will appeal to the following result due to Elliott, which will be useful for us in light of our Proposition 8.1.

Theorem

[26, Thm. 6] Let $0< a < b \le 1$. Let $g: \mathbb {N} \rightarrow \mathbb {C}$ be an additive function, and for $y \ge 10$ define

$$\begin{aligned} \theta (y) := \sum _{y^{a} < p^k \le y^{b}} \frac{1}{p^k} |g(p^k)-A_g(y) + A_g(y/p^k)|. \end{aligned}$$

Then for all $\varepsilon , B > 0$ there exist $X_0 = X_0(a,b,\varepsilon ,B)$ and $c > 0$ such that if $X \ge X_0$ then, uniformly over $X^{\varepsilon } < t \le X$,

$$\begin{aligned} A_g(t) = G(X) \log t - \eta (X) + O(Y(X)), \end{aligned}$$

where $G,\eta$ are measurable functions and

$$\begin{aligned} Y(X) := \sup _{X^c < w \le X} \theta (w) + (\log X)^{-B} \sum _{p^k \le X} \frac{|g(p^k) |}{p^k} + \max _{X^c \le p^k \le X} |g(p^k) |p^{-k}. \end{aligned}$$

Corollary 8.8

Let $\delta \in (0,1/2)$. Suppose $g: \mathbb {N} \rightarrow \mathbb {R}$ is an additive function such that $|\mathcal {B}(X) |= o(X)$. Then, uniformly over all $X^{\delta } \le t \le X$ we have

$$\begin{aligned} A_g(t) = \lambda (X)\log t - \eta (X) + o(B_g(X)), \end{aligned}$$

where $\lambda (X)$ and $\eta (X)$ are measurable functions such that for each fixed $0 < u \le 1$,

$$\begin{aligned} \lambda (X^u) = \lambda (X) + o(\tfrac{B_g(X)}{\log X}), \quad \quad \eta (X^u) = \eta (X) + o(B_g(X)). \end{aligned}$$

Proof

By combining Lemmas 8.3 and 8.5 , we have

$$\begin{aligned} \sum _{X^{\delta } \le p^k \le X} \frac{|g(p^k)-A_g(X) + A_g(X/p^k)|}{p^k} = o(B_g(X)), \end{aligned}$$

for any fixed $\delta > 0$. Applying Elliott’s theorem with $a = \varepsilon = \delta$, $b = 1$, $B = 1$, we have

$$\begin{aligned} Y(X) = o(B_g(X)) + O\left( \frac{\sqrt{\log \log X}}{\log X} B_g(X) + B_g(X)X^{-\delta /2}\right) = o(B_g(X)), \end{aligned}$$

using Lemma 3.4 to treat the second error term, and the bound $|g(p^k) |p^{-k/2} \le B_g(X)$ for all $p^k \le X$ in the third. We thus deduce the existence of G(X) such that

$$\begin{aligned} A_g(t) = G(X) \log t - \eta (X) + o(B_g(X)). \end{aligned}$$

(59)

For $X^{\delta } < t_1 \le t_2 \le X$,

$$\begin{aligned} A_g(t_2)-A_g(t_1) = G(X) \log (t_2/t_1) + o(B_g(X)), \end{aligned}$$

so we have removed the term $\eta (X)$. Now, by Proposition 8.1 we also know that in the same range,

$$\begin{aligned} A_g(t_2)-A_g(t_1) = \lambda (X)\log (t_2/t_1) + o(B_g(X)). \end{aligned}$$

Applying this with $t_1 = X^{1/2}$, $t_2 = X$, we deduce readily that

$$\begin{aligned} G(X) = \lambda (X) + o\left( \frac{B_g(X)}{\log X}\right) , \end{aligned}$$

and hence, from (59), that for all $X^{\delta } < t \le X$,

$$\begin{aligned} A_g(t) = \lambda (X) \log t - \eta (X) + o(B_g(X)). \end{aligned}$$

The slow variation of $\lambda (X)$ is a consequence of Proposition 8.1(iii). To obtain the corresponding property for $\eta$ we evaluate $A_g(X^u)$ in (59), once as written and once with X replaced by $X^u$, obtaining

$$\begin{aligned} A_g(X^u) = u\lambda (X^u) \log X -\eta (X^u) + o(B_g(X^u)) = u\lambda (X) \log X - \eta (X) + o(B_g(X)), \end{aligned}$$

from which it also follows, using the slow variation of $\lambda$, that

$$\begin{aligned} \eta (X^u) = \eta (X) + u(\lambda (X^u) - \lambda (X)) \log X + o(B_g(X)) = \eta (X) + o(B_g(X)) \end{aligned}$$

for each fixed $\delta \le u \le 1$, as required. $\square$

Proof of Theorem 1.9

By Lemma 8.5 (with $\alpha = 1$),

$$\begin{aligned} \frac{1}{X}\sum _{n \le X} |g(n) - A_g(X) |= o(B_g(X)) \end{aligned}$$

so that for all but o(X) integers $n \le X$ we have

$$\begin{aligned} g(n) = A_g(X)+ o(B_g(X)). \end{aligned}$$

(60)

By Corollary 8.8 and Proposition 8.1(i), we deduce that

$$\begin{aligned} g(n) = \lambda (X) \log X - \eta (X) + o(B_g(X)) = \lambda (X) \log n - \eta (X) + o(B_g(X)) \end{aligned}$$

for all but o(X) integers $X/\log X < n \le X$, and thus for all but o(X) integers $n \le X$, proving the claim of Theorem 1.9. $\square$