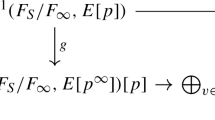Abstract
Let \(E_{/\mathbb {Q}}\!\) be an elliptic curve, \(p>3\) a good ordinary prime for E, and \(K_\infty \) a p-adic Lie extension of a number field k. Under some standard hypotheses, we study the asymptotic growth in both the Mordell–Weil rank and Shafarevich–Tate group for E over a tower of extensions \(K_n/k\) inside \(K_\infty \); we obtain lower bounds on the former, and upper bounds on the latter’s size.

Similar content being viewed by others
References
Darmon, H.: Tian, Ye: Heegner points over towers of Kummer extensions. Can. J. Math. 62(5), 1060–1081 (2010)
Dokchitser, T.: Dokchitser, Vladimir: Regulator constants and the parity conjecture. Invent. Math. 178(1), 23–71 (2009)
Greenberg, R.: Iwasawa Theory, Projective Modules, and Modular Representations, vol. 211, no. 992. Memoirs of the American Mathematical Society (2011)
Guo, L.: General Selmer groups and critical values of Hecke \(L\)-functions. Math. Ann. 297(2), 221–233 (1993)
Greenberg, R.: Galois theory for the Selmer group of an abelian variety. Compos. Math. 136(3), 255–297 (2003)
Cuoco, A.A., Monsky, P.: Class numbers in \({\mathbf{Z}}^{d}_{p}\)-extensions. Math. Ann. 255(2), 235–258 (1981)
Perbet, G.: Sur les invariants d’Iwasawa dans les extensions de Lie \(p\)-adiques. Algebr. Number Theory 5(6), 819–848 (2011)
Gonzalez-Sanchez, J., Klopsch, B.: Analytic pro-p groups of small dimensions. J. Group Theory 12(5), 711–734 (2009)
Delbourgo, D., Lei, A.: Transition formulae for ranks of abelian varieties. Rocky Mt. J. Math. 45(6), 1807–1838 (2015)
Coates, J., Fukaya, T., Kato, K., Sujatha, R.: Root numbers, Selmer groups, and non-commutative Iwasawa theory. J. Algebr. Geom. 19(1), 19–97 (2010)
Dokchitser, V.: Root numbers of non-abelian twists of elliptic curves. Proc. Lond. Math. Soc. (3) 91, 300–324 (2005). With an appendix by Tom Fisher
Delbourgo, D.: Peters, Lloyd: Higher order congruences amongst Hasse-Weil \(L\)-values. J. Aust. Math. Soc. 98(1), 1–38 (2015)
Zhang, S.W.: Gross-Zagier Formula for \({{\rm GL}}(2)\). II, Heegner Points and Rankin \(L\)-Series. Mathematical Sciences Research Institute Publications. Cambridge University Press, Cambridge (2004)
Skinner, C., Urban, E.: The Iwasawa main conjectures for \({{\rm GL}}_2\). Invent. Math. 195(1), 1–277 (2014)
Zerbes, S.L.: Selmer groups over \(p\)-adic Lie extensions. J. Lond. Math. Soc. 70(3), 586–608 (2004)
Harris, M.: \(p\)-Adic representations arising from descent on abelian varieties. Compos. Math. 39(2), 177–245 (1979)
Coates, J.: Fragments of the \({{\rm GL}}_2\) Iwasawa theory of elliptic curves without complex multiplication. In: Arithmetic Theory of Elliptic Curves (Cetraro, 1997). Lecture Notes in Mathematics, vol. 1716, pp. 1–50. Springer, Berlin (1999)
Serre, J.P.: Cohomologie Galoisienne, Cours au Collège de France, vol. 1962. Springer, Berlin (1962/1963)
Hachimori, Y., Venjakob, O.: Completely faithful Selmer groups over Kummer extensions. Kazuya Kato’s fiftieth birthday. Doc. Math., Extra vol., 443–478 (2003) (electronic)
Burns, D., Venjakob, O.: On descent theory and main conjectures in non-commutative Iwasawa theory. J. Inst. Math. Jussieu 10(1), 59–118 (2011)
Howson, S.: Euler characteristics as invariants of Iwasawa modules. Proc. Lond. Math. Soc. 3(85), 634–658 (2002)
Venjakob, O.: On the structure theory of the Iwasawa algebra of a \(p\)-adic Lie group. J. Eur. Math. Soc. (JEMS) 4(3), 271–311 (2002)
Ritter, J., Weiss, A.: Toward equivariant Iwasawa theory. III. Math. Ann. 336(1), 27–49 (2006)
Bourbaki, N.: Éléments de mathématique. Fasc. XXXI. Algèbre commutative. Chapitre 7: Diviseurs, Actualités Scientifiques et Industrielles, vol. 1314. Hermann, Paris (1965)
Kobayashi, S.: Iwasawa theory for elliptic curves at supersingular primes. Invent. Math. 152(1), 1–36 (2003)
Coates, J.: Elliptic Curves—The Crossroads of Theory and Computation. Lecture Notes in Computer Science, vol. 2369, pp. 9–19 (2002)
Matsuno, K.: Finite \(\Lambda \)-submodules of Selmer groups of abelian varieties over cyclotomic \({\mathbb{Z}}_p\)-extensions. J. Number Theory 99(2), 415–443 (2003)
Coates, J., Schneider, P., Sujatha, R.: Links between cyclotomic and \({\text{ GL }}_2\) Iwasawa theory. Kazuya Kato’s fiftieth birthday. Doc. Math. Extra vol., 187–215 (2003) (electronic)
Delbourgo, D., Lei, A.: Non-commutative Iwasawa theory for elliptic curves with multiplicative reduction. Math. Proc. Cambridge Philos. Soc. 160(1), 11–38 (2016)
Venjakob, O.: A non-commutative Weierstrass preparation theorem and applications to Iwasawa theory. J. Reine Angew. Math. 559, 153–191 (2003). With an appendix by Denis Vogel
Acknowledgments
The majority of this work was carried out during the first named author’s visit to Université Laval in May–June 2015, and he would like to thank them for their generous hospitality, and in particular Hugo Chapdelaine. The authors would also like to thank Wei Lu for his comments on an earlier version of this article.
Author information
Authors and Affiliations
Corresponding author
Additional information
The second named author’s research was supported by FRQNT’s Établissement de nouveaux chercheurs universitaires program 188809.
Appendix: Skew power series rings and characteristic ideals
Appendix: Skew power series rings and characteristic ideals
Let G be a d-dimensional torsion-free p-adic Lie group, given by \(H\rtimes \Gamma \), where \(\Gamma \cong \mathbb Z_p\) and H is a uniform pro-p group. Let \(\Lambda (\star )\) be the Iwasawa algebra \(\mathbb Z_p[[\star ]]\) for \(\star \in \{G, H,\Gamma \}\). Suppose that \(\Gamma =\overline{\langle \gamma \rangle }\) and \(H=\overline{\langle \sigma _1,\ldots ,\sigma _{d-1}\rangle }\). An element of \(\Lambda (G)\) if a (possibly infinite) sum of \((\sigma _1-1)^{n_1}\cdots (\sigma _{d-1}-1)^{n_{d-1}}\cdot (\gamma -1)^n\) for some non-negative integers \(n_1,\ldots ,n_{d-1},n\). We may identify \(\Lambda (G)\) with the skew power series ring \(R\llbracket X;\sigma ,\delta \rrbracket \), where \(R=\Lambda (H)\), X is an indeterminant, which can be identified with \(\gamma -1\), \(\sigma :R\rightarrow R\) is a ring homomorphism and \(\delta :R\rightarrow R\) is a \(\sigma \)-derivation. If \(r\in R\),
More generally, for \(n\ge 1\), we have
where \((X^nr)_i\) are elements of R.
For \(f=\sum _{i=0}^\infty r_iX^i\), we say that f has finite reduced order if \(r_i\in \Lambda (H)^\times \) for some \(i\ge 0\). Recall the Weierstrass Preparation Theorem of Venjakob in [30] states that such f admits the factorization
where \(u\in \Lambda (G)^\times \) and \(\tilde{f}\) is a polynomial over \(\Lambda (H)\) in X.
Lemma 5.1
Let \(M=\Lambda (G)/I\) be a \(\Lambda (G)\)-module that is finitely generated over \(\Lambda (H)\). Then, there exists \(f\in I\) that has finite reduced order.
Proof
Let \(\mathfrak {m}\) be the maximal ideal of \(\Lambda (H)\). For each element \(f\in I\), we may write \(f=\sum _{i=0}^\infty r_iX^i\). Suppose that f does not have finite reduced order. Then, \(r_i\in \mathfrak {m}\) for all i.
Note that we have the following isomorphism of \(\Lambda (H)\)-modules:
The image of \(\Lambda (G)f\) at the i-th component is
as given by (5.1). Since we assume that \(r_\ell \in \mathfrak {m}\) for all \(\ell \), the \(\Lambda (H)\)-module above is contained in \(\mathfrak {m}\) by [30, Lemma 2.1]. If this is the case for all \(f\in I\), the image of M under \(s_H\) in \(\Lambda (H)^\mathbb {N}\) is non-trivial at all components, which contradicts the fact that M is finitely generated over \(\Lambda (H)\). Therefore, we conclude that there must exist \(f\in I\) with finite reduced order. \(\square \)
Lemma 5.2
Let \(f=\sum _{i=0}^nr_iX^i\) be a polynomial in \(\Lambda (G)\). There exists \(r_0',\ldots ,r_n'\in \Lambda (H)\) such that
Proof
Note that for all \(m\ge 0\) and \(h\in H\), there exists \(h'\in H\) such that \(\gamma ^mh=h'\gamma ^m\) by the fact that H is normal in G. The result follows by identifying X with \(\gamma -1\). \(\square \)
For all \(n\ge 1\), we write \(H_n=H^{p^n}\), which is a subgroup of H and \(H/H^{p^n}\) is a p-group of order \(p^{(d-1)n}\) by the uniformality of H.
Proposition 5.3
Let \(M=\Lambda (G)/I\) be a \(\Lambda (G)\)-module that is finitely generated over \(\Lambda (H)\) such that I contains a polynomial f in X of degree \(\tau \). Then, \(M_{H_n}\) is a finitely generated \(\Lambda (\Gamma )\)-torsion module. Furthermore, its characteristic power series factorizes into polynomial of degree \(\le \tau \).
Proof
Note that \(\Lambda (G)_{H_n}\) can be identified with \(\Lambda (H/H_n\rtimes \Gamma )=\mathbb Z_p[H/H_n]\llbracket X;\sigma ,\delta \rrbracket \). We fix a set of coset representatives of \(H/H_n\), say \(\{h_i:i=1,\ldots , p^{(d-1)n}\}\). Each element of \(\Lambda (G)_{H_n}\) can be written as \(\sum _{i}f_ih_i\), where \(f_i\) are some elements of \(\Lambda (\Gamma )\). As \(\Lambda (\Gamma )\)-modules, we have the isomorphism
We know that \(M_{H_n}\) is a quotient of \(\Lambda (G)_{H_n}/I_{H_n}\), so it suffices to prove our result for the latter. Since, in particular, \(s_\Gamma (\Lambda (G)_{H_n})/s_\Gamma (I_{H_n})\) is a quotient of \(\Lambda (\Gamma )^{\oplus p^{dn}}\), it is finitely generated over \(\Lambda (\Gamma )\).
By Lemma 5.2, the image of f under \(s_\Gamma \) is a polynomial of degree \(\tau \) at each component. Therefore, \(s_\Gamma (\Lambda (G)_{H_n})/s_\Gamma (I_{H_n})\) may be decomposed as a direct sum of \(\Lambda (\Gamma )\)-modules where each summand is killed by a polynomial of degree d. \(\square \)
Corollary 5.4
Let \(M=\Lambda (G)/I\) be a \(\Lambda (G)\)-module that is finitely generated over \(\Lambda (H)\). Then, \(M_{H_n}\) is a finitely generated \(\Lambda (\Gamma )\)-torsion module for all \(n\ge 1\). Furthermore, there exists an integer \(\tau \), independent of n, such that the characteristic power series of \(M_{H_n}\) factorizes into polynomial of degree \(\le \tau \).
Proof
By Lemma 5.1, I contains an element of f that is of finite reduced order. Venjakob’s Weierstrass Preparation Theorem tells us that we may replace f by a polynomial in X, say of degree \(\tau \). The result now follows from Proposition 5.3. \(\square \)
Rights and permissions
About this article
Cite this article
Delbourgo, D., Lei, A. Estimating the growth in Mordell–Weil ranks and Shafarevich–Tate groups over Lie extensions. Ramanujan J 43, 29–68 (2017). https://doi.org/10.1007/s11139-016-9785-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11139-016-9785-1