Alternating knots, planar graphs, and $q$-series

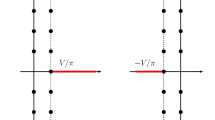
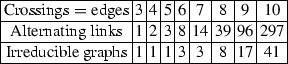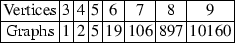Abstract

Recent advances in Quantum Topology assign $q$-series to knots in at least three different ways. The $q$-series are given by generalized Nahm sums (i.e., special $q$-hypergeometric sums) and have unknown modular and asymptotic properties. We give an efficient method to compute those $q$-series that come from planar graphs (i.e., reduced Tait graphs of alternating links) and compute several terms of those series for all graphs with at most 8 edges drawing several conclusions. In addition, we give a graph-theory proof of a theorem of Dasbach-Lin which identifies the coefficient of $q^k$ in those series for $k=0,1,2$ in terms of polynomials on the number of vertices, edges, and triangles of the graph.

Appendix 1: Tables

In this section, we give various tables of graphs, and their corresponding alternating knots (following Rolfsen’s notation [18]) and links (following Thistlethwaite’s notation [5]) and several terms of $\Phi _G(q)$. In view of an expected positive answer to Question 1.6, we will list irreducible graphs, i.e., simple planar 2-connected graphs which are not of the form $G_1 \cdot G_2$ (for the operation $\cdot$ defined in Sect. 1.3).

• The first table gives number of alternating links with at most 10 crossings and the number of irreducible graphs with at most 10 edges

  

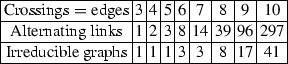  (28)

  To list planar graphs, observe that they are sparse: if $G$ is a planar graph which is not a tree, with $V$ vertices and $E$ edges, then

  $$\begin{aligned} V \le E \le 3V-6 \,. \end{aligned}$$

• The next table gives the number of planar 2-connected irreducible graphs with at most 9 vertices

  

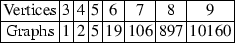  (29)

• Figures 5, 6, 7 and 8 give the list of irreducible graphs with at most 9 edges. These tables were constructed by listing all graphs with $n \le 9$ vertices, selecting those which are planar, and further selecting those that are irreducible. Note that if $G$ is a planar graph with $E \le 9$ edges, $V$ vertices, and $F$ faces, then $E-V=F-2 \ge 0$, and hence $V \le E \le 9$.

• Figures 9 and 10 give the reduced Tait graphs of all alternating knots and links (and their mirrors) with at most 8 crossings. Here, $P_r$ is the planar polygon with $r$ sides, and $-K$ denotes the mirror of $K$. Moreover, the notation $G=G_1\cdot G_2\cdot G_3$ indicates that $\Phi _G(q)=\Phi _{G_1}(q)\Phi _{G_2}(q)\Phi _{G_3}(q)$ by Lemma 1.5.

• Figure 11 gives the alternating knots and links with at most 8 crossings for the irreducible graphs with at most 8 edges.

• Figure 12 gives the first 21 terms of of $\Phi _G(q)$ for all irreducible graphs with at most 8 edges (Fig. 13). Many more terms are available from http://www.math.gatech.edu/~stavros/publications/phi0.graphs.data/

Fig. 5

The irreducible planar graphs $G_0^3,G_0^4$, and $G_0^5$ with 3, 4, and 5 edges

Fig. 6

The irreducible planar graphs with 6 and 7 edges: $G_0^6,G_1^6$, and $G_2^6$ on the top and $G_0^7,G_1^7$, and $G_2^7$ on the bottom

Fig. 7

The irreducible planar graphs with 8 edges: $G_0^8,\dots ,G_3^8$ on the top (from left to right) and $G_4^8,\dots ,G_7^8$ on the bottom

Fig. 8

The irreducible planar graphs with 9 edges: $G_0^9,\dots ,G_5^9$ on the top, $G_6^9,\dots ,G_{11}^9$ on the middle and $G_{12}^{9},\dots ,G_{16}^9$ on the bottom

Fig. 9

The reduced Tait graphs of the alternating knots with at most 8 crossings

Fig. 10

The reduced Tait graphs of the alternating links with at most 8 crossings

Fig. 11

The irreducible planar graphs with at most 8 edges and the corresponding alternating links

Fig. 12

The first 21 terms of $\Phi _G(q)$ for the irreducible planar graphs with at most 8 edges

Fig. 13

Plot of the coefficients of $\Phi _{G^6_2}(q)$ on the top and $h_4(q)^2$ (keeping in mind that $G^6_2$ has two bounded square faces) on the bottom