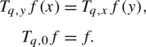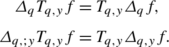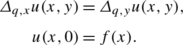The q-cosine Fourier transform and the q-heat equation

Abstract

The aim of this work is to establish in great detail The q-Fourier analysis related to the q-cosine. The wise reader will note that the considered q-cosine coincides with the one given by T.H. Koornwinder and S.F. Swarttouw. Through the q-cosine product formula, we define and analyze the properties of the q-even translation and the q-convolution. Adopting the Titchmarsh approach, we study the q-cosine Fourier transform and its inverse formula.

The second theme of this paper is an application of the q-Fourier analysis developed earlier. We extend the heat representation theory inaugurated by P.C. Rosenbloom and D.V. Widder to the q-analogue. We construct the q-solution source, the q-heat polynomials and solve the q-analytic Cauchy problem.

1 Introduction

During the last years, an intensive work was founded about the so-called q-basic theory. Taking account of the well-known Ramanujan works shown at the beginning of this century by Jackson ([9, 10]), many authors such as Askey, Gasper, Ismail, Rogers, Andrew, Koornwinder, and others (see references) have recently developed this topic.

The present article is devoted to the study of the q-analogue of the Fourier transforms and to showing how it plays a central role in solving the q-heat equation associated to the second q-derivative operator. The method used here differs from those given by T.H. Koornwinder and R.F. Swarttouw, who discovered a q-analogue of Hankel’s Fourier–Bessel via some q-analogue orthogonality relations. We note that Ph. Feinsilver [4] gave a q-Harmonic Analysis for a q-Laplace transform with inversion formula.

Without entering into a dilemma through the analysis presented here, it seems that the point of view of T.H. Koornwinder and R.F. Swarttouw [12] is more suitable for harmonic analysis. We take as definition of the q-cosine the one given by the previous authors with a simple change and we prefer to write it as a series of functions denoted as b _n (x;q ²). This q-cosine appears as an eigenfunction of the operator Δ _q . Owing to a nice paper [12], we give a product formula written with the q-Jackson integral and we study the q-translation and the q-convolution. Next we define the q-analogue of the cosine Fourier transform with the purpose to find the transformation inverse. To this end, we prove the equivalent of the so-called Riemann–Lebesgue Lemma and discover that the Titchmarsh approach holds [15].

A motivation behind this work is to state some result about the q-heat equation associated to Δ _q operator. We attempt to extend the heat representation theory studied in many cases ([5, 7, 14], etc.). We define the q-heat polynomials and find that they are linked to the q-Hermite polynomials [13] and constitute with the q-associated functions a biorthogonal system. We conclude by solving the q-analytic Cauchy problem related to the q-heat equation.

2 Notations and preliminaries

We begin by recalling some q-elements of quantum analysis adapting the notation used in the book of Gasper and Rahman [6]. Let a and q be real numbers such that 0<q<1, the q-shift factorial is defined by

$$ (a;q)_{0}=1,\qquad (a;q)_{n}={\prod_{k=0}^{n-1}} \bigl(1-aq^{k} \bigr),\quad n=1,2,\ldots ,\infty. $$

(1)

A basic hypergeometric series is

$${}_{r}\varphi_{s}(a_{1},\ldots ,a_{r};b_{1},\ldots ,b_{s};q,z)=\sum _{k=0}^{\infty}\frac{(a_{1},\ldots ,a_{r};q)_{k}}{(b_{1},\ldots ,b_{s},q;q)_{k}} \bigl[ (-1)^{k}q^{\binom{k}{2}} \bigr]^{1+s-r}z^{k}. $$

A function f is q-regular at zero if lim _n→∞ f(xq ⁿ)=f(0) exists and is independent of x.

The q-derivative D _q f of a function f is defined by

$$ D_{q}f(x)=\frac{f(x)-f(qx)}{(1-q)x},\quad x\neq0. $$

(2)

The q-derivative at zero is defined by

$$D_{q}f ( 0 ) =\lim_{n\rightarrow\infty}\frac{f ( xq^{n} ) -f ( 0 ) }{xq^{n}}, $$

if it exists and does not depend on x.

We introduce the set

$$\mathbb{R}_{q}= \bigl\{q^{k};k\in\mathbb{Z} \bigr\}.$$

The q-integral of Jackson is defined by

The q-integration by parts is given for suitable functions f and g by

$$ {\int_{0}^{\infty}} f(x)D_{q}g(x)\,d_{q}x= \bigl[ f(x)g(x) \bigr]_{0}^{\infty}-{\int _{0}^{\infty}} f(x)D_{q}g \bigl(q^{-1}x \bigr)\,d_{q}x. $$

(3)

The q-analogue of the Gamma function is defined as

$$ \varGamma_{q}(x)=\frac{(q;q)_{\infty}}{(q^{x};q)_{\infty}}(1-q)^{1-x}, $$

(4)

which tends to Γ(x) when q tends to 1⁻.

3 q-Trigonometric functions

We define the q-cosine as

$$ \cos \bigl(x;q^{2} \bigr)={_{1}\phi_{1}} \bigl(0;q;q^{2},(1-q)^{2}x^{2} \bigr)=\sum _{n=0}^{\infty }(-1)^{n}b_{n} \bigl(x;q^{2} \bigr), $$

(5)

where we have put

$$ b_{n} \bigl(x;q^{2} \bigr)=b_{n} \bigl(1;q^{2} \bigr)x^{2n}=q^{n(n-1)} \frac{(1-q)^{2n}}{(q;q)_{2n}}x^{2n}. $$

(6)

In the same way, the q-sine is given by

$$\sin \bigl(x;q^{2} \bigr)= ( 1-q ) x{_{1} \phi_{1}} \bigl(0;q^{3};q^{2},(1-q)^{2}x^{2} \bigr)=\sum_{n=0}^{\infty}(-1)^{n}c_{n} \bigl(x;q^{2} \bigr), $$

with

$$c_{n} \bigl(x;q^{2} \bigr)=c_{n} \bigl(1;q^{2} \bigr)x^{2n+1}=\frac{q^{n(n-1)}(1-q)^{2n+1}}{(q;q)_{2n+1}}x^{2n+1}. $$

These q-trigonometric functions differ and should not be confused with the functions cos _q and sin _q considered in [6, p. 23]; but coincide with the one given in [12] and [15] with a minor change of variable. Furthermore, we have

Proposition 3.1

The following statements hold:

• 1.
  $$b_{n} \bigl(0,q^{2} \bigr)=\delta_{n,0},\qquad \varDelta_{q}b_{n} \bigl(x;q^{2} \bigr)=b_{n-1}\bigl(x;q^{2} \bigr),\quad n\geq1; $$
• 2.
  $$\bigl \vert b_{n} \bigl(x;q^{2} \bigr) \bigr \vert \leq \frac{x^{2n}}{ ( 2n ) !}, $$

where

$$ \varDelta_{q}u ( x ) = \bigl( D_{q}^{2}u \bigr) \bigl( q^{-1}x \bigr) . $$

(7)

Proof

We only prove Part 2 since Part 1 is deduced from the definition of Δ _q .

The coefficients b _n (1;q ²), defined by (6), can be written as

where we have put q=e ^−t, t>0.

Since the functions

$$f(t)=\frac{e^{-jt}-e^{-(j+1)t}}{1-e^{-(j+1)t}}\quad \mbox{and}\quad g(t)=\frac {e^{-jt}-e^{-(j+1)t}}{1-e^{-(2j+2)t}}, $$

decrease on ]0,∞[, we obtain

$$b_{n} \bigl(1;q^{2} \bigr)\leq{\frac{1}{{(2n)!}}}. $$

 □

As a consequence of the previous proposition, we can show that for λ∈ℂ the function

$$\cos \bigl(\lambda x;q^{2} \bigr)=\sum_{0}^{\infty}(-1)^{n}b_{n} \bigl(x;q^{2} \bigr){\lambda}^{2n},$$

is the unique analytic solution of the q-differential equation

$$ \varDelta_{q}u(x)=-{\lambda}^{2}u(x), $$

(8)

with

$$ u(0,q)=1,\qquad ( D_{q}u ) ( 0 ) =0. $$

(9)

Proposition 3.2

For x∈ℝ _q and $\frac{\operatorname{Log}(1-q)}{\operatorname{Log}(q)}\in\mathbb{Z}$, we have

• 1.
  $$\bigl \vert \cos \bigl(x,q^{2} \bigr) \bigr \vert \leq \frac{1}{(q;q^{2})_{\infty}^{2}}; $$
• 2.
  $$\lim_{x\rightarrow\infty}\cos \bigl(x,q^{2} \bigr)=0; $$
• 3.
  $$\bigl \vert \sin \bigl(x,q^{2} \bigr) \bigr \vert \leq \frac{1}{(q;q^{2})_{\infty}^{2}}; $$
• 4.
  $$\lim _{x\rightarrow\infty}\sin \bigl(x,q^{2} \bigr)=0. $$

Proof

To prove Parts 1 and 2, we use the properties of ₁ ϕ ₁ given in [12] and their connection to the q-cosine. We obtain

$$ \bigl|\cos \bigl(q^{1+n};q^{2} \bigr)\bigr|\leq{\frac{1}{{(q;q^{2})_{\infty}^{2}}}}\left\{\begin{array}{l@{\quad }l} 1& \mbox{if}\ n\geq0,\\ q^{n^{2}} & \mbox{if}\ n\leq0. \end{array}\right.$$

(10)

hence Parts 1 and 2 follow. A similar argument shows Parts 3 and 4. □

Now we try to find a product formula for the q-cosine functions. We begin by proving the following result.

Proposition 3.3

For reals x and y, y≠0, we have

(11)

Note that this formula can be expressed in terms of ₁ φ ₁ as follows

(12)

Proof

To show (11) and (12), we begin by expanding the q-cosines in series absolutely and uniformly convergent on every compact of ℝ. From the product rule of series and the fact that

$$\frac{1}{(q;q)_{2n-2k}}=\frac{(q^{2n-2k+1},q)_{\infty}}{(q;q)_{\infty}}=0,\quad k>n, $$

we obtain for y≠0

$$\cos \bigl(x;q^{2} \bigr)\cos \bigl(y;q^{2} \bigr)=\sum _{k=0}^{\infty}{\frac{q^{2k^{2}}}{{(q;q)_{2k}}}} \biggl({ \frac{x}{y}} \biggr)^{2k}\sum_{n=0}^{\infty}(-1)^{n} \frac{q^{n^{2}-n}}{(q;q)_{2n-2k}}q^{-2nk}y^{2n}. $$

On the other hand, we have

$$\frac{1}{(q;q)_{2n-2k}}=\frac{q^{-k(2k-1)+2nk}}{(q;q)_{2n}}{ \sum _{s=-k}^{s=k}} ( -1 )^{k-s}\frac{q^{\binom{k-s}{2}}}{ ( q;q )_{k-s} ( q;q )_{k+s}}q^{2ns}.$$

We deduce (11) after the interchange of summation order. To prove (12), we write

$$\cos \bigl(x;q^{2} \bigr)\cos \bigl(y;q^{2} \bigr)=I+J, $$

with

$$I=\sum_{s=0}^{\infty}\cos \bigl(q^{s}y;q^{2} \bigr)\sum_{k\geq s}q^{k} \biggl( \frac{x}{y}\biggr)^{2k}\frac{(-1)^{k-s}q^{\frac{(k-s)(k-s-1)}{2}}}{(q;q)_{k+s}(q;q)_{k-s}},$$

$$J=\sum_{s=-\infty}^{-1}\cos \bigl(q^{s}y;q^{2} \bigr)\sum_{k\geq-s}q^{k} \biggl( \frac{x}{y}\biggr)^{2k}\frac{(-1)^{k-s}q^{\frac{(k-s)(k-s-1)}{2}}}{(q;q)_{k-s}(q;q)_{k+s}}.$$

In I, we make the change k−s into k and use the equality

$$(q;q)_{k+2s}=(q;q)_{2s} \bigl(q^{1+2s};q \bigr)_{k}, $$

to obtain

$$I=\sum_{s=0}^{\infty}q^{s} \biggl({ \frac{x}{y}} \biggr)^{2s}\frac{(q^{2s+1};q)_{\infty}}{(q;q)_{\infty}}{_{1} \phi_{1}} \bigl(0;q^{1+2s};q,q \bigl(q^{2}/y^{2} \bigr) \bigr)\cos \bigl(q^{s}y;q^{2} \bigr). $$

Now we make the change k+s into k in J and use the equalities

$$(q;q)_{k-2s}=(q;q)_{-2s} \bigl(q^{1-2s};q \bigr)_{k},\quad -s\geq1, $$

$${\frac{(k-2s)(k-2s-1)}{2}}={\frac{(k-2)(k-3)}{2}}-2sk+2s^{2}-1, $$

and

This identity is easily deduced from [11]. Then we obtain

$$J=\sum_{s=-\infty}^{-1}q^{s} \bigl(x^{2}/y^{2} \bigr)^{2s}\frac{(q^{1+2s};q)_{\infty}}{(q;q)_{\infty}}{_{1} \phi_{1}} \bigl(0;q^{1+2s};q,qx^{2}/y^{2} \bigr)\cos \bigl(q^{s}y;q^{2} \bigr). $$

We add these sums to find that (12) holds. □

Remark 3.4

(1) If we replace y by q ^y, x by q ^x, and assume the proposition the hypothesis, we obtain from (12) that the following integral representation holds

(2) The product formula (11) leads to

$$ \cos \bigl(x;q^{2} \bigr)\cos \bigl(y;q^{2} \bigr)=\sum _{n=0}^{\infty}b_{n} \bigl(x;q^{2} \bigr) \varDelta_{q}^{n}\cos \bigl( y;q^{2} \bigr) . $$

(13)

4 q-Translation and q-convolution

We define, for x and y in ℝ _q , the measure

$$ d_{q}\mu_{(x,y)}=\sum_{s=-\infty}^{\infty} \mathcal{{D}} \bigl(x,y;q^{s} \bigr)q^{s}\delta_{yq^{s}}, $$

(14)

where δ _u denotes the unit mass supported at u, and

$$ \mathcal{{D}} \bigl(x,y;q^{s} \bigr)= \biggl({\frac{x}{y}} \biggr)^{2s}\frac{(q({\frac{x}{y}})^{2};q)_{\infty}}{(q;q)_{\infty}}{_{1}\phi_{1}} \biggl(0;q \biggl({\frac{x}{y}}\biggr)^{2};q,q^{1+2s} \biggr). $$

(15)

Proposition 4.1

(1) For x and y in ℝ _q , we have

$$d_{q}\mu_{ ( x,y ) }=d_{q}\mu_{ ( y,x ) }. $$

(2) d _q μ _(x,y) is of bounded variation.

(3)

$${\int} d_{q} \mu_{ ( x,y ) }(t)=1. $$

Proof

For n,m∈ℤ, the relation (2.3) from [12] leads to

$$\mathcal{{D}} \bigl(q^{n},q^{m};q^{s} \bigr)= \mathcal{{D}} \bigl(q^{m},q^{n};q^{s+m-n} \bigr). $$

We obtain Part 1 after the change s−n+m by s.

To prove Part 2, we suppose $|{\frac{x}{y}}|\leq1$; from the formulas (2.4) in [12] we have

$$ |d_{q}\mu_{(x,y)}|_{var}\leq \biggl( \frac{|y|^{2}+q|x|^{2}}{|y|^{2}-q|x|^{2}}\biggr)\frac{(q|{\frac{x}{y}}|^{2};-q,q)_{\infty}}{(q,q)_{\infty}}. $$

(16)

Finally, from (2.8) in [12], we can show that Part 3 is true. □

We introduce the q-translation which generalizes the even translation given by ${\frac{1}{2}}(\delta_{x+y}+\delta_{x-y})$.

Let f be a function with support in ℝ _q , the q-translation is defined for x and y in ℝ _q by

$$ T_{x,q}f(y)=\int_{0}^{\infty}f(t)\,d_{q} \mu_{(x,y)}(t). $$

(17)

From the previous proposition and the q-product formula (12), we have

Proposition 4.2

Let f be a function with compact support in ℝ _q . We have

• (i)
  $$T_{q,y}\cos \bigl( x;q^{2} \bigr) =\cos \bigl( x;q^{2} \bigr) \cos \bigl( y;q^{2} \bigr) . $$
• (ii)
  
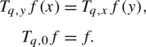
• (iii)
  

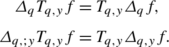
• (iv) The function u(x,y)=T _q,y f(x) is a solution of the problem

  

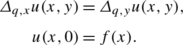
From the relation

$$\varDelta_{q}^{n}(f) ( x ) =\frac{q^{(2-n)n} ( q;q )_{2n}}{ ( 1-q )^{2n}}{\sum_{k=-n}^{n}} ( -1 )^{n-k} \frac{q^{\binom{n-k}{2}}}{ ( q;q )_{n-k} ( q;q )_{n+k}}f \bigl( q^{k}x \bigr) , $$

we can write the q-translation of a function f as

$$ T_{q,y}f ( x ) ={\sum _{n=0}^{\infty}} b_{n} \bigl(y,q^{2} \bigr)\varDelta_{q,x}^{n}f ( x ) , $$

(18)

and have in the limit when q tends to 1⁻ the classical even translation cited before.

Now we denote by $L_{q}^{1}(\mathbb{R}_{q})$ the space of functions f defined on ℝ _q such that

$$\Vert f\Vert _{1,q}=\int_{-\infty}^{\infty}\bigl|f(t)\bigr|\,d_{q}t< \infty. $$

Then we are able to define the q-convolution by

$$ f\star_{q}g(x)=\frac{(1+q^{-1})^{1/2}}{\varGamma_{q^{2}}(1/2)}\int_{0}^{\infty }T_{x,q}f(y)g(y)\,d_{q}y, $$

(19)

where f and g are two functions in $L_{q}^{1}(\mathbb{R}_{q})$. We can show that this space is an algebra.

5 q-Analogue of Fourier-cosine

In this section, we suppose $\frac{\operatorname{Log}(1-q)}{\operatorname{Log}(q)}\in\mathbb{Z}$. The q-analogue of Fourier transform is defined for λ∈ℝ _q by

$$ \mathcal{F}(f) (\lambda)={\frac{(1+q^{-1})^{1/2}}{\varGamma_{q^{2}}(1/2)}}\int_{0}^{\infty}f(t) \cos \bigl(\lambda t;q^{2} \bigr)\,d_{q}t, $$

(20)

where f is a function in $L_{q}^{1}(\mathbb{R}_{q})$.

This definition is the same (after a minor change) as that given by T.H. Koornwinder and R.F. Swarttouw (see [12]).

Proposition 5.1

For $f, g\in L_{q}^{1}(\mathbb{R}_{q})$, the following properties hold:

• (1)
  $$ \bigl \vert \mathcal{F}_{q} ( f ) ( \lambda ) \bigr \vert \leq \frac{1}{ [ q ( 1-q ) ]^{\frac{1}{2} } ( q;q )_{\infty}} \Vert f\Vert_{1,q},\quad \lambda\in\mathbb{R}_{q}; $$

  (21)
• (2)
  $$ \mathcal{F}_{q} ( \mathcal{T}_{q,x}f ) ( \lambda ) =\cos \bigl(\lambda x;q^{2} \bigr)\mathcal{F}_{q} ( f ) ( \lambda ) ,\quad \lambda\in\mathbb{R}_{q};$$

  (22)
• (3)
  $$\mathcal{F}_{q}(f\star_{q}g)=\mathcal{F}_{q}(f) \mathcal{F}_{q}(g). $$

Proof

Part 1. The inequality (21) follows from Proposition 3.2 and the identity

$$\bigl(q;q^{2} \bigr)_{\infty} \bigl(q^{2};q^{2} \bigr)_{\infty}=(q;q)_{\infty}. $$

Part 2 is a direct consequence of the q-product formula (12).

Part 3 is obtained after the exchange of the integration order and taking into account the invariability of the q-integral by the q-translation. □

Now we focus our attention on the inversion of the linear map $\mathcal{F}_{q}$. We proceed by looking at the q-analogue of the Riemman–Lebesgue Lemma, the localization theorem, and we show that the Titchmarsh approach holds in the q-theory.

Proposition 5.2

Let f be a function in $L_{q}^{1} ( \mathbb{R}_{q} )$, then

$$\lim_{\lambda\longrightarrow\infty}\mathcal{F}_{q} ( f ) (\lambda)=0,\quad \lambda\in\mathbb{R}_{q}. $$

Proof

To prove this, first we have from Proposition 3.2

$$\bigl \vert f(x)\cos \bigl(\lambda x;q^{2} \bigr) \bigr \vert \leq \frac{1}{(q;q^{2})_{\infty}^{2}} \bigl \vert f(x) \bigr \vert \in L_{q}^{1} ( \mathbb{R}_{q} ) ,\quad x,\lambda\in\mathbb{R}_{q}. $$

And for λ∈ℝ _q we have

$$\lim _{\lambda\rightarrow\infty}f(x)\cos \bigl(\lambda x;q^{2} \bigr)=0,\quad \lambda \in\mathbb{R}_{q}, $$

so the result is true. □

Proposition 5.3

We have the identity

$$\int_{0}^{\infty}\frac{\sin ( x;q^{2} ) }{x}\,d_{q}x= \frac {\varGamma_{q^{2}}^{2} ( \frac{1}{2} ) }{1+q^{-1}}. $$

Proof

This is a consequence of (2.8) in [12]. □

Proposition 5.4

Let f:(0,∞)→ℂ satisfy the conditions:

• (1) $f\in L_{q}^{1} ( \mathbb{R}_{q} )$,

• (2) For a∈ℝ _q , there exists C(a)>0 such that

  $$\bigl \vert f \bigl( aq^{k} \bigr) -f ( 0 ) \bigr \vert \leq C ( a ) q^{k},\quad k=0,1,2,\ldots . $$

Then

$$\lim _{\lambda\rightarrow+\infty}\int_{0}^{\infty}f ( x ) \frac{\sin ( \lambda x;q^{2} ) }{x}\,d_{q}x=\frac{\varGamma_{q^{2}}^{2} ( \frac{1}{2} ) }{1+q^{-1}}f ( 0 ) . $$

Proof

Indeed, the first hypothesis shows that for an arbitrary ε>0 we have for large q ^−N,N=0,1,… , that

$$\int_{q^{-N}}^{\infty} \biggl \vert \frac{f ( x ) }{x} \biggr \vert \,d_{q}x\leq\frac{\varepsilon}{2} \bigl(q;q^{2} \bigr)_{\infty}^{2}$$

and

The second hypothesis and Proposition 3.2 show that

$$\biggl \vert \frac{f ( q^{k-N} ) -f ( 0 ) }{q^{k-N}}\sin \bigl( \lambda q^{k-N};q^{2} \bigr) \biggr \vert \leq\frac{C ( N ) }{q^{-N} ( q,q^{2} )_{\infty}^{2}}. $$

Since from Proposition 3.2 we have that sin(λx;q ²) tends to zero as λ tends to ∞, the proposition is then a direct consequence. □

Theorem 5.5

(The q-cosine Fourier integral theorem)

If $f\in L_{q}^{1} ( \mathbb{R}_{q} )$ is such that for a∈ℝ _q there exist positive constants C(a) such that

$$ \bigl|T_{x,q}f \bigl(aq^{k} \bigr)-f \bigl(q^{k} \bigr)\bigr| \leq C(a)q^{k},\quad k=0,1,\ldots, $$

(23)

then

(24)

6 q-Heat equation and q-heat polynomials

In this section, the two q-analogues of the elementary exponential functions are crucial and they are defined by

(25)

and

$$ e \bigl(x;q^{2} \bigr)=\frac{1}{((1-q^{2})x;q^{2})_{\infty}}=\sum _{0}^{\infty}\frac{(1-q^{2})^{n}}{(q^{2};q^{2})_{n}}x^{n}, \quad |x|<\frac{1}{1-q^{2}}. $$

(26)

These functions satisfy the identity

$$e \bigl(x;q^{2} \bigr)E \bigl(-x;q^{2} \bigr)=1, $$

and have as limit, when q tends to 1⁻, the classical exponential function.

Now we purpose to give the q-analogue of the heat equation associated to the second derivative operator (even in x)

$$ \frac{\delta^{2}u}{\delta x^{2}}=\frac{\delta u}{\delta t},\quad x\in \mathbb{R},\ t>0. $$

(27)

We consider as q-heat equation associated to the second q-derivative operator the partial q-difference equation

$$ (\varDelta_{q,x}u) (x,t)=(D_{q^{2},t}u) (x,t). $$

(28)

We take as the initial condition

$$ u(x,0)=f(x),\quad f\in L_{q}^{1} ( \mathbb{R}_{q} ) . $$

(29)

6.1 q-Solution source

To find the solution source related to the q-heat equation, we apply the Fourier method with the adapted q-Fourier cosine studied before.

Putting

$$U(\lambda,t)=\mathcal{{F}} \bigl(u(x,t) \bigr) (\lambda), $$

Eq. (28) becomes

$$D_{q^{2},t}U(\lambda,qt)=-{\lambda}^{2}U(\lambda,t), $$

and, taking into account conditions (29), we obtain

$$U(\lambda,t)=\mathcal{{F}}(f) (\lambda)e \bigl(-{\lambda}^{2}t;q^{2} \bigr). $$

The problem consists in finding the function which has e(−λ ² t;q ²) as its q-Fourier-cosine transform. For this end, we need the following lemma.

Lemma 6.1

For n=0,1,2,… and t>0, we have

Proof

From (26) we find

$$\int _{0}^{\infty}e \biggl(-\frac{\lambda^{2}}{qt(1+q)^{2}},q^{2} \biggr)\lambda^{2n}\,d_{q}\lambda=(1-q)\sum_{-\infty}^{\infty}\frac{q^{ ( 2n+1 ) k}}{ ( -\frac{1-q}{1+q}\frac{q^{2k}}{qt},q^{2} )_{\infty}}\mathtt{.}$$

Secondly, the use of the well-known Ramanujan [8] identity

$$\sum _{-\infty}^{\infty} \frac{z^{k}}{ ( bq^{k},q )_{\infty }}=\frac{ ( bz,q/bz,q,q )_{\infty}}{ ( b,z,q/b,q )_{\infty}},\quad b\neq0, $$

leads to the result after minor computation. □

Proposition 6.2

$$\frac{ ( 1+q^{-1} )^{1/2}}{\varGamma_{q^{2}} ( 1/2 ) }{\int_{0}^{\infty}} e \biggl(-\frac{\lambda^{2}}{qt(1+q)^{2}},q^{2} \biggr)\cos \bigl( \lambda x,q^{2} \bigr)\,d_{q}\lambda=A \bigl( t,q^{2} \bigr) e \bigl( -tx^{2},q^{2} \bigr), $$

where

$$ A \bigl( t,q^{2} \bigr) = \bigl[ (1-q)q^{-1} \bigr]^{1/2}\frac{ ( -\frac{1+q}{1-q}q^{2}t,-\frac{1-q}{1+q}\frac{1}{t},q^{2} )_{\infty}}{ ( -\frac{1-q}{1+q}\frac{1}{qt},-\frac{1+q}{1-q}q^{3}t;q^{2} )_{\infty}}. $$

(30)

As an immediate consequence we are now able to define the q-source solution associated to the q-heat equation (28) by

$$ G \bigl(x,t,q^{2} \bigr)= \bigl(A \bigl( t,q^{2} \bigr) \bigr)^{-1}e \biggl(-\frac{x^{2}}{qt(1+q)^{2}};q^{2} \biggr). $$

(31)

In the same manner as in the classical heat equation theory, we put

$$ G \bigl(x,y,t;q^{2} \bigr)=T_{y,q}G \bigl(x,t;q^{2} \bigr), $$

(32)

with T _y,q being the q-translation studied in Sect. 4.

Through this approach we show that the solution of the q-Cauchy problem (28) and (29) can been written in the form of

$$ u(x,t)= \bigl(G \bigl(\cdot,t;q^{2} \bigr)\star_{q}f \bigr) (x)=\int_{0}^{\infty}G \bigl(x,y,t;q^{2} \bigr)f(y)\,d_{q}y. $$

(33)

It is natural to ask how other properties such as the positivity of G(x,t;q ²) and the existence of the q-semigroup can be established.

6.2 q-Heat polynomials

Proposition 6.3

It is easy to see that, for x∈ℝ and t>0, the analytic function

$$\lambda\rightarrow e{ \bigl(-{\lambda}^{2}t;q^{2} \bigr)\cos \bigl(\lambda x;q^{2} \bigr)}, $$

is a solution of (28) and it has the expansion

$$e \bigl( -\lambda^{2}t,q^{2} \bigr) \cos \bigl(\lambda x,q^{2} \bigr)=\sum _{n=0}^{\infty} ( -1 )^{n}v_{2n}(x,t,q)\lambda^{2n},$$

where

$$ v_{2n}(x,t,q)=\sum _{k=0}^{n}b_{k} \bigl( x,q^{2} \bigr) \frac {(1-q^{2})^{n-k}}{(q^{2};q^{2})_{n-k}}t^{n-k}, $$

(34)

with the functions b _n being given by (6).

From Proposition 3.1 we deduce immediately the following properties:

We note that formula (34) can be inverted:

$$ b_{n} \bigl(x;q^{2} \bigr)=\sum _{k=0}^{n}(-1)^{n-k}v_{2k}(x,t;q)q^{ ( n-k ) ( n-k-1 ) } \frac{(1-q^{2})^{n-k}}{(q^{2};q^{2})_{n-k}}t^{n-k}. $$

(35)

Proposition 6.4

The q-heat polynomials (34) possess the q-integral representation

• (1)
  $$ v_{2n}(x,t;q)={\int _{0}^{\infty}} G \bigl(x,y,t,q^{2} \bigr)b_{n} \bigl(y;q^{2} \bigr)\,d_{q}y. $$

  (36)
• (2)
  $$ b_{n} \bigl(x;q^{2} \bigr)={\int_{0}^{\infty}} G \bigl(x,y,t,q^{2} \bigr)v_{2n} \bigl(q^{-1/2}y,t;q^{-1} \bigr)\,d_{q}y. $$

  (37)

Proof

We have

and

 □

In [14], the authors defined the so-called associated functions by the Appell transform. We extend this notion by defining for t>0 the q-associated functions of v _2n by

$$ w_{2n}(x,t;q)= ( -1 )^{n} \varDelta_{q,y}^{n}G \bigl(x,y,t;q^{2}\bigr) \bigl\vert_{y=0}. $$

(38)

It is easy to see that

$$ w_{2n}(x,t;q)=\frac{ ( 1+q^{-1} )^{1/2}}{\varGamma_{q^{2}} ( 1/2 ) }{ \int_{0}^{\infty}} e \bigl(-t \lambda^{2},q^{2} \bigr)\lambda^{2n}\cos \bigl( \lambda x,q^{2} \bigr)\,d_{q}\lambda. $$

(39)

Proposition 6.5

(Biorthogonality)

For t>0 and n,m∈ℕ, we have

$${\int_{0}^{\infty}} w_{2m}(x,t;q)v_{2n} \bigl(q^{1/2}x,-t;q \bigr)\,d_{q}x= ( -1 )^{m}\delta_{n,m}. $$

Proof

By (37), we have

$$\varDelta_{q}^{m}b_{n} \bigl(x;q^{2} \bigr)={\int_{0}^{\infty}} \varDelta_{q}^{m}G \bigl(x,y,t,q^{2} \bigr)v_{2n} \bigl(q^{-1/2}y,t;q^{-1} \bigr)\,d_{q}y. $$

Putting x=0, we obtain

$${\int_{0}^{\infty}} w_{2m}(y,t;q)v_{2n} \bigl(q^{-1/2}y,t;q^{-1} \bigr)\,d_{q}y= ( -1 )^{m}\delta_{n,m}. $$

 □

6.3 Convergence of ∑ _n≥0 α _n v _2n (x,t;q)

Now we establish the following estimates that will be needed later

Lemma 6.6

For n=0,1,… and $0< \frac{x_{0}^{2}}{t_{0}} <+\infty$, we have

$$\bigl| v_{2n}(x_{0},t_{0},q)\bigr| \geq \frac{(1-q^{2})^{n}}{(q^{2};q^{2})_{n}}\vert t_{0}\vert ^{n}\geq \frac{\vert t_{0}\vert ^{n}}{n!}. $$

Proof

Indeed, the first inequality is a consequence of b ₀(1;q ²)=1 and the hypothesis, and the second follows from

$$\frac{1}{n!}\leq\frac{(1-q^{2})^{n}}{(q^{2};q^{2})_{n}}. $$

 □

Corollary 6.7

For n=0,1,… and $0 < \frac{x_{0}^{2}}{t_{0}}< +\infty$, we have

$$\big| v_{2n}(x_{0},t_{0},q)\big| \geq Cn^{-\frac{1}{2}} \biggl( \frac{\vert t_{0}\vert e}{n} \biggr)^{n}, $$

where C is a constant depending on x ₀ and t ₀.

Lemma 6.8

For n=0,1,…,δ>0, and $\vert \frac{x^{2}}{\delta ( 1+q ) }\vert <1$, we have

$$ \frac{(1-q^{2})^{n}}{(q^{2};q^{2})_{n}}\bigl| v_{2n} \bigl(\vert x\vert ,\vert t\vert ,q \bigr)\bigr| \leq q^{-n ( n-1 ) }\frac{ ( \delta+\vert t\vert )^{n}}{n!}e \biggl( \frac{x^{2}}{\delta ( 1+q ) };q \biggr) . $$

(40)

Proof

To show (40), we note that

$$(q;q)_{2k}= \bigl(q,q^{2};q^{2} \bigr)_{k},$$

and

$$\bigl(q;q^{2} \bigr)_{k}\geq(q;q)_{k}. $$

For δ>0, and by using the fact that

$$\frac{(1-q)^{k}}{(q;q)_{k}}\frac{|x|^{2}}{(\delta(1+q))^{k}}\leq q^{-\binom {k}{2}}\exp \biggl( \frac{\vert x\vert ^{2}}{\delta(1+q)} \biggr), $$

we obtain

The inequalities

$$\biggl(-\frac{|t|}{\delta};q^{2} \biggr)_{n}\leq \biggl( \frac{|t|}{\delta}+1 \biggr)^{n}, $$

and

$$q^{\binom{n}{2}}n!\leq\frac{ ( q;q )_{n}}{ ( 1-q )^{n}}\leq n! , $$

give the result. □

By the Stirling formula, we obtain

Corollary 6.9

For n=0,1,…,δ>0, and $\vert \frac{x^{2}}{\delta ( 1+q ) }\vert <1$, we have

$$ v_{2n} \bigl(\vert x\vert ,\vert t\vert ,q \bigr)\leq K q^{-n ( n-1 ) } \biggl( \bigl( \delta+\vert t\vert \bigr) \frac{n}{e} \biggr)^{n}, $$

(41)

where K is a constant depending δ.

Theorem 6.10

Let (α _n ) be a sequence of real or complex numbers such that

$$\overline{\lim_{n\rightarrow\infty}} {\frac{n}{e}}q^{-2(n-1)}| \alpha_{n}|^{1/n}={\frac{1}{\sigma}}<+\infty. $$

Then the series

$$\sum_{n\geq0}\alpha_{n}v_{2n}(x,t;q), $$

converges in the strip

$$ S_{\sigma}= \bigl\{(x,t),x\in\mathbb{R},\ |t|<\sigma \bigr\}, $$

(42)

and converges uniformly in any region of this strip.

To prove the theorem, we adopt the same approach as in [14] by taking account of the q-equivalent estimation (41).

Remark

If we write u(x,t) as the sum of the previous series, then this function satisfies the q-heat equation (28) and

$$u(x,0)=\sum_{n=0}^{\infty}\alpha_{n}b_{n} \bigl(x;q^{2} \bigr), $$

where the b _n (x;q ²) is given by (6).

6.4 Analytic Cauchy problem related to the q-heat equation

Lemma 6.11

Under the hypothesis of Theorem 6.10 and putting

$$ u ( x,t ) =\sum_{n\geq0}\alpha_{n}v_{2n}(x,t;q), $$

(43)

u(x;t) is an analytic function of two variables x and t in the strip S _σ given by (42) and satisfies the q-heat equation (28). Furthermore, the coefficients α _n are given by

$$ \alpha_{n}= \varDelta_{q}^{n}u ( x,t ) \bigl\vert_{ ( x,t ) = ( 0,0 ) }. $$

(44)

Proof

To show this, we note that the theorem gives that u(x,t) is analytic in the whole strip S _σ . Now for a fixed integer p the series

$$\sum_{n\geq0}\alpha_{n+p}v_{2n}(x,t;q) $$

converges uniformly in any compact region of S _σ . To prove (44), it suffices to see that for integers n and p we have

$$\bigl(\varDelta_{q,x}^{n}v_{2p}(x,t;q)\bigr)\bigl|_{(0,0)}= \delta_{n,p}, $$

where δ _n,p is the Kronecker symbol. □

Finally the following statement is established.

Theorem 6.12

Under the hypothesis of Lemma 6.11, the function u(x,t) given by (43) has the q-Maclaurin expansion

$$u(x,t)=\sum_{m,p\geq0}\beta_{m,p} \frac{(1-q^{2})^{m}}{(q^{2};q^{2})_{m}}x^{2p}t^{m}, $$

where

$$ \beta_{m,p}=\alpha_{m+p}b_{p} \bigl( 1,q^{2} \bigr) . $$

(45)

If for x∈ℝ and |t|<σ then function

$$u(x,t)=\sum_{m,p}\beta_{m,p} \frac{(1-q^{2})^{m}}{(q^{2};q^{2})_{m}}x^{2p}t^{m}, $$

satisfies the q-heat equation (28) with the coefficients β _m,p given by (44), then u(x,t) can be extended to an analytic function in the strip S _σ and we have

$$u(x,t)=\sum_{n\geq0}\alpha_{n}v_{2n}(x,t;q). $$