Identifying anomalous patterns in ecological communities’ diversity: leveraging functional boxplots and clustering of normalized Hill’s numbers and their integral functions

Abstract

Diversity is fundamental in many disciplines, such as ecology, business, biology, and medicine. From a statistical perspective, calculating a measure of diversity, whatever the context of reference, always poses the same methodological challenges. For example, in the ecological field, although biodiversity is widely recognised as a positive element of an ecosystem, and there are decades of studies in this regard, there is no consensus measure to evaluate it. The problem is that diversity is a complex, multidimensional, and multivariate concept. Limiting to the idea of diversity as variety, recent studies have presented functional data analysis to deal with diversity profiles and their inherently high-dimensional nature. A limitation of this recent research is that the identification of anomalies currently still focuses on univariate measures of biodiversity. This study proposes an original approach to identifying anomalous patterns in environmental communities’ biodiversity by leveraging functional boxplots and functional clustering. The latter approaches are implemented to standardised and normalised Hill’s numbers treating them as functional data and Hill’s numbers integral functions. Each of these functional transformations offers a peculiar and exciting point of view and interpretation. This research is valuable for identifying warning signs that precede pathological situations of biodiversity loss and the presence of possible pollutants.

1 Introduction

Biodiversity is widely acknowledged as one of the most critical components of healthy ecosystems, and conserving it has become a top priority for environmental management (Laurila-Pant et al. 2015; Worm et al. 2006; Kremen 2005). Despite its prominence, many investigations have shown that the diversity of species, genetics, and communities is declining at an alarming rate (e.g. UNEP 2002, 2010; Cardinale 2014). According to the International Union for Conservation of Nature (IUCN), 24% of all mammal species and 12% of all bird species are at risk of extinction (Hilton-Taylor and Brackett 2000). In 2002 and 2010, the Convention on Biological Diversity (CBD) issued strong international signals to reduce the current rate of biodiversity loss. To achieve this, a set of indicators has been suggested, but due to the complex and multivariate nature of biodiversity, there is currently no scientific consensus on which criteria to use (Royal Society 2003; Di Battista and Gattone 2003; Gattone and Di Battista 2009; Di Battista et al. 2017; Maturo and Di Battista 2018).

The CBD (UNEP 1992) defines biodiversity as “the variability among living organisms from all sources including, inter alia, terrestrial, marine and other aquatic ecosystems and the ecological complexes of which they are part; this includes diversity within species, between species and of ecosystems”. Biological diversity refers to living things’ different types, amounts, and locations, including species, ecosystems, and genes (EASAC 2005). Because of its multifaceted nature, biodiversity cannot be measured by a single index (e.g., see Chao et al. 2014; Hill 1973).

Due to the inherent complexity of biodiversity, it is essential to clarify that our focus is specifically on the “variety of living organisms in a delineated study area” (Patil and Taillie 1982; Pielou 1975). Even when we narrow our scope to species variety, we encounter a challenge stemming from the multidimensional nature of biodiversity. This intricacy arises from the intertwining of species richness (the number of different species) and evenness (the equitable distribution of abundances among species) (Ricotta et al. 2003). Accordingly, various biodiversity indices, which weigh these two aspects differently, may yield inconsistent rankings when applied to ecological communities (e.g., see Di Battista et al. 2016, 2017).

An innovative approach to addressing this challenge was put forth by Hill (1973), who offered the notion of diversity profiles as a solution. These profiles comprise a parametric family of diversity indices designed to provide a unified framework. They introduce functions dependent on a parameter, allowing for rare and abundant species sensitivity. Hence, they offer a spectrum of biodiversity measures, providing a comprehensive graphical representation of community diversity (Chao et al. 2014). The graphical representation of these curves can offer direct insight into the relative biodiversity among ecological communities: if the curves do not intersect, a straightforward biodiversity ranking is evident. Nonetheless, numerous studies have stressed that when the profiles cross, achieving a singular ranking becomes problematic (e.g., see Di Battista et al. 2016).

To address this limitation, recent research has introduced the application of functional data analysis to diversity profiles (Maturo et al. 2016). A method for ranking ecological communities has also emerged through the so-called Hill’s numbers integral function (Maturo and Di Battista 2018). This function, derived from Hill’s diversity profiles, encourages the attainment of a definitive ranking among ecological communities, overcoming the intersecting profiles.

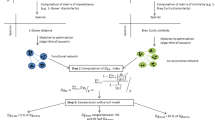
Current research in this field has yet to address the challenge of systematically identifying anomalous ecological communities; in other words, the identification of anomalies still focuses on univariate measures of biodiversity and neglects the multidimensional nature of biodiversity. This paper introduces an innovative approach to biodiversity analysis. Our method employs an outlier detection system combining modified band depth (Lopez-Pintado and Romo 2019) and different transformations of Hill’s numbers (Hill 1973). This strategy provides a novel approach for identifying and characterising anomalous ecological communities within biodiversity studies. At the same time, we propose a functional clustering method to identify groups of biodiversity profiles with similar patterns. This method can also be used to notice groups of ecological communities at risk. As discussed in the article, Hill’s profiles are limited for certain statistical methodologies, such as clustering or other outlier detection methods based on distance. The main problem is that the magnitude of functional variability of diversity profiles is different across the domain. This results in a distance bias that will always be dominated by richness, which can be found in the first part of Hill’s numbers domain. Instead, we need a trade-off between the importance of richness and evenness in calculating functional distance. Solving the latter problem is the second objective of the paper and is synergistically integrated with the first objective of identifying biodiversity outliers.

The ultimate goal of these methods is to equip policymakers and other stakeholders with more robust statistical tools that consider the multivariate aspect of biodiversity, encompassing the countless potential combinations of evenness and richness (the complete spectrum of diversity profiles). This will allow them to identify possible indications of environmental quality decline more effectively.

The paper is organized as follows: The second section explores the leading classical biodiversity indices, Hill’s numbers, and their limitations. The third section introduces standardised and normalised Hill’s functions, Hill’s number integral functions, and the outlier detection strategies. The fourth and fifth sections propose a practical application of the method to a real dataset and a simulation study on two scenarios. Finally, the paper concludes with a summary of the findings and future research directions.

2 Background

One typical way to evaluate biodiversity is by examining patterns of $\alpha$-diversity indices. The standard methods of measuring biodiversity rely on species counts (richness index) and composite indices, such as Shannon-Wiener (Shannon 1948) or Simpson indices (Simpson 1949), which are widely used in ecology because they are easy to comprehend and apply (Lamb et al. 2009). The richness index is a measure of the total number of species that exist in a particular ecological community. It is the simplest way to represent biodiversity and is commonly used. However, it has a few limitations. Firstly, it does not consider the relative abundance of species. Secondly, it is susceptible to the size of the sample collected to represent the community. Incomplete samples are common in biodiversity studies, leading to underestimating the true species richness. Lastly, species richness is strongly influenced by the presence of rare species, and therefore, it is not ideal for detecting early warning signals of biodiversity change.

The Shannon-Wiener index (Eq. 1) (Shannon 1948) is given by:

$$\begin{aligned} \triangle _{S_1}=-\sum _{i=1}^k f_i \log (f_i) \end{aligned}$$

(1)

The Shannon-Wiener (Shannon 1948) index is a biodiversity measure ranging from zero to log(k), where k is the number of species. The Shannon-Wiener index is affected by the number of species and their evenness. It measures the diversity of the entire community, but its drawback is that it is susceptible to rare categories in an ecological community. It is easy to see that the exponential of the Shannon-Wiener index (Eq. 2) represents the number of species in equivalent terms:

$$\begin{aligned} \triangle _{S_2}=e^{-\sum _{i=1}^k f_i \log (f_i)} \end{aligned}$$

(2)

The expression’s minimum value is 1, which occurs when e is raised to the power of 0. On the other hand, its maximum value is k, which is obtained when e is raised to the power of log(k).

The Simpson index (Simpson 1949) considers the number of species and their relative abundances (as shown in Eq. 3). It can be expressed as follows:

$$\begin{aligned} \triangle _{K_1}=1-\sum _{i=1}^k f_i^2 \end{aligned}$$

(3)

where $f_i$ is the relative frequency of the i-th species, and k is the total number of species in an ecological community. The Simpson’s index is a measure that can range from zero to $(k - 1)/k$. The number of species present in an ecosystem determines its maximum value. It occurs when they are evenly distributed, while its minimum value happens when only one species exists. This index is influenced by both evenness and richness, making it a good indicator of the dominance of one or a few species over others. However, it is not a reliable predictor of richness since it is susceptible to changes in the relative abundances of the most dominant species. Therefore, it is mainly considered a measure of dominance concentration rather than richness. One limitation of this index is that it cannot indicate volume or describe population growth and decline changes. Instead, it only reflects changes in species composition. An alternative but similar metric is the Simpson’s Reciprocal Index (Eq. 4). It is given by:

$$\begin{aligned} \triangle _{K_2}=\frac{1}{\sum _{i=1}^k f_i^2} \end{aligned}$$

(4)

The reciprocal of the Simpson’s index ranges from 1 (minimum biodiversity) to k (maximum biodiversity) and is expressed in an equivalent number of species.

Abundance-weighted heterogeneity indices provide a richer understanding than solely assessing richness and exhibit sensitivity to changes within populations. Nevertheless, it’s crucial to note that these indices’ approaches to weighting richness and relative abundance may vary (Maturo et al. 2018). Recognized by practitioners and scholars, a single index significantly oversimplifies the intricate nature of biodiversity (Gove et al. 1994; Di Battista et al. 2014, 2016). Addressing the limitations inherent in traditional indices, Hill introduced a comprehensive framework for biodiversity estimation, commonly known as Hill’s numbers:

$$\begin{aligned} N_q=\left( \sum _{i=1}^k f_i^q\right) ^{\frac{1}{1-q}} \end{aligned}$$

(5)

The formula for calculating the diversity number includes three components. Firstly, q is the order of the diversity number, which indicates its tendency to contain or exclude the rarer species. Secondly, $f_i$ represents the relative abundance of the species ‘i’ in the sample. Finally, k is the total number of species.

Traditional diversity indices provide a single numerical value that describes the structure of an ecological community. In contrast, Hill’s numbers offer a continuum of diversity measures that vary in their sensitivity to the presence of rare species, depending on the value of the parameter q. One advantage of Hill’s numbers is that as q increases, they become less sensitive to the presence of rare species, which can be helpful in certain contexts (Ricotta et al. 2003). Effectively, for $q=+\infty$, only the commonest species are considered. Conversely, for $q=-\infty$, they consider only the rarest species.¹ Another advantage of Hill’s numbers is their capacity to facilitate natural interpretation. They are expressed in effective numbers of species, allowing for a more intuitive understanding of diversity dynamics. This characteristic has led to their frequent designation as true diversity indices (Jost 2007).

Hill (1973) emphasized that diversity numbers of different orders highlight different community characteristics, and relying on only one Hill’s number would oversimplify the complexity of biodiversity. Therefore, Hill recommended analyzing an ecological community using diverse numbers of different orders as a good practice. However, Chao et al. (2014) stated that a diversity profile, which is a plot of $N_q$ vs. q from $q = 0$ to $q=4$, can provide a complete representation of species diversity in ecological communities. Although Hill’s numbers can be calculated for $q < 0$ and $q > 4$, Chao argued that these values are less informative because the frequencies of rare species dominate them for $q < 0$. For $q > 4$, the profile changes are negligible.

Hill’s numbers are an exceptional discovery in the study of biodiversity, but they do have some limitations. One of the main limitations is that the number of individuals sampled can greatly impact the value of $N_0$. However, Hill noted that this under-sampling bias becomes less severe for higher-order Hill’s numbers. Another significant drawback of Hill’s numbers is that it is not possible to establish a unique ranking among ecological communities when the profiles intersect. This means that richness indices, the exponential of the Shannon-Weiner index or Simpson’s Reciprocal Index, may result in conflicting results. To address this issue, a different approach for considering the whole q-domain of biodiversity profiles is needed, as a single index can significantly reduce the complexity of biodiversity.

In the literature of ecological statistics there are also other diversity profiles besides Hill’s numbers. One of the best known is certainly the Patil and Taillie’s biodiversity profiles, which are known as Beta Profiles (Patil and Taillie 1979, 1982) and are given by:

$$\begin{aligned} \Delta _\beta =\sum _{i=1}^k \frac{\left( 1-f_i^\beta \right) }{\beta } f_i \quad \beta \ge -1 \end{aligned}$$

(6)

where the value of $\beta$ denotes the relative importance of richness and evenness. The meaning is very similar to Hill’s profile, but there are some small differences. The most commonly used indicators of biodiversity are special cases: $\beta =-1$ generates the richness index minus one; $\lim _{\beta \rightarrow 0}$ represents the Shannon diversity index; and $\beta =1$ results in the Simpson index. In recent literature, however, Hill’s numbers are preferred because they are expressed in the equivalent number of species and thus are easy to interpret.

3 Material and methods

3.1 Treating Hill’s numbers via functional data analysis

3.1.1 Hill’s numbers functional data (HF)

The idea behind using Functional Data Analysis (FDA) to analyse Hill’s numbers is that the latter is a function in a fixed domain and thus can be observed as a continuous function rather than a simple sequence of observations. Indeed, Hill’s numbers are generally computed for specific values of the q domain because they correspond to the classical biodiversity indexes and their transformations. Instead, in the FDA context, the datum can be considered a single entity expressed by a specific smoothed function. The benefit of this method is that it overcomes the limitations of the univariate approach by considering the entire domain, allowing for a multivariate concept of biodiversity. Hence, the curve considers the classical indices and their infinite shades simultaneously.

Following this approach, we can approximate Hill’s Functions (HF) as a linear combination of a possibly variable number of basis functions, $\phi _t(q)$, $t=1,..., T$, as follows:

$$\begin{aligned} N_i(q) \approx \sum _{t=1}^T \beta _{it}\phi _{t}(q) \end{aligned}$$

(7)

where i is a generic ecological community, and the coefficients in the T-dimensional vector $\beta_i$ determine the expansion in terms of T basis functions $\phi _t(q)$. Theoretically, we could consider the entire domain, but as mentioned above, it would make little sense from a practical point of view; therefore, we consider q in [0, 4].

3.1.2 Standardized Hill’s functions (SHFs) and normalized Hill’s functions (NHFs)

Hill’s functions take a decreasing form, and their interpretation is straightforward because the higher the profile, the more biodiversity an ecological community. One problem that needs attention is that any statistical approach based on profiles is biased if we ignore variability. Profiles are characterized by functional variability in the first part of the domain, which is much higher than functional variability in the second part of the q domain. In other words, maximum variability at the point $q=0$ and minimum variability between functions at the point $q=4$. In other words, functional variance gradually decreases as we give less importance to richness than evenness. This consideration implies that if we apply, for example, an unsupervised classification method, the functional distance will be entirely dominated by the part of the domain that has the most significant variability if we do not weigh the distance between curves with a measure of functional variability. In practice, any methodology that involves calculating a distance may be affected by this problem. Therefore, in the case of clustering, we will classify ecology communities mainly according to richness because the latter has variability and an order of magnitude much higher than the Shannon or Simpson index and their variants.

For these reasons, we propose new tools for evaluating biodiversity: the Standardized Hill Functions (SHF) and the Normalized Hill Functions (NHF). Standardization transforms data with a functional mean equal to zero and a functional standard deviation equal to one. This process is particularly useful when we aim to eliminate scale differences between variables, allowing us to compare variable magnitudes directly. A common example of standardization is the functional z-score transformation as follows:

$$\begin{aligned} N_i^z(q) = \frac{N_i(q) - \bar{{\textbf {N}}}(q)}{SD({\textbf {N}}(q))} \end{aligned}$$

(8)

where $\bar{{\textbf {N}}}(q)$ is the functional mean of a set of bioversity profiles, whereas $SD({\textbf {N}}(q))$ is the functional standard deviation of the same group of ecological communities.

Normalization is a more general term and can refer to several methods of transforming data into a standard or desired format. Normalization can include standardization but can also refer to different processes. For example, normalization can transform variable values to a specific range between 0 and 1. This can be useful when we aim to interpret variable values in a particular context or to ensure that the data is within a specific range. The great advantage of normalizing biodiversity profiles is that it gives us an immediate idea of their value at every point of the domain compared to other ecological communities. Knowing what the minimum and maximum are, we can also make a relative assessment of biodiversity in terms of the individual community. Normalized Hill’s Functions (NHF) can be expressed as follows:

$$\begin{aligned} N_i^n(q) = \frac{N_i(q) - \min {{\textbf {N}}(q)}}{\max {{\textbf {N}}(q)}-\min {{\textbf {N}}(q)}} \end{aligned}$$

(9)

As a borderline case, if a biodiversity profile is always above the others, NHF will be a constant straight line equal to one. On the contrary, if we have an ecological community whose biodiversity profile is below the others for every q, then NHF will be a horizontal line equal to 0.

Although SHF and NHF have the disadvantage that the value of the function at a point is not expressed in an equivalent number of species, such as the original Hill’s numbers, they have several practical advantages. First, the methodologies implemented on standardized or normalized profiles are unaffected by the magnitude of curves variability in the domain zone characterized by more significant variability. Second, we can compare different ecological communities to each other as if all the infinite shades of richness and evenness had the same order of magnitude. In other words, the biodiversity profiles are purified by the measuring unit, allowing a “vertical” comparison (between profiles) and “horizontal” comparison (at different points of the domain of the single profile).

3.1.3 Hill’s numbers integral functions (HIF)

Recently, Maturo (2018) proposed using the “Hill’s numbers integral function” for solving the ranking problem when profiles intersect. Although this tool does not have the advantage of being standardised, it is beneficial to understand what community has the most biodiversity, considering specific parts of the q domain.

The Hill’s Integral Function (HIF) can be defined as follows:

$$\begin{aligned} I(x)= \int _{0}^{x} N(q) \, dq \end{aligned}$$

(10)

where $x \in [0,4]$. Follows that, fixed $x=x_0$, $I(x_0)$ becomes a scalar.

The function has the following features: the higher I(x), the more diverse an ecological community (considering $0\le q \le x$); I(x) is monotonous concerning richness and evenness; $I(0)=N(0)$ provides the richness index; $I(4)=\int _{0}^{4} N(q) \, dq$, if computed for different ecological communities, provides a unique ranking among them according to their biodiversity (variety); I(x) is an increasing monotone function; fixed the number of species, I(x) tends to be more curved in case of high dominance of one or few categories; and finally, given the number of species, I(x) tends to grow more constantly in case of evenness, i.e. when the relative frequencies of all species tend to $\frac{1}{k}$ (maximum evenness).

As an example, Fig. 1 shows the meaning of the Hill’s integral function in the interval [0, 2],

$$\begin{aligned} I(2)= \int _{0}^{2} N(q) \, dq \end{aligned}$$

(11)

Fig. 1

Hill’s integral function I(2)

HIFs allow us to compare different ecological communities according to their total variety despite their diversity profiles intersecting. This is a flexible tool because, fixed the importance of the trade-off between richness and evenness, we can get a unique ranking.

3.2 Identification of anomalous groups of biodiversity profiles’ transformations via the functional K-means algorithm

Proximity among statistical units is crucial. The Euclidean norm of a vector $\varvec{x}^{\prime }=\left( x_1, x_2, \ldots , x_n\right)$ in $\mathbb {R}^n$ is used in finite-dimensional spaces: $\Vert \varvec{x}\Vert ^2=\sqrt{\sum _{i=1}^n x_i^2}$. Hence, the distance between vectors x and y can be expressed as $d(\varvec{x}, \varvec{y})=\Vert x-y\Vert =\sqrt{\sum _{i=1}^n\left( x_i-y_i\right) ^2}$. When dealing with FDA, observations exist in an infinite dimensional space, where choosing a preliminary norm is crucial due to the failure of equivalence between norms and distances (Ferraty and Vieu 2003). Various methods for calculating distances between functional objects have been suggested in the literature. However, the most comprehensive spaces for functional data are complete metric spaces. If the metric $d(\cdot , \cdot )$ is associated with a norm so that $d(X(q), Y(q))=\Vert X(q)-Y(q)\Vert$, we have a normed space (Banach space). In some cases, the norm $\Vert \cdot \Vert$ is associated with an inner product $\langle \cdot , \cdot \rangle$ and thus $\Vert X(q)\Vert =\langle X(q), X(q)\rangle ^{1 / 2}$. A Banach space whose norm derives from an inner product is called a Hilbert space; an important example is the space $L_2[a, b]$ of real square-integrable functions defined on [a, b] with $\langle X(q), Y(q)\rangle =\int _a^b X(q) Y(q) d q$. Focusing on the $L_2$-norm, a commonly used distance between functional elements is given by:

$$\begin{aligned} \Vert X(q)-Y(q)\Vert _2=\left( \frac{1}{\int _a^b w(t) d q} \int _a^b|X(q)-Y(q)|^2 w(q) d q\right) ^{1 / 2} \end{aligned}$$

(12)

where w are the weight and the observed points on each curve are equally spaced. In the ecological context, this equation provides the distance between two profiles on the considered dimension (SHF, NHF, or HIF).

Equation 12 is the starting point of any clustering algorithm. Other metrics and semi-metrics exist in the FDA literature to calculate the distance between curves. However, if there are no specific reasons to choose a different one, Eq. 12 can be used.

This section introduces a possible unsupervised classification method for creating similar groups of transformed biodiversity profiles. The goal is to understand which groups of ecological communities are at risk or have recurring patterns. Numerous clustering methods are used in the FDA literature. In the following, we focus on functional k-means.

Let f(q) be a generic function with $q \in [0,4]$ that can be alternatively take the form of $N_i^n(q)$, $N_i^z(q)$, or $I(q)=I(4)= \int _{0}^{4} N(q) \, dq$ defined as follows:

$$\begin{aligned} f(q) = {\left\{ \begin{array}{ll} N_i^z(q) &{}\quad \text {if interested in SHF} \\ N_i^n(q) &{}\quad \text {if interested in NHF} \\ I(q) &{}\quad \text {if interested in HiF.} \end{array}\right. } \end{aligned}$$

(13)

Given a set of E ecological communities, the functional k-means algorithm aims to partition the E observations into $e \leqslant E$ sets $S=S_1, S_2, \ldots , S_e$ minimising the within-cluster sum of squares. The iterative procedure starts by fixing the number e of clusters and selecting e initial centroids, $\left\{ c_1^{(0)}(q), \ldots , c_e^{(0)}(q)\right\}$. At the m-th iteration, each function is assigned to the cluster whose centroid is nearest according to the chosen distance from the previous iteration.

$$\begin{aligned} C_i^{(m)}=\underset{j=1,2, \ldots , e}{\arg \min } \sum _{i=1}^{n_j} \sum _{j=1}^e\left\| f_{ij}(q)-\psi _j^{m-1}(q)\right\| ^2 \end{aligned}$$

(14)

where $C_i^{(m)}$ is the m-th cluster assignment of the i-th function, $i=1,2, \ldots , E$. When all the communities have been assigned to a cluster, the cluster means are updated as follows: $\psi _j^m(q)=\sum _{f_i(q) \in c_j} \frac{f_i(q)}{n_j}$, where $n_j$ is the number of functions in the j-th cluster, $C_j$. This process continues until a maximum number of iterations is reached or no further changes in cluster assignment occur (Maturo et al. 2020, 2019; Maturo and Verde 2024).

Different functional k-means may be implemented to recognise outliers and peculiar patterns in a sample of E curves f(q) computed starting from smoothed Hill’s numbers. The approach can be used for SHF, NHF, or HIF where each of these transformations provides a different and particular interpretation.

3.3 Anomaly identification of biodiversity profiles’ transformations via functional boxplots

Different functional depth measures may be used to recognize outliers in a sample of E f(q) (SHF, NHF, or HIF) computed starting from smoothed Hill’s numbers. This research concentrates on the modified band depth (MBD) (Lopez-Pintado and Romo 2019) to overcome some limitations of the classical band depth (BD) proposed by Lopez-Pintado and Romo (2019). The concept of BD is simple: the higher the depth, the more a curve is contained within the bands defined by other curves in the functional data set. For further details, please refer to Lopez-Pintado and Romo (2019). However, it is important to note that this approach considers an indicator function equal to one only when a curve is entirely contained within the band. MDB overcomes the issue of having too many depth ties by considering the proportion of times that a function is in the band.

It is a generalization of BD as follows. For any of the functions f(q) in $f(q)_1,...,f(q)_n$, let

$$\begin{aligned} A_b(f(q))&\equiv A(f(q); \,f(q)_{i_1}, ..., f(q)_{i_b}) \\&\equiv \left\{ q \in \Theta : \min _{r=i_1,..,i_b}f(q)_r\le f(q) \right. \\&\qquad \left. \le \max _{r=i_1,..,i_b}f(q)_r\right\} , \; b \ge 2, \end{aligned}$$

be the set of the q interval where the curve f(q) is in the band determined by $f(q)_{i_1},...., f(q)_{i_b}$.

If $\lambda$ is a Lebesgue measure on q, $\lambda _r\left( A_b(f(q);\, f(q)_{i_1},..., f(q)_{i_b})\right) =\frac{\lambda (A_b(f(q))}{\lambda (q)}$ provides the proportion of times that f(q) is in the band. Therefore, the MBD for the i-th curve can be computed as follows:

$$\begin{aligned} MBD_{n,B}(f(q))=\sum _{b=2}^BMBD_{n}^{(b)}(f(q)), \; B \ge 2, \end{aligned}$$

(15)

where

$$\begin{aligned} MBD_{n}^{(b)}(f(q))=\left( {\begin{array}{c}n\\ b\end{array}}\right) ^{-1} \sum _{1\le i_1<i_2<.... <i_b\le n}\lambda _r\left( A(f(q); \,f(q)_{i_1}, ..., f(q)_{i_b}) \right) , \;\; b \ge 2. \end{aligned}$$

(16)

Functions with the lowest depth values are considered suspect functions. This means they might be outliers and are identified using an outlier detection rule. A common approach is to extend the classical boxplot to the functional context (FB). The central region can be identified by the band delimited by the $\alpha$ proportion $(0< \alpha <1)$ of the deepest curves from the sample. Generally, $\alpha =0.5$ can be fixed to get the middle $50\%$ of the functional data, whose border is defined as the envelope representing the “box”. In the case in which $x=4$, we get:

$$\begin{aligned} C_{0.5}=\left\{ (q, f(q): \min _{r=1, \ldots ,\lceil n / 2]} f(q)_{[r]} \le f(q) \le \max _{r=1, \ldots ,\lceil n / 2\rceil } f(q)_{[r]}\right\} . \end{aligned}$$

(17)

Equation (17) can be compared to the non-functional interquartile range and provides information on the spread of $C_{0.5}$. The whiskers in the functional box-plot show the maximum range of the dataset, excluding any functional outliers. To identify outlying curves, the fences are determined by expanding the $50\%$ central region envelope by 1.5 times its range.

4 Application to fish biodiversity of Lazio rivers (Italy)

Section 4 provides an application on a real dataset called “Bioittica”. The latter is available at the website “http://dati.lazio.it/catalog/it/dataset/bioittica” and has been analysed using the “R” statistical software. It collects and systematises the distributions and abundances of indigenous and alien fish species in the running waters of Lazio’s central region, providing a display of the fish biodiversity in the area. The following information is provided in Fig. 2: the first image displays the location of the provinces of Lazio in Italy (https://upload.wikimedia.org/). In contrast, the second image shows the watercourses map of Lazio (http://www.arpalazio.gov.it/). The data presented is from 2015 and indicates that 54 fish species were found distributed differently across 33 rivers listed in Table 1. We utilised the R packages Febrero-Bande and Oviedo de la Fuente (2012), Ramsay (2023), Wickham (2016), and Wolf (2019) for our application.

Fig. 2

Lazio Region in Italy (https://upload.wikimedia.org/) and its watercourses (http://www.arpalazio.gov.it/)

Table 1 Lazio rivers and values of the classical biodiversity indexes

Figure 3 shows the violin plots with the distributions based on the three classic biodiversity indices. The picture identifies the rivers which, according to their biodiversity calculated with the individual indices, are anomalous, both in positive and negative terms. As we can observe, based on the richness index, the only river that presents an anomalous value is the Tiber (Tevere), as it has a significantly higher richness than the other rivers. However, based on the the Shannon-Weiner index, there are no outliers. Based on the the Simpson index, on the contrary, the presence of two outliers is denoted: the Tronto river and the Ratto river. These two waterways appear anomalous because they have a much lower biodiversity than the others. Figure 4 illustrates the bagplots of the classic indexes. In this way, it is possible to establish the existence of bivariate outliers based on the traditional biodiversity indices. In each plot, only one outlier is detected.

Fig. 3

Violin plots of the classical biodiversity indexes (Lazio’s rivers). The dots are blue and move left and right so as not to overlap when there are other dots with the same value

Fig. 4

Lazio’s rivers classical indexes bag plots

Figure 5 displays the diversity profiles of the 33 rivers, as described in Eq. 5. The Tiber (in Italian, “Tevere”) is the most diverse river with 33 species. On the other hand, the least diverse rivers are Ratto, Quesa, and Tronto, with only one or two species each. However, it’s important to note that this graph cannot be used to rank the rivers based on biodiversity, as it’s impossible to determine which river has the most biodiversity when their profiles overlap.

Fig. 5

Diversity profiles of Lazio’s rivers

Figure 6a shows the Standardized Hill’s Functions (SHFs). This graph allows us to make an immediate comparison between ecological communities and the different points of the domain of the same function because, through standardisation, we purify the variability that is not constant in the functional domain. For example, if we look at the Tiber, the river with the most remarkable diversity, we can see that the standardised curve is decreasing. From an ecological point of view, this information is fascinating because it means that, the difference between the Tiber and other rivers decreases compared to the case in which we evaluate it by focusing above all on richness (the first part of the domain). The difference compared to the non-standardized case is that this decrease in functional difference is real this time and is not due to the incorrect perception caused by the decrease in functional variability in the second part of the domain. Figure 6b shows the functional boxplot applied to SHFs. We can see that this outlier detection strategy shows the presence of three anomalous curves, two with too much diversity and the other with little diversity.

Figure 6c highlights the Normalized Hill’s Functions (NHFs). As we can appreciate, this representation provides a fascinating view of the profiles because the highest and lowest profiles automatically become straight lines parallel to the q-axis (as highlighted previously, this extreme case occurs only when the minimum and maximum profile remains such across the entire domain). Therefore, the river with the greatest diversity automatically becomes a horizontal line and always equals one. On the contrary, the river with less diversity automatically becomes a horizontal line equal to zero. All the considerations that can be made starting from these two ecological communities have the great advantage that they provide information both in relative terms to these two communities and in terms of the magnitude of the diversity of the individual communities; indeed, we know, by construction, that the maximum value of the functions is one and the minimum is zero. Figure 6d illustrates the functional boxplot applied to NHFs. Also, in this case, we can appreciate the presence of three outliers that are the same as those highlighted by the previous methodology.

Figure 6e instead shows Hill’s Integral Functions (HIFs). This representation allows us to rank the rivers based on their biodiversity. By their nature, these functions are monotonous and increasing because they are cumulative. These will enable us to order the communities by fixing the weight we want to give to the trade-off between richness and evenness. Figure 6f shows us the functional boxplot applied to HIFs. Using the modified band depth strategy, the only river that appears to be anomalous for biodiversity is the Tiber. The Tiber is abnormal in a positive sense because it enjoys the maximum biodiversity in the Lazio Region.

Fig. 6

a Standardized Hill’s Functions (SHFs), c Normalized Hill’s Functions (NHFs), e Hill’s integral functions (HIFs) of Lazio’s rivers, and their functional boxplots (charts b, d, f) based on the modified band depth, respectively

Figure 7 shows the results of functional k-means clustering applied to the three functional representations. All methodologies implement five groups as suggested by the Elbow method applied to b-spline scores and illustrated in Fig. 7d, e, and f. Clearly, Fig. 7a, 7b, and 7c can lead to different partitions; in fact we see that the Tiber forms a group alone in the Fig. 7c but is in the group of communities with greater biodiversity in the Fig. 7a and 7b. The red curves are of particular interest in all the figures because they identify the group of ecological communities with low biodiversity and are, therefore, at risk.

Fig. 7

a Standardized Hill’s Functions (SHFs) functional K-means, b Normalized Hill’s Functions functional K-means (NHFs), c Hill’s integral functions functional K-means (HIFs) of Lazio’s rivers, and their Elbow plots (d, e, f) to select the number of groups

5 Application to simulated datasets

The model simulates the typical dynamics of ecological communities using the number of species, dominance factor, and probability of zero abundance for each community randomly generated for each species. Species abundances are then simulated, considering random interaction rates and variable carrying capacities. This simulation produces a data frame representing species abundances for 110 communities. Each row of the data frame represents a community, and each column represents a species. We can always think about biodiversity data, but we must emphasise how the methodology can be applied in any context in which diversity is of interest, (e.g. Maturo et al. 2018, 2019).

For each community, the simulation begins by generating random interaction coefficients $(\textit{coeff}\_\textit{interaction})$ from a uniform distribution bounded by the dominance factor. These coefficients represent the strength of interactions between species. Additionally, the model assigns initial abundances $(\textit{abundances})$ to each species. However, to introduce variability, there’s a chance for certain species to have zero abundance. This probability is determined by a random binomial distribution with a parameter $(\textit{prob}\_\textit{zero})$. Species abundances are then sampled from a uniform distribution ranging from 10 to 1000 individuals, ensuring a diverse initial population. Furthermore, carrying capacities $(\textit{carrying}\_\textit{capacities})$ are randomly assigned to each species, representing the maximum population size a species can sustain in its environment. These capacities are sampled from a uniform distribution ranging from 100 to 2000 individuals. Once the initial parameters are set, the model simulates the community dynamics over a predefined number of time steps (100 in this case). At each time step, the growth rates of species are calculated based on their interaction coefficients, current abundances, and carrying capacities. The growth rates are then used to update the abundances of each species, taking into account the constraints imposed by the carrying capacities.

The model generates a realistic representation of species abundance within ecological communities by iterating through these steps. This approach allows for exploring various community structures, from highly dominant to heterogeneous, while also capturing the stochasticity inherent in ecological systems.

5.1 Scenario 1

We have 110 ecological communities in total. The initial model includes 100 communities, each with a different number of species, ranging from 5 to 30. The dominance factor is randomly generated from a uniform distribution with parameters between 0.1 and 1. The probability of zero abundance for each ecological community is also randomly determined by a uniform distribution with parameters between 0.01 and 0.9. To generate potential outliers, we make changes to the initial parameters. We randomly generate ten potential outliers by varying the number of species from 5 to 50. The dominance factor is also randomly generated from a uniform distribution with parameters between 0.9 and 1. The probability of zero abundances is determined randomly with the same parameters as the initial model. This simulation system enables us to generate potential outliers regarding richness and strong dominance.

Figure 8 shows violinplots and outliers according to classical indices. Based on richness, we would have only one anomalous value, two with the Shannon index and five with the Simpson index. Figure 9 shows bivariate outliers according to classical indices. We can see that, in this case, we have some abnormal communities varying between two and three. Contrary to what we have observed for the rivers of Lazio, in this case, the functional approach evidences the presence of many outliers decidedly higher than the classical indices (see Fig. 10a and 10b, and 10c and 10d). On the contrary, focusing on HIFs, we do not appreciate outliers with low biodiversity but only with high biodiversity (see Fig. 10e and 10f). Regarding the results of clustering, the optimal number of groups varies between 4 and 5 (see Fig. 11d, 11e, and 11f). Figure 11a, 11b, and 11c highlight the presence of distinct groups that create groups of ecological communities based on their biodiversity.

Fig. 8

Simulated scenarios n. 1. Violin plots of the classical Biodiversity indexes. The dots are blue and move left and right so as not to overlap when there are other dots with the same value

Fig. 9

Simulated scenarios n. 1. Classical indexes bag plots

Fig. 10

a Standardized Hill’s Functions (SHFs), c Normalized Hill’s Functions (NHFs), e Hill’s integral functions (HIFs) of Scenario 1, and their functional boxplots (charts b, d, f) based on the modified band depth

Fig. 11

Simulated scenarios n. 1: a Standardized Hill’s Functions (SHFs) functional K-means, b Normalized Hill’s Functions functional K-means (NHFs), c Hill’s integral functions functional K-means (HIFs) of Lazio’s rivers, and their Elbow plots (d, e, f) to select the number of groups

5.2 Scenario 2

We have 110 ecological communities, out of which the starting model simulates 100 communities. The number of species in each community ranges from 5 to 30. We generate the dominance factor using a uniform parameter distribution [0.1,0.8]. Similarly, the probability of zero abundance is randomly selected for each ecological community using a uniform distribution with parameters [0.01,0.8]. Furthermore, we generate ten potential outliers by introducing changes to the starting parameters. The number of species in these outliers ranges from 3 to 30. We use a uniform distribution with parameters [0.01,0.99] to generate the dominance factor for the outliers. The probability of zero abundances for each ecological community in the outliers is randomly determined using a uniform distribution with parameters [0.2,0.8]. We can generate potential outliers with highly variable dominance and almost the same richness as the starting model using this simulation system.

Figures 12, 13, 14, and 15 retrace the same scheme illustrated for the rivers of Lazio and Scenario 1. What is worth highlighting in Scenario 2 is that the functional approach on all dimensions is more conservative. In other words, while the Simpson index highlights numerous outliers, using SHFs and NHFs we only appreciate one community with very low biodiversity and no outliers with HIFs.

Fig. 12

Simulated scenarios n. 2. Violin plots of the classical Biodiversity indexes. The dots are blue and move left and right so as not to overlap when there are other dots with the same value

Fig. 13

Simulated scenarios n. 2. Classical Indexes Bag Plots

Fig. 14

a Standardized Hill’s Functions (SHFs), c Normalized Hill’s Functions (NHFs), e Hill’s integral functions (HIFs) of Scenario 2, and their functional boxplots (charts b, d, f) based on the modified band depth

Fig. 15

Simulated scenarios n. 2: a Standardized Hill’s Functions (SHFs) functional K-means, b Normalized Hill’s Functions functional K-means (NHFs), c Hill’s integral functions functional K-means (HIFs) of Lazio’s rivers, and their Elbow plots (d, e, f) to select the number of groups

6 Discussion and conclusions

There is widespread agreement that monitoring is crucial to preserving and managing biodiversity. This is because the diversity of species is an indicator of the condition of an ecosystem and, therefore, the quality of the environment in which they live. Hence, institutions, scholars, and experts have debated this issue in recent decades. In this context, one of the main challenges is identifying an appropriate measure of biodiversity. To be effective, a monitoring program should use statistically reliable methods to assess changes in biodiversity over time (Magurran 2021). However, although several metrics have been proposed, there is currently no consensus on which measure is best.

There are three main reasons why biodiversity indicators can be problematic (Maturo and Di Battista 2018). Firstly, an indicator of biodiversity must meet many criteria, which can be challenging. Secondly, the Convention on Biological Diversity has provided a broad definition of biodiversity, which can make it hard to measure. Lastly, scholars and stakeholders have different interests and needs when measuring biodiversity. Due to the complex nature of the concept of biodiversity, no single indicator can satisfy all requirements. All metrics are questionable because no single index can fully encapsulate a concept as multidimensional and multivariate as biodiversity.

Remarkably, after a critical review of the primary methods for assessing biodiversity, we have proposed a new methodology for detecting outliers, overcoming the issues of the classical indicators in a functional framework. Exploiting functional data analysis, we have proposed the following tools: the functional boxplot based on the modified band depth extended to the context of biodiversity profiles treated as functional data; functional k-means to identify groups of ecological communities with similar biodiversity patterns; and finally, different functional transformations of Hill’s numbers to improve interpretation (NHFs), solving the ranking issue when profiles intersect (HIFs), and overcoming the problems related to non-homogeneous functional variability over the q-domain (SHFs).

The interpretation of why an ecological community is an outlier is exciting when evaluated compared to the average of a specific area. It is exciting to note that in both the application to real and simulated data, approaches based on classic indices always show contrasting results and contrast with the proposed new approach. We expected the contrast with the new strategy because the latter is based on an infinite dimensional evaluation. In contrast, the classic indices are based on only one dimension of diversity at a time. After all, this is precisely the reason why we introduce an approach of this type. The contradictory nature of the classic indices results confirms that a multidimensional approach was to be considered. This last aspect means that a practitioner dealing with an unchanged instrument would be unable, based on the classical indices, to understand which ecological communities should be considered at risk and would have to rely purely on qualitative assessments because the classical indices conflict. For this reason, we propose an analytical tool that tries to solve the problem of classical indices.

An interesting aspect to highlight is that, in some cases, the functional approach turns out to be more conservative in outlier detection. This was expected because we consider multiple dimensions simultaneously (infinite in reality). Therefore, it would be like combining an infinite number of variants of the classic indices simultaneously. Another curious aspect is that traditional indices often present notable limitations. The study highlights how the richness index can usually select only outliers with a high number of species, while the exponential of the Shannon index and the reciprocal of the Simpson index seem only to be able to highlight outliers with little diversity. On the contrary, the functional approach seems to capture both types of anomalies indifferently. Further studies and simulations could confirm or deny this situation.

Our research aims to provide ecologists, policymakers, and scholars with additional tools to rank ecological communities and detect areas with high environmental risks. However, our method is not without limitations. Indeed, the function we introduce is unaffected by species’ absolute abundance. This means that if all species in a community are multiplied by a common factor, the value of the function will remain the same because it depends on the weight of each species in the community. Therefore, our method can only be used to analyse variety within ecological communities and not the total biomass. However, it is essential to note that biodiversity is multidimensional, and no metric can perfectly capture all its aspects.