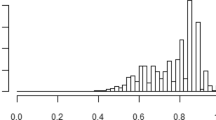
Abstract
The aim of this paper is to apply the Zenga distribution for equivalent disposable income from the last two waves of European Quality of Life Surveys for Germany and France (both for total society and selected socio-economic groups) and to assess the goodness of fit to empirical data. The Zenga distribution has not been used to describe the income distribution in these countries yet. The obtained parameters were assessed for fitting to empirical data using two measures—the Wasserstein-Kantorovich and the Wasserstein-Kantorovich standardized measure. The analysis of the results received allows for the conclusion that the Zenga distribution can fit the income distributions both for small as well as large values. It was also shown that the Zenga distribution fits the data well even with small and very small samples. The article uses a new measure to assess the fit of the distribution to empirical data, based on the Wasserstein-Kantorovich measure assessing the distance between the empirical and theoretical cumulative distribution function. The modification consisted in standardizing the Wasserstein-Kantorovich measure by dividing the field between distributors by the rectangle area, where length is maximum income and width is maximum value of the cumulative distribution function. The proposed measure is not sensitive to extreme values, often found in the analysis of income distribution, and can be applied even in very small samples.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The research on income and its distribution occupies an important place in economic theory, and its results are a valuable source of information both for scientists as well as for public institutions as a basis for shaping social policy. Income distribution is also an important element of research on the living conditions of the society and the general condition of the economy.
The income distribution can be described in several ways. The first one consists in providing a synthetic index characterizing a selected trait of distribution, mainly inequality, for example Gini coefficient (Gini 1912, 1914, 1921), Lorenz curve (1905), Pietra inequality index (Pietra 1915) as well as Zenga inequality index (Zenga 2007). The contrast of the Gini and Zenga indices, application them for the analysis of incomes in various countries, and development empirical estimation methodologies for light- and heavy-tailed distributions is the subject of the work of Gresselin et al. (2010, 2013, 2014).
More complete information on the distribution of income can be obtained using an empirical distribution, for example, a histogram or quantiles. In this case, however, it is not always possible to determine all values of the distribution characteristics, e.g. modal, without grouping the data. On the other hand, using only grouped data may be a source of problems with closing extreme class intervals, which is necessary to determine many other distribution characteristics. The above problems can be avoided by using the theoretical distribution as an income distribution model.
The first theoretical function describing the distribution of income was proposed by Pareto in 1897 in Cours d'Economie Politique, formulating it in the form of the Pareto law (Pareto 1964). A detailed description of the Pareto distribution and the research conducted with the participation of this distribution was described by Arnold (1983). Another very popular theoretical model of income distribution is the log-normal (LN) distribution. It was popularized by Aitchison and Brown (1957). In the literature, the LN distribution is available in two versions—two-parameter and three-parameter distribution, but the three-parameter distribution differs from the two-parameter distribution only in position, and not in shape or variance.
Another group of 12 theoretical distributions was proposed by Burr. Some of the Burr distributions are used in the literature under other names, e.g. the type III Burr distribution is sometimes called the Dagum distribution (Dagum 1985), and the Burr distribution of the XII type by the Singh-Maddali distribution (cf. Singh and Maddala 1976). Burr distributions of type III and XII are special cases of generalized beta distribution (McDonald and Xu 1995; Ulman 2011).
Other theoretical models of wage and income distributions include the gamma distribution used by Salem and Mount (1974) to describe the US income distribution in 1960–69, the family of functions to describe Champernowne's (1953) pre-tax income distribution, and the distribution of Gram-Charlier type A used by Rutherford (1955).
In this paper, a new three-parameter model for distributions proposed by Zenga (2010) was applied. This model is a Beta mixture defined for non-negative distributions indicated for describing income, financial and actuarial distributions. Zenga model has three parameters: \(\mu\) is a scale parameter and it is equal to the expected value, \(\alpha\) and \(\theta\) are shape parameters that inequality depends on. It means that this distribution controls the location and inequality separately so restrictions on the expected value and inequality measure can be imposed separately (Arcagni and Porro 2013). The estimated parameters of Zenga distribution can be found, through D’Addario’s invariants method (Zenga et al. 2010a; Arcagni 2011).
The Zenga model was used to describe the income distributions for Italy, Swiss, the United States, the United Kingdom (Zenga et al. 2010b), Poland (Jędrzejczak and Trzcińska 2018), the Czech Republic (Trzcińska 2022). The parameters for Germany and France have not been estimated.
The aim of this paper is to apply the Zenga distribution for equivalent disposable income from the last two waves of European Quality of Life Surveys for Germany and France (both for total society and selected socio-economic groups) and to assess the goodness of fit to empirical data. For this purpose, a new measure of fit based on the distance between empirical and theoretical distribution was applied.
2 Mathematical and statistical properties of Zenga distribution
The three-parameter model was introduced by Zenga (2010, 2010a, 2012). The density function \(f(x:\mu ;\;\alpha ;\;\theta )\) in Zenga distribution has been obtained as a mixture of Polisicchio’s (2008) following truncated Pareto density:
a fixed \(\mu >0\) and all the values of k in the interval \((0;1)\). The density on the parameter k is given by the beta density and has the following form:
where \(B(\alpha;\;\theta )\) is the beta function.
The model is characterized by the probability density function \(f(x:\mu ;\alpha ;\theta )\), (\(\mu >0; \alpha >0; \theta >0\)) for non-negative variables:
Graphs of the density function of Zenga distribution for different levels of parameters \(\theta\) (on the left) and \(\alpha\) (on the right) are presented in Fig. 1.
It is easy to see that
and
In the case \(\theta >0\), the cumulative distribution function \(F(x:\mu ;\alpha ;\theta )\) is described by the equation
where
is the incomplete beta function.
Graphs of the cumulative distribution function of Zenga distribution for different levels of parameters \(\theta\) (on the left) and \(\alpha\) (on the right) are presented in Fig. 2.
It is interesting to note that the parameter \(\alpha\) governs the behavior of the density function as x tends to 0, while the value of the parameter \(\theta\) regulates the finiteness of the function in the neighborhood of \(\mu\). The parameter α is an inverse inequality indicator and \(\theta\) is a direct inequality indicator. In particular the bigger value of the parameter α the less unequal the distribution (Porro 2015). The expected value \(E(X)\) is always equal to the parameter μ.
3 Data and methods
In this paper all calculations are based on the data from research European Quality of Life Surveys (EQLS), the data of monthly household income has been recalculated into the net equivalent income per member of the household expressed in Euro. The purpose of the European Quality of Life Surveys is to measure both objective and subjective indicators of the standard of living of citizens and their households. The Zenga model for the socio-economic group in Germany and France was used for two periods: 2007 and 2016.
To investigate the goodness of fit of theoretical distribution to the empirical one Zenga proposed: the Mortara index \({A}_{1}\), the quadratic K. Pearson index \({A}_{2}\) and the modified quadratic index \({A}_{2}^{^{\prime}}\) which are described by the following formulas (Zenga et al. 2012):
where \({n}_{j}\) and \({\widehat{n}}_{j}\) are respectively the empirical and the estimated frequencies of the jth interval.
However, all these measures are not suitable for small data sets because they require data aggregation. To find a degree of adjustments of a theoretical distribution to the empirical one, the Wasserstein-Kantorovich distance was applied. This measure has a long history and continues to attract interest from diverse fields in statistics, machine learning, and computer science, in particular image analysis Santambrogio (2015), Peyre and Cuturi (2019), and Panaretos and Zemel (2020).
The Wasserstein-Kantorovich distance between empirical \({F}_{p}\) and theoretical \({F}_{q}\) cumulative distribution function is computed as:
It should be noted that the maximum value of the income affects the distance between cumulative distribution functions. The distance is greater the higher the maximum income is. To overcome this dependency and compare the goodness of fit of the Zenga distribution between the studied countries as well as in various socio-economic groups, the Wasserstein-Kantorovich measure was normalized. The area between theoretical and empirical cumulative distribution function was divided by the rectangle area, where length is the value of the highest income in a given set and width is maximum value of the cumulative distribution function, which equals to 1. This allows for the standardization of the distance between cumulative distribution functions in the range from [0, 1). The measure equal to 0 means full compliance (overlapping of the empirical and theoretical cumulative graphs). This is rather theoretical situation in which the area between the empirical and theoretical cumulative distribution functions is equal to 0. A value close to 1 means a full cumulative mismatch. The presented measures of distributions similarity have a clear interpretation. The lower the value of \({d}_{W}\), and normalized \({d}_{W}\) the higher the consistency of compared distributions.
The parameters estimates were obtained by means of D’Addario’s invariants method, as it is described in (D’Addario 1934, 1939; Zenga 2010). Numerical methods of optimization were carried out using Mathematica program.
4 Results of applying Zenga distribution for equivalized income in France and Germany
In this chapter, the results of applying Zenga distribution for equivalent income in France and Germany are discussed. Table 1 presents descriptive characteristics of the data set.
The data sets range from 994 observations for France in 2016 to 1437 observations for Germany. Each of the above distributions is extremely right-sided asymmetric. The biggest asymmetry is for France in 2007–it is caused by extremely high maximum observation, which equals 46,700€. Both measures of differentiation and shape measures (asymmetry, kurtosis) are higher for France than for Germany.
Table 2 presents estimation results and measures of goodness of fit for income distributions in Germany and France.
Considering the measure of the Wasserstein-Kantorovich distance, the best match was recorded for Germany in 2007. It is easy to see that the fit measured with this measure is better the larger the sample size. As expected, a significantly higher value of the Wasserstein-Kantorovich measure was observed for France in 2007. In this data set, the maximum value of income was almost 2 times higher than for France in 2016 and almost 7 times higher than in the rest of the data. After applying the normalized measure the Wasserstein-Kantorovich distance, the best fit was obtained for Germany in 2007 and France in 2016. These observations are confirmed by Figs. 3, 4, 5 and 6 presenting the empirical distribution and density function of the Zenga distribution.
The above-described relationship can also be observed in Figs. 7, 8, 9 and 10 presenting empirical and theoretical distributions. Clearly, the worst match is for Germany in 2016 and the best for Germany in 2007.
5 Results of applying Zenga distribution for equivalized income in socio-economics groups in France and Germany
Table 3 shows the descriptive characteristics of the socioeconomic groups of France and Germany. In both studied countries, the size of the studied groups is diversified—the least numerous groups are students and unable to work. The most numerous groups are employees and retired. In the distinguished subgroups, a high or very high level of differentiation and asymmetry can be observed. In extreme cases (employed France 2007) variation coefficient equals 1.237.882 and the asymmetry coefficient—24.41. In other cases, the asymmetry coefficient ranges from 0.4441 (unable to work France 2016) to 16.78270 (retired France 2007).
A graphical presentation of the distributions for the studied countries in selected socio-economic groups is shown in Fig. 11.
For employed, a shift in the shape of the distribution (a marked change in the height of the distribution) in both countries was observed in 2016 compared to 2007. In the case of Germany, a shift to the right (towards higher income values) was also observed. Similar behavior of the distributions was noticed for the retired. The results of the approximation of the empirical income distributions in Germany and France for socio-economic groups in two periods of time by means of the Zenga model, together with the goodness of fit measures dW and normalized dW are presented in Table 4.
For socio-economic groups in France in 2007, the best match was obtained for employed. The worst fit, on the other hand, was recorded for students. It is also the smallest group—it has only 24 observations. The analysis of the distance between cumulative distribution functions in subsequent data sets confirms the observed relationship that the best match is observed for significantly more numerous groups (employed, retired) and the worst for the least numerous group in a given data subset. It should be noted, however, that the Zenga distribution fits well even for small and very small samples. In 4 out of 15 cases where the group size was less than 100 observations, and in 4 out of 8 cases when the group size was less than 50, the distance between cumulative distribution function is less than 0.05. The greatest distance between cumulative distribution function was observed for the unable to work, whose number was less than 20 observations, yet this measure was 0.070985, which is less than 0.1.
6 Conclusions
In the article, the Zenga distribution was applied to description of the distribution of equivalent income for France and Germany for the last two waves of the EQLS research (2007 and 2016). Parameters were estimated for the entire country as well as for individual socio-economic groups. The obtained parameters were assessed for fitting to empirical data using two measures—the Wasserstein-Kantorovich and the Wasserstein-Kantorovich standardized measure.
The analysis of the obtained results allows to state that the Zenga distribution can fit the income distributions both for small as well as large values. Similar results were obtained using the \({A}_{1}\), \({A}_{2}\) and \(A_{2}^{.\prime }\) measures (Zenga et al. 2010a; Arcagni and Porro 2013). It was shown that the Zenga distribution fits well with the data even with small and very small samples.
In the article, the goodness of fit measures proposed by Zenga were abandoned due to the need to aggregate data in the goodness of fit assessment procedure. It was considered that such an operation with trials of less than 100 observations may strongly influence the obtained results. For this reason, it was decided to use the Wasserstein-Kantorovich measure, which assesses the distance between the empirical and theoretical cumulative distribution function. This measure has not been used in the literature to assess the goodness of fit of the Zenga distribution yet. However, this measure is also not free from disadvantages because it is sensitive to outliers that are often found in variable distribution analyses with the Paretian right teil. For this reason, it was decided to modify the Wasserstein-Kantorovich distance by standardizing it. This was done by dividing the field between the cumulative distribution function by the rectangle area, where length is maximum income and width is maximum value of the cumulative distribution function. The applied measure allowed for the assessment of the distribution fit even in very small samples.
References
Aitchinson, J., Brown, J.A.C.: The lognormal distribution. Cambridge University Press, Cambridge (1957)
Arcagni, A.: La determinazione dei parametri di un nuovo modello distributive per variabili non negative: aspetti metodologici e applicazioni. PhD thesis, Università degli Studi di Milano Bicocca (2011)
Arcagni, A., Porro, F.: On the parameters of Zenga distribution. Stat. Methods Appl. 22(3), 285–303 (2013). https://doi.org/10.1007/s10260-012-0219-y
Arnold, B.C.: Pareto distributions fairland. International Cooperative Publishing House, Maryland (1983)
Champernowne, D.G.: A model of income distribution. Econ. J. 63(250), 318–351 (1953). https://doi.org/10.2307/2227127
D’Addario, R.: Sulla Misura Della Concentrazione dei Redditi. Poligraco dello stato, Roma (1934)
D’Addario, R.: Un metodo per la rappresentazione analitica delle distribuzioni statistiche. Ammali Dell Instituto Di Statistica Dell Universita Di Bari 16, 3–56 (1939)
Dagum C.: Analyses of Income Distribution and Inequality by Education and Sex in Canada. Adv. Econom. 4 (1985)
Gini, C.: Variabilitá e mutabilita. Tipografia di Paolo Cuppini, Bolognia (1912)
Gini, C.: Sulla Misura della Concentrazione e della Variabilità dei Caratteri. Atti del R. Istituto Veneto di Scienze, Lettereed Arti, Venezia (1914)
Gini, C.: Measurement of inequality of incomes. Econ. J. 31(121), 124 (1921). https://doi.org/10.2307/2223319
Greselin, F., Pasquazzi, L., Zitikis, R.: Zenga’s new index of economic inequality, its estimation, and an analysis of incomes in Italy. J. Probab. Stat. 2010, 1–26 (2010). https://doi.org/10.1155/2010/718905
Greselin, F., Pasquazzi, L., Zitikis, R.: Contrasting the Gini and Zenga indices of economic inequality. J. Appl. Stat. 40(2), 282–297 (2013). https://doi.org/10.1080/02664763.2012.740627
Greselin, F., Pasquazzi, L., Zitikis, R.: Heavy tailed capital incomes: Zenga index, statistical inference, and ECHP data analysis. Extremes 17(1), 127–155 (2014). https://doi.org/10.1007/s10687-013-0177-2
Jędrzejczak, A., Trzcińska, K.: Application of the Zenga distribution to the analysis of household income in Poland by socio-economic group. Statistica & Applicazioni XVI(2), 123–140 (2018)
Lorenz, M.: Methods of measuring the concentration of wealth. J. Am. Stat. Assoc. 9(70), 209 (1905). https://doi.org/10.2307/2276207
McDonald, J.B., Xu, Y.J.: A generalization of beta distribution with application. J. Econom. 66(1–2), 133–152 (1995). https://doi.org/10.1016/0304-4076(94)01612-4
Panaretos, V.M., Zemel, Y.: An Invitation to Statistics in Wasserstein Space. Springer, Cham, Switzerland (2020)
Pareto, V.: Cours d’Economie Politique, New By G. H. Bousquet et G. Busino, Librairie Droz Geneve (1964)
Peyre, G., Cucurim, M.: Computational optimal transport. Found Trends Mach. Lern 11(5–6), 355–607 (2019). https://doi.org/10.1561/2200000073
Pietra, G.: Delle relazioni tra gli indici di variabilità. Atti del Reale Istituto Veneto di Scienze, Lettere ed Arti, 74(2) (1915)
Polisicchio, M.: The continuous random variable with uniform point inequality measure. Stat. Appl. 6(2), 137–151 (2008)
Porro, F.: Zenga distribution and inequality ordering. Commun. Stat. Theory Methods 44(18), 3967–3977 (2015). https://doi.org/10.1080/03610926.2013.819921
Rutherford, R.S.G.: Income distributions: a new model. Econometrica 23(3), 277–294 (1955)
Salem, A.B., Mount, T.D.: A convenient descriptive model of income distribution: the gamma density. Econom. J. Econom. Soc. 42, 1115–1127 (1974). https://doi.org/10.2307/1914221
Santambrogio, F.: Optimal transport for applied mathematicians, PDEs and modeling. Springer-Verlag GmbH, Calculus of Variations (2015)
Singh, S.K., Maddala, G.S.: A function of size distribution of income. Econometrica 44(5), 35 (1976). https://doi.org/10.1007/978-0-387-72796-7_2
Trzcińska, K.: Income and inequality measures in households in Czech Republic and Poland based on Zenga distribution. Statistika, 102(1), 46–58 (2022). https://doi.org/10.54694/sta
Ulman, P.: Sytuacja ekonomiczna osób niepełnosprawnych i ich gospodarstw domowych w Polsce. Wydawnictwo Uniwersytetu Ekonomicznego w Krakowie, Kraków (2011)
Zenga, M.M.: Inequality curve and inequality index based on the ratios between lower and upper arithmetic means. Stat. Appl. 5(1), 3–27 (2007)
Zenga, M.M.: Mixture of polisicchio’s truncated pareto distributions with beta weights. Stat. Appl. 8(1), 3–25 (2010)
Zenga, M.M., Pasquazzi, L., Polisicchio, M., Zenga, M.: More on M.M. Zenga’s new three-parameter distribution for non-negative variables. Stat. Appl. 9(1), 5–33 (2010)
Zenga, M.M., Pasquazzi, L., Zenga, M.: First applications of a new three parameter distribution for non-negative Variables. Stat. Appl. 10(2), 131–149 (2012)
Zenga, M.M., Pasquazzi, L., Zenga, M.: First applications of a new three parameter distribution for non-negative variables, rapporto di ricerca N. 188, Dipartimento di Metodi Quantitativi per le Scienze Economiche ed Aziendali – Universita degli Studi di Milano-Bicocca (2010b)
Funding
The publication was financed from the subsidy granted to the Cracow University of Economics - Project nr 084/EIT/2022/POT.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no relevant financial or non-financial interests to disclose.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ćwiek, M., Trzcińska, K. Assessment of goodness of fit of income distribution in France and Germany based on the Zenga distribution. Qual Quant 57, 4013–4027 (2023). https://doi.org/10.1007/s11135-022-01556-w
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11135-022-01556-w