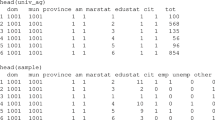
Abstract
A variety of data is of geographic interest but is not available at a small area level from large-scale national sample surveys. Small area estimation can be used to estimate parameters of target variables to detailed geographical scales based on relationships between the target variables and relevant auxiliary information. Small area estimation of proportions is a topic of great interest in many fields of study, where binary variables are diffused, such as in labour force, business, and social exclusion surveys. The univariate generalised mixed model with logit link function is widely adopted in this context. The small area estimation literature has shown that multivariate small area estimators, where correlations among response variables are taken into account, provide more efficient estimates than the traditional univariate approaches. However, the estimation problem of multivariate proportions has not been studied yet. In this article, we propose a bivariate small area estimator of proportions based on a bivariate generalised mixed model with logit link function. A simulation study and an application are presented to evaluate the good properties of the bivariate estimator compared to its univariate setting. We found that the extent of the improved efficiency of the bivariate over the univariate approach is associated with the degree of correlation of the area-specific random effects and the intraclass correlation, whereas it is not strongly related to the area sample size.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Large-scale national sample surveys are usually designed to produce precise and accurate estimates for large population domains, for example large geographical areas. However, many phenomena, such as poverty, well-being, and social exclusion present spatial heterogeneity. Thus, policy makers in charge of implementing policies at sub-national level ask for disaggregated estimates. Direct estimates obtained for these areas may return large variability due to small sample sizes (Rao and Molina 2015).
In the last decade, there has been an increasing attention to the development of efficient small area estimators based on different approaches. In particular, mixed models have become prominent in this field (Rao and Molina 2015; Rao 2003; Jiang and Lahiri 2006).
Since many social phenomena are multidimensional, thus naturally correlated, (Betti and Lemmi 2013) we argue, in line with the literature, that this property can be used to further improve the efficiency of the small area estimates. This is carried out by taking into account for the correlation in the data in the model estimation stage by including correlated random-area effects (Moretti et al. 2020a, 2021; Benavent and Morales 2016; Ubaidillah et al. 2019; Fabrizi et al. 2005; Moretti et al. 2020b; Guha and Chandra 2021). Importantly, this problem finds also its motivation in the statistical modelling literature. In fact, as pointed by Klein et al. (2015), although the vast majority of regression models are implemented for each single response variable separately, modelling multivariate correlated response variables simultaneously can be extremely relevant, given that it is possible to gain detailed information on the joint stochastic behaviour of multivariate response vectors accounting for complex regression effects. Specifically, Klein et al. (2015) propose a unified Bayesian framework for multivariate structured additive distributional regression analysis considering a large class of continuous, discrete and latent multivariate response distributions. This point is also stressed in Gueorguieva (2001), where it is discussed that there are important advantages of estimating the multivariate model over fitting separate models. In particular, these include better control over the type I error rates and potential gains in efficiency in the parameter estimates. In addition, practitioners can answer multivariate questions.
The focus of this article is on the unit-level approach where we assume that the auxiliary variables are known for all units of the sample. Fuller and Harter (1987) introduce the multivariate variance components model in small area estimation, later used by Datta et al. (1999) to estimate small area mean vectors of multiple characteristics, and, particularly, use this in empirical best linear unbiased and empirical Bayes prediction. Molina (2009) studies a multivariate mixed model under a logarithmic transformation, and Baíllo and Molina (2009) focus on a particular case of the multivariate nested error regression model for uncorrelated random effects. Recently, Moretti et al. (2020a) investigate the multivariate small area estimation problem of latent well-being indicators and Moretti et al. (2020b) use a parametric bootstrap to estimate the mean squared error of a multivariate Empirical Best Linear Unbiased Predictor (EBLUP) of small area means. However, all these articles focus on continuous variables only. Therefore, an important gap in the literature is how to deal with the multivariate small area estimation issue in presence of non-continuous response variables, in our case binary variables. In fact, these types of variables are widely diffused in social surveys. For example, there are poverty and well-being indicators that are based on binary variables (Betti and Lemmi 2013). Some social indicators estimated on Labour Force Surveys by Official Statistics are also constructed on dichotomous variables (see e.g. Chambers et al. (2016)). Therefore, there is the need to estimate small area proportions as target parameters.
The aim of this article is to provide a small area estimation approach to compute estimates of a multidimensional characteristic depending on correlated dichotomous response variables. Particularly, our target characteristic is a vector of small area proportions, based on these binary response variables. The response is a vector of observations of K binary variables, taking values 0 or 1, for a unit nested in a small area. For example, from a sample survey two binary variables can be constructed, i.e., an employment indicator, and poverty indicator. Hence, the goal could be estimating two proportions, i.e., the proportions of unemployed persons and the proportion of people living in a household with the income below a certain poverty line. In this article, we focus on the bivariate (two response variables only) small area estimation problem only.
Our approach extends the traditional univariate Generalised Linear Mixed Model (GLMM) with logit link function i.e. logistic mixed model. A pioneer work on the use of logistic mixed models in univariate small area estimation is MacGibbon and Tomberlin (1987). The reason why we are focusing on an extension of this model is firstly motivated by the fact that the univariate model is extensively adopted and studied in national statistical agencies for a variety of estimation problems in labour force and more widely social surveys. However, so far, there has not been attention to the multivariate extension in this context which shows potential from a modelling perspective. Second, the properties of small area predictors based on the univariate GLMM are well studied in both the small area estimation literature (Chandra et al. 2018; Chambers et al. 2016) and statistical modelling literature (Coull and Agresti 2000; Rabe-Hesketh and Skrondal 2001; Berridge and Crouchley 2011). Finally, it allows for taking into account for unit-level information available in the sample (auxiliary variables).
Under this framework, once the model parameters are estimated, an Empirical Plug-in Predictor (EPP) under a GLMM is used to provide small area estimates of proportions. This is widely adopted in Official Statistics (Chandra et al. 2018; Molina and Strzalkowska-Kominiak 2020; Chandra et al. 2012; Salvati et al. 2012; Rao and Molina 2015). As pointed by Chandra et al. (2018), the EPP predictor is not the most efficient under the model, compared to empirical best predictors. We refer to Jiang and Lahiri (2001) for a detailed study on the Empirical Best Predictor (EBP) that minimises the Mean Squared Error (MSE) for binary response variables. However, since the EBP does not have a closed-form expression it has to be computed via numerical approximations. This is not a straightforward exercise. For instance, the Office for National Statistics (in the United Kingdom) and the Australian Bureau of Statistics prefer the use of approximations such as the EPP (Chandra et al. 2018; Chambers et al. 2016). There are also other applications in Official Statistics, such as in the United States, where small area predictors are evaluated under the traditional univariate GLMM and EPPs are used (Slud 1999, 2004). Thus, the EPP under a GLMM is used in practice as a good alternative to the EBP (Jiang 2003). We also refer to Molina et al. (2007) and López-Vizcaíno et al. (2013) for other studies that evaluate this type of small area predictor.
It is important to acknowledge that there are other modelling strategies that can be implemented in case of correlated multivariate binary variables. For example, the multivariate probit model is also proposed (Edwards and Allenby 2003). However, the main drawback here is that the computations involve high-dimensional integrals which cannot be solved analytically. Numerical integration methods are proposed, but the literature has shown that these are not very accurate in case of probit models and can be slow in case high dimensions. Hence, simulation-based approaches are often implemented (Cappellari and Jenkins 2006). To overcome these problems, the multivariate logit modelling approach is often used (Bel et al. 2018). This is the focus of our research. Considering other techniques to treat compositional data, Aitchison (1982) developed a unified approach to the statistical analysis of compositional data. A range of methods are proposed in this work. Interestingly, Hijazi and Jernigan (2009) investigate the Dirichlet covariate model as an alternative to the logratio techniques. This model is of a particular interest given that it is possible to simultaneously assess the effects of the covariates on the relative contributions of the different components of a particular measure (Gueorguieva et al. 2008).
The remainder of this article is organised as follows. In Sect. 2, we describe the small area estimation problem and multivariate GLMM we used to provide the predictor. In Sect. 3, we describe a parametric bootstrap approach to estimate the mean squared error of the bivariate predictor. In Sect. 4, we present a model-based simulation study and its results are discussed. In Sect. 5, we show an application. We conclude the article in Sect. 6 with a final discussion and future research directions.
2 Small area estimation of proportions
2.1 Notation and small area problem
We consider a target finite population U of size N partitioned in D non-overlapping small areas, \(U_d\), \(d=1,...,D\) of size \(N_d\) such that \(\cup _{d=1}^D=U\) and \(\sum _{d=1}^D N_d=N\). From U we select a random sample s of size n, with \(n_d\) denoting the sample size in small area d, such that \(\sum _{d=1}^Dn_d=n\).
Let \({\mathbf {y}}_{di}=(y_{di1},y_{di2})^T\) denotes a vector of the values of \(k=1,2\) variables of interest \({\mathbf {Y}}\) for unit i in area d. Suppose that \(y_{dik}\) is binary, i.e., \(y_{dik} = 0\) or 1. Thus, the population parameter of interest is a vector of proportions of \({\mathbf {Y}}\) for area d, and denoted by \({\mathbf {p}}_d=({p}_{d1},{p}_{d2})\), where the generic element related to variable k is given as follows:
where \(s_d\) denotes the sample elements and \(r_d\) the out of sample elements in area d.
The direct estimator for the k th small area proportion \(p_{dk}\) is given by:
where \(w_{di}\) denotes the survey weight for unit i in area d. We refer to Särndal et al. (2003) for details of the variance of 2. Estimator 2 is based on area-specific sample information only, thus, it becomes unstable when the sample size in area d is small. In particular, the direct estimates may return larger variability. In addition, the estimator cannot be computed for areas with zero sample sizes. Hence, model-based small area estimation methods that ’borrow strength’ across areas via the use of statistical models are used to produce accurate and precise small area estimates of 1 (Rao and Molina 2015).
Estimator 2 is based on area-specific sample information only, thus, it becomes unstable when the sample size in area d is small. In particular, the direct estimates may return large variability. In addition, the estimator cannot be computed for areas with zero sample sizes. Hence, model-based small area estimation methods that ’borrow strength’ from auxiliary information via the use of statistical models are used to produce accurate and precise small area estimates of the target parameter given by 1 (Rao and Molina 2015).
2.2 The bivariate binomial-logit mixed model
Statistical models with random area-specific effects taking into account for between and within areas variability are often used to build indirect small area estimators. As we preliminary stated in the Introduction, the small area EPP for proportions under a GLMM with logit link function is widely adopted in the literature and Official Statistics. We refer to Chandra et al. (2012, 2018); Molina and Strzalkowska-Kominiak (2020); Rao (2003); Rao and Molina (2015) for detailed discussions around this topic.
In Sect. 2.1, we assumed that \(y_{dik}\) is binary, i.e., \(y_{dik} = 0\) or 1. Suppose \({\mathbf {x}}_{dik}\) denotes the vector of observed values of p unit-level auxiliary information (including intercept) for unit i in area d related to \(y_{dik}\), which is the observation of variable k for unit i in area d.
Let \(\pi _{dik}\) be the probability that unit i in small area d assumes value equal to 1 related to variable k. We assume that the following bivariate GLMM with logistic link function relates \({\mathbf {x}}_{dik}\) to \(y_{dik}\), for \(i=1,...,N_d\), \(d=1,...,D\) and \(k=1,2\) (Coull and Agresti 2000; Rabe-Hesketh and Skrondal 2001; Berridge and Crouchley 2011):
where \(\varvec{\beta }_K\) is a p-dimensional vector of regression coefficients for response k, \(u_{dk}\) is the random area effect for area d and response k, and it measures the difference between the average of the variable for area d and its average in the entire sample. Therefore, the random area effects take into account for the variability that is not explained by the fixed effects. We assume these following a bivariate Normal distribution, i.e. \({\mathbf {u}}_d=(u_{d1},u_{d2})^T \sim N({\mathbf {0}}, \varvec{\Sigma }_u)\), where \(\varvec{\Sigma }_u\) denotes a \(2 \times 2\) an unknown positive-definite variance-covariance matrix. Its off-diagonal elements are the covariances between \(u_{dv}\) and \(u_{dj}\) with \(v \ne j\).
Furthermore, we assume that \(y_{dik}|u_{dk} \sim \text {Binomial}(1, \pi _{dik})\) with \(\pi _{dik} = \text {E}(y_{dik}|u_{dk})\). Thus, it holds that (Gueorguieva 2001; Coull and Agresti 2000; Rabe-Hesketh and Skrondal 2001):
That is the characteristic for unit i in area d related to a specific variable k is Bernoulli distributed conditionally on the random effects (Jiang et al. 2019).
Note that when the covariances between \(u_{dv}\) and \(u_{dj}\) with \(v \ne j\) are equal to 0, model 3 and 4 is equivalent to two separate GLMM models for the two response variables (Gueorguieva 2001).
Model 3 and 4 can be written for the sample elements \(i=1,...,n_d\) without loss of generality. Hence, the model parameters are estimated on a random sample s drawn from U (Rao and Molina 2015).
In order to estimate the model parameters we follow the Maximum Likelihood (ML) approach. We refer to McCulloch (1997), McCulloch (1994) and Booth and Hobert (1999) for the theory and Berridge and Crouchley (2011) for its implementation. In addition, we also refer to Rabe-Hesketh and Skrondal (2008), Skrondal and Rabe-Hesketh (2004) and Gueorguieva (2001) for other practical implementations.
2.3 Small area predictor
We can now present the Empirical Plug-in Predictor of the small area proportions for area d under 3 and 4 introduced in Sect. 2.2. This is given as follows:
with \({\hat{\mu }}_{dik} = {\hat{E}}(y_{dik }| u_{dk}) = \text {exp}({\mathbf {x}}_{dik}^T \hat{\varvec{\beta }}_k+ {\hat{u}}_{dk}) [1 + \text {exp}({\mathbf {x}}_{dik}^T \hat{\varvec{\beta }}_k+ {\hat{u}}_{dk})]^{-1}\), where \(\hat{\varvec{\beta }}_k\) and \({\hat{u}}_{dk}\) denote the estimates of the regression coefficients and predictions of random effects, respectively.
In practice, the auxiliary variables are available for the sample units and area-specific aggregates are available for the population, e.g. from the Census or administrative data. Thus, 5 cannot be applied and a modification is available in the literature (Rao and Molina 2015; Chandra et al. 2018). In the economy of space, we write the estimator only for the general proportion k, that is given by, assuming small sampling fractions:
where \({\hat{p}}_{dk}=n_d^{-1} \sum _{i \in s_d} y_{dik}\) , \(f_d=\frac{n_d}{N_d}\), and \(\bar{{\mathbf {X}}}_{dk}\) denotes the means of the auxiliary variable for the population (e.g., from the Census).
3 Mean squared error estimation via parametric bootstrap
In this section, we describe a parametric bootstrap algorithm we used to estimate the Mean Squared Error of \({\hat{p}}_{dk}^{EPP1}\), denoted by \(MSE({\hat{p}}_{dk}^{EPP1})\). This type of bootstrap for GLMM with logit link function is well-known and widely studied in the literature. The reader may want to refer to González-Manteiga et al. (2007) where its properties are also evaluated. There are also applications of this algorithm in the literature, such as in Chandra et al. (2018) and Hobza et al. (2018). Moreover, the algorithm is extended in small area estimation under bivariate mixed models e.g. Moretti et al. (2020b) following the same ideas.
The parametric bootstrap algorithm steps are the following:
-
1.
Estimate the GLMM given in Sect. 2.2 on the random sample s and the following estimates are obtained: \(\hat{\varvec{\Sigma }}_u\) and \(\hat{\varvec{\beta }}_k\) for \(k=,1,2\).
-
2.
Generate the bootstrap area-specific effects as follows \({\mathbf {u}}_d^{*(b)} \sim N({\mathbf {0}}, \hat{\varvec{\Sigma }}_u)\). ’*’ denotes the bootstrap quantities and b denotes the \(b^{th}\) bootstrap replication, \(b=1,...,B\).
-
3.
Calculate the true proportion for variable k and small area d of the bootstrap population:
$$\begin{aligned} {\hat{p}}_{dk}^{*(b)} = \text {exp}(\bar{{\mathbf {X}}}_{dk} \hat{\varvec{\beta }}_k + u_d^{*(b)}) [1 + \text {exp}(\bar{{\mathbf {X}}}_{dk} \hat{\varvec{\beta }}_k + u_d^{*(b)})]^{-1} \end{aligned}$$(7) -
4.
Generate the bootstrap responses \(y_{dik}^{*(b)}\) according to model in Sect. 2.2 as follows:
$$\begin{aligned}&y_{dik}^{*(b)} | u_{dk}^{*(b)} \sim \text {Binomial} (1, \pi _{dik}^{*(b)}), \nonumber \\&\text {with}, \pi _{dik}^{*(b)}= \text {exp}(\bar{{\mathbf {x}}}_{dik}^T \hat{\varvec{\beta }}_k + u_d^{*(b)}) [1 + \text {exp}(\bar{{\mathbf {x}}}_{dik}^T \hat{\varvec{\beta }}_k + u_d^{*(b)})]^{-1}, i \in s_d. \end{aligned}$$(8) -
5.
Estimate model in Sect. 2.2 on the responses generated at Step 4 and obtain the bootstrap EPP1 according to 6. This is denoted by \({\hat{p}}_{dk}^{EPP1*(b)}\).
-
6.
Repeat steps 2-5 B times, and the bootstrap estimator for the MSE of \({\hat{p}}_{dk}^{EPP1.1}\) is given by:
$$\begin{aligned} {\hat{MSE}}_{boot}({\hat{p}}_{dk}^{MEPP1}) = B^{-1} \sum _{b=1}^B \left( {\hat{p}}_{dk}^{EPP1*(b)} - {\hat{p}}_{dk}^{*(b)} \right) ^2, \end{aligned}$$(9)for \(d=1,...,D\) and \(k=1,2\).
In this article we choose \(B=500\) (Hobza et al. 2018).
There are other bootstrap algorithms that are helpful in case of dependent data. This is an area of ongoing research in small area estimation. We can find some applications of block bootstrap in (Mokhtarian and Chambers 2013). Wild bootstrap is also study in (Rojas-Perilla et al. 2020) in case there are some mild model failures such as non-normality after using transformations (see also Feng et al. (2011)).
4 Model-based simulation study
In this section, we present the results of a model-based simulation study designed to evaluate the performances of the bivariate predictor of small area proportions compared to the univariate case under different scenarios. In addition, we also evaluate the performance of the MSE bootstrap estimator described in Sect. 3. Given the computational burdens, this has been carried out for some scenarios only.
In order to choose the setting of this simulation, we follow model-based simulation studies in small area estimation (see Chambers et al. (2016) and González-Manteiga et al. (2007)).
All the computations in this section are produced in R. The mixed models parameter estimates are computed using the software developed by Crouchley and Crouchley (2012).
4.1 Simulation parameters
In this section, we show all the parameters used to generate the population in Sect. 4.2 (first bullet point) so that the experiment can be replicated by users.
Two binary response variables are generated in the population according to the GLMM model introduced in 3 and 4 with the following parameters:
-
regression coefficients, \(\varvec{\beta _1} = (0.05 , 1)\), and \(\varvec{\beta _2} = (0.05 , 2)\). The first element of each vector is related to the intercept.
-
area-specific random effect are generated from a bivariate Normal distribution (according to assumption in model 3 and 4 ): \({\mathbf {u}}_d \sim N({\mathbf {0}}, \varvec{\Sigma }_u)\), with variance-covariance matrix: \(\varvec{\Sigma }_u = \begin{bmatrix} \sigma _{u1}^2 &{} \rho _{u} \cdot \sqrt{\sigma _{u1}^2 \cdot \sigma _{u2}^2} \\ \rho _{u} \cdot \sqrt{\sigma _{u2}^2 \cdot \sigma _{u1}^2} &{} \sigma _{u2}^2 \end{bmatrix}\).
\(\sigma _{u1}^2\) and \(\sigma _{u2}^2\) denote the variances of the random effects related to responses 1 and 2, respectively. \(\rho _u\) denotes the correlation coefficient. We choose two realistic levels of correlation in \(\varvec{\Sigma }_u\) (small and large correlation) i.e. \(\rho _{u} =\{0.09, 0.40\}\).
Regarding the values of the variances \(\sigma _{u1}^2\) and \(\sigma _{u2}^2\), these are chosen as a function of the intraclass correlation. This is practice in model-based simulation studies in small area estimation (see e.g. Moretti and Whitworth (2020), Moretti et al. (2020a) and Burgard and Münnich (2014)). Indeed, the variability of small area estimators depends on this coefficient (Moretti and Whitworth 2020; Moretti et al. 2020a) and it affects the accuracy of mixed models parameter estimates (see Goldstein (2011)).
The intraclass correlation coefficient, denoted by \(\text {ICC}_k\) for variables \(k=1,2\), gives information on the partition of the total variance which is between-areas and within-areas. In particular, it measures the degree of homogeneity of the units belonging to the same areas and is between 0 and 1.
The intraclass correlation of variable \(k = 1, 2\) in case of generalised mixed models with logit link function is given as follows (Guo and Zhao 2000):
As outlined in Table 1 below, we chose a wide range of ICC values. For example, for a fixed ICC equal to 0.18, one can obtain the variance \(\sigma _{uk}^2\) by solving this for \(\sigma _{uk}^2\) : \(0.18 = \frac{{\sigma }_{uk}^{2}}{{\sigma }_{uk}^{2} + \frac{\pi ^3}{3}}.\)
As pointed in Moretti and Whitworth (2020), in the social sciences, the intraclass correlation does not often assume very large values. For example, in economic wellbeing indicators Moretti et al. (2021) note an ICC close to 0.20. Whereas, in medical or agricultural applications, the intraclass correlation coefficient can reach large values (Koo and Li 2016; Pleil et al. 2018). Regarding ICC in health indicators we refer also to (Castelli et al. 2013), where large ICCs e.g. about 0.40 are noted.
The population size in each small area d is \(N_d=100\), and the number of areas is equal to \(D=50\). We keep this in small scale for computational reasons. The auxiliary variable is generated from a Uniform distribution i.e. \(x_{di} \sim \text {Unif}(-1,20)\), and it is kept fixed over the simulations.
Table 1 shows the scenarios that we consider in this simulation study.
4.2 Simulation steps
The simulation consists in the following steps, where \(l=1,...,L\), with \(L=500\) denotes the repetitions:
-
1.
Generate the population values \(U^{l} = \cup _{d=1}^{D} U_d^{(l)}\) where \(U_d^{(l)} = \{( y_{di1}^{(l)}, y_{di2}^{(l)}, x_{di}), i=1,...,N_d \}\) \(y_{di1}^{(l)}\) and \(y_{di2}^{(l)}\) are generated according to the bivariate model given in 3 and 4 with parameters presented in Sect. 4.1.
-
2.
Sampling: select a random sample \(s^{(l)}_d\) without replacement of size \(n_d=5\) from \(U_d^{(l)}\) for \(d=1,...,D\). We also evaluate an additional scenario where \(n_d\) varies across small areas, and in this case \(n_d \sim \text {Unif}(1, 10)\) (values are rounded). This is to evaluate the impact of the sample size in area d onto the estimators.
-
3.
Estimate the bivariate model given in 3 and 4 and its univariate version in each sample \(s^{(l)}_d\) and obtain the univariate and bivariate predictors for both small area proportion using 6. These are denoted, for variable \(k=1,2\), by \(\hat{{\bar{y}}}^{MEPP1(l)}_{d1}\), \(\hat{{\bar{y}}}^{MEPP1(l)}_{d2}\) and \(\hat{{\bar{y}}}^{UEPP1(l)}_{d1}\), \(\hat{{\bar{y}}}^{UEPP1(l)}_{d2}\), for the bivariate and univariate case, respectively. The direct estimates are also calculated and denoted by \(\hat{{\bar{y}}}^{DIR(l)}_{d1}\), \(\hat{{\bar{y}}}^{DIR(l)}_{d2}\)
For some scenarios only (A, C, F, see Table 1 for the details) we evaluate the bootstrap MSE estimator described in Sect. 3.
-
4.
The following measures of performance are also calculated in order to evaluate the estimators for \(k=1,2\) in both the univariate and bivariate case (here, \({\bar{y}}_{dk}^{(l)}\) denotes any estimator for \({\bar{y}}_{dk}\), for proportion k and area d):
Absolute Relative Bias (ARB)
$$\begin{aligned} \text {ARB}(\hat{{\bar{y}}}_{dk}) = \left|\frac{L^{-1} \sum _{l=1}^{L} (\hat{{\bar{y}}}_{dk}^{(l)} - {\bar{y}}_{dk}^{(l)})}{L^{-1} \sum _{l=1}^L {\bar{y}}_{dk}^{(l)}} \right|, \end{aligned}$$(11)Root Mean Squared Error (RMSE)
$$\begin{aligned} \text {RMSE}(\hat{{\bar{y}}}_{dk}) = \sqrt{L^{-1} \sum _{l=1}^{L} (\hat{{\bar{y}}}_{dk}^{(l)} - {\bar{y}}_{dk}^{(l)})^2}, \end{aligned}$$(12)Relative Root Mean Squared Error (RRMSE)
$$\begin{aligned} \text {RRMSE}(\hat{{\bar{y}}}_{dk}) = \frac{\sqrt{L^{-1} \sum _{l=1}^{L} (\hat{{\bar{y}}}_{dk}^{(l)} - {\bar{y}}_{dk}^{(l)})^2}}{L^{-1} \sum _{l=1}^L {\bar{y}}_{dk}^{(l)}}, \end{aligned}$$(13)where \({\bar{y}}_{dk}^{(l)}=N_d^{-1}\sum _{i=1}^D y_{dik}^{(l)}\).
% Relative Reduction in Terms of RMSE (RelRed%)
$$\begin{aligned} \text {RelRed}(\hat{{\bar{y}}}_{dk})\% = L^{-1} \sum _{l=1}^L \frac{\text {RMSE}(\hat{{\bar{y}}}^{MEPP1(l)}_{dk}) - \text {RMSE}(\hat{{\bar{y}}}^{UEPP1(l)}_{dk})}{\text {RMSE}(\hat{{\bar{y}}}^{UEPP1(l)}_{dk})} \times 100. \end{aligned}$$(14)
Equation 14 can be seen as a measure of efficiency, since our hypothesis is that the RMSE of the bivariate small area estimator is smaller than its univariate setting (Moretti et al. 2020a). In order to present summary statistics, the median across the small areas D is shown as a robust central tendency measure that avoids the impact of extreme values in some small areas (Giusti et al. 2014). The mean values across the small areas are also presented in parenthesis in the outputs. In this case, the same notation as above is used but the index ’d’ is dropped.
4.3 Results
In this section, we present the results of the simulation study. In order to present results relevant to users, we split this section according to the focus of the discussion.
In particular, we are investigating how the correlation in the variance-covariance matrix of the random effects, intraclass correlation and sample size impact on the the quality measures.
4.3.1 Summary of model parameter estimates
Table 2 shows the evaluation of the bivariate model parameter estimates of \(\beta\) and \(\varvec{\Sigma }_u\). In order to evaluate their quality we show the averages of the estimates of those across the simulations S. The biases were negligible, i.e. very close to zero, hence they have been omitted. \({\hat{\sigma }}_1^{2}\), \({\hat{\sigma }}_2^{2}\) and \({\hat{\rho }}\) are the averages across the simulations of the elements in \(\varvec{\Sigma }_u\). These results can be compared to the true values that are used to generate the population and given in Table 1 above.
4.3.2 Role of correlation \(\rho _u\) (Scenarios A and B)
In this section, we present the results of the impact of the correlation coefficients \(\rho _u\) between random effects on the quality measures. In particular, we are focusing in scenarios A and B (Table 1), with \(\rho _u = \{0.09, 0.40\}\).
Table 3 shows the median across the small areas of the RRMSE and Table 4 shows the median across the small areas of the absolute relative bias of the estimators for both \(\rho _u=0.09\) and \(\rho _u=0.40\) cases. Mean values are shown in parenthesis.
Overall, looking at Table 3, in line with the literature, we can see smaller RRMSE when model-based small area estimates are used compared to direct estimates. We can also see that the bivariate predictor provides estimates with smaller RRMSE than the univariate case, and this is in line with the bivariate small area estimation literature of continuous response variables (see e.g. Datta et al. (1999) and Moretti et al. (2020a)).
In addition, it can be seen from Table 4 that both the predictors provide small area estimates with a negligible ARB; both the bivariate and univariate predictors produce estimates with a very small bias. We also calculated the relative bias, however, these are also close to zero, hence, negligible. Thus, we present the ARB only.
Table 5 shows the median values of the percentage relative reductions in terms of root mean squared error of the small area estimates across the areas varying \(\rho _u\) i.e. \(\rho _u=\{0.09,0.40\}\). Mean values are shown in parenthesis. For example, in Table 5\(RelRed({\hat{{\bar{y}}}_{1}})\) relates to the % relative difference in terms of RMSE of the bivariate predictor over the univariate predictor for \(k=1\) proportion. Larger gains in efficiency are obtained when \(\rho _u=0.40\). When \(\rho _u\) becomes smaller, \(\rho _u=0.09\), there are still good performances in terms of efficiency of the bivariate estimator over the univariate estimator. If \(\rho _u=0\), the bivariate case corresponds to the univariate case and the performances of the estimators would be the same (see e.g. Datta et al. (1999)).
4.3.3 Role of intraclass correlation \(ICC_k\) (Scenarios B, C, D, E)
In this section, we present the results of the impact of the intraclass correlation on the quality measures of the estimators. Particularly, we are considering scenarios B, C, D and E of Table 1 where different levels of intraclass correlations are selected.
We show in Table 6 the % relative reductions in terms of RMSE of the small area estimators under different level of ICC, indicated again in the table to compare the results easily.
It can be seen that, the largest gains in efficiency of using the bivariate predictor over the univariate predictor are obtained when the intraclass correlation is large. In this case, the variables borrow more strength from each other, achieving larger reduction in terms of RMSE. The smaller the intraclass correlation, the higher is the improvement of the model-based estimates over the direct estimates. Thus, we expect that the univariate estimates return a large efficiency already, compared to the direct estimates. Therefore, the reductions in terms of RMSE of the bivariate estimates compared to their univariate setting are modest here. Although, as shows in Table 6 there are still gains in efficiency of using the bivariate estimator over its univariate setting in case of smaller ICC (see scenario E).
We present in Table 7 the ARB of the small area estimators under different level of ICC. We still can see that the small area estimates produced by the model-based estimators show a negligible small ARB. Smaller biases can be observed in case of larger ICC.
4.3.4 Role of the area sample size \(n_d\) (Scenario F)
We present now the results of scenario F, which we reminder to the reader, is the scenario where the sample size in area d, \(n_d\), varies across areas i.e. between 1 and 10. This is to evaluate the impact of the \(n_d\) onto the small area estimates. As exercise, we also run a small scale simulation study where \(n_d\) varied between 20 and 50, and we observed similar patterns to what we found here under scenario F. In the economy of space, those results are omitted.
We found that there is a moderate relationship between the percentage relative reductions in terms of RMSE and the small area sample size. In fact, the estimates of Pearson correlation coefficient between \(n_d\) and \(RelRed({\hat{{\bar{y}}}_{1}})\) and \(RelRed({\hat{{\bar{y}}}_{2}})\) are modest and equal to − 0.163 and − 0.129, respectively. This means that when the area sample size becomes larger, the percentage relative reductions in terms of RMSE of using the bivariate predictor over the univariate predictor become smaller. However, this relationship is not large. The median values across the areas of the % Relative Reductions are equal to − 11.607% and − 41.959% for \(k=1\) and \(k=2\), respectively. We present the ARB and RRMSE of the model-based small area estimators in Table 8. This shows that the estimates present a negligible bias and that there is a gain in efficiency by using the bivariate estimator over the univariate predictor. This is consistent to our previous results of the sections above.
We also depict in Figs. 1 and 2 the RRMSE of the model-based estimators, univariate versus bivariate case, for the small area means of the responses \(k=1,2\), respectively. The estimates are ordered by growing sample size in area d. The dotted line shows the RRMSE for the bivariate estimator, whereas the continuous line shows the RRMSE of the univariate estimator. As noted above, we can see gains in efficiency when the bivariate predictor is used, and these are larger for the second response, given that its ICC is larger than the one of reponse \(k=1\) (Fig. 2).
4.3.5 Evaluations of the bootstrap MSE
In this section, we present the evaluation of the bootstrap MSE estimator. Since simulation studies to evaluate bootstrap MSE estimators are computationally heavy, we focus on some of the scenarios only, i.e. A, C, and F. Table 9 shows the Empirical MSE (EMSE), the average values of the bootstrap MSE across the simulations and their ARB. Median (and average) values across the small area are presented as summary statistics, as in the tables above.
By looking at Table 9 it can be seen that, the bootstrap algorithm presented in this article provides good estimates of the EMSE of the bivariate small area estimators. In fact, the average of the bootstrap MSE across the simulation approximates well the EMSE. In addition, the ARB are negligible (i.e., very close to zero). This is in line with other studies in bivariate small area estimation on the bootstrap MSE estimation (see, Moretti et al. (2020b)).
4.4 Final remarks on the simulation study
This simulation study shows good performances of the bivariate small area predictor under all the scenarios considered. By good performance, we mean that the bivariate approach does not introduce bias in the estimates, thus, it provides estimates with smaller variance. This shows that the bivariate small area estimates are more efficient than the univariate small area estimates. Larger gains in efficiency are obtained when the correlation in \(\varvec{\Sigma }_u\) (\(\rho _u\)) is larger. Even when the correlation is smaller, equal to 0.09, we can see good gains in efficiency, i.e. the mean squared error is smaller, thus the efficiency improves. The bivariate predictor provides more efficient estimates when the intraclass correlation increases. When this is small instead, we notice a smaller gain, but the results are still satisfactory. We do not find a strong relationship between small area sample size and gains in efficiency, indeed, the relationship was moderate under the scenarios considered.
5 Application
In this section, we present an application where the performances of the univariate EPP are compared to the bivariate EPP. For the estimators i.e. EPP and bootstrap MSE related to the univariate case we refer to Chandra et al. (2018), Molina and Strzalkowska-Kominiak (2020), and Rao and Molina (2015).
5.1 Data
Data from Lehtonen and Veijanen (2016) is used and this is available from Pratesi (2016). The data was derived from AMELIA data (see Burgard et al. (2017) and Lehtonen and Veijanen (2016) for the details). AMELIA is a synthetic dataset that allows for comparative and reproducible research. The aim of the project was to generate a synthetic and realistic data based on European Union Statistics for Income and Living Conditions (EU-SILC) variables. Although the data is not a real dataset, it mimics the statistical properties of the real data behind (Burgard et al. 2017).
In particular, the sample size is equal to \(n=2000\) and we use the “Districts” (\(D=40\)) as small areas with sample sizes ranging between 25 and 84 and average sampling fraction \({\bar{f}}_d=0.002\).
We create two binary variables and their proportions are the target parameters for which we produce the small area estimates. Based on the variable RB210 (Basic activity status) we create a binary variables called ’Employed’, \(Y_1\), taking value 1 if the unit is employed and 0 otherwise. We also create another variable, \(Y_2\) which is called ’Poor’. This variable takes value 1, denoting that the unit is poor, if the value of the income of the unit is below the poverty line calculated as 60% of the median of the income (Chatterjee 2011).
5.2 Small area estimates
The target parameters are the proportion of employed people and people with an income below the poverty line. We compute the direct estimates and their standard deviations using the survey weights according to (2); these are denoted by \({\hat{p}}_d^{Employed, DIR}\) and \({\hat{p}}_d^{Poor, DIR}\), respectively, for \(d=1,...,40\). In addition, model-based small area estimates are computed under the univariate GLMM and bivariate GLMM for both proportions. The following auxiliary variables are used: Age, Sex, Education level (Highest ISCED level attained) and Degree of urbanisation. These are available for the sample and aggregates are available for the population. The estimates of the variance components of the models are \({\hat{\sigma }}_u^{2Employed}=0.195\) and \({\hat{\sigma }}_u^{2Poor}=0.040\) for the univariate GLMMs and \(\hat{\varvec{\Sigma }}_u=\begin{bmatrix} 0.195 &{} -0.010\\ -0.010 &{} 0.040 \end{bmatrix}\) , for the bivariate GLMM.
We also check the normality of the random effects estimated from both univariate and bivariate models and the Kolmogorov-Smirnov test (with \(\alpha =0.05\)) is performed to investigate the normality of the area-specific random effects predicted for both the univariate and bivariate GLMMs. The null hypothesis of the test is that the data is normally distributed. The results, with p-value in parenthesis, for the univariate case are 0.161 (0.224) and 0.091 (0.864) for employed and poor, respectively; and for the bivariate case 0.068 (0.986) and 0.103 (0.755) for employed and poor, respectively. Given that the p-value are larger than \(\alpha =0.05\), we cannot reject the null hypothesis and we can say that the distributions of the random effects are not statistically different from the normal distribution.
Figures 3 and 4 show the Relative Root Mean Squared Error (RRMSE) % of the small area estimates for employed and poor proportions, respectively. These are ordered by growing sample size. The RRMSE of the direct estimates can be approximated by the coefficient of variation (standard deviation divided by direct estimate) (Rao and Molina 2015).
It can be seen that, in line with the simulation study, the use of the bivariate GLMM provides more efficient estimates that the univariate model for both small area proportions. The median percentage relative reductions in terms of RMSE across the areas is 48.8% for employment and 26.4% for poor, showing important gains in efficiency. We can also see that the RRMSE% estimates of the small area proportions obtained via the bivariate predictors are all below 20%, thus, reliable for many statistical agencies, see for example Commonwealth Department of Social Services (2015).
6 Conclusion
In this article, we studied the bivariate small area estimation problem of proportions. This is an important problem in applications, since many variables present a binary nature. For example, many variables related to labour force, deprivation, poverty, health are binary. Here, we focus on the problem of providing small area estimates based on sample surveys that are not representative for small domains. We recognise that the use of geo-referenced administrative data is still important to study social phenomena. However, there might some privacy and confidentiality issues regarding their access at small area level. In addition, the availability of administrative data varies depending on the country. Future research will take into account for it. Sample surveys, such as the European Statistics on Income and Living Conditions (EU-SILC), are still very much important to study social phenomena, since they contain crucial information on poverty and social exclusion variables, and they can be used to estimate a large variety of poverty indicators, such as the Laeken indicators (see also Betti and Lemmi (2013)).
In this work, we compared the univariate empirical plug-in predictor i.e. EPP under a unit-level generalised linear mixed model (GLMM) with logit link function to its bivariate extension. As mentioned in the Introduction, the univariate predictor is used by statistical agencies given its good properties and simplicity. The performances of the small area estimators are compared via a model-based simulation study and an application. Our results show that the use of the bivariate generalised mixed model provides more efficient small area estimates of proportions compared to the use of its univariate setting in all scenarios considered. We found that good gains in efficiency can also be seen when the correlation of the area-specific random effects is small e.g. \(\rho =0.09\). This is an important result, since in applications correlations may be small. Of course, as expected, larger gains are obtained when the correlation is large. It is however important to stress that the performances of the multivariate estimator depend also on the intraclass correlation coefficient. In fact, these gains in efficiency become larger when the intraclass correlation increases. Thus, larger correlation between random effects does not always guarantee a large reduction in the mean squared error. We did not find a large effect of the area sample size on the quality measures considered. In fact, the relationship is rather modest. We can also see that the RRMSE% values of the small area proportions obtained via the bivariate predictors are all below 20%, thus, reliable for many statistical agencies for example Statistics Canada (Spagnolo et al. 2018).
Our findings are in line with those from the multivariate small area estimation for continuous outcome variables (Moretti et al. 2020a, b), these results have been studied theoretically in Datta et al. (1999) for the Normal case. However, (Normal) continuous variables are rarely present in real data, especially, in poverty and well-being field. Our results pose the basis for extending the use of bivariate generalised mixed models in small area estimation of social indicators, given the different types of variables that are available in social surveys (e.g., binary, count, ordinal etc.).
In practice, when multivariate regression models are applied, users need to consider model selection issues, taking into account for the choice of a response distribution and predictors. The reader may want to refer to Klein et al. (2015), where the authors discuss guidelines that facilitate the model choice in presence of multivariate models. In summary, regarding model choice in multivariate distributional regression, the Deviance Information Criterion (DIC) (Spiegelhalter et al. 2002), normalized quantile residuals (Dunn and Smyth 1996), and proper scoring rules (Gneiting and Raftery 2007) are studied in the literature. In order to evaluate sensitivity against distributional choices, we also recommend to perform simulation studies, which can be based on real data that users aim to use in their applications.
The object of this article was the bivariate case. However, extensions to more than two outcomes can be derived. Here, computational problems need to be considered. In the multivariate small area estimation literature (Moretti et al. 2020a) consider four responses for the continuous case, and show good performances (in terms of bias and mean squared error) of the multivariate approach compared to the univariate approach. To overcome issues where the aim is to estimate many single indicators, they propose the use of data dimensionality reduction techniques, such as factor analysis. Thus, the multivariate small area estimation problem can be reduced to a small number of variables (in their application on well-being two variables). Their work can be interestingly extended to the binary variables scenario.
In case one is interested in estimating one indicator only, other small area estimation techniques can be used to improve the small area estimates obtained via traditional methods. For example, the use of spatial models where borrowing strength from related small area can produce more reliable estimates (Pratesi and Salvati 2008).
We argue that the use of bivariate small area estimators is very useful for data users. In fact, auxiliary variables may not be good enough to explain the between areas variation. Users might be restricted to the use of these variables for privacy and confidentiality reasons, thus they need to rely on covariates that suffer from that issue. As pointed in Benavent and Morales (2016) the use of complex statistical modelling, taking into account for additional relationships between variables can produce small area estimates with higher quality i.e. in terms of precision, than simpler models such as univariate models.
Since multivariate small area estimation of proportions is a field under investigation, there are still areas that need to be explored. In particular, in this article we considered a parametric bootstrap approach to estimate the mean squared error of the small area predictors. This is a well-known algorithm applied in small area estimation (see Rao and Molina (2015)). However, analytical methods based on a linearization techniques need to be studied in small area estimation under multivariate GLMM. Thus, comparisons to the boostrap mean squared error can be carried out, as it is practice in small area estimation. This topic is highly challenging in under multivariate GLMM. Model-robust approaches related to parametric bootstrap methods under GLMM in the multivariate setting are also interesting future areas of research. Future research will also consider other bootstrap approaches under this model, e.g., wild and block bootstraps, these are studied in the literature for other types of models (see Mokhtarian and Chambers (2013); Rojas-Perilla et al. (2020)). The use of generalised models using other link functions in small area estimation is another interesting topic of further work. Spatial extensions of this model need also to be considered where random area effects depend on a spatial process which may improve the small area estimates. In the multivariate small area estimation literature, there is some work on the use of spatial models, however, this is for the area-level case (see for example Porter et al. (2015)). There is potential to use these models in the context of unit-level multivariate small area estimation as well.
References
Aitchison, J.: The statistical analysis of compositional data. J. Royal Stat. Soc. Series B (Methodol.) 44(2), 139–160 (1982)
Baíllo, A., Molina, I.: Mean-squared errors of small-area estimators under a unit-level multivariate model. Statistics 43(6), 553–569 (2009)
Bel, K., Fok, D., Paap, R.: Parameter estimation in multivariate logit models with many binary choices. Econom. Rev. 37(5), 534–550 (2018)
Benavent, R., Morales, D.: Multivariate fay-herriot models for small area estimation. Comput. Stat. Data Anal. 94, 372–390 (2016)
Berridge, D.M., Crouchley, R.: Multivariate Generalized Linear Mixed Models Using R. CRC Press, Boca Raton (2011)
Betti, G., Lemmi, A.: Poverty and Social Exclusion: New Methods of Analysis. Routledge, London (2013)
Booth, J.G., Hobert, J.P.: Maximizing generalized linear mixed model likelihoods with an automated monte carlo em algorithm. J. Royal Stat. Soc. Series B (Stat. Methodol.) 61(1), 265–285 (1999)
Burgard, J.P., Kolb, J.-P., Merkle, H., Münnich, R.: Synthetic data for open and reproducible methodological research in social sciences and official statistics. AStA Wirtschafts-und Sozialstatistisches Archiv 11(3–4), 233–244 (2017)
Burgard, J.P., Münnich, R.: Sae teaching using simulations (2014)
Cappellari, L., Jenkins, S.P.: Calculation of multivariate normal probabilities by simulation, with applications to maximum simulated likelihood estimation. Stata J. 6(2), 156–189 (2006)
Castelli, A., Jacobs, R., Goddard, M., Smith, P.C.: Health, policy and geography: insights from a multi-level modelling approach. Soc. Sci. Med. 92, 61–73 (2013)
Chambers, R., Salvati, N., Tzavidis, N.: Semiparametric small area estimation for binary outcomes with application to unemployment estimation for local authorities in the uk. J. Royal Stat. Soc. Series A (Stat. Soc.) 179(2), 453–479 (2016)
Chandra, H., Chambers, R., Salvati, N.: Small area estimation of proportions in business surveys. J. Stat. Comput. Simul. 82(6), 783–795 (2012)
Chandra, H., Kumar, S., Aditya, K.: Small area estimation of proportions with different levels of auxiliary data. Biom. J. 60(2), 395–415 (2018)
Chatterjee, D.K.: Encyclopedia of Global Justice: A-I. Springer Science & Business Media, Berlin (2011)
Commonwealth Department of Social Services (2015). Survey of disability, ageing and carers, 2012. modelled estimates for small areas, projected 2015. Australian Bureau of Statistics, Release 1
Coull, B.A., Agresti, A.: Random effects modeling of multiple binomial responses using the multivariate binomial logit-normal distribution. Biometrics 56(1), 73–80 (2000)
Crouchley, R., Crouchley, M.R.: Package ‘sabrer’ (2012)
Datta, G.S., Day, B., Basawa, I.: Empirical best linear unbiased and empirical bayes prediction in multivariate small area estimation. J. Stat. Plan. Inference 75(2), 269–279 (1999)
Dunn, P.K., Smyth, G.K.: Randomized quantile residuals. J. Comput. Graph. Stat. 5(3), 236–244 (1996)
Edwards, Y.D., Allenby, G.M.: Multivariate analysis of multiple response data. J. Market. Res. 40(3), 321–334 (2003)
Fabrizi, E., Ferrante, M.R., Pacei, S.: Estimation of poverty indicators at sub-national level using multivariate small area models. Stat. Trans. 7(3), 587–608 (2005)
Feng, X., He, X., Hu, J.: Wild bootstrap for quantile regression. Biometrika 98(4), 995–999 (2011)
Fuller, W.A., Harter, R.: The multivariate components of variance model for small area estimation. In: Platek, R., Rao, J.N.K., Sarndal, C.E., Singh, M.P. (Eds.), Small Area Statistics pp. 103-123 (1987)
Giusti, C., Tzavidis, N., Pratesi, M., Salvati, N.: Resistance to outliers of m-quantile and robust random effects small area models. Commun. Stat.-Simul. Comput. 43(3), 549–568 (2014)
Gneiting, T., Raftery, A.E.: Strictly proper scoring rules, prediction, and estimation. J. Am. Stat. Assoc. 102(477), 359–378 (2007)
Goldstein, H.: Multilevel Statistical Models, vol. 922. John Wiley & Sons, Hoboken (2011)
González-Manteiga, W., Lombardía, M.J., Molina, I., Morales, D., Santamaría, L.: Estimation of the mean squared error of predictors of small area linear parameters under a logistic mixed model. Comput. Stat. Data Anal. 51(5), 2720–2733 (2007)
Gueorguieva, R.: A multivariate generalized linear mixed model for joint modelling of clustered outcomes in the exponential family. Stat. Modell. 1(3), 177–193 (2001)
Gueorguieva, R., Rosenheck, R., Zelterman, D.: Dirichlet component regression and its applications to psychiatric data. Comput. Stat. Data Anal. 52(12), 5344–5355 (2008)
Guha, S., Chandra, H.: Measuring and mapping disaggregate level disparities in food consumption and nutritional status via multivariate small area modelling. Soc. Indic. Res. 154(2), 623–646 (2021)
Guo, G., Zhao, H.: Multilevel modeling for binary data. Ann. Rev. Sociol. 26(1), 441–462 (2000)
Hijazi, R.H., Jernigan, R.W.: Modelling compositional data using dirichlet regression models. J. Appl. Probab. Stat. 4(1), 77–91 (2009)
Hobza, T., Morales, D., Santamaría, L.: Small area estimation of poverty proportions under unit-level temporal binomial-logit mixed models. Test 27(2), 270–294 (2018)
Jiang, H.-Y., Yue, R.-X., Zhou, X.-D.: Optimal designs for multivariate logistic mixed models with longitudinal data. Commun. Stat.-Theory Methods 48(4), 850–864 (2019)
Jiang, J.: Empirical best prediction for small-area inference based on generalized linear mixed models. J. Stat. Plan. Inference 111(1–2), 117–127 (2003)
Jiang, J., Lahiri, P.: Empirical best prediction for small area inference with binary data. Ann. Inst. Stat. Math. 53(2), 217–243 (2001)
Jiang, J., Lahiri, P.: Mixed model prediction and small area estimation. Test 15(1), 1 (2006)
Klein, N., Kneib, T., Klasen, S., Lang, S.: Bayesian structured additive distributional regression for multivariate responses. J. Royal Stat. Soc. Series C (Appl. Stat.) 64(4), 569–591 (2015)
Koo, T.K., Li, M.Y.: A guideline of selecting and reporting intraclass correlation coefficients for reliability research. J. Chiropr. Med. 15(2), 155–163 (2016)
Lehtonen, R., Veijanen, A.: Model-assisted method for small area estimation of poverty indicators. Analysis of poverty data by small area estimation, 109–127 (2016)
López-Vizcaíno, E., Lombardía, M.J., Morales, D.: Multinomial-based small area estimation of labour force indicators. Stat. Modell. 13(2), 153–178 (2013)
MacGibbon, B., Tomberlin, T.J.: Small area estimates of proportions via empirical Bayes techniques. Citeseer (1987)
McCulloch, C.E.: Maximum likelihood variance components estimation for binary data. J. Am. Stat. Assoc. 89(425), 330–335 (1994)
McCulloch, C.E.: Maximum likelihood algorithms for generalized linear mixed models. J. Am. Stat. Assoc. 92(437), 162–170 (1997)
Mokhtarian, P., Chambers, R.: An outlier robust block bootstrap for small area estimation (2013)
Molina, I.: Uncertainty under a multivariate nested-error regression model with logarithmic transformation. J. Multivar. Anal. 100(5), 963–980 (2009)
Molina, I., Saei, A., José Lombardía, M.: Small area estimates of labour force participation under a multinomial logit mixed model. J. Royal Stat. Soc. Series A (Stat. Soc.) 170(4), 975–1000 (2007)
Molina, I., Strzalkowska-Kominiak, E.: Estimation of proportions in small areas: application to the labour force using the swiss census structural survey. J. Royal Stat. Soc. Series A (Stat. Soc.) 183(1), 281–310 (2020)
Moretti, A., Shlomo, N., Sakshaug, J.W.: Multivariate small area estimation of multidimensional latent economic well-being indicators. Int. Stat. Rev. 88(1), 1–28 (2020)
Moretti, A., Shlomo, N., Sakshaug, J.W.: Parametric bootstrap mean squared error of a small area multivariate eblup. Commun. Stat.-Simul. Comput. 49(6), 1474–1486 (2020)
Moretti, A., Shlomo, N., Sakshaug, J.W.: Small area estimation of latent economic well-being. Sociol. Methods Res. 50(4), 1660–1693 (2021)
Moretti, A., Whitworth, A.: Development and evaluation of an optimal composite estimator in spatial microsimulation small area estimation. Geogr. Anal. 52(3), 351–370 (2020)
Pleil, J.D., Wallace, M.A.G., Stiegel, M.A., Funk, W.E.: Human biomarker interpretation: the importance of intra-class correlation coefficients (icc) and their calculations based on mixed models, anova, and variance estimates. J. Toxicol. Environ. Health Part B 21(3), 161–180 (2018)
Porter, A.T., Wikle, C.K., Holan, S.H.: Small area estimation via multivariate fay-herriot models with latent spatial dependence. Aust. New Zealand J. Stat. 57(1), 15–29 (2015)
Pratesi, M.: Analysis of Poverty Data by Small Area Estimation. John Wiley & Sons, Hoboken (2016)
Pratesi, M., Salvati, N.: Small area estimation: the eblup estimator based on spatially correlated random area effects. Stat. Methods Appl. 17(1), 113–141 (2008)
Rabe-Hesketh, S., Skrondal, A.: Parameterization of multivariate random effects models for categorical data. Biometrics 57(4), 1256–1263 (2001)
Rabe-Hesketh, S., Skrondal, A.: Multilevel and longitudinal modeling using Stata. STATA press (2008)
Rao, J.: Some new developments in small area estimation (2003)
Rao, J., Molina, I.: Small Area Estimation. John Wiley & Sons, Hoboken (2015)
Rojas-Perilla, N., Pannier, S., Schmid, T., Tzavidis, N.: Data-driven transformations in small area estimation. J. Royal Stat. Soc. Series A (Stat. Soc.) 183(1), 121–148 (2020)
Salvati, N., Chandra, H., Chambers, R.: Model-based direct estimation of small-area distributions. Aust. New Zealand J. Stat. 54(1), 103–123 (2012)
Särndal, C.-E., Swensson, B., Wretman, J.: Model Assisted Survey Sampling. Springer Science & Business Media, Berlin (2003)
Skrondal, A., Rabe-Hesketh, S.: Generalized Latent Variable Modeling: Multilevel, Longitudinal, and Structural Equation Models. Chapman and Hall/CRC, Boca Raton (2004)
Slud, E.: Models for simulation and comparison of saipe analyses. Census Bureau preprint, posted at SAIPE web-site (see below) (1999)
Slud, E.: Small area estimation errors in saipe using glm versus fh models. In Proceedings of the American Statistical Association, Section on Survey Research Methods, pp. 4402–4409 (2004)
Spagnolo, F.S., D’Agostino, A., Salvati, N.: Measuring differences in economic standard of living between immigrant communities in italy. Qual. Quant. 52(4), 1643–1667 (2018)
Spiegelhalter, D.J., Best, N.G., Carlin, B.P., Van Der Linde, A.: Bayesian measures of model complexity and fit. J. Royal Stat. Soc. Series B (Stat. Methodol.) 64(4), 583–639 (2002)
Ubaidillah, A., Notodiputro, K.A., Kurnia, A., Mangku, I.W.: Multivariate fay-herriot models for small area estimation with application to household consumption per capita expenditure in indonesia. J. Appl. Stat. (2019)
Funding
The authors declare that no funds, grants, or other support were received during the preparation of this manuscript.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no relevant financial or non-financial interests to disclose.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Moretti, A. Estimation of small area proportions under a bivariate logistic mixed model. Qual Quant 57, 3663–3684 (2023). https://doi.org/10.1007/s11135-022-01530-6
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11135-022-01530-6