“… practitioners and researchers alike often forget that numbers are not all created equal”
(Abran et al. 2012, p. 585)
Abstract
Quantitative data are generated differently. To justify inferences about real-world phenomena and establish secured knowledge bases, however, quantitative data generation must follow transparent principles applied consistently across sciences. Metrological frameworks of physical measurement build on two methodological principles that establish transparent, traceable—thus reproducible processes for assigning numerical values to measurands. Data generation traceability requires implementation of unbroken, documented measurand-result connections to justify attributing results to research objects. Numerical traceability requires documented connections of the assigned values to known quantitative standards to establish the results' public interpretability. This article focuses on numerical traceability. It explores how physical measurement units and scales are defined to establish an internationally shared understanding of physical quantities. The underlying principles are applied to scrutinise psychological and social-science practices of quantification. Analyses highlight heterogeneous notions of ‘units’ and ‘scales’ and identify four methodological functions; they serve as (1) ‘instruments’ enabling empirical interactions with study phenomena and properties; (2) structural data format; (3) conceptual data format; and (4) conventionally agreed reference quantities. These distinct functions, employed in different research stages, entail different (if any) rationales for assigning numerical values and for establishing their quantitative meaning. The common numerical recoding of scale categories in tests and questionnaires creates scores devoid of quantitative information. Quantitative meaning is created through numeral-number conflation and differential analyses, producing numerical values that lack systematic relations to known quantity standards regarding the study phenomena and properties. The findings highlight new directions for the conceptualisation and generation of quantitative data in psychology and social sciences.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Current world record in women’s 100 metres race is 10.49 seconds. European neonates, on average, are 49.7 centimetres long and weigh 3.5 kilogrammes, which equals 7.7 pounds (Janssen et al. 2007). Quantitative information is ubiquitous in our lives. Crucially, we understand it all the same way. Indeed, our globalised world could not function without a shared understanding of quantitative information. But how is this actually achieved? In what ways are these numerical values assigned to quantities of length, time, weight and other properties to enable this global understanding?
Quantitative information is also used in social sciences and psychology. But their numerical data feature striking peculiarities—they are typically without measurement units (caution: not to be confused with scale types, e.g., featuring interval units; see below). That is, they do not specify a particular property to which the numerical values refer, as this is the case for quantitative information expressed in measurement units (e.g., metre units indicate the property of length, kilogram units indicate mass). For example, the Human Development Index 2019 of the nations’ average achievements regarding their people’s capabilities (Conceição 2019) lists for Norway an HDI-score of 0.954 and for Nepal of 0.579. But 0.579 of what? Without a unit indicating the property measured, such scores cannot be readily understood. Instead, their meaning is derived from comparisons with other countries’ scores, revealing that, out of 189 countries, Norway ranked 1st and Nepal 149th. But how much ‘human development’ do these ranks reflect? Numerical values without measurement units, commonly called scores, are also often generated with rating methods. Yet what does a ‘happiness’ rating score of 2.68 signify—how ‘happy’ is that? The meaning of rating scores, as well, is derived from comparisons (e.g., between individuals). But why is that so? How are quantitative psychological and social-science data generated at all? And why do they, unlike physical measurement data, typically have no property-indicating unit? Given these striking differences, are these quantitative data at all comparable in their accuracy and reliability as expected for measurement results and as needed for establishing a secured knowledge base about the phenomena of the world?
Indeed, quantitative psychological and social-science data yielded some paradoxes when contrasting individual-level scores with their aggregates on collective levels. For example, within countries, wealthier persons rate themselves ‘happier’ than poorer persons. But when these scores are averaged on the country level, wealthier countries appear not to ‘be happier’ than poorer countries—a surprising finding replicated also longitudinally (Easterlin et al. 2010). It would correspond to finding that, although within countries, men tend to be taller than women this would not be reflected in the nations’ averages. How can such paradoxes emerge in quantitative data given the greater accuracy generally attributed to them?
The demand for transparent and transferable quantitative information about human capital is growing (Fisher 2009)—as are discussions about replication crises (Hanfstingl 2019; Nosek et al. 2015), validity (Buntins et al. 2017; Newton 2012) and quantitative methods in psychology and social sciences (Michell 2003; Tafreshi et al. 2016; Thomas 2020; Uher 2021c, 2021d; Valsiner 2017; Westerman 2014). Current debates primarily concern issues of data analysis (e.g., significance testing, effect sizes and robust statistics (Epskamp 2019; Open Science Collaboration 2015). Much less attention is paid to the processes by which quantitative data are generated in the first place before they are being processed and analysed (Uher 2018a, b, c, 2019, 2021a). Indeed, many debates on ‘measurement’ (e.g., in psychometrics) actually concern only data modelling but not data generation (Uher 2021c, 2021d). Data analyses, however, can reveal valid information about the study objects only if—during data generation—relevant properties have been encoded into the data in appropriate ways. So, how are quantitative data generated in different fields?
1.1 Transdisciplinary and philosophy-of-science analyses
This article applies transdisciplinary and philosophy-of-science approachesFootnote 1 to explore how numerical data are generated in psychology and social sciences as compared to metrology (the science of measurement) and physics. Transdisciplinary approaches are needed because quantitative data are used by different sciences to describe and explore real-world phenomena. The generation of these data must therefore be based on some common principles that ensure that mathematical and statistical analyses of these data allow to make inferences that are appropriate, accurate and justified—with regard to the study phenomena and properties (rather than to, e.g., statistical assumptions as in psychometrics; Uher 2021c, 2021d). This is essential for obtaining information that can be set in relation to findings from other investigations in the same and other sciences—thus, for establishing a secured knowledge base.
Many assume quantitative research in psychology and social sciences would require a ‘soft’ or ‘wide’ definition of measurement (Finkelstein 2003; Mari et al. 2013; 2015). Changing the definition of a key scientific activity, however, cannot establish its comparability across sciences. Much in contrast, it undermines comparability because it fails to provide guiding principles that specify how measurement processes can be implemented in comparable ways given the peculiarities of different sciences’ study phenomena. Labelling different procedures uniformly as ‘measurement’ also obscures essential and necessary differences in established practices as well as inevitable limitations. Ultimately, measurement is not just any activity for creating numerical values but involves specific processes that justify the high public trust placed in it (Abran et al. 2012; Porter 1995). Measurement denotes structured processes that (1) justify the assumption that the generated quantitative information is indeed attributable to the study phenomena (research objects) and properties and that (2) establish a shared understanding of its quantitative meaning regarding these phenomena and properties. Basic principles of measurement that are applicable in the same ways across sciences are essential for scrutinising established research practices and for guiding necessary adaptations to particular study phenomena and properties. The aim of this transdisciplinary approach, however, is not to develop new measurement theories but instead to scrutinise—on the abstract philosophy-of-science level—the basic concepts underlying key theories established in different sciences and to highlight commonalities and differences (Uher 2020). This entails the necessity to clearly distinguish—regardless of any disciplinary boundaries—data generation processes that meet the basic principles of measurement from other quantification processes that do not (see below).
Such transdisciplinary explorations are complicated, however, because the different sciences developed their quantitative approaches largely independently from one another (Berglund et al. 2012), and therefore established different terminologies, concepts and practices. This entails terminological fallacies that are hard to identify because, in different sciences, different terms may denote the same concept (jangle-fallacies; Kelley 1927) and the same term may denote different concepts (jingle-fallacies; Thorndike 1903)—such as the term ‘measurement’ itself. Thus, when intuitively relying on their own discipline-specific terminology, scientists may unintentionally misread works from other disciplines. Commonalities and differences between discipline-specific terms and concepts can therefore be identified only on metatheoretical and methodological levels—but not on the levels of concrete methods (models, operations and practices). This also applies to the different types of measurement theories (for an overview, see Tal 2020). For this reason, the article adopts a more abstract philosophy-of-science level of consideration and a corresponding terminology in order to explore basic concepts and approaches and to identify common principles of measurement applicable across sciences.
1.2 Outline of this article
First, the article outlines philosophy-of-science concepts that are relevant for measurement and quantitative investigations in all sciences. Then, it briefly introduces to social scientists and psychologist the two basic methodological principles of measurement (data generation traceability and numerical traceability) that were shown to underlie metrologists’ structural frameworks of physical measurement and that are key for developing frameworks applicable also to psychological and social-science research. These two principles are needed (1) to justify the attribution of quantitative results to the study phenomena and (2) to establish the data’s shared quantitative meaning and that are therefore key to distinguish measurement from other quantification processes (Uher 2018a, 2020).
This article focusses on the principle of numerical traceability to explore the ways in which quantitative meaning is established for numerical data in different sciences. It will show how metrologists have used this principle to build the International System of Units and to establish a shared global understanding of measurement units and scales and the physical properties to which they refer. This principle will then be applied to scrutinise the use of ‘units’ and ‘scales’ in psychology and the social sciences, highlighting heterogeneous meanings and functions that entail different (if any) rationales for making numerical assignments—and thus different abilities for implementing numerical traceability. Finally, the analyses will pinpoint fallacies that frequent conflations of the heterogeneous notions of ‘units’ and ‘scales have for the interpretation of results and will outline new directions in the conceptualisation and generation of quantitative data in psychology and social-sciences.
2 Basic concepts relevant for quantitative investigations in all sciences
This section briefly outlines philosophy-of-science concepts that are foundational for quantitative investigations in all sciences.
2.1 Quality versus quantity: the distinction between target property and measurand
Objects or phenomena cannot be measured in themselves; only some of their properties can be. Commonly, objects and phenomena feature various properties. A metal box features, amongst others, the properties of length, mass and temperature; a person’s talking behaviour features sound intensity, temporal and spatial properties, amongst others. This requires specification of the particular property being studied in an object or phenomenon—called the target property. Any given study object or phenomenon features of a given target property only a specific entity (e.g., a box’s specific weight) or even several specific entities (e.g., a box’s specific length versus width versus height; the specific temporal durations of persons’ monologues versus dialogues). Therefore, scientists must specify the particular entity of the target property that is to be measured in the study object—called the measurand (e.g., the box’s width rather than its height or length; temporal duration only of an individual’s monologues rather than any talking behaviour). Metrologists commonly refer to the target property as the general property, and to the specific entity of the general property featured by an object as the specific property (Mari et al. 2017). This terminology, however, blurs the important distinction between quality and quantity.
Qualities are properties that differ in kind (Latin qualis for "of what sort"). Length is qualitatively different from mass and temperature; temporal duration is qualitatively different from sound intensity. Quantities (from Latin quantus for “how much, how many”), in turn, are divisible properties of entities of the same kind—thus, of the same quality (Hartmann 1964). That is, even if the specific entities change in magnitude (e.g., by adding or dividing them), their meaning as entities of the given target property remains unchanged—they are all qualitatively homogeneous. Placing several boxes side-by-side changes the magnitude of their joint width but does not alter its quality as being that of length. Any divisible entities of the same quality differ only quantitatively, never qualitatively (Michell 2012; Uher 2021c, d).
2.2 Phenomenon–quality–quantity conflation
Often, however, any qualitative property featuring divisible (quantitative) properties is simply called a ‘quantity’, which again conflates quality with quantity. This may be of less concern to metrologists and physicists who focus on those qualitative properties that do feature quantitative structures. But it entails profound fallacies for other scientists who explore many qualitative properties that do not feature quantitative properties as well. Indeed, quality—quantity conflation may fuel the belief (widespread in psychology and social sciences) that quantities would exist in themselves and could be studied without any reference to the qualities in which they occur. This misleads scientists to overlook that “[q]uantities are of qualities, and a measured quality has just the magnitude expressed in its measure” (Kaplan 1964, p. 207). All quantitative research ultimately has a qualitative grounding (Campbell 1974).
To explore quality—quantity conflation as well as further fallacies, these important concepts will be clarified here by distinguishing (1) the qualitative properties (qualities, target property) under study from (2) the divisible, thus quantitative properties that may occur in them, and of which (3) specific quantitative properties or specific quantities (measurands) are studied in a given research object or phenomenon. This terminology may appear cumbersome but it is essential to avoid fallacies that entail numerous problematic practices (see below; Uher 2021a, c, d). Indeed, these differentiations highlight clear implications for measurement that are also reflected in the basic axioms of quantity (see e.g., Barrett 2003). Specifically, data-generating persons, whether operating measuring devices or generating data directly (e.g., observation), must first demarcate the entities to be studied (e.g., measurands) and categorise them regarding their e-quality or ine-quality. Entities of the same (equal, homogeneous) quality can then be compared in their divisible properties (quantities) regarding that target quality in terms of their order, distance, ratio and further relations (e.g., measurand with metering ruler or timer). Finally, data-generating persons must encode the identified quantitative relations by assigning to the measurands particular quantity values, thereby producing numerical data (Uher 2018a). Thus, measurement requires both categorisation of the quality of interest and determination of the specific quantity of that quality that is to be studied (measurand) in the study phenomenon or object.
This shows that the common dichotomisation of qualitative versus quantitative research (e.g., methods data) reflects a profound misconception, implying quantities could be determined independently of the quality studied. But all data represent qualitive properties (what they are about) and only some contain, additionally, quantitative information about these properties (how many/much of that quality; Uher 2018a). Psychologists and social scientists, however, often do not specify the quality studied, such as when speaking about ‘measuring behaviour’ or ‘measuring attitudes’. This jargon ignores that not objects and phenomena in themselves but only properties can be measured and that various, qualitatively different properties may be measurable in any given phenomenon (e.g., behaviours’ spatial or temporal properties). This phenomenon—quality—quantity conflation (Uher 2021c, d) underlies various conceptual problems that will be analysed below.
2.3 Multitudes versus magnitudes
Two basic kinds of quantity are distinguished, which are central for defining measurement units (see below). Multitude (plurality) is a discontinuous and discrete quantity that is divisible into indivisibles and discontinuous parts, which are countable (numerable) and can therefore be expressed as a number (e.g., dogs have 42 teeth). Thus, multitudes are quantities by their ontological nature. Magnitude (unity), by contrast, is a continuous and unified quantity, which is divisible into divisibles and continuous parts. Magnitude is an entity’s specific quantitative property that can be compared to that of other entities of the same quality (e.g., specific lengths of different fingers) so that they can be ordered (ranked) in terms or ‘more’, ‘less’ or ‘equal’ (Hartmann 1964).
2.4 Numerical data: numerals versus numbers
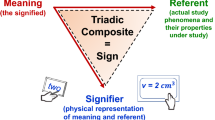
Data are sign systems (e.g., Indo-Arabic numerals, Greek letters) that scientists use to represent information about the study phenomena in semiotic ways. This allows to manipulate, decompose and recompose, thus, to analyse this semiotic information (e.g., mathematical symbols on computer) in lieu of the actual properties and phenomena under study and in ways not applicable to these latter in themselves (e.g., individuals’ body weight or behaviours cannot be dissected or averaged). The inherently representational function of sign systems, however, is often overlooked likely because their symbolic nature is inherent to human thinking and everyday language and therefore often no longer explicitly noticed. Given this, scientists must clearly distinguish the phenomena and properties under study (e.g., metal boxes’ properties, individuals’ talking behaviour) from the means used for their exploration (e.g., data, methods, models, terms, concepts). This is particularly challenging in psychological and social-science research where many study phenomena are unobservable in themselves and accessible only through language and where, therefore, descriptions of the study phenomena are often mistaken for these phenomena in themselves. Indeed, common jargon often blurs this important distinction, such as when the term ‘variable’ is used to denote both the study phenomena (e.g., age, beliefs, behaviours) and the sign systems encoding information about them (e.g., lexical variable names and numerical variable values; Uher 2021a, b, c).
Signs are generally arbitrary—they typically bear no inherent relations to the objects they denote (e.g., no resemblanceFootnote 2). Hence, signs mean something only by agreed convention (Deutscher 2006). With regard to numerical data, numerals (chiffres, Ziffern) must be distinguished from numbers (nombres, Zahlen); ignoring this distinction (numeral—number conflation) entails numerous fallacies. Numerals are invented by humans; therefore, they vary in forms (e.g., Arabic, Roman or Tamil numerals look as diverse as 2, 5, 10; II, V, X; or  ,
,  ,
,  ) and can be assigned different meanings (e.g., Roman numbers can signify both numerals and letters). Numerals (e.g., written symbols) are often used to represent numbers (Michels 1982) but numerals can also represent just order (e.g., 1st, 2nd, 3rd) or only categorical—qualitatively different—properties that have no quantitative meaning at all (e.g., registration or phone ‘numbers’; Campbell 1919/2020). Both numerals and natural numbers have a definite order. The order of natural numbers arises from ontological interrelations among real phenomena, whereas the order of numerals derives only from human invention (Campbell 1957; Hartmann 1964). Thus, when numerals are used as data, their meanings must be made explicit—an important point for the analyses of numerical traceability below.
) and can be assigned different meanings (e.g., Roman numbers can signify both numerals and letters). Numerals (e.g., written symbols) are often used to represent numbers (Michels 1982) but numerals can also represent just order (e.g., 1st, 2nd, 3rd) or only categorical—qualitatively different—properties that have no quantitative meaning at all (e.g., registration or phone ‘numbers’; Campbell 1919/2020). Both numerals and natural numbers have a definite order. The order of natural numbers arises from ontological interrelations among real phenomena, whereas the order of numerals derives only from human invention (Campbell 1957; Hartmann 1964). Thus, when numerals are used as data, their meanings must be made explicit—an important point for the analyses of numerical traceability below.
2.5 Measurement versus quantification versus quantitative data (outcomes, results)
In different sciences, the terms ‘measurement’ and ‘quantification’ have different meanings and are therefore prone to jingle-jangle fallacies. For metrologists, measurement denotes a structured process whereas quantification denotes primarily a result (Mari et al. 2013). Social scientists and psychologists, by contrast, often treat these terms as synonyms for any process of quantitative data generation as well as for the outcomes. Distinguishing data generation processes from their outcomes is however important because not all quantitative data are results of measurement (Abran et al. 2012). And precisely for this reason, it is equally important to distinguish procedures that meet the criteria of measurement (justified attribution of the results to the study phenomena and properties; shared understanding of the results’ quantitative meaning regarding these phenomena and properties) from those that do not (e.g., opinions, judgements; Mari et al. 2015, 2017; Uher 2020). Here, measurement processes are distinguished from quantification processes and both, in turn, from their outcomes (results, quantitative data).
To establish measurement processes and distinguish them from other quantification processes, two methodological principles are crucial.
3 Two basic methodological principles of measurement
Measurement is the assignment of numerical values to properties, whereby the measurand is represented mathematically (e.g., in data variables and numerical values)—but neither just any assignment of numerical values nor purely mathematical processes are measurements. Performing a measurement always requires an empiricalFootnote 3 stage, thus, an interaction with the target property in the given study object (phenomenon) as well as a structured framework establishing traceable relations from the measurand to the numerical value assigned to it (Mari et al. 2015). Transdisciplinary analyses showed that the structural framework of physical measurement developed in metrology (for details, e.g., Mari et al. 2017) builds on two basic methodological principles—data generation traceability and numerical traceability. These principles are—on the abstract philosophy-of-science level of consideration of methodology but not on the level of methodFootnote 4—applicable also across sciences (for details; Uher 2020).
This section briefly outlines these two principles. They will be applied in the subsequent sections to explore how the different sciences define and use ‘units’ and ‘scales’ and assign numerical values in order to generate quantitative data.
3.1 Data generation traceability: designing unbroken documented measurand—result connections
The first methodological principle of measurement, data generation traceability, concerns the process structure needed to ensure that the results do provide information about the measurands. This is established by making the entire measurement process—from the specific quantities of the target property to be measured (measurands) in a study object up to the assignment of quantity values to them—fully transparent, and thus traceable and reproducible. To justify that the generated results are attributable to the measurands, this process must be designed from knowledge about the objects and properties under study (called object-dependence or object-relatedness in metrology; Mari et al. 2017). This requires explanations of how the operative structures allow to make numerical assignments such that they reveal reliable and valid information about the measurands, and only about them but not also about other properties (Mari et al. 2015).
This knowledge must be implemented in unbroken documented connection chains that connect the measurand (if necessary, via mediating properties) with a property that humans can accurately and intersubjectively perceive (for an example, see footnoteFootnote 5). At each step, the interconnected qualities empirically interact, thereby establishing proportional relations between their divisible properties (quantities)—i.e., quantitative relations—along the chain from measurand up to result (Uher 2019, 2020). Developing such connection (conversion) chains (e.g., for instrument development) requires knowledge of systematic quantitative (lawful) connections among different qualitative properties (Mari et al. 2017; Mari and Wilson 2015). By implementing documented unbroken connection chains, metrologists establish processes that allow to trace a result, in the inverse direction, back to the measurand as well as to the reference unit used to determine the result comprising a numerical value together with a measurement unit. Data generation traceability allows to make this entire process—and not just the results—reproducible by other persons, in other contexts and at other times (Mari et al. 2015). Detailed comparisons with quantitative data generation processes established in psychology and social sciences are elaborated elsewhere (Uher 2018a, 2020, 2021c, d). Here, the focus is on comparisons regarding the second principle, numerical traceability.
3.2 Numerical traceability: connecting results to known quantitative standards
The final step of measurement involves the assignment of numerical values to the measurands. But how should this assignment be made? Why is the specific mass we know as 1 kilogram labelled with 1 and not with 2 or 0.453? And how do we all come to know how much weight 1 kilogram exactly is? These questions refer to the methodological principle of numerical traceability, which requires that the numerical value assigned to a measurand is systematically connected, in documented and transparent ways, not only to the measurand but also to a reference quantity of the given target property, which has already been independently defined and conventionally established and which also defines a measurement unit (see below). To guarantee that measurement results are reliably interpretable and always represent the same quantitative information across time and contexts (e.g., specific weight of 1 kilogram), metrologists define primary references, which are internationally accepted (e.g., through legislation) and assumed to be stable (e.g., the international prototype kilogram). From a given primary reference, metrologists establish unbroken documented connection chains to all working references that are used in (non-metrological) research and everyday life for measuring a given target property (e.g., laboratory weighing scales, household thermometers; JCGM200:2012, 2012). These are called calibration chains because, along the connections in the chain, they specify uncertainties as a quantitative indication of the measurement quality of a result to assess its reliability (JCGM100:2008, 2008).
Documented networks of calibration chains, rooted in the same primary references, are used to disseminate measurement units internationally (Maul et al. 2019). These networks guarantee that any comparisons with working references that are traced back to the same primary reference produce for the same measurand comparable results (De Silva 2002), thereby establishing the results’ numerical traceability (called metrological traceability in metrology; JCGM200:2012, 2012). These conditions ensure that quantitative results (e.g., the specific weight of 1 kilogram) can be understood everywhere in the same ways; in other words, that the generated results are invariant with respect to the particular persons (subjects; e.g., operators, users) involved (called subject-independence or intersubjectivity in metrology; Mari et al. 2017).
Through numerical traceability, measurands become quantitatively comparable by comparing them to one another not only empirically but also mathematically via the numerical values assigned to them (Maul et al. 2019). This establishes for the numerical values in themselves, in conjunction with the measurement units used for their generation, a publicly shared universal meaning. Nowadays, all persons (relying on the SI) can understand how much a neonatal weight of 3.5 kilogrammes is and can make—from this numerical information alone—direct comparisons. This is a historic achievement. Over centuries, metrologists invested considerable efforts to standardise and unify the many different and locally varying measurement references and units that had been used before (see below). The importance of the universal meaning of measurement results in our globalised world underlines the crucial role that numerical traceability plays in measurement.
4 Units, scales and quantitative data in metrology and physical sciences
The importance of numerical traceability will now be further explored by scrutinising the concepts and practices by which ‘units’ and ‘scales’ are defined and used in different sciences to generate numerical data. This section will explore those established in metrology and physical sciences, the subsequent section those from psychology and social sciences.
4.1 Methodological principles for defining measurement units
Key for establishing numerical traceability in metrology and physical sciences is to designate for a given target property (e.g., mass) specific entities that serve as reference quantities and that are used to define measurement units (JCGM200:2012, 2012). That is, measurement units specify both a particular quality and a particular quantity of that quality. By designating reference quantities as units (the term unit generally mean oneness, singularity), scientists create multitudes, which are countable. When comparing a measurand’s specific quantity (e.g., an object’s specific mass) with standardised reference entities (units) of the same target property (e.g., calibrated gram weights), their ratio can be expressed as a numeral indicating the measurand’s quantity value (e.g., “2”) together with some lexical symbols (e.g., “g”, “oz”) indicating the reference unit used and thus also the target property studied (e.g., mass). Hence, quantity values cannot be understood without their reference unit because their meaning is established only with regard to the given target quality (e.g., 1 gram ≠ 1 minute ≠ 1 metre). Thus, in measurement, scientists assign not numbers as widely believed in psychology and social sciences (Uher 2021c, 2021d) but numerals, which are defined as quantity values of a particular qualitative property (e.g., “2 gram”; Mari et al. 2015). This is a key point that will be taken up again below.
Given that measurement units determine which quantity value must be assigned to a measurand, their definition plays a crucial role in measurement. Many physical measurement units were originally derived from historical conventions about arbitrarily defined references (Hand 2016). Some of the oldest units of length measurement refer to human body parts (e.g., ell, foot, hand), which are always “at hand” but vary among individuals. Standardisation was therefore reached by authoritative decree—by fiat.Footnote 6 For example, one inch was legally defined, amongst others, by King Edward II of England in 1324 as the length of three barley grains placed lengthwise end-to-end (Klein 1974). Many decreed entities constitute multitudes. For example, carob seeds, given their uniformity, were used to define a unit of weight (carat, ct) with one seed equalling one carat (later standardised to equal 0.2 gram). Other historical measurement units involve defined magnitudes of qualitative properties of material objects that are directly and publicly perceivable and in which persons can therefore reliably and intersubjectively demarcate divisible entities that are (almost) identical, or at least sufficiently similar to serve as units (e.g., marks on metre sticks). The durability of material objects facilitates the construction of prototypes that can be physically preserved at least for some time—an important element for standardisation. For example, around 970 already, Saxon King Edgar is said to have kept in his palace a wooden "yardstick", decreed to equal 36 inches, as the official standard of measurement (Naughtin 2009).
With the availability of sophisticated technologies, and building on the knowledge developed from decreed measurement units, physicists increasingly replaced the originally arbitrary definitions of established reference units with artefact-free definitions that are based on natural constants and therefore not subject to deterioration or destruction but that are reproducible any time and any place (Quinn 2010). Examples are the redefinitions of the standard unit of one metre as the length of the path travelled by light in vacuum during a time interval of 1/299,792,458 of a second (BIPM 2006), and, just recently, of the standard unit of one kilogram in terms of the Planck constant, speed of light and the Caesium atom’s resonant frequency (BIPM 2019). History thus shows that measurement units can be defined by fiat (arbitrarily) as long as they are explicitly and conventionally defined and systematically connected through documented unbroken connection chains that establish quantitative relations from the primary references to all working references used (with known calibration uncertainties)—that is, as long as the principle of numerical traceability is met.
4.2 The international system of units (SI)
To define physical measurement units, scientists encounter two challenges. First, they must identify the structural—i.e., both qualitative and quantitative—connections that exist between physical properties (e.g., natural constants). Second, they must establish explicit and agreed measurement units codifying reference quantities of the given qualities together with conventional definitions of their interrelations. This has been done and codified in the International System of Units (Système International d’Unités, SI). In this coherent system, all known physical qualities featuring divisible (quantitative) properties together with their internationally established units are systematically interrelated in determinative ways and on the basis of non-contradictory mathematical equations (BIPM 2006; Czichos 2011). In metrology, properties that cannot be expressed in terms of other physical properties featuring divisible properties are called ‘base quantities’ (e.g., mass, length, time, temperature)—an established metrological term reflecting the common quality—quantity conflation.Footnote 7 The conventionally defined entities that are used as their references are called base units (e.g., gram, metre, second, Kelvin). These base properties are used to define all other known qualities featuring divisible properties, called ‘derived quantities’ (e.g., velocity, area, mass density)—a term likewise reflecting quality—quantity conflation. The corresponding quantitative standard entities, called derived units (e.g., metre per second, square metre, kilogram per cubic metre), are defined as products of powers of the base units according to algebraic relations that are specified in internationally agreed equations (e.g., velocity from length and time; BIPM 2006). This system allows to convert measurement results between different units (e.g., neonates’ weight in kilogram or pound) without loss of information regarding the specific quantity that they denote (JCGM200:2012, 2012)—an important condition for establishing numerical traceability and thus a secured body of knowledge about real-world phenomena. (For details on the SI’s structure, challenges of its establishment and issues of uncertainty of measurement, not considered here, see BIPM 2006; White, Fsarrance, & AACB Uncertainty of Measurement Working Group 2004).
4.3 The fundamental idea behind measurement scales in metrology and physics
Measurands are assumed to be entities that are empirically given by the study object; their initially unknown specific quantity is determined through measurement. Measurement units, by contrast, are entities of a specific quantity that are designed on purpose and hence known before a measurement is executed. This is done in a process often called scale construction, which produces a structure of classifiers (e.g., measurement units) that are assumed to be adequate for a given measurand (Mari and Giordani 2012).
The term ‘scale’ has slightly different meanings in metrology and physics, which, however, are all based on the same fundamental idea. Primarily, measurement ‘scales’ denote a (physical or conceptual) concatenation of identical measurement units (e.g., metre scale, Celsius scale) to create countable multitudes of known magnitude (going back to Euclid; Tal 2020). This facilitates the intersubjective determination of the measurands’ initially unknown magnitudes and hence of the numerical values that are to be assigned to them. But many properties are not directly accessible by humans or not accurately enough (Uher 2020), and concatenation is not possible for derived quantities (Rossi 2007). Maybe therefore, the term scale also denotes measuring instruments (e.g., weighing scales), thus, the physical devices engineered to enable an empirical interaction with the measurand and to implement unbroken documented connection chains between measurand and result. Specifically, measuring instruments connect the measurand as the input property (via mediating properties if needed) with an output property, thereby establishing proportional relations between the specific quantities of the different qualitative properties interconnected in a given chain (data generation traceability). The specific quantity of the output property is then compared with that of the (calibrated) standard reference implemented in the instrument, which in turn is connected in unbroken calibration chains to an established primary reference (numerical traceability). Where this comparison is not automated but executed by persons, instruments (e.g., spring scales) often involve visual displays featuring identical units that are spatially concatenated into a measurement scale.
A further meaning of the term scale refers to the order of magnitude in which numerical information is depicted in graphs, charts, drawings or maps. For example, size relationships between the graphical features and the real world are indicated using linear (e.g., 1:1000 scale) or non-linear relationships (e.g., logarithmic scale). But this as well reflects the fundamental idea of measurement scales—the determination of a measurand’s initially unknown magnitude (i.e., a continuous unified quantity) through comparison with a concatenation of identical, conventionally defined magnitudes serving as multitudes (i.e., discontinuous and discrete quantities). The countability of multitudes allows for testing which quantity axioms are met (von Helmholtz 1887; Hölder 1901) and for generating numerically traceable results.
5 Units, scales and quantitative data in psychology and social sciences
Building on the insights gained from analysing the principles underlying measurement units and scales in metrology and physical sciences, this section will now scrutinise the use of ‘units’ and ‘scales’ in psychology and social sciences, focussing on selected applications with examples. It will highlight heterogeneous meanings and functions that will be further explored subsequently.
5.1 Jingle-jangle fallacies and terminological differentiations used here
Psychologists and social scientists use the terms ‘measurement unit’, ‘measurement scale’ and ‘scale unit’ not just when measuring physical properties (e.g., electric skin resistance; reaction times) but also for quantitative investigations of their “non-physical” study phenomena (e.g., constructs like ‘happiness’ or ‘Human Development’). For clear distinctions, here, the terms measurement unit and measurement scale exclusively refer to the units and scales used in processes that meet the principles of data generation traceability and numerical traceability (see above). All other ‘units’ and ‘scales’ will be labelled in line with common psychological and social-science jargon, thus not necessarily with metrological jargon.
5.2 ‘Units’: diverse applications in research processes
In psychology and social sciences, the term ‘unit’ is used in at least five different ways (ignoring many variations and mixtures). It is used for U1) ‘answer units’ in questionnaires (e.g., multi-stage answer categories); U2) ‘variable units’ indicating properties ascribed to a variable’s values (e.g., nominal, ordinal, interval); (U3) ‘psychometric units’ derived from data modelling (featuring, e.g., equal distances); (U4) measurement units from metrology (e.g., millisecond in reaction time measurement), and also for (U5) the sets of entities forming the basis for investigation or analysis (e.g., ‘unit of analysis’). Some examples illustrate typical applications.
Standardised rating methods involve sets of statements or questions (called items) describing the phenomena of interest (e.g., behaviours, attitudes). Respondents indicate their pertinent judgements (assessments, ratings, opinions) in standardised ‘answer units’ (categories) that are intended to indicate varying degrees of, for example, judged agreement, intensity, frequency or typicality. Such ‘answer units’ vary substantially in number (e.g., 2, 5, 10 categories) and format; for example, they may be labelled lexically (e.g., ‘never’, ‘rarely’, ‘sometimes’, ‘often’, ‘always’), numerically (e.g., ‘1’, ’2’, ‘3’, ‘4’, ‘5’) or otherwise nonverbally (e.g., icons, colours, lines). In sum, ‘answer units’ are used both to elicit and to encode responses in a standardised bounded format. To create numerical data, researchers recode respondents’ chosen (non-numerical) ‘answer units’ into numerals in highly standardised ways (e.g., ‘sometimes’ always into ‘3’, ‘often’ always into ‘4’). The numerical data generated for different individuals on different items are then pooled and analysed jointly (see below).
Given that numerals can encode numbers, order or just categorically (qualitatively) different properties, researchers must specify the meanings that they ascribe to the numerical data created (e.g., when recoding answer categories). For this purpose, four types of ‘variable units’ are popular (Stevens 1946). ‘Nominal units’ encode categorical (including binary) information (e.g., ‘Nepal’, ‘Norway’; ‘correct’/ ‘incorrect’), indicating qualitatively different and thus indivisible properties. ‘Ordinal units’ encode sequence information, indicating relative quantity differences that are not further specified and that thus cannot be assumed to be of equal size. ‘Interval units’ encode sequence information with specified intervals that are determined by arbitrarily defining reference points and dividing the magnitude thus-defined arbitrarily into equal ‘units’; this, however, precludes interpretation of relative between-unit differences (e.g., 15 °C cannot be said to be half as warm as 30 °C). ‘Ratio units’, in turn, encode numerical information featuring order, equal distances and an absolute zero-point indicating absence of the target property; for example, zero Kelvin (K = − 273 °C) is the lowest temperature at which molecules stop moving. Therefore, ‘ratio units’ represent absolute quantity differences, enabling the determination of ratio relations and conversion of quantitative information between different ‘ratio units’ (e.g., between metre and inch). Although widely used, Steven’s category system is neither exhaustive nor universally accepted (Thomas 2020; Velleman & Wilkinson 1993). Alternative systems involve, for example, grades to encode ordered labels (e.g., ‘lecturer’, ‘reader’, ‘professor’); ranks to encode sequences starting from 1 as either the smallest or the largest (e.g., ‘1st’, ‘2nd’, ‘3rd’); counted fractions to encode numerical values that are bounded by a specific range but that do not constitute interval units (e.g., percentages); counts to encode non-negative integers; amounts to encode non-negative real numbers; and balances to encode unbounded ranges of numerals, which can have both positive and negative values (Velleman and Wilkinson 1993). In sum, ‘variable units’ serve to define the type of information encoded in the values that a given data variable can take, which determines the applicability of statistical methods of analysis.
Among the most important psychological and social-science study phenomena are constructs (e.g., ‘intelligence’, ‘happiness’, ‘Human Development’). Constructs are conceptual entities that refer to various phenomena and properties (e.g., different intellectual performances) on an abstract level of consideration (theoretical construct definition). As abstractions, constructs are non-observable in themselves; they can thus be studied only indirectly through sets of specific phenomena and properties that are chosen to serve as construct indicators in given studies (operational construct definition). Quantitative information about construct indicators is encoded in so-called manifest (data)Footnote 8variables. Empirical structures underlying the numerical values of various manifest (data) variables are statistically analysed and modelled in fewer (or even just one) synthesised variables, called latent (data) variables. This is done by using psychometric models, which specify statistical assumptions about the interrelations between manifest and latent (data) variables (e.g., item response functions). Such models allow to transform the values of manifest (data) variables, typically featuring binary or ordinary ‘units’ (e.g., correctness or rating data), into values of latent (data) variables, which are commonly aimed at featuring interval or ratio ‘units’. The latent data structures are modelled such as to maximise the fit to the statistical assumptions specified in the model, which can be tested empirically. In sum, ‘psychometric units’ describe properties of numerical data that are synthesised through statistical modelling. Although aligned to statistical assumptions rather than to properties of the study phenomena, psychometrically modelled data are commonly assumed to reflect quantitative information about the constructs and the various phenomena to which they refer (Uher 2021c).
Psychologists and social scientists also use metrological units (SI) to measure physical properties using pertinent measuring devices (e.g., reaction times in milliseconds, electrical skin resistance in Ohm). As established in metrology and physics, the known magnitudes of conventionally defined measurement units are thereby used to determine the unknown magnitude of a measurand (or an output property connected to it) through comparison of their ratio.
Finally, the term ‘unit’ is also used to denote the sets of entities under study, such as the particular phenomena (e.g., behaviours, ‘traits’, attitudes, social interactions), or particular members or larger collections of the entities studied (e.g., individual, organisation, country). For example, ‘sampling unit’ denotes the entities sampled from a statistical population (e.g., schools in a district). ‘Experimental unit’ denotes the smallest entity to which an intervention is applied (e.g., teaching method applied in some classes), ‘observational unit’ denotes the entities about which the single data points are generated (e.g., individual students). ‘Unit of analysis’ denotes the level on which the data are being analysed (e.g., individual, class, country) but also the type of information that is being explored (e.g., variabilities, averages). Their particular definition depends on the research question (e.g., individual development, international comparison) and influences the methodology and analytical methods. In qualitative analyses (e.g., textual content analysis), ‘unit of analysis’ denotes the portion of content chosen as the basis for developing codes (e.g., words, tweets, entire interviews). For consistent coding, researchers also specify what constitutes the ‘units of meaning’ in their analysis (e.g., word frequencies, treatment of themes; Roller and Lavrakas 2015).
Before these heterogeneous notions and uses of ‘units’ will be further explored, what about the term ‘scales’?
5.3 ‘Scales’: disparate notions and meanings
Psychologists and social scientist use the term ‘scales’ variously for (S1) ‘answer scales’ in terms of the set of answer categories provided in tests or questionnaires; (S2) ‘item scales’ in terms of the sets of test or questionnaire items presented to respondents; (S3) ‘scale types’ indicating properties ascribed to the values that data variables can take; (S4) ‘psychometric scales’ obtained from statistically modelling latent structures underlying the values of many (manifest) data variables; and (S5) measurement scales from metrology applied for measuring physical properties. Some examples briefly illustrate typical applications.
‘Answer scales’ may involve sets of multi-stage answer categories intended to indicate graded degrees (‘rating scale’), such as ‘agreement scales’ (called ‘Likert scales’; Likert 1932) that may feature as ‘units’, for example, ‘strongly disagree’, ‘disagree’, ‘neither disagree nor agree’, ‘agree’, ‘strongly agree’. Such sets of pre-defined ‘answer units are commonly called a ‘scale’, likely because their presentation (e.g., horizontally next to each other) resembles the concatenation of measurement units. But because ‘answer scales’ always refer to a particular content to be judged, the term ‘scale’ may also denote the set of questionnaire items (‘multi-item scale’) or just single items (‘single item scale’), often including a specific ‘answer scale’ (e.g., ‘happiness scales’).
The data that are generated by applying such ‘answer scales’ and ‘item scales’ are encoded in data variables that, given the meaning they are intended to reflect, are ascribed particular properties regarding the values that they can take. This is often referred to as ‘scale types’ (Stevens 1946), such as ‘ordinal scales’ or ‘ratio scales’. Synthesised latent variables, psychometrically modelled to feature interval or ratio ‘units’ (e.g., through Rasch-modelling) are called ‘psychometric scales’. Furthermore, measurement scales for measuring physical properties are used in line with established metrological practice (e.g., Time scales, Ohmmetre scale).
6 Methodological functions underlying the diverse notions of ‘units’ and ‘scales’
The diverse notions and uses that ‘units’ and ‘scales’ have in the different sciences will be explored in this section in more detail. Generally, the term ‘scale’ may refer to structures into which ‘units’ are embedded in research processes. But the diverse notions highlighted in the previous sections refer to structures that have different functions and that are employed in different stages of research processes. Four distinct methodological functions can be identified that involve different, if any, rationales for making numerical assignments and that thus impact the possibilities for establishing numerical traceability.
-
1.
‘Instruments’ to enable empirical interactions with the study phenomena and properties
A first methodological function, underlying the notions of ‘units’ and ‘scales’ as the items and answer categories of tests and questionnaires, is that of ‘stimuli’ triggering and enablingFootnote 9 empirical interactions with the study phenomena and properties. Item and answer ‘scales’ are therefore often called ‘instruments’ (e.g., ‘rating instruments’), in analogy to physical measuring instruments (e.g., weighing scales). But, in themselves, language-based ‘instruments’ cannot interact with anything. Instead, it is the data-generating persons who must interact with (i.e., perceive and interpret) both the study phenomena (e.g., emotions) and the investigatory methods (e.g., verbal descriptions presented in ‘questionnaire scales’), leading to complex triadic interactions (Uher 2018a). Hence, whereas technical instruments are developed to overcome limitations in human abilities, the application of language-based ‘instruments’ inherently relies on human abilities (Uher 2019, 2020). Moreover, technical instruments are constructed to implement explicit and determinative assignment rules; instances of the same properties must always be encoded with the same numerical values so that these always represent the same information (Ellis 1966). In standardised language-based ‘instruments’, by contrast, the rationales for choosing particular answer categories are neither specified nor even known but, instead, are left to respondents’ everyday-language interpretations and intuitive decisions (Uher 2018a). That is, the function of ‘units’ and ‘scales’ as ‘instruments’ is interpreted differently in the sciences.
-
2.
Structural data format to encode information about the study phenomena and properties
A second methodological function, underlying the notions of ‘answer units’ and item and answer ‘scales’, is to serve as structural format for data generation. Items are typically intended to specify the study phenomena; answer categories to specify the quality of interest and particular divisible properties of it (quantities). By choosing for each item one single answer category, respondents generate data in a highly standardised format, in which the items serve as data variables and the chosen ‘answer units’ as variable values. Measurement results as well involve a structured data format. The units always indicate the target quality as well as a specified reference quantity of it; the numerical values indicate the ratio of the measurand’s quantity with that of the reference quantity.
-
3.
Conceptual data format to ascribe particular meaning to numerical values
A third methodological function, underlying the notion of ‘scale types’ and ‘scale units’ as specifying the properties that researchers ascribe to their data variables regarding the values that these can take, is to implement a conceptual data format. For measurement, the conceptual properties ascribed to numerical values must be derived from the target properties of the empirical study system, which are determined experimentally. For example, the Kelvin scale, is ‘ratio scaled’ because it features an absolute zero-point indicating absence of temperature, whereas the Celsius and Fahrenheit scales are only ‘interval scaled’ because their zero-points are defined arbitrarily. Conceptual properties form an elementary part of any symbolic (data) system and determine the permissible transformations that maintain its mapping relations with the empirical system under study.
In standardised language-based methods, by contrast, the conceptual properties that researchers ascribe to the numerical values are commonly derived either from a) (untested) presumptions about the properties of interest (e.g., intended ordinal meaning in ‘agreement ratings’), b) statistical assumptions made for data modelling (e.g., ‘interval units’ in psychometrics), or c) preconditions of particular statistical methods of analysis that researchers wish to apply to answer their questions (e.g., metric analysis). Statistical assumptions and preconditions, however, are mere mathematical concepts, which are unrelated to the empirical study systems (Toomela 2021) and applied only after data generation is already completed.
The function of ‘scales’ for implementing a conceptual data format furthermore underlies their notion as the order of magnitude by which numerical information is visually depicted. It is also behind the notion of ‘units’ as the sets of entities that form the basis for investigation or analysis.
-
4.
Conventionally agreed reference quantities of defined magnitudes
A fourth methodological function, underlying the notion of measurement units and scales as reference quantities of a given target quality (e.g., SI scales with units of mass like gram or ounce), is to establish a conventionally agreed and traceable quantitative meaning of the numerical values assigned to measurands. Standard reference quantities are conventionally agreed and thus known before a measurement is executed. Unbroken documented connection chains from established (international) primary references to the working refences (e.g., gauged measuring devices) used for empirical comparisons with measurands allow to establish a subject-independent and conventionally shared meaning of measurement results—thus, numerical traceability. This makes these numerical results comparable even just mathematically, such as those indicating neonates’ weight in different world regions.
An analogous implementation of this methodological function of ‘units’ and ‘scales’ as agreed reference quantities is largely absent in psychological and social-science research as will be explored now.
7 Establishing numerical traceability in psychological and social-science research: possibilities and limitations of current practices
This section will now scrutinise practices that are currently established in psychological and social-science research for implementing the different methodological functions of ‘scales’ and ‘units’ and will explore the consequences that these entail for the establishment of numerical traceability. The focus will be on the widely-used language-based quantification methods (e.g., tests, questionnaires).
7.1 Standardised item and answer ‘scales’ fail to establish both data generation traceability and numerical traceability
Identical wording and formatting of item and answer ‘scales’ is often assumed to be sufficient as standardisation for enabling quantitative investigations. To make these ‘scales’ applicable to a broad range of individuals, phenomena and contexts; their wordings are often abstract and even vague (e.g., ‘often’, ‘sometimes’). This entails that items and answer categories reflect not specific target qualities and particular quantities of them as required for measurement but instead concepts, which mostly refer to conglomerates of qualitatively heterogeneous properties and study phenomena (Uher 2018b, 2021c). Insufficient specification of concrete study phenomena, the target property and its divisible (quantitative) properties to be studied in them, however, promotes phenomenon—quality—quantity conflation. Given this, it is unsurprising that individuals construct for the same standardised items heterogeneous meanings and for multi-stage answer categories not mutually exclusive, quantitative meanings but instead overlapping and often even qualitatively different meanings (Lundmann and Villadsen 2016; Rosenbaum and Valsiner 2011; Uher and Visalberghi 2016). This precludes the establishment of standardised and traceable processes of data generation (Uher 2018a).
Particular problems for numerical traceability arise from the narrow range of values in ‘answer scales’. Bounded value ranges are also used for some measurement units; but these are either repeating, and thus unlimited (e.g., clock time), or inherent to the target property (e.g., degrees in a circle). Other quantitative categories with bounded value ranges refer to specified samples of unlimited size (e.g., percentages, counted fractions), thus indicating quantity values that are traceable. By contrast, the numerical values created from standardised ‘answer scales’ are conceived to be bounded from the outset—regardless of the diverse phenomena, qualities and quantities to which they may be applied. As a consequence, data-generating persons must assign a broad range of quantitative information flexibly to a predetermined, narrow range of values. But how do they do this? For example, how often is “often” for a phenomenon to occur, given that general occurrence rates vary for different phenomena (e.g., talking versus sneezing) and also across contexts (Uher 2015a)? To fit their ideas into narrow ‘answer scales’, respondents sometimes seem to intuitively weigh the study phenomena’s observed occurrences against their presumed typical occurrence rates in given contexts (e.g., sex/gender or age groups; Uher 2015c; Uher and Visalberghi 2016; Uher et al. 2013b)—just like Procrustes, the stretcher and subduer from Greek mythology, who forced people to fit the size of an iron bed by stretching them or cutting off their legs.
Without knowing the specific quantitative relations by which this intuitive fitting is done (unlike logarithmic scales), however, the quantitative data thus-generated can reflect quantitative information neither of the actual (inaccessible) phenomena and properties of interest nor of those used as their (accessible) indicators. Indeed, the requirement to assign diverse ranges of quantities flexibly to a bounded range of values can distort and even inverse quantitative relations, thereby introducing shifts in the quantitative meaning of the data produced. A simple hypothetical example illustrates this. Assumed we judged the size of different bicycles on a verbal ‘answer scale’ (e.g., ‘small’, ‘medium’, ‘large’) and did the same also for different cars and different trains using that same ‘scale’. Although any ‘large’ bicycle is smaller than any ‘small’ train, the assigned answer values would suggest otherwise. Hence, the same values do not always represent the same quantitative information, thereby precluding the establishment of numerical traceability.
7.2 Numerical recoding of answer categories fails to establish numerical traceability
Assumed these problems in data generation could be ignored and a target property is specified, such as agreement in ‘Likert scales’. Could researchers establish numerical traceability by systematically assigning numerical values to respondents' chosen answer categories (e.g., ‘1’ to ‘strongly disagree’, ‘2’ to ‘disagree’, ‘3’ to ‘neither disagree nor agree’, ‘4’ to ‘agree’, ‘5’ to ‘strongly agree’)? To ensure that these numerals can indicate quantitative information, the answer categories must reflect divisible properties of the target property.
Referring to Steven’s ‘scale’ types, what would this mean? Regarding ‘interval scales’, often assumed for data analysis, can we assume that the difference between ‘strongly disagree’ and ‘disagree’ equals that between ‘disagree’ and ‘neither disagree nor agree’? Regarding ‘ordinal scales’, one could certainly say that ‘strongly agree’ indicates more agreement than ‘agree’. But could ‘agree’ reflect more agreement than ‘neither agree nor disagree’—which respondents often choose to indicate having no opinion or finding the item inapplicable (Uher 2018a)? And does ‘disagree’ really reflect a lower level of agreement than ‘agree’—or is disagreeing with something not rather an entirely different idea than agreeing with it? Likewise, what tells us that, in ‘happiness scales’, feeling ‘pretty happy’ versus ‘not too happy’ reflects only differences in intensity—thus, divisible properties of the same kind of emotion rather than emotions of qualitatively different kind, like joy and sadness? Semantically, two different qualities can be easily merged into one conceptual dimension (as done in semantic differentials; Snider and Osgood 1969). But what divisible (quantitative) properties could be identified in such conglomerates of heterogeneous qualities?
Further inconsistencies occur. Recall that measurement scales involve identical units of defined magnitude. The conventional meaning of the magnitude of a 4-cm long measurand is established through the equality of its length to that of four concatenated centimetre units—it covers a rulers’ first, second, third and fourth centimetre-unit. But this does not apply analogously to ‘agreement scales’—to indicate ‘agree’, one cannot also tick ‘strongly disagree’, ‘disagree’ and ‘neither disagree nor agree’ without introducing fundamental contradictions in meaning. That is, the (hypothesised) quantities that verbal ‘answer scales’ are intended to reflect do not match the quantitative relations ascribed to their numerically recoded values—not even when just ordinal properties are assumed—and thus fail to meet at least basic axioms of quantity.
Moreover, the numerical assignment procedure differs fundamentally from that used in measurement. In ‘rating-scale’ based investigations, researchers do not assign numerals to measurands compared with a unit. Instead, they recode the ‘answer units’ in themselves into numerals. Unit-free values, however, can provide information about neither the particular target property studied nor any specific quantity of it. But the same numerical value has, necessarily, different quantitative meanings—with regard to both different units indicating the same target quality (e.g., ‘4’ grams, ‘4’ ounces, ‘4’ tons) and different target properties (e.g., ‘4’ kilogrammes, ‘4’ metres, ‘4’ minutes). Moreover, in measurement, numerical values are assigned with reference to the conventionally agreed and numerically traceable standard quantity indicated by the measurement unit. In ‘answer scales’, by contrast, the assigned numerals depend on study-specific decisions about the structural data format. For example, depending on the value range chosen for ‘answer scales’ in a given study, their middle category can be recoded into very different numerical values (e.g., ‘0’, ‘3’, ‘4’ or ‘50’)—even when referring to the same item and meant to indicate the same quantitative information.
Recoding the heterogeneous meanings of the verbal values of ‘answer scales’ into numerical values entails further problems because it implies that they would reflect homogeneous meanings. Numeral–number conflation promotes the frequent ascription of mathematical properties to numerals (e.g., that ‘4’ is more than ‘3’ and this more than ‘2’), ignoring that these quantity relations do not apply to the meanings of the verbal values thus-recoded. This creates the illusion that the numerical recoding of ‘answer units’ could establish a universal meaning for the variable values thereby enabling mathematical exploration of the phenomena and properties described. Following this erroneous belief, unit-free scores are often treated as if they would represent ontological quantities that can be ordered, added, averaged and quantitatively modelled—ignoring, that this applies neither to the answer categories used for data generation nor to the conglomerates of heterogeneous study phenomena and properties commonly described in rating ‘scales’.
7.3 Differential analyses cannot establish numerical traceability
Without unbroken documented connections both to the measurand of the target property studied (data generation traceability) and to a known quantity reference of that target property (numerical traceability), unit-free values are meaningless in themselves. The only option to create meaning for such scores is to compare different cases with one another.Footnote 10 For this purpose, psychologists and social scientists apply a differential perspective when analysingFootnote 11 and interpreting scores by considering not the absolute scores in themselves that are ascribed to cases but instead the relative between-case differences that these reflect.
This shift in perspective justifies merging values obtained for different properties and study phenomena, as this is commonly done to compute overall indices for constructs from the values obtained for their various construct indicators. For example, the Human Development Index is a summary score computed from various normalised values obtained for ‘life expectancy at birth’, ‘years of schooling’, and ‘cross national income per capita’ (Conceição 2019). Clearly, values in units of years and of monetary currencies cannot be meaningfully merged or compared in themselves because they refer to different qualities. This is possible only with regard to the differential information that they reflect (Uher 2011; Uher et al. 2013a). Differential analyses can enable meaningful comparisons and may circumvent problems arising from arbitrary algorithms for merging heterogeneous scores. But, although statistically derived, differentially standardised scores do not establish systematic proportional relations to the primary quantity values from which they were derived—not even when these are measurement results (e.g., response times in milliseconds)—because differential standardisation is based on the score distributions in specific samples. Consequently, differential summary scores of heterogeneous qualities are derived through processes of artificial quantification but not ‘construct measurement’ as widely believed (Uher 2020).
Assumed we could ignore the problem that quantity values referring to different qualities cannot be meaningfully merged, could we at least summarise numerical values that are derived from answer categories meant to indicate the same quality? As the above analyses (e.g., of ‘agreement scales’) already showed, upon closer reflection, different answer categories actually do not reflect the quantitative properties implied by their numerically recoded values and thus cannot be quantitatively merged. Or would it be reasonable to assume that answering twice ‘neither disagree nor agree’ (3)—often used to indicate ‘no opinion’ or ‘not applicable’—could correspond to (roughly) the same quantity of agreement as does answering once ‘strongly disagree’ (1) and once ‘strongly agree’ (5)—that is, having a split opinion or different item interpretations? In both cases, the arithmetic average of the numerically recoded answer categories would amount to ‘3’. Ignoring the meanings that verbal answer categories can actually have and that the data-generating persons may actually have in mind entails shifts in the quantitative meaning ascribed to numerical data derived from recoding answer categories.
Regardless of these problems, score distributions obtained from statistical modelling are often interpreted as reflecting the distributions of the (hypothesised) target property’s magnitudes in a sample. But differential scores cannot indicate quantities of a particular target property as in measurement because the quantitative meaning attributed to differential values depends on the distribution of all values in the sample considered, leading to reference group effects. For example, persons 1.70 m tall will obtain higher differential scores when compared to a sample of mostly shorter persons and lower differential scores when compared to mostly taller persons. That is, meaning for the quantity values that are ascribed to the still unknown magnitudes of the measurands of individual cases is created by comparing these ascribed values with one another—thus, by comparing many unknowns. This differs fundamentally from measurement where the measurand’s unknown quantity is compared with that of a known and specified reference quantity.
Differential analyses may enable pragmatic quantification that is useful in many fields of research. But they have paved the way for the widespread fallacy to interpret between-case differences as reflecting real quantities that are attributable to the single cases being compared. This problem is inherent also to psychometric ‘scaling’.
7.4 Modelling ‘psychometric scales’ cannot establish numerical traceability
Psychometric modelling, as well, involves the transformation of numerical values based on their distribution patterns in given samples, thus on the normalisation of variable values. Many ‘IQ scales’, for example, are standardised such that the sample’s average is set to 100 and one standard deviation to 15. In a norm distribution, the scores of 68% of a sample’s individuals fall within one standard deviation from the sample’s average in both directions (IQ range 85–115) and the scores of 95% of the individuals fall within two standard deviations (IQ range of 70–130). To maintain their ascribed differential meaning, IQ scores are normalised in various ways, such as for different age groups and different educational levels but in particular for different cohorts given substantial increases during the twentieth century and recent decreases (Flynn 2012; Teasdale and Owen 2005). That is, persons are ascribed particular IQ scores on the basis of the norm variations established for their particular reference group.
Given this, the ‘units’ of ‘IQ scales’ do not indicate specific quantities with regard to a hypothesised target property. Instead, they refer to the proportion of cases in the norming sample that obtained particular numerical summary scores (indicating, e.g., correctness on multiple test items). That is, ‘IQ scale units’ are ‘interval scaled’ with regard to the ranges of numerical summary scores—the meaning of which, however, varies with their distribution patterns in the samples studied. Hence, ‘IQ scale units’ refer to a population (sample) parameter. The common practice of normalising ‘IQ scales’ would correspond to defining metre scales on the basis of people’s average body heights. Given that average human height varies, such as by gender, country and socio-economic factors (e.g., in industrialised countries during the twentieth century), the specific reference quantities that would be defined in this way as the length of a 1-metre unit would vary over space and time—and thus, the measurement results obtained for one and the same measurand. This fundamentally contradicts the meaning and merits of measurement. Indeed, if all cases would have the same quantity of a (hypothesised) target property, the differential approach (and thus also psychometric modelling) would be unable to determine their magnitude—in lack of a specified quantity reference.
Normalising allows to create meaning for scores through differential comparisons but this entails shifts in the quantitative meaning that can be ascribed to these scores because this meaning is bound to the sample studied. Although based on scores ascribed in some ways to individual cases (e.g., correctness, speed in response), differential scores cannot be interpreted as reflecting properties of these cases in themselves. Normalising may be useful for pragmatic purposes but is entirely different from measurement.
7.5 Statistical results are commonly not interpreted in terms of the information actually encoded in the data
Further shifts in meaning occur during result interpretation. Let us consider again the example of ‘agreement scales’, which are clearly intended to reflect levels of agreement (ignoring the problems shown above). Surprisingly, the statistically analysed results are typically interpreted not as reflecting the respondents’ levels of agreement as inquired during data collection but instead as hypothetical magnitudes regarding the actual phenomena of interest (e.g., those described in constructs of ‘extraversion’, ‘neuroticism’, ‘happiness’ or ‘honesty’). Can agreement be reasonably assumed to be a property inherent to these diverse phenomena or does agreement not rather form part of the judgement process itself? Ultimately, people can agree on the length of different lines (as in Solomon Asch’s classical social conformity experiments; Asch 1955); still this agreement is not a property of these lines but of the persons judging them. While this is an obvious example, in psychological and social-science investigations, it is difficult to disentangle the psychical phenomena involved in the judgement processes from the phenomena to be judged—thus, to distinguish the means of investigation from the phenomena under study.
8 Conclusions and implications
The article scrutinised the uses and notions of ‘units’ and ‘scales’ in different sciences as well as the rationales used for assigning numerical values to measurands in order to generate quantitative data and for establishing meaning for such numerical data with regard to the phenomena and properties studied. The analyses highlighted four methodological functions underlying the diverse notions of ‘units’ and ‘scales’; they serve as (1) ‘instruments’ enabling empirical interactions with the study phenomena and properties; (2) structural data format; (3) conceptual data format; and (4) conventionally agreed reference quantities of particular target qualities. These methodological functions are distinct and employed in different stages of research processes. Importantly, they differ in their ability to help establish numerical traceability—the systematic connection of numerical results to quantity standards that are known and conventionally agreed with regard to the target property, which is essential for establishing the values’ public interpretability. The present analyses highlight important differences in the ways in which the sciences interpret and use ‘units’ and ‘scales’ and establish quantitative meaning for their numerical data. They also show new directions for development in the conceptualisation and generation of quantitative data in psychological and social-science research.
8.1 Conflation of heterogeneous notions of ‘units’ and ‘scales’ entails erroneous beliefs about their interchangeability and the requirements of measurement
In psychology and social sciences, the different notions of ‘units’ and ‘scales’ are often used interchangeably, such as when ‘rating scales’, Steven’s ‘scale types’ or ‘psychometric scales’ are all referred to as measurement scales. The analyses showed that their equation is not warranted. Rather, lack of differentiation of the four methodological functions of ‘units’ and ‘scales’ and their frequent conflation entail serious fallacies that compromise the establishment of processes that adhere to the basic principles of measurement, and thus compromise also the interpretation of results. This occurs, for example, when properties that are conceptually ascribed to the symbolic (data) system (e.g., when numerically recoding answer categories or given particular statistical assumptions) are attributed also to the empirical study system although systematic unbroken connections of the thus-generated quantitative data both to the measurands (data generation traceability) and to known quantity standards (numerical traceability) have not been established (e.g., in ‘rating scales’). Standardisation is important for implementing measurement processes, but standardisation of just the data format, as often assumed for language-based test and questionnaires (e.g., standardised items and answer categories), is insufficient. By contrast, limiting the values to narrow bounded ranges, regardless of the phenomena and properties to which they may refer, introduces serious shifts in meaning of the numerical values thus-created. In sum, the four methodological functions of units and scales are not interchangeable with one another. Common (implicit) beliefs that implementing just some of these functions in a research process could establish the remaining functions as well are not warranted.
8.2 All four methodological functions implemented in measurement units and scales
Measurement units and scales feature the special constellation that all four methodological functions are implemented in the same process. They are connected, through comparison, with the measurand (directly or via mediators), thus serving as important components of measuring instruments. For encoding information, measurement units and scales specify a particular structural data format as well as a conceptional data format ascribed to these data, indicating both the target property and a particular quantity of it. Finally, the quantity information indicated in measurement units and scales is systematically connected to conventionally agreed and well-defined reference quantities to enable its public interpretability (numerical traceability).
This highlights that the four different functions cannot substitute one another but must all be involved in the same process in order to establish both data generation traceability and numerical traceability. That is, none of the four methodological functions in itself is sufficient for a process to meet these two basic methodological principles of measurement. Their fulfillment is required (1) to justify the attribution of quantitative results to the study phenomena and properties and (2) to establish the data’s shared quantitative meaning. These two basic principles are therefore key to distinguish measurement from other quantification processes (e.g., judgements, opinions). The four different methodological functions of ‘scales’ and ‘units’ identified in this article provide important guiding criteria for how implementation of numerical traceability can be accomplished.
8.3 New directions in the conceptualisation and generation of quantitative data in psychology and social-sciences
Quantitative research in psychology and social sciences often involves only three of the four methodological functions and not always in the same data generation process. The fourth function for connecting the numerical result to conventionally agreed and known reference quantities, however, is still seldom considered. Although the quantitative meaning ascribed to numerical values is key to any quantification process, little attention has so far been devoted to how this meaning is being established in psychological and social-science research.
Numerical data generated in psychology and social sciences often constitute differential summary scores that have no quantity meaning in themselves (e.g., construct indices). Instead, their meanings are created through between-case comparisons and are therefore always bound to the particular sample studied, thus precluding the numerical values’ comparability across studies and disciplines. This does not contradict their utility for pragmatic purposes. Indeed, the meaning of differential summary scores can be made publicly interpretable (e.g., through reference scores for particular samples provided in manuals)—if they are derived from primary data that meet the two principles of measurement (e.g., ‘intellectual performance’ derived from binarily coded correctness of test answers; Human Development Index derived from ‘life expectancy at birth’, ‘years of schooling’, and ‘cross national income per capita’). But this is not possible for summary scores derived from quantitative data generated through ‘rating scales’ because these methods do not even allow to establish data generation traceability, not to mention numerical traceability. The very necessity to assign a broad range of quantitative information flexibly to a predetermined, narrow range of values alone can lead to paradoxical findings, such as those emerging in quantitative happiness ratings, not to mention further serious methodological problems inherent to ‘rating scales’ (for details; Uher 2018a).
A key problem in quantitative psychological and social-science research is the frequent lack of specification of the target qualities studied and of possible divisible properties that may occur in them (quantities). Phenomenon—quality—quantity conflation often misleads researchers to overlook that specifying the target quality, its divisible properties (quantities) and the specific measurand to be explored in the study phenomena (research objects) is essential for any quantification process. Their erroneous yet widespread conflation also entails shifts in meaning in the interpretation of results (e.g., agreement as a quantitative property of both happiness and neuroticism?).
Particular conceptual efforts must be devoted to specify what is actually meant to be quantified and how this is aimed to be achieved. This is prerequisite for further major efforts that are needed to devise ways for implementing all four methodological functions of ‘units’ and ‘scales’ in the same research process. Given the peculiarities of psychological and social-science study phenomena, the specific ways in which conventionally agreed and traceable quantitative meanings can be established for numerical data (numerical traceability) may necessarily differ from those developed in the physical sciences.
The article highlighted ways that psychologists and social scientists must develop to meet the basic methodological principles of measurement, which underlie the structural frameworks established in metrology and physical sciences, while carefully considering their study phenomena’s peculiarities. The two methodological principles of data generation traceability and numerical traceability are essential to ensuring the robustness and usefulness of quantitative information. They enable public scrutiny, transparency and replicability, and maintain a high degree of interpretability of the results regarding their referents—the real-world phenomena under study.
Notes
The present analyses rely on the Transdisciplinary Philosophy-of-Science Paradigm for Research on Individuals (TPS Paradigm; Uher 2015b, 2018c) in which established concepts from various disciplines, complemented by novel ones, have been integrated into overarching philosophical, metatheoretical and methodological frameworks that coherently build upon each other. These frameworks highlight connections, differences, and communalities across sciences, and thus starting points for cross-scientific collaboration (Uher 2020). The TPS-Paradigm has already been applied 1) to integrate and expand on previous concepts of individuals’ psyche, behavior, language and contexts (Uher 2013, 2015d, 2016a, b, 2021b); 2) to refine and newly develop concepts and methodologies for taxonomising and comparing individual differences in various kinds of phenomena and populations (Uher 2015a, c, d, 2018b, c), and 3) to critically analyze concepts, theories and practices of data generation, quantification and measurement across the sciences (Uher 2019, 2020) as well as in quantitative psychology and psychometrics (Uher 2018a, 2021a, c, d). Applications are demonstrated in multi-method studies (e.g., (Uher 2015a, 2018a; Uher et al. 2013a, b; Uher & Visalberghi, 2016). http://researchonindividuals.org.
With very few exceptions (e.g., icons, onomatopoeia).
This empirical process, necessarily, is affected by errors, which entails uncertainty (not further discussed here; for details, e.g., Mari et al. 2015).
Methodology denotes the system of principles underlying scientific enquiry, thus the philosophical and theoretical foundations of the ways (approaches) in which research objects can be explored and that make particular operations suited for this purpose and others not, together with explanations of what their results indicate and why. Method denotes the selection and construction of specific behaviours and instruments (practices, techniques) used to perform particular research operations (e.g., observing, self-reporting). Hence, methodology is the higher-order concept, comprising the classification of methods and their underlying philosophical and theoretical rationales (Uher 2020).
Thermometers illustrate this principle. Temperature (within a particular range) is structurally connected to the spatial expansion of mercury. When tubed, the expansion length of mercury (mediator) is systematically connected to the tube length. The latter is publicly and (relatively) accurately perceivable, enabling the intersubjective definition of identical (or highly similar) units (e.g., marked on the tube). To generate results, measurement-executing persons must visually compare the length of the tubed mercury with the length of the tube and the units marked on it and convert the quantitative information thus-obtained (e.g., by counting units) into semiotically encoded information as data (e.g., by writing down “20 °C”). The connection chain thus involves ‘temperature’—'length of tubed mercury’, chained by physical laws, and ‘length of tubed mercury’—'length of scale units’—‘data variable names and values’, chained by measurement-executing persons through visual comparison and semiotic encoding, respectively (unless digitised; Uher 2020).
Derived from the Latin fiat for “let it be done”.
The quality—quantity conflation reflected in this term is unproblematic only in metrology and physical sciences given their focus on qualities featuring quantitative properties as well.
For within-case comparisons, the meaning of unit-free values can be created though comparison with the individual’s base-line over time. Mostly, however, even in within-individual analyses, the meaning of scores is determined on the basis of the scores obtained by other individuals for both their baseline and their variability (e.g., comparisons of heart-rate variability).
This may entail changing the numerical values assigned to individuals, such as through z-standardisation, setting the sample’s average to zero and its standard deviation to one. This transforms the bounded range of typically non-negative values obtained from recoding ‘agreement scales’, commonly ascribed at least ordinal properties, into an unbounded range with positive and negative values centred around zero and often ascribed interval properties.
References
Abran, A., Desharnais, J.-M., Cuadrado-Gallego, J.J.: Measurement and quantification are not the same: ISO 15939 and ISO 9126. J. Softw. Evol. Process 24(5), 585–601 (2012). https://doi.org/10.1002/smr.496
Asch, S.E.: Opinions and social pressure. Scientific American, 193(5), 31–35 (1955). Retrieved from http://www.jstor.org/stable/24943779
Barrett, P.: Beyond psychometrics. J. Manag. Psychol. 18(5), 421–439 (2003). https://doi.org/10.1108/02683940310484026
Barrett, P.: The EFPA test-review model: when good intentions meet a methodological thought disorder. Behav. Sci. 8(1), 5 (2018). https://doi.org/10.3390/bs8010005
Berglund, B., Rossi, G.B., Townsend, J.T., Pendrill, L.: Measurement with Persons: Theory, Methods, and Implementation Areas. Taylor Francis, New York (2012)
BIPM (2006) BIPM: The international system of units (SI) (8th ed). Organisation Intergouvernementale de la Convention du Mètre. Retrieved from http://www.bipm.org/
BIPM (2019) BIPM: The international system of units (SI) (9th ed). Organisation Intergouvernementale de la Convention du Mètre. Retrieved from http://www.bipm.org/en/publications/guides/
Buntins, M., Buntins, K., Eggert, F.: Clarifying the concept of validity: from measurement to everyday language. Theory Psychol. 27(5), 703–710 (2017). https://doi.org/10.1177/0959354317702256
Campbell, N.R.: Foundations of Science: The Philosophy of Theory and Experiment. Dover Publications, New York (1957)
Campbell, N.R.: Foundations of Science. Salzwasser Verlag, Frankfurt am Main (1919/2020)
Campbell, D.T.: Qualitative knowing in action research. Kurt Lewin Award address. In Society for the Psychological Study of Social Issues, presented at the meeting of the American Psychological Association. New Orleans, LA (1974)
Conceição, P.: Human development report. United Nations Development Programme (2019)
Czichos, H.: Introduction to metrology and testing. In Springer handbook of metrology and testing (pp. 3–22). Berlin, Heidelberg: Springer (2011). https://doi.org/10.1007/978-3-642-16641-9_1
Deutscher, G.: The unfolding of language: The evolution of mankind’s greatest invention. Arrow (2006)
De Silva, G.M.S.: Basic Metrology for ISO 9000 Certification. Butterworth-Heinemann (2002)
Easterlin, R.A., McVey, L.A., Switek, M., Sawangfa, O., Zweig, J.S.: The happiness-income paradox revisited. Proc. Natl. Acad. Sci. USA 107(52), 22463–22468 (2010). https://doi.org/10.1073/pnas.1015962107
Ellis, B.: Basic concepts of measurement. Cambridge University Press, Cambridge, UK (1966).
Epskamp, S.: Reproducibility and replicability in a fast-paced methodological world. Adv. Methods Pract. Psychol. Sci. 2(2), 145–155 (2019). https://doi.org/10.1177/2515245919847421
Finkelstein, L.: Widely, strongly and weakly defined measurement. Measurement 34(1), 39–48 (2003).
Fisher, W.P.: Invariance and traceability for measures of human, social, and natural capital: theory and application. Measurement 42(9), 1278–1287 (2009). https://doi.org/10.1016/J.MEASUREMENT.2009.03.014
Flynn, J. R.: Are we getting smarter? Rising IQ in the twenty-first century. Cambridge University Press, Cambridge (2003)
Hand, D.J.: Measurement: A Very Short Introduction. Oxford University Press, Oxford (2016)
Hanfstingl, B.: Should we say goodbye to latent constructs to overcome replication crisis or should we take into account epistemological considerations? Front. Psychol. 10, 1949 (2019). https://doi.org/10.3389/fpsyg.2019.01949
Hartmann, N.: Der Aufbau der realen Welt. Grundriss der allgemeinen Kategorienlehre [The Structure of the Real World. Outline of the General Theory of Categories], 3rd edn. Walter de Gruyter, Berlin (1964)
Hölder, O.: Die Axiome der Quantität und die Lehre vom Mass (Band 53). Leipzig: Berichte über die Verhandlungen der Königlich Sächsischen Gesellschaft der Wissenschaften zu Leipzig, Mathematisch—Physische Classe (1901)
Janssen, P.A., Thiessen, P., Klein, M.C., Whitfield, M.F., Macnab, Y.C., Cullis-Kuhl, S.C.: Standards for the measurement of birth weight, length and head circumference at term in neonates of European, Chinese and South Asian ancestry. Open Med. 1(2), e74-88 (2007)
JCGM100:2008: Evaluation of measurement data—Guide to the expression of uncertainty in measurement (GUM). Joint Committee for Guides in Metrology (originally published in 1993) (2008). http://www.bipm.org/en/publications/guides/gum.html
JCGM200:2012.: International vocabulary of metrology—Basic and general concepts and associated terms (VIM 3rd edition). Working Group 2 (Eds.), Joint Committee for Guides in Metrology (2012). Retrieved from https://www.bipm.org/utils/common/documents/jcgm/JCGM_200_2012.pdf
Kaplan, A.: The Conduct of Inquiry: Methodology for Behavioral Science. Chandler Publishing Co, Scranton (1964)
Kelley, T. L.: Interpretation of Educational Measurements. Yonkers, NY: World (1927)
Klein, H.A.: The World of Measurements: Masterpieces, Mysteries and Muddles of Metrology. Simon and Schuster, New York (1974)
Likert, R.: A technique for the measurement of attitudes. Arch. Psychol. 22(140), 1–55 (1932)
Lundmann, L., Villadsen, J. W.: Qualitative variations in personality inventories: subjective understandings of items in a personality inventory. Qual. Res. Psychol. 13(2), 166–187 (2016). https://doi.org/10.1080/14780887.2015.1134737
Mari, L.: A quest for the definition of measurement. Measurement 46(8), 2889–2895 (2013). https://doi.org/10.1016/j.measurement.2013.04.039
Mari, L., Giordani, A.: Quantity and quantity value. Metrologia 49(6), 756–764 (2012). https://doi.org/10.1088/0026-1394/49/6/756
Mari, L., Wilson, M.: A structural framework across strongly and weakly defined measurements. In 2015 IEEE International Instrumentation and Measurement Technology Conference (I2MTC) Proceedings, pp. 1522–1526. IEEE (2015). https://doi.org/10.1109/I2MTC.2015.7151504
Mari, L., Maul, A., Irribarra, D.T., Wilson, M.: Quantification is neither necessary nor sufficient for measurement. J. Phys: Conf. Ser. 459(1), 012007 (2013). https://doi.org/10.1088/1742-6596/459/1/012007
Mari, L., Carbone, P., Petri, D.: Fundamentals of hard and soft measurement. In Ferrero, A., Petri, D., Carbone, P., Catelani, M. (Eds.), Modern Measurements: Fundamentals and Applications (pp. 203–262). Hoboken, NJ: John Wiley & Sons (2015). https://doi.org/10.1002/9781119021315.ch7
Mari, L., Carbone, P., Giordani, A., Petri, D.: A structural interpretation of measurement and some related epistemological issues. Stud. Hist. Philos. Sci. 65–66, 46–56 (2017). https://doi.org/10.1016/j.shpsa.2017.08.001
Maul, A., Mari, L., Wilson, M.: Intersubjectivity of measurement across the sciences. Measurement 131, 764–770 (2019). https://doi.org/10.1016/J.MEASUREMENT.2018.08.068
Michels, E.: Evaluation and research in physical therapy. Physic. Therapy 62, 828–834 (1982).
Michell, J.: The quantitative imperative. Theory Psychol. 13(1), 5–31 (2003). https://doi.org/10.1177/0959354303013001758
Michell, J.: Alfred Binet and the concept of heterogeneous orders. Front. Psychol. 3, 261 (2012). https://doi.org/10.3389/fpsyg.2012.00261
Naughtin, P.: Which inch? (2009). Retrieved from http://metricationmatters.com/articles.html retrieved 29/10/2014
Newton, P.E.: Clarifying the consensus definition of validity. Meas. Interdiscip. Res. Perspect. 10(1–2), 1–29 (2012). https://doi.org/10.1080/15366367.2012.669666
Nosek, B.A., Alter, G., Banks, G.C., Borsboom, D., Bowman, S.D., Breckler, S.J., Yarkoni, T.: Promoting an open research culture: author guidelines for journals could help to promote transparency, openness, and reproducibility. Science (New York, N.Y.), 348(6242), 1422–1425 (2015). https://doi.org/10.1126/science.aab2374
Open Science Collaboration.: Estimating the reproducibility of psychological science. Science , 349(6251), aac4716. (2015). https://doi.org/10.1126/science.aac4716
Porter, T. M.: Trust in numbers: The pursuit of objectivity in science and public life. Princeton University Press (1995)
Quinn, T.J.: From Artefacts to Atoms: The BIPM and the Search for Ultimate Measurement Standards. Oxford University Press, Oxford (2010)
Roller, M. R., Lavrakas, P. J.: Applied qualitative research design: A total quality framework approach. Guilford Press (2015)
Rosenbaum, P. J., Valsiner, J.: The un-making of a method: From rating scales to the study of psychological processes. Theory Psychol. 21(1), 47-65 (2011). https://doi.org/10.1177/0959354309352913
Rossi, G. B.: Measurability. Measurement 40(6) 545–562 (2007). https://doi.org/10.1016/j.measurement.2007.02.003
Snider, J. G., Osgood, C. E.: Semantic differential technique: A sourcebook. Aldine, Chicago (1969)
Stevens, S. S.: On the theory of scales of measurement. Science, 103, 667–680 (1946)
Tafreshi, D., Slaney, K.L., Neufeld, S.D.: Quantification in psychology: Critical analysis of an unreflective practice. J. Theor. Philos. Psychol. 36(4), 233–249 (2016). https://doi.org/10.1037/teo0000048
Tal, E.: Measurement in science. In E. N. Zalta (Ed.), The Stanford Encyclopedia of Philosophy (Fall 2020). Metaphysics Research Lab, Stanford University (2020). Retrieved from https://plato.stanford.edu/archives/fall2020/entries/measurement-science
Teasdale, T. W., Owen, D. R.: A long-term rise and recent decline in intelligence test performance: The Flynn Effect in reverse. Personal. Indiv. Diff. 39(4), 837-843 (2005). https://doi.org/10.1016/j.paid.2005.01.029
Thomas, M.A.: Mathematization, not neasurement: a critique of Stevens’ scales of measurement. J. Methods Meas. Soc. Sci. 10(2), 76–94 (2020). https://doi.org/10.2458/v10i2.23785
Thorndike, E.L.: Notes on Child Study, 2nd edn. Macmillan, New York (1903)
Toomela, A.: Problems with measurement in psychology—Just a tip of the iceberg. J. Theoret. Philos. Psychol. 41(2), 134–138 (2021). https://doi.org/10.1037/teo0000185
Uher, J.: Individual behavioral phenotypes: An integrative meta-theoretical framework. Why “behavioral syndromes” are not analogs of “personality”. Develop. Psychobiol. 53(6), 521–548 (2011). https://doi.org/10.1002/dev.20544
Uher, J.: Personality Psychology: Lexical Approaches Assessment Methods and Trait Concepts Reveal Only Half of the Story—Why it is Time for a Paradigm Shift. Integ. Psychol. Behav. Sci. 47(1), 1-55 (2013). https://doi.org/10.1007/s12124-013-9230-6
Uher, J.: Comparing individuals within and across situations, groups and species: Metatheoretical and methodological foundations demonstrated in primate behaviour. In D. Emmans & A. Laihinen (Eds.), Comparative neuropsychology and brain imaging (Vol. 2), Series Neuropsychology: An interdisciplinary approach (pp. 223–284). Lit Verlag, Berlin (2015a). https://doi.org/10.13140/RG.2.1.3848.8169
Uher, J.: Conceiving “personality”: Psychologist’s challenges and basic fundamentals of the transdisciplinary philosophy-of-science paradigm for research on individuals. Integ. Psychol. Behav. Sci. 49(3), 398–458 (2015b). https://doi.org/10.1007/s12124-014-9283-1
Uher, J.: Developing “personality” taxonomies: Metatheoretical and methodological rationales underlying selection approaches methods of data generation and reduction principles. Integ. Psychol. Behav. Sci. 49(4), 531–589 (2015c). https://doi.org/10.1007/s12124-014-9280-4
Uher, J.: Interpreting “personality” taxonomies: Why previous models cannot capture individual-specific experiencing behaviour functioning and development. Major taxonomic tasks still lay ahead. Integ. Psychol. Behav. Sci. 49(4), 600-655 (2015d). https://doi.org/10.1007/s12124-014-9281-3
Uher, J.: Exploring the workings of the Psyche: Metatheoretical and methodological foundations. In J. Valsiner, G. Marsico, N. Chaudhary, T. Sato, & V. Dazzani (Eds.), Psychology as the science of human being: The Yokohama Manifesto (pp. 299–324). New York: Springer International Publishing. (2016a). https://doi.org/10.1007/978-3-319-21094-0_18
Uher, J.: What is behaviour? and (when) is language behaviour? A metatheoretical definition. J. Theory Social Behav. 46(4), 475–501 (2016b). https://doi.org/10.1111/jtsb.12104
Uher, J.: Quantitative data from rating scales: An epistemological and methodological enquiry. Front. Psychol. 9, 2599 (2018a). https://doi.org/10.3389/fpsyg.2018.02599
Uher, J.: Taxonomic models of individual differences: a guide to transdisciplinary approaches. Philos. Trans. of Royal Soc. B: Biological Sciences, 373(1744) (2018b). https://doi.org/10.1098/rstb.2017.0171
Uher, J.: The transdisciplinary philosophy-of-science paradigm for research on individuals: Foundations for the science of personality and individual differences. In V. Zeigler-Hill & T. K. Shackelford (Eds.), The SAGE handbook of personality and individual differences: Volume I: The science of personality and individual differences (pp. 84–109). London, UK: SAGE (2018c). https://doi.org/10.4135/9781526451163.n4
Uher, J.: Data generation methods across the empirical sciences: differences in the study phenomena’s accessibility and the processes of data encoding. Qual. Quant. 53(1), 221–246 (2019). https://doi.org/10.1007/s11135-018-0744-3
Uher, J.: Measurement in metrology psychology and social sciences: data generation traceability and numerical traceability as basic methodological principles applicable across sciences. Qual. Quant. 54(3), 975–1004 (2020). https://doi.org/10.1007/s11135-020-00970-2
Uher, J.: Problematic research practices in psychology: Misconceptions about data collection entail serious fallacies in data analysis. Theor. Psychol. 31(3), 411-416 (2021a). https://doi.org/10.1177/09593543211014963
Uher, J.: Psychology’s status as a science: Peculiarities and intrinsic challenges. Moving beyond its current deadlock towards conceptual integration. Int. Psychol. Behav. Sci. 55(1), 212–224 (2021b). https://doi.org/10.1007/s12124-020-09545-0
Uher, J.: Psychometrics is not measurement: Unraveling a fundamental misconception in quantitative psychology and the complex network of its underlying fallacies. J. Theoret. Philos. Psychol. 41(1), 58-84 (2021c). https://doi.org/10.1037/teo0000176
Uher, J.: Quantitative psychology under scrutiny: Measurement requires not result-dependent but traceable data generation. Personal. Indiv. Diff. 170, 110205 (2021d). https://doi.org/10.1016/j.paid.2020.110205
Uher, J., Addessi, E., & Visalberghi, E.: Contextualised behavioural measurements of personality differences obtained in behavioural tests and social observations in adult capuchin monkeys (Cebus apella). J. Res. Personal. 47(4), 427–444 (2013). https://doi.org/10.1016/j.jrp.2013.01.013
Uher, J., Visalberghi, E.: Observations versus assessments of personality: A five-method multi-species study reveals numerous biases in ratings and methodological limitations of standardised assessments. J. Res. Personal. 61, 61–79 (2016). https://doi.org/10.1016/j.jrp.2016.02.003
Uher, J., Werner, C.S., Gosselt, K.: From observations of individual behaviour to social representations of personality: Developmental pathways attribution biases and limitations of questionnaire methods. J. Res. Personality 47(5), 647–667 (2013). https://doi.org/10.1016/j.jrp.2013.03.006
Valsiner, J.: From Methodology to Methods in Human Psychology. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-61064-1
Velleman, P.F., Wilkinson, L.: Nominal ordinal interval and ratio typologies are misleading. American Statis. 47(1), 65–72 (1993). https://doi.org/10.1080/00031305.1993.10475938
von Helmholtz, H.: Zählen und Messen, erkenntnistheoretisch betrachtet. Fuess Verlag, Leipzig (1887)
Westerman, M.A.: Examining arguments against quantitative research: “Case studies” illustrating the challenge of finding a sound philosophical basis for a human sciences approach to psychology. New Ideas Psychol. 32, 42–58 (2014). https://doi.org/10.1016/J.NEWIDEAPSYCH.2013.08.002
White, G.H., Farrance, I., AACB Uncertainty of Measurement Working Group.: Uncertainty of measurement in quantitative medical testing: a laboratory implementation guide. Clin. Biochem. Rev., 25(4), S1-24 (2004)
Acknowledgements
The author thanks the editor and two anonymous reviewers for their constructive comments on a previous draft. This research was funded by a Marie Curie Fellowship of the European Commission’s FP7 Programme awarded to the author (EC Grant Agreement Number 629430).
Funding
This research was funded by a Marie Curie Fellowship of the European Commission’s FP7 Programme (EC Grant Agreement Number 629430).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Uher, J. Functions of units, scales and quantitative data: Fundamental differences in numerical traceability between sciences. Qual Quant 56, 2519–2548 (2022). https://doi.org/10.1007/s11135-021-01215-6
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11135-021-01215-6