Stability of a cascade system with two stations and its extension for multiple stations

Abstract

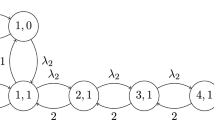
We consider a two-station cascade system in which waiting or externally arriving customers at station 1 move to the station 2 if the queue size of station 1 including an arriving customer itself and a customer being served is greater than a given threshold level $c_{1} \ge 1$ and if station 2 is empty. Assuming that external arrivals are subject to independent renewal processes satisfying certain regularity conditions and service times are i.i.d. at each station, we derive necessary and sufficient conditions for a Markov process describing this system to be positive recurrent in the sense of Harris. This result is extended to the cascade system with a general number k of stations in series. This extension requires certain traffic intensities of stations $2,3,\ldots , k-1$ for $k \ge 3$ to be defined. We finally note that the modeling assumptions on the renewal arrivals and i.i.d. service times are not essential if the notion of the stability is replaced by a certain sample path condition. This stability notion is identical with the standard stability if the whole system is described by the Markov process which is a Harris irreducible T-process.

Appendix

1.1 The equivalence of (a) and (c) in Proposition 2.2

We prove that (a) is equivalent to (c) in Proposition 2.2. We first note that, under the assumption that $X(\cdot )$ is a Harris irreducible T-process, $X(\cdot )$ is either Harris recurrent or $\sigma$-transient by the irreducibility and the Doeblin decomposition (see Theorem 3.1 of [16]), where $X(\cdot )$ is said to be $\sigma$-transient if S is a countable union of measurable sets $A_{i}$ for $i \ge 1$ such that $\mathbb {E}_{x}(\eta _{A_{i}}) < \infty$ for all $x \in S$ and for all $i \ge 1$, in which case each $A_{i}$ is said to be uniformly transient. If $X(\cdot )$ is positive Harris recurrent, then it has an invariant probability measure. Denote it by $\nu$. Then, (2.5) is immediate from (2.2) in Remark 2.1 because there exists a compact set $C \subset S$ such that $\nu (C) > 0$ by the tightness of $\nu$ on S.

Conversely, if (2.5) holds, then $\mathbb {E}_{x}(\eta _{C}) = \infty$ for the compact set C. Hence, $X(\cdot )$ cannot be $\sigma$-transient, and therefore it is Harris recurrent by the Doeblin decomposition. Thus, there is a unique invariant measure. Suppose that this $X(\cdot )$ is null recurrent, then it follows from (2.3) in Remark 2.1 that, for all $x \in S$ and any compact set $C \subset S$,

$$\begin{aligned} \limsup _{t \rightarrow \infty } \frac{1}{t} \int _{0}^{t} \mathbb {P}_{x}(X(u) \in C) {\textrm{d}}u = 0. \end{aligned}$$

(A.1)

This contradicts (2.5), so $X(\cdot )$ must be positive Harris recurrent.

1.2 Proof of (ii) of Lemma 3.1

By (i) of Lemma 3.1${\varvec{X}}(\cdot )$ is a T-process. Let $\varphi (B) = T({\varvec{x}}^{*},B)$, then $T({\varvec{x}}^{*},B) > 0$ implies that $T({\varvec{y}},B) > 0$ for $\forall {\varvec{y}}$ in some open set $V({\varvec{x}}^{*})$ containing ${\varvec{x}}^{*}$ by the lower semi-continuity of $T(\cdot ,B)$. Furthermore, let e be the exponential distribution with unit mean, then $K_{e}({\varvec{x}},V({\varvec{x}}^{*})) = \int _{0}^{\infty } \mathbb {P}_{{\varvec{x}}}({\varvec{X}}(u) \in V({\varvec{x}}^{*})) e^{-u} {\textrm{d}}u > 0$ for $\forall {\varvec{x}} \in S$ since ${\varvec{x}}^{*}$ is reachable from any ${\varvec{x}} \in S$. Hence, for the sampling distribution a by which ${\varvec{X}}(\cdot )$ is a T-process,

$$\begin{aligned} K_{e * a}({\varvec{x}},B)&\ge \int _{V_{\varepsilon }({\varvec{x}}^{*})} K_{e}({\varvec{x}},d{\varvec{y}}) K_{a}({\varvec{y}}, B)\\ {}&\ge \int _{V_{\varepsilon }({\varvec{x}}^{*})} K_{e}({\varvec{x}},d{\varvec{y}}) T({\varvec{y}}, B) > 0, \quad \forall {\varvec{x}} \in S, \end{aligned}$$

where $e * a$ is the convolution of distributions e and a on $\mathbb {R}_{+}$, and $K_{e * a}(\cdot ,\cdot )$ is $e * a$-sampling K-chain. This proves that ${\varvec{X}}(\cdot )$ is $\varphi$-irreducible because distribution $e * a$ has an absolutely continuous component with respect to Lebesgue measure on $\mathbb {R}_{+}$.

1.3 Proof of Lemma 3.2

Obviously, (2.5) implies (3.8) for $X(\cdot ) = {\varvec{X}}(\cdot )$, so we only need to prove that (3.8) implies (2.5). Recall that ${\varvec{X}}_{2}(\cdot )$ is the Markov process describing the queue of class-2 customers. We first show that ${\varvec{X}}_{2}(\cdot )$ is a positive Harris recurrent if (3.8) holds for $i=2$. Since $R_{e,2}(\cdot )$ is a regenerative process with cycles $\tau _{e,2}(\cdot )$ and $R_{s,2}(\cdot )$ is dominated by such a regenerative process $Y(\cdot )$ with cycles $\tau _{s,2}(\cdot )$ in the sense that

$$\begin{aligned} \int _{0}^{t} 1(R_{s,2}(u) \le x) {\textrm{d}}u \le \int _{0}^{t} 1(Y(u) \le x){\textrm{d}}u, \qquad x \ge 0, t \ge 0. \end{aligned}$$

both of $R_{e,2}(\cdot )$ and $R_{s,2}(\cdot )$ are tight on average. Hence, by Proposition 2.2, for any ${\varvec{x}}_{2} \in S$, any $\varepsilon > 0$ and $v = e, s$, there is a compact subset $C_{v,2} \subset \mathbb {R}_{+}$ such that

$$\begin{aligned} \liminf _{t \rightarrow \infty } \frac{1}{t} \int _{0}^{t} \mathbb {P}_{{\varvec{x}}_{2}}(R_{v,2}(u) \in C_{v,2}) {\textrm{d}}u \ge 1 - \varepsilon . \end{aligned}$$

(A.2)

Let $\widetilde{C}_{2} = C_{2,e} \times C_{2,s}$, then

$$\begin{aligned} \mathbb {P}_{{\varvec{x}}_{2}}({\varvec{X}}_{2}(u) \in \{0\} \times \widetilde{C}_{2})&\ge \mathbb {P}_{{\varvec{x}}_{2}}(Q_{2}(u)=0) - \mathbb {P}_{{\varvec{x}}_{2}}(R_{e,2}(u),R_{s,2}(u)) \not \in \widetilde{C}_{2})\\&\ge \mathbb {P}_{{\varvec{x}}_{2}}(Q_{1}(u)=0) - \big (\mathbb {P}_{{\varvec{x}}_{2}}(R_{e,2}(u) \not \in C_{e,2}) + \mathbb {P}_{{\varvec{x}}}(R_{s,2}(u) \not \in C_{s,2})\big )\\&\ge \mathbb {P}_{{\varvec{x}}_{2}}(Q_{1}(u)=0) - 2 \varepsilon . \end{aligned}$$

Integrating this inequality for $u \in [0,t]$, it follows from (3.8) for $i=2$ that there is some ${\varvec{x}}'_{2} \in S$,

$$\begin{aligned} \limsup _{t \rightarrow \infty } \frac{1}{t} \int _{0}^{t} \mathbb {P}_{{\varvec{x}}'_{2}}({\varvec{X}}_{2}(u) \in \{0\} \times \widetilde{C}_{2}) {\textrm{d}}u > 0. \end{aligned}$$

By Proposition 2.2, this proves that ${\varvec{X}}_{2}(\cdot )$ is positive recurrent. Furthermore, it is tight on average by (b) of Proposition 2.2. Since $Q_{1|2}(t) \le 1$ for $\forall t \ge 0$, $\{Q_{1|2}(t); t \ge 0\}$ is obviously tight on average. Similar to $R_{e,2}(\cdot )$ and $R_{s,2}(\cdot )$, $R_{e,1}(\cdot )$, $R_{s,1}(\cdot )$ and $R_{s,1|2}(\cdot )$ are also tight on average. Hence, by a similar argument to ${\varvec{X}}_{2}(\cdot )$, (3.8) for $i=1$ implies (2.5) for $X(\cdot ) = {\varvec{X}}(\cdot )$.

1.4 Proof of Lemma 3.3

Note that, under Assumption 3.1, ${\varvec{X}}(\cdot )$ is $\varphi$-irreducible T-process by Lemma 3.1. (i) Since ${\varvec{X}}(\cdot )$ is positive Harris recurrent, it has the stationary distribution $\nu$, and, by (2.2) in Remark 2.1,

$$\begin{aligned} \lim _{t \rightarrow \infty } \frac{1}{t} \int _{0}^{t} \mathbb {P}_{{\varvec{x}}}(Q_{i}(u) \ge 1){\textrm{d}}u = \mathbb {P}_{\nu }(Q_{i} \ge 1), \qquad \forall {\varvec{x}} \in S, i =1,2. \end{aligned}$$

Integrating both sides of this equation by $\xi$ and applying the dominated convergence theorem, we have

$$\begin{aligned} \lim _{t \rightarrow \infty } \frac{1}{t} \int _{0}^{t} \Big (\int _{S} \mathbb {P}_{{\varvec{x}}}(Q_{i}(u) \ge 1) \xi (\textrm{d}{\varvec{x}}) \Big ) {\textrm{d}}u = 1 - \mathbb {P}_{\nu }(Q_{i}(0)=0). \end{aligned}$$

This and the definition of $\rho ^{*}_{i}(\xi )$ prove (3.12).

(ii) By Lemma 3.2, we only need to show that $\rho ^{*}_{i}(\xi ) < 1$ for $i=1,2$ is equivalent to (3.8) for some ${\varvec{x}} \in S$ and some $\ell \ge 0$. Assume that $\rho ^{*}_{i}(\xi ) < 1$ for $i=1,2$. Because, by Fatou’s lemma,

$$\begin{aligned} \rho ^{*}_{i}(\xi ) \ge \int _{S} \Big (\liminf _{t \rightarrow \infty } \frac{1}{t} \int _{0}^{t} \mathbb {P}_{{\varvec{x}}}(Q_{i}(u) \ge 1) {\textrm{d}}u \Big ) \xi (d{\varvec{x}}), \end{aligned}$$

we have

$$\begin{aligned}&\int _{S} \Big ( \limsup _{t \rightarrow \infty } \frac{1}{t} \int _{0}^{t} \mathbb {P}_{{\varvec{x}}}(Q_{i}(u) = 0) {\textrm{d}}u \Big ) \xi (d{\varvec{x}}) \\&\quad = \int _{S} \Big ( 1- \liminf _{t \rightarrow \infty } \frac{1}{t} \int _{0}^{t} \mathbb {P}_{{\varvec{x}}}(Q_{i}(u) \ge 1) {\textrm{d}}u \Big ) \xi (d{\varvec{x}}) \ge 1 - \rho ^{*}_{i}(\xi ) > 0. \end{aligned}$$

Hence, (3.8) holds for $i=1,2$, $\ell =0$ and some ${\varvec{x}}_{i} \in S$.

Conversely, assume (3.8) for $i=1,2$ and some ${\varvec{x}}_{i} \in S$ and some $\ell = 0$. Then, ${\varvec{X}}(\cdot )$ is positive Harris recurrent by Lemma 3.2. Hence, (3.12) holds by (i) of Lemma 3.3, and therefore we only need to show that $\mathbb {P}_{\nu }(Q_{i}(0)=0) > 0$ for $i=1,2$. To prove this, we first note that ${\varvec{X}}(\cdot )$ is Harris $\varphi$-irreducible for $\varphi (B) = T({\varvec{x}}^{*},B)$ by Lemma 3.1. Hence, $\varphi (B) > 0$ implies $K_{a}({\varvec{x}},B) > 0$ for $\forall {\varvec{x}} \in S$ for some sampling distribution a by Definition 2.2. Then, for the stationary distribution $\nu$ of ${\varvec{X}}(\cdot )$, for any sampling distribution a on $\mathbb {R}_{+}$,

$$\begin{aligned} \nu (B) \ge \int _{S} \nu (d{\varvec{x}}) K_{a}({\varvec{x}},B) > 0. \end{aligned}$$

Hence, $\varphi (B) > 0$ implies $\nu (B) > 0$ for any $B \in {\mathscr {B}}(S)$. From the definition of $\varphi$, $\varphi (G) > 0$ for any open set G containing ${\varvec{x}}^{*}$ of Lemma 3.1. As this G, we choose $G_{0}$ defined by

$$\begin{aligned} G_{0} = \{0\} \times \mathbb {Z}_{+} \times \{0,1\} \times \mathbb {R}_{+}^{5} \subset S, \end{aligned}$$

which obviously contains ${\varvec{x}}^{*}$. Since the discrete topology is taken on $\mathbb {Z}_{+}^{2} \times \{0,1\}$, $G_{0}$ is an open set. Hence, $\varphi (G_{0}) > 0$, which implies that $\mathbb {P}_{\nu }(Q_{1}(0)=0) = \nu (G_{0}) > 0$. This proves that $\rho _{1}^{*}(\xi ) < 1$. Similarly, $\rho ^{*}_{2}(\xi ) < 1$ is proved.