Dispatching to parallel servers

Abstract

Policy iteration techniques for multiple-server dispatching rely on the computation of value functions. In this context, we consider the continuous-space M/G/1-FCFS queue endowed with an arbitrarily designed cost function for the waiting times of the incoming jobs. The associated relative value function is a solution of Poisson’s equation for Markov chains, which in this work we solve in the Laplace transform domain by considering an ancillary, underlying stochastic process extended to (imaginary) negative backlog states. This construction enables us to issue closed-form relative value functions for polynomial and exponential cost functions and for piecewise compositions of the latter, in turn permitting the derivation of interval bounds for the relative value function in the form of power series or trigonometric sums. We review various cost approximation schemes and assess the convergence of the interval bounds these induce on the relative value function, namely Taylor expansions (divergent, except for a narrow class of entire functions with low orders of growth) and uniform approximation schemes (polynomials, trigonometric), which achieve optimal convergence rates over finite intervals. This study addresses all the steps to implementing dispatching policies for systems of parallel servers, from the specification of general cost functions toward the computation of interval bounds for the relative value functions and the exact implementation of the first-policy improvement step.

Appendices

On policy iteration and first-policy improvement

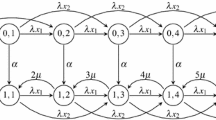
Recall the system depicted in Fig. 1, where jobs, arriving according to a Poisson process with rate $\lambda$, are dispatched upon arrival toward one of the $k$ servers ($1,\dots ,k$) selected by a (possibly random) dispatching policy $\pi (u,x)$, where $u=(u_{1},\dots ,u_{k})\in \mathbb {R}_{{\ge 0}}^k$ denotes the server backlog vector and $x=(x_{1},\dots ,x_{k})\in \mathbb {R}_{{\ge 0}}^k$ are the prospective service times of an incoming job at the servers. By taking snapshots at initial time $n=0$ and at the job arrival times ($n=1,2,3,\dots$), the continuous-time system reduces to a MDP, $(\Phi ^{\pi }_{n})_{n\in \mathbb {N}}$, with state $\Phi ^{\pi }_{n} = ( U_{n} , X_{n} ) \in \Omega \equiv \mathbb {R}_{{\ge 0}}^k\times \mathbb {R}_{{\ge 0}}^k$, where $X_{n}$ is the service time vector of the $n$th job and $U_{n}$ is the backlog of the system at the time of arrival, and with transition probability kernel $P=(P_{1},\dots ,P_{k})$ such that, for any $n$ and every $(u,x)\in \Omega$, $\mathcal {S}\subset \Omega$,

$$\begin{aligned} \begin{array}{c} P_{i}(u,x,\mathcal {S}) {:}{=}Prob (\Phi ^{\pi }_{n+1}\in \mathcal {S}| \Phi ^{\pi }_{n} = ( u,x),\, \pi (u,x) = i) = P_{i}((u_{1},\dots ,u_{i}+x,\dots ,u_{k}) , 0,\mathcal {S}) . \end{array} \end{aligned}$$

Assume that the performance of the system is measured by a cost function $f$, where $f(i,u,x) \equiv f_{i}(u_{i}) \, \mathbf {1}_{\mathbb {R}_{>0}}(x)$ models a penalty incurred when a job with service time $x$ joins server $i$, given backlog state $u=(u_{1},\dots ,u_{k})$. We would like to minimize the long-run average cost, defined by

$$\begin{aligned} J_\pi = \limsup _{N\rightarrow \infty } \frac{1}{N} \sum _{n=1}^{N} \mathbb {E}\left[ f\left( \pi (\Phi ^{\pi }_{n}) ,\Phi ^{\pi }_{n} \right) \right] , \end{aligned}$$

independently of $\Phi ^{\pi }_{0}$. The optimality equations of the system are

$$\begin{aligned} g({u,x})&\textstyle = \min _i\left[ f_{i}(u_{i}) + P_{i} g({u,x})\right] - \varsigma , \end{aligned}$$

(OEa)

$$\begin{aligned} \pi (u,x)&\textstyle \in \arg \min _i\left[ f_{i}(u_{i}) + P_{i} g({u,x})\right] , \end{aligned}$$

(OEb)

where $P_{i} g({u,x}) = \int _\Omega g({t,y}) P_{i}(u,x,d(t,y)) \equiv P_{i} g({(u_{1},\dots ,u_{i}+x_{i},\dots ,u_{k}),0}) .$ If one can find $\varsigma ^*>0$, a policy $\pi ^*$, and an integrable function $g$ such that $(g,\varsigma ^*)$ solves (OEa) and $\pi ^*$ satisfies (OEb), then $\pi ^*$ is the optimal policy and

is the optimal cost of the system [2, 25, 31, 32]. The policy iteration algorithm for solving (OE) can be described as follows [17]: Given an initial policy $\pi ^{(0)}$, find, for $k\ge 0$, a function ${g}^{(k)}$, a mean cost $\varsigma ^{(k)}$, and a policy $\pi ^{(k+1)}$ satisfying

$$\begin{aligned} \textstyle {g}^{(k)}(u,x)&\textstyle = f( \pi ^{(k)}{(u,x)} ,u,x) + P_{\pi ^{(k)}{(u,x)}} {g}^{(k)}(u,x) - \varsigma ^{(k)}, \end{aligned}$$

(PIa)

$$\begin{aligned} \textstyle \pi ^{(k+1)}{(u,x)}&\textstyle \in \arg \min _i\left[ { f_{i}(u_{i}) } + {v}^{(k)}(u_{1},\dots ,u_{i}+x_{i},\dots ,u_{k}) \right] , \end{aligned}$$

(PIb)

where (PIa) is the policy evaluation step, (PIb) is the policy improvement step and ${v}^{(k)}(u) := \int _\Omega {g}^{(k)}(t,y) \, P({u,0},d(t,y)) - \varsigma ^{(k)}$ defines the relative value function under policy $\pi ^{(k)}$. Under favorable conditions, $( \pi ^{(k)}, \varsigma ^{(k)})$ eventually converges toward a solution $(\pi ^*,\varsigma ^*)$ [31, 32]. Solving (PIb), however, is generally difficult.

The first iteration of (PI) may still be implemented easily if the initial policy $\pi ^{(0)}\equiv \pi$ is a random Bernoulli split between the servers. In that case, the Poisson process separates into $k$ independent Poisson processes with rates $\lambda _{1},\dots ,\lambda _{k}$, where $\lambda _{1}+\cdots +\lambda _{k}=\lambda$, and the multiple-server system decomposes into $k$ independent M/G/1 queues with arrival rates $\lambda _{1},\dots ,\lambda _{k}$ and transition probability kernels $P^{{(\lambda _{1})}},\ldots ,P^{{(\lambda _{k})}}$. The relative value function under the initial random policy then takes the additively separable form $v(u) = \sum _{i=1}^{k} v_{i}(u_{i})$, where $v_{i}(u_{i}) {:}{=}P^{{(\lambda _{i})}} g_{i}({u_{i},0}) - \varsigma _{i}$ is the relative value function at server $i$, and $g_{i}$ satisfies

$$\begin{aligned} g_{i}({u_{i},x_{i}}) = P^{{(\lambda _{i})}} g_{i}({u_{i},x_{i}}) + f_{i}(u_{i}) - \varsigma _{i} \qquad (i=1,\dots ,k). \end{aligned}$$

(FPIa)

Since $f_{i}(u_{i}) + v(u_{1},\dots ,u_{i}+x_{i},\dots ,u_{k}) = f_{i}(u_{i}) + v(u) + v_{i}(u_{i}+x_{i}) - v_{i}(u_{i})$, (PIb) reduces to

$$\begin{aligned} \hat{\pi }{(u,x)} \in \arg \min _i\mathcal {A}_{i}(u,x) , \end{aligned}$$

(FPIb)

where $\mathcal {A}_{i}(u,x) = f_{i}(u_{i}) + v_{i}(u_{i}+x_{i}) - v_{i}(u_{i})$ is the admission cost at server $i$. The first-policy improvement approach then consists in stopping the PI algorithm after a single iteration, by solving (FPIa)–(FPIb). Observe that (FPIa) is an instance of the Poisson equation $g= Pg+ f$ under $\int f(u)\, \nu ({du}) = 0$, where $\nu$ denotes the nontrivial measure invariant for the transition kernel P (i.e., $P \nu = \nu$) [3, 34, 35]. In (FPIa), $\nu$ coincides with the asymptotic probability measure of the waiting times at server i.

Characterization of the value function

Before showing Propositions 1–2, and Theorem 1, we characterize $W^{*}$ in the complex plane.

Proposition B.1

(Analyticity of $W^{*}$ and pole location) Under Assumption 1:

• (i) The dominant singularity $p_{W}$ of $W^{*}$ (i.e., that with largest real value) is a pole with degree 1 lying on the negative real axis $\mathbb {R}_{<0}$. The dominant singularity $p_{X}$ of $X^{*}$ is real, negative (possibly infinite) and satisfies $p_{X}<p_{W}$. $X^{*}$ is analytic on $\{s\in \mathbb {C}\, | \,\mathfrak {R}\left( s\right) > p_{W}\}$.

• (ii) $W^{*}$ is analytic on $\{s\in \mathbb {C}_{0}\, | \,\mathfrak {R}\left( s\right) > p_{W}\}$, where $\lim \nolimits _{s\rightarrow \infty }|W^{*}(s)|\le 1$.

• (iii) One can find $\epsilon >0$ such that $W^{*}$ is analytic on $\{s\in \mathbb {C}_{0}\setminus \{p_{W}\}\, | \,\mathfrak {R}(s)>p_{W}-\epsilon \}$.

• (iv) $W^{*}$ is analytic in a neighborhood of 0, where it can be rewritten as the series

  $$\begin{aligned} W^{*}(s) = \sum \nolimits _{k=0}^\infty w_{k}\, (-s)^k , \quad \forall s\in \{\sigma \in \mathbb {C}_{0}:|\sigma -a| < |p_{W}| \}, \end{aligned}$$

  (B1)

  in which the coefficients $\{w_{k}\}$ are given by (III3) in Table 1, and satisfy $w_{k}=\mathbb {E}\big [W^k\big ]/ {k}!$, for $k\in \mathbb {N}$. The series $\{w_{k}\}$ is asymptotically geometric with asymptotic rate $|p_{W}|^{-1}$.

• (v) At any point $a\in \mathbb {C}_{0}$ where $W^{*}$ is analytic, $W^{*}$ can be rewritten as the series

  $$\begin{aligned} W^{*}(s) = \sum \nolimits _{k=0}^{\infty } w_{{a}:{k}} (a-s)^{k} , \quad \forall s\in \{\sigma \in \mathbb {C}:|\sigma -a| < r_{a} \} , \end{aligned}$$

  (B2)

  where $r_{a}$ denotes the distance from $a$ to the closest singularity of $W^{*}$. The coefficients $\{w_{{a}:{k}}\}$ are given by (III4) in Table 1.

Next, we derive the identities of Sect. 3.1 for the value function.

Proof

(Proposition 1) Start the queue at state $u$. The quantity $V(u,t)$ appearing in (VF) can be rewritten, for any $T\ge 0$ and for $t$ large enough, as $V(u,t) = V(u,T) + V(U({T}),t-T)$, where $U({T})$ denotes the backlog observed after time $T$. It follows from the Markov property of the system and from Definition (VF) of the value function that

$$\begin{aligned} v(u) = \mathbb {E}\big [ V(u,T) - \lambda \bar{f}T\big ] + \mathbb {E}\big [ v(U({T})) \big ] . \end{aligned}$$

(B3)

Now, consider the function

$$\begin{aligned} \textstyle g({u,x}) = \lim \nolimits _{N\rightarrow \infty }\{ \sum _{n=1}^{N} \mathbb {E}\left[ f(U_{n} ) -\bar{f}\right] \, | \,(U_{1},X_{1})=(u,x) \} + \bar{f}, \quad \forall u,x\in \mathbb {R}_{{\ge 0}},\nonumber \\ \end{aligned}$$

(B4)

which can be verified to satisfy Eq. (PE) by application of the Markov property to the MDP. The function $g$ defined by (B4) can be seen as a discrete-time counterpart of the value function (VF), which follows from (B4) by using the convention $(U_{0},X_{0})=(u,0)$ and setting $v(u)\equiv Pg({u,0}) - \bar{f}$ or, equivalently, from (B3) by defining $T$ as the arrival time of the first job so that $\mathbb {E}\big [ V(u,T) - \lambda \bar{f}T\big ] = -\bar{f}$ and $\mathbb {E}\big [ v(U({T})) \big ] \equiv Pg({u,0})$. $\square$

Proof

(Theorem 1) A simple calculation reveals that $\Updelta (u)=0$ if $u<0$, and $\textstyle \Updelta (u) = (P- \widehat{P}) g({u,0}) = \kappa e^{-\lambda u}$, for $u\ge 0$, with $\kappa$ satisfying

$$\begin{aligned} \textstyle \kappa = \mathbb {E}\big [ g({0,X_{0}}) - \lambda \int _{-\infty }^{0} g({u,X}) \, e^{\lambda u} \, du\big ] . \end{aligned}$$

(B5)

We characterize the extended value function $\widehat{v}:u\in \mathbb {R}\mapsto \widehat{v}(u)=g({u,0}) - f(u)$ associated with some $g$ solution of (PE’). Note that, by construction, $\widehat{v}$ coincides with the value function on $\mathbb {R}_{{\ge 0}}$, i.e., $\widehat{v}(u) \equiv v(u)$ if $u\ge 0$. Once $\widehat{v}$ is known, it will be possible to recover $g$ using

$$\begin{aligned} g({u,x}) = g({u+x,0}) - f(u+x) + f(u) = \widehat{v}(u+x) + f(u) . \end{aligned}$$

(B6)

Consider $s$ in the region of absolute convergence of $\mathcal {B}_{\widehat{v}}$, where the orders of integration in our developments may be permuted. The two-sided Laplace transform of $\widehat{v}$ is given by

Solving the above equation for $\mathcal {B}_{\widehat{v}}(s)$ and using $W^{*}(-s) = 1+{\lambda \mathbb {E}\big [X^2\big ]}/[{2(1-\rho )}]s+o(s)$ yields, after computations,

(B7)

where $h(s)$ has no singularities on $\{s\in \mathbb {C}\, | \,\mathfrak {R}\left( s\right) <- p_{W}\}$, and $\varepsilon$ is given by

$$\begin{aligned} \varepsilon = {\kappa }/{(1-\rho )}-{\hat{X}^{*}_{2}(\lambda )\bar{f}}/{(1-\rho )^2} , \end{aligned}$$

(B8)

with $\hat{X}^{*}_{2}(\lambda ){:}{=}1-\lambda \mathbb {E}\big [X\big ]+\lambda ^2\mathbb {E}\big [X^2\big ]/2$. Since $\widehat{v}$ is expected to be asymptotically flat for $u\rightarrow -\infty$, the $- {\lambda \bar{f}}/[{(1-\rho )s^2}]$ term in (B7) is necessarily due to a term $-{\lambda \bar{f}}/({1-\rho })\, u$ on $\mathbb {R}_{{\ge 0}}$ in the backlog domain. By inverse transformation of (B7), we find

where $r$ satisfies $\mathcal {L}_{r(-\cdot )}(s) = -[{h(-s)+\varepsilon }]/{s}$. The general form for $g$ follows from (B6), ($\widehat{\text {S}}$) and $\widehat{v}(u) \equiv v(u)$ on $\mathbb {R}_{{\ge 0}}$. The nonempty ROC of $\mathcal {B}_{\partial _{+}\widehat{v}}$ follows from $-p_{W}\in ROC (\mathcal {L}_{f})$.

It remains to show that the function $r$ is identical for all solutions or, equivalently, that the quantity $\kappa$ in (B5) is the same for all $g$.

To see this, consider a solution $g_{1}$ of (PE’) with associated value function $\widehat{v}_{1}$ and jump $\varepsilon _{1}$ at $u=0$. The value function for every other solution $g_{2}$ can be rewritten as $\widehat{v}_{2}=\alpha + (\widehat{v}_{1} - \varepsilon _{2} + \varepsilon _{1} ) \mathbf {1}_{\mathbb {R}_{<0}}+ \widehat{v}_{1} \mathbf {1}_{\mathbb {R}_{{\ge 0}}}$, where $\varepsilon _{1}$, $\varepsilon _{2}$ and $\alpha$ are constants. We show that $\varepsilon _{1}=\varepsilon _{2}$. If we successively compute expression (B8) for $\varepsilon _{1}$ and $\varepsilon _{2}$, using (B5), (B6) and the extension of (PE), we get, after simplifications, $\varepsilon _{2} = \varepsilon _{1} - ( \varepsilon _{1} - \varepsilon _{2} ) X^{*}(\lambda ) /{(1-\rho )}$. Exploiting twice the strict convexity of $e^{-x}$, we find $X^{*}(\lambda ) = \mathbb {E}\big [ e^{-\lambda X} \big ]> e^{-\lambda \mathbb {E}\big [X\big ] } > 1 - \lambda \mathbb {E}\big [X\big ] = 1-\rho$. Hence, $X^{*}(\lambda ) /{(1-\rho )} \ne 1$ and, consequently, $\varepsilon _{1}=\varepsilon _{2}$. $\square$

Proof

(Proposition 2) (i) Consider $s$ in the region of absolute convergence of $\mathcal {B}_{\widehat{v}}$. Since $\mathcal {B}_{\partial _{+}{c}}(s)=s\mathcal {B}_{{c}}(s)$, (C) can be rewritten as

$$\begin{aligned}{}[s+ \lambda (1- X^{*}(-s)) ] \, \mathcal {B}_{c}(s) \overset{\text {\tiny {(PK)}}}{=} \lambda \mathcal {L}_{f}(s) + s\mathcal {L}_{r(-\cdot )}(-s) \left[ 1+ \lambda /s(1- X^{*}(-s)) \right] , \end{aligned}$$

while transformation of ($\widehat{\text {S}}$) gives $\mathcal {B}_{c}(s)= \mathcal {B}_{\widehat{v}}(s) + {\lambda \bar{f}}/[{(1-\rho )s^2}]$. Besides,

$$\begin{aligned} X^{*}(-s) \mathcal {B}_{\widehat{v}}(s)= & {} \mathbb {E}\big [{sX}\big ]\int _{-\infty }^{+\infty } \widehat{v}(u) e^{-su} du= \mathbb {E}\big [ \int _{-\infty }^{+\infty } \widehat{v}(u) e^{-s(u-X)} du\big ]\\= & {} \mathbb {E}\big [ \int _{-\infty }^{+\infty } \widehat{v}(t+X) e^{-st} dt\big ] = \int _{-\infty }^{+\infty } \mathbb {E}\big [ \widehat{v}(t+X) \big ] e^{-st} dt= \mathcal {B}_{\mathbb {E}\big [\widehat{v}(\cdot +X)\big ]}(s). \end{aligned}$$

Combining the above with $\mathcal {B}_{\partial _{+}\widehat{v}}(s)=s\mathcal {B}_{\widehat{v}}(s)$, we get, after computations,

$$\begin{aligned} \mathcal {B}_{\partial _{+}\widehat{v}}(s) = \lambda \left[ \mathcal {L}_{f}(s) -\bar{f}/s+ \mathcal {B}_{\mathbb {E}\big [\widehat{v}(\cdot +X)\big ]}(s) - \mathcal {B}_{\widehat{v}}(s)\right] + \tilde{h}(s) , \end{aligned}$$

(B9)

where $\tilde{h}(s)$ shows no singularity on $\{s\in \mathbb {C}\, | \,\mathfrak {R}\left( s\right) <- p_{W}\}$, and we have used Proposition B.1(i) and $1+ \lambda /s(1- X^{*}(-s)) = 1-\rho +o(1)$. Inverse Laplace transformation of (B9) then gives, at every $u\ge 0$ where $\widehat{v}$ is differentiable,

$$\begin{aligned} \widehat{v}^{\prime }(u) = \lambda \left( f(u) - \bar{f}+ \mathbb {E}\left[ \widehat{v}(u+X)- \widehat{v}(u) \right] \right) , \end{aligned}$$

(B10)

which holds for almost every $u>0$ by piecewise continuity of $f$. Since by construction $v(u)\equiv \widehat{v}(u)$ for $u\ge 0$, we find (DE). From Theorem 1, we have

$$\begin{aligned} \textstyle \widehat{v}(0) = g({0,0}) - f(0) \overset{\text {\tiny {(PE')}}}{=} Pg({0,0}) - \bar{f}\overset{\text {\tiny {(II1)}}}{=} \mathbb {E}\big [\widehat{v}(X_{0})\big ] + f(0) - \bar{f}, \end{aligned}$$

(B11)

which yields (BCa). Finally, we find (BCb) by taking the limit of (B10) as $u\rightarrow 0^+$,

(ii) Equation (S) follows directly from ($\widehat{\text {S}}$) and the fact that $v(u)\equiv \widehat{v}(u)$ for $u\ge 0$. It remains to compute $\partial _{+}c$. From Theorem 1, we get

(B12)

where we have used $f(u)=0$ if $u<0$. Equation (C) follows by inversion of (B12). $\square$

Splitting schemes for the Pollaczek–Khinchin formula

This section includes further details on the transform splitting scheme (III12), which proves very useful when computing value functions with discrete service time distributions. See also [9] for a step-by-step derivation of the core function in the case of jobs with identical service times.

1.1 Discrete service time distributions

Consider the M/D/1 queue, where all the jobs have equal service time $x$. In this scenario, the transform $W^{*}$ is given by (PK) with $X^{*}(s)=e^{-sx}$ and can be rewritten as

$$\begin{aligned} \begin{array}{ll} W^{*}(s) = [\Upsilon (-s)]^m W^{*}(s) +\frac{(1-\lambda x)s}{s- \lambda } \sum \nolimits _{k=0}^{m-1} [\Upsilon (-s)]^k ,&\quad \forall m\in \mathbb {N}_{>0}, \end{array} \end{aligned}$$

(C1)

where $\Upsilon (s) {:}{=}[{\lambda }/({s+\lambda })]\,e^{sx}$. It can be seen that (III12) holds if

$$\begin{aligned} \textstyle W^{l}_{u}(s) = [\Upsilon (-s)]^ {\tilde{m}({u})} W^{*}(s) ,\quad W^{r}_{u}(s) = \frac{s(1-\rho ) }{s-\lambda } \sum \nolimits _{k=0}^{\tilde{m}({u})-1} [\Upsilon (-s)]^k , \end{aligned}$$

with $\tilde{m}({u})=\left\lceil ({\tau -u})/{x}\right\rceil$.

1.2 Degenerate cases

The decomposition scheme (C1) is not possible for all discrete service time distributions. Consider, for instance, the geometric service time distribution $F_{X}({u})= (e^{\varsigma }-1) \sum \nolimits _{k=1}^{\infty } e^{- k\varsigma } \theta (u-kx)$ for $u\in \mathbb {R}_{{\ge 0}}$, where $x>0$ and $\lambda <(1-e^{-\varsigma })/x$. We have $\mathbb {E}\big [ X\big ] = x/(1-e^{-\varsigma })$, $X^{*}(s) = (e^{\varsigma }-1)/(e^{\varsigma +sx}-1)$, and $W^{*}$ degenerates into

$$\begin{aligned} W^{*}(s) = \frac{ b(e^{\varsigma +sx}-1) s}{(s- \lambda ) e^{\varsigma +sx} -s+\lambda e^{\varsigma } } = b-s(e^{\varsigma +sx}-1) \, f(s) , \end{aligned}$$

(C2)

where $b= ({1-e^{-\varsigma }-\lambda x})/({1-e^{-\varsigma }})$ and $f(s) = [(\lambda -s) e^{\varsigma +sx} +s-\lambda e^{\varsigma } ]^{-1}$. Although $f(s)$ decreases like $O(r^{-1})$ as $|s|\rightarrow \infty$ (i.e., not fast enough for counterclockwise integration along $\mathcal {C}_{r}$), it decomposes as follows:

$$\begin{aligned} \textstyle f(s) = [\tilde{\Upsilon }(-s)]^{m } f(s) + \sum \nolimits _{k=1}^{m} [\tilde{\Upsilon }(-s)]^{k} /({\lambda e^{\varsigma }-s}), \quad (m=1,2,\dots ), \end{aligned}$$

(C3)

where $\textstyle \tilde{\Upsilon }(s)= ({ s+\lambda e^{\varsigma }})/{(s+ \lambda ) } \, e^{sx-\varsigma }$ is $O( e^{\mathfrak {R}(s)x} )$ with just one pole at $-\lambda$. By distributing (C2) and using (C3) twice with parameters $m+1$ and m, we find, after computations, that (III12) holds if we set

$$\begin{aligned} \begin{array}{rcl} W^{l}_{u}(s) &{}=&{} \lambda b\frac{s( e^{\varsigma }-1 )( \lambda e^{\varsigma }-s)^{\tilde{m}_{l}({u})-1}}{(\lambda -s)^{\tilde{m}({u})}\, [ s- \lambda -(s-\lambda e^{\varsigma }) e^{-(sx+\varsigma )} ] } \, e^{-\tilde{m}({u})(sx+\varsigma )},\\ W^{r}_{u}(s) &{}=&{} \frac{s-b}{s-\lambda } + \lambda b\frac{ (e^{\varsigma }-1 ) -s}{(s-\lambda ) (s-\lambda e^{\varsigma })} \sum \nolimits _{k=1}^{\tilde{m}({u})-1} \big (\frac{s-\lambda e^{\varsigma }}{s-\lambda } \big )^{k} e^{-k(sx+\varsigma )} , \end{array} \end{aligned}$$

with $\tilde{m}({u})=\lceil ({\tau -u})/{x}\rceil$.

System interpretation of Taylor series CVF

In view of (C), the core function can be seen as the answer to the input $f$ of a linear filter with transfer function ${\lambda }/{(1-\rho )} \,W^{*}(-s)$. Similarly, the Taylor series (IV3) for the CVF of an analytic cost function is reminiscent of digital filtering in signal processing. Indeed, for $n\in \mathbb {N}$, consider the vector of derivatives $\tilde{f}^{(n)}=(\tilde{f}_{0},\dots , \tilde{f}_{n-1} )$, where $\tilde{f}_{k} ={f^{(k)}(0)}$, and the vector $\tilde{c}^{(n)}=(\tilde{c}^{(n)}_{0}, \dots ,\tilde{c}^{(n)}_{n-1})$, where $\tilde{c}^{(n)}_{k}$ is defined by (IV2). Using the matrix inversion lemma, one shows that the Toeplitz, upper triangular matrices

satisfy $W^{(n)}({I^{(n)}}/{\lambda }-X^{(n)}) = I^{(n)}$ for all $n$, where $I^{(n)}$ denotes the identity matrix. Besides, (IV2) rewrites in matrix form as $\tilde{c}^{(n)}=W^{(n)} \tilde{f}^{(n)}$.

As $n\rightarrow \infty$, $\{\tilde{c}_{t}\}$ becomes the output (at nonnegative times) of the cross-correlation of $\{\tilde{f}_{t}\}$ with the sequence defined by $\tilde{h}[t]= {\lambda }/({1-\rho })\,w_{t}$ for $t\ge 0$, thus giving us an interpretation for analytic functions of Proposition 2(ii), where $c^{\prime }$ was obtained by cross-correlation of $f(u)$ with $\lambda /(1-\rho ) F^{\prime }_{W}({u})$. Similarly, (IV3b) expresses $c^{\prime }(u)$ as the cross-correlation of the sequence of derivatives of $f$ at $u$ with the sequence $\tilde{h}[t]$.

From our observation it follows that the Z-transforms of the sequences satisfy

$$\begin{aligned} \mathcal {Z}_{\tilde{c}^{(\infty )}}(z) = \mathcal {Z}_{\tilde{h}}({1}/{z})\, \mathcal {Z}_{\tilde{f}^{(\infty )}}(z) , \end{aligned}$$

(D1)

where $\mathcal {Z}_{h}(z) = \sum \nolimits _{k=0}^{\infty } h[k] z^{-k}$ denotes the Z-transform of a sequence $h[t]$. The vector $\tilde{c}^{(\infty )}$ can be recovered from (D1) by inverse Z-transform, provided that the regions of convergence of $\mathcal {Z}_{\tilde{f}^{(\infty )}}(z)$ and $\mathcal {Z}_{\tilde{h}}({1}/{z})$ intersect on a nonempty circular band – this condition is to be linked to those of Theorem 2(i).

Conversely, inverting $W^{(n)}$ yields $\tilde{f}^{(n)}=({I^{(n)}}/{\lambda }-X^{(n)}) \tilde{c}^{(n)}$ and, as $n\rightarrow \infty$,

$$\begin{aligned} \tilde{f}_{k} = {\tilde{c}_{k}}/{\lambda } - \sum \nolimits _{t=0}^\infty [{\tilde{c}_{t+k}}/{{(t+1)}!}]\, \mathbb {E}\big [X^{t+1}\big ] , \end{aligned}$$

(D2)

which provides us with a converse for Theorem 2, where the source cost function of a given core function with germ $\{\tilde{c}_{k}\}$ can be recovered from $c$ through (D2), on the condition that $c$ grows slower than the exponential type $|p_{X}|$ – where $p_{X}$ denotes the dominant pole of $X$ – , in which case $({I^{(n)}}/{\lambda }-X^{(n)})\,\tilde{c}^{(n)}$ converges as $n\rightarrow \infty$. Similarly, $\mathcal {Z}_{\tilde{f}^{(\infty )}}(z) = (\mathcal {Z}_{\tilde{h}}({1}/{z}))^{-1} \mathcal {Z}_{\tilde{c}^{(\infty )}}(z)$, where $(\mathcal {Z}_{\tilde{h}}(z))^{-1}$ is the Z-transform of $\delta [{t}]/\lambda - \mathbb {E}\big [X^{t+1}\big ]/{(t+1)}!$.

Proofs and auxiliary results

Proof

(Theorem 2) (i) If $\varrho$ is the order of growth of the entire cost function $f$, and $\sigma$ is its type, then for any $\epsilon >0$ there is $k_\epsilon <\infty$ such that [30, Lecture 1]

$$\begin{aligned} \begin{array}{ll} \frac{1}{{{k}}!}|f^{({k})}(0)| < \big (\frac{e (\varrho +\epsilon )}{{k}}\big )^{\frac{{k}}{\varrho +\epsilon }} ,&\quad \forall {k}>k_\epsilon , \end{array} \end{aligned}$$

(E1a)

$$\begin{aligned} \begin{array}{ll} \frac{1}{{{k}}!}|f^{({k})}(0)| < \big (\frac{e (\sigma +\epsilon ) \varrho }{{k}}\big )^{\frac{{k}}{\varrho }} ,&\quad \forall {k}>k_\epsilon . \end{array} \end{aligned}$$

(E1b)

Consider the quantity $\tilde{c}_{{k}}= \sum \nolimits _{q=0}^{\infty } w_{q} \, f^{(k+q)}(0)$ introduced in (IV2), as well as

$$\begin{aligned} \begin{array}{ll} \bar{c}_{{k}}=\frac{\lambda }{1-\rho } \sum \nolimits _{q=0}^{\infty } w_{q} \left| f^{({k}+q)}(0)\right| ,&\quad \forall {k}\in \mathbb {N}. \end{array} \end{aligned}$$

(E2)

Recall from Proposition B.1 (iv) in Appendix B that $\lim \nolimits _{k\rightarrow \infty } w_{k+1}/w_{k} = |p_{W}|^{-1}$. Besides, it can be seen (for example, using Stirling’s approximation for the factorial) that

$$\begin{aligned} \begin{array}{ll} \lim \nolimits _{{k}\rightarrow \infty } \frac{ {({k}+1)}! \big (\frac{e s r}{{k}+{l}+1}\big )^{\frac{{k}+{l}+1}{r}} }{ {{k}}! \big (\frac{e s r}{{k}+{l}}\big )^{\frac{{k}+{l}}{r}} } = \Bigg \lbrace \begin{array}{cl} 0,&{}if r<1 \\ s,&{}if r=1 \\ \infty ,&{}if r>1 \end{array}\Bigg \rbrace ,&\quad \forall {l}\in \mathbb {N}. \end{array} \end{aligned}$$

(E3)

Equations (E1a) and (E1b) tell us that, under the assumptions of (i) and by taking $\epsilon$ sufficiently small, one can find a dominant series for $\tilde{c}_{{k}}$ and $\bar{c}_{{k}}$ that successfully passes the ratio test for convergence due to (E3), so that both $\tilde{c}_{{k}}$ and $\bar{c}_{{k}}$ are finite for all k. The finiteness of $\bar{c}_{{k}}$ allows us to interchange the integration order in the computation of $\tilde{c}_{{k}}$. Noting that $w_{q}=\mathbb {E}\big [W^q\big ]/ {q}!$ for all q [cf. Proposition B.1(iv)], we apply Fubini’s theorem and find, for ${k}\in \mathbb {N}_{\ge 0}$,

(E4)

Similarly, we introduce, for ${k}\in \mathbb {N}$,

(E5)

and $\hat{c}_{{k}}$ is finite as well. Suppose now that $|({d^{{k}}}/ {du^{{k}}})f(0)| < {{{k}}!} ({e s r}/{{k}})^{{{k}}/{r}}$ for ${k}>k_\epsilon$–in the case (i), this holds either for some $r<1$ or for $r=1$ and some finite s–, and consider the sequence

$$\begin{aligned} \textstyle \beta _{{k}}= \frac{\lambda }{1-\rho } \sum \nolimits _{q=0}^{\infty } {(q+{k})}! \, w_{q} \big (\frac{e s r}{q+{k}}\big )^{\frac{q+{k}}{r}} , \quad \forall {k}\in \mathbb {N}. \end{aligned}$$

(E6)

It is easy to see that the three sequences $\sum \nolimits _{{k}=0}^{\infty }\tilde{c}_{{k}} { u^{{k}+1}}/{{({k}+1)}!}$, $\sum \nolimits _{{k}=0}^{\infty }\bar{c}_{{k}} { u^{{k}+1}}/{{({k}+1)}!}$ and $\sum \nolimits _{{k}=0}^{\infty }\hat{c}_{{k}} { u^{{k}+1}}/{{({k}+1)}!}$ converge wherever $\sum \nolimits _{{k}=0}^{\infty } \beta _{{k}} { u^{{k}+1}}/{{({k}+1)}!}$ is convergent. Besides,

(E7)

Under the conditions of (i), we infer from E3 that the expression between brackets in (E7) tends to a finite quantity not larger than s, so that for any $\nu >0$ one can find a $k_\nu$ such that $\beta _{{k}+1}\le (\beta _{k_\nu +1}-\beta _{k_\nu }) + (s+\nu ) \beta _{{k}}$ for ${k}>k_\nu$. It follows from the ratio test that $\sum \nolimits _{{k}=0}^{\infty } \beta _{{k}} { \xi ^{{k}}}/{{{k}}!}$ converges for $\xi \in \mathbb {R}_{{\ge 0}}$, and so do $\sum \nolimits _{{k}=0}^{\infty }\tilde{c}_{{k}} { \xi ^{{k}}}/{{{k}}!} = \psi (u)$, $\sum \nolimits _{{k}=0}^{\infty }\bar{c}_{{k}} {\xi ^{{k}}}/{{{k}}!}$ and $\sum \nolimits _{{k}=0}^{\infty }\hat{c}_{{k}} {\xi ^{{k}}}/{{{k}}!}$. This last conclusion, together with (E4), (E5), and Fubini’s theorem applied to set of natural numbers with the counting measure, yields, for $u\in \mathbb {R}_{{\ge 0}}$,

where the last result follows from Proposition 2(ii). Since

$$\begin{aligned} \sum \nolimits _{{k}=0}^{\infty }\bar{c}_{{k}} \frac{\xi ^{{k}}}{{{k}}!} = \frac{\lambda }{1-\rho } \sum \nolimits _{{k}=0}^{\infty } \left( \sum \nolimits _{q=0}^{\infty }| w_{q} \, f^{({k}+q)}(0) \frac{ \xi ^{{k}}}{{{k}}!}|\right) <\infty , \quad \forall \xi \in \mathbb {R}_{{\ge 0}}, \end{aligned}$$

Fubini’s theorem applies and one may interchange the order of summation in (IV3a):

which holds for $u\in \mathbb {R}_{{\ge 0}}$.

(ii) Similarly, for any $\epsilon >0$, one can find growing sequences of naturals $\{l_{{k}}\}$ and $\{m_{{k}}\}$ such that [30, Lecture 1]

$$\begin{aligned} \begin{array}{ll} \frac{|f^{(l_{{k}})}(0)| }{{l_{{k}}}!} > \big (\frac{e (\varrho -\epsilon )}{l_{{k}}}\big )^{\frac{l_{{k}}}{\varrho -\epsilon }} ,&\quad ({k}\in \mathbb {N}_{\ge 0}), \end{array} \end{aligned}$$

(E8a)

$$\begin{aligned} \begin{array}{ll} \frac{|f^{(m_{{k}})}(0)| }{{m_{{k}}}!} > \big (\frac{e (\sigma -\epsilon ) \varrho }{m_{{k}}}\big )^{\frac{m_{{k}}}{\varrho }} ,&\quad ({k}\in \mathbb {N}_{\ge 0}). \end{array} \end{aligned}$$

(E8b)

Recall the series $\tilde{c}_{{k}}$ defined in (IV2). By taking $\epsilon$ sufficiently small in (E8a) and (E8b) and using (E3), we find that the asymptotic ratio between the moduli of two terms of (IV2) with respective indices $l_{q}-{k},l_{q+1}-{k}$ (in the case $\varrho >1$) or $m_{q}-{k},m_{q+1}-{k}$ (in the case $\varrho =1$, $\sigma >|p_{W}|^{-1}$) is greater than one for q taken large enough. Hence, one can find a subsequence of terms of (IV2) which grows in modulus, and $\tilde{c}_{{k}}$ diverges for all k. $\square$

Lemma E.1

(Coefficients $\{\tilde{\alpha }_{k}\}$ for quotients of polynomials) Let $g_{m}$ and $h_{n}$ be polynomials of degrees $m$ and $n$, and consider

$$\begin{aligned} \textstyle f(u) = \frac{g_{m}(u)}{h_{n}(u)}, \quad \forall u\in \mathbb {R}_{{\ge 0}}. \end{aligned}$$

For $\tau >0$, recall the polynomial $p_{k}$ given in Table 2 and define $f_{k}(s) = f(s) \, p_{k}({2s}/{\tau }-1)$ under the assumption $\mathcal {P}(f_{k})\cap [0,\infty )=\emptyset$. The Fourier coefficients of $f$ satisfy, for $k\ge 0$,

$$\begin{aligned} \tilde{\alpha }_{k}= & {} \sqrt{\pi } \sum \nolimits _{q=0}^{l({k})} \frac{ \zeta _{-q}\, (-\tau )^{q} }{ {q}! \Upgamma \left( \frac{1}{2}-q\right) }\nonumber \\&-\, \sum \nolimits _{a\in \mathcal {P}(f_{k})} Res _{s=a}\left( { f_{k}(s) \, {s}^{-\frac{1}{2}}]_{-\pi } {(s-\tau )}^{-\frac{1}{2}}]_{-\pi } }\right) , \end{aligned}$$

(E9)

where $l({k})=\max (0,m-n+k)$ is the largest nonnegative integer $l$ such that $\lim \nolimits _{s\rightarrow 0} s^{l} f_{k}\left( {1}/{s}\right)$ is finite, and $\{\zeta _{q}\}$ are the coefficients of the Laurent series at $+\infty$ of the analytic continuation of $f_{k}$, i.e.,

$$\begin{aligned} \begin{array}{ll} \zeta _{q} = \frac{1}{{\left( l({k})+q\right) }!} \lim \nolimits _{s\rightarrow 0} \frac{d^{l({k})+q}}{ds^{l({k})+q}} \left[ s^{l({k})} f_{k}\left( \frac{1}{s}\right) \right] ,&\quad (q=-l({k}),\dots ,\infty ). \end{array} \end{aligned}$$

(E10)

See [9] for a derivation derivation of Lemma E.1 by the technique of contour integration.