Analysis of the shortest relay queue policy in a cooperative random access network with collisions

Abstract

The aim of this work concerns the performance analysis of systems with interacting queues under the join the shortest queue policy. The case of two interacting queues results in a two-dimensional random walk with bounded transitions to non-neighboring states, which in turn results in complicated boundary behavior. Although this system violates the conditions of the compensation approach due to the transitions to non-neighboring states, we show how to extend the framework of the approach and how to apply it to the system at hand. Moreover, as an additional level of theoretic validation, we have compared the results obtained with the compensation approach with those obtained using the power series algorithm and we have shown that the compensation approach outperforms the power series algorithm in terms of numerical efficiency. In addition to the fundamental contribution, the results obtained are also of practical value, since our analysis constitutes a first attempt toward gaining insight into the performance of such interacting queues under the join the shortest queue policy. To fully comprehend the benefits of such a protocol, we compare its performance to the Bernoulli routing scheme as well as to that of the single relay system. Extensive numerical results show interesting insights into the system’s performance.

1 Introduction

In this paper, we consider a discrete-time stochastic network consisting of two interacting queues fed by a single stream of jobs according to the join the shortest queue policy (JSQ). The system under consideration is primarily motivated by emerging applications in relay-assisted cooperative random-access wireless networks [31, 38].

Cooperative communication is a new communication paradigm in which different terminals (i.e., nodes, devices) in a wireless network share their antennas and resources for distributed transmission and processing. Recent studies have shown that cooperative communications yield significant performance improvements for 5G networks, which need massive uncoordinated access, low latency, energy efficiency, and ultra-reliability [44].

The unprecedented growth of wireless networking, and the ever-growing demand for higher data rates and capacity over the last decades, have already pushed the limits of current cellular systems [56]. By exploiting the spatial diversity inherent to wireless channels, which is an important tool to overcome the effects of fading (decrease in signal power due to path loss), shadowing and attenuation (decrease in signal strength), relay-based cooperative communications have been proposed as the appropriate solution to achieve future needs; see, for example, [31, 38].

A typical relay-based cooperative wireless network [18, 44] operates as follows: There exists a network of a finite number of source users, a finite number of relay nodes and a common destination node. The source users transmit packets to the destination node with the cooperation of the relays. If a direct transmission of a user’s packet to the destination fails, a cooperation strategy among sources and relays is employed to specify the relays that will store the blocked packet in their buffer. Relays are responsible for the transmission of the blocked packets to the destination; for example, [45]. In a wireless network, transmission failures occur either due to packet collisions, or due to channel fading/noise and attenuation. In both cases, the packet has to be re-transmitted in a later slot. The former case occurs when more than one node transmits simultaneously [41], while the latter one refers to the probabilistic nature of transmissions; see, for example, [45, 49, 50].

In this work, we consider a simple relay-based cooperative wireless network with a single source, two infinite capacity relay nodes, and a common destination with collisions under a load balancing relay scheme. To keep the model in a simple form and enhance the readability of the paper, we assume that there is no direct link between source and destination, and, thus, the source transmits its packets to the destination with the aid of the relays. The employed cooperation strategy among source and relays is queue-based. In particular, we consider the join the shortest relay queue (JSRQ) policy and study its impact on the total transmission time, i.e., the time that is needed to transmit a packet from the source to the destination, and the total expected number of buffered packets in the system.

1.1 Related work

The analysis performed in this paper has connections with two distinct research branches.

Random-access networks Interacting queues are of practical relevance as they appropriately capture the interference in random-access networks; for example, [17, 18, 42, 43]. In addition to their practical relevance, such queueing systems are mathematically interesting as they are oftentimes formidably challenging to analyze even in their simplest forms [21, 41]. Their challenge mainly lies in the fact that the service rate of a queue depends on the state of the other queues, which in turn leads to a so-called network of coupled queues.

When dealing with such networks of coupled queues, the first point of focus concerns the characterization of the stable throughput region, aka the stability region. For small, simple networks the stability region can be fully determined, for example, [17, 43, 57], while for large, general networks, only bounds on these regions are known [12, 39, 48, 54]. For a thorough overview of several techniques used for the derivation of the stability region, the interested reader is referred to [24]. An alternative way to derive stability conditions is to use the concept of dominant systems, under which the network of interest is (stochastically) dominated by a simpler one that is easier to analyze; for example, [46, 48] and the references therein. Another powerful tool to investigate necessary and sufficient stability conditions for work-conserving queueing networks is the use of fluid models; see [11, 13, 25, 28, 51, 52].

The second point of focus in the literature concerns the computation of the joint queue length distribution. This type of performance analysis has recently regained attention due to the rapid development of real-time applications that require delay-based guarantees [26]. However, the impact of interacting queues causes severe mathematical difficulties, and there are very few studies that deal with the investigation of the queueing delay. In [42], by performing an appropriate truncation of the infinite Markov chain, the authors approximate the steady-state probability vector, within any desired degree of accuracy, whereas in [55] diffusion approximations were applied. In [17, 18, 41], the probability generating function (PGF) of the joint (relay) queue length distribution was obtained in terms of the solution of a boundary value problem. In [13, 61], fluid models were used to investigate the delay analysis of random access networks. In [53], bounds for the queueing delay in a random access network with $N>2$ nodes were also derived.

Note that, in the vast majority of the above-mentioned literature, cooperation is employed as a solution to the problem of the absence of a reliable direct link between source and destination. In our work, we additionally assume queue-aware cooperation criteria, by forwarding packets to the least loaded relay with the ultimate goal that of the optimization of the overall network performance; for example, [38]. With that in mind, we realize that the use of queue-aware load balancing schemes improves the system’s overall performance, since their mission is to effectively divide the work among the participating nodes.

Under certain conditions, the so-called JSQ policy has several strong optimality properties: The JSQ policy minimizes the overall mean delay among the class of load balancing policies that do not have any advance knowledge of the service requirements [20, 40, 59]. However, to the best of our knowledge, there is no work in the related literature that deals with the delay analysis of a cooperative random access network (i.e., a network of interacting queues with collisions) under the JSQ policy.

JSQ policy and methods of analysis The JSQ policy has been extensively studied in systems with two queues. The JSQ policy was introduced in [30], in the context of two parallel (exponential) servers and a Poisson stream of arrivals. The first major contributions toward the exact analysis of the JSQ policy for two queues were made in [23, 35], using a uniformization approach that established that the PGF of the joint equilibrium distribution of the queue lengths is meromorphic (i.e., the equilibrium distribution can be written as a linear combination—finite or infinite—of product-form terms). The generating function approach was used in combination with the theory of Riemann–Carleman–Hilbert boundary value problems to provide a compact analytical method [15, 22], but this approach does not always provide explicit expressions for the equilibrium distribution.

Although these methods are mathematically elegant and provide interesting mathematical insights, they are not so useful in the numerical computation of performance metrics. Therefore, several other numerically oriented methods were developed. In particular, the matrix geometric method (MGM) was proposed in a series of works as a possible solution; see, for example, [27, 29, 47]. Despite its algorithmic nature, MGM has several limitations as it is computationally challenging to compute the so-called rate matrix, especially in the case of quasi-birth-death systems with both infinite phases and levels resulting in an infinite dimension rate matrix. In [34], the authors investigate how to compute the infinite dimension rate-matrix for a class of simple (nearest neighbor) random walks, and they demonstrate their results by applying their analysis to the case of the JSQ model.

Another method used for the performance analysis of queueing systems is the power-series algorithm (PSA). The PSA is an algorithmic, numerically oriented procedure that has been successfully used for the analysis of JSQ systems, as well as to numerically obtain the performance measures of multi-dimensional queueing models, which fit in the class of quasi birth-and-death processes. The intrinsic idea behind the PSA is the transformation of the balance equations into a recursively solvable set of equations by adding one dimension to the state space. This is achieved by expressing the equilibrium distribution as a power series in some variable based on the model parameters (usually the load). This allows the calculation of the equilibrium joint queue length distribution. The PSA was first applied by Beneš [7] and thereafter by Hooghiemstra et al. [32]. Important generalizations were presented in [8,9,10, 19, 36, 58].

In a different direction, the precedence relation (PR) method, see, for example, [60], can be used to systematically construct bounds for any performance measure of the Markov chain under consideration.

The strength of the PSA and the PR methods is that they are not restricted to two queues, but apply equally well to more than two queues. A major weak point, however, is that the theoretical foundation of the PSA is still incomplete and that PR produces no exact results, but bounds.

The CA [3,4,5] is an alternative method, that can be used to directly solve the balance equations and it leads to an explicit solution in the form of a linear combination—finite or infinite—of product-form terms. We will further elaborate on the CA in Sect. 3.

For a comparison of some of the above-mentioned approaches used for the analysis (among others) of JSQ systems, and an exposition of their strengths and limitations, the interested reader is referred to [1].

1.2 Contribution

Application-oriented contribution In this work, we consider a slotted-time, collision-based relay-assisted cooperative communication system with the JSQ routing protocol at the relays. Relays have random access to the medium, and they are equipped with infinite capacity buffers. Such networks have not been extensively analyzed and very little is known regarding their delay performance even for small-scale networks. This is due to the strong interdependence/interaction among queues, since the successful transmission rate of a relay depends on the state of the others. In this work, we provide insights into the characterization of the delay and the performance of the system at hand. To the best of our knowledge, this is the first work that provides analytic results regarding the delay performance of the JSQ routing protocol in networks of interacting queues.

To gain more insights into the performance of the system at hand, we compare the JSRQ scheme with the Bernoulli routing scheme, as well as with the single relay system. Our numerical results reveal the superiority of the JSRQ over the Bernoulli routing scheme when the relays are more likely to remain silent, i.e., they are “slow”. At this point, regarding the Bernoulli routing protocol, we have to mention that in contrast to the continuous time setting, its stationary analysis under the slotted time setting is a challenging task (see Appendix B) since the two queues do not behave independently.

Fundamental contribution In this work, we extend for the first time the framework of the CA to a new class of random walks. We violate one of the main assumptions of the CA, viz., that of transitions being allowed only to neighboring states. We show, using the system at hand as a vehicle for illustration, that the CA can be extended to random walks in the quadrant that obey the following conditions:

Homogeneity::

The same transitions occur according to the same rates for all interior points, and similarly for all points on the horizontal boundary, and for all points on the vertical boundary.

Forbidden steps::

No transitions from interior states to the North, North–East, and East.

Bounded transitions::

Only transitions to a bounded region.

Later in our analysis we refer to the above conditions as H, F and B. Note that the CA was developed to satisfy a more restrictive setting than bounded transitions, by allowing only transition to the nearest neighbors; see, for example, [4,5,6]. We also mention the work in [3] that deals with a random walk with a similar but simpler structure.

The framework extension achieved in this paper sets the first stepping stones toward a full extension of the CA to random walks with large steps (extending the results obtained in [2]) and to queueing systems with (bounded) batch arrivals and/or (bounded) batch departures.

We demonstrate how to obtain the equilibrium joint queue length distribution through the CA and provide a detailed implementation algorithm. Moreover, we numerically validate our theoretical findings by employing the PSA and present an extensive numerical comparison discussing which method performs better in terms of accuracy and time complexity (computational time). Other validation methods are also discussed.

1.3 Paper structure

The paper is structured as follows: In Sect. 2, we describe the system under consideration in detail and provide its stability condition. The computation of the equilibrium distribution of the joint queue lengths using the CA is performed in Sect. 3. Section 4 contains various numerical results. Finally, we present conclusions and possible generalizations in Sect. 5.

2 The model

We consider a relay-assisted cooperative random access wireless network composed of a saturated source user that transmits packets to a common destination node, under the cooperation of two relay nodes. The relays are equipped with infinite capacity buffers (queues), and they assist the user by transmitting the packets that failed to reach the destination. Packets have equal length (i.e., they consist of the same fixed number of bits [14]), and time is divided into slots corresponding to the transmission time of a packet. We consider an early arrival system (EAS), under which, at the beginning of a slot, packets arrive and they are routed to the relays according to the join the shortest relay queue (JSRQ) policy. On the other hand, departures are scheduled at the end of the slot.

The number of packet arrivals are assumed i.i.d. Bernoulli random variables from slot to slot, with the average number of arrivals being $\lambda$ packets per slot. Upon the arrival of a packet, the source and the relays cooperate as follows: When the source transmits a packet, it is forwarded to the least loaded relay, i.e., to the relay with the smallest number of backlogged packets. Then, the relay node sends an acknowledgement to the source and takes over the responsibility of delivering the packet to the destination node by storing it in its queue. Such a protocol helps to keep a fair balance among the relays, as well as, enhancing the energy conservation of the relays (The relay node is usually a battery operated wireless device.). In case the numbers of packets in the relay queues are equal, a packet is routed to relay r with probability $\pi _{r}$, $r=1,2$. At the end of each slot, relay r (if it is non-empty) transmits a packet to the destination node with probability $a_{r}$, $r=1,2$. If both relays transmit at the same slot, a collision occurs, and both packets have to be retransmitted in a later slot. If only one relay transmits, then the destination node successfully decodes it, sends an acknowledgement to the corresponding relay, and the packet exits the network. The acknowledgements are assumed to be error-free, instantaneous, and broadcast to all relevant nodes. The nodes remove the successfully transmitted packets from their queues, while unsuccessful packets are retained.

In order to enhance the readability of the paper, and only for this reason, we focus hereon at the symmetric system, under which $a_{r}=a$, $r=1,2$, i.e., both relays have identical transmission parameters, and $\pi _{r}=1/2$, $r=1,2$. Note that the analysis that follows can be directly generalized to the asymmetric system case; however, this would render the notation more complicated, which would severely impact the readability of the paper.

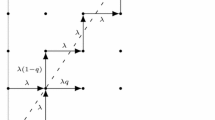
Let $Q_{r}(n)$ be the number of stored packets at the buffer of relay r, $r=1,2$, at the beginning of the n-th slot, $n \ge 0$. Then $\{\varvec{Q}(n),\, n \ge 0\}:=\{(Q_{1}(n),Q_{2}(n)),\, n \ge 0\}$ is a discrete time Markov chain with state space ${\mathcal {S}}=\{(i,j):\, i,j\ge 0\}$. The corresponding probability transition diagram is depicted in Fig. 1.

Fig. 1

The transition probability diagram of $\{\varvec{Q}(n),\, n \ge 0\}$ for a few representative states

From Fig. 1, it is evident that $\{\varvec{Q}(n),\, n \ge 0\}$ has six regions of spatial homogeneity. Namely, two angles: the upper-diagonal angle $H=\{(i,j):i>j>0\}$, and lower-diagonal angle $V=\{(i,j):j>i>0\}$; three rays: the horizontal ray $H^{\prime }=\{(i,0):i>0\}$, vertical ray $V^{\prime }=\{(0,j):j>0\}$, and diagonal ray $D=\{(i,j):j=i>0\}$; and the origin point $O=(0,0)$. These six regions govern the one-step transition probabilities, say

$$\begin{aligned}&p^{L}_{i',j'}={\mathbb {P}}\left[ \varvec{Q}(n+1)=(i+i',j+j')\, |\, \varvec{Q}(n)=(i,j)\in L\right] , \\&\quad L\in \{H,V,H^{\prime },V^{\prime },D,O\}, ~i',j'=0,\pm 1. \end{aligned}$$

• 1. For $(i,j)\in \{H,V\}$,

  $$\begin{aligned} p^V_{1,0}&=p^H_{0,1}=\lambda ({\bar{a}}^{2}+a^{2}),\,p^V_{0,-1}=p^H_{0,-1}={\bar{\lambda }}a{\bar{a}},\,p^V_{-1,0}=p^H_{-1,0}={\bar{\lambda }}a{\bar{a}},\nonumber \\ p^V_{1,-1}&=p^H_{-1,1}=\lambda a{\bar{a}}, \nonumber \\ p^V_{0,0}&=p^H_{0,0}={\bar{\lambda }}({\bar{a}}^{2}+a^{2})+\lambda a{\bar{a}}, \end{aligned}$$

  (1)

  with ${\bar{a}}=1-a$ and ${\bar{\lambda }}=1-\lambda$.

• 2. For $(i,j)\in \{H^{\prime },V^{\prime }\}$,

  $$\begin{aligned} p^{V^{'}}_{1,0}&=p^{H^{'}}_{0,1}=\lambda ({\bar{a}}^{2}+a^{2}),\,p^{V^{'}}_{0,-1}=p^{H^{'}}_{-1,0}={\bar{\lambda }}a,\,p^{V^{'}}_{1,-1}=p^{H^{'}}_{-1,1}=\lambda a{\bar{a}},\nonumber \\ p^{V^{'}}_{0,0}&=p^{H^{'}}_{0,0}={\bar{\lambda }}{\bar{a}}+\lambda a{\bar{a}}. \end{aligned}$$

  (2)

• 3. For $(i,j)\in D$,

  $$\begin{aligned} p^D_{1,0}&=p^D_{0,1}=\frac{1}{2}\lambda ({\bar{a}}^{2}+a^{2}),\,p^D_{0,-1}=p^D_{-1,0}={\bar{\lambda }}{\bar{a}}a,p^D_{0,0}={\bar{\lambda }}({\bar{a}}^{2}+a^{2})+\lambda a{\bar{a}}, \nonumber \\ p^D_{1,-1}&=p^D_{-1,1}=\frac{1}{2}\lambda {\bar{a}}a. \end{aligned}$$

  (3)

• 4. For $(i,j)\in O$,

  $$\begin{aligned} p^O_{0,1}&=p^O_{1,0}=\frac{1}{2}\lambda {\bar{a}},\,p^O_{0,0}={\bar{\lambda }}+\lambda a. \end{aligned}$$

  (4)

Remark 2.1

To better understand how the above probabilities are computed, we consider, for example, the case of $p_{1,0}^V$. This probability captures the transition from a state $(i,j) \in V$ to a state $(i+1,j)$. In this case, at the beginning of a slot, due to the EAS, with probability $\lambda$ there is a new arrival. For the transition $(i,j) \rightarrow (i+1,j)$ to occur, it is necessary on top of the arrival that no departure occurs. The latter event happens with probability ${\bar{a}}^2+a^2$. Thus, $p_{1,0}^V = \lambda ({\bar{a}}^2+a^2)$. The other transition probabilities are obtained in a similar fashion.

Remark 2.2

Note that if both relay queues are non empty, then the successful transmission rate from each of them equals ${\bar{a}}a$. If one of them is empty then the other transmits with rate a. This demonstrates that the setting under consideration is a non-work conservative setting. The only exception is the case $2{\bar{a}}a=a \iff a = 1/2 = {\bar{a}}$ (or equivalently the case $2{\bar{a}}a={\bar{a}}$). Due to the non-work conservation setting, our model incorporates two features, that of the JSRQ and that of the “coupled processors” [21]. The combination of the JSRQ feature and the coupled processor feature considerably complicates the analysis.

2.1 Stability condition

Let $({\mathbb {E}}_{x}^{k},{\mathbb {E}}_{y}^{k})$ denote the mean jump vector of $\{\varvec{Q}(n),\,n \ge 0\}$ in the angles $k=H,V$ or in the rays $k=H^{\prime },V^{\prime },D$. Then, it is readily derived that

$$\begin{aligned} {\mathbb {E}}_{x}^{H}&={\mathbb {E}}_{y}^{V}=-(\lambda a{\bar{a}}+{\bar{\lambda }}a{\bar{a}})=-a{\bar{a}}<0,\\ {\mathbb {E}}_{y}^{H}&={\mathbb {E}}_{x}^{V}=\lambda (a^{2}+{\bar{a}}^{2})+\lambda a{\bar{a}}-{\bar{\lambda }}a{\bar{a}}=\lambda -a{\bar{a}},\\ {\mathbb {E}}_{x}^{H^\prime }&={\mathbb {E}}_{y}^{V^\prime }=-a({\bar{\lambda }}+\lambda {\bar{a}})<0,\\ {\mathbb {E}}_{y}^{H^\prime }&={\mathbb {E}}_{x}^{V^\prime }=\lambda ({\bar{a}}^{2}+a^{2}+a{\bar{a}}),\\ {\mathbb {E}}^{D}_{x}&={\mathbb {E}}^{D}_{y}=\frac{\lambda }{2}(a^{2}+{\bar{a}}^{2})-{\bar{\lambda }}a{\bar{a}}=\frac{1}{2}(\lambda -2a{\bar{a}}). \end{aligned}$$

Note that $({\mathbb {E}}^{D}_{x},{\mathbb {E}}^{D}_{y})=\frac{1}{2}({\mathbb {E}}_{x}^{H}+{\mathbb {E}}_{x}^{V},{\mathbb {E}}_{y}^{H}+{\mathbb {E}}_{y}^{V})$ and that ${\mathbb {E}}_{x}^{H}+{\mathbb {E}}_{y}^{H}={\mathbb {E}}_{x}^{V}+{\mathbb {E}}_{y}^{V}=\lambda -2a{\bar{a}}$. Following the analysis in [37], we prove the following theorem.

Theorem 2.3

The system at hand is stable if and only if

$$\begin{aligned} \lambda < 2a{\bar{a}}. \end{aligned}$$

(5)

Equivalently, the stability condition for the system can be written in terms of the system load:

$$\begin{aligned} \rho = \frac{\lambda ({\bar{a}}^{2}+a^{2})}{2{\bar{\lambda }}{\bar{a}}a} <1. \end{aligned}$$

(6)

Proof

The proof of the stability condition (sufficiency and necessity) follows verbatim the analysis presented in [33], and in particular, the proof of Theorem 5 therein. Note that, although the analysis presented in [33, Theorem 5] is for a continuous time queueing network with single arrivals and departures, it can be, in the two-dimensional case, easily and in a very straightforward manner adapted to the system under consideration. For this reason, we have opted to not repeat the technical steps and instead to focus on how to apply the algorithm implemented in [33, Section 5.2] for the derivation of the stability region. Following the notation in [33], we define the vectors $u_k$ as follows:

$$\begin{aligned} u_1=(1,0),\quad u_2=(1,0),\quad u_3=(1,1),\quad u_4=(0,1),\quad u_5=(0,1), \end{aligned}$$

and the drifts as follows:

$$\begin{aligned} \delta ^{(1)}&=({\mathbb {E}}_{x}^{H^\prime },{\mathbb {E}}_{y}^{H^\prime }),\ \delta ^{(2)}=({\mathbb {E}}_{x}^{H},{\mathbb {E}}_{y}^{H}), \ \delta ^{(3)}=\frac{1}{2}({\mathbb {E}}_{x}^{H}+{\mathbb {E}}_{x}^{V},{\mathbb {E}}_{y}^{H}+{\mathbb {E}}_{y}^{V}) \\ \delta ^{(4)}&=({\mathbb {E}}_{x}^{V},{\mathbb {E}}_{y}^{V}),\ \delta ^{(5)}=({\mathbb {E}}_{x}^{V^\prime },{\mathbb {E}}_{y}^{V^\prime }). \end{aligned}$$

Using the results of [33, Section 5], the interior of the stability region can be obtained as follows:

Segment 1::

Determine a segment of the stability region in terms of $\lambda$ and a, such that there exists $c\in (0,1)$ and $A<0$ with

$$\begin{aligned} c \delta ^{(1)}+(1-c) \delta ^{(2)}=A u_2. \end{aligned}$$

(7)

This system yields $c=\frac{\lambda - a{\bar{a}}}{-{\bar{\lambda }} a{\bar{a}}}$ and it can be verified that if $\lambda <a{\bar{a}}$, then indeed there exist $c\in (0,1)$ and $A<0$ that satisfy (7). This produces one of the segments of the stability region.

Segment 2::

Similarly, for some segment of the stability region, there exists $c'\in (0,1)$ and $A'<0$ with

$$\begin{aligned} c' \delta ^{(2)}+(1-c') \delta ^{(3)}=A' u_3. \end{aligned}$$

(8)

This system yields $c'=\frac{\lambda - a{\bar{a}}}{\lambda /2}$ and it can be verified that if $2a{\bar{a}}>\lambda >a{\bar{a}}$, then indeed there exist $c'\in (0,1)$ and $A'<0$ that satisfy (8). This produces the second and last segment of the stability region.

Note that, for the symmetric model at hand, it is not necessary to use all the cones defined by the vectors $u_k$ as the system is symmetric. The union of the two stability region segments (including the set closure) produces exactly the stability condition stated in the theorem. $\square$

Remark 2.4

Theorem 2.3 can be generalized to the asymmetric case, again using [33]. This analysis would reveal that the stability condition is $\lambda -a_1(1-a_2)-(1-a_1)a_2<0$, or, equivalently in terms of the system load,

$$\begin{aligned} \frac{\lambda \left( a_1a_2 + (1-a_1)(1-a_2)\right) }{(1-\lambda )(a_1(1-a_2) + a_2(1-a_1))} < 1. \end{aligned}$$

3 The equilibrium analysis

In this section, our aim is to extend the CA to two-dimensional random walks with bounded transitions to non-neighboring states, and to apply it in the system under consideration with the two interacting queues under the join the shortest queue policy.

This section is structured as follows: We first introduce the CA and state the main results. Thereafter, we give the mathematical proofs of the main results and discuss how to implement the CA. Finally, possible model extensions that can be tackled with the CA are discussed.

The CA was developed by Adan et al. in a series of papers [4,5,6]. In these articles, the authors aim at a direct solution of the balance equations, for a sub-class of two-dimensional random walks on the lattice of the first quadrant obeying three conditions: Homogeneity, North/North–East/East forbidden states, and only transitions to neighboring states.

This method exploits the fact that the balance equations in the interior of the quarter plane are satisfied by a linear combination (finite or infinite) of product-form terms, the parameters of which satisfy a kernel equation, and that need to be chosen such that the balance equations on the boundaries are satisfied as well. As it turns out, this can be done by alternatingly compensating for the errors on the two boundaries, which eventually leads to an infinite series of product-forms.

As evident from Fig. 1, the model at hand violates the first two conditions mentioned above. In order to apply the CA, it is necessary to transform the state space (similarly to the case of the classical JSQ model [4, 5]). More concretely, we employ the following transformation:

$$\begin{aligned} \tilde{Q}_{1}(n)= \min \left\{ Q_{1}(n),Q_{2}(n)\right\} ,\,\tilde{Q}_{2}(n)= \left| Q_{2}(n)-Q_{1}(n)\right| . \end{aligned}$$

Clearly, $\{\tilde{\varvec{Q}}(n),\,n \ge 0\}:=\{(\tilde{Q}_{1}(n),\tilde{Q}_{2}(n)),\,n \ge 0\}$ is a discrete time Markov chain with state space $\tilde{{\mathcal {S}}}=\{(k,l),\,k,l\ge 0\}$. The corresponding probability transition diagram is depicted in Fig. 2.

Fig. 2

The probability transition diagram of $\{\tilde{\varvec{Q}}(n),\, n \ge 0\}$ for a few representative states

Note that the above transformation has led to a random walk that only violates the nearest neighbor condition for the application of the CA, but the new random walk has bounded transitions; see Fig. 2. Despite violating the nearest neighbor condition, we show in this paper that the CA can still be applied and it leads to an equilibrium joint queue length distribution expressed in the form of a linear combination (infinite) of product-form terms.

Let

$$\begin{aligned} \pi _{k,l}= & {} \lim _{n\rightarrow \infty }{\mathbb {P}}(\tilde{Q}_{1}(n)=k,\tilde{Q}_{2}(n)=l)\\= & {} \lim _{n\rightarrow \infty }{\mathbb {P}}(\min \{{Q}_1(n),{Q}_2(n)\}=k, |{Q}_1(n)-{Q}_2(n)|=l), \ k,l\ge 0, \end{aligned}$$

denote the equilibrium joint queue length distribution of the transformed random walk $\{\tilde{\varvec{Q}}(n),\,n \ge 0\}$.

The balance equations read as follows:

$$\begin{aligned} \pi _{k,l}&=\pi _{k,l}({\bar{\lambda }}({\bar{a}}^{2}+a^{2})+\lambda a{\bar{a}})+\pi _{k,l+1}{\bar{\lambda }}a{\bar{a}}+\pi _{k-1,l+1}\lambda ({\bar{a}}^{2}+a^{2})\nonumber \\&\quad +\pi _{k-1,l+2}\lambda {\bar{a}}a+\pi _{k+1,l-1}{\bar{\lambda }}{\bar{a}}a,\,\,\,k\ge 1,\,l\ge 3, \end{aligned}$$

(9)

$$\begin{aligned} \pi _{k,0}&=\pi _{k,0}({\bar{\lambda }}({\bar{a}}^{2}+a^{2})+\lambda a{\bar{a}})+\pi _{k,1}{\bar{\lambda }}a{\bar{a}}+\pi _{k-1,1}\lambda ({\bar{a}}^{2}+a^{2})+\pi _{k-1,2}\lambda a{\bar{a}},\,\,\,k\ge 1, \end{aligned}$$

(10)

$$\begin{aligned} \pi _{k,1}&=\pi _{k,1}({\bar{\lambda }}({\bar{a}}^{2}+a^{2})+2\lambda a{\bar{a}})+\pi _{k,2}{\bar{\lambda }}a{\bar{a}}+\pi _{k-1,2}\lambda ({\bar{a}}^{2}+a^{2})+\pi _{k-1,3}\lambda a{\bar{a}} \nonumber \\&\quad +\pi _{k,0}\lambda ({\bar{a}}^{2}+a^{2})+\pi _{k+1,0}2{\bar{\lambda }}a{\bar{a}},\,\,\,k\ge 1, \end{aligned}$$

(11)

$$\begin{aligned} \pi _{k,2}&=\pi _{k,2}({\bar{\lambda }}({\bar{a}}^{2}+a^{2})+\lambda a{\bar{a}})+\pi _{k,3}{\bar{\lambda }} a{\bar{a}}+\pi _{k-1,3}\lambda ({\bar{a}}^{2}+a^{2}) \nonumber \\&\quad +\pi _{k-1,4}\lambda a{\bar{a}}+\pi _{k+1,0}\lambda a{\bar{a}}+\pi _{k+1,1}{\bar{\lambda }}a{\bar{a}},\,\,\,k\ge 1, \end{aligned}$$

(12)

$$\begin{aligned} \pi _{0,l}&=\pi _{0,l}({\bar{\lambda }}{\bar{a}}+\lambda a{\bar{a}})+\pi _{0,l+1}{\bar{\lambda }}a+\pi _{1,l-1}{\bar{\lambda }}a{\bar{a}},\,\,\,\,l\ge 3, \end{aligned}$$

(13)

$$\begin{aligned} \pi _{0,2}&=\pi _{0,2}({\bar{\lambda }}{\bar{a}}+\lambda a{\bar{a}})+\pi _{0,3}{\bar{\lambda }}a+\pi _{1,1}{\bar{\lambda }}a{\bar{a}}+\pi _{1,0}\lambda a{\bar{a}}, \end{aligned}$$

(14)

$$\begin{aligned} \pi _{0,1}&=\pi _{0,1}({\bar{\lambda }}{\bar{a}}+2\lambda a{\bar{a}})+\pi _{0,2}{\bar{\lambda }}a+\pi _{1,0}2{\bar{\lambda }}a{\bar{a}}+\pi _{0,0}\lambda {\bar{a}}, \end{aligned}$$

(15)

$$\begin{aligned} \pi _{0,0}&=\pi _{0,0}({\bar{\lambda }}+\lambda a)+\pi _{0,1}{\bar{\lambda }}a. \end{aligned}$$

(16)

3.1 Decay rate

From the exact analysis of the system, see Sect. 3.2 and the result therein, it turns out that, although the model at hand combines both the JSRQ feature and the coupled processor feature, the dominating feature is that of the JSRQ. This is already noticeable in the decay result of the following proposition, indicating a behavior similar to that of the classical JSQ; cf. [4]. Let $Q_1$ and $Q_2$ denote the equilibrium queue length in relay 1 and 2, respectively.

Proposition 3.1

For $\rho <1$,

$$\begin{aligned} \lim _{k\rightarrow \infty }\rho ^{-2k}{\mathbb {P}}(\min \{{Q}_1,{Q}_2\}=k, |{Q}_1-{Q}_2|=l)=c\,d_0\, \delta ^l, \end{aligned}$$

(17)

with $0< \delta < 1$ and $c,d_0$ positive constants.

Proposition 3.1 can be intuitively understood by comparing the transformed model with the corresponding Geo / Geo / 2 model with one queue, Bernoulli arrivals with success probability $\lambda$, and two identical servers, each with Bernoulli service with success probability ${\bar{a}}a$. Let ${Q}_1$ and ${Q}_2$ denote the equilibrium queue lengths in the original random walk, and let Q denote the equilibrium queue length in the Geo / Geo / 2 model with one queue. It is then expected that ${\mathbb {P}}({Q}_1+{Q}_2=k)$ and ${\mathbb {P}}({Q}=k)$ have the same decay rate, since both systems will work at full capacity whenever the total number of customers grows large. Moreover, since the JSRQ protocol constantly aims at balancing the lengths of the two queues over time, it is expected that, for large values of k,

$$\begin{aligned} {\mathbb {P}}(\min \{{Q}_1,{Q}_2\}=k)\approx {\mathbb {P}}({Q}_1+{Q}_2=2k)\approx {\mathbb {P}}({Q}=2k). \end{aligned}$$

(18)

For the standard Geo / Geo / 2 model with one queue, it is well known that

$$\begin{aligned} {\mathbb {P}}({Q}=k)\approx (1-\rho )\rho ^k. \end{aligned}$$

(19)

Combining (18) and (19) leads to the following conjectured behavior of the tail probability of the minimum queue length:

$$\begin{aligned} {\mathbb {P}}(\min \{{Q}_1,{Q}_2\}=k)\approx C \rho ^{2k},\ k\rightarrow \infty , \end{aligned}$$

(20)

for some positive constant C. Hence, the decay rate of the tail probabilities for $\min \{Q_1,Q_2\}$ is conjectured to be equal to the square of the decay rate of the tail probabilities of Q. Proposition 3.1 states this conjecture, for the case when the difference of the queue sizes is fixed.

Furthermore, one can determine the decay rate of the marginal distribution of $\min \{Q_1,Q_2\}$. The latter does not follow immediately from Proposition 3.1, because the summation over the difference in queue sizes, which can be unbounded, requires a formal justification. In this paper, we derive an exact expression for $\pi _{k,l}$, which, among other things, renders the following result.

Proposition 3.2

For $\rho <1$,

$$\begin{aligned} \lim _{k\rightarrow \infty }\rho ^{-2k}{\mathbb {P}}(\min \{Q_1,Q_2\}=k)=\frac{c\,d_0}{1- \delta }, \end{aligned}$$

(21)

with $0< \delta < 1$ and $c,d_0$ positive constants.

The proofs of Propositions 3.1 and 3.2, along with several other asymptotic and exact results, are given in Sect. 3.3.

3.2 The compensation approach (CA)

As already briefly mentioned, the CA attempts to solve the balance equations by a linear combination of product-form terms. This is achieved by first characterizing a sufficiently rich basis of product-form solutions satisfying the balance equations in the interior of the state space. Subsequently this basis is used to construct a linear combination that also satisfies the equations for the boundary states. Note that the basis contains uncountably many elements. Therefore, a procedure is needed to select the appropriate elements. This procedure is based on a compensation argument (which explains the name of the method): after introducing the first term, countably many terms may subsequently be added so as to alternatingly compensate for the error on one of the two boundaries. The main steps of the analysis are briefly outlined below.

Step 1:

Characterize the set of product-forms

$$\begin{aligned} \gamma ^{k}\delta ^{l} \end{aligned}$$

satisfying the balance equations in the interior of the state space, i.e., Eq. (9). Substitution of the product-form $\gamma ^{k}\delta ^{l}$ into (9) and division by common powers yields a cubic equation in $\gamma$ and $\delta$:

$$\begin{aligned} \left( 1-\left( {\bar{\lambda }}({\bar{a}}^2+a^2) + \lambda a{\bar{a}}\right) \right) \gamma \delta =&\left( {\bar{\lambda }} {\bar{a}} a \gamma + \lambda (a^2 + {\bar{a}}^2)\right) \delta ^2 + \lambda {\bar{a}} a \delta ^3 + {\bar{\lambda }} {\bar{a}} a \gamma ^2. \end{aligned}$$

(22)

The solutions to Eq. (22) form the basis. In particular, the points on the curve defined by Eq. (22) which lie inside the region $0<|\gamma |,|\delta |<1$ characterize a continuum of product-forms satisfying the inner equations.

Step 2:

Construct a linear combination of elements in this rich basis, which is a formal solution to the balance equations. Here the word formal is used to indicate that (at this stage) we do not treat the convergence of the solution. This aspect is treated in Step 3. The formal solution is constructed as follows:

(a):

The construction of a linear combination starts with a suitable initial term $\gamma _0$ that satisfies the balance equations in the interior of the state space and also the balance equations (10)–(12). In Lemma 3.5, in Sect. 3.3, we prove that $\gamma _0=\rho ^2$. Then, from Eq. (22) we obtain the unique $\delta _0$, with $|\delta _0|<|\gamma _0|$, such that

$$\begin{aligned} \pi _{k,l} \vDash d_0 \gamma _0^k\delta _0^l,\, k>0,l\ge 0, \end{aligned}$$

satisfies Eqs. (9)–(12), where the double turnstile symbol $( \vDash )$ is used to signify that $\pi _{k,l}$ semantically entails the form $d_0\gamma _0^k\delta _0^l$. The uniqueness of the $\delta$-root is proven in Lemma 3.6. The constant $d_0$ can be set equal to one, and this will be corrected in Step 4 with the computation of the normalization constant.

(b):

The starting tuple $(\gamma _0,\delta _0)$ violates Eq. (13) on the vertical boundary. To compensate for this error, we add a new product-form term coming from the basis, such that the sum of the two terms satisfies the balance equations in all states on the vertical boundary. In particular, it is easy to show that the new tuple is $(\gamma _1,\delta _0)$. The new $\gamma$-root is uniquely determined from Eq. (22), with $|\gamma _1|<|\delta _0|$. The uniqueness of the $\gamma$-root is proven in Lemma 3.6. Then,

$$\begin{aligned} \pi _{k,l} \vDash d_0\gamma _{0}^{k}\delta _{0}^{l}+c_1\gamma _{1}^{k}\delta _{0}^{l},\, k\ge 0,l\ge 3, \end{aligned}$$

satisfies (13) if

$$\begin{aligned} c_1=-\frac{\delta _{0}(1-{\bar{\lambda }}{\bar{a}}-\lambda a{\bar{a}})-{\bar{\lambda }}a\delta _{0}^{2}-{\bar{\lambda }}a{\bar{a}}\gamma _{0}}{\delta _{0}(1-{\bar{\lambda }}{\bar{a}}-\lambda a{\bar{a}})-{\bar{\lambda }}a\delta _{0}^{2}-{\bar{\lambda }}a{\bar{a}}\gamma _{1}}d_0, \end{aligned}$$

(23)

with $d_0$ a known constant from the previous step.

(c):

Adding the new term violates the balance equations (10)–(12), hence we compensate for this error by adding a product-form solution $(\gamma _1,\delta _1)$ satisfying (22), and (10)–(12), such that

$$\begin{aligned} \pi _{k,l} \vDash {\left\{ \begin{array}{ll} d_0\gamma _{0}^{k}\delta _{0}^{l}+c_1\gamma _{1}^{k}\delta _{0}^{l}+d_1\gamma _{1}^{k}\delta _{1}^{l},\, k \ge 0,l\ge 3,\\ d_0\gamma _{0}^{k}\delta _{0}^{l}+e_{l,1}\gamma _{1}^{k}\delta _{1}^{l},\, k > 0, l=0,1,2.\\ \end{array}\right. } \end{aligned}$$

The three unknowns $e_{l,1}$, $l=0,1$, and $d_1$ can be computed from the following system:

$$\begin{aligned} A(\gamma _1,\delta _1) \begin{bmatrix} e_{0,1} \\ e_{1,1} \end{bmatrix} + B(\gamma _1, \delta _1) d_1 \delta _1^2 = - B(\gamma _1, \delta _0) c_1 \delta _0^2, \end{aligned}$$

(24)

with

$$\begin{aligned} A(\gamma ,\delta )= & {} \begin{bmatrix} \gamma (1-{\bar{\lambda }}({\bar{a}}^{2}+a^{2})-\lambda a{\bar{a}})&-(\gamma \delta {\bar{\lambda }}a{\bar{a}}+\delta \lambda ({\bar{a}}^{2}+a^{2}))\\ -\gamma (\lambda ({\bar{a}}^{2}+a^{2})+2\gamma {\bar{\lambda }}a{\bar{a}})&\gamma \delta (1-{\lambda }({\bar{a}}^{2}+a^{2})-2\lambda a{\bar{a}}) \\ \gamma ^2\lambda a {\bar{a}}&\gamma ^2\delta {\bar{\lambda }} a {\bar{a}} \end{bmatrix}, \\ B(\gamma , \delta )= & {} \begin{bmatrix} - \lambda a{\bar{a}} \\ -(\gamma {\bar{\lambda }}a{\bar{a}}+\lambda ({\bar{a}}^{2}+a^{2})+\delta \lambda a{\bar{a}}) \\ -\gamma (1-{\bar{\lambda }}({\bar{a}}^{2}+a^{2})-\lambda a{\bar{a}})+\gamma \delta \bar{\lambda a {\bar{a}}} +\delta {\lambda }({\bar{a}}^{2}+a^{2})+\delta ^2\lambda a {\bar{a}} \end{bmatrix}. \end{aligned}$$

(d):

We continue in this manner until we construct the entire formal series

$$\begin{aligned} \pi _{k,l}&\vDash \sum _{i=0}^{\infty }(d_{i}\gamma _{i}^{k}+c_{i+1}\gamma _{i+1}^{k})\delta _{i}^{l},\,~~ k\ge 0,l\ge 3,\,\text { (pairs with the same }\delta \text { -term)},\, \end{aligned}$$

(25)

$$\begin{aligned} \pi _{k,l}&\vDash d_0\gamma _0^k\delta _0^l+\sum _{i=1}^{\infty }e_{l,i}\gamma _{i}^{k}\delta _0^l,\, ~~k>0,l=0,1,2, \end{aligned}$$

(26)

and $\pi _{0,0}$, $\pi _{0,1}$ and $\pi _{0,2}$ are obtained from Eqs. (14)–(16). Note that Eq. (25) can be equivalently written as follows:

$$\begin{aligned}&\pi _{k,l} \vDash d_0\gamma _0^k\delta _0^l +\sum _{i=0}^{\infty }(c_{i+1}\delta _{i}^{l}+d_{i+1}\delta _{i+1}^{l})\gamma _{i+1}^{k},\\&\quad k\ge 0,l\ge 3,\,\text { (pairs with the same } \gamma \text { -term)}. \end{aligned}$$

Step 3:

Prove that the formal solution (25) and (26) converges. This is split up into two parts: (i) we first show in Proposition 3.7 that the sequences $\{\gamma _i\}_{i\in {\mathbb {N}}}$ and $\{\delta _i\}_{i\in {\mathbb {N}}}$ converge to zero exponentially fast, and (ii) we show in Proposition 3.10 that the formal solution converges absolutely in all states. The propositions and their proofs are in Sect. 3.3.

Step 4:

Determine the normalization constant.

Performing the steps described above for the CA yields the following main result for the equilibrium distribution.

Theorem 3.3

For $\rho <1$,

$$\begin{aligned} \pi _{k,l}&= c\sum _{i=0}^{\infty }(d_{i}\gamma _{i}^{k}+c_{i+1}\gamma _{i+1}^{k})\delta _{i}^{l},\,~~ k\ge 0,l\ge 3\, \text { (pairs with the same } \delta \text { -term)}, \nonumber \\&= c\Big (d_0\gamma _0^k\delta _0^l+\sum _{i=0}^{\infty }(c_{i+1}\delta _{i}^{l}+d_{i+1}\delta _{i+1}^{l})\gamma _{i+1}^{k}\Big ), \nonumber \\&\quad k\ge 0,l\ge 3,\,\text { (pairs with the same } \gamma \text { -term)}, \end{aligned}$$

(27)

$$\begin{aligned} \pi _{k,l}&= c \Big (d_0\gamma _0^k+\sum _{i=1}^{\infty }e_{l,i}\gamma _{i}^{k}\Big ),\,~~ k>0,l=0,1,2, \end{aligned}$$

(28)

with c denoting the normalization constant. The sequences $\{\gamma _i\}_{i\in {\mathbb {N}}}$, $\{\delta _i\}_{i\in {\mathbb {N}}}$, $\{c_i\}_{i\in {\mathbb {N}}}$, $\{d_i\}_{i\in {\mathbb {N}}}$, and $\{e_i\}_{i\in {\mathbb {N}}}$ are obtained recursively based on the analysis of Steps 1–4.

The equilibrium probabilities close to the origin, $\pi _{0,0}$, $\pi _{0,1}$ and $\pi _{0, 2}$, are obtained by directly solving the balance equations (14)–(16).

Clearly, from this result we can derive similar expressions for other performance characteristics such as the mean queue lengths, the correlation between the queue lengths, the mean waiting time, etc.

Remark 3.4

Theorem 3.3 can be generalized to the asymmetric case by replicating Steps 1–4; see [4, 5].

3.3 Proofs

Several lemmas and propositions establishing the theoretical foundations needed for the application of the CA are presented in this section.

Lemma 3.5

For $\rho =\frac{\lambda ({\bar{a}}^{2}+a^{2})}{2{\bar{\lambda }}{\bar{a}}a}<1$, the balance equations (9)–(12) have a unique solution of the form

$$\begin{aligned} \pi _{k,l}=\rho ^{2k}q(l),\,k,l\ge 0, \end{aligned}$$

(29)

with q(l) nonzero such that $\sum _{l=0}^{\infty }\rho ^{-2l}q(l)<\infty$.

Proof

We consider a modified model, which is closely related to the $\{\tilde{\varvec{Q}}(n),\, n \ge 0\}$ model and has the same asymptotic behavior. This modified model corresponds to a random walk on a slightly different grid, namely

$$\begin{aligned} \{(k,l):k\ge 0,l\ge 0\}\cup \{(k,l):k<0,k+l\ge 0\}. \end{aligned}$$

In the interior and on the horizontal boundary, the modified model has the same transition rates as the $\{\tilde{\varvec{Q}}(n),\, n \ge 0\}$ model. A characteristic feature of the modified model is that its balance equations for $k+l = 0$ are exactly the same as the ones in the interior (in this sense the modified model has no “vertical” boundary equations), and both models have the same stability region. Therefore, the balance equations for the modified model are Eq. (9)–(12) for all $k+l\ge 0$, $k\in {\mathbb {Z}}$, with only the equation for state (0, 0) being different due to the incoming rates from the states with $k+l=0$, $k\in {\mathbb {Z}}$.

Observe that the modified model, restricted to an area of the form $\{(k,l):\, k\ge k_0-l,l\ge 0,k_0=1,2,\ldots \}$, defined by a line parallel to the $k+l=0$ axis, yields exactly the same process. Hence, we can conclude that the equilibrium distribution of the modified model, say ${\hat{\pi }}_{k,l}$, satisfies

$$\begin{aligned} {\hat{\pi }}_{k+1,l}=\gamma {\hat{\pi }}_{k,l},\ k\ge -l,\ l\ge 0, \end{aligned}$$

and therefore

$$\begin{aligned} {\hat{\pi }}_{k,l}=\gamma ^k{\hat{\pi }}_{0,l},\ k\ge -l,\ l\ge 0. \end{aligned}$$

(30)

This yields

$$\begin{aligned} \sum _{l=0}^\infty {\hat{\pi }}_{-l,l}=\sum _{l=0}^\infty \gamma ^{-l}{\hat{\pi }}_{0,l}<1. \end{aligned}$$

To determine the $\gamma$, we consider levels of the form $L=\{(k,l)\,:\ 2k+l=L\}$ and let ${\hat{\pi }}_L=\sum _{2k+l=L}{\hat{\pi }}_{k,l}$. The balance equations between the levels are given by

$$\begin{aligned} \lambda ({\bar{a}}^2+a^2){\hat{\pi }}_L=2{\bar{\lambda }}{\bar{a}}a{\hat{\pi }}_{L+1},\ L\ge 1, \end{aligned}$$

(31)

since $p_{1,0}^V=2p_{0,1}^D=\lambda ({\bar{a}}^2+a^2)$ and $p_{-1,0}^V+p_{0,-1}^V=2p_{-1,0}^D=2{\hat{\lambda }}{\bar{a}}a$. Furthermore, Eq. (30) yields

$$\begin{aligned} {\hat{\pi }}_{L+1}=\sum _{2k+l=L+1}\gamma ^k {\hat{\pi }}_{0,l}=\gamma \sum _{2k+l=L-1}\gamma ^k {\hat{\pi }}_{0,l} =\gamma \, {\hat{\pi }}_{L-1}. \end{aligned}$$

(32)

Substituting (32) into (31) yields

$$\begin{aligned} \gamma =\rho ^2=\left( \frac{\lambda ({\bar{a}}^{2}+a^{2})}{2{\bar{\lambda }}{\bar{a}}a}\right) ^2. \end{aligned}$$

(33)

So far, we have shown that the equilibrium distribution of the modified model has a product-form solution which is unique up to a positive multiplicative constant. Returning to the $\{\tilde{\varvec{Q}}(n),\, n \ge 0\}$ model, we can immediately assume that the solution of the balance equations (9)–(12) is identical to the expression for the modified model as given in (29). Furthermore, the above analysis implies that this product-form is unique, since the equilibrium distribution of the modified model is unique. $\square$

Lemma 3.6

• (i) For a fixed $\gamma$, with $|\gamma |\in (0,1)$, Eq. (22) has exactly one $\delta$-root with $0<|\delta |<|\gamma |$.

• (ii) For a fixed $\delta$, with $|\delta |\in (0,1)$, Eq. (22) has exactly one $\gamma$-root with $0<|\gamma |<|\delta |$.

Proof

• (i) Divide (22) by $\gamma ^{2}$ and set $z=\delta /\gamma$. Then, after some straightforward algebra, it yields

  $$\begin{aligned} f(z)=: & {} z^2\left( {\bar{\lambda }} {\bar{a}} a \gamma + \lambda (a^2 + {\bar{a}}^2) + \lambda {\bar{a}} a \gamma z\right) \\= & {} z\left( 1-\left( {\bar{\lambda }}({\bar{a}}^2+a^2) + \lambda a{\bar{a}}\right) \right) -{\bar{\lambda }} {\bar{a}} a=:g(z). \end{aligned}$$

  Note that, for $|z|=1$,

  $$\begin{aligned} |f(z)|&=|z|^{2}|{\bar{\lambda }} {\bar{a}} a \gamma + \lambda (a^2 + {\bar{a}}^2) + \lambda {\bar{a}} a \gamma z|\le {\bar{\lambda }} {\bar{a}} a |\gamma | + \lambda (a^2 + {\bar{a}}^2) + \lambda {\bar{a}} a |\gamma | \\&< {\bar{\lambda }} {\bar{a}} a + \lambda (a^2 + {\bar{a}}^2) + \lambda {\bar{a}} a =\lambda (a^2 + {\bar{a}}^2)+{\bar{a}}a,\\ |g(z)|&\ge \left| |z|\left| 1-\left( {\bar{\lambda }}({\bar{a}}^2+a^2) + \lambda a{\bar{a}}\right) \right| -{\bar{\lambda }} {\bar{a}} a\right| =1-\left( {\bar{\lambda }}({\bar{a}}^2+a^2) + \lambda a{\bar{a}}\right) -{\bar{\lambda }} {\bar{a}} a \\&=\lambda (a^2 + {\bar{a}}^2)+{\bar{a}}a. \end{aligned}$$

  Then the lemma follows by applying Rouché’s theorem to f(z) and g(z) on the unit circle.

• (ii) Multiply (22) with $\gamma /\delta ^{3}$ and set ${\hat{z}}=\gamma /\delta$. The statement then follows in an analogous manner as in Assertion (i).

$\square$

Proposition 3.7

The sequences $\{\gamma _i\}_{i\in {\mathbb {N}}}$ and $\{\delta _i\}_{i\in {\mathbb {N}}}$ appearing in Eq. (27) and (28) satisfy the properties

• (i) $1>\rho ^2=|\gamma _{0}|>|\delta _{0}|>|\gamma _{1}|>|\delta _{1}|>|\gamma _2|>\ldots$,

• (ii) $0\le |\gamma _{i}|\le 0.4^{i}\rho ^2$ and $0\le |\delta _{i}|\le 0.5 \cdot 0.4^{i}\rho ^2$.

Proof

• (i) Recall that $\gamma _{0}=\rho ^2<1$. Then $\delta _{0}$ follows from (22) and, according to Lemma 3.6, $|\gamma _{0}|>|\delta _{0}|$. Assertion (i) follows upon repeating this argument and in light of Lemma 3.6.

• (ii) We prove the statement of Assertion (ii) by showing that

  • (a) for a fixed $\gamma$, with $|\gamma |\le \gamma _0$, we have $|\delta |<\frac{1}{2}|\gamma |$,

    and,

  • (b) for a fixed $\delta$, with $|\delta |\le \gamma _0/2$, we have $|\gamma |<\frac{8}{10}|\delta |$.

  Then, applying the above iteratively yields

  $$\begin{aligned}&|\gamma _i|\le \frac{8}{10}|\delta _{i-1}|\le \frac{8}{10}\frac{1}{2}|\gamma _{i-1}|\le \cdots \le \left( \frac{8}{10}\frac{1}{2}\right) ^i|\gamma _0|=0.4^i\rho ^2,\\&|\delta _i|\le \frac{1}{2}|\gamma _i|\le \frac{8}{10}\frac{1}{2}|\delta _{i-1}|\le \cdots \le \left( \frac{8}{10}\frac{1}{2}\right) ^i|\delta _0|\le \frac{1}{2}\left( \frac{8}{10}\frac{1}{2}\right) ^i|\gamma _0|=\frac{1}{2}0.4^i\rho ^2. \end{aligned}$$

  It remains to prove (a) and (b) stated above.

  • (a) For a fixed $\gamma$, we prove that $|\delta |<|\gamma |/2$ by repeating the analysis of Lemma 3.6 for $z=\delta /\gamma$ on the domain $|z|=1/2$, i.e., we show that $|f(z)|<|g(z)|$ on $|z|=1/2$. The domain $|z|=1/2$ is determined by noting that the function $g(z) =z\left( 1-\left( {\bar{\lambda }}({\bar{a}}^2+a^2) + \lambda a{\bar{a}}\right) \right) -{\bar{\lambda }} {\bar{a}} a$, defined in the proof of Lemma 3.6, has one single root in the interior of the domain $|z|=1/2$.

    For $|z|=\frac{1}{2}$,

    $$\begin{aligned} |f(z)|&=|z|^{2}\left| {\bar{\lambda }}a{\bar{a}}\gamma +\lambda ({\bar{a}}^{2}+a^{2})+\lambda a{\bar{a}}\gamma z\right| \\&\le \frac{1}{4}\left( {\bar{\lambda }}a{\bar{a}}|\gamma |+\lambda ({\bar{a}}^{2}+a^{2})+\frac{\lambda a{\bar{a}}|\gamma |}{2}\right) , \end{aligned}$$

    and

    $$\begin{aligned} |g(z)|&\ge \left| |z|\left| 1-\left( {\bar{\lambda }}({\bar{a}}^2+a^2) + \lambda a{\bar{a}}\right) \right| -{\bar{\lambda }} {\bar{a}} a\right| \\&=\frac{1}{2}\left( 1-\left( {\bar{\lambda }}({\bar{a}}^2+a^2) + \lambda a{\bar{a}}\right) \right) -{\bar{\lambda }}a{\bar{a}}\\&=\frac{1}{2}\left( \lambda ({\bar{a}}^2+a^2) + \lambda a{\bar{a}}+2{\bar{\lambda }}a{\bar{a}}\right) -{\bar{\lambda }}a{\bar{a}}=\frac{1}{2}\left( \lambda ({\bar{a}}^2+a^2) + \lambda a{\bar{a}}\right) . \end{aligned}$$

    Note that

    $$\begin{aligned} \frac{1}{2}\left( \lambda ({\bar{a}}^2+a^2) + \lambda a{\bar{a}}\right)> & {} \frac{1}{4}\left( {\bar{\lambda }}a{\bar{a}}|\gamma |+\lambda ({\bar{a}}^{2}+a^{2})+\frac{\lambda a{\bar{a}}|\gamma |}{2}\right) \\\Leftrightarrow & {} |\gamma |< \frac{2\lambda }{{\bar{a}}a(2-\lambda )} \end{aligned}$$

    and that

    $$\begin{aligned} |\gamma |\le \gamma _0=\rho ^2< \frac{2\lambda }{{\bar{a}}a(2-\lambda )}. \end{aligned}$$

    This completes the proof that $|f(z)|<|g(z)|$ on $|z|=1/2$ and the application of Rouché’s theorem follows evidently.

  • (b) For a fixed $\delta$, we prove that $|\gamma |<\frac{8}{10}|\delta |$, using a similar analysis as the one above but now for ${\hat{z}}=\gamma /\delta$ on the domain $|{\hat{z}}|=8/10$. To this end, we multiply (22) with $\gamma /\delta ^{3}$ and set ${\hat{z}}=\gamma /\delta$, yielding

    $$\begin{aligned} {\hat{f}}({\hat{z}}):= & {} {\hat{z}}^{2}{\bar{\lambda }}a{\bar{a}}={\hat{z}}\left( 1-\left( {\bar{\lambda }}({\bar{a}}^{2}+a^{2})+\lambda a{\bar{a}}\right) -{\bar{\lambda }}a{\bar{a}}\delta \right) -\left( \lambda ({\bar{a}}^{2}+a^{2})\right. \\&\quad \left. +\lambda a{\bar{a}}\delta \right) =:{\hat{g}}({\hat{z}}). \end{aligned}$$

    The domain $|{\hat{z}}|=8/10$ is determined by noting that the function ${\hat{g}}({\hat{z}})$ has one single root in the interior of the domain $|{\hat{z}}|=8/10$, namely that

    $$\begin{aligned} \left| \frac{\lambda ({\bar{a}}^{2}+a^{2})+\lambda a{\bar{a}}\delta }{1-\left( {\bar{\lambda }}({\bar{a}}^{2}+a^{2})+\lambda a{\bar{a}}\right) -{\bar{\lambda }}a{\bar{a}}\delta }\right|&\le \frac{\lambda ({\bar{a}}^{2}+a^{2})+\lambda a{\bar{a}}|\delta |}{\left| 1-\left( {\bar{\lambda }}({\bar{a}}^{2}+a^{2})+\lambda a{\bar{a}}\right) -{\bar{\lambda }}a{\bar{a}}|\delta |\right| }\\&\le \frac{8}{10}. \end{aligned}$$

    For $|{\hat{z}}|=\frac{8}{10}$,

    $$\begin{aligned} \left| {\hat{f}}({\hat{z}})\right|&=\left( \frac{8}{10}\right) ^2{\bar{\lambda }}a{\bar{a}}, \end{aligned}$$

    and

    $$\begin{aligned} \left| {\hat{g}}({\hat{z}})\right| \ge&\frac{8}{10}\left| \left( 1-\left( {\bar{\lambda }}({\bar{a}}^{2}+a^{2})+\lambda a{\bar{a}}\right) -{\bar{\lambda }}a{\bar{a}}|\delta |\right) -\left( \lambda ({\bar{a}}^{2}+a^{2})+\lambda a{\bar{a}}|\delta |\right) \right| . \end{aligned}$$

    Note that

    $$\begin{aligned}&\frac{8}{10}{\bar{\lambda }}a{\bar{a}}<\left| \left( 1-\left( {\bar{\lambda }}({\bar{a}}^{2}+a^{2})+\lambda a{\bar{a}}\right) -{\bar{\lambda }}a{\bar{a}}|\delta |\right) -\left( \lambda ({\bar{a}}^{2}+a^{2})+\lambda a{\bar{a}}|\delta |\right) \right| \\&\quad \Leftrightarrow \ |\delta |< \frac{6 a^2 \lambda +24 a^2-6 a \lambda -24 a+5 \lambda }{5 (a-1) a (\lambda +4)} \end{aligned}$$

    and that

    $$\begin{aligned} |\delta |\le \frac{\gamma _0}{2}=\frac{\rho ^2}{2}< \frac{6 a^2 \lambda +24 a^2-6 a \lambda -24 a+5 \lambda }{5 (a-1) a (\lambda +4)}. \end{aligned}$$

    This completes the proof that $|{\hat{f}}({\hat{z}})|<|{\hat{g}}({\hat{z}})|$ on $|{\hat{z}}|=8/10$ and the application of Rouché’s theorem follows evidently.

$\square$

It follows from Proposition 3.7 that the sequences $\{\gamma _i\}_{i\in {\mathbb {N}}}$ and $\{\delta _i\}_{i\in {\mathbb {N}}}$ tend to zero as $i\rightarrow \infty$. The limiting behavior of the sequences is presented in Lemma 3.8, and the limiting behavior of the coefficients is treated in Lemma 3.9. In the following lemmas, $\gamma$ is an arbitrary constant, and $\delta$ is defined using Lemma 3.6(i), and with $\delta$, ${\hat{\gamma }}$ is defined using Lemma 3.6(ii).

Lemma 3.8

• (i) Let $\gamma$, $\delta$ and ${\hat{\gamma }}$ be roots of Eq. (22) with $1>|\gamma |>|\delta |>|{\hat{\gamma }}|$. Then, as $\gamma \rightarrow 0$, ${\delta }/{\gamma }\rightarrow w$, with $|w|\in (0,1)$, and ${{\hat{\gamma }}}/{\delta }\rightarrow {1}/{{\hat{w}}}$, with $|{\hat{w}}|>1$, and w and ${\hat{w}}$ are the two distinct roots of

  $$\begin{aligned} 0&={\bar{\lambda }} {\bar{a}} a -w\left( 1-\left( {\bar{\lambda }}\left( {\bar{a}}^2+a^2\right) + \lambda a{\bar{a}}\right) \right) +\lambda \left( a^2 + {\bar{a}}^2\right) w^2. \end{aligned}$$

  (34)

• (ii) Let $\delta$, ${\hat{\gamma }}$ and ${\hat{\delta }}$ be roots of Eq. (22) with $1>|\delta |>|{\hat{\gamma }}|>|{\hat{\delta }}|$. Then, as $\delta \rightarrow 0$, ${\hat{\delta }}/{\hat{\gamma }}\rightarrow w$, with $|w|\in (0,1)$, and ${{\hat{\gamma }}}/{\delta }\rightarrow {1}/{{\hat{w}}}$, with $|{\hat{w}}|>1$, and w and ${\hat{w}}$ are the two distinct roots of Eq. (34).

Proof

By multiplying (22) with $1/\gamma ^2$, we obtain, after some straightforward calculations,

$$\begin{aligned} \frac{\delta }{\gamma }=&\left( {\bar{\lambda }}({\bar{a}}^2+a^2) + \lambda a{\bar{a}}\right) \frac{\delta }{\gamma } + \left( {\bar{\lambda }} {\bar{a}} a \gamma + \lambda (a^2 + {\bar{a}}^2)\right) \left( \frac{\delta }{\gamma }\right) ^2+ \lambda {\bar{a}} a \delta \left( \frac{\delta }{\gamma }\right) ^2 + {\bar{\lambda }} {\bar{a}} a . \end{aligned}$$

Taking now the limit as $\gamma \rightarrow 0$ (which also implies that $\delta \rightarrow 0$) and $\delta /\gamma \rightarrow w$ yields (34). By applying Rouché’s theorem in Eq. (34), it becomes immediately evident that the resulting equation has one root inside and one root outside the unit circle. This completes the proof of assertion (i). The proof of assertion (ii) follows similarly. $\square$

Lemma 3.9

• (i) Let $\gamma$, $\delta$ and ${\hat{\gamma }}$ be roots of Eq. (22) for fixed $\delta$, with $1>|\gamma |>|\delta |>|{\hat{\gamma }}|$. Then, as $\gamma \rightarrow 0$, ${\delta }/{\gamma }\rightarrow w$,

  $$\begin{aligned} \frac{c_{i+1}}{d_i}&\rightarrow -\frac{1-{\bar{\lambda }}{\bar{a}}-\lambda a{\bar{a}}-{\bar{\lambda }}a{\bar{a}}/w}{1-{\bar{\lambda }}{\bar{a}}-\lambda a{\bar{a}}-{\bar{\lambda }}a{\bar{a}}/{\hat{w}}}. \end{aligned}$$

• (ii) Let $\delta$, ${\hat{\gamma }}$ and ${\hat{\delta }}$ be roots of Eq. (22) for fixed ${\hat{\gamma }}$, with $1>|\delta |>|{\hat{\gamma }}|>|{\hat{\delta }}|$. Then, as $\delta \rightarrow 0$, ${\hat{\delta }}/{\hat{\gamma }}\rightarrow w$,

  $$\begin{aligned} \frac{e_{0,i}}{d_i \delta _i}&\rightarrow \frac{\left( 2 a^2-2 a+1\right) \lambda w ({\hat{w}}-w)}{-4 a^2 \lambda +2 a^2 \lambda {\hat{w}}+2 a^2+4 a \lambda -2 a \lambda {\hat{w}}-2 a-\lambda +\lambda {\hat{w}}}, \\ \frac{e_{1,i}}{d_i \delta _i}&\rightarrow \frac{\left( 4 a^2 \lambda -2 a^2-4 a \lambda +2 a+\lambda \right) ({\hat{w}}-w)}{-4 a^2 \lambda +2 a^2 \lambda {\hat{w}}+2 a^2+4 a \lambda -2 a \lambda {\hat{w}}-2 a-\lambda +\lambda {\hat{w}}}, \\ \frac{c_i}{d_i}&\rightarrow -\frac{w^2 \left( -4 a^2 \lambda +2 a^2 \lambda w+2 a^2+4 a \lambda -2 a \lambda w-2 a-\lambda +\lambda w\right) }{{\hat{w}}^2 \left( -4 a^2 \lambda +2 a^2 \lambda {\hat{w}}+2 a^2+4 a \lambda -2 a \lambda {\hat{w}}-2 a-\lambda +\lambda {\hat{w}}\right) }. \end{aligned}$$

Proof

The proof of the two assertions follows evidently by applying the results of Lemma 3.8 to Eq. (23) and (24), respectively. $\square$

The following proposition states that the series (25) and (26) converge absolutely.

Proposition 3.10

There exists a positive integer N such that

• (i) The series $\sum _{i=0}^{\infty }(d_{i}\gamma _{i}^{k}+c_{i+1}\gamma _{i+1}^k)\delta _{i}^{l}$, for $k+l>N$, converges absolutely.

• (ii) The series $\sum _{i=1}^{\infty }e_{l,i}\gamma _{i}^{k}\delta _0^l$, for $k>N$, $l=0,1$, converges absolutely.

• (iii) The series $\sum _{k+l>N}\sum _{i=0}^{\infty }(d_{i}\gamma _{i}^{k}+c_{i+1}\gamma _{i+1}^k)\delta _{i}^{l} +\sum _{k>N}\sum _{l=0}^1\sum _{i=1}^{\infty }e_{l,i}\gamma _{i}^{k}\delta _0^l$ converges absolutely.

Proof

It suffices to show that the series $\sum _{i=0}^{\infty }d_{i}\gamma _{i}^{k}\delta _{i}^{l}$ and $\sum _{i=0}^{\infty }c_{i+1}\gamma _{i+1}^k\delta _{i}^{l}$ converge absolutely. The rest follows along the same lines as in [4]. Note that, from Lemmas 3.8 and 3.9,

$$\begin{aligned} \left| \frac{d_{i+1}\gamma _{i+1}^{k}\delta _{i+1}^{l}}{d_{i}\gamma _{i}^{k}\delta _{i}^{l}}\right|&\rightarrow \frac{\left| \frac{1-{\bar{\lambda }}{\bar{a}}-\lambda a{\bar{a}}-{\bar{\lambda }}a{\bar{a}}/{\hat{w}}}{1-{\bar{\lambda }}{\bar{a}}-\lambda a{\bar{a}}-{\bar{\lambda }}a{\bar{a}}/w}\right| }{ \left| \frac{{\hat{w}}^2 \left( -4 a^2 \lambda +2 a^2 \lambda {\hat{w}}+2 a^2+4 a \lambda -2 a \lambda {\hat{w}}-2 a-\lambda +\lambda {\hat{w}}\right) }{w^2 \left( -4 a^2 \lambda +2 a^2 \lambda w+2 a^2+4 a \lambda -2 a \lambda w-2 a-\lambda +\lambda w\right) }\right| }\left| \frac{w}{{\hat{w}}}\right| ^{k+l}. \end{aligned}$$

(35)

As $|w|,1/|{\hat{w}}|<1$, then there exists a positive constant $N_1$ such that for $k+l>N_1$ the right-hand side of Eq. (35) is bounded by some positive constant smaller than one. Thus, the series $\sum _{i=0}^{\infty }d_{i}\gamma _{i}^{k}\delta _{i}^{l}$ is bounded by a geometric series for $k+l>N_1$, and as such converges absolutely. This concludes the proof of the absolute convergence of the series $\sum _{i=0}^{\infty }d_{i}\gamma _{i}^{k}\delta _{i}^{l}$. Similarly, one can show that the series $\sum _{i=0}^{\infty }c_{i+1}\gamma _{i+1}^k\delta _{i}^{l}$ converges absolutely for $k+l>N_2$, with $N_2$ some positive constant not necessarily equal to $N_1$. $\square$

3.4 Numerical implementation of the CA

In this section, we discuss how to numerically implement the equilibrium distribution analysis based on the CA . The equilibrium distribution $\pi _{k, l}$, $k\ge 0$, $l\ge 0$, is written as a linear combination of product-form terms, cf. (27), (28). The first step of the numerical implementation is to consider the first few terms of the series expression for $\pi _{k, l}$. More concretely, let

$$\begin{aligned} \pi _{k,l}^{(N_{\mathrm {ca}})}&= c\sum _{i=0}^{N_{\mathrm {ca}}}(d_{i}\gamma _{i}^{k}+c_{i+1}\gamma _{i+1}^{k})\delta _{i}^{l},\, ~~ k\ge 0,l\ge 2, \end{aligned}$$

(36)

$$\begin{aligned} \pi _{k,l}^{(N_{\mathrm {ca}})}&= c\Big (d_0\gamma _0^k+\sum _{i=1}^{N_{\mathrm {ca}}}e_{l,i}\gamma _{i}^{k}\Big ),\,~~ k>0,l=0,1, \end{aligned}$$

(37)

where here $N_{\mathrm {ca}}$ denotes the truncation level of the series expression obtained using the CA. From the analysis of Proposition 3.10, it follows that the inclusion of more terms of the series expression improves to a desired accuracy the computation of the equilibrium distribution, i.e., the bigger the value of $N_{\mathrm {ca}}$ the better the approximation of $\pi _{k, l}$. The constant $N_{\mathrm {ca}}$ is determined such that

$$\begin{aligned} \left| \frac{\sum \nolimits _{k,l = 0}^{T_{\mathrm {ca}}} \pi ^{{(N_{\mathrm {ca}})}}_{k, l} - \sum \nolimits _{k,l = 0}^{T_{\mathrm {ca}}} \pi ^{({N_{\mathrm {ca}}}-1)}_{k, l}}{\sum \nolimits _{k,l = 0}^{T_{\mathrm {ca}}} \pi ^{{(N_{\mathrm {ca}})}}_{k,l}}\right| < \varepsilon , \end{aligned}$$

(38)

with $\varepsilon$ denoting the precision error. This is included as the stopping criterium for the algorithm, i.e., we start with $N_{\mathrm {ca}}=1$ and, as long as Eq. (38) is not satisfied, we increase the value of $N_{\mathrm {ca}}$ by one.

Furthermore, for numerical purposes, we assume that the state-space $\tilde{{\mathcal {S}}}$ is truncated, i.e., we consider the following truncated state-space: $\tilde{{\mathcal {S}}}^{(T^{(k)},T^{(l)})}=\{(k,l):\,0\le k\le T^{(k)},0\le l\le T^{(l)}\}$. The constants $T^{(k)}$, $T^{(l)}$ are determined such that

$$\begin{aligned} c \,d_0\, \max (\gamma _0^{T^{(k)}}, \delta _0^{T^{(l)}})<\varepsilon , \end{aligned}$$

and $T^{(k)},T^{(l)}\ge 3$, so that Eqs. (27) and (28) can be applied. Note that the above are direct consequences of the asymptotic behavior of the random walk at hand, cf. Proposition 3.1. Furthermore, as $|\delta _0|<|\gamma _0|$, cf. Proposition 3.7, it suffices to choose

$$\begin{aligned} T_{ca}:=T^{(k)}=T^{(l)} \approx \max \{\lceil \log (\varepsilon )/\log (\delta _{0}) \rceil ,3\}. \end{aligned}$$

In Algorithm 1, we provide all the necessary information for the numerical implementation of the CA.

Next, we describe the time complexity of the algorithm in the Big-O notation as a function of the input size, i.e., $O(f(\cdot ))$ is measured as the maximum number of elementary steps needed to perform the algorithm, provided that each step is executed in constant (or equal) time.

3.4.1 Time complexity of Algorithm 1

We discuss the time complexity of the CA described in Algorithm 1. For a series truncation level $N_{\mathrm {ca}}$ and state-space truncation $T_{\mathrm {ca}}$, the algorithm converges with order $O\left( N_{\mathrm {ca}}\left( T_{\mathrm {ca}}\right) ^{2.376}\right)$. This order is obtained as follows:

• (i) In Steps 2 and 5, we need to compute recursively the $2(N_{\mathrm {ca}}+1)$ roots of Eq. (22). This can be done by using the Bisection method or the False position (aka regula falsi) method. With both methods, we are able to choose the bisection intervals within the interval $(0, \gamma _0)$, which results in time complexity $O(\log (\gamma _0))$ for the computation of a single root. In order to compute all the roots, the Bisection method needs to be repeated at least $2(N_{\mathrm {ca}}+1)$ times. Thus, the time complexity for the calculation of all the roots is of order $O(N_{\mathrm {ca}} \log (\gamma _0))$.

• (ii) In Step 6, we need to compute recursively the coefficients $c_i, e_{i, o}, e_{i, 1}$ and $d_i$, $i=0,1,\ldots ,N_{\mathrm {ca}}$. For this purpose, we need to solve a system of equations. The system is solved by implementing the Coppersmith–Winograd algorithm [16], which has a complexity $O(N_{\mathrm {ca}}^{2.376})$.

• (iii) In Step 7, we need to compute the equilibrium probabilities $\pi _{k, l}^{(N_{\mathrm {ca}})}$ using (36) and (37), which has time complexity $O(N_{\mathrm {ca}} (T_{\mathrm {ca}}/2))$.

• (iv) In Step 8, we need to solve a system of equations. We again use the Coppersmith–Winograd algorithm. This step has a complexity of $O( (T_{\mathrm {ca}}/2)^{2.376})$ and needs to be performed at least $N_{\mathrm {ca}}$ times. Thus, the time complexity of the entire step is of order $O\left( N_{\mathrm {ca}}\left( T_{\mathrm {ca}} /2\right) ^{2.376}\right)$.

• (v) In the construction of Algorithm 1, we have considered a part of the state-space region in which we directly use Eq. (37), cf. Step 7, and a part of the state-space region in which we solve a linear system of the equations, cf. Step 8. The sizes of these regions can be at most equal to $N_{\mathrm {ca}}$. Thus, in the worst case, this results in Step 7 requiring $O(N_{\mathrm {ca}} T_{\mathrm {ca}})$ and Step 8 requiring $O\left( N_{\mathrm {ca}}\left( T_{\mathrm {ca}}\right) ^{2.376}\right)$, respectively. Note that (iv) has the dominant time complexity, and, under the worst case scenario, it yields a time complexity of $O\left( N_{\mathrm {ca}}\left( T_{\mathrm {ca}}\right) ^{2.376}\right)$.

3.5 Applicability of the CA in case of bounded transitions

In Sect. 3, we mentioned that the model at hand violates the nearest neighbor condition for the applicability of the CA. Nonetheless, the analysis performed demonstrated that the CA can be generalized to cover a larger class of random walks permitting transitions not only to the nearest neighbors, but to a bounded region of neighboring states. From our analysis, it becomes clear that for random walks with the structure of the system at hand and bounded quasi-birth-death transitions along the rays $R_L=\{(k,l):\, 2k+l=L\}$, $L\ge L_0$, the analysis performed in Sect. 3.2 carries out to a tee. We have confirmed this for the system depicted in Fig. 3.

Fig. 3

The one-step transition probabilities diagram for a few representative states

4 Numerical results

In this section, we numerically validate our theoretical results obtained in the previous sections and compare the JSRQ routing protocol with the Bernoulli routing protocol (see Appendix B for details), as well as with the single relay system, in terms of their stability region and in terms of the total expected queue length. Furthermore, we show the superiority of the CA with respect to the PSA in terms of accuracy and efficiency. Note that the CA has the advantage of tight error bounds, while the theoretical foundation of the PSA is still incomplete and no error bounds are provided.

Before proceeding further, we have to mention that the consideration of the Bernoulli routing scheme in the slotted time setting is challenging due to the fact that the resulting arrival processes (after the Bernoulli splitting) are not independent (plus there is the interaction among the queues making the service rate of each queue dependent on the state of the other). Note that in the continuous time setting the queues behave independently; however, we consider here a discrete slotted time model so as to ensure an equivalent setting allowing for the comparison of the routing schemes. In particular, the case of the asymmetric system can be handled only with the aid of the theory of Riemann–Hilbert boundary value problems. However, for the symmetric case (which fits with the model at hand), we are able to obtain explicit expressions for the expected number of buffered packets at the relays (see Theorem B. 1). With that in mind, our contribution becomes more significant.

4.1 Comparison of JSRQ to other routing protocols

To make all systems comparable, we consider the arrival and transmission probabilities of the single relay system to be the same as in the JSRQ and Bernoulli routing systems, i.e., $\lambda$ and a are the same for the three systems.

Note that the Bernoulli routing scheme has the same stability region as the JSRQ (see Appendix B). The single server system is stable if $\lambda < a$, which implies $a \in (\lambda , 1)$. Both the JSRQ and the Bernoulli routing system are stable for $\lambda < 2a(1-a)$. Their common stability region can be equivalently written as

$$\begin{aligned} a \in (a^{-}, a^{+}) \equiv \left( \frac{1-\sqrt{1-2\lambda }}{2}, \frac{1+\sqrt{1-2\lambda }}{2}\right) , \text { for }\lambda < 1/2. \end{aligned}$$

(39)

From the above discussion, it becomes evident that the range of the stability region of the single relay system is $1-\lambda$ and of the JSRQ (as well as of the Bernoulli routing scheme) system is $\sqrt{1-2\lambda }$. For $\lambda < 1/2$, we observe that the region of the single server system contains the region of the JSQR system. Such a behavior is expected since the single relay system does not suffer from the collisions as well as from the interaction from neighbor relays, and thus it allows larger arrival rates.

For the single relay system, the total expected queue length goes to infinity as $a\downarrow \lambda$ and to zero as $a\uparrow 1$. For the JSRQ system, the total expected queue length goes to infinity as $a\rightarrow a^{+}$ or $a\rightarrow a^{-}$ (see (39)). Furthermore, for $\lambda <1/2$, it is easy to show that $a^-<\lambda<1/2<a^+$. Moreover, all systems have identical total expected queue lengths if $a=1/2$. Note that for $a=1/2$ the load of the single server system, $\lambda {\bar{a}}/{\bar{\lambda }}a$, is equal to the load of the JSRQ system, $\lambda ({\bar{a}}^{2}+a^{2})/2{\bar{\lambda }}{\bar{a}}a$.

Fig. 4

The total expected number of packets ${\mathbb {E}}[Q_1+Q_2]$ as a function of a for fixed $\lambda = 0.3$

Figure 4 shows that for $a<1/2$ the JSRQ and the Bernoulli routing scheme outperform the single relay system, for $a=1/2$ the systems perform identically, while for $a>1/2$ the single relay system performs better than the JSRQ and the Bernoulli routing system. This is an expected result, since the single relay system does not experience collisions, which in turn cause unsuccessful transmissions, i.e., the number of buffered packets will be increased. More importantly, we can observe that the JSRQ system outperforms the Bernoulli routing scheme when $a<1/2$, indicating the superiority of the JSRQ protocol even in the slotted time setting with highly interacting queues. Note that the superiority of JSRQ is observed when the relays are more likely to remain silent during a slot, i.e., when their transmission probabilities are lower than 1 / 2. In practice, this is the most reasonable scenario to apply the load balancing scheme, since relays “do not serve at efficient rates”, and it is more likely to cause significant delays.

Moreover, observe that when a takes small values, the expected number of buffered packets increases since in such a case the relays are more likely to remain silent. On the other hand, as a increases, so does the expected number of packets. This is also expected behavior, since in such a case both relays attempt to transmit with high probabilities, which in turn increases the number of collisions and results in transmission failures. This result reveals the need for consideration of an alternative channel model scheme, which allows concurrent transmissions such as the multi-packet reception scheme (see, for example, [17, 18]). Clearly, such behavior is not observed in the single relay system, since there are no collisions.

Similar observations can be deduced from Fig. 5, where we plot the total expected queue length as a function of $\lambda$ for fixed $a=0.3$. Again, we observe the superiority of JSRQ both over the Bernoulli routing scheme and over the single relay system, which is more apparent for large values of $\lambda$.

Fig. 5

The total expected number of packets ${\mathbb {E}}[Q_1+Q_2]$ as a function of $\lambda$ for fixed $\alpha = 0.3$

When we are dealing with multiple access systems, where multiple nodes try to access the medium randomly, the presence of collisions is one of the main sources of service degradation. On the other hand, the ever-increasing need for massive uncoordinated access in large and dense networks makes inappropriate the use of the single relay model, since it underestimates the interaction/interdependence between transmitting nodes and, thus, fails to describe a significant and realistic part of the network operation. Moreover, load balancing schemes are without question important for the efficient operation of such networks. Our numerical findings indicate when to use the JSRQ with respect to the Bernoulli routing scheme based on the values of the transmission probabilities (by taking into account the presence of interference among transmitting nodes). To the best of our knowledge, this characteristic has not been reported so far in the related literature.

4.2 Numerical validation of the results

As an extra step of further validation of our fundamental results, we numerically validate our main findings based on the CA using the power series algorithm, which is discussed in Appendix A. Using the CA, we can compute an explicit expression for the equilibrium distribution as a (infinite) linear combination of product-form terms. We have proven that the corresponding truncated linear combinations provide asymptotic expansions which improve as we include more terms. From this perspective, we can relatively control the error of the approach. However, for the PSA, to the best of our knowledge, there exists no error bound due to the lack of theoretical support for this approach; see [9, 10]. The error produced by the PSA implementation can be controlled somewhat by including more terms of the series. On top of that, it is sometimes unclear when this method diverges [36], but the radius of convergence of the power series can be extended using a transformation; cf. (41).

In Table 1, we depict the total expected sojourn time of a packet measured in time slots and the correlation coefficient between the queue lengths of the two relays, for various values of the load $\rho$. The total expected sojourn time of a packet is computed as ${\mathbb {E}} [S] = \frac{1}{\lambda }{\mathbb {E}}[Q_1+Q_2]$, and as expected, as $\rho$ increases, so do the values of ${\mathbb {E}} [S]$. The correlation coefficient between the queue relays is computed as ${\mathbb {R}}(Q_1, Q_2) = \frac{{\mathbb {E}}[Q_1Q_2]- {\mathbb {E}}[Q_1] {\mathbb {E}}[Q_2]}{\sqrt{{\mathbb {V}}ar[Q_1] {\mathbb {V}}ar[Q_2]}}$. For the computations performed, we choose $\rho =0.1,0.4,0.7,0.9,0.95$, so as to cover lighter and heavier traffic results. Furthermore, we choose $G = 1$ for the PSA implementation (see Algorithm 2).

As expected, as $\rho$ increases the correlation coefficient tends to one, and as the values of Table 1 indicate, it almost behaves like a linear function of $\rho$. Furthermore, it is evident, from the numerical results, that both approaches produce similar outcomes (as long as the value for $\rho$ is away from the stability region boundary $\rho =1$) differing by approximately as much as the range of the precision; cf. column $\mid \mathrm {CA} - \mathrm {PSA} \mid / \mathrm {CA}$. However, as $\rho$ approaches one, the PSA becomes highly unstable, while the CA is producing accurate results in the entire stability region. The numerical instability of the PSA can be explained observing that $\rho \rightarrow 1$ implies that $\theta \rightarrow 1$, cf. Equation (41), indicating that the power series expression is approaching the boundary of the region of convergence. This can be overcome, to a certain degree, by further increasing the value $G\ge 1$.

Table 1 Total expected sojourn time of a packet and the correlation between the queue relays

From the numerical implementation, it is notable that both the CA and the PSA provide accurate results to a desired precision. In both approaches, the time complexity of the corresponding algorithm depends on $\varepsilon$ through the determination of $T_{\mathrm {ca}}$ or $T_{\mathrm {psa}}$, cf. Step 4 of Algorithm 1, or Step 3 of Algorithm 2, respectively, which we can control. Equating $\varepsilon$ for both algorithms, we can compare the methods in terms of their algorithmic time complexity, so as to characterize the performance speed of the two approaches. As shown in Sect. 3.4.1, the compensation algorithm runs in $O\left( N_{\mathrm {ca}}\left( T_{\mathrm {ca}}\right) ^{2.376}\right)$, while for the PSA it is shown in Appendix A that Algorithm 2 runs in $O\Big ((N_{\mathrm {psa}}+1)\left( (T_{\mathrm {psa}}+1)^2/4\right) ^{2.376}\Big )$ which is equivalent to $O\left( N_{\mathrm {psa}}\left( T_{\mathrm {psa}}\right) ^{4.752}\right)$. Thus, the compensation algorithm has better big-O time complexity than the PSA.

Remark 4.1

We have numerically validated the CA with the PSA. One can observe from Table 1 that the results obtained using both approaches differ when the load approaches 1. The reason for the differences is that the PSA becomes highly unstable as $\rho \rightarrow 1$ as discussed above. This can be overcome, to a certain degree, by further increasing the value $G\ge 1$; see, for example, [9, 10]. The CA results can be also validated using the MGM instead of the PSA. Namely, in [34], the authors prove that for the class of nearest-neighbor two-dimensional random walks in the quarter plane with no transitions in the interior to the North, North–East and East, the CA and the MGM produce identical results, as the $\gamma$ terms are in fact the eigenvalues of the rate matrix and the $\delta$ terms are associated with the eigenvectors of the rate matrix. As such, we strongly believe that it provides more information to compare the results of the CA with a method which is significantly different in scope and structure, such as the PSA.

5 Conclusions and possible extensions

In this work, we focused on the application-oriented problem of characterizing the queueing delay experienced in a slotted-time relay-assisted cooperative random access wireless network with collisions under the JSRQ routing protocol. Note that due to the collisions, there is strong interdependence among the queues of the relays, resulting in different successful transmission probabilities, when both relays are busy and when one of the relays is empty. Thus, the system at hand incorporates two features: the JSRQ and the coupled processor feature. For such a system, we investigate the stability condition and apply the CA for the computation of the equilibrium joint queue (relay) length distribution. A numerical validation of the theoretical results obtained by the CA is presented. More importantly, we have applied the CA to a random walk on the positive quadrant with transitions to a bounded region of neighbors, extending the framework of the CA to a wider class of random walks (than the nearest neighbor class for which the approach was originally developed).

In a future work, we plan to generalize this work in several directions. A challenging task is related to the equilibrium analysis of a general cooperative network with a queue-aware transmission protocol under which each relay configures its transmission parameters based on the status of the other. Such a protocol serves toward self-aware and intelligent networks. Moreover, we also plan to characterize the delay using a multi-packet reception model, which allows successful transmissions even if multiple nodes (relays or source(s)) transmit simultaneously, with as ultimate goal to improve the throughput performance of the network. An interesting challenging task is the investigation of the queueing delay at a random access network with an arbitrary number of relay nodes under the JSRQ routing policy, as well as its optimality over other routing policies.

Appendices

A Equilibrium analysis: the power series algorithm

In this section, we briefly show how the PSA can be used to analyze the relay-based cooperative communication network with collisions and with the JSRQ protocol. Our aim is to numerically validate the theoretical results obtained using the CA with the PSA. To help the reader with the computations performed, we briefly present the main steps to derive a recursive, computational scheme for the equilibrium joint queue length distribution. For the analysis that follows, we use the transformed model, see Sect. 3, and the balance equations (9)–(16). Following [10], we introduce the following power-series expansion:

$$\begin{aligned} \pi _{k, l} = \sum \limits _{n = 0}^{\infty } ~\theta ^{n + k + l}~ u(n, k, l),\ k,l\ge 0, \end{aligned}$$

(40)

where $\theta$ is a bilinear conformal transformation of the real interval [0, 1) onto itself such that

$$\begin{aligned} \theta =\frac{(1+G)\rho }{1+G\rho } \iff \rho = \frac{\theta }{1 + G- G \theta }, \end{aligned}$$

(41)

where $G \ge 0$ is a parameter to be chosen [10, Section 2.3].

By applying (40) in the balance equations (9)–(16), one can obtain and solve a recursive set of equations for the coefficients u(n, k, l). Having computed the coefficients u(n, k, l), it is easy to approximate the equilibrium distribution, to any degree of required precision, using (40).

For illustration purposes, we have chosen $a=\frac{1}{2}$, so as to simplify the notation and enhance the readability of the method. Substituting $a = \frac{1}{2}, \lambda = \frac{\rho }{1 + \rho }, \rho = \frac{\theta }{1 + G- G \theta }$ and $\pi _{k, l}$ (defined in (40)) into (14)–(16)–(10) and equating the powers of $\theta$ leads to the following recursion equations for the coefficients $u(n, k, l), \ n \ge 0,\ (k,l)\in \tilde{S}$:

$$\begin{aligned} u(n-1, 0, 1)&= \frac{G}{G+1}u(n-2, 0, 1) \mathbb {1}_{\{n \ge 2\}} + \frac{1}{G+1} u(n-1, 0, 0), \ n \ge 1, ~ \end{aligned}$$

(42)

$$\begin{aligned} u(n-2, 0, 2)&= \frac{G}{G+1}u(n-3, 0, 2) \mathbb {1}_{\{n \ge 3\}}\nonumber \\&\quad -\, \frac{G-1}{G+1} u(n-2, 0, 1) + u(n-1, 0, 1) \nonumber \\&\quad -\, u(n-1, 1, 0) + \frac{G}{G+1} u(n-2, 1, 0)\nonumber \\&\quad -\, \frac{1}{G+1} u(n-1, 0, 0), \ n \ge 2, \end{aligned}$$

(43)

$$\begin{aligned} u(n-l-1, 0, l+1)&= \frac{G}{G+1} u(n-l-2, 0, l+1) \mathbb {1}_{\{n \ge l+ 2\}} \nonumber \\&\quad -\, \frac{G - \frac{3}{2}}{G+1} u(n-l-1, 0, l) \nonumber \\&\quad +\, u(n-l, 0, l) + \frac{1}{2} \frac{G}{G+1} u(n-l-1, 1, l-1) \nonumber \\&\quad - \,\frac{1}{2} u(n-l, 1, l-1) \end{aligned}$$

(44)

$$\begin{aligned}&\quad -\, \frac{1}{2(G+1)} u(n-l, 1, 0) \mathbb {1}_{\{l = 2\}}, \ n \ge l-1, l \ge 2, \end{aligned}$$

(45)

$$\begin{aligned} u(n-k, k, 0)&= \left( \frac{G - \frac{3}{2}}{G+1} u(n-k-1, k, 0) \right. \nonumber \\&\quad \left. +\, \frac{1}{2} u(n-k-1, k, 1) \right) \mathbb {1}_{\{n \ge k+1\}} \nonumber \\&\quad -\, \frac{1}{2} \frac{1}{G+1} \left( G u(n-k-2, k, 1) \right. \nonumber \\&\quad \left. -\, u(n-k-2, k-1, 2) \right) \mathbb {1}_{\{n \ge k+2\}} \nonumber \\&\quad +\, \frac{1}{G+1} u(n-k-1, k-1, 1) \mathbb {1}_{\{n \ge k+1\}}, \ n \ge k, k \ge 1, \end{aligned}$$

(46)

$$\begin{aligned} u(n-k-1, k, 1)&= \left( \frac{G - 1}{G+1} u(n-k-2, k, 1) + \frac{1}{2} u(n-k-2, k, 2) \right) \mathbb {1}_{\{n \ge k+2\}} \nonumber \\&\quad +\, \frac{1}{2} \frac{1}{G+1} \left( - G u(n-k-3, k, 2) \right. \nonumber \\&\quad \left. +\, u(n-k-3, k-1, 3) \right) \mathbb {1}_{\{n \ge k+3\}} \nonumber \\&\quad +\, \frac{1}{G+1} \left[ u(n-k-2, k-1, 2) \right. \nonumber \\&\quad \left. - \,G u(n-k-2, k+1, 0) \right] \mathbb {1}_{\{n \ge k+2\}} \nonumber \\&\quad +\,\frac{1}{G+1} u(n-k-1, k, 0) \nonumber \\&\quad +\, u(n-k-1, k+1, 0) , \ n \ge k+1, k \ge 1, \end{aligned}$$

(47)

$$\begin{aligned} u(n-k-l, k, l)&= \left( \frac{G - \frac{3}{2}}{G+1} u(n-k-l-1, k, l) \right. \nonumber \\&\quad \left. +\, \frac{1}{2} u(n-k-l-1, k, l+1) \right) \mathbb {1}_{\{n \ge k+l+1\}} \nonumber \\&\quad -\, \frac{1}{2} \frac{G}{G+1} u(n-k-l-2, k, l+1) \mathbb {1}_{\{n \ge k+l+2\}} \nonumber \\&\quad +\, \frac{1}{2} \frac{1}{G+1} \left[ u(n-k-l-2, k-1, l+2) \right] \mathbb {1}_{\{n \ge k+l+2\}} \nonumber \\&\quad +\, \frac{1}{G+1} u(n-k-l-1, k-1, l+1) \mathbb {1}_{\{n \ge k+l+1\}} \nonumber \\&\quad -\, \frac{1}{2} \frac{G}{G+1} u(n-k-l-1, k+1, l-1) \mathbb {1}_{\{n \ge k+l+1\}} \nonumber \\&\quad -\, \frac{1}{2} u(n-k-l, k+1, l-1) \nonumber \\&\quad +\, \frac{1}{2} \frac{1}{G+1} u(n-k-2, k+1, 0) \mathbb {1}_{\{l = 2\}}, \nonumber \\&\quad n \ge k + l, k \ge 1, l \ge 2. \end{aligned}$$

(48)

Plus,

$$\begin{aligned} u(0, 0, 0) = 1, \, \, \, u(n, 0, 0) = -\mathop {\sum \sum }\limits _{0 < k + l \le n} u(n - k - l, k, l). \end{aligned}$$

(49)

The coefficients u(n, k, l) can be recursively calculated from (42)–(49). Thus, using (40), one can determine the equilibrium distribution $\pi _{k, l}$.

Numerical implementation and time complexity of the PSA In order to validate the CA, we sketch below the algorithmic implementation of the PSA. Similarly to the CA, we truncate the series expression (40) to the $N_{\mathrm {psa}}$-th term.

We now discuss the time complexity of the power series algorithm described in Algorithm 2. The algorithm converges with order $O\left( (N_{\mathrm {psa}}+1)\left( (T_{\mathrm {psa}}+1)^2/4\right) ^{2.376}\right)$ for a series truncation level $N_{\mathrm {psa}}$ and state-space truncation $T_{\mathrm {psa}}$. This order is obtained as follows: In Step 5, for $0 \le n \le N_{\mathrm {psa}}$ and $0\le k, l \le T_{\mathrm {psa}}$, we compute u(n, k, l). This step determines the dominant time complexity in the PSA. These coefficients are obtained solving the system of equations (42)–(49), by implementing for example the Coppersmith–Winograd algorithm [16]. Note that this system of equations reveals that (i) the series truncation level should be chosen such that $N_{\mathrm {psa}} \le T_{\mathrm {psa}}$, and (ii) the state-space truncation should contain all states $0\le k+l \le T_{\mathrm {psa}}$. All in all, this yields that the complexity is $O\left( (N_{\mathrm {psa}}+1)\left( (T_{\mathrm {psa}}+1)^2/4\right) ^{2.376}\right)$.

B The Bernoulli routing under EAS scheme

In the following, we provide an explicit expression for the total expected number of packets at the relays for the slotted time Bernoulli routing model. To the best of our knowledge, such a model has not been analyzed in the literature so far, and this is the reason why we present it here in some detail. Note also that contrary to the continuous time model, in the slotted time Bernoulli routing model the queues do not behave independently.

Packets arrive according to a Bernoulli arrival process with parameter $\lambda$, and with probability 1 / 2 the transmitted packet is forwarded to relay 1 or relay 2 (i.e., splitting the original Bernoulli process). Note that the resulting processes are also Bernoulli with parameter $\lambda /2$, but they are not independent. The one-step transition probabilities of the resulting random walk in the quarter plane are given below (maximal space homogeneity):

$$\begin{aligned} {\mathbb {P}}\left[ \varvec{Q}(n+1)=(i+k,j+l)|\varvec{Q}(n)=(k,l)\right] =\left\{ \begin{array}{ll} p_{i,j},&{}\quad \text { for }k,l\ge 1,\\ p^{\prime }_{i,j},&{}\quad \text { for }k\ge 1,\,l=0,\\ p^{\prime \prime }_{i,j},&{}\quad \text { for }k=0,\,l\ge 1,\\ p^{O}_{i,j},&{}\quad \text { for }k=l=0, \end{array}\right. \end{aligned}$$

where

$$\begin{aligned} \begin{array}{lll} p_{1,0}=p_{0,1}=({\bar{a}}^{2}+a^{2})\frac{\lambda }{2},&{}\quad p_{0,-1}=p_{-1,0}=a{\bar{a}}{\bar{\lambda }},&{}\quad p_{0,0}=({\bar{a}}^{2}+a^{2}){\bar{\lambda }}+a{\bar{a}}\lambda ,\\ p_{1,-1}=p_{-1,1}=a{\bar{a}}\frac{\lambda }{2},&{}\quad p^{\prime }_{1,0}=p^{\prime \prime }_{0,1}=\frac{\lambda }{2}{\bar{a}},&{}\quad p^{\prime }_{0,1}=p^{\prime \prime }_{1,0}=\frac{\lambda }{2}({\bar{a}}^{2}+a^{2}),\\ p^{\prime }_{-1,0}=p^{\prime \prime }_{0,-1}=a{\bar{\lambda }},&{}\quad p^{\prime }_{0,0}=p_{0,0}^{\prime \prime }={\bar{a}}{\bar{\lambda }}+a\frac{\lambda }{2}+\frac{\lambda }{2}a{\bar{a}},&{}\quad p^{\prime }_{-1,1}=p^{\prime \prime }_{1,-1}=a{\bar{a}}\frac{\lambda }{2},\\ p^{O}_{1,0}=p^{O}_{0,1}=\frac{\lambda }{2}{\bar{a}},&{}\quad p^{O}_{0,0}={\bar{\lambda }}+\lambda a.&{}\quad \end{array} \end{aligned}$$

Stability condition Note that the underlying model satisfies the conditions of Theorem 3.3.1 in [22]. Using the notation and the theory of Fayolle et al. [22], the expected one-step transitions with respect to the x and y axis for the interior (i.e., $k,l\ge 1$) and boundary states (i.e., $k\ge 1,\,l=0$ and $k=0,\,l\ge 1$) are as follows:

$$\begin{aligned} M_{x}&=\sum _{i=-1}^{1}\sum _{j=-1}^{1}ip_{i,j}=\frac{\lambda -2a{\bar{a}}}{2}=M_{y}=\sum _{i=-1}^{1}\sum _{j=-1}^{1}jp_{i,j},\\ M_{x}^{\prime }&=\sum _{i=-1}^{1}\sum _{j=-1}^{1}ip^{\prime }_{i,j}=\frac{\lambda {\bar{a}}^2-2a{\bar{\lambda }}}{2}=M_{y}^{\prime \prime }=\sum _{i=-1}^{1}\sum _{j=-1}^{1}jp^{\prime \prime }_{i,j}, \\ M_{x}^{\prime \prime }&=\sum _{i=-1}^{1}\sum _{j=-1}^{1}ip^{\prime \prime }_{i,j}=\frac{\lambda ({\bar{a}}^{2}+a^{2}+ a{\bar{a}})}{2}=M_{y}^{\prime }=\sum _{i=-1}^{1}\sum _{j=-1}^{1}jp^{\prime \prime }_{i,j}. \end{aligned}$$

A straightforward application of Theorem 3.3.1 in [22] indicates that $\{\varvec{Q}_{n},n\ge 0\}$ is ergodic if and only if $\lambda < 2 a {\bar{a}}$.

Stationary analysis Let $\lambda < 2 a {\bar{a}}$, and denote by $\Pi (x,y)=\lim _{n\rightarrow \infty }{\mathbb {E}}(x^{Q_{1,n}}y^{Q_{2,n}})$, $|x|\le 1$, $|y|\le 1$, $n\in {\mathbb {N}}$. Then, straightforward computations yield

$$\begin{aligned} \Pi (x,y)R(x,y)=A(x,y)\Pi (x,0)+B(x,y)\Pi (0,y)+C(x,y)\Pi (0,0), \end{aligned}$$

(50)

where

$$\begin{aligned} R(x,y)&=xy\left[ 1-{\bar{\lambda }}({\bar{a}}^{2}+a^{2})-\lambda a{\bar{a}}-\frac{\lambda }{2}({\bar{a}}^{2}+a^{2})(x+y)\right] \\&\quad -\,{\bar{\lambda }}a{\bar{a}}(x+y)-\frac{\lambda }{2}a{\bar{a}}(x^{2}+y^{2}),\\ A(x,y)&=xy\left[ {\bar{\lambda }}{\bar{a}}+\frac{\lambda }{2}a +\frac{\lambda }{2}a{\bar{a}}-{\bar{\lambda }}({\bar{a}}^{2}+a^{2})-\lambda a{\bar{a}}\right. \\&\quad \left. +\,x\left( \frac{\lambda }{2}{\bar{a}} -\frac{\lambda }{2}({\bar{a}}^{2}+a^{2})\right) \right] +y{\bar{\lambda }}a^2-xa{\bar{a}}\left( {\bar{\lambda }}+\frac{\lambda }{2}x\right) ,\\ B(x,y)&=xy\left[ {\bar{\lambda }}{\bar{a}}+\frac{\lambda }{2}a +\frac{\lambda }{2}a{\bar{a}}-{\bar{\lambda }}({\bar{a}}^{2}+a^{2})-\lambda a{\bar{a}}\right. \\&\quad \left. +\,y\left( \frac{\lambda }{2}{\bar{a}} -\frac{\lambda }{2}({\bar{a}}^{2}+a^{2})\right) \right] +x{\bar{\lambda }}a^2-ya{\bar{a}}\left( {\bar{\lambda }}+\frac{\lambda }{2}x\right) ,\\ C(x,y)&={\bar{\lambda }}[xy(1-2{\bar{a}}+{\bar{a}}^{2}+a^{2})-a^{2}(x+y)]. \end{aligned}$$

Theorem B. 1

Provided that the system is stable, i.e., $\lambda < 2a{\bar{a}}$, the expected number of buffered packets in a relay node under the EAS Bernoulli routing scheme equals

$$\begin{aligned} {\mathbb {E}}[Q_{1}]={\mathbb {E}}[Q_{2}]= \frac{\lambda {\bar{a}}^2}{2a{\bar{a}}-\lambda }. \end{aligned}$$

(51)

Proof

Symmetry implies $\Pi (1,0)=\Pi (0,1)$ and $\Pi _{1}(1,0)=\Pi _{2}(0,1)$, where $\Pi _{1}(x,y)$ (resp. $\Pi _{2}(x,y)$) denotes the first-order derivative with respect to x (resp. y). The proof is outlined in the following steps:

• Step 1. Plugging $y=1$ in (50), dividing both sides by $x-1$, then differentiating with respect to x and setting $x=1$ yields

  $$\begin{aligned} (2a{\bar{a}}-\lambda ){\mathbb {E}}[Q_1] = (1 - a {\bar{a}}) \lambda - a^2 (2 - \lambda ) \Pi _1(1,0) - a^2 \lambda \Pi (1, 0). \end{aligned}$$

  (52)

• Step 2. Similar to the above steps, plugging $x=y$ in (50), dividing both sides by $x(x-1)$, then differentiating with respect to x and setting $x = 1$, we obtain

  $$\begin{aligned} 2(2a{\bar{a}}-\lambda ){\mathbb {E}}[Q_1] = (1 - 2 a {\bar{a}}) \lambda + a (1 - 2 a) (2 - \lambda ) \Pi _1(1,0) + a (1 - 2 a) \lambda \Pi (1,0). \end{aligned}$$

  (53)

• Step 3. Dividing (52) by $a^2$ and (53) by $a(1-2a)$ and then adding them yields the desired result.

$\square$