1 Introduction

We consider a tandem network of queues \(0,\dots , s-1.\) Customers arrive one-by-one at queue 0 according to a Poisson process with rate \(\lambda \). There are s independent batch service processes at exponential rates \(\mu _0, \dots , \mu _{s-1}\). Service process i, \(i=0, \dots , s-1\), at rate \(\mu _i\) is such that all customers of all queues \(0, \dots , i\) simultaneously receive service and move to the next queue.

This system does not satisfy partial balance in classical form at queue 0, since customers arrive one-by-one and are served in batches. Therefore, our system cannot fall in the class of Kelly–Whittle networks [12] and it does not fall in the class of batch routing queueing networks with product form [6, 14].

In isolation, queue 0 can be modeled as a queue with disasters [9]; customers arrive one-by-one and the entire queue is emptied according to a Poisson process of triggers with rate \(\mu _0+\dots +\mu _{s-1}\). However, our tandem network of queues cannot be modeled as a network with triggers or negative customers (see, for example, [5] for a description of these networks). The reason is that in a tandem network with triggers or negative customers that empty the entire queue, a trigger or a negative customer that finds a queue empty is lost. In our system the contents of queues \(0,\dots ,i\) are shifted to queues \(1,\dots ,i+1\) also when some of the queues \(0,\dots ,i\) are empty.

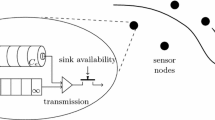
Our model is motivated by applications in data collection from a wireless sensor network (WSN). In particular, we investigate the case where clients arriving at the network are interested in collecting data from different sensors for data fusion. These sensors broadcast their data, i.e., all clients receive the data of a sensor when it is transmitted. A client needs to obtain data from an arbitrary set of \(s\in \mathbb {N}\) different sensors in order to be able to apply a fusion algorithm. Examples of such applications are i) localization for client positioning [3]; ii) the retrieval of various noisy measurements of the same attribute for data fusion [16].

Data fusion in WSNs has been studied extensively in, for instance, [2, 17, 19,20,21]. Scheduling for WSNs has been extensively studied in, for example, [1, 11]. However, little work has been done on sensor transmission schedules that support data fusion [16, 18], as aimed at here. Sensor transmission schedules affect the time for a client to receive sufficient data from distinct sensors in order to be able to apply a data fusion algorithm. In this work, we consider a tandem queueing model and we show it can be used to analyze sensor transmission schedules under which clients collect a fixed number of sensor observations to be able to apply data fusion algorithms.

The problem of providing a fixed number of units of service (in our case, a set of s observations) to all clients has been studied in, for instance, [8, 13, 15]. In [8] a discrete-time multi-server queueing model with a general arrival process is considered, where each client is interested in receiving s units of service. Contrary to our model, in each time slot each client is guaranteed to receive a unit of service. In [15] a discrete-time queue is considered with geometric arrivals and arbitrarily distributed service requirements (number of units of service required). Contrary to our model, a single class of customers and a single server is considered. Our model has similarities to gated service polling models [4]. In particular, we could place customers of each class at different queues and provide gated batch service [7] at one of these queues.

The contributions of this paper are as follows. We model our system as a multi-class tandem network of queues with batch service and demonstrate that our system has a geometric product-form steady-state distribution. Moreover, we determine the service allocation strategies that minimize the expected waiting time in the system and state conditions to approximate such optimal allocations. We also provide a closed form expression for the Hellinger distance to an optimal allocation. We show that this queueing model has applications in data collection from a WSN where the class of a client in the queueing model corresponds to the number of observations that a client has already collected from a WSN. Analyzing a scheduling mechanism for the WSN data collection application now reduces to analyzing this multi-class queue under a specific assignment of service rates for these classes. As special cases, we consider a decentralized and an optimal centralized broadcasting schedule and determine the performance gap between the two with respect to waiting time, for arbitrarily large WSNs. As such, this paper introduces a novel product-form queueing model that is of theoretical interest in itself and has interesting practical applications to WSNs.

The remainder of this paper is organized as follows. In Sect. 2 we formulate the model and introduce some notation. In Sect. 3 we analyze our model and obtain the steady-state distribution. In Sect. 4 we determine optimal service allocations with respect to waiting time and state conditions to approximate such allocations. Applications to sensor networks are provided in Sect. 5. In Sect. 6 we discuss the results and provide conclusions.

2 Model and notation

We consider a tandem network of queues \(0, \ldots , s-1\) in which there are s customer classes, labeled \(0, \dots , s-1\). Customers arrive according to a Poisson process with rate \(\lambda \) and have class 0. There are s independent batch service processes at exponential rates \(\mu _0, \dots , \mu _{s-1}\). Service process i, \(i=0, \dots , s-1\), at rate \(\mu _i\) is such that all customers of all classes \(0, \dots , i\) simultaneously receive service (but not those of class \(i+1, \ldots , s-1\)). Customers of classes \(0, \dots , s-2\) that receive service increase their class by 1 and remain in the system. Customers of class \(s-1\) that receive service leave the system.

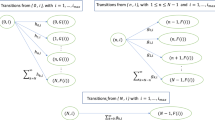
We will describe the continuous-time Markov chain, \(X=(X(t), t\ge 0)\), that captures the dynamics of this queueing model, but before doing so we introduce the following notation. Let \(\mathbb {N}_0 = \{0, 1, \dots \}\). For \(n\in \mathbb {N}_0^s\) we denote its elements through subscripts, i.e., \(n=(n_0,\dots ,n_{s-1})\). Next, consider s functions \(U_i:\mathbb {N}_0^s \rightarrow \mathbb {N}_0^s\), \(0 \le i \le s-1\), where \(U_i(n)=(0, n_0, \ldots , n_{i-1}, n_i+n_{i+1}, n_{i+2}, \ldots , n_{s-1})\) for \(i=0, \dots , s-2,\) and \(U_{s-1}(n)=(0, n_0, \ldots , n_{s-2})\).

We have a continuous-time Markov chain X on the state space \(\mathbb {N}_0^s\) in which \(n\in \mathbb {N}_0^s\) represents the state in which there are \(n_i\) customers of class i, \(i=0, \dots , s-1,\) in the system. The outgoing transitions from state n are as follows. For each \(0\le i\le s-1\) a transition occurs from n to \(U_i(n)\) at a rate \(\mu _i\). Also, there is a transition at rate \(\lambda \) from n to \(n+e_0\), where \(e_0 = (1, 0, \dots , 0)\) is of length s.

If n contains zeros, some care is required with the above definition of the transition rates. We illustrate this by means of two examples. Firstly, let \(0<i\le s-1\) and consider \(n_j=0\) iff \(j=i\). In this case \(U_i(n)=U_{i-1}(n)\). Therefore, the transition rate from n to \(U_{i-1}(n)\) is \(\mu _{i-1}+\mu _i\). Secondly, let \(0<i\le s-1\) and consider \(n_j=0\) iff \(j\le i\). In this case \(U_{0}(n)=U_{1}(n)=\dots =U_{i}(n)=n\). Note that we do not have a transition from n to \(U_j(n)\) for \(j\le i\) in this case.

For notational convenience in the next section, we introduce the functions \(S_{i}: \mathbb {Z} \times \mathbb {Z}^{s}\rightarrow \mathbb {Z}_0^s\), for \(i=0,\dots ,s-1\). These functions are defined as \(S_i(x,n) = (n_1, \ldots , n_{i}, x, n_{i+1}-x, n_{i+2}, \ldots , n_{s-1})\) for \(i=0,\dots ,s-2\) and \(S_{s-1}(x,n) = (n_1, \ldots , n_{s-2}, x).\) The functions \(U_i\) and \(S_i\) are illustrated in Fig. 1. Finally, let \(\bar{\mu }_i=\sum _{k=i}^{s-1} \mu _k\). This is the total rate at which customers of class i receive service and change their class to \(i+1\). Note that \(\bar{\mu }_0=\sum _{k=0}^{s-1} \mu _k\) and \(\bar{\mu }_{s-1}=\mu _{s-1}\).

Fig. 1
figure 1

States of the general continuous-time Markov chain

Full size image

3 Analysis

In this section, we discuss the balance equations of the Markov chain X and derive the steady-state distribution \(\pi (n)\) (\(n \in {\mathbb N}_0^{s}\)) of the system in Sect. 2.

The reason for introducing \(S_{i}\) in the previous section is that \(S_{i}(x, n)\) provides a convenient means to describe the states with a transitions into n. Indeed, ignoring boundary conditions for the moment and considering \(n\in \mathbb {Z}^s\) with \(n_0=0\), we have \(U_i(S_{i}(x, n))=n\) for all \(0\le i\le s-1\) and all \(x\in \mathbb {Z}\). In other words, for all \(0\le i\le s-1\) and \(x\in \mathbb {Z}\), \(S_i(x, n)\) has a transition to n with rate \(\mu _i\). The one thing we need to deal with is that \(S_i(x, n)\) itself must be an element of the state space, i.e., we need \(S_i(x, n)\in \mathbb {N}_0^s\). It is readily verified that for \(0\le i\le s-2\) this is true iff \(n\in \mathbb {N}_0^{s}\) and \(0\le x\le n_{i+1}\). Also, \(S_{s-1}(x, n)\in \mathbb {N}_0^s\) iff \(n\in \mathbb {N}_0^{s}\) and \(x\ge 0\).

Before we determine the steady-state distribution of this system, we first discuss the balance equations. Let \(k=\min \{i \,|\, n_i>0, 0 \le i \le s-1 \}\). Note that, as discussed in Sect. 2, \(U_i(n)=n\) for \(0\le i\le k-1\). Note, in addition, that \(S_i(x, n)=n\) for \(0\le i\le k-2\) and \(0\le x\le n_{i+1}\). Also, \(S_{k-1}(0, n)=n\). Now, for \(n_0=0\), the resulting balance equation is

$$\begin{aligned} \pi (n)\left( \lambda +\sum _{i=k}^{s-1}\mu _i\right)= & {} \sum _{x=1}^{n_{k}} \mu _{k-1} \pi (S_{k-1}(x, n)) \nonumber \\&+ \sum _{i=k}^{s-2} \sum _{x=0}^{n_{i+1}} \mu _i \pi (S_{i}(x, n))+ \sum _{x=0}^{\infty } \mu _{s-1} \pi (S_{s-1}(x, n)).\qquad \end{aligned}$$
(3.1)

Adding \(\pi (n)\mu _i=\sum _{x=0}^{n_{i+1}}\pi (S_i(x, n))\mu _i=\pi (S_i(0, n))\mu _i\) for \(0\le i\le k-2\), as well as \(\pi (n)\mu _{k-1}=\pi (S_{k-1}(0, n))\mu _{k-1}\) to the left-hand side as well as the right-hand side of (3.1), (3.1), i.e., the balance equation for \(n_0=0\), becomes

$$\begin{aligned} \pi (n)\left( \lambda +\sum _{i=0}^{s-1}\mu _i\right) = \sum _{i=0}^{s-2} \sum _{x=0}^{n_{i+1}} \mu _i \pi (S_{i}(x, n))+ \sum _{x=0}^{\infty } \mu _{s-1} \pi (S_{s-1}(x, n)). \end{aligned}$$
(3.2)

For the case \(n_0>0\), it is readily verified that the balance equation is as follows:

$$\begin{aligned} \pi (n)\left( \lambda +\sum _{i=0}^{s-1}\mu _i\right) = \lambda \pi (n-e_{0}). \end{aligned}$$
(3.3)

We next determine the steady-state distribution of the Markov chain X.

Theorem 3.1

The steady-state probability distribution of the continuous-time Markov chain X defined above is

$$\begin{aligned} \pi (n)= \prod _{i=0}^{s-1} \left( \frac{\lambda }{\lambda + \bar{\mu }_i} \right) ^{n_i} \prod _{i=0}^{s-1} \frac{ \bar{\mu }_i}{\lambda +\bar{\mu }_i}, \end{aligned}$$
(3.4)

where \(n_i \ge 0\) for \(0 \le i \le s-1\).

Proof

First, it is readily verified that (3.4) satisfies (3.3) for \(n_0>0\).

For \(n_0=0\), we use induction on s to prove that (3.4) satisfies (3.2). As a base case, we consider \(s=1\). For \(s=1\), by observing that in this case \(\bar{\mu }_0 =\mu _0\), (3.2) reduces to

$$\begin{aligned} \pi (0) (\lambda +\mu _0)&= \mu _0 \sum _{x=0}^{\infty } \pi (S_{0}(x, n)) = \mu _0 \sum _{x=0}^{\infty } \pi (x), \end{aligned}$$
(3.5)

which is clearly satisfied by the geometric distribution (3.4).

Before considering the general case \(s>1\), for clarity, observe that, using (3.4), for \(0 \le i \le s-1\),

$$\begin{aligned} \pi (S_{i}(x, n))= & {} \pi (n_1, \ldots , n_i, x, n_{i+1}-x, n_{i+2}, \ldots , n_{s-1}) \nonumber \\&= \prod _{j=0}^{i-1} \left( \frac{\lambda }{\lambda + \bar{\mu }_j} \right) ^{n_{j+1}} \left( \frac{\lambda }{\lambda + \bar{\mu }_i} \right) ^{x} \left( \frac{\lambda }{\lambda + \bar{\mu }_{i+1}} \right) ^{n_{i+1}-x} \nonumber \\&\quad \cdot \prod _{j=i+2}^{s-1} \left( \frac{\lambda }{\lambda + \bar{\mu }_j} \right) ^{n_j} \prod _{i=0}^{s-1} \frac{ \bar{\mu }_i}{\lambda +\bar{\mu }_i}, \end{aligned}$$
(3.6)

where we note that the exponent of the first i terms is \(n_{j+1}\).

We now consider the general case \(s>1\). First, we consider (3.2) for the (\(s-1\))-dimensional system with service rates \(\mu _0, \mu _1, \dots , \mu _{s-3}, \mu _{s-2}+ \mu _{s-1}\). Note that \(\bar{\mu }_{s-2}=\mu _{s-2}+ \bar{\mu }_{s-1}\). We assume that (3.2) for this \((s-1)\)-dimensional system has the solution provided in (3.4). Based on this induction hypothesis, we will show that  (3.2) for an s-dimensional system has the solution provided in (3.4).

Now, writing (3.2) for this \((s-1)\)-dimensional system in detail with the product-form steady-state distribution according to (3.4) gives

$$\begin{aligned}&\prod _{i=0}^{s-2}\left( \frac{\lambda }{\lambda +\bar{\mu }_i}\right) ^{n_i}\left( \lambda +\bar{\mu }_0\right) \nonumber \\&\quad = \sum _{i=0}^{s-3}\sum _{x=0}^{n_{i+1}}\mu _i \prod _{j=0}^{i-1}\left( \frac{\lambda }{\lambda +\bar{\mu }_j}\right) ^{n_{j+1}} \left( \frac{\lambda }{\lambda +\bar{\mu }_i}\right) ^x \left( \frac{\lambda }{\lambda +\bar{\mu }_{i+1}}\right) ^{n_{i+1}-x}\prod _{j=i+2}^{s-2} \left( \frac{\lambda }{\lambda +\bar{\mu }_j}\right) ^{n_j} \nonumber \\&\qquad +\;\bar{\mu }_{s-2}\sum _{x=0}^\infty \prod _{i=0}^{s-3}\left( \frac{\lambda }{\lambda +\bar{\mu }_i}\right) ^{n_{i+1}}\left( \frac{\lambda }{\lambda +\bar{\mu }_{s-2}}\right) ^{x}. \end{aligned}$$
(3.7)

Note that in both sides of (3.7), the constant \(\prod _{i=0}^{s-2} \frac{ \bar{\mu }_i}{\lambda +\bar{\mu }_i}\) is cancelled.

We next show that (3.2) has the solution provided in (3.4) for an s-dimensional system. Let \(\gamma _{s} = \prod _{i=0}^{s-1} \frac{ \bar{\mu }_i}{\lambda +\bar{\mu }_i}\). Multiplying all terms in (3.7) with \((\lambda /(\lambda +\bar{\mu }_{s-1}))^{n_{s-1}} \gamma _s\), and using that \(\bar{\mu }_{s-2} \sum \limits _{x=0}^\infty \left( \frac{\lambda }{\lambda +\mu _{s-2}}\right) ^x = \lambda + \bar{\mu }_{s-2}\), gives

$$\begin{aligned} \pi (n)\left( \lambda +\bar{\mu }_0\right)&= \sum _{i=0}^{s-3}\sum _{x=0}^{n_{i+1}}\mu _i\pi (S_{i}(x, n)) \nonumber \\&\quad + (\lambda +\bar{\mu }_{s-2})\prod _{i=0}^{s-3}\left( \frac{\lambda }{\lambda +\bar{\mu }_i}\right) ^{n_{i+1}}\left( \frac{\lambda }{\lambda +\bar{\mu }_{s-1}}\right) ^{n_{s-1}} \gamma _{s}. \end{aligned}$$
(3.8)

Note that, in (3.8), n is of length s. It remains to show that the second term of the right-hand side of (3.8) equals

$$\begin{aligned} (\lambda +\bar{\mu }_{s-2})\prod _{i=0}^{s-3}\left( \frac{\lambda }{\lambda +\bar{\mu }_i}\right) ^{n_{i+1}}\left( \frac{\lambda }{\lambda +\bar{\mu }_{s-1}}\right) ^{n_{s-1}} \gamma _s&=\mu _{s-2}\sum _{x=0}^{n_{s-1}}\pi (S_{s-2}(x, n)) \nonumber \\&\quad + \mu _{s-1}\sum _{x=0}^{\infty }\pi (S_{s-1}(x, n)). \end{aligned}$$
(3.9)

The first term on the right-hand side of (3.9) is

$$\begin{aligned} \mu _{s-2}\sum _{x=0}^{n_{s-1}}\pi (S_{s-2}(x, n))&= \prod _{i=0}^{s-3}\left( \frac{\lambda }{\lambda +\bar{\mu }_i}\right) ^{n_{i+1}}\left( \frac{\lambda }{\lambda +\bar{\mu }_{s-1}}\right) ^{n_{s-1}} \nonumber \\&\quad \cdot \left( \lambda +\bar{\mu }_{s-2}-\frac{\left( \lambda +\bar{\mu }_{s-1}\right) ^{n_{s-1}+1}}{\left( \lambda +\bar{\mu }_{s-2}\right) ^{n_{s-1}}}\right) \gamma _s, \end{aligned}$$
(3.10)

where we used that \(\mu _{s-2}=\bar{\mu }_{s-2}-\bar{\mu }_{s-1}\) and we have evaluated the geometric sum \(\displaystyle \sum \limits _{x=0}^{n_{s-1}} \left( \frac{\lambda + \bar{\mu }_{s-1}}{\lambda + \bar{\mu }_{s-2}}\right) ^x\).

Similarly, the second term on the right-hand side of (3.9) is

$$\begin{aligned} \mu _{s-1}\sum _{x=0}^{\infty }\pi (S_{s-1}(x, n)) =&\ \mu _{s-1}\prod _{i=0}^{s-2}\left( \frac{\lambda }{\lambda +\bar{\mu }_i}\right) ^{n_{i+1}} \sum _{x=0}^{\infty }\left( \frac{\lambda }{\lambda +\bar{\mu }_{s-1}}\right) ^{x} \gamma _s \nonumber \\ =&\ \prod _{i=0}^{s-2}\left( \frac{\lambda }{\lambda +\bar{\mu }_i}\right) ^{n_{i+1}}\left( \lambda +\bar{\mu }_{s-1}\right) \gamma _s, \end{aligned}$$
(3.11)

where in the last equation we used that \(\bar{\mu }_{s-1}=\mu _{s-1}\).

It is easy to verify that (3.9) follows from (3.10) and (3.11). The proof that (3.4) satisfies (3.2) now follows from (3.8) and (3.9). \(\square \)

From Little’s law we readily obtain that the expected waiting time for a customer in a system with s customer classes is

$$\begin{aligned} \sum _{i=0}^{s-1} 1/\bar{\mu }_i. \end{aligned}$$
(3.12)

From Theorem 3.1, we also readily obtain that the expected length of the busy period of the system is

$$\begin{aligned} \lambda ^{-1} \left( \left( \prod \limits _{i=0}^{s-1} \frac{ \bar{\mu }_i}{\lambda +\bar{\mu }_i} \right) ^{-1} - 1 \right) . \end{aligned}$$
(3.13)

4 Optimal assignment of service rates

Consider the system introduced in Sect. 2. We further assume that the total service rate \(\mu \) is distributed over \(\mu _i\), \(i=0,\ldots , s-1\), i.e., \(\mu = \mu _1 + \ldots + \mu _{s-1}\). In this section, we determine the service allocation that minimizes the expected waiting time, and the conditions to approximate such optimal allocations. The following lemma formalizes the intuitive fact that it is best to choose \(\mu _{s-1}\) as large as possible.

Lemma 4.1

The system with \(\mu _i=0\) for \(0 \le i < s-1\) and \(\mu _{s-1}=\mu \) minimizes the expected waiting time among all systems with the property that \(\mu _0 +\ldots + \mu _{s-1}= \mu \).

Proof

From (3.12), it immediately follows that the expected waiting time is minimized when all \(\bar{\mu }_i\) take their maximal value. As \(\bar{\mu }_0= \mu _0 +\ldots + \mu _{s-1}= \mu \), and \(\bar{\mu }_0 \ge \bar{\mu }_1 \ge \ldots \ge \bar{\mu }_{s-1}=\mu _{s-1}\), this maximum is attained when \(\bar{\mu }_0=\bar{\mu }_1=\ldots =\bar{\mu }_{s-1}=\mu \), which corresponds to the service rate assignment stated in the lemma. \(\square \)

Consider the optimal service rate assignment

$$\begin{aligned} \mu _i = {\left\{ \begin{array}{ll} 0,\quad &{}\text {if } 0\le i< s-1,\\ \mu ,\quad &{}\text {if } i=s-1. \end{array}\right. } \end{aligned}$$
(4.1)

From Lemma 4.1 it follows that the steady-state distribution \(\pi ^C\) of this system is as follows. Here, we used the superscript C to indicate that to achieve such an optimal rate assignment we would require central coordination.

Corollary 4.2

For \(n_i \ge 0\), \(0 \le i \le s-1\), the steady-state distribution of the system under the optimal service rate assignment is

$$\begin{aligned} \pi ^C(n)=\frac{\mu ^s}{(\lambda +\mu )^s} \prod _{i=0}^{s-1} \left( \frac{\lambda }{\lambda +\mu } \right) ^{n_i}, n \ne 0, \end{aligned}$$

with expected waiting time, denoted by \(W_s^C\),

$$\begin{aligned} \mathbb {E}[W_s^C] = s/\mu . \end{aligned}$$

We next determine the Hellinger distance [10] between a distribution \(\pi \), corresponding to a general system with \(\mu _i\) as defined in Sect. 2, and the optimal system \(\pi ^C\), as defined in Corollary 4.2. We denote the Hellinger distance between \(\pi _1\) and \(\pi _2\) by \(H(\pi _1, \pi _2)\), where

$$\begin{aligned} H(\pi _1, \pi _2) = \frac{1}{\sqrt{2}}\sqrt{\sum _n \left( \sqrt{\pi _1(n)}-\sqrt{\pi _2(n)} \right) ^2}. \end{aligned}$$

Also,

$$\begin{aligned} 1-H^2(\pi _1, \pi _2) = \sum _n \sqrt{\pi _1(n) \pi _2(n)}. \end{aligned}$$

The Hellinger distance \(H(\pi _1, \pi _2)\) and the total variation distance, denoted by \( \delta (\pi _1, \pi _2)\), satisfy

$$\begin{aligned} H^2(\pi _1, \pi _2) \le \delta (\pi _1, \pi _2) \le \sqrt{2} H(\pi _1, \pi _2). \end{aligned}$$

The maximum distance 1 between the two distributions is achieved when \(\pi _1\) assigns probability 0 to every set to which \(\pi _2\) assigns a positive probability, and vice versa.

From Theorem 3.1 and Corollary 4.2, it is readily verified that \(H(\pi , \pi ^C)\) is as follows:

Lemma 4.3

$$\begin{aligned} H(\pi , \pi ^C)&= \left( 1- \prod _{i=0}^{s-1} \frac{ \sqrt{\mu \bar{\mu }_i}}{\sqrt{(\lambda +\mu )(\lambda +\bar{\mu }_i)}-\lambda } \right) ^{1/2}. \end{aligned}$$

We next investigate under which conditions an arbitrary system can have a Hellinger distance approaching zero to the optimal system. To this end, consider the system introduced in Sect. 2, with s independent batch service processes at exponential rates \(\mu _0, \dots , \mu _{s-1}\). Assume \(\mu _i\) depends on s and N, so \(\mu _i = \nu _i(s,N)\), \(i=0,\ldots ,s-1\), where N is, for the moment, an arbitrary system parameter denoting the size of the WSN.

Using the fact that \(\bar{\mu }_i = \sum _{k=i}^{s-1} \mu _i\) and Lemma 4.3, the next result follows.

Lemma 4.4

For any \(\lambda >0\), \(\lim _{N \rightarrow \infty } H(\pi , \pi ^C) = 0\) iff \(\lim _{N \rightarrow \infty } \nu _i(s,N) = 0 \) for \(0 \le i < s-1\) and \(\lim _{N \rightarrow \infty } \nu _{s-1}(s,N)=\mu \).

Proof

Note that \(H(\pi , \pi ^C)\) is 0 only if the product in Lemma 4.3 tends to 1 in the limit. As for each \(i=0,\ldots ,s-1\) each term

$$\begin{aligned} \frac{ \sqrt{\mu \bar{\mu }_i}}{\sqrt{(\lambda +\mu )(\lambda +\bar{\mu }_i)}-\lambda } \le 1, \end{aligned}$$

the product tends to 1 only if each term individually tends to 1. By straightforward calculations it follows that \( \sqrt{\mu \bar{\mu }_i}/\sqrt{(\lambda +\mu )(\lambda +\bar{\mu }_i)}-\lambda = 1\) only if \(\lambda =0\) or \(\bar{\mu }_i=\mu \). Thus, \(H(\pi , \pi ^C) \rightarrow 0\) iff \(\bar{\mu }_i \rightarrow \mu \) for any \(i, 0 \le i \le s-1\). We next evaluate under which conditions \(\bar{\mu }_i \rightarrow \mu , \forall i\). For \(i=s-1\), it follows that \(\mu _{s-1} \rightarrow \mu \). For \(0 \le i < s-1\) this follows from the observation that \(\mu = \mu _0+\ldots +\mu _{s-1}= \bar{\mu }_0 \ge \bar{\mu }_1 \ge \ldots \ge \bar{\mu }_{s-1}=\mu \). \(\square \)

5 Applications in wireless sensor networks

In this section, we show that the problem of collecting a fixed number of sensor observations from a WSN to be able, for instance, to apply data fusion algorithms, can be modeled using the queueing system introduced in Sect. 2.

Consider a WSN consisting of N sensors. Clients arrive at the network according to a Poisson process at rate \(\lambda \) and need to obtain s observations from distinct sensors in order to apply a fusion algorithm. We assume that any set of s observations from distinct sensors suffices and that there is a one-to-one correspondence between sensors and observations, i.e, different sensors transmit different observations. The sensors broadcast their data, i.e., all clients receive the data of a sensor when it is transmitted. A transmission schedule determines which sensor transmits at which time. In the remainder of this section, we analyze two different scheduling strategies and their impact on the system’s performance. We also quantify the performance gap between the two schedules with respect to waiting time, for arbitrarily large WSNs.

First we show that the WSN described above can be modeled using the queueing system in Sect. 2.

Lemma 5.1

All clients that have obtained i different observations, \(0\le i\le s-1\), have the same set of observations. Moreover, the observations of the clients that have obtained i observations are a subset of the observations obtained by clients that have \(j>i\) observations.

Proof

Initially there are no clients in the network and the conditions are satisfied. The proof directly follows from an induction over the number of events by considering two possible events: i) arrival of a client and ii) transmission of an observation (which is useful to all or part of the clients in the system). \(\square \)

It follows from Lemma 5.1 that we can identify customers of class \(0\le i\le s-1\) in the queueing system with those clients that have obtained i different observations and that are waiting to collect \(s-i\) additional observations. Indeed, if customers of class i receive service (obtain a new observation), then also clients of classes \(0, 1, \dots , i-1\) receive service, since their observations form a subset of those of class i customers. It remains to quantify the values of the service rates \(\mu _0, \dots , \mu _{s-1}\). In the next two subsections, we will do this for two specific broadcasting schedules.

5.1 Decentralized broadcasting and optimal broadcasting

First, we consider a decentralized broadcasting schedule, D, where each sensor transmits independently of the other sensors at an exponential rate \(\mu ^D/N\). Note that the overall transmission rate of observations is \(\mu ^D\).

Lemma 5.2

Under a decentralized broadcasting schedule

$$\begin{aligned} \mu _i = {\left\{ \begin{array}{ll} \frac{\mu ^D}{N},\quad &{}\text {if } 0\le i< s-1,\\ \mu ^D\left( 1-\frac{s-1}{N}\right) ,\quad &{}\text {if } i=s-1. \end{array}\right. } \end{aligned}$$
(5.1)

Proof

For \(0\le i< s-1\), \(\mu _i\) is the rate at which all customers of classes \(0, \dots , i\), but no customers of classes \(i+1, \dots , s-1\), receive a new observation. From Lemma 5.1 it follows that this new observation must be exactly the one observation that has already been received by customers of class \(i+1\), but not by customers of class i. Thus, this rate corresponds to the rate at which one specific sensor is transmitting, which is \(\mu ^D/N\). If \(i=s-1\), all \(N-(s-1)\) observations that have not yet been received by customers of class \(s-1\) will cause them to increase their class. These observations are transmitted by \(N-(s-1)\) sensors that transmit independently at rate \(\mu ^D/N\). \(\square \)

From Theorem 3.1 and Lemma 5.2 it follows that the steady-state distribution of the system under the D schedule is as follows:

Corollary 5.3

For \(n_i \ge 0\), \(0 \le i \le s-1\), the steady-state distribution of the system under the D schedule is

$$\begin{aligned} \pi ^D(n)= \prod _{i=0}^{s-1} \left( \frac{\lambda }{\lambda +\mu ^D (1-i/N)} \right) ^{n_i} \prod _{i=0}^{s-1} \frac{ \mu ^D (1-i/N)}{\lambda +\mu ^D (1-i/N)}, \end{aligned}$$

with expected waiting time, denoted by \(\mathbb {E}[W_s^D]\),

$$\begin{aligned} \sum _{i=0}^{s-1} (\mu ^D(1-i/N))^{-1}. \end{aligned}$$

Next we consider the following centralized broadcasting schedule C: at an exponential rate \(\mu ^C\) an observation is broadcast from a sensor whose observation causes all clients in the system to increase their class, i.e, the observation is broadcast by a sensor that has not transmitted its observation to any of the clients present in the network. One way to achieve an optimal schedule is to follow a round-robin schedule, in which the N sensors are scheduled sequentially in a cyclic way. Another way is to keep track of the sensors that have broadcast observations to the customers present in the system and not schedule these sensors for transmission. As discussed in Sect. 4, we have

$$\begin{aligned} \mu _i = {\left\{ \begin{array}{ll} 0,\quad &{}\text {if } 0\le i< s-1,\\ \mu ^C,\quad &{}\text {if } i=s-1. \end{array}\right. } \end{aligned}$$
(5.2)

From Lemma 4.3, Lemma 5.2 and (5.2) the next corollary follows.

Corollary 5.4

If \(\mu ^D= \mu ^C\), then

$$\begin{aligned} H(\pi ^D, \pi ^C)&= \left( 1- \prod _{i=0}^{s-1} \frac{\mu \sqrt{1-i/N}}{\sqrt{(\lambda +\mu )(\lambda +\mu (1-i/N))}-\lambda } \right) ^{1/2}. \end{aligned}$$

From Corollary 5.4, we readily have that for \(N \rightarrow \infty \), \(H(\pi ^D, \pi ^C)\rightarrow 0\).

Fig. 2
figure 2

\(H(\pi ^D, \pi ^C)\), \(s=10\)

Full size image

Figure 2 shows \(H(\pi ^D, \pi ^C)\) for finite N. Under the parameters considered, the distance \(H(\pi ^D, \pi ^C)\) rapidly decreases as a function of the network size N.

Clearly, when \(\mu ^D= \mu ^C\) it follows from the results of Sect. 4 that the decentralized schedule D is asymptotically optimal in the sense that, for \(i=0, \ldots , s-2\), \(\lim _{N \rightarrow \infty } \mu _i^{D} = 0\) and \(\lim _{N \rightarrow \infty } \mu _i^{D} = \mu ^C\). However, even when \(\mu ^D \ne \mu ^C\) we next quantify the performance penalty that occurs when we still demand \(\mathbb {E}[W_s^D]=\mathbb {E}[W_s^C]\), i.e., we quantify the additional amount of resources (in terms of the total transmission rate) that needs to be spent such that the performance of the decentralized schedule meets the performance of the centralized schedule in terms of waiting time.

Theorem 5.5

If \(\mu ^D = \gamma (s,N)\mu ^C\), where

$$\begin{aligned} \gamma (s, N) = s^{-1}\sum _{i=0}^{s-1}\left( 1-\frac{i}{N}\right) ^{-1}, \end{aligned}$$
(5.3)

then \(\mathbb {E}[W^D_s] = \mathbb {E}[W^C_s]\).

If we jointly let \(N\rightarrow \infty \) and \(s\rightarrow \infty \) while keeping \(N = \delta s\) then

$$\begin{aligned} \lim _{s,N\rightarrow \infty } \gamma (s,N) = -\delta \log \left( 1-\frac{1}{\delta }\right) , \end{aligned}$$
(5.4)

where the result follows from evaluating \(\lim _{s \rightarrow \infty } s^{-1} \int _{0}^{s-1} (1-x/(\delta s))^{-1} dx\).

Lastly, if s is kept constant while \(N\rightarrow \infty \), we have \(\lim _{N\rightarrow \infty } \gamma (s,N) = 1\).

6 Conclusions

We have introduced a new type of multi-class tandem network of queues with batch service and demonstrated that this system has a geometric product-form steady-state distribution. Moreover, we have shown that in order to have an optimal service allocation with respect to waiting time it is required to maximize the service rate of the last queue in the tandem network of queues considered. We have shown that our queueing model has applications in data collection in WSNs. As specific WSN applications, we considered optimal centralized and decentralized sensor broadcasting schedules. We have shown for which choices of service rates our queueing model is appropriate for the two types of schedules. We have also determined the steady-state distribution of the system under these two schedules. Lastly, we have characterized the performance gap between the two schedules with respect to waiting time, for arbitrarily large sensor networks.