Security enhancement of amplitude-shift keying-type asymmetric quantum communication systems

Abstract

Recently, we proposed an amplitude-shift keying asymmetric quantum communication system and evaluated its reliability when using the quasi-Bell state and two-mode squeezed vacuum state (TSVS) as an entangled light source. In this paper, we evaluate the security of the system and find that either security or reliability can be enhanced depending on the entangled light sources. We also consider an approach to enhance the security of the system as well as its reliability by increasing the number of signal modes. Interestingly, we find that the quasi-Bell state always performs better than the TSVS under certain conditions.

1 Introduction

Entanglement is an important resource for quantum protocols. Well-known protocols use entanglement such as the E91 quantum cryptographic protocol [1], superdense coding [2], and quantum teleportation [3]. Furthermore, quantum illumination [4] and quantum reading [5], which are quantum sensing protocols proposed in 2008 and 2011, respectively, have also attracted attention in recent years.

In the 2020s, on the basis of those quantum sensing protocols, we proposed an asymmetric quantum communication (AQC) system that employs an entanglement-based secure communication protocol. The system is expected to improve the reliability and security of asymmetric communication systems such as satellite-to-terrestrial, mobile device-to-base station, and Internet of Things (IoT) device-to-base station communications [6,7,8]. We also discussed its performance based on the error probability criterion when using two different modulation methods, amplitude-shift keying (ASK) and phase-shift keying (PSK), and demonstrated its superiority over the conventional method, which does not utilize entanglement. For the PSK-type AQC system, we introduced an optimal entangled state in a noiseless environment and investigated its error performance to evaluate the reliability and security when several quantum states are used in both noiseless and attenuated environments [7, 8]. By contrast, for the ASK-type AQC system, we also investigated its error performance to evaluate its reliability when several quantum states are used, but the evaluation of its security was reserved for future work [6].

An entangled cat state is generally called a quasi-Bell state [9], which was proposed by Hirota and Sasaki in 2001, and plays an important role in many quantum information processing tasks (e.g., [10,11,12,13,14,15]). In both the ASK-type and PSK-type AQC systems, the quasi-Bell state can also be used as the main entangled resource to improve performance [6,7,8]. In this paper, we focus on evaluating the security of the ASK-type AQC systems using the quasi-Bell state and another entangled state called a two-mode squeezed vacuum state (TSVS), which was mentioned as future work in [6]. This evaluation is based on the error probability criterion that was used in [7, 8]. We also consider an approach to enhance the security of these systems. By using the approach that increases the number of signal modes, we can significantly reduce the legitimate receiver’s error probability while keeping that of the eavesdropper at about 0.5. This fact indicates the enhancement of both security and reliability.

The paper is organized as follows: In Sect. 2, we briefly review the model of an ASK-type AQC system. In Sect. 3, we evaluate the security of this system when using the quasi-Bell state and TSVS. In Sect. 4, we consider an approach to enhance the security of the system. In Sect. 5, we present the discussion and conclusion of this paper.

2 Brief review of ASK-type AQC systems

The ASK-type AQC systems proposed in [6] consist of two sides, Alice and Bob. Alice, who represents satellites, mobile phones, IoT devices, and so on, plays the role of the sender, but she does not deliver any substance nor emit any energy such as light pulses in the system. In contrast, Bob, who represents ground base stations, mobile phone base stations, IoT base stations, and so on, plays the role of the receiver, and he does need to deliver some substance or emit some energy such as light pulses in the system.

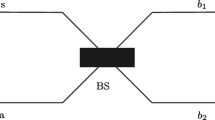
In fact, because of the difference in the transmission capabilities of Alice and Bob, which is caused by the differences in their physical resources, Alice is generally required to use a low power supply and is limited by low processing capacity. Therefore, there is a security problem for Alice when she transmits data to Bob: how to reduce energy costs and improve security against an eavesdropper, Eve, who may use a high power supply and have high processing capabilities, including a quantum computer. The ASK-type AQC systems employ a new approach to solving the problem by utilizing entangled states of light whose two modes are labeled S and A, unlike conventional methods such as lightweight cryptography, post-quantum cryptography, and conventional quantum cryptography. The protocol of such a system is given as follows (Fig. 1) [6]:

Fig. 1

Protocol of an ASK-type AQC system

• 1. Bob inputs the light corresponding to mode A directly into his detector.

• 2. Bob emits the light corresponding to mode S toward Alice, who operates two beam splitters with reflectivities of $R_0$ and $R_1$ $(R_0 < R_1)$, respectively; Alice then switches the two beam splitters to encode the binary information of “0” and “1.”

• 3. The light subsequently reflected from Alice, subject to a reflectivity of either $R_0$ or $R_1$, is then collected by Bob’s detector.

• 4. Bob decodes the binary information received at his detector by performing a joint measurement of both light beams.

Bob generates the entangled states of light as an information medium and carries the cost of its propagation. To encode the information that low-cost Alice wants to send to Bob, she only needs to reduce the light corresponding to mode S to different amplitudes. Note that $R_0=0$ is a special case in which Alice does not reflect light, and it corresponds to an on-off keying modulation. Moreover, because Eve—we assume that Eve and Bob have exactly the same receiving environment and capacity—cannot access the light corresponding to mode A, which remains concealed by Bob, there is a difference in the reception performance of Eve and Bob. This difference in reception performance creates the security of the ASK-type AQC systems. Note that energy attenuation caused by the environment has been included in this model. To discuss the security of the system, we focus on the difference in error probability when Eve obtains all of the light corresponding to mode S and when Bob obtains all of it. We consider that when the error probability of Eve is increased, the security of the system is increased. Moreover, when the error probability of Bob is decreased, the reliability of the system is increased.

3 Security evaluation

To evaluate the security of the system, we need to calculate the error probability when Eve exists. In the following, for Eve, we derive the error probabilities that occur when either the quasi-Bell state or the TSVS is used. The error probabilities of Bob have been presented in [6], and we present them again in Sect. 3.3. To evaluate the security of the systems, we also perform numerical calculations using the above and obtain the error performance.

3.1 Error probability of the AQC system using a quasi-Bell state

The quasi-Bell state, which is constructed by the coherent states $|\alpha \rangle$, is used as the main entangled resource in [6]. Following the results of that study, we clarified that of the two types of quasi-Bell state, the non-maximum quasi-Bell state and maximum quasi-Bell state, the latter offers an advantage over the former under most conditions. Therefore, a maximum quasi-Bell state is used in this paper and represented as the quantum states of the composite system SA as follows:

$$\begin{aligned} |\Psi \rangle _\textrm{SA} = h\left( |\alpha \rangle _\textrm{S}|\alpha \rangle _\textrm{A} - |-\alpha \rangle _\textrm{S}|-\alpha \rangle _\textrm{A}\right) , \end{aligned}$$

(1)

where

$$\begin{aligned} h= \frac{1}{\sqrt{2\left( 1 - \kappa ^2\right) }}, \; \; \; \; \; \kappa = \langle \alpha | -\alpha \rangle = \langle -\alpha | \alpha \rangle = \textrm{e}^{-2\left| \alpha \right| ^2}, \end{aligned}$$

(2)

and $\alpha$ is the complex amplitude of the coherent state. Note that the average number of photons in mode S is $\langle n \rangle _\textrm{QBS}= \left| \alpha \right| ^2 \coth ( 2\left| \alpha \right| ^2 )$, and $\inf \langle n \rangle _\textrm{QBS} = 0.5$.

To clarify the error probability of Eve when using the quasi-Bell state as an entangled resource, we consider a method to derive its analytical expression in the same way as the method in [6]. The method is explained below.

First, we describe the received quantum states eavesdropped by Eve in her detector, because Eve can discriminate the two quantum states $\{{\Psi }_\textrm{S}^{(\mathrm b)}\}$ corresponding to the two respective reflectivities $\{R_\textrm{b}\}$ to eavesdrop the binary information $b \in \{0,1\}$ encoded by Alice. The received quantum state (i.e., its density operator) before being eavesdropped by Eve can be represented by:

$$\begin{aligned} {\Psi }_\textrm{SA}^{(\textrm{b})}= & {} \,\textrm{Tr}\,_\textrm{E}\left\{ \bigl (\mathbb {U}_\textrm{SE}^{(R_\textrm{b})}\!\otimes \!\mathbb {I}_\textrm{A}\bigr ) \bigl (|\Psi \rangle _\textrm{SA}\langle \Psi | \!\otimes \! |0\rangle _\textrm{E}\langle 0|\bigr ) \bigl (\mathbb {U}_\textrm{SE}^{(R_\textrm{b})}\!\otimes \!\mathbb {I}_\textrm{A}\bigr )^{\dagger } \right\} \nonumber \\= & {} h^2 \left( |\sqrt{R_\textrm{b}}\alpha \rangle _\textrm{S} \langle \sqrt{R_\textrm{b}}\alpha | \!\otimes \! |\alpha \rangle _\textrm{A} \langle \alpha |-L_\textrm{b} |\sqrt{R_\textrm{b}}\alpha \rangle _\textrm{S} \langle -\sqrt{R_\textrm{b}}\alpha |\!\otimes \! |\alpha \rangle _\textrm{A} \langle -\alpha |\right. \nonumber \\{} & {} \left. -L_\textrm{b} |-\sqrt{R_\textrm{b}}\alpha \rangle _\textrm{S} \langle \sqrt{R_\textrm{b}}\alpha |\!\otimes \! |-\alpha \rangle _\textrm{A} \langle \alpha |+ |-\sqrt{R_\textrm{b}}\alpha \rangle _\textrm{S} \langle -\sqrt{R_\textrm{b}}\alpha |\!\otimes \! |-\alpha \rangle _\textrm{A} \langle -\alpha |\right) , \nonumber \\ \end{aligned}$$

(3)

where

$$\begin{aligned} L_\textrm{b}=\textrm{e}^{-2(1-R_\textrm{b})|\alpha |^2}, \end{aligned}$$

(4)

$|0\rangle _\textrm{E}$ is the vacuum state in environment mode E, and $\mathbb {I}_\textrm{A}$ is the identity operator in mode A. Moreover, $\mathbb {U}_\textrm{SE}^{(R_\textrm{b})}$ is the unitary operator on modes S and E, and it describes the interaction between modes S and E subject to the energy attenuation corresponding to Alice’s beam splitter with $R_\textrm{b}$. Since Eve cannot access mode A, which is concealed by Bob, she can only eavesdrop on mode S and obtain the received quantum state ${\Psi }_\textrm{S}^{(\mathrm b)}$, which is expressed as follows:

$$\begin{aligned} {\Psi }_\textrm{S}^{(\mathrm b)}=\,\textrm{Tr}\,_\textrm{A} {\Psi }_\textrm{SA}^{(\mathrm b)}&=h^2\left( |\sqrt{R_\textrm{b}}\alpha \rangle _\textrm{S} \langle \sqrt{R_\textrm{b}}\alpha | -L_\textrm{b}\kappa |\sqrt{R_\textrm{b}}\alpha \rangle _\textrm{S} \langle -\sqrt{R_\textrm{b}}\alpha | \right. \nonumber \\&\;\;\;\;\;\; \; \; \left. -L_\textrm{b} \kappa |-\sqrt{R_\textrm{b}}\alpha \rangle _\textrm{S} \langle \sqrt{R_\textrm{b}}\alpha | + |-\sqrt{R_\textrm{b}}\alpha \rangle _\textrm{S} \langle -\sqrt{R_\textrm{b}}\alpha | \right) . \end{aligned}$$

(5)

Then, we express the received quantum state ${\Psi }_\textrm{S}^{(\mathrm b)}$ using a finite matrix, because the quasi-Bell state constructed by the coherent state $|\alpha \rangle =\sum _{n=0}^{\infty }\frac{\alpha ^n}{\sqrt{n!}}\textrm{e}^{-\frac{1}{2}|\alpha |^2}|n\rangle$ with number state $|n\rangle$ is an infinite-dimensional vector, which is difficult to use in calculation. Observing Eq. (3) reveals that the two received quantum states $\{{\Psi }_\textrm{S}^{(\mathrm b)}\}$ consist of the following four coherent states:

$$\begin{aligned} \{ |-\sqrt{R_0}\alpha \rangle _\textrm{S}, |\sqrt{R_0}\alpha \rangle _\textrm{S}, |-\sqrt{R_1}\alpha \rangle _\textrm{S}, |\sqrt{R_1}\alpha \rangle _\textrm{S}\} . \end{aligned}$$

Taking the four-dimensional subspace of a Hilbert space that is spanned by the four coherent states, a convenient orthonormal basis can be chosen from the measurement state of the square-root measurement (SRM) [16]. One of the merits of using the SRM is that a four-dimensional vector representation of these coherent states in the four-dimensional subspace can be obtained from the square root of their Gram matrix. Then, the four-dimensional vector representation of these coherent states is given as follows:

$$\begin{aligned}&|-\sqrt{R_0}\alpha \rangle _\textrm{S}=\left[ \begin{array}{c} \gamma _{11}^{(+)} \\ \gamma _{11}^{(-)}\\ \gamma _{13}^{(+)}\\ \gamma _{13}^{(-)} \end{array} \right] , \;\; |\sqrt{R_0}\alpha \rangle _\textrm{S}=\left[ \begin{array}{c} \gamma _{11}^{(-)} \\ \gamma _{11}^{(+)}\\ \gamma _{13}^{(-)}\\ \gamma _{13}^{(+)} \end{array} \right] , \nonumber \\&|-\sqrt{R_1}\alpha \rangle _\textrm{S}=\left[ \begin{array}{c} \gamma _{13}^{(+)} \\ \gamma _{13}^{(-)}\\ \gamma _{33}^{(+)}\\ \gamma _{33}^{(-)} \end{array} \right] , \;\; |\sqrt{R_1}\alpha \rangle _\textrm{S}=\left[ \begin{array}{c} \gamma _{13}^{(-)} \\ \gamma _{13}^{(+)}\\ \gamma _{33}^{(-)}\\ \gamma _{33}^{(+)} \end{array} \right] , \end{aligned}$$

(6)

where the details can be found in Appx. A, and the expression of the received quantum state ${\Psi }_\textrm{S}^{(\mathrm b)}$ can be obtained by substituting Eq. (6) into Eq. (5). To derive an analytical expression of the error probability, we prepare an expression of the difference between the two received quantum states, ${\Psi }_\textrm{S}^{(\mathrm 0)}-{\Psi }_\textrm{S}^{(\mathrm 1)}(=:U^\mathrm{(QBS)})$, which is expressed as

$$\begin{aligned} U^\mathrm{(QBS)}=h^2\left[ \begin{array}{cccc} A &{} B &{} C &{} D \\ B &{}A &{} D &{} C \\ C &{} D &{} E &{} F \\ D &{} C &{} F &{} E \end{array} \right] , \end{aligned}$$

(7)

where

$$\begin{aligned} A&={\gamma _{11}^{(+)}}^2-2L_0 \kappa {\gamma _{11}^{(+)}}{\gamma _{11}^{(-)}}+{\gamma _{11}^{(-)}}^2-{\gamma _{13}^{(+)}}^2+2L_1\kappa {\gamma _{13}^{(+)}}{\gamma _{13}^{(-)}}-{\gamma _{13}^{(-)}}^2, \end{aligned}$$

(8)

$$\begin{aligned} B&=2{\gamma _{11}^{(+)}}{\gamma _{11}^{(-)}}-L_0\kappa ({\gamma _{11}^{(+)}}^2+{\gamma _{11}^{(-)}}^2)-2{\gamma _{13}^{(+)}}{\gamma _{13}^{(-)}}+L_1\kappa ({\gamma _{13}^{(+)}}^2+{\gamma _{13}^{(-)}}^2), \end{aligned}$$

(9)

$$\begin{aligned} C&=-L_0\kappa {\gamma _{11}^{(-)}}{\gamma _{13}^{(+)}}+{\gamma _{11}^{(-)}}{\gamma _{13}^{(-)}}+{\gamma _{11}^{(+)}}({\gamma _{13}^{(+)}}-L_0\kappa {\gamma _{13}^{(-)}})\nonumber \\&\;\;\;\;\;\;\;\;\;\;\; -{\gamma _{13}^{(+)}}{\gamma _{33}^{(+)}}+L_1\kappa {\gamma _{13}^{(-)}}{\gamma _{33}^{(+)}}+L_1\kappa {\gamma _{13}^{(+)}}{\gamma _{33}^{(-)}}-{\gamma _{13}^{(-)}}{\gamma _{33}^{(-)}}, \end{aligned}$$

(10)

$$\begin{aligned} D&={\gamma _{11}^{(-)}}{\gamma _{13}^{(+)}}+{\gamma _{11}^{(+)}}{\gamma _{13}^{(-)}}-L_0\kappa ({\gamma _{11}^{(+)}}{\gamma _{13}^{(+)}}+{\gamma _{11}^{(-)}}{\gamma _{13}^{(-)}})\nonumber \\&\;\;\;\;\;\;\;\;\;\;\;+L_1\kappa {\gamma _{13}^{(+)}}{\gamma _{33}^{(+)}}-{\gamma _{13}^{(-)}}{\gamma _{33}^{(+)}}-{\gamma _{13}^{(+)}}{\gamma _{33}^{(-)}}+L_1\kappa {\gamma _{13}^{(-)}}{\gamma _{33}^{(-)}},\end{aligned}$$

(11)

$$\begin{aligned} E&={\gamma _{13}^{(+)}}^2-2L_0\kappa {\gamma _{13}^{(+)}}{\gamma _{13}^{(-)}}+{\gamma _{13}^{(-)}}^2-{\gamma _{33}^{(+)}}^2+2L_1\kappa {\gamma _{33}^{(+)}}{\gamma _{33}^{(-)}}-{\gamma _{33}^{(-)}}^2,\end{aligned}$$

(12)

$$\begin{aligned} F&=2{\gamma _{13}^{(+)}}{\gamma _{13}^{(-)}}-L_0\kappa ({\gamma _{13}^{(+)}}^2+{\gamma _{13}^{(-)}}^2)-2{\gamma _{33}^{(+)}}{\gamma _{33}^{(-)}}+L_1\kappa ({\gamma _{33}^{(+)}}^2+{\gamma _{33}^{(-)}}^2).\nonumber \\ \end{aligned}$$

(13)

Finally, we derive the analytical expression of the error probability. In this paper, we assumed that Alice sends the binary information with equal a priori probabilities, and thus, the error probability when discriminating the two received quantum states with an optimum quantum measurement for Eve is given as follows [17]:

$$\begin{aligned} P_\textrm{e}=\frac{1}{2}\left( 1-\sum _{\lambda _{i}>0}\lambda _{i}\right) , \end{aligned}$$

(14)

where $\{\lambda _i\}$ denotes the eigenvalues of the difference between these quantum states. The eigenvalues can be obtained immediately by a spectral decomposition of $U^\mathrm{(QBS)}$ and are given as follows:

$$\begin{aligned} \lambda _{\pm }^{(+)}&=\frac{h^2}{2}\left\{ A+B+E+F\pm \sqrt{(A+B-E-F)^2+4(C+D)^2}\right\} ,\end{aligned}$$

(15)

$$\begin{aligned} \lambda _{\pm }^{(-)}&=\frac{h^2}{2}\left\{ A-B+E-F\pm \sqrt{(A-B-E+F)^2+4(C-D)^2}\right\} . \end{aligned}$$

(16)

We confirm directly that only two of the eigenvalues $\{\lambda _{+}^{(\pm )}\}$ are greater than 0. Substituting $\{\lambda _{+}^{(\pm )}\}$ into Eq. (14), we have the analytical expression of the error probability

$$\begin{aligned} P_\textrm{Eve}^\mathrm{(QBS)}=\frac{1}{4}\left\{ 2-h^2 \left( 2d L_1 \kappa -2a L_0 \kappa +\sqrt{\Upsilon ^{(+)}} +\sqrt{\Upsilon ^{(-)}} \right) \right\} , \end{aligned}$$

(17)

where

$$\begin{aligned} \Upsilon ^{(\pm )}=\{\kappa (a L_0+d L_1\pm L_0\pm L_1)\mp a\mp d-2\}^2-4 (b\pm c)^2 (\kappa L_0\mp 1) (\kappa L_1\mp 1), \end{aligned}$$

(18)

and

$$\begin{aligned} a=\textrm{e}^{-2 R_0 |\alpha |^2}, \;\;\; b=\textrm{e}^{\sqrt{R_0 R_1}|\alpha |^2-\frac{1}{2}|\alpha |^2(R_0+R_1)}, \nonumber \\ c=\textrm{e}^{-\sqrt{R_0 R_1}|\alpha |^2-\frac{1}{2}|\alpha |^2(R_0+R_1)}, \;\;\; d=\textrm{e}^{-2 R_1 |\alpha |^2}. \end{aligned}$$

(19)

3.2 Error probability of an AQC system using the TSVS

The TSVS is another important entangled state not only in an ASK-type AQC system but in various quantum information processing tasks (e.g., [5, 18,19,20]). The TSVS can be represented by:

$$\begin{aligned} |\psi \rangle _\textrm{SA}=\sum _{n=0}^{\infty }\sqrt{\frac{N_\textrm{S}^n}{(N_\textrm{S}+1)^{n+1}}}|n\rangle _\textrm{S}|n\rangle _\textrm{A}, \end{aligned}$$

(20)

where $\langle n \rangle _\textrm{TSVS}=N_{\textrm{S}}{}$ represents the average number of photons in mode S. In this paper, we also consider an ASK-type AQC system when using the TSVS as an entangled resource, and the error probability of Eve is required for the calculation and evaluation.

Similar to the approach in Sect. 3.1, we first describe the received quantum states eavesdropped by Eve in her detector. The received quantum state before being eavesdropped by Eve can be represented by:

$$\begin{aligned} \psi _\textrm{SA}^{(\textrm{b})}=\sum _{k=0}^{\infty }\left\{ \bigl (\mathbb {E}_k^{(R_\textrm{b})}\bigr )_\textrm{S}\otimes \mathbb {I}_\textrm{A} \right\} |\psi \rangle _\textrm{SA}\langle \psi | \left\{ \bigl (\mathbb {E}_k^{(R_\textrm{b})}\bigr )_\textrm{S}\otimes \mathbb {I}_\textrm{A} \right\} ^{\dag }, \end{aligned}$$

(21)

where

$$\begin{aligned} \mathbb {E}_k^{(R_\textrm{b})}=\sum _{n}\sqrt{ \left( \begin{array}{c}n\\ k \end{array} \right) }\sqrt{R_\textrm{b}^{n-k}(1-R_\textrm{b})^k}|n-k \rangle \langle n | \end{aligned}$$

(22)

is the Kraus operator [21] for the attenuation channel with respect to the energy transmissivity $R_\textrm{b}$. Since Eve cannot access mode A, which is hidden by Bob, she can only eavesdrop on mode S and obtain the received quantum state $\psi _\textrm{S}^{(\textrm{b})}$, which is expressed as follows:

$$\begin{aligned} \psi _\textrm{S}^{(\textrm{b})}=\,\textrm{Tr}\,_\textrm{A} \psi _\textrm{SA}^{(\textrm{b})}=\sum _{ l=0}^{\infty }\sum _{k=0}^{l}\frac{N_{\textrm{S}}{}^l}{(N_{\textrm{S}}{}+1)^{l+1}}\left( \begin{array}{c}l\\ k \end{array} \right) R_\textrm{b}^{l-k} (1-R_\textrm{b})^k |l-k \rangle _\textrm{S} \langle l-k |. \end{aligned}$$

(23)

Then, we prepare the expression of the difference between the two received quantum states, ${\psi }_\textrm{S}^{(\mathrm 0)}-{\psi }_\textrm{S}^{(\mathrm 1)}(=:U^\mathrm{(TSVS)})$, which is expressed as a diagonal matrix

$$\begin{aligned} U^\mathrm{(TSVS)}&=\sum _{ l=0}^{ \infty }\sum _{k=0}^{l}\frac{N_{\textrm{S}}{}^l}{(N_{\textrm{S}}{}+1)^{l+1}}\left( \begin{array}{c}l\\ k \end{array} \right) \nonumber \\&\; \; \; \; \; \; \; \; \; \times \left\{ R_\textrm{0}^{l-k} (1-R_\textrm{0})^k -R_\textrm{1}^{l-k} (1-R_\textrm{1})^k \right\} |l-k \rangle _\textrm{S} \langle l-k | \nonumber \\&:=\textrm{diag} (\lambda _1,\lambda _2,\cdots ,\lambda _m), \end{aligned}$$

(24)

where $m=1,2,\ldots ,\infty$. Finally, substituting $\{\lambda _m\}$ into Eq. (14), we have the expression of the error probability

$$\begin{aligned} P_\textrm{Eve}^\mathrm{(TSVS)}=\frac{1}{2}\left( 1-\sum _{\lambda _m>0} \lambda _m \right) . \end{aligned}$$

(25)

Because the diagonal matrix is an infinite matrix, we calculate $\{\lambda _m\}$ using a suitable finite value of m based on a conventional numerical calculation method (e.g., [6, 14, 22]).

3.3 Error performance of the ASK-type AQC systems

In this subsection, we evaluate the security of the ASK-type AQC systems using the quasi-Bell state and TSVS. We also compare these with an asymmetric classical communication (ACC) system that does not use entanglement.

We have derived the error probabilities Eqs. (17) and (25) of Eve when using the quasi-Bell state and TSVS, respectively, in the above subsections. To calculate the error probabilities of Bob, we introduce the results of [6] when the quasi-Bell state is used and that of [19] when the TSVS is used. As given in [6], the error probability $P_\textrm{Bob}^{(\mathrm QBS)}$ when the quasi-Bell state is used is expressed as

$$\begin{aligned} P_\textrm{Bob}^{(\mathrm QBS)}=\frac{1}{2}\left\{ 1\!-\!\frac{1}{2} \left( \sqrt{{\Lambda _\textrm{N}^{(+)}}^2\!-\!4 \Xi _\textrm{N}^{(+)}} \!-\!\Lambda _\textrm{N}^{(+)} \right) - \frac{1}{2} \left( \sqrt{{\Lambda _\textrm{N}^{(-)}}^2\!-\!4\Xi _\textrm{N}^{(-)}}\!-\!\Lambda _\textrm{N}^{(-)} \right) \right\} , \end{aligned}$$

(26)

where

$$\begin{aligned} \Lambda _\textrm{N}^{(\pm )}&=-\frac{ (L_0\mp 1)(a\kappa \mp 1)- (1\mp L_1)(1 \mp d\kappa ) }{2(\kappa ^2+1)}, \end{aligned}$$

(27)

$$\begin{aligned} \Xi _\textrm{N}^{(\pm )}&=-\frac{ (L_0 \mp 1)(L_1 \mp 1) \{ (a\kappa \mp 1 ) (d\kappa \mp 1) -(b\mp c\kappa )^2 \} }{4(\kappa ^2+1)^2}. \end{aligned}$$

(28)

The error probability $P_\textrm{Bob}^{(\mathrm TSVS)}$ when the TSVS is used is difficult to calculate. In this case, the upper bound $P_\textrm{Bob, UB}^{(\mathrm TSVS)}$ and lower bound $P_\textrm{Bob, LB}^{(\mathrm TSVS)}$ on error probability $P_\textrm{Bob}^{(\mathrm TSVS)}$ are generally used, as follows [19]:

$$\begin{aligned} P_\textrm{Bob, LB}^{(\mathrm TSVS)}&= \frac{1}{2} \left[ 1-\sqrt{1-\left\{ \left( 1-\sqrt{R_0R_1}-\sqrt{(1-R_0)(1-R_1)}\right) N_{\textrm{S}}{}+1 \right\} ^{-2}}\right] , \end{aligned}$$

(29)

$$\begin{aligned} P_\textrm{Bob, UB}^{(\mathrm TSVS)}&= {\left\{ \begin{array}{ll} \frac{1}{2} \left\{ \left( 1-\sqrt{R_0}\right) N_{\textrm{S}}{}+1\right\} ^{-2}&{} (R_1=1) \\ \frac{1}{2} \left( \Sigma \sigma ^z-\Theta \theta ^z \right) ^{-1} &{} (R_1 \ne 1) \end{array}\right. }, \end{aligned}$$

(30)

where

$$\begin{aligned} \sigma&=\frac{(1-R_0)N_{\textrm{S}}{}+1}{(1-R_1)N_{\textrm{S}}{}+1}, \end{aligned}$$

(31)

$$\begin{aligned} \theta&=\frac{1-R_0}{1-R_1}, \end{aligned}$$

(32)

$$\begin{aligned} \Sigma&=\frac{\left\{ \left( 1-\sqrt{R_0R_1}\right) N_{\textrm{S}}{}+1\right\} ^2}{(1-R_0)N_{\textrm{S}}{}+1}, \end{aligned}$$

(33)

$$\begin{aligned} \Theta&=(1-R_1)N_{\textrm{S}}{}, \end{aligned}$$

(34)

$$\begin{aligned} z&={\left\{ \begin{array}{ll} 0&{} \left( \frac{\theta ^{\Theta }}{ \sigma ^{\Sigma }} \ge 1\right) \\ 1&{} \left( \frac{\theta ^{\Theta }}{ \sigma ^{\Sigma }}<1 \mathrm{\;\;\; and \;\;\;} \xi \ge 1 \right) \\ \xi &{} \left( \frac{\theta ^{\Theta }}{ \sigma ^{\Sigma }}<1 \mathrm{\;\;\; and \;\;\;} \xi < 1 \right) \end{array}\right. }, \end{aligned}$$

(35)

$$\begin{aligned} \xi&=\frac{\ln \frac{\ln \sigma ^{\Sigma }}{\ln \theta ^{\Theta }}}{\ln \frac{\theta }{\sigma }}. \end{aligned}$$

(36)

In the case of the ACC system, we assume that any classical light sources and measurement approaches are allowed, and the lower bound $P_\textrm{Cla}$ of its error probability is given by [5] as follows:

$$\begin{aligned} P_\textrm{Cla}=\frac{1-\sqrt{1-\textrm{e}^{- N_\textrm{C}(\sqrt{R_1}-\sqrt{R_0})^2 }}}{2}, \end{aligned}$$

(37)

where the average number of photons is $\langle n \rangle _\textrm{Cla}=N_\textrm{C}$. Because the ACC system has no mode A, Eq. (37) represents the performance limitations of both Bob and Eve.

Fig. 2

Error probabilities with respect to the average number of photons $\langle n \rangle$ when $R_0=0.5$ and $R_1=1$

Fig. 3

Error probabilities with respect to the average number of photons $\langle n \rangle$ when $R_0=0.3$ and $R_1=0.6$

Fig. 4

Error probabilities with respect to the average number of photons $\langle n \rangle$ when $R_0=0.2$ and $R_1=0.8$

Fig. 5

Error probabilities with respect to the average number of photons $\langle n \rangle$ when $R_0=0$ and $R_1=0.3$

Figures 2, 3, 4, and 5 show the error probabilities obtained when the average number of photons $\langle n \rangle$(:=$\langle n \rangle _\textrm{QBS}=\langle n \rangle _\textrm{TSVS}=\langle n \rangle _\textrm{Cla}$) is varied from 0.5 to 100, for which the reflectivities $\{R_0, R_1\}$ were fixed at $\{ 0.5, 1\}$, $\{0.3, 0.6\}$, $\{ 0.2, 0.8\}$, and $\{ 0,0.3\}$, respectively. The red dot-dash line, dotted line, and dashed line indicate the error probability $P_\textrm{Eve}^\mathrm{(TSVS)}$ for Eve, the upper bound $P_\textrm{Bob, UB}^{(\mathrm TSVS)}$ for Bob, and the lower bound $P_\textrm{Bob, LB}^{(\mathrm TSVS)}$ for Bob, respectively, when the AQC system with the TSVS is used. The blue dot-dash line and dashed line indicate the error probabilities $P_\textrm{Eve}^\mathrm{(QBS)}$ for Eve and $P_\textrm{Bob}^\mathrm{(QBS)}$ for Bob, respectively, when the AQC system with the quasi-Bell state is used. The green solid line represents the lower bound on the error probability $P_\textrm{Cla}$ for both Bob and Eve when the ACC system allows any classical light source.

Figures 2, 3, 4, and 5 show that the error probability of the AQC system using the quasi-Bell state improves rapidly as the average number of photons increases. Although in some cases such as $\{R_0, R_1\}=\{ 0.5, 1\}$, the error probability for Bob is slightly superior to that of Eve, we find that overall, the gap between these error probabilities is small and that Eve has almost the same reception performance as Bob. Moreover, because these error probabilities almost overlap with that of the ACC system allowing any classical light source, the performance, including the security and reliability, of the AQC system using the quasi-Bell state is almost the same as that of the ACC system. Therefore, we consider that these systems have high reliability but low security.

By contrast, the gap between the error probabilities for Bob and Eve when the AQC system uses the TSVS widens as the average number of photons increases. However, we find that the improvement of the error probability of Bob slows as the average number of photons increases, although the reception performance of Bob is superior to that of Eve. Therefore, compared with the AQC system using the quasi-Bell state, the system using the TSVS has higher security but lower reliability.

In the next section, we discuss an approach to enhance the security as well as reliability of the AQC systems.

4 Security enhancement

The results of Sect. 3.3 suggest that we need to consider an approach to enhance the security, i.e., widen the gap in the error probabilities of Bob and Eve. Many quantum information processing tasks such as those in [4, 5, 18, 19] have shown that using a large amount of the same quantum state signals, expressed as $\rho ^{\otimes M}:=\underbrace{\rho \otimes \cdots \otimes \rho }_{M}$, may improve performance for some quantum protocols. Note that M is the total number of signal modes and can be considered the signal bandwidth [5]. For the binary discrimination between $\rho _0^{\otimes M}$ and $\rho _1^{\otimes M}$ with equal a priori probabilities, which represent binary information “0” and “1,” respectively, the error probability with an optimum quantum measurement is difficult to calculate because a large composite Hilbert space is required. A common criterion for evaluating system performance in these cases is the quantum Chernoff bound [23], a mathematical method that obtains the upper bound on the error probability. In this section, in contrast to using $M=1$, as in the above section, we consider an approach that sets $M>1$ to enhance security. Therefore, the quantum Chernoff bound is an important criterion needed by Bob to evaluate his error probability with an upper bound. When using the quasi-Bell state, the upper bound represented by the quantum Chernoff bound on the error probability is expressed as:

$$\begin{aligned} P_{\textrm{Bob,UB},M}^{(\mathrm QBS)} := \frac{1}{2} \left\{ \min _{0\le s \le 1} \,\textrm{Tr}\,{\Psi _\textrm{SA}^{(1)}}^s {\Psi _\textrm{SA}^{(0)}}^{1-s}\right\} ^M, \end{aligned}$$

(38)

where $\Psi _\textrm{SA}^{(0)}$ and $\Psi _\textrm{SA}^{(1)}$ can be represented by an $8 \times 8$ matrix [6]. Moreover, when $R_0=0$, $\Psi _\textrm{SA}^{(0)}$ and $\Psi _\textrm{SA}^{(1)}$ can be represented by a $6 \times 6$ matrix [15]. Here, $R_1=1$ is known as a special case in which the minimum s is 0, and the upper bound can be expressed as:

$$\begin{aligned} \left. P_{\textrm{Bob,UB},M}^{(\mathrm QBS)} \right| _{R_1=1}= \frac{1}{2} \left\{ {}_\textrm{SA}\langle \Psi | \Psi _\textrm{SA}^{(0)} |\Psi \rangle _\textrm{SA} \right\} ^M= \frac{1}{2} \left\{ \frac{(1+L_0)(e-f\kappa )^2}{2(\kappa ^2-1)^2} \right\} ^M, \end{aligned}$$

(39)

where

$$\begin{aligned} e=\textrm{e}^{\sqrt{R_0}|\alpha |^2-\frac{1}{2}|\alpha |^2(1+R_0)}, \;\;\;\; f=\textrm{e}^{-\sqrt{R_0}|\alpha |^2-\frac{1}{2}|\alpha |^2(1+R_0)}. \end{aligned}$$

(40)

When using the TSVS, the upper bound on the error probability is given in [19], as follows:

$$\begin{aligned} P_{\textrm{Bob, UB},M}^{(\mathrm TSVS)}&= {\left\{ \begin{array}{ll} \frac{1}{2} \left\{ \left( 1-\sqrt{R_0}\right) N_{\textrm{S}}{}+1\right\} ^{-2M}&{} (R_1=1) \\ \frac{1}{2} \left( \Sigma \sigma ^z-\Theta \theta ^z \right) ^{-M} &{} (R_1 \ne 1) \end{array}\right. }, \end{aligned}$$

(41)

where $P_{\textrm{Bob, UB},M}^{(\mathrm TSVS)} |_{M=1}=P_{\textrm{Bob, UB}}^{(\mathrm TSVS)}$.

In addition, we also need a criterion for Eve to evaluate the lower bound on her error probability. Reference [24] derived a lower bound on the error probability for a binary discrimination problem, based on the Jozsa–Uhlmann fidelity [25, 26] and expressed as follows:

$$\begin{aligned} \frac{1}{2}\left[ 1-\sqrt{1-F(X,Y)}\right] \le P_\textrm{e}, \end{aligned}$$

(42)

where $F(X,Y)=(\,\textrm{Tr}\,\sqrt{\sqrt{X}Y\sqrt{X}})^2$ is the fidelity in terms of quantum states X and Y. However, for the binary discrimination between $\rho _0^{\otimes M}$ and $\rho _1^{\otimes M}$, the calculation of $F(\rho _0^{\otimes M},\rho _1^{\otimes M})$ is difficult for the same reason as above. The question then becomes whether we can remove the Kronecker product from the calculation of fidelity. To answer this question, we prove the following theorem.

Theorem 1

For any binary quantum state signals $\{\rho _0,\rho _1\}$, the error probability $P_{\textrm{e}, M}$ with an optimum quantum measurement when discriminating M copies of $\rho _0$ (i.e., $\rho _0^{\otimes M}$) from that of $\rho _1$ (i.e., $\rho _1^{\otimes M}$), which have equal a priori probabilities, satisfies

$$\begin{aligned} \frac{1}{2}\left( 1-\sqrt{1-O^M}\right)&\le \frac{1}{2}\left[ 1-\sqrt{1-\left\{ F(\rho _0,\rho _1)\right\} ^M}\right] \nonumber \\&= \frac{1}{2}\left\{ 1-\sqrt{1-F(\rho _0^{\otimes M},\rho _1^{\otimes M})}\right\} \le P_{\textrm{e}, M}, \end{aligned}$$

(43)

where $O=|\langle \tau _0|\tau _1\rangle |^2$ is the overlap for the purifications $\{ |\tau _0\rangle ,|\tau _1\rangle \}$ of $\{\rho _0,\rho _1\}$, and $F(X,Y)=(\,\textrm{Tr}\,\sqrt{\sqrt{X}Y\sqrt{X}})^2$ is the fidelity.

Proof of Theorem 1

The first inequality holds according to Uhlmann’s theorem [25, 26] that $O \le F(\rho _0,\rho _1)$ holds. The second inequality holds according to Fuchs’s theorem [24]. The equal sign connecting the two inequalities holds because of the following:

$$\begin{aligned} F(\rho _0^{\otimes M},\rho _1^{\otimes M})&=\left( \,\textrm{Tr}\,\sqrt{\sqrt{\rho _0^{\otimes M}}\rho _1^{\otimes M}\sqrt{\rho _0^{\otimes M}}}\right) ^2\\&=\left\{ \,\textrm{Tr}\,\sqrt{(\sqrt{\rho _0})^{\otimes M}\rho _1^{\otimes M}(\sqrt{\rho _0})^{\otimes M}}\right\} ^2\\&=\left\{ \,\textrm{Tr}\,\sqrt{(\sqrt{\rho _0}\rho _1\sqrt{\rho _0})^{\otimes M}}\right\} ^2\\&=\left\{ \,\textrm{Tr}\,\left( \sqrt{\sqrt{\rho _0}\rho _1\sqrt{\rho _0}}\right) ^{\otimes M}\right\} ^2\\&=\left( \,\textrm{Tr}\,\sqrt{\sqrt{\rho _0}\rho _1\sqrt{\rho _0}}\right) ^{2M}\\&=\{F(\rho _0,\rho _1)\}^M, \end{aligned}$$

where the second and fourth equalities hold according to $\sqrt{X \otimes Y}=\sqrt{X}\otimes \sqrt{Y}$ for any operators X and Y, the third equality holds according to the mixed-product property of Kronecker product, and the fifth equality holds according to $\,\textrm{Tr}\,X\otimes Y=\,\textrm{Tr}\,X \,\textrm{Tr}\,Y$. $\square$

Therefore, Thm. 1 suggests that we can calculate $F(\rho _0,\rho _1)$ to the power of M easily instead of calculating $F(\rho _0^{\otimes M},\rho _1^{\otimes M})$. There is also a simpler lower bound based on overlap O, albeit a loose one. Here, we use the formula based on the fidelity to calculate the lower bound $P_{\textrm{Eve, LB},M}^{(\mathrm QBS)}$ on the error probability for Eve when the quasi-Bell state is used, as follows:

$$\begin{aligned} P_{\textrm{Eve, LB},M}^{(\mathrm QBS)}&= \frac{1}{2}\left[ 1-\sqrt{1-\left\{ F(\Psi _\textrm{S}^{(0)},\Psi _\textrm{S}^{(1)})\right\} ^M}\right] \nonumber \\&=\frac{1}{2}\left[ 1-\sqrt{1-\left\{ \frac{\sqrt{\Delta ^{(+)}}+\sqrt{\Delta ^{(-)}}}{2(1-\kappa ^2)} \right\} ^{2M}} \right] , \end{aligned}$$

(44)

where

$$\begin{aligned} \Delta ^{(\pm )}=(b\pm c)^2(1\mp L_0\kappa )(1\mp L_1\kappa ). \end{aligned}$$

(45)

Similarly, we also use the formula to calculate the lower bound $P_{\textrm{Eve, LB},M}^{(\mathrm TSVS)}$ on the error probability for Eve when the TSVS is used, as follows:

$$\begin{aligned} P_{\textrm{Eve, LB},M}^{(\mathrm TSVS)}&= \frac{1}{2}\left[ 1-\sqrt{1-\left\{ F(\psi _\textrm{S}^{(0)},\psi _\textrm{S}^{(1)})\right\} ^M}\right] \nonumber \\&=\frac{1}{2} \left[ 1- \sqrt{ 1-\left\{ \sum _m \sqrt{\lambda _m^{(0)}\lambda _m^{(1)}}\right\} ^{2M} } \right] , \end{aligned}$$

(46)

where $\lambda _m^{(0)}$ and $\lambda _m^{(1)}$ are the m-th diagonal elements of $\psi _\textrm{S}^{(0)}$ and $\psi _\textrm{S}^{(1)}$, respectively.

Fig. 6

Bounds on error probability with respect to number of modes M when $R_0=0.99$, $R_1=1$, and the average number of photons per mode is 0.51

Fig. 7

Bounds on error probability with respect to number of modes M when $R_0=0.9$, $R_1=1$, and the average number of photons per mode is 0.51

Fig. 8

Bounds on error probability with respect to number of modes M when $R_0=0.98$, $R_1=0.99$, and the average number of photons per mode is 0.51

Fig. 9

Bounds on error probability with respect to number of modes M when $R_0=0.99$, $R_1=1$, and the average number of photons per mode is 3

Fig. 10

Bounds on error probability with respect to number of modes M when $R_0=0$, $R_1=1$, and the average number of photons per mode is 0.51

Figures 6, 7, and 8 show the error probabilities obtained when the number of modes M is varied from 1 to 5000, for which the reflectivities $\{R_0, R_1\}$ were fixed at $\{ 0.99, 1\}$, $\{0.9, 1\}$, and $\{ 0.98,0.99\}$, respectively, and the average number of photons per mode $\langle n \rangle _M$(:=$\langle n \rangle _\textrm{QBS}=\langle n \rangle _\textrm{TSVS}$) was fixed at 0.51. In Fig. 9, the settings are the same as in Fig. 6, but the average number of photons per mode is changed to 3. Figure 10 shows the error probabilities obtained when M is varied from 1 to 35, for which $\{R_0, R_1\}$ were fixed at $\{ 0, 1\}$ and $\langle n \rangle _M$ were fixed at 0.51. The red dot-dash line and dashed line represent the lower bound on the error probability $P_{\textrm{Eve, LB},M}^{(\mathrm TSVS)}$ for Eve and the upper bound on that $P_{\textrm{Bob, UB},M}^{(\mathrm TSVS)}$ for Bob, respectively, when the AQC system with the TSVS is used. The blue dot-dash line and dashed line represent the lower bound on the error probability $P_{\textrm{Eve, LB},M}^{(\mathrm QBS)}$ for Eve and the upper bound on that $P_{\textrm{Bob, UB},M}^{(\mathrm QBS)}$ for Bob, respectively, when the AQC system with the quasi-Bell state is used. The green solid line represents the lower bound on the error probability $P_\textrm{Cla}$ for both Bob and Eve when the ACC system allows any classical light sources including a light source that it is divided into M modes and the average number of photons $\langle n \rangle _\textrm{Cla}=\langle n \rangle _M M$ is used.

From Fig. 6, we know that the reliability of an AQC system can be enhanced by increasing M. In addition, we confirm that the error probability of Eve remained approximately 0.5 despite the increase in M, and hence, the reception performance of Eve cannot be significantly improved while the security of the system can be enhanced. In contrast, in the ACC system, the error probabilities of Bob and Eve are both approximately equal to 0.5, and thus, the reliability and security of the system have not been improved. Figure 7 shows that the reliability of the AQC system can be significantly enhanced by decreasing $R_0$. However, it should be noted that Eve’s reception performance may also be improved, leading to a decrease in the security of the system. By comparing Figs. 6 and 9, we can see that when the average number of photons per mode is increased, only Bob’s reception performance is enhanced while Eve’s reception performance is hardly improved. From Fig. 8, we know that the reliability of the AQC system reduces sharply when $R_1$ is decreased. In this case, by applying the results in Fig. 9 and increasing the average number of photons per mode, we note that only Bob’s reception performance is significantly enhanced. Regarding the comparison of the AQC systems using the quasi-Bell state and TSVS, as shown in Fig. 10, there is a case in which the error probability of Bob when the quasi-Bell state is used is significantly superior to that when the TSVS is used even when M is small.¹ The error probability is also significantly superior to that when $M=1$, i.e., a one-shot pulse, with the same average number of photons, although increasing M may need a highly advanced technique (e.g., $P_{\textrm{Bob,UB},M}^\mathrm{(QBS)}|_{\langle n \rangle _\textrm{QBS}=0.51, M=35} \approx 3\times 10^{-22}$ vs. $P_\textrm{Bob}^\mathrm{(QBS)}|_{\langle n \rangle _\textrm{QBS}=17.85} \approx 3\times 10^{-9}$ when $\{R_0, R_1\}=\{0,1 \}$). By contrast, the reception performance of Eve when using the quasi-Bell state is also improved. Therefore, we suggest using the TSVS and quasi-Bell state appropriately depending on the required performance.

Figure 10 also demonstrates an interesting fact: in the absence of constraints on large thermal noise and energy attenuation, there exists an entangled state, the performance of which is superior to the TSVS in the quantum illumination protocol as well as classical light sources in the single-mode protocol. The result is different from that reported in [27], which stated that the TSVS is optimal for any level of thermal noise when evaluating the quantum Fisher information in a quantum illumination protocol. We present a simple different perspective based on the quantum Chernoff bound criterion here to justify our findings. When $|\alpha |\rightarrow 0$, the quasi-Bell state becomes a Bell state [10], and hence, the former can be seen as a generalization of the latter. Using Eq. (39), we have

$$\begin{aligned} \lim _{|\alpha | \rightarrow 0} \left\{ \left. P_{\textrm{Bob,UB},M}^{(\mathrm QBS)} \right| _{R_0=0, R_1=1}\right\} =2^{-2M-1}, \end{aligned}$$

(47)

where the average number of photons per mode in mode S of the Bell state is 0.5. Using Eq. (41), we have

$$\begin{aligned} \left. P_{\textrm{Bob, UB},M}^{(\mathrm TSVS)} \right| _{R_0=0, R_1=1,N_\textrm{S}=0.5}=2^{2M-1} \times 3^{-2M} , \end{aligned}$$

(48)

where the average number of photons per mode in mode S of the TSVS is 0.5. Then, taking the ratio of Eq. (48) to Eq. (47), we have

$$\begin{aligned} \frac{2^{2M-1} \times 3^{-2M}}{2^{-2M-1}}=\left( \frac{4}{3}\right) ^{2M}. \end{aligned}$$

(49)

The value of Eq. (49) is always greater than 1 and grows exponentially as M increases because $\frac{4}{3}>1$ and $M\ge 1$. Therefore, Eq. (49) demonstrates that there is a case such that the quasi-Bell state (or the Bell state) is always superior to the TSVS despite the value of M.

The above results support the findings of previous studies that entanglement is not a unique resource [28] and the amount of entanglement with 1 ebit is sufficient [15] in a quantum illumination protocol because the amount of entanglement of the TSVS is about 1.377 ebit when $N_\textrm{S}=0.5$, whereas that of the quasi-Bell and Bell state is 1 ebit. Although we have not determined all the resources of quantum illumination, we believe that an analysis of non-Gaussian states such as the quasi-Bell state will give us more insight. Another issue is the reason the quasi-Bell state outperforms the TSVS. Reference [6] suggested that the robustness against attenuation of the coherent states, i.e., the nonorthogonal states that compose the quasi-Bell state, may be the reason. Comparing the Bell state, which is composed of orthogonal states, and the quasi-Bell state, which is composed of nonorthogonal states, in the above results, we find that both can significantly outperform the TSVS. Therefore, the robustness of the coherent states may not be an important reason. Because the received state $\rho _0$ of the Bell and quasi-Bell states when the target is absent are composed of the maximally mixed state (and the vacuum state) while the TSVS is not, we further speculate that when $\rho _0$ is closer to the maximally mixed state, this may increase the performance over that of the TSVS. We will revisit this issue in the future.

5 Conclusions

In this paper, we focused on a security evaluation of the ASK-type AQC systems using the quasi-Bell state, TSVS, and an ACC system allowing any classical light source. We first derived the error probability of Eve, which is considered to be an evaluation criterion of system security, when the quasi-Bell state and TSVS are used. By comparing those results with the error probabilities of Bob in the previous study [6], which are considered to be an evaluation criterion of system reliability, we found that the reliability is high and security is low when the quasi-Bell state is used, and the opposite is true when the TSVS is used. We also found that the ACC system cannot offer security because both Bob and Eve access the same received quantum state signals. By contrast, in the AQC systems, Bob can access mode A of the entangled state, whereas Eve cannot because Bob keeps it private. Then, we considered an approach to enhance the security as well as reliability of the AQC systems. By increasing the signal modes, which can be treated as the signal bandwidth, we found that we can significantly reduce Bob’s error probability while keeping that of Eve at about 0.5, which indicates the enhancement of both security and reliability. Finally, we discussed an interesting case in which the quasi-Bell state is always superior to the TSVS in the quantum illumination protocol in the absence of constraints on large thermal noise and energy attenuation, which can be considered a special case of AQC systems.

Future work will include consideration of the physical implementation of the methods and the countermeasures against active attack methods such as spoofing attacks. In addition, although we introduced energy attenuation into the model of the AQC system [6], many factors in channel may affect system security. It is necessary to elucidate in detail the influences due to these factors, including energy attenuation, thermal noise, phase noise, and so on, and to develop approaches or protocols that reduce these influences. Another important issue is to elucidate the principles other than entanglement that ASK, a simple modulation method, provides security. Moreover, the extensibility of the AQC systems is also an interesting topic [29,30,31], and we will revisit this topic in the future.

Appendix A Details of Eq. (6)

The elements $\{\gamma _{11}^{(\pm )}, \gamma _{13}^{(\pm )}, \gamma _{33}^{(\pm )} \}$ are given as follows [6]:

$$\begin{aligned} \gamma _{11}^{(\pm )}=&\sum _{i=0}^{1} \frac{\sqrt{(-1)^i e_+ +a+d+2} \left\{ (-1)^i e_+ +a-d\right\} ^2}{2 \sqrt{2} \left[ \left\{ (-1)^i e_+ +a-d\right\} ^2+4 (b+c)^2\right] } \nonumber \\&\pm \sum _{j=0}^{1} \frac{\sqrt{(-1)^j e_- -a-d+2} \left\{ (-1)^j e_- -a+d\right\} ^2}{2 \sqrt{2} \left[ \left\{ (-1)^j e_- -a+d\right\} ^2+4 (b-c)^2\right] }, \end{aligned}$$

(50)

$$\begin{aligned} \gamma _{13}^{(\pm )}=&\sum _{i=0}^{1} \frac{(b+c) \sqrt{(-1)^i e_+ +a+d+2} \left\{ (-1)^i e_+ +a-d\right\} }{\sqrt{2} \left[ \left\{ (-1)^ie_+ +a-d\right\} ^2+4 (b+c)^2\right] } \nonumber \\&\pm \sum _{j=0}^{1} \frac{(b-c) \sqrt{(-1)^j e_- -a-d+2} \left\{ (-1)^j e_- -a+d\right\} }{\sqrt{2} \left[ \left\{ (-1)^j e_- -a+d\right\} ^2+4 (b-c)^2\right] },\end{aligned}$$

(51)

$$\begin{aligned} \gamma _{33}^{(\pm )}=&\sum _{i=0}^{1} \frac{\sqrt{2} (b+c)^2 \sqrt{(-1)^i e_+ +a+d+2}}{\left\{ (-1)^i e_+ +a-d\right\} ^2+4 (b+c)^2} \nonumber \\&\pm \sum _{j=0}^{1} \frac{\sqrt{2} (b-c)^2 \sqrt{(-1)^j e_- -a-d+2}}{\left\{ (-1)^j e_- -a+d\right\} ^2+4 (b-c)^2}, \end{aligned}$$

(52)

$$\begin{aligned} e_{\pm }=&\sqrt{(\pm a \mp d)^2+4(b \pm c)^2}, \end{aligned}$$

(53)

where a, b, c, d are given in Eq. (19).