Adjustable-depth quantum circuit for position-dependent coin operators of discrete-time quantum walks

Abstract

Discrete-time quantum walks with position-dependent coin operators have numerous applications. For a position dependence that is sufficiently smooth, it has been provided in Nzongani et al. (Quantum circuits for discrete-time quantum walks with position-dependent coin operator, arXiv:2211.05271, 2022) an approximate quantum-circuit implementation of the coin operator that is efficient. If we want the quantum-circuit implementation to be exact (e.g., either, in the case of a smooth position dependence, to have a perfect precision, or in order to treat a non-smooth position dependence), but the depth of the circuit not to scale exponentially, then we can use the linear-depth circuit of the previous reference, which achieves a depth that is linear at the cost of introducing an exponential number of ancillas. In this paper, we provide an adjustable-depth quantum circuit for the exact implementation of the position-dependent coin operator. The lower the depth of the circuit is, the more we have to add ancillary qubits, so this adjustable-depth circuit we propose is the right tool for a good adaptation to the experimental platform: one will typically reduce the depth as much as the experimental platform can handle the added ancillary qubits that go with the reduction of the depth. This adjustable-depth circuit consists in (i) applying in parallel, with a linear-depth circuit, only certain operator-packs of coin operators (rather than all of them as in the original linear-depth circuit), each pack contributing linearly to the depth, and in (ii) applying sequentially these packs, which contributes exponentially to the depth. Hence, given an input position state, one has to wait the right operator-pack to apply the coin operator to the coin state of this position. The key technical point of this work, which is the main technical novelty with respect to the previous reference, is that the one-hot encoding of the ancillary positions at the beginning of each operator-pack is selective, that is, we perform this encoding only for certain positions (those whose internal state we want to apply the coin operator to).

Appendices

Explicit definition of $Q_{1,i}^{(n,m)}$

As mentioned in Sect. 3.3, the only difference between $Q_{1,i}^{(n,m)}$ and $Q_1^{(n)}$ of Ref. [1] is, apart from the number of ancillary qubits, the fact that the first NOT gate of $Q_{11}^{(n)}$ is replaced by a generalized $(n-m)$-Toffoli gate in $Q_{11,i}^{(n,m)}$ (that we are going to define). To describe $Q_{1,i}^{(n,m)}$ explicitly, we thus follow exactly the construction of $Q_1^{(n)}$ in Ref. [1, Appendix C3]. Thus, the explicit definition of operator $Q_{1,i}^{(n,m)}$ can be written

$$\begin{aligned} Q_{1,i}^{(n,m)} :={Q_{10}^{(n,m)}}^{\dag } Q_{11,i}^{(n,m)}Q_{10}^{(n,m)} \, , \end{aligned}$$

(A1)

where $Q_{10}^{(n,m)}$ makes the copies of the values of the position qubits on the ancillary coins, in order to be able to perform the controlled SWAPs in parallel via $Q_{11,i}^{(n,m)}$, and then one undoes the copies via ${Q_{10}^{(n,m)}}^\dag$. The amount of copies and SWAPs is no longer quantified by n as in Ref. [1], but by the parameter m. In Fig. 11, we have depicted the quantum circuits implementing $Q_{1,i}^{(n,m)}$ for $n=3$ and $m=2$, so that $i=0,1$. Let us now write explicitly the copies operation, $Q_{10}^{(n,m)}$, and the controlled SWAPs operation, $Q_{11,i}^{(n,m)}$.

Fig. 11

Quantum circuits implementing $Q_{1,i}^{(n=3,m=2)}$ for $i=0,1$. We recall that each $Q_{1,i}^{(n,m)}$ initializes the ancillary position states of the $2^m$ positions treated by the operator-pack $U_i^{(n,m)}$. This initialization is necessary because then each of the $2^m$ parallel coin operations applied with $Q_{0,i}^{(n,m)}$ must be controlled on the corresponding ancillary position

1.1 The copies: $Q_{10}^{(n,m)}$

We have

$$\begin{aligned} Q_{10}^{(n,m)} :=\mathop {{\mathop {\prod }\nolimits ^L}}\limits _{j=0}^{m-2}q_{10}^{(n,m)}(j) \, , \end{aligned}$$

(A2)

where $\forall j \ge 0$,

$$\begin{aligned} q_{10}^{(n,m)}(j) :=\mathop {{\mathop {\prod }\nolimits ^L}}\limits _{k=j+1}^{m-1}J_k^{(j)}\, , \end{aligned}$$

(A3)

with

$$\begin{aligned} J_k^{(0)}&:=K_{b_k,s_{l_k}}(X) \end{aligned}$$

(A4a)

$$\begin{aligned} J_k^{(j\ge 1)}&:=\left( \mathop {{\mathop {\prod }\nolimits ^L}}\limits _{l'=0}^{2^j-2}K_{s_{l_k}+l',s_{l_k} +l'+2^j}(X)\right) K_{b_k,s_{_{l_k}}+\sum _{u=1}^j2^{u-1}}(X) \, , \end{aligned}$$

(A4b)

where we have defined

$$\begin{aligned} \begin{aligned} l_0&:=1 \\ l_k&:=2^{k-1}-1+l_{k-1},\forall k \ge 1 \, , \end{aligned} \end{aligned}$$

(A5)

and where we remind the reader that $K_{a,b}(C)$ corresponds to applying the one-qubit gate C on qubit $\mathinner {|{b}\rangle }$ while controlling it on qubit $\mathinner {|{a}\rangle }$ (we apply C only if $a=1$).

1.2 The controlled SWAPs: $Q_{11,i}^{(n,m)}$

The operator $Q_{11,i}^{(n,m)}$ is composed of the generalized $(n-m)$-Toffoli gate, that we denote by $T_i^{(n,m)}$, and of the controlled-SWAP operations. We can write it as

$$\begin{aligned} Q_{11,i}^{(n,m)} :=\Bigg (\underbrace{\mathop {{\mathop {\prod }\nolimits ^L}}\limits _{j=0}^{m-1}B_j}_{\text {controlled SWAPs}}\Bigg ) T_{i}^{(n,m)}\, , \end{aligned}$$

(A6)

where we are going to define $T_{i}^{(n,m)}$ and the $B_j$’s below.

1.2.1 The generalized multi-Toffoli gate

What we call generalized multi-Toffoli gate is a multi-Toffoli gate for which the controls can be positive (i.e., on 1) or negative (i.e., on 0). The question here is how to express a negative control in terms of a positive control.

A first, naive idea is to express a negative control by the sequence of a NOT gate, then, a positive control, and finally another NOT gate. But, have in mind that we do not apply $Q_{11,i}^{(n,m)}$ alone, we apply the Hermitian conjugate ${Q_{11,i}^{(n,m)}}^\dag$ later on. Moreover, the $n-m$ last position qubits, on which the multi-Toffoli gate is controlled, are used by no other operation within $U_i^{(n,m)}$, neither the copies $Q_{10,i}^{(n,m)}$, nor the controlled SWAPs of $Q_{11,i}^{(n,m)}$, nor $Q_2^{(n,m)}$. So, what we can do is simply applying a NOT gate before applying a positive control in order to obtain a negative control, and then we just wait until the application of ${Q_{11,i}^{(n,m)}}^\dag$ to undo these operations on the $n-m$ last position qubits. One thus has to flip the qubit, i.e., to (i) apply a NOT gate on $\mathinner {|{b_j}\rangle }$, with $j=m,\dots , n-1$, whenever the bit $h_{j-m}$ of $i_2$ is equal to 0, and then to (ii) apply a positive control, which delivers in total a negative control on $\mathinner {|{b_j}\rangle }$.

Thus, we replace $T_i^{(n,m)}$ by

$$\begin{aligned} \tilde{T}_{i}^{(n,m)} :=\underbrace{{K}_{\alpha ,b'_0}^{\text {multi}}(X)}_{\text {(n-m)-Toffoli}} \left( \underbrace{\left( \bigotimes _{k=m}^{n-1}g_{i,k-m}^{b_{k}}\right) }_{\text {bit flips}}\otimes I_{2^m}\otimes I_{2^{(2^m)}}\otimes I_{2^{(2^m)}}\right) \, , \end{aligned}$$

(A7)

which we call almost generalized multi-Toffoli gate. In this equation, the function $g^{b_k}_{i,j}$ indicates when to place the NOT gates on the control position qubit $\mathinner {|{b_k}\rangle }$:

$$\begin{aligned} g_{i,j}^{b_k}:={\left\{ \begin{array}{ll} X \text { if } \lfloor \frac{i}{2^j} \! \! \! \mod 2 \rfloor = 0 \\ I_2 \text { otherwise} \end{array}\right. } \, . \end{aligned}$$

(A8)

Moreover, ${K}_{\alpha ,b'_0}^{\text {multi}}(C)$ is the multiply controlled operation that applies gate C on qubit $\mathinner {|{b'_0}\rangle }$ whenever all qubits are 1 in the set of $n-m$ control qubits

$$\begin{aligned} \alpha :=\bigcup _{k=m}^{n-1} \{\mathinner {|{b_{k}}\rangle }\} \, . \end{aligned}$$

(A9)

In Appendix D, we present an alternative method for reducing the amount of NOT gates used in the generalized multi-Toffoli gate.

1.2.2 The controlled SWAPs

We can write

$$\begin{aligned} B_j :=\left( \bigotimes _{k=1}^{2^j-1}E_{b'_k,b'_k+2^j}^{s_{j+k-1}}\right) E_{b'_0,b'_{2^j}}^{b_j} \, , \end{aligned}$$

(A10)

where $E_{b,c}^{a}$ denotes the controlled-SWAP operation that swaps $\mathinner {|{b}\rangle }$ and $\mathinner {|{c}\rangle }$, controlling this by $\mathinner {|{a}\rangle }$.

Explicit definition of $Q_{2}^{(n,m)}$

In this appendix, we give an explicit definition of $Q_{2}^{(n,m)}$, which is the same as that of $Q^{(n)}_2$ of Ref. [1] except for the number of ancillary wires. In Fig. 12, we show the quantum circuits implementing $Q_{2}^{(n,m)}$ for $n=3$ and $m=0,1,2,3$. The operation $Q_{2}^{(n,m)}$ can be written

$$\begin{aligned} Q_{2}^{(n,m)} :=Q_{21}^{(n,m)}Q_{20}^{(n,m)} \, , \end{aligned}$$

(B1.)

where $Q_{20}^{(n,m)}$ corresponds to the starting series of CNOT operations, and $Q_{21}^{(n,m)}$ to the controlled-SWAP series followed by CNOTs. The explicit definition of $Q_{20}^{(n,m)}$ reads

$$\begin{aligned} Q_{20}^{(n,m)} :=I_{2^n}\otimes I_{2^{(2^m)}}\otimes \left[ \mathop {{\mathop {\prod }\nolimits ^L}}\limits _{j=0}^{m-2}\left( \bigotimes _{k=0}^{2^{m-j-1}-2}K_{b'_{2^m-1-2^{j+1}(\frac{1}{2}+k)},b'_{2^m-1-k2^{j+1}}}(X)\right) \right] \, , \end{aligned}$$

(B2.)

while the explicit definition of $Q_{21}^{(n,m)}$ reads

$$\begin{aligned} Q_{21}^{(n,m)} :=I_{2^n}\otimes \left[ \mathop {{\mathop {\prod }\nolimits ^L}}\limits _{j=0}^{m-1}C_{m,j}\left( \bigotimes _{k=0}^{2^j-1}E_{s_{k2^{m-j}},s_{2^{m-j}(\frac{1}{2}+k)}}^{b'_{(k+1)2^{m-j}-1}}\right) \right] \, , \end{aligned}$$

(B3.)

where the CNOTs following the controlled SWAPs are given by

$$\begin{aligned} C_{m,j} :=\left\{ \begin{array}{ll} \bigotimes _{l=0}^{2^{j+1}-2}K_{b'_{2^m-1-2^{m-j-1}(\frac{1}{2}+l)},b'_{2^m-1-l2^{m-j-1}}}(X) \ {} &{} \ \text {if} \ j < m-1 \\ I_{2^{(2^m)}} \otimes I_{2^{(2^m)}} \ {} &{} \ \text {if} \ j = m-1 \end{array} \right. \end{aligned}$$

(B4.)

Fig. 12

Quantum circuits implementing $Q_{2}^{(n=3,m)}$, for $m=0,1,2,3$. We recall that $Q_{2}^{(n=3,m)}$ initializes, i.e., gives the appropriate value to, each of the ancillary coin states, at the beginning of each operator-pack $U_i^{(n,m)}$, in order for the $2^m$ coin operators of each operator-pack to be applicable in parallel on these ancillary coin states

Depth calculation details

Fig. 13

A way of expressing the SWAP operation, with 3 CNOT gates

In this appendix, we prove the result for the depth of the circuit, given in Eq. (11).

First, we recall that the depth of a SWAP operation counts for 3, as shown in Fig. 13.

Now, the depth of $U^{(n,m)}$, defined in Eqs. (3) and (6), is

$$\begin{aligned} d(U^{(n,m)})&= \sum _{i=0}^{2^{n-m}-1}d(U_i^{(n,m)}) \end{aligned}$$

(C1.a)

$$\begin{aligned}&= \sum _{i=0}^{2^{n-m}-1} d({Q_{1,i}^{(n,m)}}^{\dagger }) + d({Q_{2}^{(n,m)}}^{\dagger }) + d(Q_{0,i}^{(n,m)}) + d(Q_{2}^{(n,m)}) + d(Q_{1,i}^{(n,m)}) \, . \end{aligned}$$

(C1.b)

Since we apply $2^m$ coin operators in parallel with $Q_{0,i}^{(n,m)}$, defined in Eq. (7) and illustrated in Fig. 4, we have that

$$\begin{aligned} d(Q_{0,i}^{(n,m)}) = 1 \, . \end{aligned}$$

(C2.)

The depth of the operator $Q_{2}^{(n,m)}$, defined in Eqs. (B1.), (B2.), (B3.) and (B4.), and illustrated in Fig. 12, is

$$\begin{aligned} \begin{aligned} d(Q_{2}^{(n,m)})&= 3\underbrace{m}_{\text {SWAPs}} + \underbrace{2(m-1)}_{\text {CNOTs}} \\ {}&= 5m-2 \, . \end{aligned} \end{aligned}$$

(C3.)

If $m=0$, we get a negative depth for $d(Q_{2}^{(n,m)})$, and the minimum value of the depth must be 0. To solve this problem, we perform the following modification,

$$\begin{aligned} d(Q_{2}^{(n,m)}) = 5m - 2(1-\delta _{m,0}) \, . \end{aligned}$$

(C4.)

Moreover, we have that

$$\begin{aligned} d(Q_{2}^{(n,m)}) = d({Q_{2}^{(n,m)}}^\dagger ) \, . \end{aligned}$$

(C5.)

Lastly, the depth of the operator $Q_{1,i}^{(n,m)}$, defined in Eqs. (A1), (A2) and (A6), and illustrated in Fig. 11, is,

$$\begin{aligned} d(Q_{1,i}^{(n,m)}) = d({Q_{10,i}^{(n,m)}}^{\dagger }) + d(Q_{11,i}^{(n,m)}) + d(Q_{10,i}^{(n,m)}) \, , \end{aligned}$$

(C6.)

where

$$\begin{aligned} d(Q_{10,i}^{(n,m)}) = d(Q_{10,i}^{(n,m)\dagger }) \, , \end{aligned}$$

(C7.)

and

$$\begin{aligned} d(Q_{10,i}^{(n,m)}) = m-1 \, . \end{aligned}$$

(C8.)

If $m=0$, we obtain a negative depth for $d(Q_{10,i}^{(n,m)})$; we therefore perform the following modification,

$$\begin{aligned} d(Q_{10,i}^{(n,m)}) = m-1+\delta _{m,0} \, . \end{aligned}$$

(C9.)

As shown in Eq. (A6), the operator $Q_{11,i}^{(n,m)}$ can be separated into two operations: the $(n-m)$-Toffoli gate on $\mathinner {|{b'_0}\rangle }$, and the series of controlled SWAPs. Let us first treat the $(n-m)$-Toffoli gate. As mentioned in Sect. 3.3, one has to flip some of the position qubits before applying the $(n-m)$-Toffoli gate; the only pack i for which no flip is needed is when $i=2^{n-m}-1$, i.e., the last pack; therefore, we get a contribution $1-\delta _{i,2^{n-m}-1} + \varepsilon _d(n-m)$ to $d(Q_{11,i}^{(n,m)})$, where we recall that $\varepsilon _d(n-m)$ denotes the depth of the $(n-m)$-Toffoli gate. Let us now treat the controlled SWAPs. The depth of the non-parallelized controlled SWAPs is $3\sum _{k=0}^{m-1}2^k=3(2^m-1)$; however, as one parallelizes this step in the circuit, the depth becomes only 3m. Therefore, the depth of $Q_{11,i}^{(n,m)}$ finally reads

$$\begin{aligned} d(Q_{11,i}^{(n,m)}) = 1-\delta _{i,2^{n-m}-1} + \varepsilon _d(n-m) + 3m \, . \end{aligned}$$

(C10.)

Inserting Eqs. (C7.), (C9.) and (C10.) into Eq. (C6.), one gets,

$$\begin{aligned} d(Q_{1,i}^{(n,m)})&= d(Q_{10,i}^{(n,m)\dagger }) + d(Q_{11,i}^{(n,m)}) + d(Q_{10,i}^{(n,m)}) \end{aligned}$$

(C11.a)

$$\begin{aligned}&= 2d(Q_{10,i}^{(n,m)}) + d(Q_{11,i}^{(n,m)}) \end{aligned}$$

(C11.b)

$$\begin{aligned}&= 2(m-1+\delta _{m,0}) + 1-\delta _{i,2^{n-m}-1} + \varepsilon _d(n-m) + 3m \end{aligned}$$

(C11.c)

$$\begin{aligned}&= 5m + \varepsilon _d(n-m) + 2\delta _{m,0} - \delta _{i,2^{n-m}-1} - 1 \, . \end{aligned}$$

(C11.d)

Moreover, we have that

$$\begin{aligned} d(Q_{1,i}^{(n,m)}) = d({Q_{1,i}^{(n,m)}}^\dagger ) \, . \end{aligned}$$

(C12.)

Inserting now Eqs. (C5.) and (C12.), and then (C2.), (C4.) and (C11.d), into the expression of $d(U^{(n,m)}_i)$ given by Eq. (C1.b), we obtain

$$\begin{aligned} d(U_i^{(n,m)})&= d(Q_{1,i}^{(n,m)\dagger }) + d(Q_{2}^{(n,m)\dagger }) + d(Q_{0,i}^{(n,m)}) + d(Q_{2}^{(n,m)}) + d(Q_{1,i}^{(n,m)}) \end{aligned}$$

(C13.a)

$$\begin{aligned}&= 2(d(Q_{2}^{(n,m)}) + d(Q_{1,i}^{(n,m)})) + d(Q_{0,i}^{(n,m)}) \end{aligned}$$

(C13.b)

$$\begin{aligned}&= 2(5m - 2(1-\delta _{m,0}) + 5m + \varepsilon _d(n-m) + 2\delta _{m,0} - \delta _{i,2^{n-m}-1} - 1) + 1 \end{aligned}$$

(C13.c)

$$\begin{aligned}&= 20m + 2\varepsilon _d(n-m) - 2\delta _{i,2^{n-m}-1} + 8\delta _{m,0} - 5 \, . \end{aligned}$$

(C13.d)

The only term of $d(U_i^{(n,m)})$ which depends on i is $-2\delta _{i,2^{n-m}-1}$, which is equal to -2 when $i=2^{n-m}-1$ and 0 for the rest; thus, inserting Eq. (C13.d) into Eq. (C1.a), we get

$$\begin{aligned} d(U^{(n,m)})&= \sum _{i=0}^{2^{n-m}-1}d(U_i^{(n,m)}) \end{aligned}$$

(C14.a)

$$\begin{aligned}&= \sum _{i=0}^{2^{n-m}-1}20m + 2\varepsilon _d(n-m) - 2\delta _{i,2^{n-m}-1} + 8\delta _{m,0} - 5 \end{aligned}$$

(C14.b)

$$\begin{aligned}&= (2^{n-m}-1)(20m + 2\varepsilon _d(n-m)+8\delta _{m,0}-5) + 20m + 2\varepsilon _d(n-m) \nonumber \\&\quad + 8\delta _{m,0} - 7 \end{aligned}$$

(C14.c)

$$\begin{aligned}&= 2^{n-m}(20m+2\varepsilon _d(n-m) + 8\delta _{m,0}-5)-2 \, , \end{aligned}$$

(C14.d)

which is the result announced in Eq. (11).

Optimizing the number of NOT gates used in $Q_{1,i}^{(n,m)}$

The NOT gates applied in order to realize the almost generalized multi-Toffoli gate $\tilde{T}_i^{(n,m)}$ (see Eq. (A7)), i.e., applied with the function $g^{b_k}_{i,j}$ before the standard multi-Toffoli gate, are applied again when applying the conjugate transposed ${Q_{1,i}^{(n,m)}}^{\dag }$, and part of these NOT gates of $(\tilde{T}_i^{(n,m)})^{\dag }$ cancel out with the NOT gates applied in order to realize the next almost generalized multi-Toffoli gate $\tilde{T}_{i+1}^{(n,m)}$. Therefore, it makes sense to devise a function that only applies the NOT gates remaining after the cancelling out. More precisely, this function replaces $g^{b_k}_{i,j}$ and is applied only to implement $\tilde{T}_i^{(n,m)}$, i.e., only before the standard multi-Toffoli gate of $Q_{11,i}^{(n,m)}$, and not after applying the same standard multi-Toffoli gate of ${Q_{11,i}^{(n,m)}}^{\dag }$. This is indeed possible because the operations which are in between $(\tilde{T}_i^{(n,m)})^{\dag }$ and $\tilde{T}_{i+1}^{(n,m)}$, namely, the conjugate transposed of the copies ${Q_{10}^{(n,m)}}^{\dag }$ and the copies ${Q_{10}^{(n,m)}}$ (which by the way simplify each other apart from the last stage), do not involve the wires on which $(\tilde{T}_i^{(n,m)})^{\dag }$ controls.

So, in each $U_i^{(n,m)}$, we do the following modifications: (i) instead of applying $\tilde{T}_i^{(n,m)}$ in $Q_{1,i}^{(n,m)}$ (see Eq. (A7)), we apply the same operation but replacing $g_{i,j}^{b_k}$ given in Eq. (A8) by

$$\begin{aligned} h_{i,j}^{b_k} :={\left\{ \begin{array}{ll} X \ \ \text {if } i \text {\hspace{-2mm}}\mod 2^j = 0 \\ I_2 \ \text { otherwise} \end{array}\right. } , \end{aligned}$$

(D1.)

which amounts to replacing $Q_{1,i}^{(n,m)}$ by an operation that we call $P_{1,i}^{(n,m)}$; (ii) moreover, instead of applying $(\tilde{T}_i^{(n,m)})^{\dag }$, we simply apply the standard $(n-m)$-Toffoli gate ${K}_{\alpha ,b'_0}^{\text {multi}}(X)$, which amounts to replacing ${Q_{1,i}^{(n,m)}}^{\dag }$ by an operation that we call $\bar{P}_{1,i}^{(n,m)}$. In total, we have replaced $U_i^{(n,m)}$ by

$$\begin{aligned} (U_i^{(n,m)})' :=\bar{P}_{1,i}^{(n,m)} {Q_{2}^{(n,m)}}^\dagger Q_{0,i}^{(n,m)}Q_{2}^{(n,m)}{P}_{1,i}^{(n,m)} \, . \end{aligned}$$

(D2.)

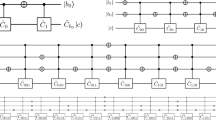
Let us notice that $h_{i,j}^{b_k}$ implements the NOT gates as in the naive circuit of Ref. [1]. In Fig. 14, we show how part of the NOT gates of the almost generalized multi-Toffoli gates $(\tilde{T}_i^{(n,m)})^\dag$ and $\tilde{T}_{i+1}^{(n,m)}$ cancel between each other, and which NOT gates remain, that we encode via $h_{i,j}^{b_k}$.

Fig. 14

In the top figure, we show the adjustable-depth circuit $U^{(n=3,m=0)}$. In the middle figure, we replace the generalized multi-Toffoli gates by the $\tilde{T}_i^{(n,m)}$’s, which enables to see that part of the NOT gates of the $(\tilde{T}_i^{(n,m)})^\dag$’s cancel out with those of the $\tilde{T}_{i+1}^{(n,m)}$’s. In the bottom figure, we show the optimized adjustable-depth circuit $(U^{(n,m)})'$, obtained by taking the product of the optimized operator-packs $(U_i^{(n,m)})'$, defined in Eq. (D2.)

Pseudocode

The pseudo-code used to code, with Qiskit, the adjustable-depth quantum circuit, is given below:

Algorithm 1

$Q_{1,i}^{(n,m)}$ and $P_{1,i}^{(n,m)}$

Algorithm 2

$Q_{2}^{(n,m)}$

Algorithm 3

$Q_{0,i}^{(n,m)}$

Universal set of gates used for the compilation of our circuits in Sect. 4

The compilation of the circuits in Sect. 4 has been done with the following universal set of gates:

$$\begin{aligned} R_X(\theta )&:=\begin{bmatrix} \cos \frac{\theta }{2} &{} -i \sin \frac{\theta }{2} \\ -i \sin \frac{\theta }{2} &{} \cos \frac{\theta }{2} \end{bmatrix} \end{aligned}$$

(F1.a)

$$\begin{aligned} R_Y(\theta )&:=\begin{bmatrix} \cos \frac{\theta }{2} &{} - \sin \frac{\theta }{2} \\ \sin \frac{\theta }{2} &{} \cos \frac{\theta }{2} \end{bmatrix} \end{aligned}$$

(F1.b)

$$\begin{aligned} R_Z(\lambda )&:=\begin{bmatrix} e^{-i \frac{\lambda }{2}} &{} 0 \\ 0 &{} e^{i \frac{\lambda }{2} } \end{bmatrix} \end{aligned}$$

(F1.c)

$$\begin{aligned} P(\lambda )&:=\begin{bmatrix} 1 &{} 0 \\ 0 &{} e^{i {\lambda }} \end{bmatrix} \end{aligned}$$

(F1.d)

$$\begin{aligned} CNOT&:=\begin{bmatrix} 1 &{} 0 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 \\ 0 &{} 0 &{} 1 &{} 0 \end{bmatrix} \, . \end{aligned}$$

(F1.e)