Automatic evolutionary design of quantum rule-based systems and applications to quantum reinforcement learning

Abstract

Explainable artificial intelligence is a research topic whose relevance has increased in recent years, especially with the advent of large machine learning models. However, very few attempts have been proposed to improve interpretability in the case of quantum artificial intelligence, and many existing quantum machine learning models in the literature can be considered almost as black boxes. In this article, we argue that an appropriate semantic interpretation of a given quantum circuit that solves a problem can be of interest to the user not only to certify the correct behavior of the learned model, but also to obtain a deeper insight into the problem at hand and its solution. We focus on decision-making problems that can be formulated as classification tasks and propose a method for learning quantum rule-based systems to solve them using evolutionary optimization algorithms. The approach is tested to learn rules that solve control and decision-making tasks in reinforcement learning environments, to provide interpretable agent policies that help to understand the internal dynamics of an unknown environment. Our results conclude that the learned policies are not only highly explainable, but can also help detect non-relevant features of problems and produce a minimal set of rules.

1 Introduction

Quantum machine learning (QML) [1] lies at the intersection of classical machine learning (ML) and quantum computing. It attempts to migrate classical ML to a quantum computing paradigm and develop new techniques that take advantage of quantum mechanisms such as superposition, entanglement, parallelism or tunneling to solve supervised, unsupervised and reinforcement learning (RL) tasks. Successful QML models inspired by classical ML are quantum Support Vector Machines (qSVM) [2], quantum Neural Networks [3, 4], or quantum K-Means and other clustering methods [5], to mention just a few. On the other hand, other QML techniques that are not inspired by classical ML have also stood out in tasks such as search and optimization, such as the variational quantum eigensolver (VQE), the quantum approximate optimization algorithm (QAOA) or the Grover search method [4]. The advantages of QML techniques and models range from improved performance over their classical counterpart [6], to improved efficiency (in either time or space) in solving a particular task [7].

In this work, our experiments focus on quantum reinforcement learning (QRL) problems [8]. The most commonly used configuration in QRL encompasses a quantum agent interacting with a classical environment where the agent implements an action selection policy to return the best possible action to perform in an unknown environment. Examples of these policies in the literature are the Grover operator [9], variational quantum circuits (VQC) [10, 11] or the quantum analogue of the classical policy iteration method [12]. In particular, VQC-based proposals are heavily influenced by classical deep reinforcement learning (DRL) methods using neural networks, and are trained using DRL ideas such as deep Q-learning [13] or policy-gradient algorithms as REINFORCE [10]. Different mechanisms such as data re-uploading or deep variational layers have been studied in the literature [3, 13] with outstanding results in performance [14] and space efficiency [15].

Other approaches attempt to use concepts coming from the area of Quantum Computing to develop classical RL methods, although they cannot be considered in the QRL field since they are not targeted at providing an implementation in quantum computers or simulators. In the past decade, the work [16] Dong and Chen proposed is one of the first quantum-inspired methods able to perform probabilistic action selection, by means of using the quantum state formalism to represent a discrete action set together with the probabilities to choose an action, and then applying amplitude amplification methods to improve the policy. Other recent work in this category is [17], where a replay buffer for deep Q-networks is built using the Grover operator to select the probabilities to sample experiences for training. Recently, [18] proposes a framework to develop different quantum-inspired models (Q-learning, deep Q-networks, policy gradient methods, etc.). The proposal is built considering partial observability of states and probabilistic action selection under the formalism of quantum states and their collapse, and the application in energy efficiency control tasks shows their superiority with respect to classical approaches. Our approach lies in the QRL category, since the proposed method attempts to create implementable quantum circuits able to be run in quantum hardware.

Despite the important advantages in the field of QML (and QRL in particular), we have detected a gap between the final VQC that solves a problem and the interpretability/explainability of its behavior. Generally, VQCs used in QRL are chosen due to their high problem generalization ability [10, 13, 14] or efficiency in space [15], but their final behavior is difficult to interpret or explain. This fact makes it difficult to certify the correctness of a solution except through the use of extensive data-driven testing. In classical artificial intelligence, explainable artificial intelligence (XAI) methods [19] attempt to develop techniques to extract a graphical or natural language interpretation of the behavior of an ML model. In the particular case of RL, we find approaches to find interpretable agent policies such as [20], which uses a trained policy to generate a dataset to extract a decision tree able to explain the policy behavior. Recently, another approach use evolutionary algorithms to evolve RL policies modeled as CART-type decision trees [21], therefore creating interpretable policies. A different approach using human-friendly prototypes has been proposed in [22] using a new neural network model specially designed to wrap the resulting prototypes. Other previous proposals are also summarized in the review technical report [23]. However, in the case of QML, the explainability of VQC models has not been studied as thoroughly as in its classical counterpart, but we can find some recent progress in [24, 25].

Another different approach to improve the explainability of a quantum model consists of designing the model with an internal structure that is highly interpretable, as is the case of quantum decision trees [26], quantum decision forests [27] or quantum rule-based systems [28, 29], all these models aimed at solving classification problems. These models allow the extraction of rules once the correct behavior is learned, in the form of ”If condition is true, then conclusion”. Our proposal is inspired by the later works [28, 29], where an original model is proposed to represent a rule-based system in a quantum rule-based database, along with the mechanisms to deal with uncertainty. In [28], the structure of a quantum rule-based system (QRBS) is proposed as a quantum circuit containing rules implemented with CNOT and Toffoli gates to derive intermediate facts and conclusions, applied to a proof-of-concept classification task in the field of medicine. The later work [29] explored the benefits of quantum computing as a representation and inference mechanism for a QRBS under data uncertainty. The authors studied the formulation of a QRBS from the point of view of knowledge-based systems, so they did not develop a learning process for QRBS in a data-driven environment.

In this work, we propose a QRBS learning mechanism to solve classification tasks, with applications in the field of QRL. Unlike classical classification tasks in supervised learning, where an existing dataset is known in advance, in RL and QRL there is no prior data and the models learn online through interaction with an unknown environment. This setup makes the learning problem more difficult than in the supervised learning approach. Our proposal aims to find a QRBS capable of optimally solving a reinforcement learning problem. To do so, we formulate the task of learning a QRBS as a binary optimization problem and solve it using evolutionary computation algorithms [30]. We experimentally demonstrate that the rules in the learned QRBS help explain the agent’s behavior in solving the action selection task, which is useful not only to certify the correctness of the learned behavior by a human user, but also to obtain a deeper knowledge about the structure of the problem. The remaining of the manuscript is structured as follows: Sect. 2 describes the fundamentals of the methods used in our approach. After that, Sect. 3 explains the proposal to represent and learn a QRBS to solve RL problems. Then, Sect. 4 shows the results obtained in state-of-the-art reference RL scenarios, and Sect. 5 concludes.

2 Methods

2.1 Foundations of rule-based systems for classification

A traditional rule-based system (RBS) [31] comprises three components: (a) a knowledge base containing a set of rules; (b) a working memory that contains known and inferred information; and (c) an inference engine to derive new knowledge from existing data in the working memory. The early foundations of an RBS come from the field of logic, where each rule is modeled as an implication $A\rightarrow C$ (A is a well-formed formula called antecedent, C the consequent), and an inference mechanism such as Modus Ponendo Ponens is used to infer the fact C once A is in the working memory. Some RBS representation models, such as decision trees [32], include additional constraints on the antecedent, such as A must be in conjunctive normal form of atoms. On the other hand, contemporary inference engines must take into account not only classical inference tools, but also mechanisms to address imperfect knowledge and conflict resolution, e.g., contradictory derivations.

A classification problem contains two types of data: a set of input features $F=\{F^i\}$ where each feature $F^i$ can contain a value of the set $\{v^i_j\}$, and an output class C that contains a discrete set of labels $\{c_l\}$. An RBS for classification contains rules of the manner shown in Eq. 1. The inference process begins with the input features of an observation in the working memory and evaluates each rule to distinguish a possible set of outputs to label observation in one class or another, considering the conflict resolution mechanisms and the treatment of uncertainty of the inference engine.

$$\begin{aligned} F^{i_1}=v^{i_1}_{j_1}\wedge ...\wedge F^{i_n}=v^{i_n}_{j_n}\rightarrow C=c_l \end{aligned}$$

(1)

The proposal of this work creates a quantum rule-based system that contains rules inspired by the structure shown in Eq. 1, where the antecedent is in conjunctive normal form and the consequent contains a single derivation. As in [28], we rely heavily on controlled-NOT (CX) and Toffoli gates, although we extend the model to multiple controlled-NOT (MCX) gates to implement each rule. Thus, the mapping from a classical RBS to a QRBS will be designed as follows: (a) the knowledge base of the QRBS will be implemented in a quantum circuit that contains a sequence of MCX gates, one for each rule of the system; (b) the working memory will be the quantum state of the system; and (c) the inference engine will be implemented as the natural evolution of an initial quantum state through the circuit. A detailed description of the proposal is provided in Sect. 3.

2.2 Reinforcement learning

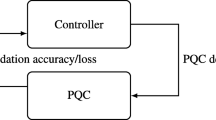
Reinforcement learning [33] is one of the main types of learning in machine learning. Unlike supervised and unsupervised machine learning, in RL there is no prior dataset to learn from. Instead, the learning process takes place dynamically over time, through the interaction between the learner (agent) and an unknown environment. Figure 1 shows the main cycle of an RL task: At each time instant t, the agent perceives the state of the environment $s_t$ as input. It then selects an action $a_t$ from an available action set and performs the action in the environment. Finally, the environment evolves from state $s_t$ to state $s_{t+1}$ based on its current state and the agent’s action, and returns an immediate reward $r_{t+1}$ to inform the agent about the action’s suitability in the context of $s_t$. This reward may depend on the initial state $s_t$, the final state $s_{t+1}$, the agent’s action $a_t$ or a combination of the three and is represented as $r_t(s_t, a_t, s_{t+1})$. Generally, the environment is stochastic and its behavior is assumed to be governed by an underlying unknown Markov decision process [34] of the environment. Therefore, it holds the first-order Markov assumption, and the agent’s goal is to find a correct policy for action selection $\pi (a_t | s_t)$ that maximizes the cumulative reward $R_t$ over time as it is shown in Eq. 2, where $\gamma \in [0,1]$ is called discount factor to prevent the cumulative reward from going to infinity while training the agent.

Fig. 1

Cycle of Reinforcement Learning (Color figure online)

$$\begin{aligned} R_t= r_t(s_t, a_t, s_{t+1}) + \gamma R_{t+1} \end{aligned}$$

(2)

In this work, we learn a quantum rule-based system as a suitable agent’s policy capable of providing optimal performance in a given RL environment. In our experiments, we assume a quantum reinforcement learning setup where the agent implements a quantum policy and the environment is classical.

2.3 Evolutionary computation and the CHC algorithm

Evolutionary algorithms [35] are a subset of gradient-free metaheuristic optimization methods whose behavior is inspired by natural phenomena; for example, genetic algorithms (GA) whose principles follow the simulation of Darwinian evolution. In summary, a GA comprises a set of candidate solutions (called population) uniquely determined by their genes (free parameters to optimize). In each iteration of a GA (called generation), some members of the population are selected and grouped generally in pairs to form the parents set. These parents are usually chosen using a selection operator that follows the principle of survival of the fittest, i.e., those individuals that are best adapted to their environment (that is, those that best solve the optimization problem) are more likely to transmit their genetic information to future generations. The parents are then combined using a recombination/crossover operator to create a new population (offspring) containing genetic information from their parents and, additionally, possible mutations introduced by a mutation operator with certain probability. After that, the offspring replace the initial population and a new evolutionary cycle begins. Being inspired by evolutionary principles, the population is expected to increase its quality every generation to solve the optimization problem and eventually provide an optimal solution. Evolutionary algorithms, and especially GAs, are considered a type of global search methods and have been successfully used in a wide variety of problems over the last two decades [30].

The CHC evolutionary algorithm [36] is a type of GA with special focus on finding a balance in exploration of the solution space and exploitation to achieve convergence. It was initially designed to solve binary optimization problems, although it has been adapted to other types of encoding in [37, 38]. CHC achieves a balance in population diversity and convergence through the design of four components: a) Elitist selection to create the population of the next generation using the best individuals from both the parent and offspring populations; b) the use of the HUX uniform crossover to generate two children from two parents as different as possible to improve exploration; c) an incest prevention mechanism to prevent two genetically similar parents from recombining; and d) reinitialization to restart the population once it has converged to a local optimum.

Fig. 2

Flow diagram of the Binary CHC optimization algorithm (Color figure online)

Figure 2 shows the main flow of the CHC algorithm, where N is a positive even integer hyperparameter containing the population size, L if the length of the solutions (i.e., the number of free variables to be optimized), d is the recombination threshold for the incest prevention mechanism, M is a positive integer hyperparameter to control the selective pressure in the reinitialization mechanism, and $r\in (0, 1)$ is the last hyperparameter that controls elitism and the recombination threshold after divergence. The difference(x,y) method implements a distance measurement to evaluate how much the solutions x, y differ. In the case of binary optimization, the method is usually the Hamming distance which returns the number of pairwise variables/genes with different values in x and y. Finally, the procedure HUX(x,y) is the recombination method for solutions x, y. It creates a copy of each solution $c1=x, c2=y$, and swaps exactly half of the differing genes between both solutions c1, c2 at random.

In this work, we use the classical binary evolutionary algorithm CHC as an optimization method to learn optimal quantum rule-based systems in RL problems, as a suitable procedure that maintains a balance in the exploration and exploitation of the solution space. The main idea is to design a binary encoding mechanism capable of representing a QRBS into a solution and to use the algorithm to evolve a population of QRBS solutions evaluated in RL environments to assess their performance.

3 Description of the proposal

Our proposal focuses on the automatic learning of a QRBS that solves a given classification problem. To do so, the structure of a quantum rule and a QRBS used in this work are first described in Sect. 3.1. After that, Sect. 3.2 explains the representation of QRBS to be optimized using evolutionary binary optimization algorithms, and finally Sect. 3.3 particularizes the approach to solve reinforcement learning problems.

3.1 Rule design

The article [28] proposed a model to represent a general quantum rule-based system in a quantum circuit based on the extensive use of CNOT and Toffoli gates, along with intermediate variables implemented as additional qubits for the inference process. In our proposal, we simplify the process to define the set of rules that provides the final result, since our goal is to solve data-driven classification tasks with no intermediate facts to derive. We also constrain the QRBS rules to have the form described in Eq. 1, to reduce the search space to find a QRBS that solves a problem. Taking these considerations into account, our approach defines a quantum rule as a single multiple controlled NOT gate (MCX) with variable control states with values 0 or 1. To use an MCX gate as a quantum rule, we distinguish two types of qubits:

• Input qubits encoding classical input data, that can be used as control qubits. The number of input qubits depends on the nature of the encoded classical data: for continuous values or binary information, a single qubit will be used. On the other hand, discrete values will be enumerated and transformed into a binary number. In this case, the number of qubits will be equal to the number of bits needed to encode the discrete value.

• Output qubits, whose number is equal to the number of class labels in the classification task. Therefore, an MCX targets to a specific output qubit (class label) that is controlled by several input qubits.

Fig. 3

Example of classical data encoding and two quantum rules (Color figure online)

The quantum embedding mechanisms considered in this work to transfer classical data to quantum states are basis encoding for discrete/binarized data or angle encoding for continuous values, although other embedding techniques such as amplitude encoding or Q-Sample [39] could also have been selected. We implement both encoding techniques as rotation gates $R_x(\theta \pi )$, where $\theta \in [0,1]$. An arbitrary example of quantum encoding and two possible rules is shown in Fig. 3, considering a discrete input characteristic Size with four possible values ${\text {Small}}\mapsto {|{00}\rangle }, {\text {Medium}} \mapsto {|{01}\rangle }, {\text {Large}}\mapsto {|{10}\rangle }, {\text {Extra-Large}}\mapsto {|{11}\rangle }\}$, a continuous input value Intensity$\in [0,1]$, and two possible outcomes Danger$\in$Low,High. The first MCX gate implements the rule If ${|{\text {Size}_0}\rangle }={|{1}\rangle }$ and ${|{\text {Intensity}}\rangle }={|{0}\rangle }$ then ${|{\text {Low}}\rangle }={|{1 }\rangle }$, and the second MCX can be read as If ${|{Size_0 Size_1}\rangle }= {|{10}\rangle }$ and ${|{\text {Intensity}}\rangle }={|{1}\rangle }$ then ${|{\text {High}}\rangle }={|{1}\rangle }$. We can see that both rules fit into the structure of Eq. 1. However, if translated into natural language by interpreting the quantum embedding mechanism, we get If (Size = Large or Size = Extra-Large) and Intensity = 0 Then Danger = Low for Rule 1, and If Size = Large and Intensity = 1 Then Danger = High for Rule 2. Therefore, even with the restrictions introduced by Eq. 1, the natural interpretation of the rules in the QRBS could contain a richer set of operators in the antecedents to form more complex rules.

According to the example, the complete quantum rule-based system will be composed of an initial subcircuit containing the quantum embedding mechanism and the ansatz as a sequence of MCX operations where each MCX implements a rule. The inference of the possible outcomes is governed by the effect of each MCX on the corresponding output qubits of the quantum state, which will be measured as a final step.

3.2 QRBS optimization using evolutionary algorithms

We propose to use gradient-free binary optimization algorithms to learn a suitable QRBS that solves a given classification problem. In particular, we use the CHC binary evolutionary algorithm in this work because it is a global search procedure that maintains a balance in solution space exploration and convergence. The CHC algorithm is intended to evolve a population where each solution is a binary-encoded QRBS that is evaluated according to its performance in solving the classification task.

The key problem to solve here is to find a compact and necessarily injective mapping from a sequence of binary digits (solution in the population) to a quantum circuit that implements the ansatz of the encoded QRBS: Compact to reduce the search space as much as possible, and injective so that each solution can be translated into a unique QRBS. However, we are constrained by the limitation that the length of the solutions in a typical population-based optimization algorithm is fixed (parameter L of the CHC algorithm), so that all candidate solutions contain the same number of parameters to optimize. Since we do not know in advance the optimal number of rules of the target QRBS, we are forced to set a value $N_R$ for the maximum number of rules allowed for a QRBS as a hyperparameter, and to introduce a mechanism to activate/deactivate rules in the binary representation. A similar procedure must be established to select which input qubits will be used for the antecedent of each rule and its control value. With these considerations, our proposal covers the following design to encode a QRBS in a solution in the population, assuming $N_I$ input qubits and $N_O$ possible class labels:

• A QRBS is implemented as a concatenated sequence of $N_R$ rules. It contains a fixed structure with $N_R*(2*N_I + \lceil {\text {log}}_2 N_o\rceil + 1)$ bits.

• Each rule i in a QRBS is encoded as a concatenated sequence of binary digits $[A_i C_i]$, where $A_i$ encodes the antecedent and $C_i$ the consequent. The length of a sequence that implements a rule is set to $2*N_I + \lceil log_2 N_o\rceil + 1$ binary values.

• The antecedent $A_i$ of the i-th rule contains $2*N_I$ bits with the structure $([a^i_1, c^i_1], [a^i_2, c^i_2],..., [a ^i_{N_I}, c^i_{N_I}])$, where $a^i_j$ has the value 1 if the j-th input qubit is active in the rule and the value 0 otherwise, and $c^ i_j$ is the control value in case the qubit is used.

• The consequent $C_i$ of the i-th rule is encoded as a bit sequence $[a^i, t^i_1, t^i_2,..., t^i_{\lceil {\text {log}}_2 N_o\rceil }]$, where $a^i$ contains the value 1 if the i-th rule is active and therefore a member of the QRBS, and the value 0 otherwise. The remaining bits from $t^i_1$ to $t^i_{\lceil {\text {log}}_2 N_o\rceil }$ contain the binary representation of the position of the output qubit that is used as a target in the MCX gate in case the rule is active, in the range $\{0,..., N_o - 1\}$.

This design is compact considering the limitations regarding the fixed length of all solutions in the population, and it is also injective. Furthermore, it allows the representation of any possible QRBS containing a maximum number of rules $N_R$. However, if the number of class labels is not a power of two, encoding the target qubit in a solution could result in invalid targets. In these cases, we solve this situation by considering the rule as not active. As an example, the following sequence is a possible representation of Rule 1 in the QRBS in Fig. 3: [ [1, 1], [0, 1], [1, 0], [1, 0] ]. The first pair [1, 1] means that the first input qubit $Size_0$ is active with the control value 1. The second pair [0, 1] translates to the fact that the qubit $Size_1$ is not used in the rule (the control value is unused in this case), and the third pair [1, 0] activates the qubit Intensity with control value 0. The consequent is encoded with the last pair [1, 0], which means that the rule is active and targets to the qubit Low. This sequence could be concatenated with [ [1, 1], [1, 0], [1, 1], [1, 1] ] as the representation of Rule 2 to define the full QRBS with $N_R=2$ rules in the figure.

3.3 Evaluation of a quantum rule-based system for reinforcement learning

In our experiments, the CHC evolutionary algorithm is used to evolve a population of QRBS containing the structure defined in the previous section as a sequence of binary digits. Evaluating each QRBS in a reinforcement learning environment is similar to a classification task. In RL, the QRBS implements the agent policy and must return a selected action $a_t$ to be executed if state $s_t$ is perceived at time t. In this work, we assume a deterministic policy where the action whose output qubit contains the maximum expected probability of returning ${|{1}\rangle }$ is selected. We achieve this by using the $\sigma _z$ observable in the range $[-1, 1]$ over the output qubits. We name ${|{\psi _o^t}\rangle }={|{q^t_1 q^t_2...q^t_{N_o}}\rangle }$ to the partial quantum state corresponding to the output qubits in a t-th arbitrary time instant. We measure the output qubits and calculate the expectation of each action as shown in Eq. 3. After that, the action chosen by the agent is obtained using Eq. 4, that is, the action with the closest value to -1 is selected and, if two or more actions have the same expectation, the first action with such value is selected.

$$\begin{aligned} {\text {ActionSet}}=({\langle {\psi ^t_o}|}\sigma _z I_{N_o-1} {|{\psi ^t_o}\rangle }, {\langle {\psi ^t_o}|}I\sigma _z I_{N_o-2} {|{\psi ^t_o}\rangle },..., {\langle {\psi ^t_o}|}I_{N_o-1}\sigma _z {|{\psi ^t_o}\rangle } ) \end{aligned}$$

(3)

$$\begin{aligned} {\text {action}}= {\text {min}}\{{\text {argmin}} \{{\text {ActionSet}}\} \} \end{aligned}$$

(4)

Since an RL environment is stochastic, multiple QRBS runs and tests are required to evaluate the true performance of a given policy. A series of predefined T episodes are executed between the agent’s QRBS and the environment to calculate the suitability of a solution. The performance of the final agent is calculated as the average of the cumulative reward obtained for each episode as shown in Eq. 5, where $s^j_t$ is the perceived environment state at time t of the j-th episode and $\pi _{QRBS}(a^j_t | s^j_t)$ is the action selected by the QRBS under evaluation in each state perception.

$$\begin{aligned} {\text {fitness}}({\text {QRBS}})= {1\over T}\sum _{j=1}^T \sum _{t=0} r^j_t(s^j_t, \pi _{\text {QRBS}}( a^j_t | s^j_t), s^j_{t+1}) \end{aligned}$$

(5)

Each QRBS in the population is evaluated based on its fitness value. In a RL problem, it is desirable to obtain policies that provide the maximum return, so the objective of the proposed CHC method is to maximize the fitness of the solutions.

4 Experiments

We test the proposal in simulated RL and quantum environments. The goal of the simulations is to experimentally show the capabilities of our approach to learn interpretable optimal policies in quantum reinforcement learning scenarios, provided as a quantum rule-based system. To that end, the binary CHC evolutionary optimization algorithm was implemented in Python as an agent policy learning mechanism using the representation model shown in Sect. 3.2, and the policy evaluation was performed in a quantum simulation software using Tensorflow Quantum v0.7.2. The experiments were run on a desktop computer with Intel(R) Core(TM) i5-9600K CPU at 3.70 GHz with 32 GB of RAM equipped with an NVIDIA GeForce RTX 2060 GPU to accelerate the quantum circuit simulation. The RL environments selected for experimentation are described in Sect. 4.1. Then, Sect. 4.2 shows the experimental setup. Section 4.3 analyzes and discusses the results, and finally Sect. 4.4 provides a comparison with classical (non-quantum) RL interpretability models.

4.1 Description of reinforcement learning environments and preprocessing

We tested the proposal in RL simulation environments of the software Gymnasium from the Farama Foundation (formerly Gym from OpenAI), since it is an extended testbed widely used for research and training in RL. The software is freely available online at https://gymnasium.farama.org for the Python programming language. The data reported in the OpenAI’s Gym Leaderboard at https://github.com/openai/gym/wiki/Leaderboard to solve the environments is used as the main baseline to assess the suitability of our approach. We selected five environments with discrete action sets to test our approach as an action classification task, although the structure of the environment states varies from discrete to continuous features:

• The FrozenLake environment (Fig. 4a) simulates a discrete 4x4 grid world containing traversable cells and holes where the agent could fall (16 possible states). The agent starts at the top left cell (0,0), and the goal is to reach the bottom right cell (3,3) without falling into the holes. A simulation ends if the agent reaches the goal or falls into a hole. The agent receives a reward of + 1 if it succeeds in its task and 0 otherwise. The perception at each time step is the cell where the agent is located, and it can decide between four actions to move up, down, left or right. There are two versions of the environment: Slippery, where the agent could end up in a different cell than the desired one if it slips, and non-slippery, where the next cell is completely determined from the current cell and the agent’s action. In our simulations, we use the non-slippery version for illustrative purposes. Therefore, the environment is considered solved if the agent can reach the target cell with the policy learned in one simulation of a given policy.

• The BlackJack environment (Fig. 4b) simulates a simplified version of the classic casino game Black Jack. The value of face cards (Jacks, Queens, Kings) is 10, numerical cards from 2 to 9 have a value equal to their number and Aces can count as 11 or 1. A game begins with the dealer’s card visible. The agent can hit a new card until the sum exceeds 21 or stop (2 actions). The dealer then draws cards until reaching a total value of 17 or more. The winner is the one whose sum is closest to 21 without exceeding this value and, if both exceed, there is a tie. During the game, the agent perceives the state as a tuple (player’s sum, dealer’s value, ace) where ace contains 1 if the player has a usable ace and 0 otherwise (704 possible states). The reward is provided to the agent at the end of a game and contains a value of +1 for a win, −1 for a loss, and 0 for a tie. We consider the environment is solved if the agent obtains an average cumulative reward of $-$0.05 or higher over 1000 simulated games with the same policy.

• The CartPole environment (Fig. 4c) is a classic control problem in which the end of a pole is connected to a 2-D cart. The agent controls the cart by pushing left or right at each time instant with a constant force (2 actions). At each time step, the agent’s perception contains the position of the cart on the screen in the range [$-$4.8, 4.8], the pole angle in the range [$-$0.418, 0.418] rads, and the speed of the cart and the angular velocity of the pole in the range $(-\infty , \infty )$. Therefore, the state space contains four features with continuous values. The goal is to keep the pole on top without falling (absolute value of the pole angle less than 0.21 rads) for as long as possible. The agent receives a reward +1 every time instant the pole is up, and 0 if the pole falls or the cart leaves the screen. The simulation ends when the pole falls, the cart leaves the screen, or 500 time steps are simulated. The environment is considered solved if the agent can maintain the pole for an average of 500 time steps over 100 simulations using the same policy.

• The MountainCar environment (Fig. 4d) is another classic control problem. A 2-D car is stochastically located in a valley between two hills. It can take one of three actions to move left with constant acceleration, move right with constant acceleration, and do not accelerate. The car’s goal is to plan accelerations to reach the top of the right hill in the minimum time, taking into account the car’s position along the x-axis in the range [$-$1.2, 0.6] and the speed of the car in the range [$-$0.07, 0.07]. Therefore, the state space contains two continuous features. The reward obtained by the agent is −1 for each time step that the car is not in the target state, and the simulation ends either if the target state is reached, or after 200 time steps. The environment is considered solved if the agent obtains an average cumulative reward of −110 in 100 simulations with the same policy.

• The Acrobot environment (Fig. 4e) is another control problem. Here, two links are connected by a joint. One end of one of the links is in a fixed position but can rotate. The joint between both links can be controlled by an agent applying a torque of −1 N m, $+$1 N m or 0 N m (3 actions), making the links to swing. The objective of the environment is to plan a sequence of torques to be applied so that the links reach a certain height. If $\theta _1, \theta _2$ are the relative angles of the links, the agent perceives ${\text {cos}}(\theta _1), {\text {sin}}(\theta _1), {\text {cos}}(\theta _2), {\text {sin}}(\theta _2), \omega _{\theta _1}, \omega _{\theta _2}$ at each time instant, where $\omega _{\theta _1}\in [-4\pi , 4\pi ]$ and $\omega _{\theta _2}\in [-9\pi , 9\pi ]$ are the angular velocities of both joints. Thus, the agent’s perception contains 6 features with continuous values. For each instant in which the system does not reach a target state, the agent receives a reward of −1. The simulation terminates if a target state is not reached after 500 time steps, or if a target height is achieved, defined as $-{\text {cos}}(\theta _1) - {\text {cos}}(\theta _2 + \theta _1) > 1.0$. Unlike previous environments, there is no specific criteria to indicate when the environment is considered resolved for Acrobot. However, in this work we established the criterion to obtain a minimum average cumulative reward of −80 in 10 simulations with the same policy, as a balance between the computational time required to run our experiments and the best solutions reported in the Open AI Gym’s online leaderboard.

Fig. 4

Snapshots of environment’s rendering using Farama Foundation’s Gymnasium software (Color figure online)

The agent’s state perception requires preprocessing for all environments, so that it can be fed as input to the QRBS policy under evaluation. To that end, quantum embedding is designed in our experiments using angle encoding with gates $R_x(\theta \pi )$ with $\theta \in [0, 1]$. Table 1 shows the preprocessing applied to each state component for the environments studied, along with the number of qubits needed to represent the information. We consider three types of preprocessing: (a) binarization, which transforms a non-negative integer to its binary representation; (b) scaling, which scales data in a range [l, u] to the interval [0, 1], and (c) arctan, which calculates the arctan of a value and performs a rescaling from $[- \pi /2, \pi /2]$ to [0, 1]. With these considerations in mind, the number x in parentheses in the cells of the Type column means the number of different values that the feature in column 2 can contain, from $0..x-1$, and the number in parentheses in the Preprocessing column represents the number of bits required to binarize the state characteristic value.

Table 1 Environment’s states preprocessing for quantum embedding

Each preprocessed feature is encoded into a quantum state using the number of qubits shown in the Required Qubits column. The total number of qubits used in each policy is equal to the sum of the number of qubits for each environment’s feature plus the number of possible actions in the environment, since we establish a single qubit to determine whether each action is executed or not. Therefore, the total number of qubits required for a policy to solve FrozenLake is 8, for BlackJack is 12, it is 6 for CartPole, 5 for MountainCar, and 9 for Acrobot.

4.2 Experimental settings

Before running the final experiments, we performed a pre-experimentation to find suitable hyperparameters capable of solving each problem, using a classic trial-and-error procedure. The final hyperparameters used to learn each environment are shown in Table 2, where column 1 describes the environment, column 2 shows the population size of the CHC algorithm, column 3 sets the number of copies of the best solution to reinitialize the population after the divergence of the CHC algorithm, column 4 prints the percentage of random changes in the copies of the best solution after the divergence in CHC, column 5 indicates the maximum number of rules allowed in a QRBS, and column 6 remarks the number of policy evaluations to calculate the average performance of the solutions. We performed 30 runs of the CHC algorithm to learn each environment and to be able to analyze the results statistically. Each run was stopped if a QRBS in the population solved the environment, or if a maximum of 1000 iterations of the CHC algorithm was reached (except for the MountainCar environment, which was set to 500 iterations to reduce execution time).

Table 2 Experimental settings to solve each environment

4.3 Results

Table 3 Summary of results to solve each environment

Fig. 5

QRBS obtained for the FrozenLake environment with best performance and minimum number of rules (Color figure online)

Algorithm 1

Interpretation of rules of the FrozenLake QRBS in Figure 5

Fig. 6

QRBS obtained for the BlackJack environment with best performance and minimum number of rules (Color figure online)

Algorithm 2

Interpretation of rules of the BlackJack QRBS in Figure 6

Fig. 7

QRBS obtained for the CartPole environment with best performance and minimum number of rules (Color figure online)

Algorithm 3

Interpretation of rules of the CartPole QRBS in Figure 7

Fig. 8

QRBS obtained for the MountainCar environment with best performance and minimum number of rules (Color figure online)

Algorithm 4

Interpretation of rules of the MountainCar QRBS in Figure 8

Fig. 9

QRBS obtained for the Acrobot environment with best performance and minimum number of rules (Color figure online)

Algorithm 5

Interpretation of rules of the Acrobot QRBS in Figure 9

Fig. 10

Evolution of the average Return ($R_t$) and its standard deviation in all experiments (blue: average return for the whole CHC’s populations; orange: average return for the best solution in the populations) (Color figure online)

Table 3 shows a summary of the results obtained to learn a QRBS implementing a quantum agent policy to solve each environment. We analyze the average cumulative reward obtained in the 30 runs and its standard deviation (rows 2–3) considering a discount factor $\gamma =1.0$, the best and worst cumulative rewards obtained in each problem (rows 4–5), the average, standard deviation and the minimum number of rules of the QRBS learned in all experiments (rows 6–8), the average number of iterations required by the CHC algorithm to obtain the optimal solution and its standard deviation (rows 9–10), and the average and s.d. calculation time in seconds required for a single execution on rows 11–12. The subscripts in rows 2, 4, 5 indicate the number of runs that provided a QRBS that solves the environment, and the number of times the best and worst performance were obtained, respectively.

The first thing we may notice in Table 3 is that all the runs were able to solve the environments, except for the cases of FrozenLake and MountainCar. This might be expected as they are the least informed environments about the performance of a given policy, and an extensive exploration is required to find a solution. However, all environments were solved in at least 20 separate experiments of 30. We remark that CartPole was solved optimally in all runs with very few CHC iterations. We can also verify an increase in the average number of CHC iterations and the execution time required to solve each environment, according to its complexity and the number of times the environment was solved. For this reason, FrozenLake and MountainCar hold the maximum number of average iterations and computational time required for a single CHC execution. It is also striking that the average and minimum number of rules used by the best QRBS found in each run is usually low, which means that the strategy designed to activate/deactivate rules in a QRBS during the learning process is effective and can provide simple solutions with minimum size. It is especially notable in the cases of BlackJack, CartPole and Acrobot, where only two rules can be used to solve the environments. However, the solution with two rules in the latter environment is not the one that provides the best $R_t$.

Figure 10 provides the evolution of $R_t$ in all problems studied to give support to the previous analysis. The X axis contains the number of the current CHC iteration, and the Y axis the $R_t$ value. We remark in blue the average of the mean return of solutions in the CHC population at each iteration, considering the unfinished experiments only. Also, we highlight in orange the average return of the best solutions found in all executions at each iteration. Figure 10b and c corresponds to the BlackJack and CartPole environments, which were solved in fewer iterations with our approach. As it is expected, the populations increase their quality over time, and so it does the better solution returned. The case of FrozenLake in Fig. 10a should also be mentioned due to the high variability in the value of the best return and the almost constant population $R_t$ value. This problem was unsolved in 9 of 30 executions, which justifies the high variability in the best return. Also, since the return is binary ($R_t=0$ or $R_t=1$), the population return remains constant until a solution that solves the environment is found. The most interesting behavior to us is provided by the problems MountainCar and Acrobot in Fig. 10d and e. Although the $R_t$ values of the best solution have a regular behavior and increase with the number of iterations, we observe a high variability in the average $R_t$ with regards to the population. This behavior is a direct consequence of the CHC algorithm components and, in particular, the reinitialization step after divergence in Fig. 2. When the CHC algorithm converges to a local optimum, the elements in the population are reinitialized to random solutions. This fact decreases substantially the quality of the solutions in the population until a few iterations are executed.

To deepen into the analysis of the best solutions found, Figs. 5–9 plot the QRBS obtained for each problem with best $R_t$ and minimum number of rules (if two or more QRBS obtained the same performance). A possible interpretation for these QRBS is provided in the rule sets in Algorithms 1–5. These rules must be interpreted after applying preprocessing. Additionally, the supplementary material for this article includes five videos containing five rendered runs for each environment using these QRBS as agent policies, to evaluate each QRBS visually in practice.

The first thing that catches our attention in Fig. 5 corresponding to the QRBS of FrozenLake is Rule 1, which activates the action Right without antecedent. This was an unexpected behavior for us, because we designed the QRBS model with Equation 1 in mind for the structure of rules. However, the type of rules like Rule 1 have a place in classical RBS and are called default rules. Default rules fire when no other rules do, to provide an output decision by default. The representation proposed in Sect. 3.2 allows the emergence of default rules during evolutionary learning of the optimal QRBS if all input qubits are deactivated for a rule, and this fact enabled the QRBS in Fig. 5 to have a minimum number of possible rules to learn the FrozenLake environment. As can be seen in the supplementary material, this policy implements the Right action by default, except when the agent is in the third column and first, second or third rows (Rules 2-3 in the diagram in Fig. 5), which activate the action Down. In this case, even if both actions Right and Down are activated with the same probability, Down is selected due to the deterministic action selection mechanism imposed in Eq. 4. Finally, it can also be verified that the output qubits for the actions Left and Up are not used, which means that the agent can dispense with these actions to implement its behavior and therefore reduce the size of the quantum circuit implementing the policy.

A similar situation arose in the best solution found for the BlackJack environment in Fig. 6, where the action Stop is selected by default except when Rules 2 or 3 are activated, which cause the agent to select the action Hit. Furthermore, the QRBS obtained for BlackJack is a clear example that the rules obtained in the QRBS should not be interpreted alone, but in the context of the complete QRBS due to the inference process performed by the evolution of the quantum state. In fact, the action Hit is selected only when either Rule 2 or Rule 3 is activated, but not both, since the input values are discrete and both rules can be activated with probability 0 or 1. Thus, the interpretation provided in the Algorithm 2 would be more readable from the point of view of human reasoning if Rules 2 and 3 are replaced by ”If the antecedent of Rule 2 is True and the antecedent of Rule 3 is False, or the antecedent of Rule 2 is False and the antecedent of Rule 3 is True, then Hit”. As it was the case in the example shown in Sect. 3.1, designing a quantum rule structure as indicated in Eq. 1 could lead to more complex rule structures after interpretation. In this case, the proposed rule to replace Rules 2 and 3 in the BlackJack environment contains logical NOT, AND, and XOR operations in the antecedent.

The circuit in Fig. 7 corresponds to the QRBS obtained to solve the CartPole environment. In this case, the learned QRBS is capable of solving the environment optimally according to the criteria existing in the literature, disregarding the two input features Cart Position and Cart Velocity. It uses a minimum set of 2 rules that depend on the Pole Angular Velocity and Pole Angle features separately. Since both features can have continuous values, activating Rules 1 and 2 could produce a probability of selecting Left or Right actions in the range [0, 1]. If both actions can be selected with equal probability, then Left is chosen due to the criteria implemented in Eq. 4. The degree of activation of each rule varies depending on the values of the Pole angular velocity for Rule 2, and the Pole angle for Rule 3. Thus, the inference process plays a very important role in this problem to control the cart by switching between degrees of rule activation. This behavior is clearly visualized in the video of the QRBS CartPole included in the supplementary material.

The circuit in Fig. 8 for MountainCar solves the environment with four rules, and it is another example to show that the rules should not be analyzed separately, but in the context of the entire QRBS. The main rules that produce acceleration are Rule 1 and Rule 4, both depending on the input feature Velocity. They are complementary: Rule 1 accelerates to the right when the car goes up the slope on the right and rule 4 accelerates to the left when it goes up the slope on the left. In this QRBS we can also find contradictory rules such as Rules 2 and 4, which activate actions No acceleration and Accelerate to the left with equal probabilities. In this case, Rule 3 resolves the conflict as it changes the probability of not accelerating when the car is on the hill on the right. The effect of rules 2 and 3 cancel each other when the velocity is negative on the right side of the environment (i.e., the car moves toward the valley from the right), where it accelerates to the left. Combining the outputs of these rules produces appropriate behavior as shown in the video in the supplementary material.

Finally, Fig. 9 plots the circuit that obtained the best performance in the Acrobot environment. It contains a set of 3 rules and shows that the input features ${\text {cos}}(\theta _1), {\text {cos}}(\theta _2), \omega _{\theta _1}$ are not necessary to solve the environment with a minimum average performance of $R_t=-80$ in 10 tests, as well as the action Do not apply torque. The first thing we notice is that Rules 1 and 3 are complementary, since they apply a negative torque when $\omega _{\theta _2}$ has a negative value (before preprocessing), and a positive torque when $\omega _{\theta _2 }$ is positive. Rule 2 forces the agent to also apply a positive torque, when the sin of both joints is negative. As it can be seen in the video for Acrobot supplementary material, these 3 rules are enough to solve the environment correctly.

To conclude the discussion of the results, we can summarize the outcomes of the proposed procedure for learning QRBS in QRL environments as successful, since it has been experimentally shown that the approach is capable of providing adequate solutions in all tested RL environments, including the learning of default rules to reduce the set of rules. Furthermore, it has been proven that a reduced set of rules can be achieved to solve most of the problems thanks to the designed mechanism to activate/deactivate rules. All inferred quantum rule-based systems contain a set of highly interpretable rules, which helped to not only explain optimal behavior, but also determine which input features and actions could be discarded in some of the problems studied. For this reason, we believe that the QRBS design developed in this work, and also the use of gradient-free binary optimization methods to learn QRBS, could be powerful tools to obtain explainable quantum circuits that solve classification tasks, and especially in reinforcement learning setups.

4.4 Comparison with classic approaches

In this section, we compare the quality of the QRBS obtained in our work with state-of-the-art methods. We perform the comparison with classical (non-quantum) models, since there are no similar interpretable approaches in the QML research area, and QRL in particular. We selected decision trees as the target classical model for comparison for two reasons: first, decision trees are one of the classical machine learning models with the highest interpretability and inference efficiency; and secondly, the rules that can be extracted from a decision tree follow the same structure of Eq. 1 as our proposal. Although the comparison between such different classical and quantum methods is difficult, this choice could make the comparison fairer.

In terms of theoretical efficiency, the proposed QRBS evaluates a rule in $\mathcal {O}(1)$ operations, since these are implemented as a single MCX gate where all antecedent inputs and consequent are evaluated simultaneously. In a classical decision tree, evaluating a single rule is $\mathcal {O}(d)$ where d stands for the tree depth, i.e., the number of nodes that must be evaluated in the path from the root to the target leaf node. However, if we focus in the number of rules $N_R$, the QRBS needs to evaluate all rules to provide an output, so that QRBSs can be executed in $\mathcal {O}(N_R)$. On the contrary, a classical non-probabilistic inference engine for decision trees provides an output in $\mathcal {O}(log(N_R))$, since a single path from the root to a target leaf node is evaluated. This improvement in the classical decision tree could be worse in we consider inference with a probabilistic inference engine. In probabilistic inference, all nodes in the tree are evaluated in the worst case, so that the efficiency falls to $\mathcal {O}(N_R)$. In such probabilistic case, an upper bound of the number of operations required to provide an output can be calculated with the number of nodes in the tree as $\sum _{i=0}^d w^i$, where w stands for the maximum number of children a node could have. However, the quantum approach considering QRBS performs a maximum of $N_R=w^d$ operations only because each path from the root to a leaf is evaluated in $\mathcal {O}(1)$. Therefore, the QRBS outperforms classical probabilistic inference in decision trees in terms of theoretical efficiency, although it is less competitive when it is compared with the crisp (non-probabilistic) case.

Regarding the experimental comparison, we followed the proposed methodology in [20] for classical RL to extract interpretable policies as decision trees from learned black-box models. The procedure is straightforward: First, a neural network model implementing a policy is trained with a classical RL algorithm to solve an environment. After that, the learned model is used in the environment to generate a large enough dataset containing environment states as input, and the action selection decision of the learned policy as output. As a final step, a decision tree is used to learn the policy from the dataset.

Table 4 Experimental settings to solve each environment

In our experiments, we created different network policies for the environments described in Sect. 4.1 with a classic multi-layer perceptron (MLP) feedforward neural network. Each MLP is fed with the same preprocessed data used to train the QRBS, in order to establish an experimental setting as similar as possible to the one used in our approach. The MLPs provide a Q-value as output for each possible action in the corresponding environment. They were trained with the classic double deep Q-network (DDQN) algorithm [40] using the hyperparameters described in Table 4. In addition, the DDQN target policy was modified at every iteration of the DDQN method using a soft update strategy with $\alpha =0.1$ [41]. Finally, the discount factor was set to $\gamma =0.99$ for the training stage in all experiments.

In all cases, the policies were tested every 10 trained episodes. An additional stopping criterion was set for early stopping if the trained policy solved each environment in test under the same conditions than in the QRBS. Both MLPs and DDQN were implemented in Tensorflow and Python and were executed for 30 times in the same hardware than the QRBS under simulation. After these experiments were finished, we selected the learned policies with the best $R_t$ in test to generate a supervised learning classification dataset containing 100.000 patterns (policy network-environment interactions) for each problem. The decision tree model selected to learn these datasets was CART, since CART can handle input features with continuous data and there is a standard implementation of this type of decision tree in the Scikit-Learn library for Python. During decision tree learning, we limited the maximum tree depth to the number of input features/qubits for QRBS, so that the maximum number of atoms in the antecedent of each generated rule equals the maximum number of atoms in the antecedent of the learned QRBSs in the previous section. This choice helps to mitigate the differences between the experimental settings in both quantum and classical approaches, so that all models possess rules with the same input structure.

Table 5 Summary of results to solve each environment with classical MLPs

Table 5 shows the results after learning the MLPs for each problem, containing the mean $R_t$ and its standard deviation, the best and worst $R_t$ found, and the mean number of iterations and time required for the learning, together with their standard deviation. It is noticeable that, despite the QRBSs were learned under simulation, the training time for CartPole and Acrobot of QRBS was substantially lower than for the MLPs. However, in the remaining problems the training time of the MLPs is much better than the time of the quantum approach, which is the behavior one could expect. Other remarkable result relates to th fact that MLPs solved all environments in all runs, including MountainCar and FrozenLake where the QRBS was unable to solve in 10 and 9 executions of 30, respectively. Also, MLPs were able to achieve solutions with better best $R_t$ in BlackJack and MountainCar.

As we mentioned previously, we used the MLPs with best $R_t$ to create a supervised learning dataset containing 100.000 experiences where the input features are the state perceptions, and the target output is the action selected by the MLP. The input features were also preprocessed with the settings of Table 1 except for binarization, since decision trees can handle numerical values. Then, we used these datasets to create interpretable RL policies as CART decision trees with the information entropy as node splitting criterion. Results regarding decision tree extraction are shown in Table 6, where Column Problem describes the environment, Column Maximum Tree Depth sets the tree depth constraint for each problem, Training Accuracy shows the percentage of correct classification rate of decision tree prediction for each dataset, and Column #Rules prints the number of leaf nodes in the generated tree, that equals the number of rules that model the solution’s behavior.

Table 6 Results for decision tree extraction

In Table 6, we may verify that the decision trees were unable to learn the complete datasets except for the FrozenLake problem. This is a direct consequence of the maximum tree depth imposed for each problem, which limits the size of the antecedent in the generated rules. Of course, removing this constraint solves this situation but with the added cost of increasing the number of rules and antecedent complexity. Being compared with our approach, which is studied in this article as a QML model with inherent interpretability that learns from data directly, the interpretation of MLP policies with Decision Trees show relevant limitations regarding accuracy with respect to the QRBS. Moreover, if we focus in the number of generated rules, the generated decision trees have provided a significantly higher number of rules in general, except for the FrozenLake and MountainCar environments where the number of rules equal the results of our approach with QRBS. Figure 11 plots these generated trees, which serve as a sample to show their general structure. In general, they are very populated trees with maximum number of nodes up to their maximum depth, except for the cases of FrozenLake and BlackJack. Due to the large size of some of these trees and the page size limitation, it is difficult to assess the true behavior of each tree except for Fig. 11a, which inferred an equivalent set of rules to the QRBS in the FrozenLake problem.

Fig. 11

Decision trees generated from the MLP policies for each problem

To end up the comparison with classical interpretable methods, we can summarize the findings of this section in two main outcomes: First, theoretical efficiency improvements of a quantum model such as QRBS could be achieved against classical decision trees with probabilistic inference mechanisms, while this is not the case for the crisp classical model. Secondly, the proposed method was able to learn policies from data, while the interpretability of a policy neural network with decision trees could lead to incomplete modeling of the network policy if the size of the antecedent is constrained. In any case, the QRBS model could be useful to reduce the number of rules extracted. This could be a desirable property of an interpretable model in many cases, which makes the QRBS competitive in the QML research area, but also being compared with classical models.

5 Conclusion

In this article, we have proposed quantum rule-based systems as interpretable methods for quantum machine learning classification in reinforcement learning tasks. The proposal includes a simple definition of rules whose antecedent is in conjunctive normal form and the consequent provides a target class label. The QRBS model is based on a sequence of multiple controlled NOT gates to facilitate the construction and explainability of the rules.

The contribution of the manuscript also addresses the learning of a QRBS suitable for classification, formalized as a binary optimization problem. The CHC evolutionary method was proposed to perform the learning task. The proposal was tested in reinforcement learning scenarios and the results suggest that our approach is capable of not only optimally solving the studied environments, but also returning QRBS with minimal sets of rules, including default rules, that can help to identify relevant and irrelevant input features and actions to solve an RL problem. We also found that the inference engine, considered as the evolution of an initial quantum state in the QRBS quantum circuit, could affect the interpretability of the rules separately and therefore a contextual analysis that considers the entire QRBS is required to unravel the correct behavior of the extracted rules. We believe that our approach could be an important step forward in achieving explainable and interpretable quantum machine learning models, but also that it can serve as a tool to gain deeper knowledge about the problem to be solved and its solution. Although this manuscript has focused on classification tasks for RL, future works will be conducted to extend the approach to other problem statements such as regression or clustering.