Abstract
We propose a quantum circuit that implements a delayed-choice quantum eraser via bipartite entanglement with the extension that the degree of entanglement between the two paired quantons is adjustable. This provides a broader setting to test complementarity relations between interference visibility and which-way distinguishability in the scenario that the which-way information is obtained through entanglement without direct contact with the quantum state for interference. The visibility-distinguishability relations are investigated from three perspectives that differ in how the which-way information is taken into consideration. These complementarity relations can be understood in terms of entropic uncertainty relations in the information-theoretic framework and the triality relation that incorporates single-particle and bipartite properties. We then perform experiments on the quantum computers provided by the IBM Quantum platform to verify the theoretical predictions. We also apply the delay gate to delay the measurement of the which-way information to affirm that the measurement can be made truly in the “delayed-choice” manner.













Similar content being viewed by others
Data availability
The data generated in this study are available from the corresponding author on reasonable requests.
Notes
However, it should be noted that, in the interference experiments in quantum circuits, the interference is between different qubit states, typically \(\vert {0}\rangle \) and \(\vert {1}\rangle \), which are analogues to different optical paths in optical interferometers but are usually not spatially separated states. In this sense, unlike optical interferometers, the visibility-distinguishability duality is not to be understood in terms of wave-particle duality. Nevertheless, from the information-theoretic viewpoint, the visibility-distinguishability complementarity in a quantum circuit shares exactly the same mathematical structure as that of an optical experiment and thus can be understood as the same effect.
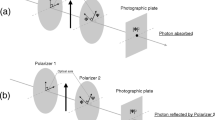
The same idea of using a Mach-Zehnder interferometer for the delayed-choice quantum eraser has been considered in the literature (see e.g., [29, 30]). Particularly, our setup in Fig. 1 is very similar to Figure 1 in [30], except that the latter investigates a different issue and does not consider an adjustable phase shift.
The adjustable phase shift \(\theta \) can also be realized by tilting the second beam splitter.
The main merit of using the EOM is that the switch between the closed and open configurations can be made very fast, which is crucial for Wheeler’s delayed-choice experiment. If the switch speed is not a concern, one can simply replace the EOM with a half-wave plate that rotates the input polarization by \(45^\circ \) for the closed configurations, and remove the half-wave plate for the open configuration. The arrangement devised to recombine the two paths can alternatively be replaced by the method proposed in Figure 1 in [30].
However, because of the unitary freedom for density matrices, \(\rho _{\gamma _1}\) also admits infinitely many different interpretations. For example, \(\frac{1}{2}\mathbb {1}_{2\times 2}\) can be alternatively interpreted as having an arbitrarily specific polarization (e.g., clockwise polarized) by 50% probability and having the orthogonal polarization (e.g, counterclockwise polarized) by the other 50%. The resulting detection probabilities of \(D_1\) and \(D_2\) nevertheless are independent of the interpretation. If a different interpretation is adopted, each individual photon \(\gamma _1\) may not be said to travel either of the two paths and thus the two paths still interference to a certain degree depending on the interpretation, but the probabilistic nature of \(\frac{1}{2}\mathbb {1}_{2\times 2}\) turns out to “conceal” the two-path interference of each individual event in the accumulated result.
The fact that the \(D'_1\) and \(D'_2\) outcome deduces how \(\gamma _1\) travels the two paths can be empirically verified by the concurrence counts between \(D_1/D_2\) and \(D'_1/D'_2\) in the open configuration (i.e., the applied voltage for the EOM is turned off).
Rigorously speaking, as commented in Footnote 5, the which-way information is neither marked in the first place nor erased in a later time. Rather, it is the ambiguity of interpretations that is removed upon the delayed-choice measurement. It has been argued that no information is erased at all in a quantum eraser and the term “quantum eraser” is a misleading misnomer (see e.g., [29, 32]). However, also see [33] for different opinions.
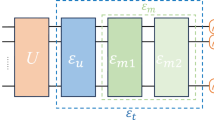
We label the objects associated in the upper quantum wire with the superscript or subscript “i” for “interference” and those in the lower wire with “d” for “delayed-choice”.
Prior to the first H gate, the qubit states \(\vert {0}\rangle _i\) and \(\vert {1}\rangle _i\) are analogous to the photon states of \(45^\circ \) and \(135^\circ \) diagonal polarizations, which become \(1/\sqrt{2}\left( \vert {\mathrm {Path\ 1}}\rangle \pm \vert {\mathrm {Path\ 2}}\rangle \right) \) after entering the first PBS. After the second H gate, the qubit states \(\vert {0}\rangle _i\) and \(\vert {1}\rangle _i\) are analogous to the photon states of horizontal and vertical polarizations, which enter \(D_1\) and \(D_2\), respectively. In the Mach-Zehnder interferometer as shown in Fig. 1, an entering beam is split into two beams, which are recombined and strike either \(D_1\) or \(D_2\) in the end. By contrast, in the quantum circuit analogy, there is only one qubit throughout the whole “interferometer”, which is measured with the 0/1 readouts by \(D_i\) in the end.
However, the value of \(\phi '\) in \(R_y(\phi ')\) is not to be directly identified with the value of \(\phi '\) in WP(\(\phi '\)) by the analogy. In accordance with the comment in Footnote 9, the qubit states \(\vert {0}\rangle \) and \(\vert {1}\rangle \) before the \(R_y(\phi ')\) gate are analogous to the photon states of \(45^\circ \) and \(135^\circ \) diagonal polarizations. Consequently, in particular, \(R_y(\phi '=0)\) corresponds to WP(\(\phi '=\pi /4\)), and \(R_y(\phi '=\pi /2)\) corresponds to WP(\(\phi '=0\)).
Note that the upper right and lower right grouped blocks do not touch each other at all. Therefore, the exact position of the \(R_y(\phi ')\) gate relative to the gates of the upper grouped block is not important. In fact, the \(R_y(\phi ')\) gate can be positioned even after the delay gate. It is only convenient for illustration and calculation that the \(R_y(\phi ')\) gate is depicted in this particular position.
If a composite AB system is in a pure state, the Schmidt decomposition implies that the density matrices \(\rho ^A\) and \(\rho ^B\) for the A and B subsystems, respectively, have the same eigenvalues.
In the special case that \(\cos \phi \cos \phi '=1\), we have \(p(0_d)=1\) and \(p(1_d)=0\), and thus \(p(0_i|1_d)\) and \(p(1_i|1_d)\) appearing in (4.5) are ill defined. Similarly, in the special case that \(\cos \phi \cos \phi '=-1\), we have \(p(0_d)=0\) and \(p(1_d)=1\), and thus \(p(0_i|0_d)\) and \(p(1_i|0_d)\) are ill defined. Nevertheless, for both special cases, \(p_\textrm{succ}\) in (4.5) and thus \({\mathcal {D}}\) in (4.6) are still well defined, as \(p_\textrm{succ}\) simply reduces to \(p(1_d)p(1_i|1_d)\) or \(p(0_d)p(0_i|0_d)\), respectively, when \(p(0_d)=0\) or \(p(1_d)=0\).
As remarked in Footnote 13, we have to pay special attention to the two special cases. In the case that \(\cos \phi \cos \phi '=1\), there are no events in the \(1_d\) subensemble (i.e., \(p(1_d)=0\)), and \({\mathcal {D}}_{1_d}\) and \({\mathcal {V}}_{1_d}\) are both ill defined. Similarly, in the case that \(\cos \phi \cos \phi '=-1\), there are no events in the \(0_d\) subensemble (i.e., \(p(0_d)=0\)), and \({\mathcal {D}}_{0_d}\) and \({\mathcal {V}}_{0_d}\) are both ill defined.
As remarked in Footnote 14, in the special case that \(\cos \phi \cos \phi '=1\), \({\mathcal {D}}_{1_d}\) and \({\mathcal {V}}_{1_d}\) are ill defined; in the special case that \(\cos \phi \cos \phi '=-1\), \({\mathcal {D}}_{0_d}\) and \({\mathcal {V}}_{0_d}\) are ill defined. Nevertheless, for both special cases, \({\mathcal {V}}_\textrm{avg}\) and \({\mathcal {D}}_\textrm{avg}\) are still well defined, because the ill defined part is multiplied by \(p(1_d)=0\) or \(p(0_d)=0\) in (4.18) and (4.19).
Also note that, in the open configuration, the phase gate \(P(\theta )\) has no effect on the outcome of \(D_i\).
As the delay gate is also applied, there is no doubt that the retroactive effect of the quantum erasure is experimentally realized in quantum circuits. The only remaining doubt pertains to whether this experiment can be interpreted in the same way as the optical experiment of quantum erasure (also see Footnote ). This however is a matter of philosophical interpretation, for more discussions of which we refer interested readers to [33] and references therein.
The simulated data already agree closely with the theoretical ones when we perform 5000 shots for each setting. This ensures that the number of 5000 shots is large enough to average out probabilistic fluctuations for real experiments. In Figs. 4, 5, 6, we present the simulated data with 40,000 shots for each setting. The deviation from the theory is almost inappreciable with the large number of 40,000 shots.
The simulated data indeed yield no \(1_d\) events when \(\phi '=0\) and \(\phi =0\equiv 2\pi \). In Fig. 6a, the points where \({\mathcal {D}}_{1_d}\) and \({\mathcal {V}}_{1_d}\) are ill defined are indicated by the hollow squares and hollow diamonds.
By contrast, the same error does not lead to significant deviations in the total-ensemble perspective and the average perspective as shown in Figs. 4 and 5. The total visibility \({\mathcal {V}}\) defined in (4.4) does not involve \(p(0_d)\) or \(p(1_d)\) and thus is insusceptible to the errors on \(p(0_d)\) and \(p(1_d)\). On the other hand, for \({\mathcal {D}}\) in (4.6) with (4.5), \({\mathcal {V}}_\textrm{avg}\) in (4.18), an \({\mathcal {D}}_\textrm{avg}\) in (4.19), the errors on \(p(1_i|1_d)\), \({\mathcal {V}}_{1_d}\), and \({\mathcal {D}}_{1_d}\) are greatly “tamed” through the multiplication by \(p(1_d)\), which in the presence of noise remains close to 0 when \(\phi \approx 0\) and \(\phi \approx 0\equiv 2\pi \). In fact, theoretically, \({\mathcal {V}}\), \({\mathcal {D}}\), \({\mathcal {V}}_\textrm{avg}\), and \({\mathcal {D}}_\textrm{avg}\) are all well defined even if \(p(0_d)=0\) or \(p(1_d)=0\) (recall Footnote 13 and Footnote 15).
This picture of the layout is obtained from the Qiskit software development kit [34].
References
Bohr, N.: The quantum postulate and the recent development of atomic theory. Nature 121, 580 (1928). https://doi.org/10.1038/121580a0
Scully, M.O., Englert, B.-G., Walther, H.: Quantum optical tests of complementarity. Nature 351, 111 (1991). https://doi.org/10.1038/351111a0
Jaeger, G., Shimony, A., Vaidman, L.: Two interferometric complementarities. Phys. Rev. A 51, 54 (1995). https://doi.org/10.1103/PhysRevA.51.54
Englert, B.-G.: Fringe visibility and which-way information: An inequality. Phys. Rev. Lett. 77, 2154 (1996). https://doi.org/10.1103/PhysRevLett.77.2154
Dürr, S.: Quantitative wave-particle duality in multibeam interferometers. Phys. Rev. A 64, 042113 (2001). https://doi.org/10.1103/PhysRevA.64.042113
Björk, G., Karlsson, A.: Complementarity and quantum erasure in welcher Weg experiments. Phys. Rev. A 58, 3477 (1998). https://doi.org/10.1103/PhysRevA.58.3477
Englert, B.-G., Bergou, J.A.: Quantitative quantum erasure. Opt. Commun. 179, 337 (2000). https://doi.org/10.1016/S0030-4018(99)00718-X
Jakob, M., Bergou, J.A.: Complementarity and entanglement in bipartite qudit systems. Phys. Rev. A 76, 052107 (2007). https://doi.org/10.1103/PhysRevA.76.052107
Jakob, M., Bergou, J.A.: Quantitative complementarity relations in bipartite systems: Entanglement as a physical reality. Opt. Commun. 283, 827 (2010). https://doi.org/10.1016/j.optcom.2009.10.044
Roy, A.K., Pathania, N., Chandra, N.K., Panigrahi, P.K., Qureshi, T.: Coherence, path predictability, and \(I\) concurrence: a triality. Phys. Rev. A 105, 032209 (2022). https://doi.org/10.1103/PhysRevA.105.032209
Dürr, S., Rempe, G.: Can wave-particle duality be based on the uncertainty relation? Am. J. Phys. 68, 1021 (2000). https://doi.org/10.1119/1.1285869
Busch, P., Shilladay, C.: Complementarity and uncertainty in Mach-Zehnder interferometry and beyond. Phys. Rep. 435, 1 (2006). https://doi.org/10.1016/j.physrep.2006.09.001
Coles, P.J., Kaniewski, J., Wehner, S.: Equivalence of wave-particle duality to entropic uncertainty. Nat. Commun. 5, 1 (2014). https://doi.org/10.1038/ncomms6814
Coles, P.J.: Entropic framework for wave-particle duality in multipath interferometers. Phys. Rev. A 93, 062111 (2016). https://doi.org/10.1103/PhysRevA.93.062111
Bera, M.N., Qureshi, T., Siddiqui, M.A., Pati, A.K.: Duality of quantum coherence and path distinguishability. Phys. Rev. A 92, 012118 (2015). https://doi.org/10.1103/PhysRevA.92.012118
Qureshi, T., Siddiqui, M.A.: Wave-particle duality in n-path interference. Ann. Phys. 385, 598 (2017). https://doi.org/10.1016/j.aop.2017.08.015
Angelo, R., Ribeiro, A.: Wave-particle duality: an information-based approach. Found. Phys. 45, 1407 (2015). https://doi.org/10.1007/s10701-015-9913-6
Bagan, E., Bergou, J.A., Cottrell, S.S., Hillery, M.: Relations between coherence and path information. Phys. Rev. Lett. 116, 160406 (2016). https://doi.org/10.1103/PhysRevLett.116.160406
Ma, X.-S., Kofler, J., Zeilinger, A.: Delayed-choice Gedanken experiments and their realizations. Rev. Mod. Phys. 88, 015005 (2016). https://doi.org/10.1103/RevModPhys.88.015005
Ionicioiu, R., Terno, D.R.: Proposal for a quantum delayed-choice experiment. Phys. Rev. Lett. 107, 230406 (2011). https://doi.org/10.1103/PhysRevLett.107.230406
IBM Quantum, https://www.ibm.com/quantum, https://quantum-computing.ibm.com/
Amico, M., Dittel, C.: Simulation of wave-particle duality in multipath interferometers on a quantum computer. Phys. Rev. A 102, 032605 (2020). https://doi.org/10.1103/PhysRevA.102.032605
Schwaller, N., Dupertuis, M.-A., Javerzac-Galy, C.: Evidence of the entanglement constraint on wave-particle duality using the IBM Q quantum computer. Phys. Rev. A 103, 022409 (2021). https://doi.org/10.1103/PhysRevA.103.022409
Pozzobom, M.B., Basso, M.L.W., Maziero, J.: Experimental tests of the density matrix’s property-based complementarity relations. Phys. Rev. A 103, 022212 (2021). https://doi.org/10.1103/PhysRevA.103.022212
Cruz, P.M.Q., Fernández-Rossier, J.: Testing complementarity on a Transmon quantum processor. Phys. Rev. A 104, 032223 (2021). https://doi.org/10.1103/PhysRevA.104.032223
Scully, M.O., Druhl, K.: Quantum eraser: a proposed photon correlation experiment concerning observation and “delayed choice’’ in quantum mechanics. Phys. Rev. A. 25, 2208 (1982). https://doi.org/10.1103/PhysRevA.25.2208
Kim, Y.-H., Yu, R., Kulik, S.P., Shih, Y., Scully, M.O.: Delayed “choice’’ quantum eraser. Phys. Rev. Lett. 84, 1 (2000). https://doi.org/10.1103/PhysRevLett.84.1
Walborn, S.P., TerraCunha, M.O., Pádua, S., Monken, C.H.: Double-slit quantum eraser. Phys. Rev. A 65, 033818 (2002). https://doi.org/10.1103/PhysRevA.65.033818
Qureshi, T.: Demystifying the delayed-choice quantum eraser. Eur. J. Phys. 41, 055403 (2020). https://doi.org/10.1088/1361-6404/ab923e
Qureshi, T.: The delayed-choice quantum eraser leaves no choice. Int. J. Theor. Phys. 60, 3076 (2021). https://doi.org/10.1007/s10773-021-04906-w
Jacques, V., Wu, E., Grosshans, F., Treussart, F., Grangier, P., Aspect, A., Roch, J.-F.: Experimental realization of Wheeler’s delayed-choice Gedanken experiment. Science 315, 966 (2007). https://doi.org/10.1126/science.1136303
Kastner, R.: The ‘delayed choice quantum eraser’ neither erases nor delays. Found. Phys. 49, 717 (2019). https://doi.org/10.1007/s10701-019-00278-8
Chiou, D.-W.: Delayed-choice quantum erasers and the Einstein-Podolsky-Rosen paradox. Int. J. Theor. Phys. 62, 120 (2023). https://doi.org/10.1007/10773-023-05370-4
Qiskit contributors, Qiskit: An open-source framework for quantum computing (2023). https://doi.org/10.5281/zenodo.2573505
Brydges, T., Elben, A., Jurcevic, P., Vermersch, B., Maier, C., Lanyon, B.P., Zoller, P., Blatt, R., Roos, C.F.: Probing Rényi entanglement entropy via randomized measurements. Science 364, 260 (2019). https://doi.org/10.1126/science.aau4963
Dieguez, P.R., Guimarães, J.R., Peterson, J.P., Angelo, R.M., Serra, R.M.: Experimental assessment of physical realism in a quantum-controlled device. Commun. Phys. 5, 1 (2022). https://doi.org/10.1038/s42005-022-00828-z
Acknowledgements
This work was supported in part by the National Science and Technology Council, Taiwan under the Grants 111-2112-M-004-008, 111-2119-M-007-009, 110-2112-M-110-015, 111-2112-M-110-013, 111-2119-M-002-012, and 112-2119-M-002-017. The availability of accessing the IBM Quantum cloud services via the IBM Q Hub at National Taiwan University is gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The two authors contributed equally.
Appendices
Appendix A: An elementary account of (4.17)
It is notable that the complementarity relation (4.17) from the separate subensemble perspective is saturated to unity. Its meaning and significance can be understood in view of the triality relation (5.12) as discussed in Sec. 5.2. Here, we present a simple account for (4.17).
First, we express the state at slice 5 in Fig. 2 in the generic form
The state at slice 6 is then given by
The contrast for the \(0_d\) subensemble defined in (4.10) is computed from \(\vert {\psi _6}\rangle \) as
Because the phase gate \(P(\theta )\) acting on the interference qubit, we have \(a^*b+ab^*=2|a||b|\cos \theta \). Consequently, the visibility \({\mathcal {V}}_{0_d}\) defined in (4.11) is given by
Meanwhile, the distinguishability for the \(0_d\) subensemble defined in (4.16) is computed from \(\vert {\psi _5}\rangle \) as
It follows that \({\mathcal {D}}_{0_d}^2+{\mathcal {V}}_{0_d}^2=1\). In the subensemble perspective, the complimentary relation always saturates.
Appendix B: System calibration data
The experimental results presented in the main text are performed on ibm_auckland, and more experimental results presented in Appendix C are performed on ibmq_toronto. Both ibm_auckland and ibmq_toronto share the same qubit layout as shown in Fig. 14.Footnote 21
The interference visibility and path distinguishability in the total-ensemble perspective on ibmq_toronto with \(t_\text {delay}=0\) (a–c) and \(t_\text {delay}=100\,\text {dt}\) (d–f). From the left to right columns, \(\phi ^{\prime }=0\), \(0.25\pi \), and \(0.5\pi \) The calibration data of the selected physical qubits for the pairs we have chosen. The data were retrieved directly from the IBM Quantum website on the same days of the experiments. \(T_1\) is the longitudinal (thermal) relaxation time, and \(T_2\) is the transverse (dephasing) relaxation time
We select three different pairs for our “i” and “d” qubits: (i) physical qubits 4 and 7 on ibm_auckland, (ii) physical qubits 1 and 4 on ibm_auckland, and (iii) physical qubits 1 and 4 on ibmq_toronto. The calibration data of these pairs were retrieved directly from the IBM Q website on the same days of the experiments and are reported in Table 1. Pair (i) is used for Fig. 4, 5, 6. Pair (ii) is used for Fig. 3 and Figs. 7, 8, 9, 10, 11, 12 , 13. Pair (iii) is used for the figures in Appendix C.
More experimental data
In order to know more about the nature of noises in the real devices of IBM Quantum, in addition to experiments performed on ibm_auckland, we also perform experiments on ibmq_toronto for comparison.
The experimental results on ibmq_toronto from the total ensemble perspective, the average perspective, and the subensemble perspective are presented in Figs. 15, 16, and 17, respectively. The top panels (a–c) show the results with the delay time \(t_{\text {delay}}=0\,\text {dt}\) in the delay gate, while the bottom panels (d–f) show the results with \(t_{\text {delay}}=100\,\text {dt}\). Compared with the experimental results performed on ibm_auckland as presented in the main text, the visibility and distinguishability are much noisier. Moreover, the time delay has stronger effect on ibmq_toronto than on ibm_auckland: the effect is appreciable with \(t_{\text {delay}}\sim 100\,\text {dt}\) on the former, but it is not appreciable until \(t_{\text {delay}}\sim 10^5\,\text {dt}\) on the latter. The fact that ibmq_toronto is much noisier than ibm_auckland is in agreement with the fact that the former has shorter relaxation times and a larger CNOT error rate, according to the daily calibration data provided by IBM Quantum as shown in Table 1.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Chiou, DW., Hsu, HC. Complementarity relations of a delayed-choice quantum eraser in a quantum circuit. Quantum Inf Process 23, 18 (2024). https://doi.org/10.1007/s11128-023-04214-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11128-023-04214-8