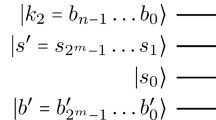Quantum circuits for discrete-time quantum walks with position-dependent coin operator

Abstract

The aim of this paper is to build quantum circuits that implement discrete-time quantum walks having an arbitrary position-dependent coin operator. The position of the walker is encoded in base 2: with n wires, each corresponding to one qubit, we encode $2^n$ position states. The data necessary to define an arbitrary position-dependent coin operator is therefore exponential in n. Hence, the exponentiality will necessarily appear somewhere in our circuits. We first propose a circuit implementing the position-dependent coin operator, that is naive, in the sense that it has exponential depth and implements sequentially all appropriate position-dependent coin operators. We then propose a circuit that “transfers” all the depth into ancillae, yielding a final depth that is linear in n at the cost of an exponential number of ancillae. The main idea of this linear-depth circuit is to implement in parallel all coin operators at the different positions. Reducing the depth exponentially at the cost of having an exponential number of ancillae is a goal which has already been achieved for the problem of loading classical data on a quantum circuit (Araujo in Sci Rep 11:6329, 2021) (notice that such a circuit can be used to load the initial state of the walker). Here, we achieve this goal for the problem of applying a position-dependent coin operator in a discrete-time quantum walk. Finally, we extend the result of Welch (New J Phys 16:033040, 2014) from position-dependent unitaries which are diagonal in the position basis to position-dependent $2\times 2$-block-diagonal unitaries: indeed, we show that for a position dependence of the coin operator (the block-diagonal unitary) which is smooth enough, one can find an efficient quantum-circuit implementation approximating the coin operator up to an error $\epsilon$ (in terms of the spectral norm), the depth and size of which scale as $O(1/\epsilon )$. A typical application of the efficient implementation would be the quantum simulation of a relativistic spin-1/2 particle on a lattice, coupled to a smooth external gauge field; notice that recently, quantum spatial-search schemes have been developed which use gauge fields as the oracle, to mark the vertex to be found (Zylberman in Entropy 23:1441, 2021), (Fredon arXiv:2210.13920). A typical application of the linear-depth circuit would be when there is spatial noise on the coin operator (and hence a non-smooth dependence in the position).

Appendices

Appendix A: Fujiwara et al.’s scheme, also called increment and decrement (ID) scheme, for the shift operator

In the case of a uniform total coin operator, i.e., when for each k, $C_k = C$, then the total coin operator given by Eq. (8) reads

$$\begin{aligned} {C}^{(n)}_{\text {unif.}} = I_{2^n} \otimes C. \end{aligned}$$

(A1)

What is proven in Ref. [80] is that ${W}^{(n)}$ can be implemented by the following circuit,

$$\begin{aligned} {W}^{(n)} = D^{(n)} {C}^{(n)}_{\text {unif.}}, \end{aligned}$$

(A2)

since the displacement operator $D^{(n)}$, also called increment and decrement (ID) scheme, can be shown to be equal to the coin-dependent shift operator ${S}^{(n)}$ (see Ref. [80]), i.e.,

$$\begin{aligned} D^{(n)} = {S}^{(n)}, \end{aligned}$$

(A3)

and it is defined by

$$\begin{aligned} D^{(n)} {:}{=}K_1^{n}(Z^{n}_{\uparrow }) (I_{2^n} \otimes X) K_1^{n}(Z^{n}_{\downarrow }) (I_{2^n} \otimes X), \end{aligned}$$

(A4)

where $K_m^{m'}(M)$ is the application of the gate M occupying $m'$ wires and being controlled by the first m wires starting from wire 0, where $X = \sigma ^1 = \begin{bmatrix} 0 &{} 1 \\ 1 &{} 0 \end{bmatrix}$, and where the left and right displacement operators are respectively defined by

$$\begin{aligned} Z^{n}_{\uparrow }&{:}{=}\mathop {{\mathop {\prod }\nolimits ^L}}\limits _{p=0}^{n-1} I_{2^{n-1-p}} \otimes K_p^{1}(X) \end{aligned}$$

(A5a)

$$\begin{aligned} Z^{n}_{\downarrow }&{:}{=}\mathop {{\mathop {\prod }\nolimits ^R}}\limits _{p=0}^{n-1} I_{2^{n-1-p}} \otimes K_p^{1}(X) \, , \end{aligned}$$

(A5b)

where the superscripts L and R mean respectively that the product is performed from right to left (and hence towards the left) or from left to right (and hence towards the right).

In Fig. 12 we show the circuits implementing the left and right shift operators, respectively $Z^n_{\uparrow }$ and $Z^n_{\downarrow }$, defined respectively Eqs. (A5a) and (A5b), and in Fig. 13 we show the circuit implementing the uniform DQW characterized by the walk operator of Eq. (A2).

Fig. 12

Circuits implementing the left (left figure) and right (right figure) shift operators, respectively $Z^n_{\uparrow }$ and $Z^n_{\downarrow }$, defined respectively in Eqs. (A5a) and (A5b), introduced in Ref. [80]

Fig. 13

Circuit implementing the uniform discrete-time quantum walk characterized by the walk operator of Eq. (A2), introduced in Ref.  [80]

Appendix B: Proof of $U^{(n)} = {C}^{(n)}$, by induction on n

It is easy to show that $U^{(1)} = {C}^{(1)}$. Let us now show that assuming $U^{(n)} = {C}^{(n)}$ for a certain n implies $U^{(n+1)} = {C}^{(n+1)}$. We start by expressing $U^{(n+1)}$, given by Eq.  (17), as the product of two circuits,

$$\begin{aligned} U^{(n+1)} = P^{(1)}_{n+1} P^{(0)}_{n+1}, \end{aligned}$$

(B1)

where

$$\begin{aligned} P^{(a)}_{n+1} {:}{=}\mathop {{\mathop {\prod }\nolimits ^L}}\limits _{k=0}^{2^n-1} G_{n+1}(C_{2^na + k}) T_{n+1}(k). \end{aligned}$$

(B2)

Considering the definition of the towers $T_n$ given in Eq. (18b), it makes sense to write $P^{(a)}_{n+1}$ given in Eq. (B2) as

$$\begin{aligned} P_{n+1}^{(a)} = \Big \{ \, \mathop {{\mathop {\prod }\nolimits ^L}}\limits _{k=1}^{2^n-1} G_{n+1}(C_{2^na + k}) T_{n+1}(k) \Big \} \Big \{ G_{n+1}(C_{2^na}) T_{n+1}(0) \Big \} \end{aligned}$$

(B3)

Now, using the definitions of Eqs. (18b) and (20b), we can rewrite Eq. (B3) as

$$\begin{aligned}&P_{n+1}^{(a)} = \Bigg \{ \, \mathop {{\mathop {\prod }\nolimits ^L}}\limits _{k=1}^{2^n-1} \begin{bmatrix} I_{2^{n+1}} &{} 0 \\ 0 &{} G_n(C_{2^n a + k}) \end{bmatrix} \begin{bmatrix} T_n(k \ \text {mod} \ 2^{n-1} ) &{} 0 \\ 0 &{} T_n(k \ \text {mod} \ 2^{n-1} ) \end{bmatrix} \Bigg \}\nonumber \\&\Bigg \{ \begin{bmatrix} I_{2^{n+1}} &{} 0 \\ 0 &{} G_n(C_{2^n a}) \end{bmatrix} \begin{bmatrix} 0 &{} T_n(0) \\ T_n(0) &{} 0 \end{bmatrix} \Bigg \} \end{aligned}$$

(B4a)

$$\begin{aligned}&= \Bigg \{ \, \mathop {{\mathop {\prod }\nolimits ^L}}\limits _{k=1}^{2^n-1} \begin{bmatrix} T_n(k \ \text {mod} \ 2^{n-1} ) &{} 0 \\ 0 &{} G_n(C_{2^n a + k}) T_n(k \ \text {mod} \ 2^{n-1} ) \end{bmatrix} \Bigg \} \begin{bmatrix} 0 &{} T_n(0) \\ G_n(C_{2^n a}) T_n(0) &{} 0 \end{bmatrix} \, . \end{aligned}$$

(B4b)

Now, it is easy to show the following formula,

$$\begin{aligned} \begin{bmatrix} A_N &{} 0 \\ 0 &{} B_N \end{bmatrix} \cdots \begin{bmatrix} A_1 &{} 0 \\ 0 &{} B_1 \end{bmatrix} \begin{bmatrix} 0 &{} D \\ C &{} 0 \end{bmatrix} = \begin{bmatrix} 0 &{} A_N... A_1 D \\ B_N... B_1 C &{} 0 \end{bmatrix}, \end{aligned}$$

(B5)

which, applied to Eq. (B4b), leads to

$$\begin{aligned} P^{(a)}_{n+1} = \begin{bmatrix} 0 &{} Q_n \\ R_n^{(a)} &{} 0 \end{bmatrix}, \end{aligned}$$

(B6)

with

$$\begin{aligned} Q_n&{:}{=}\mathop {{\mathop {\prod }\nolimits ^L}}\limits _{k=0}^{2^n-1} T_n( k \ \text {mod} \ 2^{n-1} ) \end{aligned}$$

(B7a)

$$\begin{aligned} R_n^{(a)}&{:}{=}\mathop {{\mathop {\prod }\nolimits ^L}}\limits _{k=0}^{2^n-1} G_n(C_{2^na+k}) T_n( k \ \text {mod} \ 2^{n-1} ) \, . \end{aligned}$$

(B7b)

We immediately notice, see Eq. (17), that

$$\begin{aligned} R_n^{(0)} = U^{(n)}, \end{aligned}$$

(B8)

which by induction assumption is equal to ${C}^{(n)}$, and we also have that

$$\begin{aligned} R_n^{(1)} = \mathop {{\mathop {\prod }\nolimits ^L}}\limits _{k=0}^{2^n-1} G_n(C_{2^n+k}) T_n( k \ \text {mod} \ 2^{n-1} ), \end{aligned}$$

(B9)

so that we can also use the induction assumption and obtain

$$\begin{aligned} R_n^{(1)} = {C}^{(n)}_{\text {bis}}, \end{aligned}$$

(B10)

with

$$\begin{aligned} {C}^{(n)}_{\text {bis}} {:}{=}\sum _{k=2^n}^{2^{n+1}-1} \mathinner {|{k_2}\rangle } \! \! \mathinner {\langle {k_2}|} \Big |_{{\mathcal {S}}} \otimes {\tilde{C}}_{k_2} = \begin{bmatrix} C_{2^n} &{} &{} 0 \\ &{} \ddots &{} \\ 0 &{} &{} C_{2^{n+1}-1} \end{bmatrix}, \end{aligned}$$

(B11)

where $\mathinner {|{k_2}\rangle } \! \! \mathinner {\langle {k_2}|} \Big |_{{\mathcal {S}}}$ means that we consider the operator $\mathinner {|{k_2}\rangle } \! \! \mathinner {\langle {k_2}|}$ restricted to the subspace ${\mathcal {S}}$ formed by the vectors $\mathinner {|{k_2}\rangle }$ for $k_2=2^n,...,2^{n+1}-1$. Moreover, it is easy to show by induction on n that

$$\begin{aligned} Q_n = I_{2^n}. \end{aligned}$$

(B12)

Hence, using Eq. (B6) for $a=0$ and 1 in Eq. (B1) leads to

$$\begin{aligned} U^{(n+1)}&= \begin{bmatrix} 0 &{} I_{2^n} \\ {C}^{(n)}_{\text {bis}} &{} 0 \end{bmatrix} \begin{bmatrix} 0 &{} I_{2^n} \\ {C}^{(n)} &{} 0 \end{bmatrix} \end{aligned}$$

(B13a)

$$\begin{aligned}&= \begin{bmatrix} {C}^{(n)} &{} 0 \\ 0 &{} {C}^{(n)}_{\text {bis}} \end{bmatrix} \end{aligned}$$

(B13b)

$$\begin{aligned}&= {C}^{(n+1)} \, , \end{aligned}$$

(B13c)

which completes the proof.

Appendix C: Initializing the ancillary positions: $Q_1$

1.1 Basic requirement on $Q_1$

Let $\mathinner {|{K}\rangle }$ be a state of the following form,

$$\begin{aligned} \mathinner {|{K}\rangle } {:}{=}\mathinner {|{k_2}\rangle } \mathinner {|{s_0}\rangle } \mathinner {|{s'=0}\rangle } \mathinner {|{b'=0}\rangle }. \end{aligned}$$

(C1)

We want a unitary operator $Q_1$ which acts on states $\mathinner {|{K}\rangle }$ of the form of Eq. (C1) as follows,

$$\begin{aligned} \begin{aligned}&Q_1 \left( \mathinner {|{k_2}\rangle } \mathinner {|{s_0}\rangle } \mathinner {|{s'=0}\rangle } \mathinner {|{b'=0}\rangle } \right) \\&\ \ \ \ \ \ \ \ \ \ = \mathinner {|{k_2}\rangle } \mathinner {|{s_0}\rangle } \mathinner {|{s'=0}\rangle } \mathinner {|{(2^{k})_2}\rangle }, \end{aligned} \end{aligned}$$

(C2)

where we have used the notation

$$\begin{aligned} \mathinner {|{(2^{k})_2}\rangle } {:}{=}| \underbrace{0...0(b'_k=1)0...0 }_{ 2^n \ \text {locations}} \rangle . \end{aligned}$$

(C3)

In simple words, the action of $Q_1$ on such a state $\mathinner {|{K}\rangle }$ is to change the kth bit of $\mathinner {|{b'}\rangle }$ from $b'_k=0$ to $b'_k=1$.

Fig. 14

Diagrammatic representation of the naive scheme for $Q_1$ for $n=1$ (left figure), $n=2$ (middle figure), and $n=3$ (right figure). In this naive scheme, all operations inside a same blue box cannot be executed in parallel (except of course for the depth-1 box), which makes the circuit depth exponential in the number of position wires. We remedy this problem by parallelizing these circuits, see Fig. 15

1.2 Naive scheme

We want an operator $Q_1$ that is unitary and that satisfies Eq. (C2); we call this a valid $Q_1$. We are going to prove that the circuit depicted in Fig. 14 for $n=1,2,3$, is a valid $Q_1$ for any n.

1.2.1 Definition / Construction

We use the notation

$$\begin{aligned} {\textbf{Q}}^{(n)}_1 {:}{=}{Q}_1, \end{aligned}$$

(C4)

which makes explicit the dependence in n. We define ${\textbf{Q}}^{(n)}_1$ by induction as follows:

$$\begin{aligned} {\textbf{Q}}^{(1)}_1&{:}{=}E^{b_0}_{b'_0,b'_1} (I_{2} \otimes I_{2} \otimes I_2 \otimes I_2 \otimes X) \end{aligned}$$

(C5a)

$$\begin{aligned} {\textbf{Q}}^{(n+1)}_1&{:}{=}B^{(n+1)} {\textbf{Q}}^{(n)}_1 \, , \end{aligned}$$

(C5b)

with

$$\begin{aligned} B^{(n+1)} {:}{=}\mathop {{\mathop {\prod }\nolimits ^L}}\limits _{i=0}^{2^n-1} E^{b_n}_{b'_i,b'_{i+2^n}}. \end{aligned}$$

(C6)

In Eqs. (C5a) and (C6), we have introduced the controlled exchange (i.e., SWAP) operators $E^{b_n}_{b'_i,b'_{i+2^n}}$, that swap $b'_i$ and $b'_{i+2^n}$ controlling on $b_n$. In Eqs. (C5a) and (C6), we have purposely omitted to multiply the $E^{b_n}_{b'_i,b'_{i+2^n}}$ operators by the appropriate identity tensor factors, in order to lighten the notations. In Eq. (C5b), we have also purposely omitted to multiply ${\textbf{Q}}^{(n)}_1$ by the appropriate identity tensor factors, again in order to lighten the notations.

1.2.2 Proof

Let us prove by induction on n that the operator ${\textbf{Q}}^{(n)}_1$ defined by Eqs. (C5) is a valid $Q_1$ operator, i.e., is unitary and satisfies Eq. (C2). Unitarity is trivial by induction, let us then show the main validity condition.

Let us start by $n=1$, see Eq. (C5a). Let us also start with a state $\mathinner {|{K}\rangle }$ of the form of Eq. (C1), and let us apply ${\textbf{Q}}^{(1)}_1$. After the X gate on $\mathinner {|{b_0'}\rangle }$, we have that $b'_0 = 1$. Now, if $k=b_0=0$, then the SWAP operation $E^{b_0}_{b'_0,b'_1}$ acts as the identity, and we stay with $b'_0=1$ and $b'_1=0$, which is what we want, i.e., $\mathinner {|{b'=(2^k)_2}\rangle }=\mathinner {|{01}\rangle }$. But, if $k=b_0=1$, then the SWAP operation $E^{b_0}_{b'_0,b'_1}$ does swap $b'_0$ and $b'_1$, so that we obtain $b'_0=0$ and $b'_1=1$, which is what we want, i.e., $\mathinner {|{b'=(2^k)_2}\rangle }=\mathinner {|{10}\rangle }$. This completes the proof for $n=1$.

Let us now assume that Eq. (C2) is true for $Q_1 = {\textbf{Q}}^{(n)}_1$, and let us show that this implies that it is also true for $Q_1 = {\textbf{Q}}^{(n+1)}_1$. There are two situations to be distinguished: either (i) $k \le 2^n-1$, or (ii) $k\ge 2^n$. Let us consider situation (i). We have that

$$\begin{aligned} {\textbf{Q}}^{(n+1)}_1 \mathinner {|{K}\rangle }&\equiv B^{(n+1)} {\textbf{Q}}^{(n)}_1 \mathinner {|{K}\rangle } \end{aligned}$$

(C7a)

$$\begin{aligned}&= B^{(n+1)} \left( \mathinner {|{k_2}\rangle } \mathinner {|{s_0}\rangle }\mathinner {|{s'=0}\rangle } \mathinner {|{(2^k)_2}\rangle }\right) \, , \end{aligned}$$

(C7b)

where the first equality (C7a) holds by definition of ${\textbf{Q}}^{(n+1)}_1$ in Eq. (C5b), and the second equality (C7b) holds by induction assumption (it is trivial that this assumption holds when augmenting the Hilbert space from n to $n+1$). We thus now have to prove that $B^{(n+1)}$ acts as the identity (because the state $\mathinner {|{k_2}\rangle } \mathinner {|{s_0}\rangle }\mathinner {|{s'=0}\rangle } \mathinner {|{(2^k)_2}\rangle }$ is already what we want): this is trivial because all operations in $B^{(n+1)}$ are controlled by $b_n$, but since $k\le 2^n-1$ we have that $b_n=0$, so that $B^{(n+1)}$ indeed acts as the identity, which completes the proof for $k\le 2^n-1$.

Let us now treat situation (ii), $k\ge 2^n$. We have that

$$\begin{aligned} k = \underbrace{1}_{=b_n} \times 2^n + l, \end{aligned}$$

(C8)

where

$$\begin{aligned} l {:}{=}b_{n-1} 2^{n-1} + \dots + b_1 2^1 + b_0. \end{aligned}$$

(C9)

Now, ${\textbf{Q}}^{(n)}_1$ acting on the appropriate total Hilbert space for $n+1$ is blind to what is on $\mathinner {|{b_n}\rangle }$, and so it simply does by induction assumption what it would do on the Hilbert space for n, that is, it encodes $\mathinner {|{l}\rangle }$ on the ancillary positions, that is,

$$\begin{aligned} {\textbf{Q}}^{(n+1)}_1 \mathinner {|{K}\rangle }&\equiv B^{(n+1)} {\textbf{Q}}^{(n)}_1 \left( \mathinner {|{(2^n+l)_2}\rangle } \mathinner {|{s_0}\rangle }\mathinner {|{s'=0}\rangle } \mathinner {|{(b'=0}\rangle } \right) \end{aligned}$$

(C10a)

$$\begin{aligned}&= B^{(n+1)} \left( \mathinner {|{(2^n+l)_2}\rangle } \mathinner {|{s_0}\rangle }\mathinner {|{s'=0}\rangle } \mathinner {|{(2^l)_2}\rangle }\right) \, , \end{aligned}$$

(C10b)

where the first equality (C10a) holds by definition of ${\textbf{Q}}^{(n+1)}_1$ in Eq. (C5b), and the second equality (C10b) holds by induction assumption as we have just explained above. We now have to prove that $B^{(n+1)}$ swaps the $b'_l=1$ that is on the ancillary position l in $\mathinner {|{b'}\rangle }$ with $b'_{2^n+l}=0$. But this is almost immediate since because $k\ge 2^n$ we have that $b_n=1$ so all the SWAP operations of $B^{(n+1)}$ do swap the relevant qubits, that is, by definition, they scan one by one the $b'_i$s ($i \le 2^n-1$) and swap them with their corresponding $b'_{i+2^n}$, an operation which is the identity since all ancillary qubits are 0 except precisely for $b'_l=1$: hence, Eq. (C10b) delivers

$$\begin{aligned} \begin{aligned}&B^{(n+1)} \left( \mathinner {|{(2^n+l)_2}\rangle } \mathinner {|{s_0}\rangle }\mathinner {|{s'=0}\rangle } \mathinner {|{(2^l)_2}\rangle }\right) \\&\ \ \ \ \ \ = \mathinner {|{(2^n+l)_2}\rangle } \mathinner {|{s_0}\rangle }\mathinner {|{s'=0}\rangle } \mathinner {|{(2^{2^n+l})_2}\rangle }, \end{aligned} \end{aligned}$$

(C11)

which completes the proof for $k\ge 2^n$.

Fig. 15

Diagrammatic representation of the parallelized scheme for $Q_1$ for $n=1$ (top left figure), $n=2$ (top middle figure), $n=3$ (top right figure), and $n=4$ (bottom figure). In this parallelized scheme, all operations inside a same blue or green box can be executed in parallel, which makes the total depth of the circuit linear in n

Fig. 16

Diagrammatic representation of the parallelized scheme for $Q_1$, for $n=5$. In this parallelized scheme, all operations inside a same blue or green box can be executed in parallel, which makes the total depth of the circuit linear in n

1.3 Parallelized scheme

The circuit depicted in Fig. 14 and defined via Eqs. (C5) implements a valid $Q_1$, but its depth is exponential in the number of position wires, i.e., in n, as it can be seen in Eq. (C6), since the product goes up to $i=2^n-1$ and all the SWAPs it implements are controlled on the same position qubit $b_{n-1}$. We want to parallelize these SWAP operations. For that, our idea is to copy the information contained in the position qubits onto the ancillary coins, which are available and in exponential number, and from the resulting ancillary coins we can initialize all ancillary positions at once as wished, since each SWAP can be controlled on a different ancillary coin, on which an appropriate copy of a position qubit has been done, after which we undo the copy operations performed on the ancillary coins.

Such a parallelized circuit is shown in Fig. 15 for $n=1$ to 4, and in Fig. 16 for $n=5$.

1.3.1 Definition / Construction

The parallelized circuit is defined as

$$\begin{aligned} Q_1 = Q_{10}^{\dag } Q_{11} Q_{10}, \end{aligned}$$

(C12)

where $Q_{10}$ corresponds to the operation of doing copies of the position qubits onto the ancillary coins, which we call “copies operation”, and $Q_{11}$ corresponds to the parallelized controlled SWAPs. With $Q_{10}^{\dag }$ we undo the copies, so that after $Q_{10}^{\dag }$ all the ancillary coins $s_i$ are set back to 0, as they were before applying $Q_{10}$.

The copies operation is performed with a series of CNOT gates applied appropriately; it is defined as follows,

$$\begin{aligned} Q_{10} {:}{=}\mathop {{\mathop {\prod }\nolimits ^L}}\limits _{i=0}^{n-2} Q^{(i)}_{10} \, , \end{aligned}$$

(C13)

where, for $i\ge 0$,

$$\begin{aligned} Q_{10}^{(i)} {:}{=}\mathop {{\mathop {\prod }\nolimits ^L}}\limits _{m=i+1}^{n-1} J_m^{(i)}, \end{aligned}$$

(C14)

with

$$\begin{aligned}&\ \ \, J_m^{(0)} {:}{=}K_{b_m,s_{l_m}}(X) \end{aligned}$$

(C15a)

$$\begin{aligned}&J_m^{(i\ge 1)} {:}{=}&\left( \mathop {{\mathop {\prod }\nolimits ^L}}\limits _{l'=0}^{2^i-2} K_{s_{l_m+l'},s_{l_m+l'+2^i}}(X) \right) K_{b_m,s_{l_m+\sum _{u=1}^i 2^{u-1}}}(X) \, , \end{aligned}$$

(C15b)

and where we have defined

$$\begin{aligned} l_0&{:}{=}1 \end{aligned}$$

(C16a)

$$\begin{aligned} l_m&{:}{=}2^{m-1}-1 + l_{m-1} \ \ \text {for} \ m \ge 1 \, . \end{aligned}$$

(C16b)

One can convince oneself that the copies operation (i) copies as many position qubits as needed on the ancillary coins, and (ii) is linear in n, since it doubles the number of copies performed at each incremented i in Eq. (C13).

It is easy to define $Q_{11}$ from Figs. 15 and 16: the difference with the naive scheme is that this time each SWAP is controlled on a different ancillary coin (instead of on the same position qubit an exponential number of times), so that all these SWAPs can be applied simultaneously.

Appendix D: Initializing the ancillary coins: $Q_2$

1.1 Basic requirement on $Q_2$

The operator $Q_1$ acts as Eq. (C2) on states $\mathinner {|{K}\rangle }$, so on states $\mathinner {|{S}\rangle }$ of the form of Eq. (27) it acts as

$$\begin{aligned} Q_1 \mathinner {|{S}\rangle } = \sum _{k=0}^{2^n-1} \sum _{s_0=0,1} \alpha _{k,s_0} \mathinner {|{k_2}\rangle } \mathinner {|{s_0}\rangle } \mathinner {|{s'=0}\rangle } \mathinner {|{(2^k)_2}\rangle }. \end{aligned}$$

(D1)

Equation (D1) is the most general form of the state at the output of $Q_1$, and we want a unitary operator $Q_2$ which acts as follows on such a state:

$$\begin{aligned}&Q_2 \left( Q_1 \mathinner {|{S}\rangle } \right) \equiv \sum _{k=0}^{2^n-1} Q_2 \left[ \mathinner {|{k_2}\rangle } \left( \sum _{s_0=0,1} \alpha _{k,s_0} \mathinner {|{s_0}\rangle } \right) \mathinner {|{s'=0}\rangle } \mathinner {|{(2^k)_2}\rangle }\right] \nonumber \\&\quad = \sum _{k=0}^{2^n-1} \mathinner {|{k_2}\rangle } \mathinner {|{s_{2^n-1}=0}\rangle } ... \mathinner {|{s_{k+1}=0}\rangle } \! \nonumber \\&\quad \left( \sum _{s_0=0,1} \alpha _{k,s_0} \mathinner {|{s_0}\rangle } \right) \! \mathinner {|{s_{k-1}=0}\rangle } ... \mathinner {|{s_0=0}\rangle } \mathinner {|{(2^k)_2}\rangle } \, . \end{aligned}$$

(D2)

That is, $Q_2$ replaces the superposition that is on the 0th coin by $\mathinner {|{0}\rangle }$, and puts this superposition on the kth coin instead of $\mathinner {|{s_{k}=0}\rangle }$.

Fig. 17

Diagrammatic representation of $Q_2$ for $n=1$ (top left figure), $n=2$ (top middle figure), $n=3$ (top right figure), and $n=4$ (bottom figure). All operations inside a same green box can be executed in parallel, which makes the total depth of the circuit linear in n

1.2 Definition / Construction of $Q_2$

We want an operator $Q_2$ that is unitary and that satisfies Eq. (D2); we call this a valid $Q_2$.

We could use the position qubits in order to initialize the ancillary coins, similarly to how we have used them to initialize the ancillary positions, but then in order to parallelize the operations we would have to do copies as we have done to initialize the ancillary positions. Instead, we are going to use the ancillary position qubits (which already contain all the information of the position qubits) to initialize the ancillary coins.

One can show that the circuit depicted in Fig. 17 for $n=1,2,3,4$, is a valid $Q_2$. Let us briefly outline the proof, but before, let us define that circuit.

We use the notation

$$\begin{aligned} {\textbf{Q}}^{(n)}_2 {:}{=}Q_2, \end{aligned}$$

(D3)

which makes explicit the dependence in n. We define $Q_2$ by induction as follows:

$$\begin{aligned} {\textbf{Q}}^{(1)}_2&{:}{=}E^{b'_1}_{s_0,s_1} \end{aligned}$$

(D4a)

$$\begin{aligned} {\textbf{Q}}^{(n+1)}_2&{:}{=}M^{(n+1)} V^{(n+1)} F({\textbf{Q}}^{(n)}_2) V^{(n+1)} \, , \end{aligned}$$

(D4b)

where

$$\begin{aligned} V^{(n+1)}&{:}{=}\bigotimes _{m=1}^{2^n-1} K_{b'_{2m},b'_{2m+1}}(X) \end{aligned}$$

(D5a)

$$\begin{aligned} M^{(n+1)}&{:}{=}\bigotimes _{l=0}^{2^n-1} E^{b'_{1+2l}}_{s_{2l},s_{1+2l}} \, , \end{aligned}$$

(D5b)

and where F(.) takes the circuit ${\textbf{Q}}^{(n)}_2$ and multiplies by 2 all “heights”, that is, it performs a vertical homothety, or dilation, of factor 2, with center on $s_0$ and $b'_{2^n-1}$. In Eqs. (D4a) and (D5), we have purposely omitted the various tensor factors $I_2$ on all remaining qubits, in order to lighten notations.

Let us explain a bit how ${\textbf{Q}}^{(n+1)}_2$ works, i.e., let us outline the proof to show that the circuit defined via Eqs. (D4) is a valid $Q_2$. If we apply solely $F({\textbf{Q}}^{(n)}_2)$ to an input state for which the auxiliary position $b'_k$ that is “turned on” (i.e., the value of which is 1) is even, i.e., $k=2p$ with p an integer, no operation is performed. If we now apply this $F({\textbf{Q}}^{(n)}_2)$ to an input state for which $b'_k=1$ for k odd, then the auxiliary coins which are swapped are $s_0$ and $s_{k-1}$ (and recall that we want $s_k$ instead of $s_{k-1}$). Thanks to $V^{(n+1)} \cdot V^{(n+1)}$, applying $V^{(n+1)} F({\textbf{Q}}^{(n)}_2) V^{(n+1)}$ to an input state for which $b'_k=1$ for k even does swap $s_0$ and $s_k$, without the need of $M^{(n+1)}$. What $M^{(n+1)}$ does is to have the auxiliary coin that is exchanged with $s_0$ when $b'_k=1$ for k odd, pass from $s_{k-1}$ to $s_k$; $M^{(n+1)}$ only acts on odd auxiliary positions.

The depth of both $V^{(n+1)}$ and $M^{(n+1)}$ is 1, and that of $F({\textbf{Q}}^{(n)}_2)$ is the same as that of ${\textbf{Q}}^{(n)}_2$, so that the depth of $Q_2$ is linear in n.

Appendix E: Proof that $U^{(n)}_{\mathrm {lin.}}$ coincides with ${C}^{(n)}$ on all relevant states

On the one hand, the state at the output of $Q_2$ has the form of Eq. (D2). On the other hand, $Q_0$ is defined by Eq. (24). So, $Q_0$ acting on $Q_2Q_1 \mathinner {|{S}\rangle }$ gives

$$\begin{aligned}&Q_0Q_2Q_1 \mathinner {|{S}\rangle } = \sum _{k=0}^{2^n-1} \mathinner {|{k_2}\rangle } \mathinner {|{s_{2^n-1}=0}\rangle }... \mathinner {|{s_{k+1}=0}\rangle } \nonumber \\&\quad \left( C_k \sum _{s_0=0,1} \alpha _{k,s_0} \mathinner {|{s_0}\rangle } \right) \mathinner {|{s_{k-1}=0}\rangle }... \mathinner {|{s_0=0}\rangle } \mathinner {|{(2^k)_2}\rangle } \end{aligned}$$

(E1)

We know from Eq. (D2) how $Q_2^{-1}$ acts on states of the form of the right-hand side of Eq. (D2), that is, states that can be written under the form $Q_2 Q_1 \mathinner {|{S}\rangle }$. Now, because each $C_k$ is unitary, it is easy to prove that the state $Q_0 Q_2 Q_1 \mathinner {|{S}\rangle }$ is also of the form of the right-hand side of Eq. (D2), i.e., it is a state of the form

$$\begin{aligned}{} & {} Q_0Q_2Q_1 \mathinner {|{S}\rangle } = \sum _{k=0}^{2^n-1} \mathinner {|{k_2}\rangle } \mathinner {|{s_{2^n-1}=0}\rangle }... \mathinner {|{s_{k+1}=0}\rangle } \left( \sum _{s_0=0,1} {\tilde{\alpha }}_{k,s_0} \mathinner {|{s_0}\rangle } \right) \nonumber \\{} & {} \quad \mathinner {|{s_{k-1}=0}\rangle }... \mathinner {|{s_0=0}\rangle } \mathinner {|{(2^k)_2}\rangle }, \end{aligned}$$

(E2)

with $\sum _{k=0}^{2^n-1} \sum _{s_0=0,1} |{\tilde{\alpha }}_{k,s_0}|^2 = \sum _{k=0}^{2^n-1} \sum _{s_0=0,1} |{\alpha }_{k,s_0}|^2 = 1$. Hence, we know that

$$\begin{aligned} Q_2^{-1} Q_0Q_2Q_1 \mathinner {|{S}\rangle }&= \sum _{k=0}^{2^n-1} \mathinner {|{k_2}\rangle } \left( \sum _{s_0=0,1} {\tilde{\alpha }}_{k,s_0} \mathinner {|{s_0}\rangle } \right) \mathinner {|{s'=0}\rangle } \mathinner {|{(2^k)_2}\rangle } \end{aligned}$$

(E3a)

$$\begin{aligned}&= \sum _{k=0}^{2^n-1} \sum _{s_0=0,1} {\tilde{\alpha }}_{k,s_0} \mathinner {|{k_2}\rangle } \mathinner {|{s_0}\rangle } \mathinner {|{s'=0}\rangle } \mathinner {|{(2^k)_2}\rangle } \, . \end{aligned}$$

(E3b)

We know from Eq. (D1) how $Q_1^{-1}$ acts on states of the form of Eq. (E3b) (i.e., of the form $Q_1 \mathinner {|{S}\rangle }$). Hence, applying $Q_1^{-1}$ to $Q_2^{-1} Q_0Q_2Q_1 \mathinner {|{S}\rangle }$ given by Eq. (E3b) yields

$$\begin{aligned}&Q_1^{-1} Q_2^{-1} Q_0 Q_2 Q_1 \mathinner {|{S}\rangle } = \sum _{k=0}^{2^n-1} \sum _{s_0=0,1} {\tilde{\alpha }}_{k,s_0} \mathinner {|{k_2}\rangle } \mathinner {|{s_0}\rangle } \mathinner {|{s'=0}\rangle } \mathinner {|{b'=0}\rangle } \end{aligned}$$

(E4a)

$$\begin{aligned}&\quad = \sum _{k=0}^{2^n-1} \mathinner {|{k_2}\rangle } \left( C_k \sum _{s_0=0,1} \alpha _{k,s_0} \mathinner {|{s_0}\rangle } \right) \mathinner {|{s'=0}\rangle } \mathinner {|{b'=0}\rangle } \end{aligned}$$

(E4b)

$$\begin{aligned}&\quad = \sum _{k=0}^{2^n-1} \sum _{s_0=0,1} \alpha _{k,s_0} \mathinner {|{k_2}\rangle } (C_k \mathinner {|{s_0}\rangle }) \mathinner {|{s'=0}\rangle } \mathinner {|{b'=0}\rangle } \end{aligned}$$

(E4c)

$$\begin{aligned}&\quad = \left[ \left( \sum _{k'=0}^{2^n-1} \mathinner {|{k'_2}\rangle } \! \mathinner {\langle {k'_2}|} \otimes C_k \right) \sum _{k=0}^{2^n-1} \sum _{s_0=0,1} \alpha _{k,s_0} \mathinner {|{k_2}\rangle } \mathinner {|{s_0}\rangle } \right] \mathinner {|{s'=0}\rangle } \mathinner {|{b'=0}\rangle } \end{aligned}$$

(E4d)

$$\begin{aligned}&\quad = \left( {C}^{(n)} \sum _{k=0}^{2^n-1} \sum _{s_0=0,1} \alpha _{k,s_0} \mathinner {|{k_2}\rangle } \mathinner {|{s_0}\rangle } \right) \mathinner {|{s'=0}\rangle } \mathinner {|{b'=0}\rangle } \end{aligned}$$

(E4e)

$$\begin{aligned}&\quad = \left( {C}^{(n)} \otimes I_{2^{(2^n-1)}} \otimes I_{2^{(2^n)}} \right) \left( \sum _{k=0}^{2^n-1} \sum _{s_0=0,1} \alpha _{k,s_0} \mathinner {|{k_2}\rangle } \mathinner {|{s_0}\rangle } \mathinner {|{s'=0}\rangle } \mathinner {|{b'=0}\rangle }\right) \end{aligned}$$

(E4f)

$$\begin{aligned}&\quad = \left( {C}^{(n)} \otimes I_{2^{(2^n-1)}} \otimes I_{2^{(2^n)}} \right) \mathinner {|{S}\rangle } \, . \end{aligned}$$

(E4g)

The right-hand side of Eq. (E4g) is that of Eq. (26), and the left-hand side of Eq. (E4g) is also that of Eq. (26) because $Q_1^{-1} = Q_1^{\dag }$, $Q_2^{-1} = Q_2^{\dag }$, and $U_{\text {lin.}}^{(n)}$ is defined by Eq. (25), which completes the proof.

Appendix F: Efficient quantum circuit for a smooth position-dependent coin operator

1.1 The exact, complete circuit, for a complete Walsh decomposition

We follow the same computational steps as in Ref. [2]. In this subappendix, we first derive an exact quantum circuit for $C^{(n)}_{f,\sigma }$ using the development of f into a Walsh series.

1.1.1 $C^{(n)}_{f,\sigma }$ as a product of Walsh terms $U_j$

First, let us define the Walsh functions: for any natural number j and real number $x \in [0,1]$, the jth Walsh function at point x is

$$\begin{aligned} w_j(x){:}{=}(-1)^{\sum _{i=1}^nj_ix_{i-1}}, \end{aligned}$$

(F1)

where $j_i$ is the ith bit in the binary expansion $j=\sum _{i=1}^nj_i2^{i-1}$, with n the most significant non-vanishing bit of j, and $x_i$ the ith bit in the dyadic expansion⁸$x=\sum _{i=0}^{\infty } x_i/ 2^{i+1}$. The Walsh functions form a complete set of orthonormal functions. For a finite number of points $x_p$ one can define the discrete Walsh functions $w_{jp} {:}{=}w_j(x_p)$. The set of discrete Walsh functions is still complete and orthormal: $\frac{1}{2^n}\sum _{p=0}^{2^n-1}w_{jp}w_{lp}=\delta _{jl}$ and $\frac{1}{2^n}\sum _{j=0}^{2^n-1}w_{jp}w_{jl}=\delta _{pl}$. Thus, one can expand the $f(x_p)$’s in terms of discrete Walsh functions as

$$\begin{aligned} f(x_p)=\sum _{j=0}^{2^n-1} a_j w_{jp}, \end{aligned}$$

(F2)

where the $a_j$ are real numbers such that

$$\begin{aligned} a_j{:}{=}\frac{1}{2^n}\sum _{p=0}^{2^n-1}f(x_p)w_{jp}. \end{aligned}$$

(F3)

The Walsh functions at a given position can only take the value $+1$ or $-1$, making their associated Walsh operators a tensor product of Z Pauli operators. Indeed, we define the Walsh operators as

$$\begin{aligned} {\hat{w}}_j=(Z_{n-1})^{j_n}\otimes \cdots \otimes (Z_0)^{j_1}, \end{aligned}$$

(F4)

where $Z_i$ is a third Pauli matrix applied on qubit i, and $j=0,\cdots ,2^n-1$. Therefore, for each real number $x_p=\sum _{i=0}^{n-1}b_i/2^{i+1}$, with $b_i\in \{0,1\}$, one has

$$\begin{aligned} {\hat{w}}_j\mathinner {|{k_2}\rangle }&\equiv {\hat{w}}_j\mathinner {|{b_{n-1}\cdots b_0}\rangle } \end{aligned}$$

(F5a)

$$\begin{aligned}&= (-1)^{\sum _{i=1}^nj_ib_{i-1}}\mathinner {|{b_{n-1}\cdots b_0}\rangle } \end{aligned}$$

(F5b)

$$\begin{aligned}&= w_{jp}\mathinner {|{k_2}\rangle } \, . \end{aligned}$$

(F5c)

The operator $C^{(n)}_{f,\sigma }$, defined in Eq. (39), can now be rewritten in terms of Walsh operators:

$$\begin{aligned} C^{(n)}_{f,\sigma }&{:}{=}e^{i{\hat{f}}\otimes \sigma } \end{aligned}$$

(F6a)

$$\begin{aligned}&=e^{i\sum _{j=0}^{2^n-1}a_j{\hat{w}}_j \otimes \sigma } \end{aligned}$$

(F6b)

$$\begin{aligned}&=\prod _{j=0}^{2^n-1} U_j \, , \end{aligned}$$

(F6c)

where

$$\begin{aligned} U_j {:}{=}e^{ia_j{\hat{w}}_j\otimes \sigma }, \end{aligned}$$

(F7)

and where, in going from the second to the third line in Eqs. (F6), we have used the following commutation relations, $\forall j,j'$, $[{\hat{w}}_j\otimes \sigma ,{\hat{w}}_{j'} \otimes \sigma ]=0$.

1.1.2 Quantum circuits for the Walsh terms $U_j$

Let us now derive the quantum circuits for the operators $U_j$. Let us consider, in the expression the Walsh operators ${{\hat{w}}}_j$, Eq. (F4), only the Z Pauli matrices on the relevant qubits (i.e., one for each $j_i=1$), and omit the other, $I_2$ tensor factors (i.e., one for each $j_i=0$). Let r be the number of such Z Pauli matrices. Now, we first remark that every tensor product of a number r of Z Pauli matrices can be rewritten using CNOT matrices:

$$\begin{aligned} Z_{r-1}\otimes \cdots \otimes Z_1 \otimes Z_0 = A_r(I_{2^{(r-1)}}\otimes ...\otimes I_{2^{(1)}}\otimes Z_0)A_r^{-1}, \end{aligned}$$

(F8)

where $A_r {:}{=}CNOT_{1}^{0} \cdot CNOT_{2}^{0}...CNOT_{r-1}^{0}$ and $CNOT_i^j$ is the CNOT quantum gate controlled by qubit i and applied on qubit j. Therefore, the operator $U_j$ written as acting on the r relevant position qubits and the coin qubit, can be written in terms of quantum gates as

$$\begin{aligned} U_j=(A_r\otimes I_{2})(I_{2^{(r-1)}}\otimes ...\otimes I_{2^{(1)}}\otimes e^{i a_jZ\otimes \sigma })(A_r^{-1}\otimes I_{2}). \end{aligned}$$

(F9)

1.1.3 Quantum circuits for the terms $e^{i a_jZ\otimes \sigma }$

Let us finally derive a quantum circuit for each $e^{i a_jZ\otimes \sigma }$, for $\sigma =X,Y,Z$. For $\sigma =Z$, the quantum circuit is simply

$$\begin{aligned} e^{i a_jZ\otimes Z}&=CNOT(I_{2}\otimes e^{ia_jZ})CNOT \end{aligned}$$

(F10a)

$$\begin{aligned}&=CNOT(I_{2}\otimes R_Z(-2a_j))CNOT \, , \end{aligned}$$

(F10b)

where $R_Z(\theta )=\begin{bmatrix} e^{-i\frac{\theta }{2}}&{}0 \\ 0&{}e^{i\frac{\theta }{2}}\end{bmatrix}$.

For $\sigma =Y$:

$$\begin{aligned} e^{ia_jZ\otimes Y}&= \begin{bmatrix} e^{ia_jY} &{} 0 \\ 0 &{} e^{-ia_jY} \end{bmatrix} \end{aligned}$$

(F11a)

$$\begin{aligned}&= \begin{bmatrix} e^{ia_jY} &{} 0 \\ 0 &{} e^{ia_jXYX} \end{bmatrix} \end{aligned}$$

(F11b)

$$\begin{aligned}&= \begin{bmatrix} e^{ia_jY} &{} 0 \\ 0 &{} Xe^{ia_jY}X \end{bmatrix} \end{aligned}$$

(F11c)

$$\begin{aligned}&= CNOT(I_{2}\otimes e^{ia_jY})CNOT \end{aligned}$$

(F11d)

$$\begin{aligned}&=CNOT(I_{2}\otimes R_Y(-2a_j))CNOT \, , \end{aligned}$$

(F11e)

where $R_Y(\theta )=\begin{bmatrix} \cos (\frac{\theta }{2})&{}-\sin (\frac{\theta }{2}) \\ \sin (\frac{\theta }{2})&{}\cos (\frac{\theta }{2}) \end{bmatrix}$.

For $\sigma =X$:

$$\begin{aligned} e^{ia_jZ\otimes X}&= \begin{bmatrix} e^{ia_jX} &{} 0 \\ 0 &{} e^{-ia_jX} \end{bmatrix} \end{aligned}$$

(F12a)

$$\begin{aligned}&= \begin{bmatrix} e^{ia_jY} &{} 0 \\ 0 &{} e^{ia_jZXZ} \end{bmatrix} \end{aligned}$$

(F12b)

$$\begin{aligned}&= \begin{bmatrix} e^{ia_jX} &{} 0 \\ 0 &{} Ze^{ia_jX}Z \end{bmatrix} \end{aligned}$$

(F12c)

$$\begin{aligned}&= {\widehat{CZ}}(I_{2}\otimes e^{ia_jX}){\widehat{CZ}} \end{aligned}$$

(F12d)

$$\begin{aligned}&= {\widehat{CZ}}(I_{2}\otimes R_X(-2a_j)){\widehat{CZ}} \, , \end{aligned}$$

(F12e)

where $R_X(\theta ){:}{=}\begin{bmatrix} \cos (\frac{\theta }{2})&{}-i\sin (\frac{\theta }{2}) \\ -i\sin (\frac{\theta }{2})&{}\cos (\frac{\theta }{2}) \end{bmatrix}$ and ${\widehat{CZ}}{:}{=}\text {diag}(1,1,1,-1)$ is the controlled-Z gate.

Since the operators $U_j$ commute with each other, the implementation of $C^{(n)}_{f_m,\sigma }=\prod _{j=0}^{2^m-1}U_j$ can be optimized by choosing the right sequence that cancels a maximum number of CNOT gates. This can be done by using the Gray code [90], resulting into only one CNOT gate per Walsh operator implemented and improving polynomialy the complexity of the scheme. Such an optimization could perhaps also be done by the transpiler of the used quantum computer.

We have finally obtained an exact quantum circuit $C^{(n)}_{f,\sigma }=\prod _{j=0}^{2^n-1}U_j$, where the order of the terms in the product is determined by the previous optimization.

1.2 Approximation by truncation of the complete circuit, and related efficiency

1.2.1 Idea

The idea here is the following. Instead of implementing the exact, complete decomposition $C^{(n)}_{f,\sigma }=\prod _{j=0}^{2^n-1}U_j$, the depth of which scales exponentially with n, we truncate the circuit up to some $j=2^m$, i.e., we approximate $C^{(n)}_{f,\sigma }$ by some truncation $C^{(n)}_{f_m,\sigma } = \prod _{j=0}^{2^m-1}U_j$, where we have introduced the truncation $f_m{:}{=}\sum _{j=0}^{2^m-1} a_j w_{j}$ of the Walsh development of a function f up to the term $2^m$. This is interesting only if m does not scale exponentially with n. Notice that even if we truncate the quantum circuit $C^{(n)}_{f,\sigma }$ into $C^{(n)}_{f_m,\sigma }$, we still need the full decomposition of the function f in order to compute accurately the coefficients $a_j$ of the decomposition.

1.2.2 Approximation error and smoothness condition

Let $\epsilon$ be a positive real number. One can show that $\sup _x|f(x)-f_m(x)|<\frac{\sup _{x \in [0,1]} f'(x)}{2^m}$ [91, 92], where x is a continuous or discrete variable in [0, 1]. This implies that for m such that $\frac{\sup _{x \in [0,1]} f'(x)}{2^m} = \epsilon$, the approximating coin operator $C^{(n)}_{f_m,\sigma }$ is close to the real coin operator $C^{(n)}_{f,\sigma }$ up to $\epsilon$ in terms of the spectral norm. Therefore, only $2^m \propto 1/\epsilon$ Walsh operators have to be implemented to approximate the coin operator up to $\epsilon$, resulting in a quantum circuit with a total number of one-qubit and two-qubit quantum gates of $O(1/\epsilon )$. The condition for the quantum circuit to be efficient is $m\ll n$, i.e., $2^m \ll 2^n$, i.e., $\epsilon 2^m \ll \epsilon 2^n$, which, using the fact that $\sup _{x \in [0,1]} f'(x) = \epsilon 2^m$, yields Eq. (40), which is a smoothness condition on f.

Fig. 18

Circuit implementing the block-diagonal unitary matrix $C^{(n)}_{f,\sigma }{:}{=}e^{i{\hat{f}}\otimes \sigma }$ for f being a linear function $f(x) {:}{=}ax$. This circuit only uses n two-qubit gates

1.3 Linear position dependence

In the particular case of a unitary operator $C^{(n)}_{f,\sigma }{:}{=}e^{i{\hat{f}}\otimes \sigma }$ with ${\hat{f}}$ the operator associated to a function f that is linear, i.e., $f(x) {:}{=}ax$ where $x \in [0,1]$ and $a \in {\mathbb {R}}$, one can derive a quantum circuit using only n two-qubit gates. Indeed, let us consider the quantum circuit of Fig. 18 acting on the state $\mathinner {|{\psi }\rangle }=\mathinner {|{x_{n-1}}\rangle }\cdots \mathinner {|{x_0}\rangle }\mathinner {|{\phi }\rangle }$, and let $R(\theta ) {:}{=}e^{i\theta \sigma }$. Each rotation controlled by $\mathinner {|{x_i}\rangle }$ can be written as $R(x_i\theta /2^{i+1})$ where $x_i=0,1$. The final state can be written as

$$\begin{aligned} \mathinner {|{\psi }\rangle }&=\mathinner {|{x_{n-1}}\rangle }\cdots \mathinner {|{x_{0}}\rangle }R(a\sum _{i=0}^{n-1}x_i/2^{i+1})\mathinner {|{\phi }\rangle } \end{aligned}$$

(F13a)

$$\begin{aligned}&=\mathinner {|{x_{n-1}}\rangle }\cdots \mathinner {|{x_{0}}\rangle }R(ax)\mathinner {|{\phi }\rangle } \, , \end{aligned}$$

(F13b)

where $x=\sum _{i=0}^{n-1}x_i/2^{i+1}$ is given by its dyatic expansion. This quantum circuit applied on a general state $\mathinner {|{\psi }\rangle }_i=\sum _x \mathinner {|{x}\rangle }(c_x^0\mathinner {|{0}\rangle }+c_x^1\mathinner {|{1}\rangle })$ will give the final state:

$$\begin{aligned} \mathinner {|{\psi }\rangle }_f&=\sum _x c_x\mathinner {|{x}\rangle } R(ax)(c_x^0\mathinner {|{0}\rangle }+c_x^1\mathinner {|{1}\rangle }) \end{aligned}$$

(F14a)

$$\begin{aligned}&=e^{i{\hat{f}}\otimes \sigma }\mathinner {|{\psi }\rangle }_i \, . \end{aligned}$$

(F14b)