Numerical analysis of bipartite entanglement evolution in simple cubic 1/2-spin system with additional spin 1 dopant

Abstract

The system in consideration is a singular simple cubic cell of spins $s = \frac{1}{2}$ doped in centre with additional spin $S = 1$. The structure is located in external magnetic field and is undergoing dissipative, Markovian evolution. The analysis of system time evolution is focused on the entanglement evaluation and determination of its behaviour over time. We found out the distinct effect of doping the structure with additional spin $S = 1$ in the time evolution of the bipartite entanglement in $\vert W \rangle$ state. We also distinguished the raising and lowering spin interaction with environment and determined its impact on decoherence. Furthermore, we have shown that the entanglement between spins is in the form of a damped superposition of Gaussian functions. Its pulsed nature results from the unitary evolution in spin structure, while the damping is caused by the influence of the environment.

1 Introduction

The entanglement, specific correlation between the elements of composite quantum system, turned out to be one of the most surprising features of a quantum theory, alongside with its non-determinism and discretisation of physical parameters. Since the famous papers by Schrödinger [1] and Einstein, Podolsky and Rosen [2] it remains one of the most frequently discussed topics of modern physics. Development of quantum information theory drew attention to possibility of utilising the entanglement as a resource: in quantum cryptography [3,4,5], quantum computation [6, 7] and quantum information processing [8,9,10]. Due to this reason, the gathering knowledge on the entanglement formation and behaviour over time is highly anticipated, and determining the set of parameters for which the entanglement in particular quantum system will be high and stable over time may be used as a guideline for manufacturing the real layouts to implement the quantum informatics protocols on.

Recently, the spin structures gather popularity as a mean of system for analysis of this particular quantum correlation [11,12,13,14,15,16,17,18,19,20,21]. They were analysed, among others, in terms of thermal entanglement [18, 19, 22,23,24], in the presence of Dzyaloshinskii–Moriya interaction [16, 17, 20, 25], Kaplan–Shekhtman–Entin-Wohlman–Aharony interactions [26, 27] or three spin interaction [22, 28], and for various magnetic fields [17, 19]. Also, the time evolution of quantum entanglement was discussed for numerous models of coupling to the environment [16, 20, 27, 29, 30]. However, most of this work is focused on the single pair of coupled spins.

There exist quantum states that are highly entangled and states with low entanglement or even without any entanglement at all. There are multiple ways to quantitatively express the amount of entanglement in system: one of them is to determine the conditions on the elements of density matrix to represent separable states in accordance to the Peres–Horodecki criterion [31, 32] and then calculating the distance between the analysed entangled state and the set of all separable states, utilising the Schmidt–Hilbert norm [33, 34]—the further the state is from the set, the more entangled it is. Other measures include among others: negativity [32], relative entropy of entanglement [33], entanglement of formation [35] or, probably the most common, concurrence [36]. This last measure proven to be a reliable mean to evaluate the amount of entanglement for coupled systems of dimensionality $2 \otimes 2$ and $2 \otimes 3$ [37] and therefore was utilised in presented analysis.

The aim of this work is to determine the time behaviour of the bipartite entanglement in a three-dimensional finite spin structure coupled with Markovian environment. To this end, the Lindblad master equation was applied, and it was solved by numerical finite step method, using the Runge–Kutta algorithm. Entanglement concurrence time evolution was computed for $\frac{1}{2}$ - $\frac{1}{2}$ spins and for $\frac{1}{2}$ and 1 spins using initial state, which is equivalent of $\vert W \rangle$ state [38, 39] for the system without the $S = 1$ dopant.

The paper is organised as follows: In Sect. 2, we present the analysed structure and describe the mathematical formalism behind the system Hamiltonian and time evolution of the structure state; we also present the tools to quantify the entanglement in the system. Section 3 covers the presentation and discussion of obtained results. Finally, Sect. 4 serves as a summary of the research.

2 Model

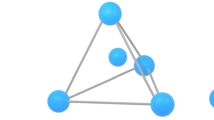
The analysed model is a finite, three-dimensional structure similar to simple cubic cell with spins $s = \frac{1}{2}$, placed in the corners. The structure consists also an additional dopant with spin $S = 1$ in the centre. The entire system is located in an external magnetic field (0, 0, h), acting along the z axis. The visualisation of the model is shown in Fig.1.

Fig. 1

The model in consideration. Spins $s = \frac{1}{2}$ are marked by the blue spheres and are labelled for convenience with letters: a to the left on the dopant, and b to the right, and with numbers, to easily determine the order of coupling by exchange interactions. Red sphere in the centre is the aforementioned dopant, with spin $S = 1$

If we assume that spins coupling range does not exceed the lattice constant, and they interact according to Heisenberg XXX model, the Hamiltonian of the analysed structure can be written as:

$$\begin{aligned} \hat{H}= & {} - j \left[ \sum \limits _{i = 1}^4 \vec {s}_{a,i} \vec {s}_{b,i} + \sum \limits _{q= a,b} \left( \vec {s}_{q,1} + \vec {s}_{q,3} \right) \left( \vec {s}_{q,2} + \vec {s}_{q,4} \right) \right] \nonumber \\ {}{} & {} - J \vec {S} \cdot \sum \limits _{i = 1}^4 \left( \vec {s}_{a,i} + \vec {s}_{b,i} \right) - h \cdot \left( \hat{S}^Z + \sum \limits _{i = 1}^4 ( \hat{s}^Z_{a,i} + \hat{s}^Z_{b,i} ) \right) \end{aligned}$$

(1)

where j is exchange integral for spins $s = \frac{1}{2}$ and J is the integral for exchange interaction between spin $S = 1$ and $s = \frac{1}{2}$. The superscript z indicates the component of spin in the direction of the external magnetic field. We are primarily interested in time evolution of system coupled to dissipative environment satisfying the Born–Markov condition, which can be realized for example in a form of a large bosonic reservoir. In aim to determine the change over time of density matrix $\rho (t)$ describing the overall state of the system, we utilize the Lindblad equation:

$$\begin{aligned} \frac{d}{dt} \rho (t) = -i \left[ \hat{H}, \rho (t) \right] + \mathcal {D}(\rho ). \end{aligned}$$

(2)

In (2), the first term (commutator) describes coherent time evolution governed by the Hamiltonian, while the second $\mathcal {D}(\rho )$ indicates the dissipator, assumed here as:

$$\begin{aligned} \mathcal {D}(\rho ) = \left( \gamma _P \left[ \mathcal {L}(\hat{S}^+) + \sum _{q=a,b} \sum \limits _{i=1}^4 \mathcal {L}(\hat{s}_{q,i}^+ ) \right] + \gamma _N \left[ \mathcal {L}(\hat{S}^-) + \sum _{q=a,b} \sum \limits _{i=1}^4 \mathcal {L}(\hat{s}_{q,i}^- ) \right] \right) \end{aligned}$$

(3)

with $\mathcal {L}$ being Lindblad operator:

$$\begin{aligned} \mathcal {L}(\hat{X}) = \hat{X} \rho (t) \hat{X}^\dagger - \frac{1}{2} \hat{X}^\dagger \hat{X} \rho (t) - \frac{1}{2} \rho (t)\hat{X}^\dagger \hat{X}. \end{aligned}$$

(4)

Parameters $\gamma _P$ and $\gamma _N$ are decoherence rates connected with spin raising and lowering effect of the system interaction with the reservoir, and the operators $\hat{s}_{q,i}^+ (\hat{s}_{q,i}^-)$ and $\hat{S}^+ (\hat{S}^-)$ denote the raising (lowering) operators for spins 1/2 and 1, respectively. Individual forms of these operators result from formulas:

$$\begin{aligned} \hat{s}^\pm = \hat{s}^X \pm i\hat{s}^Y, ~~~~ \hat{S}^\pm = \hat{S}^X \pm i\hat{S}^Y \end{aligned}$$

and in calculational basis they can be represented as:

$$\begin{aligned}{} & {} \hat{s}^+ = \begin{bmatrix} 0 &{} 1 \\ 0 &{} 0 \end{bmatrix}, ~~~~\hat{s}^- = \begin{bmatrix} 0 &{} 0 \\ 1 &{} 0 \end{bmatrix},\\{} & {} \hat{S}^+ = \begin{bmatrix} 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 1 \\ 0 &{} 0 &{} 0 \end{bmatrix}, ~~~~\hat{S}^- = \begin{bmatrix} 0 &{} 0 &{} 0\\ 1 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 \end{bmatrix}. \end{aligned}$$

Fig. 2

Time evolutions of bipartite entanglement in isolated system in the absence of dopant (Fig. a) and with dopant with spin S=1, (Fig. b)

Fig. 3

The example of decomposition of bipartite entanglement $C_{1/2, 1/2}$ into Gauss modes for some period of time. The solid line represents the evolution of entanglement and the dashed lines the corresponding Gaussian modes

Fig. 4

Time dependence of entanglement concurrence for various exchange integrals between spins $s = \frac{1}{2}$. Model parameters are set as $J =1$, $h=0$ and $\gamma _P = \gamma _N =0.005$. The magnitude or sign of j exchange integral seem to have no impact on entanglement dynamics in analysed state

Fig. 5

Time dependence of entanglement concurrence for various magnetic fields. Model parameters are set as $j =1$, $J = 1$ and $\gamma _P = \gamma _N =0.005$. Magnetic field has no impact on the behaviour of the concurrence in considered model

Fig. 6

Time dependence of entanglement concurrence for various exchange integrals between spins $s = \frac{1}{2}$ and spin $S = 1$. Model parameters are set as $j =1$, $h=0$ and $\gamma _P = \gamma _N =0.005$

Fig. 7

Time dependence of entanglement concurrence for decoherence parameters, $\gamma _P = \gamma _N$. Model parameters are set as $j =1$, $J = 2$ and $h= 0$

Fig. 8

Time dependence of entanglement concurrence for decoherence parameters $\gamma _P < \gamma _N$. Model parameters are set as $j =1$, $J = 2$ and $h= 0$

Fig. 9

Time dependence of entanglement concurrence for decoherence parameters $\gamma _P > \gamma _N$. Model parameters are set as $j =1$, $J = 2$ and $h= 0$

To quantitatively describe the strength of bipartite entanglement in the system, the concurrence measure is applied [35, 36]. For the entanglement between the two adjacent spins $s = \frac{1}{2}$, this measure must be calculated in respect to subsystem consisting only the two examined spins (be it subsystem A, in no way related to spins $s_{a,i}$), so the overall density matrix has to be reduced to a smaller form, in accordance with the formula:

$$\begin{aligned} \hat{\rho }_{\frac{1}{2}, \frac{1}{2}} = \text {Tr}_B \rho = \sum \limits _{j = 1}^{\text {dim}(\mathcal {H}_B)} ( \hat{I}_A \otimes \langle \phi ^B_j \vert ) \cdot \rho \cdot (\hat{I}_A \otimes \vert \phi ^B_j \rangle ) \end{aligned}$$

(5)

where $\text {Tr}_B \rho$ denotes partial trace of the density matix $\rho$ over the subsystem B consisting of six remaining spins $s = \frac{1}{2}$ and spin $S = 1$; states $\lbrace \vert \phi _j^B \rangle \rbrace _j$ span complete basis in subsystem B. Concurrence of the entanglement is calculated for the reduced density matrix as:

$$\begin{aligned} \mathcal {C}_{\frac{1}{2}, \frac{1}{2}} = \text {max} \lbrace 0 , \sqrt{\lambda _4} - \sqrt{\lambda _3} - \sqrt{\lambda _2} - \sqrt{\lambda _1} \rbrace . \end{aligned}$$

(6)

In equation above $\lambda _4 \ge \lambda _3 \ge \lambda _2 \ge \lambda _1$ are the eigenvalues of a matrix resulted from following transformation on the reduced density matrix:

$$\begin{aligned} R_{\frac{1}{2}, \frac{1}{2}} = \hat{\rho }_{\frac{1}{2}, \frac{1}{2}} \left( \sigma ^Y_2 \otimes \sigma ^Y_2 \right) \hat{\rho }_{\frac{1}{2}, \frac{1}{2}}^\dagger \left( \sigma ^Y_2 \otimes \sigma ^Y_2 \right) \end{aligned}$$

(7)

where $\sigma ^Y_2$ is Y-Pauli matrix-lower index to describe the dimensionality of it and does not correspond to the position of spin in the spin structure.

To calculate the concurrence value between the spins $S = 1$ and $s = \frac{1}{2}$, the density matrix also needs to be reduced, in this case, however, the reduction takes place in respect to subsystem of dimensionality $2 \otimes 3$ (therefore $B'$ in equation below is the subsystem consisting the seven spins $s = \frac{1}{2}$ that are not taken into consideration):

$$\begin{aligned} \hat{\rho }_{\frac{1}{2},1} = \text {Tr}_{B'} \rho . \end{aligned}$$

(8)

Concurrence for the systems of mentioned dimensionality is calculated similarly to (6):

$$\begin{aligned} \mathcal {C}_{\frac{1}{2},1} = \text {max} \lbrace 0 , \sqrt{\lambda _6} - \sqrt{\lambda _5} - \sqrt{\lambda _4} - \sqrt{\lambda _3} - \sqrt{\lambda _2} - \sqrt{\lambda _1} \rbrace \end{aligned}$$

(9)

where $\lambda _6 \ge \lambda _5 \ge \lambda _4 \ge \lambda _3 \ge \lambda _2 \ge \lambda _1$ are the eigenvalues of the matrix [40, 41]:

$$\begin{aligned} R_{\frac{1}{2},1} = \hat{\rho }_{\frac{1}{2},1} \left( \sigma ^Y_2 \otimes \mathcal {O}_3 \right) \hat{\rho }_{\frac{1}{2},1}^\dagger \left( \sigma ^Y_2 \otimes \mathcal {O}_3 \right) , \end{aligned}$$

(10)

in which the operator $\mathcal {O}_3$ is a particular composition of all possible cyclic operators for qutrits with appropriate phases, defined in calculational basis as [42, 43]:

$$\begin{aligned} \mathcal {O}_3 = \begin{bmatrix}0 &{} -i &{} i \\ i &{} 0 &{} -i \\ -i &{} i &{}0 \end{bmatrix} . \end{aligned}$$

(11)

3 Time evolution of entanglement concurrence

The time behaviour of the entanglement in the system was calculated by numerical methods. Analytical solution for the system without the environment taken into account and cursory solution of this problem with environment included is provided in appendix; however, due to the scale of the problem the results presented below were obtained by computer-assisted calculations. Equation (2) is solved approximately by multi-step method using fourth-order Runge–Kutta algorithm, and for each step the concurrences were computed in accordance to the formulas above. As an initial state, we choose partially entangled state $\vert \alpha \rangle$, which can be presented in the form:

$$\begin{aligned} \vert \alpha \rangle = \frac{1}{2 \sqrt{2}} \left( \vert \downarrow \uparrow \uparrow \uparrow \uparrow \uparrow \uparrow \uparrow \rangle + \vert \uparrow \downarrow \uparrow \uparrow \uparrow \uparrow \uparrow \uparrow \rangle +... + \vert \uparrow \uparrow \uparrow \uparrow \uparrow \uparrow \uparrow \downarrow \rangle \right) \otimes \vert 0 \rangle , \end{aligned}$$

where the first term of the tensor product corresponds to one excitation in a ferromagnetically ordered frame of spins $s = \frac{1}{2}$, while the second represents the state of the $S=1$ spin. In other words, the first term is equivalent of $\vert W \rangle$ state for the frame, in notation below the arrows refers to values of spins $s = \frac{1}{2}$ z-projection-$\uparrow : m_S =\frac{1}{2}$, $\downarrow : m_S = -\frac{1}{2}$, the second term can in general take three values; $-1$, 0 and 1 and refer to value of spin $S = 1$ z-projection.

Since our system is highly symmetric, to determine the structure of bipartite entanglement it is sufficient to calculate the entanglement between two spins 1/2 and between any spin 1/2 and spin 1 of the considered spin system. In Fig. 2a, we present evolution of the bipartite entanglement for spins a1 and b1 for the case of no interaction with spin $S =1$ ($J=0$). If we then turn on the interaction of spins 1/2 with spin 1 ($J\ne 0$), then the evolution of bipartite entanglement proceeds as shown in Fig. 2b.

Without the $S = 1$ dopant, the $\vert \alpha \rangle$ state is an eigenstate of the frame of spins $s = \frac{1}{2}$, therefore in isolated system the time evolution does not change the initial bipartite entanglement; in other words, during unitary evolution all 1/2 spins are equally entangled with concurrence equal to 0.25 (see Fig. 2a). Introduction of the dopant into the structure changes the behaviour of the bipartite entanglement which becomes a time dependent and periodic, both for $\mathcal {C}_{\frac{1}{2},\frac{1}{2}}$ and for $\mathcal {C}_{\frac{1}{2},1}$ (see Fig. 2b). Within one period, peaks of highest concurrence can be observed: $\mathcal {C}_{\frac{1}{2},\frac{1}{2}}$ reaches 0.25 at the begging and the end of the period, while $\mathcal {C}_{\frac{1}{2},1}$ exceeds the value 0.3 twice during that period. The peaks within one period can be decomposed into a sum of Gaussian modes what suggests the pulsed nature of entanglement between spins in considered quantum system, where each peak has the form of a Gaussian mode. The example of decomposition of entanglement $C_{1/2, 1/2}$ into Gauss modes for some period of time is presented in Fig. 3.

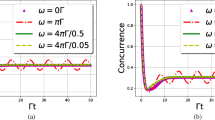
The series of numerical simulations showed that the time evolution of the state $\vert \alpha \rangle$ does not depend on exchange integral j between spins $s = \frac{1}{2}$, neither it does not depend on applied external field. Illustrative results of simulations confirming the lack of dependence on j and h are shown in Figs. 4, 5.

In contrast to the interaction integral between the spins located at the vertices of the cubic structure under consideration, the dopant interaction integral is relevant. By varying the value of the J integral, we can adjust the period of the entanglement variation by changing its frequency, as shown in Fig. 6. The change in frequency of entanglement evolution holds for both kinds of entanglement: for $\mathcal {C}_{\frac{1}{2},\frac{1}{2}}$ and for $\mathcal {C}_{\frac{1}{2},1}$-the periods for the former are longer. It is, however, noteworthy that without dopant time of total concurrence loss for $\mathcal {C}_{\frac{1}{2},\frac{1}{2}}$ is extended in comparison with situations with dopant, but the price is impossibility of utilising the entanglement between spins $s = \frac{1}{2}$ and $S = 1$.

The next step of our simulations was to analyse the different characteristics of dissipative environment. We prepared three sets of various dissipative parameters and conducted a comparative analysis on them. The sets correspond to situations, where there is an equal probability that environment raise or lower any spin in structure ($\gamma _N = \gamma _P$); the environment prefers to lower spins than to raise them ($\gamma _N > \gamma _P$); the environment prefers to raise spins than lower them ($\gamma _N < \gamma _P$). The results are presented in Figs. 7, 8 and 9.

Looking at Fig. 7, it is easy to see that an increase of $\gamma _P$ and $\gamma _N$ parameters has a strongly dampening influence on the entanglement of both $\mathcal {C}_{\frac{1}{2},\frac{1}{2}}$ and $\mathcal {C}_{\frac{1}{2},1}$. However, if we compare the red and blue plots in Figs. 8 and 9, it can be seen that the decisive influence on the decoherence rate is exerted by the spin-lowering factors from the environment. Difference between the plots in Fig. 8 is minimal (due to identical values of $\gamma _N$) and is difficult to notice even in close-up (see Fig. 10a), while similar difference for Fig. 9 can be spotted on the original figure-for sake of clarity; we nevertheless pictured the close-up in Fig. 10b-here, the $\gamma _P$ have identical values, so the results confirm the previously stated observation.

Fig. 10

Close-ups of comparisons for particular concurrence behaviours

4 Conclusion

We have conducted a numerical analysis of bipartite entanglement evolution in simple cubic cell of spins $s = \frac{1}{2}$ with addition of spin $S = 1$ in the centre, placed in external magnetic field and in dissipative, Markovian environment. We successfully applied the open system formalism, namely Lindblad master equation, in research focused on determining the impact of additional spin on the behaviour of bipartite entanglement between spins $s = \frac{1}{2}$ and between spin $s = \frac{1}{2}$ and spin $S = 1$. As an initial state, we assumed the equivalent of W state for structure devoid of an additional node. We compared the behaviour of concurrence in isolated system with and without additional spin, and for different exchange integrals and applied magnetic fields. Moreover, we analysed various environment parameters to determine its impact on the decoherence. We found out that inclusion of the additional spin introduces the state into a behaviour where entanglement pulses can be distinguished (the periods of increased entanglement), which is a direct result of getting the structure out of its eigenstate by expanding the Hilbert space of the system (it gains additional degrees of freedom). We would especially like to draw the readers attention to two periods of entanglement between $s = \frac{1}{2}$ and $S = 1$, where, in isolated system, the concurrence $\mathcal {C}_{\frac{1}{2},1}$, a resource available only in doped system, reaches its maxima, which, in turn, are greater than the maximal value of the concurrence between two spins $s = \frac{1}{2}$. We found out that for initial state $\vert \alpha \rangle = \vert W \rangle \otimes \vert 0 \rangle$ neither the external magnetic field, nor the exchange integral between spins $s = \frac{1}{2}$ has any impact on the concurrence behaviour in time. However, the exchange integral between spins of the frame and spin $S = 1$ has-the increase of exchange interaction strength results in higher frequency of the entanglement pulses. In open systems, the analysis showed that both concurrences decrease exponentially; decrease rate is dictated by the environment parameters. However, for our definition of W state it turned out that the rate of lowering spins $\gamma _N$ has a bigger impact on decoherence time than its raising spins counterpart $\gamma _P$, yet this conclusion appears to result solely from the definition on initial state.

Appendix A

1.1 Analytical solution for density matrix elements

First step in obtaining the explicit form of density matrix undergoing the time evolution is to examine it without the external influence of the bosonic environment. The Liouville–von Neumann equation (closed system equivalent of Lindblad formula) reads:

$$\begin{aligned} \frac{d}{dt} \rho (t) =-i \left[ \hat{H}, \rho (t) \right] . \end{aligned}$$

Both operators can be expressed in basis constructed from the eigenvectors of Hamiltonian:

$$\begin{aligned} \hat{H} = \sum \limits _{k=1} E_k \vert \epsilon _k \rangle \langle \epsilon _k \vert ,~~~~~\rho (t) = \sum \limits _{k,l} p_{k,l} (t) \vert \epsilon _k \rangle \langle \epsilon _l \vert . \end{aligned}$$

(A1)

Without the loss of generality, one can determine the form of k, l-th element of density matrix:

$$\begin{aligned} \frac{d}{dt} p_{k,l} (t)= & {} -i \left[ \hat{H}, \rho (t) \right] _{k,l} = -i \langle \epsilon _k \vert \hat{H} \rho (t) - \rho (t) \hat{H} \vert \epsilon _l \rangle \nonumber \\ {}= & {} -i \langle \epsilon _k \vert \hat{H} \rho (t)\vert \epsilon _l \rangle + i \langle \epsilon _k \vert \rho (t) \hat{H} \vert \epsilon _l \rangle . \end{aligned}$$

(A2)

It is easy to see which components of sums from (A1) would be equal to zero due to scalar products of different basis vectors ($\langle \epsilon _\alpha \vert \epsilon _\beta \rangle = 0$ when $\alpha \ne \beta$) after substituting them to (A2), and what remains is:

$$\begin{aligned} \frac{d}{dt} p_{k,l} (t) = -i \langle \epsilon _k \vert E_k \vert \epsilon _k \rangle \langle \epsilon _k \vert p_{k,l} \vert \epsilon _k \rangle \langle \epsilon _l \vert \epsilon _l \rangle + i \langle \epsilon _k \vert p_{k,l} \vert \epsilon _k \rangle \langle \epsilon _l \vert E_l \vert \epsilon _l \rangle \langle \epsilon _l \vert \epsilon _l \rangle . \end{aligned}$$

(A3)

All the scalar products above are equal to one and therefore can be omitted in the expression:

$$\begin{aligned} \frac{d}{dt} p_{k,l} (t) = -i p_{k,l} \left( E_k - E_l \right) , \end{aligned}$$

(A4)

which translates to following form of denisty matrix elements:

$$\begin{aligned} p_{k,l} (t) = p_{k,l} (0) \cdot e^{ -i \left( E_k - E_l \right) t} . \end{aligned}$$

(A5)

However, at this point it should be marked that this form corresponds to basis constructed with eigenvectors of Hamiltonian. In aim to translate this result to the calculational basis, that allows to determine the entanglement between the particular spins of the structure, the change of basis is required. Eventually, the element in the m-th row and n-th column of density matrix in this calculational basis, denoted by $\rho _{m,n}$, is expressed by:

$$\begin{aligned} \rho _{m,n} = \sum \limits _{k,l} \langle m \vert \epsilon _k \rangle p_{k,l}(0) e^{-i (E_k - E_l)t} \langle \epsilon _l \vert n \rangle , \end{aligned}$$

where $\vert m \rangle$ and $\vert n \rangle$ are the base vectors of calculational basis. Further calculations (reduction of he Hilbert space, determination of concurrence using (6) or (9)) do not require any complex calculation methods; nevertheless, they are extremely labour-intensive and their determination is best entrusted to the computational software.

In order to attempt an analytical solution for an open system, we start the analysis with determining the effect of the dissipator on the $p_{k,l}$ element of density matrix, initially for only one dissipative operator $\hat{A}$ in Lindblad equation:

$$\begin{aligned} \mathcal {D}(\rho ) = \gamma \mathcal {L}(\hat{A}). \end{aligned}$$

(A6)

All the operators we used in dissipator act on the space spanned by the computational basis vectors; therefore, they can be decomposed to the form:

$$\begin{aligned} \hat{A} = \sum _{k,l} A_{k,l} \vert k\rangle \langle l\vert , \end{aligned}$$

which allows to write the k,l-th element of dissipator as:

$$\begin{aligned}{}[\mathcal {D}]_{k,l}= & {} \langle k \vert \gamma \mathcal {L}(\hat{A}) \vert l \rangle \\ {}= & {} \gamma \langle k\vert 2 \hat{A} \rho (t) \hat{A}^\dagger - \hat{A}^\dagger \hat{A} \rho (t) - \rho (t) \hat{A}^\dagger \hat{A} \vert l \rangle \\ {}= & {} \gamma \left( 2 \langle k \vert \hat{A} \rho (t) \hat{A}^\dagger \vert l \rangle - \langle k \vert \hat{A}^\dagger \hat{A} \rho (t) \vert l\rangle - \langle k \vert \rho (t) \hat{A}^\dagger \hat{A} \vert l \rangle \right) \end{aligned}$$

Proceeding as in the case of a closed system, one can derive the result:

$$\begin{aligned}{}[\mathcal {D}]_{k,l} = 2 \gamma \sum _{m,n} \left( A_{k,m} A^*_{l,n} \cdot \rho _{m,n}(t) - \frac{1}{2} A^*_{m,k} A_{m,n}\cdot \rho _{n,l}(t) -\frac{1}{2} A^*_{n,m} A_{n,l} \cdot \rho _{k,m}(t) \right) \end{aligned}$$

(A7)

As one can notice, a complete solution to determine the explicit form of the density matrix requires solving a system of interconnected differential equations. However, the case discussed in paper allows for two more simplification: firstly, the operators in dissipator are of two kinds—raising and lowering spin operators. In their calculation basis matrix form, they have only two types of elements—0 and 1. The only terms that will not be zeroed out in the above equation are those that relate to the two elements of the matrix $\hat{A}$ that both are equal to one. What is more, the initial state consists of several calculational basis vectors, all of them with the same probability amplitude (for $\vert \alpha \rangle$ this amplitude is $\rho _0 = \frac{1}{8}$). Assuming operationally that $\left[ \hat{H}, \rho (t) \right] = 0$, the Lindblad equation for the situation considered in paper simplifies to:

$$\begin{aligned} \frac{d}{dt} \rho _{k,l}(t) = \sum _{\alpha , \beta } \eta \gamma _x \cdot \rho _{\alpha ,\beta }(t) \end{aligned}$$

(A8)

where $\eta$ can be equal to either $+2$ or $-1$, depending on what part of Lindblad operator this term originates from, x can be P (for spin raising operator) or N(for spin lowering operator), and $\rho _{\alpha ,\beta }$ are the terms from (A7) that were associated with two nonzero elements of operator matrix. The selection of these elements can be laborious, yet it is perfectly doable knowing the matrix forms of the operators in question. The implicit form of particular density matrix element reads:

$$\begin{aligned} \rho _{k,l}(t) = \sum _{\begin{array}{c} {\text {all nonzero}} \\ \\ \text {elements from (A7)} \end{array}} \rho _0 \cdot e^{\eta \gamma _X t}. \end{aligned}$$

(A9)

While solution (A9) is far from rigorous, it allows, along with (A5), to draw some conclusions: the unitary density matrix evolution for discussed system without the bosonic environment consists of periodic changes in the population of states that are not eigenstates, while the inclusion of the dissipative environment into account will result in exponential change in time of the density matrix elements. Both of these findings have their confirmation in numerical results presented in the main paper.