1 Introduction

Reinforcement learning can be used for a large variety of applications, ranging from autonomous robots [1] to determining optimal social and economical interactions [2]. Reinforcement learning designs intelligent agents that are able to interact with the outer world to successfully accomplish specific tasks, such as finding a goal or obtaining certain rewards. Over the years, reinforcement learning has seen many improvements, most notably the use of neural networks to encode the quality of state-action combinations. Since then, it has been successfully applied to complex games such as Go [3] and solving a Rubik’s cube [4].

Reinforcement learning models are useful for exploring an unknown environment cost-effectively. In hostile environments, choosing the best course of action can be a matter of life and death. Therefore, artificial machine learning models often aid in making the best decision. Reinforcement learning models can find a cost-effective path through unknown or unexplored environments. By presenting the reinforcement learning model with a simplified overview of the environment, together with the goal and possibly dangerous locations or paths that enemy parties control, the model searches for a path that reaches the objective while incurring the least amount of cost. The definition of cost differs per use case. If we wish to find a route between two points, we can define the cost as the length of the route found, however, in hostile situations, we should instead define the cost as a measure of the safety of a specific route.

The reinforcement learning model effectively learns a policy that dictates which action a should be taken in a state s. The expected cumulative future reward of a given state-action combination, given by Q(s, a), determines the quality of a given policy.

In simple environments, one can easily find the optimal policy, even without explicitly computing the Q values. However, in complex environments with many variables, humans would have difficulties finding an optimal path and computer models take over. As environments become more complex, even computers can have difficulties and their computational power sometimes proves insufficient [5]. This gives rise to learning enhancements, such as curriculum learning where we gradually complicate the environment [6]; hardware-based computation enhancements, such as distributed reinforcement learning on CPU-GPU Systems [7]; and quantum (assisted) reinforcement learning [8, 9].

For the latter, much research is done recently, both using gate-based quantum computers and annealing-based quantum computers as computation platform. Gate-based approaches can use Grover’s search algorithm to find the best new action [10, 11] or model complex interactions between the agent and the environment in superposition [8, 12]. Here, the learning phase is partially quantum and the optimal policy is stored using either classical or quantum resources. The annealing-based quantum approach comprises an algorithm to train a quantum Boltzmann machine efficiently using a quantum annealer [13, 14]. The quantum Boltzmann machine stores the optimal policy.

Current quantum hardware is still under development and hardware typically is noisy. Therefore, current quantum devices are called noisy-intermediate scale quantum (NISQ) devices [15]. Yet, even these NISQ devices already prove useful in solving specific problems [16]. Gate-based NISQ devices can for instance help simulate quantum many-body systems [17]. Furthermore, both gate-based and annealing-based NISQ devices can help solve optimization problems. Examples include threathing AES encryption by formulating it as an optimization problem [18] and implementing quantum machine learning models [19, 20] and quantum neural networks [21].

In this work, we analyse the capabilities of quantum machine learning for reinforcement learning. We compare the performance of both the gate-based and the annealing-based quantum approach with that based on classical deep reinforcement learning. We specifically consider agents in an unknown environment that have to reach an objective. The unknown environment can have both obstructed states and penalty states. Visiting a penalty state will incur a large cost. We also allow for stochasticity in the actions of the agents: given a state and an action, agents only move to intended state with some probability and otherwise move to an adjacent grid position. We also introduce an improved learning technique called curriculum learning, where the environment is gradually made more complex. In [13, 14], an approach to grid traversal for single agents is presented using quantum annealers. This work has later been extended to settings with multiple agents collectively reaching certain objectives in [22].

In the next sections, we will first introduce the two quantum approaches to implement the reinforcement learning models. Next, we will explain the experimental set-up and compare and discuss the results with classical reinforcement learning. We will conclude with a summary and give pointers for future research.

2 Quantum computing approaches

Quantum computers exploit quantum effects to perform computations. The way in which quantum computers implement these operations and which operations are supported can, however, differ. Two common approaches to quantum computing are annealing-based quantum computing and gate-based quantum computing. The approaches are analogues to classical analogue computing and classical digital computing, respectively.

2.1 Annealing-based quantum computing approach

Annealing-based quantum computing (or quantum annealing) is based on the work of Kadowaki and Nishimore [23]. Many problems have already been solved using quantum annealing, giving reasonable solutions in real time [24] or giving optimal or very good solutions faster than classical alternatives [25]. Applications of quantum annealing are diverse and include traffic optimisation [24], finance [26], cyber security problems [27] and machine learning [13, 25, 28]. In quantum annealing, qubits are brought in an initial superposition state, after which a problem-specific Hamiltonian is applied to the qubits. If the Hamiltonian is applied slowly enough, the qubits remain in the desired ground-state and a measurement will reveal the answer to the considered problem. We encode the Hamiltonian either as a quadratic unconstrained binary optimization (QUBO) problem or in the Ising formulation [29].

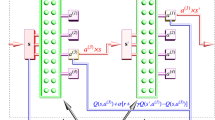
The proposed annealing-based quantum approach explicitly computes the Q-function to determine the optimal policy. This Q-function can be encoded by a Boltzmann machine: a neural network in which all nodes can be connected. Restricted Boltzmann machines are a special type of Boltzmann machine: the nodes are subdivided in visible nodes v and hidden nodes h and connections only exist between nodes of different groups. The visible nodes relate to the possible states and actions. We can further subdivide the hidden nodes in multiple hidden layers. In that case, connections only exist between nodes of subsequent layers.

Edges connect different nodes and weights can be assigned to these edges. A positive (negative) weight indicates a preference for the two linked nodes to attain the same (opposite) value. Nodes take one of two possible values \(\pm 1\). Using weights assigned to nodes, we can indicate a preference for one of the two values.

Restricted Boltzmann machines are stochastic Ising models. Therefore, quantum annealers can help determine the energy associated with a restricted Boltzmann machine. The energy of a restricted Boltzmann machine is given by

$$\begin{aligned} E(v,h) = -\sum _i w_{ii} v_i - \sum _j w_{jj} h_j -\sum _i \sum _j w_{ij} v_i h_j, \end{aligned}$$
(1)

where \(v_i\) and \(h_j\) are variables indicating the values of the visible and hidden nodes and \(w_{ij}\) indicates the weight between nodes i and j. By definition, \(w_{ij}=0\) if nodes i and j are not in subsequent layers. All weights are bidirectional.

To train a restricted Boltzmann machine, we first fix the visible nodes, which effectively fixes a state-action combination. Then, we use the quantum annealer to efficiently determine the energy for this pair, and finally, we update the weight of the restricted Boltzmann machine to improve performance, based on some metric. The used metric can differ between use cases. For our application, we consider the expected reward obtained with the current weights of the restricted Boltzmann machine. More details on the implementation are given in [13, 14, 22].

We can enhance the performance of the restricted Boltzmann machine by applying replica stacking: Multiple copies of the same layout are simultaneously mapped to the hardware and corresponding variables in different replicas are coupled. This lowers the probability of finding suboptimal configurations. Note that the available hardware, the size of the encoded environment and the number of actions naturally impose a limit on the number of replicas we can use.

The restricted Boltzmann machine and its weights encode the provisional policy. By tuning the weights, we can learn a better policy.

2.2 Gate-based quantum approach

Gate-based quantum computing is in many ways similar to conventional digital computers. Most classical concepts are replaced by their direct quantum equivalent: quantum bits (qubits) replace bits and qubit operations replace bit operations. A key difference is that the quantum operations have to be reversible. All classical operations can, however, be made reversible by adding additional bits. Gate-based quantum computers perform operations by carefully manipulating specific qubits in a specific order. The resulting quantum state then holds the answer and a measurement reveals only one of the possible outcomes with probability proportional to the square of the amplitude of that specific outcome.

For the gate-based quantum approach, we chose to explore an approach that uses Grover’s search algorithm [30] to find the best action, instead of modelling complex agent–environment interactions in a quantum way, as the Grover-approach [31] is more suited to NISQ devices. Instead, an implementation that models complex agent–environment interactions in superposition requires significant overhead for error-correction.

Another reason we consider the Grover’s approach is the option to evaluate the effect of multiple sequential steps: What are the best n sequential steps to take from my current position to reach the objective?

The gate-based quantum approach stores a provisional policy during learning, which keeps the best action for every state, together with the expected reward from that state. The approach returns the stored policy once training is finished. In each iteration, we search for the best action starting from some state, using Grover’s search algorithm. We let the number of used Grover-iterations depend on the expected reward of the provisional state-action combination of the policy. That way, we assure that we find good actions more often, once we have found them and included them in the provisional policy.

3 Experiments and results

3.1 Experimental set-up

To implement the reinforcement learning model, we have two quantum approaches, an annealing-based quantum approach that implements a restricted Boltzmann machine and a gate-based quantum approach that uses Grover’s search algorithm to find the optimal action. We compare both quantum models with a classical deep reinforcement learning approach. We evaluate the performance of these approaches on multiple different environments. During the training phase of each of the approaches, the best policy, given by state-action combinations, is learned.

3.1.1 Used environments

Fig. 1 shows the used environments. The environments contain one or more starting states S and one or more target states G. An agent starts in a starting state and follows a learned policy to reach the target G. The policy is learned using one of the three considered approaches. The environments furthermore contain obstructed states W and penalty states P. From each state, agents can take four actions: move up, down, left and right. If an action would make an agent move outside of the environment, or into an obstructed state, the time-step advances without the agent changing position. Agents that visit a penalty state incur a negative reward of minus two hundred, whereas reaching the goal state gives a positive reward of two hundred. We take the magnitude of both values to be equal, as a penalty state should be avoided just as much as the target should be reached. Agents incur a small negative reward of minus ten if they take a step. We explicitly chose this value significantly smaller than the reward in the target state. This small cost of taking a step favours direct paths over detours.

Fig. 1
figure 1

The four considered environments. S denotes the starting position, W denotes an obstructed state, P denotes a penalty state, and G denotes the objective state

Full size image

3.1.2 Stochastic actions

We allow the agents to take either deterministic or stochastic actions. With stochastic actions, an agent takes an action with tunable probability p and with probability \((1-p)/2\) one of the two adjacent actions is taken instead. For example, for \(p=0.9\), an agent moves up with probability 0.9 and moves to the right or left each with probability 0.05. If \(p=1\), we refer to the action as deterministic, otherwise, we call them stochastic. In practice, agents can deviate from the action suggested by the model, for instance, because a path is closed unexpectedly. Stochastic actions take this uncertainty into account. We expect the performance of the model to drop initially; however, as the learning stage proceeds, we expect the model to still learn the optimal policy with the same performance as the deterministic approach achieves.

3.1.3 Performance measure

We can quantify the performance of a learned policy using the expected reward.

Previous works also considered the fidelity of a policy. The fidelity equals the fraction of states that have the correct action assigned to it. Determining the correct action per state usually requires explicit evaluation of the environment. This is only viable for small and relatively simple environments and we therefore only used the fidelity for developing and testing the performance of an approach, not for the eventual evaluation.

To calculate expected reward, we follow the actions given by the policy, starting from a predefined starting state, and keep track of the sum of the rewards per step. This measure is simple to evaluate, independent of the size of the environment. We therefore only consider the expected reward in evaluating the performance of a policy.

3.1.4 Training phase and learning strategies

We train for a fixed number of training iterations and compute the expected reward throughout training. In both quantum approaches, each training iteration consists of a single state-action combination. For the classical deep reinforcement learning approach, a single training iteration is one evaluation of a path from the starting point to the goal. We choose for this difference as otherwise the number of training iterations for the classical deep reinforcement approach would be too high.

To compute the expected reward, we start in a starting position S and follow the policy until either a goal state is reached or a maximum number of states have been visited. This maximum number of states is taken as the number of distinct states in the considered environment. In case of stochastic actions, we repeat this process thirty times and average the results. In total, we independently train the three approaches ten times and average the found results over these ten runs. This compensates for possible variability during the training phase.

We also employ two different training strategies. In the first training strategy, we present each of the three approaches with the whole environment, whereas in the second strategy we gradually increase the complexity of the environment during training. We call the first strategy direct learning and the second strategy curriculum learning [6]. In curriculum learning, the environment initially only contains obstructed states. After a fixed number of training iterations, we complicate the environment by adding penalty states and later also stochastic actions. We also introduce the stochastic actions gradually, by first learning with high p values and gradually lowering p, where p is the probability of correctly taking the action.

3.1.5 Hyperparameter choice

The three approaches considered have some hyperparameters we have to set, such as the number of hidden layers and the number of replicas in the quantum annealing-based approach and the exploration rate in the classical approach. For both quantum approaches, we also have to determine the number of quantum samples we have to take in each training iteration. The last two hyperparameters are the learning rate and the discount factor. This discount factor weighs the current value of future rewards: A future reward is worth less than the same reward obtained now.

We chose candidate values for each of the hyperparameters based on [22] and performed a grid-search over the possible combinations to find the best setting. We determined the quality of each setting by computing the fidelity of the learned policy. We used the \(5\times 3\)-environment shown in Fig. 1b to find the hyperparameters as we can find the optimal policy for this environment by a quick visual inspection. We chose the hyperparameter settings that gave the highest average fidelity over five independent runs. If two settings showed similar average performance, we chose the settings with the most stable performance and the fastest convergence.

Note that ideally one would tune the hyperparameters to each environment specifically. This, however, significantly increases the computational load and hence does not scale well. We expect that our way of choosing the hyperparameters is scalable and performance for other environments will remain acceptable.

3.1.6 Simulation set-up

We compared the results of both quantum approaches with a classical deep reinforcement learning approach. In this classical approach, an agent starts exploring the environment from the starting state and hopes to find a target state. Given enough training time, the strategy of the agent will improve and he will find a target state faster. The way of training differs from the two quantum approaches, most notably in that no explicit policy is kept and that in a single training iteration of the classical deep reinforcement learning approach we update the model for a whole path, instead of for a single state-action combination.

We trained the classical deep reinforcement learning approach locally on a modest personal computer. We simulated both quantum approaches: The quantum annealing-based approach using simulated annealing models provided by the Ocean software package by D-Wave [32] and the gate-based quantum approach using the Qiskit quantum software package [33]. We expect that both quantum approaches will show similar performance on real quantum hardware, even on NISQ devices are still subject to noise. For the quantum annealing-based approach, we expect during training, the effect of noise on the outcome will be counteracted by a suitable choice of weights. For the gate-based quantum approach, we expect that the noise will have a small effect because the circuit is shallow. Because the difference in how we test the approaches, we only compare the performance based on the number of training steps taken and not on the actual running times.

3.2 Results of curriculum learning versus direct learning

In this section, we compare the performance of curriculum learning versus direct learning, using some of the environments of Fig. 1. For each environment, we added penalty states after half of the training steps, thereby complicating the environment. We used the expected reward to quantify the performance of a policy.

In the first tests, we have set the stochasticity to zero and compared the results of curriculum learning with that of direct learning. We find that the gate-based approach learns relatively quickly, whereas the quantum annealing-based approach takes more training iterations to learn. Similarly, we do see the classical reinforcement learning approach requires more training steps to learn a policy. Initially, the found reward is low for all three approaches, as the agent is effectively performing a random walk in the environment. With curriculum learning, no penalty states are present yet, so the only penalty comes from taking steps.

In all results, we also see some variability in the reward found, resulting from stochasticity inherent in the learning method. For both quantum approaches, this is the chosen state-action combination to consider in that iteration and for the classical approach this is the path chosen to explore. Furthermore, we see a drop in the found reward once we complicate the environment.

Figures 2 and 3 show the results for the \(5\times 3\) environment shown in Fig. 1b for both direct learning and curriculum learning. The classical deep reinforcement learning approach learns a good policy; however with curriculum learning, performance is more stable. Both quantum approaches perform similarly for curriculum learning and learn the optimal policy relatively quickly. In direct learning, we see that both approaches do not learn the optimal path as this would constitute a reward of 150: 200 from the goal and \(-50\) for five steps.

The gate-based quantum approach shows improvement over time, whereas the quantum annealing-based approach quickly learns a policy, but then stops learning. A visual inspection of the policy learned that the path found leads the agent through the penalty state before reaching the end state, resulting in an overall reward of roughly zero. The drops in performance in the classical approaches most likely follow from uncertainty in the learning process, or from two paths that initially seem equally good, but one path having a significantly lower reward. We expect a similar reason to cause the drops in performance for the gate-based and annealing-based quantum approaches.

Fig. 2
figure 2

Expected reward for classical deep reinforcement learning in the \(5\times 3\) environment shown in Fig. 1b

Full size image
Fig. 3
figure 3

Expected reward for gate-based reinforcement learning and quantum annealing-based reinforcement learning in the \(5\times 3\) environment shown in Fig. 1b

Full size image

If we complicate the environment, we do see a different behaviour. Figures 3 and 4 show the results for the \(4\times 3\) environment shown in Fig. 1a. Even though this environment is smaller, it is more complex than the \(5\times 3\) environment, and hence, we already expected a worse performance. Both quantum approaches initially learn faster with curriculum learning than with direct learning. With curriculum learning, we do see a sharp drop in the expected reward once we introduce penalty states in the environment. We expect that this follows from the first learning stage in curriculum learning, where a policy is learned that is suboptimal in the more complex environment and which is too hard to unlearn fast. A visual inspection of the policy learned by both quantum approaches under curriculum learning learned that only a single state had the wrong action, which caused the agent to move in circles, explaining the low reward found. In trying to overcome this, the agent sometimes ends up in a penalty state, hence the drops in reward for the quantum annealing-based approach.

3.3 Quantifying the effect of stochastic actions

In this section, we analyse the performance of our approaches in stochastic settings to see if they can coop with that. Therefore, we considered two independent runs of direct learning, one with deterministic actions and one with stochastic actions. We did this for each of the three approaches and compared the expected reward over time. As the absolute performance under stochastic actions is lower, we mainly consider the relative performance between the two.

We again see that the models initially find a low reward, as the agent effectively performs a random walk. For some environments, the model has difficulty finding a good policy and performance stays relatively constant during the training phase, especially for the larger environments combined with any of the two quantum approaches. Another effect of the stochasticity is that the reward shows more variance over time than with deterministic actions.

Figures 6b and 7b show the performances of the classical deep reinforcement learning approach and both quantum approaches for the \(8\times 10\) environment. This environment is the largest and most complex environment considered. Performance with stochastic actions is similar as performance with deterministic actions for all three approaches. For both quantum versions, the expected reward starts lower, but we see improvements due to learning, indicating that after sufficient training steps the expect reward for deterministic and stochastic actions will coincide.

Fig. 4
figure 4

Expected reward for classical deep reinforcement learning in the \(4\times 3\) environment shown in Fig. 1a

Full size image
Fig. 5
figure 5

Expected reward for gate-based reinforcement learning and quantum annealing-based reinforcement learning in the \(4\times 3\) environment shown in Fig. 1a

Full size image
Fig. 6
figure 6

Expected reward for classical deep reinforcement learning in the \(8\times 10\) environment shown in Fig. 1d

Full size image
Fig. 7
figure 7

Expected reward for gate-based reinforcement learning and quantum annealing-based reinforcement learning in the \(8\times 10\) environment shown in Fig. 1d

Full size image

As a final test, we considered the combined effect of our two extensions: curriculum learning with stochastic actions. The procedure applied with curriculum learning is that we introduce penalty states after a quarter of the training steps. After half of the training step, we introduce stochastic actions with a high p value; and, after three quarters of the training steps, we lower the p value leading to more stochasticity in the actions. We double the number of training steps for each of the environments considered.

Figures 8a and 9a show the performance of the classical deep reinforcement learning approach and the two quantum approaches for the \(5\times 4\) environment, shown in Fig. 1c. We see that the classical deep reinforcement learning approach reaches similar rewards with, but does so sooner. Similarly, the gate-based approach reaches a similar performance for both learning strategies, but with curriculum learning, the reward is more stable. The quantum annealing-based approach shows a significant improvement when using curriculum learning over direct learning, the absolute performance is, however, lower than that of the other two approaches. An interesting aspect is that with curriculum learning we see significant drops in performance once we complicate the environment. This drop indicates that the learned policy so far was suboptimal for the more complex environment. The approach should thus relearn part of the policy for this new environment.

Fig. 8
figure 8

Expected reward for classical deep reinforcement learning in the \(5\times 4\) environment shown in Fig. 1c

Full size image
Fig. 9
figure 9

Expected reward for gate-based reinforcement learning and quantum annealing-based reinforcement learning in the \(5\times 4\) environment shown in Fig. 1c

Full size image

4 Discussion

In the previous section, we presented the results of multiple experiments run for the classical approach and the two quantum approaches for grid traversal. We considered the effect of curriculum learning and the effect of stochastic actions on the performance on the approaches. We found that on some environments, the two quantum approaches required significantly fewer training steps than the classical deep reinforcement learning approach to attain similar performance. On other environments, performance of the quantum approaches lacked behind slightly, however, still using significantly fewer training iterations. A possible solution would be a better tuning of hyperparameters or a change in the learning set-up. Time wise we have no comparison between the different approaches as we simulated the quantum approaches and used different hardware backends for these simulations and the classical results. As a result, the run time of the experiments is incomparable and left out.

Our first extension of the models is a different learning technique: curriculum learning. With curriculum learning, we gradually complicate the environment in hope of quicker learning. With the exception of the \(4\times 3\) environment, we observe quicker convergence to a policy with a high expected reward when using curriculum learning instead of direct learning. An artefact we do observe in especially the quantum environments is a sharp drop in performance once we complicate the environment. We expect that the two quantum approaches learned a policy for the simple environment and have difficulty unlearning the suboptimal parts of this policy in the more complex environment. A solution for this is moving to a more complicated environment once a certain performance level is achieved instead of after a fixed number of training iterations.

Our second extension was allowing for stochastic actions taken by the agents. With some probability, a different action is taken than initially intended. We found that for each approach the performance under deterministic actions is close to the performance under stochastic actions. When combining both extensions, we see that especially the quantum annealing-based approach benefits from the curriculum learning strategy. The other two approaches show a similar final performance for both learning strategies.

A note of attention is the difference in learning between the classical deep reinforcement learning approach and the two quantum approaches. The classical approach lets an agent explore the environment from a starting state and uses the whole path taken to update the policy for each training iteration. The two quantum approaches only consider single state-action combinations in each training iteration and update the policy based only on the results for that state-action combination.

5 Conclusion

In this paper, we considered two quantum approaches to grid traversal using reinforcement learning, a gate-based approach and a quantum annealing-based approach. We extended previous models by including stochastic actions and using a new learning technique called curriculum learning. We compared the expected reward of a policy learned with a quantum approach with a policy learned using classical deep reinforcement learning, and we did that for both extensions. We found that for some environments the quantum approaches learn faster than the classical approach by a factor of almost one hundred in terms of the number of training steps. For other environments, the difference is likely smaller as the performance of the quantum approaches was not at the level of the classical approach’s performance. We expect that, as quantum hardware matures, we can also run these experiments on quantum hardware with similar performance as found in the simulations. As a result, we believe that the gap between the classical approach and the quantum approaches can grow for more complex environments and improved quantum hardware.

We furthermore analysed the performance difference between curriculum learning and direct learning. In the former, the complexity of the environment is gradually increased, in the latter, the complete environment is presented directly. We found that with curriculum learning a higher expected reward was attained sooner in all cases. The quantum annealing-based approach did show some variety in performance between different environments.

We also considered the effect of stochastic actions taken by the agents, where agents only take the intended step with some probability and move to one of the adjacent states otherwise. Here, we saw that our models perform equally well under deterministic actions compared to stochastic actions. Curriculum learning showed its potential when also considering stochastic actions, as the approaches could already learn a reasonable policy under deterministic actions before moving to more complicated stochastic actions.

Note that it is difficult to compare the performance of our approaches with previous work, such as [13, 14]. In previous work, taking a step incurred no cost. We, however, added the additional cost of taking a step, thereby favouring shorter routes over longer ones. As a result, the reward found in some environments appears low, while the policy is close to optimal. In most cases, this lower reward results from a single or a few states with incorrect actions assigned to it, which led the agents to wander in circles.

Changes to the curriculum learning strategy can also boost performance of the models, by learning an optimal policy faster. In this paper, we only complicated the environment after a fixed number of training steps. In some cases, this led to policy being learned quickly and the fortifying this optimal policy. The thus learned policy can be suboptimal, or even bad, in more complicated environments. Updating the policy proved to be hard for some environments. An improved curriculum learning strategy is to complicate the environment once a certain performance is achieved. Determining the corresponding performance thresholds when to complicate the environment does however require more knowledge of the actual considered environment. This knowledge-requirement contradicts our original goal of using the models in operational settings with limited manual user input.

An interesting direction of future work is to extend the curriculum learning technique to environments of different sizes. We considered environments of fixed size and gradually increased the complexity of those. With curriculum learning, we can also consider the effect of complicating the environment by enlarging it. Our current quantum approaches do not support this form of curriculum learning. The quantum annealing-based approach stores the policy in the weights of the restricted Boltzmann machine and the number of visible nodes correspond to the number of states and actions. So changing the size of the environment affects the layout of the restricted Boltzmann machine. Extending our implementations to also support an enlargement of the environment would require significant effort and was outside our research scope.

A second direction of future work we believe is fruitful is considering the effect of taking multiple sequential steps. We expect that performance will improve, as the approaches will traverse states even though they are bad when considering a single step, but optimal from a larger point of view. This multi-step approach is especially relevant in larger and complicated environments. We believe that minor changes to the used implementations will suffice here.

A third interesting direction for future work would be multi-agent learning under stochastic actions and with direct and curriculum learning. We believe that our implementations will, after some careful modifications, prove helpful in learning a policy in multi-agent settings. These multi-agent settings, with multiple independent agents collaboratively working towards one or more target states, have practical relevance in various use cases. The two quantum approaches might better model the complex interactions between the agents than classical deep reinforcement learning.