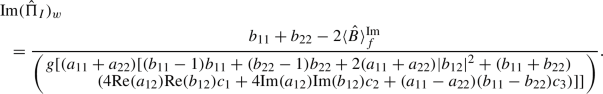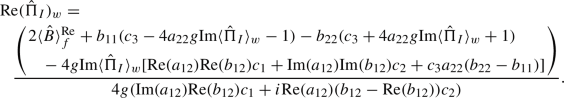Quantum information transfer using weak measurements and any non-product resource state

Abstract

Information about an unknown quantum state can be encoded in weak values of projectors belonging to a complete eigenbasis. A protocol that enables one party—Bob—to remotely determine the weak values corresponding to weak measurements performed by another spatially separated party—Alice is presented. The particular set of weak values contains complete information of the quantum state encoded on Alice’s register, which enacts the role of preselected system state in the aforementioned weak measurement. Consequently, Bob can determine the quantum state from these weak values, which can also be termed as remote state determination or remote state tomography. A combination of non-product bipartite resource state shared between the two parties and classical communication between them is necessary to bring this statistical scheme to fruition. Significantly, the information transfer of a pure quantum state of any known dimensions can be effected even with resource states of low dimensionality and purity with a single measurement setting at Bob’s end.

Appendices

Appendix A: Protocol algebraic details—transferring imaginary part of the weak value

• 1. Bob’s unnormalized state corresponding to the measurement of the imaginary part of the weak value:

  $$\begin{aligned} \rho _B^{un}= & {} \hbox {Tr}_{I,A} ( \hat{\pi }_{I}^v \rho _{tw}) \approx \hbox {Tr}_{I,A} (\hat{\pi }_{I}^v (\mathbb {I} + ig\hat{\Pi }_I \otimes \hat{A} \otimes \mathbb {I}) \rho _{I}\nonumber \\&\otimes \rho _{AB} (\mathbb {I} - ig\hat{\Pi }_I \otimes \hat{A}\otimes \mathbb {I})) \nonumber \\= & {} \hbox {Tr}_{I,A} (\hat{\pi }_{I}^v (\rho _{I} \otimes \rho _{AB} + ig\hat{\Pi }_I \rho _{I} \nonumber \\&\otimes (\hat{A} \otimes \mathbb {I}) \rho _{AB} ) (\mathbb {I} - ig\hat{\Pi }_I \otimes \hat{A} \otimes \mathbb {I})) \nonumber \\= & {} \hbox {Tr}_{I,A} (\hat{\pi }_{I}^v (\rho _{I} \otimes \rho _{AB} - ig \rho _{I} \hat{\Pi }_I \otimes \rho _{AB} ( \hat{A} \otimes \mathbb {I})\nonumber \\&+ ig\hat{\Pi }_I \rho _{I} \otimes (\hat{A} \otimes \mathbb {I}) \rho _{AB} ) ) \nonumber \\= & {} \hbox {Tr}_{I,A} ( (\hat{\pi }_{I}^v \rho _{I} \otimes \rho _{AB}) - ig \hat{\pi }_{I}^v \rho _{I} \hat{\Pi }_I \otimes \rho _{AB}\nonumber \\&( \hat{A} \otimes \mathbb {I}) + ig ( \hat{\pi }_{I}^v \hat{\Pi }_I \rho _{I} ) \otimes (\hat{A} \otimes \mathbb {I}) \rho _{AB} ) \nonumber \\= & {} \hbox {Tr}_{I} (\hat{\pi }_{I}^v \rho _{I}) ( ( \hbox {Tr}_{A} ( \rho _{AB}) - ig ( \hat{\Pi }_I )_w^* \hbox {Tr}_{A} ( \rho _{AB} ( \hat{A} \otimes \mathbb {I})) \nonumber \\&+ ig ( \hat{\Pi }_I )_w \hbox {Tr}_{A} ( (\hat{A} \otimes \mathbb {I}) \rho _{AB} ) )). \end{aligned}$$

  (A1)

• 2. Normalizing the above state:

  Cyclic property of the trace allows us to write $\hbox {Tr}_{A} ( \rho _{AB} ( \hat{A} \otimes \mathbb {I})) = \hbox {Tr}_{A} ( (\hat{A} \otimes \mathbb {I}) \rho _{AB} )$. Bob’s initial state is $\hbox {Tr}_{A} ( \rho _{AB}) \equiv \rho _B^\mathrm{{in}}$. Thus, we can write

  $$\begin{aligned} \rho _B^{un} \approx \hbox {Tr}_{I} (\hat{\pi }_{I}^v \rho _{I}) (\rho _B^\mathrm{{in}} - 2 g \hbox {Im} ( \hat{\Pi }_I )_w \hbox {Tr}_{A} ((\hat{A} \otimes \mathbb {I}) \rho _{AB}) ). \end{aligned}$$

  Further, using $\hbox {Tr}(\rho _B^\mathrm{{in}}) = 1$:

  $$\begin{aligned} \rho _{B}^N = \frac{\rho _{B}^{un}}{\hbox {Tr}(\rho _B^{un})}\approx \frac{\bigg (\rho _B^\mathrm{{in}} - 2 g \hbox {Im} ( \hat{\Pi }_I )_w \hbox {Tr}_{A} ((\hat{A} \otimes \mathbb {I}) \rho _{AB}) \bigg )}{\bigg ( 1 - 2 g \hbox {Im} ( \hat{\Pi }_I )_w \hbox {Tr}( (\hat{A} \otimes \mathbb {I}) \rho _{AB} ) \bigg )}. \end{aligned}$$

  (A2)

  In line with the weak approximation, one can bring the denominator to the numerator and Taylor expand up to the first order in g:

  $$\begin{aligned} \rho _B^N\approx & {} \bigg ( \rho _B^\mathrm{{in}} - 2 g \hbox {Im} ( \hat{\Pi }_I )_w \hbox {Tr}_{A} ((\hat{A} \otimes \mathbb {I}) \rho _{AB}) \bigg ) \bigg (1 + 2 g \hbox {Im} ( \hat{\Pi }_I )_w \hbox {Tr}((\hat{A} \otimes \mathbb {I}) \rho _{AB}) \bigg ) \nonumber \\= & {} \rho _B^\mathrm{{in}} + 2g \hbox {Im} ( \hat{\Pi }_I )_w \hbox {Tr}((\hat{A} \otimes \mathbb {I})\rho _{AB}) \rho _{B}^\mathrm{{in}} - 2g \hbox {Im} ( \hat{\Pi }_I )_w \hbox {Tr}_A ((\hat{A} \otimes \mathbb {I})\rho _{AB}) \nonumber \\= & {} \rho _B^\mathrm{{in}} + 2 g \hbox {Im} ( \hat{\Pi }_I )_w \bigg (\hbox {Tr}((\hat{A} \otimes \mathbb {I})\rho _{AB})\rho _{B}^\mathrm{{in}} - \hbox {Tr}_{A} ((\hat{A} \otimes \mathbb {I})\rho _{AB})\bigg ). \end{aligned}$$

  (A3)

• 3. Bob’s expectation value:

  $$\begin{aligned} \langle \hat{B} \rangle _f^\mathrm{{Im}}= & {} \hbox {Tr}(\hat{B} \rho _B^N) \nonumber \\\approx & {} \hbox {Tr}(\hat{B} \rho _B^\mathrm{{in}}) + 2 g \hbox {Im} ( \hat{\Pi }_I )_w\nonumber \\&\bigg ( \hbox {Tr}((\hat{A}\otimes \mathbb {I})\rho _{AB}) \hbox {Tr}(\hat{B}\rho _B^\mathrm{{in}}) - \hbox {Tr}(\hat{B} \hbox {Tr}_{A} ((\hat{A} \otimes \mathbb {I})\rho _{AB}))\bigg ). \end{aligned}$$

  (A4)

Appendix B: Protocol algebraic details—transferring real part of the weak value

• 1. Bob’s unnormalized state:

  $$\begin{aligned} \rho _B^{un}= & {} \hbox {Tr}_{I,A} ((\hat{\pi }_{I}^v \otimes \hat{\pi }_{A}^l \otimes \mathbb {I}) \rho _{tw}) \\\approx & {} \hbox {Tr}_{I,A} ((\hat{\pi }_{I}^v \otimes \hat{\pi }_{A}^l \mathbb {I}) (\mathbb {I} + ig\hat{\Pi }_I\nonumber \\&\otimes \hat{A} \mathbb {I}) \rho _{I} \otimes \rho _{AB} (\mathbb {I} - ig\hat{\Pi }_I \otimes \hat{A} \otimes \mathbb {I})) \\= & {} \hbox {Tr}_{I,A} ((\hat{\pi }_{I}^v \otimes \hat{\pi }_{A}^l \otimes \mathbb {I}) (\rho _{I} \otimes \rho _{AB} + ig\hat{\Pi }_I \rho _{I}\nonumber \\&\otimes (\hat{A} \otimes \mathbb {I}) \rho _{AB} ) (\mathbb {I} - ig\hat{\Pi }_I \otimes \hat{A} \otimes \mathbb {I})) \\= & {} \hbox {Tr}_{I,A} ((\hat{\pi }_{I}^v \otimes \hat{\pi }_{A}^l \otimes \mathbb {I}) (\rho _{I} \otimes \rho _{AB} - ig \rho _{I} \hat{\Pi }_I\otimes \rho _{AB} ( \hat{A} \otimes \mathbb {I}) \nonumber \\&+ ig\hat{\Pi }_I \rho _{I} \otimes (\hat{A} \otimes \mathbb {I}) \rho _{AB} ) )\\= & {} \hbox {Tr}_{I,A} ( (\hat{\pi }_{I}^v \rho _{I} \otimes (\hat{\pi }_{A}^l\otimes \mathbb {I}) \rho _{AB} \nonumber \\&- ig \hat{\pi }_{I}^v \rho _{I} \hat{\Pi }_I \otimes (\hat{\pi }_{A}^l \otimes \mathbb {I}) \rho _{AB} ( \hat{A}\otimes \mathbb {I}) \\&\quad + ig \hat{\pi }_{I}^v \hat{\Pi }_I \rho _{I} \otimes (\hat{\pi }_{A}^l \otimes \mathbb {I}) (\hat{A} \otimes \mathbb {I}) \rho _{AB} ) ) \\= & {} \hbox {Tr}_{I} (\hat{\pi }_{I}^v \rho _{I}) ( \hbox {Tr}_{A} ((\hat{\pi }_{A}^l \otimes \mathbb {I}) \rho _{AB}) \nonumber \\&- ig ( \hat{\Pi }_I )_w^* \hbox {Tr}_{A} ( (\hat{\pi }_{A}^l \otimes \mathbb {I}) \rho _{AB} ( \hat{A} \otimes \mathbb {I})) \\&\quad + ig ( \hat{\Pi }_I )_w \hbox {Tr}_{A} ( (\hat{\pi }_{A}^l \otimes \mathbb {I}) (\hat{A} \otimes \mathbb {I}) \rho _{AB} ) ). \end{aligned}$$

  Taking the partial trace operation over I and A inside the parenthesis, one finds:

  $$\begin{aligned} \rho _B^{un}\approx & {} ( ( \hbox {Tr}_{I} (\hat{\pi }_{I}^v \rho _{I}) \hbox {Tr}_{A} ((\hat{\pi }_{A}^l \otimes \mathbb {I}) \rho _{AB}) \nonumber \\&- ig \hbox {Tr}_{I} ( \hat{\pi }_{I}^v \rho _{I} \hat{\Pi }_I) \hbox {Tr}_{A}( (\hat{\pi }_{A}^l \otimes \mathbb {I}) \rho _{AB} ( \hat{A} \otimes \mathbb {I}))\nonumber \\&\quad + ig \hbox {Tr}_{I} ( \hat{\pi }_{I}^v \hat{\Pi }_I \rho _{I}) \hbox {Tr}_{A} ( (\hat{\pi }_{A}^l \otimes \mathbb {I}) (\hat{A} \otimes \mathbb {I}) \rho _{AB} ) )) \nonumber \\= & {} \hbox {Tr}_{I} (\hat{\pi }_{I}^v \rho _{I}) ( ( \hbox {Tr}_{A} ((\hat{\pi }_{A}^l \otimes \mathbb {I}) \rho _{AB}) \nonumber \\&- ig \hbox {Tr}_{I} ( \hat{\pi }_{I}^v \rho _{I} \hat{\Pi }_I) \hbox {Tr}_{A}( (\hat{\pi }_{A}^l \otimes \mathbb {I}) \rho _{AB} ( \hat{A} \otimes \mathbb {I})) \nonumber \\&\quad + ig \hbox {Tr}_{I} ( \hat{\pi }_{I}^v \hat{\Pi }_I \rho _{I}) \hbox {Tr}_{A} ( (\hat{\pi }_{A}^l \otimes \mathbb {I}) (\hat{A} \otimes \mathbb {I}) \rho _{AB} ) )) \nonumber \\= & {} \hbox {Tr}_{I} (\hat{\pi }_{I}^v \rho _{I}) ( \hbox {Tr}_{A} ((\hat{\pi }_{A}^l \otimes \mathbb {I}) \rho _{AB}) \nonumber \\&- ig ( \hat{\Pi }_I )_w^* \hbox {Tr}_{A} ( (\hat{\pi }_{A}^l \otimes \mathbb {I}) \rho _{AB} ( \hat{A} \otimes \mathbb {I})) \nonumber \\&\quad + ig ( \hat{\Pi }_I )_w \hbox {Tr}_{A} ( (\hat{\pi }_{A}^l \otimes \mathbb {I}) (\hat{A} \otimes \mathbb {I}) \rho _{AB} ) ). \end{aligned}$$

  (B1)

• 2. Trace of the unnormalized state:

  $$\begin{aligned} \hbox {Tr}(\rho _b^{un})\approx & {} \hbox {Tr}( \hbox {Tr}_{I} (\hat{\pi }_{I}^v \rho _{I}) ( ( \hbox {Tr}_{A} ((\hat{\pi }_{A}^l \otimes \mathbb {I}) \rho _{AB}) \nonumber \\&- ig ( \hat{\Pi }_I )_w^* \hbox {Tr}_{A}( (\hat{\pi }_{A}^l \otimes \mathbb {I}) \rho _{AB} ( \hat{A} \otimes \mathbb {I}))\nonumber \\&\quad + ig ( \hat{\Pi }_I )_w \hbox {Tr}( (\hat{\pi }_{A}^l \otimes \mathbb {I}) (\hat{A} \otimes \mathbb {I}) \rho _{AB} ) ))) \nonumber \\= & {} \hbox {Tr}_{I} (\hat{\pi }_{I}^v \rho _{I}) ( ( \hbox {Tr}((\hat{\pi }_{A}^l\otimes \mathbb {I}) \rho _{AB}) \nonumber \\&- ig ( \hat{\Pi }_I )_w^* \hbox {Tr}( (\hat{\pi }_{A}^l \otimes \mathbb {I}) \rho _{AB} ( \hat{A} \otimes \mathbb {I})) \nonumber \\&\quad + ig ( \hat{\Pi }_I )_w \hbox {Tr}( (\hat{\pi }_{A}^l \otimes \mathbb {I}) (\hat{A} \otimes \mathbb {I}) \rho _{AB} ) ))\nonumber \\= & {} \hbox {Tr}_{I} (\hat{\pi }_{I}^v \rho _{I}) \hbox {Tr}((\hat{\pi }_{A}^l \otimes \mathbb {I}) \rho _{AB}) ( ( 1 - ig ( \hat{\Pi }_I )_w^* ( \hat{A} )_{w'}^* \nonumber \\&+ ig ( \hat{\Pi }_I )_w ( \hat{A} )_{w'} )). \end{aligned}$$

  (B2)

• 3. Now, let us normalize Bob’s state using its norm in the denominator:

  $$\begin{aligned} \rho _B^{N}= & {} \frac{\rho _B^{un}}{\hbox {Tr}(\rho _B^{un})} \nonumber \\ \approx & {} \frac{ \hbox {Tr}_{I} (\hat{\pi }_{I}^v \rho _{I}) ( ( \hbox {Tr}_{A} ((\hat{\pi }_{A}^l \otimes \mathbb {I}) \rho _{AB}) - ig ( \hat{\Pi }_I )_w^* \hbox {Tr}_{A}( (\hat{\pi }_{A}^l \otimes \mathbb {I})\rho _{AB} ( \hat{A} \otimes \mathbb {I})) + ig ( \hat{\Pi }_I )_w \hbox {Tr}_{A} ( (\hat{\pi }_{A}^l \otimes \mathbb {I}) (\hat{A} \otimes \mathbb {I}) \rho _{AB} ) }{ \hbox {Tr}_{I} (\hat{\pi }_{I}^v \rho _{I}) \hbox {Tr}((\hat{\pi }_{A}^l \otimes \mathbb {I}) \rho _{AB}) ( 1 - ig ( \hat{\Pi }_I )_w^* ( \hat{A} )_{w'}^* + ig ( \hat{\Pi }_I )_w ( \hat{A} )_{w'} )}.\nonumber \\ \end{aligned}$$

  (B3)

  Using the weak approximation, the inverse of the denominator can be Taylor expanded up to the first order in g:

  $$\begin{aligned} \rho _B^{N}\approx & {} \frac{1}{\hbox {Tr}((\hat{\pi }_{A}^l \otimes \mathbb {I}) \rho _{AB})} ( \hbox {Tr}_{A} ((\hat{\pi }_{A}^l \otimes \mathbb {I}) \rho _{AB}) \nonumber \\&- ig ( \hat{\Pi }_I )_w^* \hbox {Tr}_{A} ( (\hat{\pi }_{A}^l \otimes \mathbb {I}) \rho _{AB} ( \hat{A} \otimes \mathbb {I})) \nonumber \\&+ ig ( \hat{\Pi }_I )_w \hbox {Tr}_{A} ( (\hat{\pi }_{A}^l \otimes \mathbb {I}) (\hat{A} \otimes \mathbb {I}) \rho _{AB} )) \nonumber \\&( 1 + ig ( \hat{\Pi }_I )_w^* ( \hat{A} )_{w'}^* - ig ( \hat{\Pi }_I )_w ( \hat{A} )_{w'} ) \nonumber \\= & {} \frac{1}{\hbox {Tr}((\hat{\pi }_{A}^l \otimes \mathbb {I}) \rho _{AB})} ( \hbox {Tr}_{A} ((\hat{\pi }_{A}^l \otimes \mathbb {I}) \rho _{AB}) \nonumber \\&+ ig ( \hat{\Pi }_I )_w^* ( \hat{A} )_{w'}^* \hbox {Tr}_{A} ((\hat{\pi }_{A}^l \otimes \mathbb {I}) \rho _{AB})\nonumber \\&- ig ( \hat{\Pi }_I )_w ( \hat{A} )_{w'}\hbox {Tr}_{A} ((\hat{\pi }_{A}^l \otimes \mathbb {I}) \rho _{AB}) \nonumber \\&- ig ( \hat{\Pi }_I )_w^* \hbox {Tr}_{A}( (\hat{\pi }_{A}^l \otimes \mathbb {I}) \rho _{AB} ( \hat{A} \otimes \mathbb {I})) \nonumber \\&+ ig ( \hat{\Pi }_I )_w \hbox {Tr}_{A} ( (\hat{\pi }_{A}^l \otimes \mathbb {I}) (\hat{A} \otimes \mathbb {I}) \rho _{AB} )). \end{aligned}$$

  (B4)

• 4. Bob’s expectation value:

  $$\begin{aligned}&\langle \hat{B} \rangle _f^\mathrm{{Re}} = \hbox {Tr}(\hat{B}\rho _B^{N}) \nonumber \\&\quad \approx \frac{1}{\hbox {Tr}((\hat{\pi }_{A}^l \otimes \mathbb {I}) \rho _{AB})}\bigg [ \hbox {Tr}((\hat{\pi }_{A}^l \otimes \mathbb {I}) (\mathbb {I} \otimes \hat{B}) \rho _{AB})\nonumber \\&\qquad + ig ( \hat{\Pi }_I )_w^* ( \hat{A} )_{w'}^*\hbox {Tr}((\hat{\pi }_{A}^l \otimes \mathbb {I}) (\mathbb {I} \otimes \hat{B}) \rho _{AB}) \nonumber \\&\qquad - ig ( \hat{\Pi }_I )_w ( \hat{A} )_{w'}\hbox {Tr}((\hat{\pi }_{A}^l \otimes \mathbb {I}) (\mathbb {I} \otimes \hat{B}) \rho _{AB}) \nonumber \\&\qquad - ig ( \hat{\Pi }_I )_w^* \hbox {Tr}( (\hat{\pi }_{A}^l \otimes \mathbb {I}) (\mathbb {I} \otimes \hat{B}) \rho _{AB} ( \hat{A} \otimes \mathbb {I})) \nonumber \\&\qquad + ig ( \hat{\Pi }_I )_w \hbox {Tr}( (\hat{\pi }_{A}^l \otimes \mathbb {I}) (\mathbb {I} \otimes \hat{B}) (\hat{A} \otimes \mathbb {I}) \rho _{AB} ) \bigg ] \nonumber \\&\quad = \frac{1}{\hbox {Tr}((\hat{\pi }_{A}^l \otimes \mathbb {I}) \rho _{AB})} \bigg [ \hbox {Tr}((\hat{\pi }_{A}^l \otimes \mathbb {I}) (\mathbb {I} \otimes \hat{B}) \rho _{AB}) \nonumber \\&\qquad - ig \hbox {Re} ( \hat{\Pi }_I )_w (2 i \hbox {Im} ( \hat{A} )_{w'}\hbox {Tr}((\hat{\pi }_{A}^l \otimes \mathbb {I}) (\mathbb {I} \otimes \hat{B}) \rho _{AB}) \nonumber \\&\qquad - \hbox {Tr}((\hat{\pi }_{A}^l \otimes \mathbb {I}) (\mathbb {I} \otimes \hat{B}) [(\hat{A} \otimes \mathbb {I}), \rho _{AB}] ))\nonumber \\&\qquad + g \hbox {Im} ( \hat{\Pi }_I )_w ( 2 \hbox {Re} ( \hat{A} )_{w'} \hbox {Tr}((\hat{\pi }_{A}^l \otimes \mathbb {I}) (\mathbb {I} \otimes \hat{B}) \rho _{AB}) \nonumber \\&\qquad + \hbox {Tr}((\hat{\pi }_{A}^l \otimes \mathbb {I}) (\mathbb {I} \otimes \hat{B}) \{ (\hat{A} \otimes \mathbb {I}), \rho _{AB} \} ))\bigg ], \end{aligned}$$

  (B5)

  where [x, y] and $\{x,y\}$ denote the commutator and the anticommutator, respectively.

Appendix C: Algebraic details—Proof

• 1. Now we proceed to prove that denominators of the real and imaginary parts of the weak value do not go to zero for generic choices of $\hat{A}$ and $\hat{B}$, the latter of which is made to satisfy constraints on the set derived above. Considering the extreme case, when all of the $\rho _{ij} = 0$ for a $2 \otimes 2$ resource state, $\hat{B} = \begin{bmatrix} b_{11} &{} b_{12} \\ b_{12}^* &{} b_{22} \end{bmatrix}$, $\hat{A} = \begin{bmatrix} a_{11} &{} a_{12} \\ a_{12}^* &{} a_{22} \end{bmatrix}$, $\hat{\pi }^l_A = {|{\psi }\rangle } {\langle {\psi }|}$ (where ${|{\psi }\rangle } = p_1 {|{0}\rangle } + p_2 {|{1}\rangle }$), $p_1 \equiv p_{1R} + i p_{1I}$, $p_2 \equiv p_{2R} + i p_{2I}$, and $a_{12} \equiv a_{12R} + i a_{12I}$, denominator of real part of the weak value is given by $b_{22} g (a_{12} p_2 p_1 + (2 p_2 (a_{12I} p_{1I} p_{2I} + a_{12R} p_{1R} p_{2I} - a_{12R} p_{1I} p_{2R} + a_{12I} p_{1R} p_{2R}) - i p_1 a_{12}^*) i p_2^*$ and denominator of the imaginary part of the weak value is given by $a_{22} b_{22} - a_{22} b_{22}^2 - a_{22} b_{12} b_{12}^*$. Clearly, both of these are nonzero for any choice of observables $\hat{A}$, $\hat{B}$, and $\hat{p}_1$ including those which are the set of observables.

• 2. For a $2 \times 2$ state $\rho _{AB}$, we take $\hat{B}$ to be a spin-1/2 observable $\hat{n}.\hat{\sigma }$. Since $\hat{B}^2 = 1$ and $\hbox {Tr}_A( (\hat{A} \otimes \mathbb {1}) \rho _{AB} ) = \hbox {Tr}( \hat{A} \rho _{A}^\mathrm{{in}} )$, when we equate denominator of the imaginary part (Eq. 4) to zero, we find the condition $\hbox {Tr}( \hat{B} \rho _B^\mathrm{{in}} ) = 1$. This is satisfied when Bob’s reduced state $\rho _{B}^\mathrm{{in}}$—when it is pure—is an eigenstate of $\hat{B}$. So to ensure $\hbox {Tr}( \hat{B} \rho _B^\mathrm{{in}} ) \ne 1$, set of observables $\hat{B}$ must exclude the observable whose “up” eigenstate is $\rho _{B}^\mathrm{{in}}$. When $\rho _{B}^\mathrm{{in}}$ is a mixed state, the observable set $\hat{B}$ must be such that it has the elements of a complete observable basis set $\{\hat{n_1}.\hat{\sigma }, \hat{n_2}.\hat{\sigma }, \hat{n_3}.\hat{\sigma }\}$ such that $\hat{n_1} \perp \hat{n_2} \perp \hat{n_3}$.

• 3. Consider spin-1/2 observables $B_\alpha = (1/\sqrt{n_{1\alpha }^2 + n_{2\alpha }^2 + n_{3\alpha }^2)} {\mathbf {n}}_{\alpha }.{\mathbf {\sigma }}$, $B_\beta = (1/\sqrt{n_{1\beta }^2 + n_{2\beta }^2 + n_{3\beta }^2)} {\mathbf {n}}_{\beta }.{\mathbf {\sigma }}$, and $B_\gamma = (1/\sqrt{n_{1\gamma }^2 + n_{2\gamma }^2 + n_{3\gamma }^2)} {\mathbf {n}}_{\gamma }.{\mathbf {\sigma }}$. Solving the set of equations $\hbox {Tr}(B_\alpha \rho ) = \hbox {Tr}(B_\alpha \rho '); \hbox {Tr}(B_\beta \rho ) = \hbox {Tr}(B_\beta \rho '); \hbox {Tr}(B_\gamma \rho ) = \hbox {Tr}(B_\gamma \rho ')$ (where $\rho$ and $\rho '$ are general $2 \times 2$ density matrices) leads to $\rho = \rho '$. This is easily extended to higher dimensions by considering higher dimensional versions of Pauli matrices [81, 82].

• 4. Substituting $\rho _{AB} = \rho _{A} \otimes \rho _{B}$ in Eq. (A2), which corresponds to the first set of experimental runs (imaginary part), implies:

  $$\begin{aligned} \rho _{B}^N= & {} \frac{\rho _{B}^{un}}{\hbox {Tr}(\rho _B^{un})}\approx \frac{\rho _B - 2 g \hbox {Im} ( \hat{\Pi }_I )_w \hbox {Tr}_{A} ((\hat{A} \otimes \mathbb {I}) \rho _{A} \otimes \rho _{B}) }{ \bigg (\hbox {Tr}(\rho _B) - 2 g \hbox {Im} ( \hat{\Pi }_I )_w \hbox {Tr}((\hat{A} \otimes \mathbb {I}) \rho _{A} \otimes \rho _{B}) \bigg )} \nonumber \\= & {} \frac{(1 - 2 g \hbox {Im} ( \hat{\Pi }_I )_w \hbox {Tr}_{A} (\hat{A} \rho _{A}) ) \rho _B}{(1 - 2 g \hbox {Im} ( \hat{\Pi }_I )_w \hbox {Tr}_A (\hat{A} \rho _{A} ) ) \hbox {Tr}_B \rho _{B}} \nonumber \\= & {} \rho _B. \end{aligned}$$

  (C1)

• 5. For real part of the weak value, we consider

  $$\begin{aligned} \hbox {Re} ( \hat{\Pi }_I )_w= & {} \langle \hat{B} \rangle ^\mathrm{{Re}}_f \times \hbox {Tr}((\hat{\pi }_A^l \otimes \mathbb {1}) \rho _{AB}) - \hbox {Tr}((\hat{\pi }_A^l \otimes \hat{B}) \rho _{AB}) \nonumber \\&- g \hbox {Im}( \hat{\Pi }_I )_w \big (2 \hbox {Re} ( \hat{A} )_{w'} \hbox {Tr}((\hat{\pi }_A^l \otimes \hat{B}) \rho _{AB}) \nonumber \\&+ \hbox {Tr}((\hat{\pi }_A^l \otimes \hat{B}) \{(\hat{A} \otimes \mathbb {1}),\rho _{AB}\} ) \big ) = 0. \end{aligned}$$

  (C2)

  This leads to

  $$\begin{aligned} \langle \hat{B} \rangle ^\mathrm{{Re}}_f= & {} \frac{\hbox {Tr}((\hat{\pi }_A^l \otimes \hat{B}) \rho _{AB})}{\hbox {Tr}((\hat{\pi }_A^l \otimes \mathbb {1}) \rho _{AB})}\nonumber \\&+ g \hbox {Im} ( \hat{\Pi }_I )_w \left[ \frac{\hbox {Tr}((\hat{\pi }_A^l \hat{A} \otimes \mathbb {1})\rho _{AB})}{\hbox {Tr}((\hat{\pi }_A^l \otimes \mathbb {1}) \rho _{AB})} + \frac{\hbox {Tr}((\hat{A} \hat{\pi }_A^l \otimes \mathbb {1})\rho _{AB}^\dagger )}{\hbox {Tr}((\hat{\pi }_A^l \otimes \mathbb {1}) \rho _{AB}^\dagger )} \right] \nonumber \\&\frac{\hbox {Tr}((\hat{\pi }_A^l \otimes \hat{B}) \rho _{AB})}{\hbox {Tr}((\hat{\pi }_A^l \otimes \mathbb {1}) \rho _{AB})}\nonumber \\&+ g \hbox {Im} ( \hat{\Pi }_I )_w \left[ \frac{\hbox {Tr}((\hat{\pi }^l_A \hat{A} \otimes \hat{B}) \rho _{AB}) + \hbox {Tr}((\hat{A} \hat{\pi }^l_A \otimes \hat{B}) \rho _{AB})}{\hbox {Tr}((\hat{\pi }_A^l \otimes \mathbb {1}) \rho _{AB})} \right] , \end{aligned}$$

  (C3)

  For the lth projector (total p projectors on the Hilbert space of same dimensions), $E_l \equiv \hbox {Tr}((\hat{\pi }_A^l \otimes \hat{B}) \rho _{AB})$, $N_l \equiv \hbox {Tr}((\hat{\pi }_A^l \otimes \mathbb {1}) \rho _{AB})$, and $E \equiv \hbox {Tr}(\hat{B} \rho _B^\mathrm{{in}}) = \hbox {Tr}((\mathbb {1}\otimes \hat{B}) \rho _{AB})$. We have $\sum _{l=1}^p E_l = E$. Substituting these entities in Eq. (C3) and replacing terms in the brackets corresponding to the projectors with $T1_l$ and $T2_l$, respectively, we find:

  $$\begin{aligned}&\langle \hat{B} \rangle ^\mathrm{{Re}}_f = E_l/N_l + g \hbox {Im} ( \hat{\Pi }_I )_w [T1_l] E_l/N_l + g \hbox {Im} ( \hat{\Pi }_I )_w [T2_l]\nonumber \\&\quad \implies \sum _{l=1}^p N_l \langle \hat{B} \rangle ^\mathrm{{Re}}_f = \sum _{l=1}^p E_l\nonumber \\&\quad + g \hbox {Im} ( \hat{\Pi }_I )_w \sum _{l=1}^p [T1_l] E_l + g \hbox {Im} ( \hat{\Pi }_I )_w \sum _{l=1}^p [T2_l] N_l \end{aligned}$$

  (C4)

  Since $\sum _{l=1}^p = \hat{\pi }^l_A = \mathbb {1}$, $\sum _{l=1}^p N_l = \hbox {Tr}(\rho _{AB}) = 1$. Therefore,

  $$\begin{aligned}&\langle \hat{B} \rangle ^\mathrm{{Re}}_f = E + g \hbox {Im}\langle \hat{\Pi }_I \rangle _w \sum _{l=1}^p [T1_l] E_l + g \hbox {Im} \langle \hat{\Pi }_I \rangle _w \sum _{l=1}^p [T2_l] N_l \end{aligned}$$

  (C5)

• 6. Substituting $\rho _{AB} = \rho _A \otimes \rho _B$ in Eq. (B3), corresponding to the second set of experimental runs (real part), implies:

  $$\begin{aligned}&\rho _{B}^N = \frac{\rho _{B}^{un}}{\hbox {Tr}(\rho _B^{un})}\nonumber \\&\quad \approx \frac{\hbox {Tr}_{I} (\hat{\pi }_{I}^v \rho _{I}) ( ( \hbox {Tr}_{A} (\hat{\pi }_{A}^l \rho _{A}) \rho _B - ig ( \hat{\Pi }_I )_w^* \hbox {Tr}_{A}( \hat{\pi }_{A}^l \rho _{A} \hat{A} ) \rho _B + ig ( \hat{\Pi }_I )_w \hbox {Tr}_{A} ( \hat{\pi }_{A}^l \hat{A} \rho _{A} ) \rho _B ))}{\hbox {Tr}_{I} (\hat{\pi }_{I}^v \rho _{I}) \hbox {Tr}(\rho _B) ( ( \hbox {Tr}_{A} (\hat{\pi }_{A}^l \rho _{A}) - ig ( \hat{\Pi }_I )_w^* \hbox {Tr}_{A}( \hat{\pi }_{A}^l \rho _{A} \hat{A} ) + ig ( \hat{\Pi }_I )_w \hbox {Tr}_{A} ( \hat{\pi }_{A}^l \hat{A} \rho _{A} ) ))} \nonumber \\&\quad = \frac{ \hbox {Tr}_{I} (\hat{\pi }_{I}^v \rho _{I}) ( ( \hbox {Tr}_{A} (\hat{\pi }_{A}^l \rho _{A}) - ig ( \hat{\Pi }_I )_w^* \hbox {Tr}_{A}( \hat{\pi }_{A}^l \rho _{A} \hat{A} ) + ig ( \hat{\Pi }_I )_w \hbox {Tr}_{A} ( \hat{\pi }_{A}^l \hat{A} \rho _{A} ) )) \rho _B}{\hbox {Tr}_{I} (\hat{\pi }_{I}^v \rho _{I}) ( ( \hbox {Tr}_{A} (\hat{\pi }_{A}^l \rho _{A}) - ig ( \hat{\Pi }_I )_w^* \hbox {Tr}_{A}( \hat{\pi }_{A}^l \rho _{A} \hat{A} ) + ig ( \hat{\Pi }_I )_w \hbox {Tr}_{A} ( \hat{\pi }_{A}^l \hat{A} \rho _{A} ) ))} \nonumber \\&\quad = \rho _B. \end{aligned}$$

  (C6)

  Like in case of the first set of experiments, here too, Bob’s state contains no signature of the weak measurement performed by Alice if $\rho _{AB}$ is a product state.

Appendix D: Algebraic details—Bell-diagonal state as resource

• 1. Imaginary part:

  

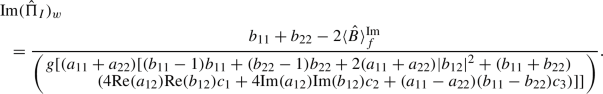  (D1)

  Here, $\langle \rangle ^\mathrm{{Im}}$ represents expectation value obtained in the set of experiments which correspond to obtaining the imaginary part of the weak value.

• 2. Real part:

  

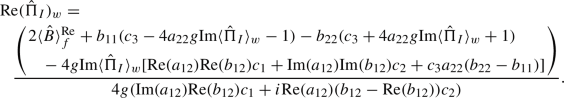  (D2)

  Here too, $\langle \rangle ^\mathrm{{Re}}$ represents expectation value obtained in the set of experiments which correspond to obtaining the real part of the weak value.

• 3. Number of classical bits to be communicated:

  The total state after weak interaction is $\rho _{twk} = U \rho _{I} \otimes \rho _{AB} U^\dagger \approx \rho _{I} \otimes \rho _{AB} + ig [{|{a_k}\rangle }{\langle {a_k}|}, \rho _{I}] \otimes [\hat{A} \otimes \mathbb {I}, \rho _{AB}]$. Similarly, $\rho _{twk}^2 = U \rho _{I}^2 \otimes \rho _{AB}^2 U^\dagger \approx \rho _{I}^2 \otimes \rho _{AB}^2 + ig {|{a_k}\rangle }{\langle {a_k}|} \rho _{I}^2 \otimes ( \hat{A} \otimes \mathbb {I} \rho _{AB}^2 ) - ig \rho _{I}^2 {|{a_k}\rangle }{\langle {a_k}|} \otimes ( \rho _{AB}^2 \hat{A} \otimes \mathbb {I})$. Here, we have chosen $\hat{\Pi }^k_I = {|{a_k}\rangle }{\langle {a_k}|}$. Substituting $\hat{\pi }_{I}^v = {|{b_0}\rangle } {\langle {b_0}|} = (1/d) \sum _{a,b = 0}^{d-1} {|{a}\rangle }{\langle {b}|}$ and $\rho _{I}^2 = \rho _{I} = \sum _{a,b = 0}^{d-1} \psi _a \psi _b^*{|{a}\rangle }{\langle {b}|}$ into Eq. (8), where the first and second terms in the parenthesis correspond to post-selection probabilities for the first and second set of experimental runs, respectively, we get:

  $$\begin{aligned} C= & {} N \sum _{k = 0}^{d-1} \bigg [ \hbox {Tr}( \hat{\pi }_{I}^v \rho _{twk}^2 ) + \hbox {Tr}( ( \hat{\pi }_{I}^v \otimes \hat{\pi }_{A}^l \otimes \mathbb {I}) \rho _{twk}^2 ) \bigg ] \nonumber \\\approx & {} N \sum _{k = 0}^{d-1} \bigg [ \hbox {Tr}( \hat{\pi }_{I}^v \rho _I \otimes \rho _{AB}^2 + i g \hat{\pi }_{I}^v {|{a_k}\rangle }{\langle {a_k}|} \rho _{I} \otimes ( \hat{A} \otimes \mathbb {I} \rho _{AB}^2 ) - i g \hat{\pi }_{I}^v \rho _{I} {|{a_k}\rangle }\nonumber \\&\qquad {\langle {a_k}|} \otimes ( \rho _{AB}^2\hat{A} \otimes \mathbb {I} ) ) + \hbox {Tr}( \hat{\pi }_{I}^v \rho _I \otimes ( (\hat{\pi }^l_A \otimes \mathbb {I}) \rho _{AB}^2 )\nonumber \\&\quad + ig \hat{\pi }_{I}^v {|{a_k}\rangle }{\langle {a_k}|} \rho _{I} \otimes (\hat{\pi }_{A}^l \otimes \mathbb {I}) ( \hat{A} \otimes \mathbb {I} \rho _{AB}^2) \nonumber \\&- ig \hat{\pi }_{I}^v \rho _{I} {|{a_k}\rangle }{\langle {a_k}|} \otimes (\hat{\pi }_{A}^l \otimes \mathbb {I}) ( \rho _{AB}^2 \hat{A} \otimes \mathbb {I}) ) \bigg ] \nonumber \\= & {} N \sum _{k = 0}^{d-1} \bigg [ \hbox {Tr}( \hat{\pi }_{I}^v \rho _I ) \hbox {Tr}( \rho _{AB}^2 ) + i g \hbox {Tr}( \hat{\pi }_{I}^v {|{a_k}\rangle }{\langle {a_k}|} \rho _{I} ) \hbox {Tr}( \hat{A} \otimes \mathbb {I} \rho _{AB}^2 ) \nonumber \\&\quad - ig \hbox {Tr}( \hat{\pi }_{I}^v \rho _{I} {|{a_k}\rangle }{\langle {a_k}|} ) \hbox {Tr}( \rho _{AB}^2 \hat{A} \otimes \mathbb {I} ) + \hbox {Tr}( \hat{\pi }_{I}^v \rho _I ) \hbox {Tr}( (\hat{\pi }^l_A \otimes \mathbb {I}) \rho _{AB}^2 )\nonumber \\&\quad + ig \hbox {Tr}( \hat{\pi }_{I}^v {|{a_k}\rangle }{\langle {a_k}|} \rho _{I} ) \hbox {Tr}(\hat{\pi }_{A}^l \hat{A} \otimes \mathbb {I} \rho _{AB}^2)\nonumber \\&\quad - ig \hbox {Tr}( \hat{\pi }_{I}^v \rho _{I} {|{a_k}\rangle }{\langle {a_k}|} ) \hbox {Tr}( (\hat{\pi }_{A}^l \otimes \mathbb {I}) ( \rho _{AB}^2 \hat{A} \otimes \mathbb {I}) ) \bigg ] \nonumber \\= & {} N \bigg [ \sum _{k = 0}^{d-1} ( \hbox {Tr}( \hat{\pi }_{I}^v \rho _I ) \hbox {Tr}( \rho _{AB}^2 ) ) + i g \hbox {Tr}\left( \hat{\pi }_{I}^v \sum _{k = 0}^{d-1} {|{a_k}\rangle }{\langle {a_k}|} \rho _{I} \right) \hbox {Tr}( \hat{A} \otimes \mathbb {I} \rho _{AB}^2 ) \nonumber \\&\quad - i g \hbox {Tr}\left( \hat{\pi }_{I}^v \rho _{I} \sum _{k = 0}^{d-1} {|{a_k}\rangle }{\langle {a_k}|} \right) \hbox {Tr}\left( \rho _{AB}^2 \hat{A} \otimes \mathbb {I} \right) \nonumber \\&\quad + \sum _{k = 0}^{d-1} \hbox {Tr}( \hat{\pi }_{I}^v \rho _I ) \hbox {Tr}( (\hat{\pi }^l_A \otimes \mathbb {I}) \rho _{AB}^2 )\nonumber \\&\quad + ig \hbox {Tr}\left( \hat{\pi }_{I}^v \sum _{k = 0}^{d-1} {|{a_k}\rangle }{\langle {a_k}|} \rho _{I} \right) \hbox {Tr}(\hat{\pi }_{A}^l \hat{A} \otimes \mathbb {I} \rho _{AB}^2) \nonumber \\&\quad - ig \hbox {Tr}\left( \hat{\pi }_{I}^v \rho _{I} \sum _{k = 0}^{d-1} {|{a_k}\rangle }{\langle {a_k}|} \right) \hbox {Tr}( (\hat{\pi }_{A}^l \otimes \mathbb {I}) ( \rho _{AB}^2 \hat{A} \otimes \mathbb {I}) ) \bigg ]; \end{aligned}$$

  (D3)

  since $\sum _{k = 0}^{d-1} {|{a_k}\rangle }{\langle {a_k}|} = \mathbb {I}$ and $\sum _{k = 0}^{d-1} 1 = d$, we have,

  $$\begin{aligned} C\approx & {} N \bigg [ d \hbox {Tr}( \hat{\pi }_{I}^v \rho _I ) \hbox {Tr}( \rho _{AB}^2 ) + i g \hbox {Tr}( \hat{\pi }_{I}^v \rho _{I} ) \hbox {Tr}( \hat{A} \otimes \mathbb {I} \rho _{AB}^2 ) \nonumber \\&\quad - i g \hbox {Tr}( \hat{\pi }_{I}^v \rho _{I} ) \hbox {Tr}( \rho _{AB}^2 \hat{A} \otimes \mathbb {I} ) \nonumber \\&\quad + d \hbox {Tr}( \hat{\pi }_{I}^v \rho _I ) \hbox {Tr}( (\hat{\pi }^l_A \otimes \mathbb {I}) \rho _{AB}^2 ) + ig \hbox {Tr}( \hat{\pi }_{I}^v \rho _{I} ) \hbox {Tr}(\hat{\pi }_{A}^l \hat{A} \otimes \mathbb {I} \rho _{AB}^2) \nonumber \\&\quad - ig \hbox {Tr}( \hat{\pi }_{I}^v \rho _{I} ) \hbox {Tr}( (\hat{\pi }_{A}^l\otimes \mathbb {I}) ( \rho _{AB}^2 \hat{A} \otimes \mathbb {I}) ) \bigg ]. \end{aligned}$$

  (D4)

  Substituting $\hat{A} = \begin{bmatrix} a_{11} &{} a_{12} \\ a_{12}* &{} a_{22} \end{bmatrix}$, and $\hat{\pi }_A^l = {|{\sigma _{zA} = -1}\rangle }{\langle {\sigma _{zA} = -1}|}$, we get

  $$\begin{aligned} C\approx & {} N [d \hbox {Tr}( \hat{\pi }_{I}^v \rho _I ) \hbox {Tr}( \rho _{AB}^2 )+ (d/2) \hbox {Tr}( \hat{\pi }_{I}^v \rho _I ) \hbox {Tr}( \rho _{AB}^2 )] \nonumber \\= & {} (3/2) N d \hbox {Tr}( \hat{\pi }_{I}^v \rho _I ) \hbox {Tr}( \rho _{AB}^2 ). \end{aligned}$$

  (D5)

  The post-selection probabilities corresponding to the first and second runs of the protocol are represented by the first and second terms in the parenthesis, respectively. As expected from the simultaneous success probability requirement, in the second set of experimental runs, post-selection succeeds exactly half the number of times it does in the first set. Considering the system state to be transferred as $\rho _I = {|{\psi }\rangle }{\langle {\psi }|} = \sum _{k=0}^{d-1} a_k a_k^* {|{a_k}\rangle } {\langle {a_k}|}$, we have $C \propto \hbox {Tr}(\hat{\pi }^v_I \rho _I) = \hbox {Tr}({|{b_0}\rangle } {\langle {b_0}|} \sum _{k=0}^{d-1} a_k^* a_l {|{a_l}\rangle } {\langle {a_k}|} ) \!=\! \hbox {Tr}((1/d) \sum _{a,b = 0}^{d-1} {|{a}\rangle } {\langle {b}|} \sum _{k,l=0}^{d-1} a_k^* a_l {|{a_l}\rangle } {\langle {a_k}|} ) \!= (1/d) \sum _{a,b=0}^{d-1} \sum _{k=0}^{d-1} a_k^* a_l {\langle {b}\rangle }{a_l} {\langle {a_k}\rangle }{a} = (1/d) \sum _{k=0}^{d-1} \sum _{a,b=0}^{d-1} a_k^* a_l \delta _{b a_l} \delta {a_k a} = \sum _{a,b = 0}^{d - 1} a_b^* a_a = 0$ (because ${\langle {b}\rangle }{a_k} = \delta _{b a_k}$ and ${\langle {a_k}\rangle }{a} = \delta _{a a_k}$). The solution space for $\sum _{k = 0}^{d - 1} a_k = 0$ is negligible compared to rest of the possibilities. Therefore, the success probability is unlikely to go to zero for any state of interest that is to be transferred.