Planar k-uniform states: a generalization of planar maximally entangled states

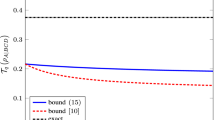
Abstract

Recently, Doroudiani and Karimipour [Phys. Rev. A 102 012427(2020)] proposed the notation of planar maximally entangled states which are a wider class of multipartite entangled states than absolutely maximally entangled states. There they presented their constructions in the multipartite systems but the number of particles is restricted to be even. Here, we first solve the remaining cases, i.e., constructions of planar maximally entangled states on systems with odd number of particles. In addition, we generalized the PME to the planar k-uniform states whose reductions to any adjacent k parties along a circle of N parties are maximally mixed. We presented a method to construct sets of planar k-uniform states which have minimal support.

Appendices

Appendix: A the proof of the Von Neumann entropy for $|\Phi _o\rangle _{{\mathcal {A}}|{\mathcal {B}}}$

Case I $t=0$. If ${\mathcal {A}}_u=\{A_{j_1},\cdots ,A_{j_s}\}$ and ${\mathcal {B}}_p=\{A_{i_{j_x}},\overline{A}_{i_{j_x}}\}_{{x=s+1}}^n$, then

$$\begin{aligned} |\Phi _o\rangle _{{\mathcal {A}}|{\mathcal {B}}}=\frac{1}{d^{s/2}}\sum _{i_{j_1},\cdots ,i_{j_s}=0}^{d-1}\left( |i_{j_1}\rangle _{A_{j_1}}\cdots |i_{j_s}\rangle _{A_{j_s}} \bigotimes |e_{i_{j_1},\cdots ,i_{j_s}}\rangle _{{\mathcal {B}}}\right) \end{aligned}$$

where $|e_{i_{j_1},\cdots ,i_{j_s}}\rangle _{{\mathcal {B}}} :=\frac{1}{d^{(n-s)/2}}\sum _{i_{j_{s+1}},\cdots ,i_{j_{n}}=0}^{d-1} |i_{j_1}\rangle _{\overline{A}_{j_1}}\cdots |i_{j_s}\rangle _{\overline{A}_{j_s}}(\otimes _{x=s+1}^n|i_{j_x}i_{j_x}\rangle _{ {A}_{j_x},\overline{A}_{j_x}}) |\oplus _{y=1}^n i_{j_y}\rangle _{B_1}.$ One can check that the set $\{|e_{i_{j_1},\cdots ,i_{j_s}}\rangle _{{\mathcal {B}}}\}_{i_{j_1},\cdots ,i_{j_s}=0}^{d-1}$ is an orthonormal set. Therefore, we have $S(|\Phi _o\rangle _{{\mathcal {A}}|{\mathcal {B}}})=s\log d$ for this bipartition. Case II $t\ge 1.$ If ${\mathcal {A}}_u=\{A_{j_1},\cdots ,A_{j_s}\}$, ${\mathcal {A}}_p=\{A_{i_{j_x}},\overline{A}_{i_{j_x}}\}_{{x=s+1}}^{s+t}$ and ${\mathcal {B}}_p=\{A_{i_{j_y}},\overline{A}_{i_{j_y}}\}_{{y=s+t+1}}^n$, then we have

$$\begin{aligned} |\Phi _o\rangle _{{\mathcal {A}}|{\mathcal {B}}}=\frac{1}{d^{(s+1)/2}}\sum _{i_{j_1},\cdots ,i_{j_s}=0}^{d-1} \sum _{i=0}^{d-1}\left( |e_{i_{j_1},\cdots ,i_{j_s},i}\rangle _{{\mathcal {A}}}\bigotimes |e_{i_{j_1},\cdots ,i_{j_s},i}\rangle _{{\mathcal {B}}}\right) \end{aligned}$$

(A1)

where $|e_{i_{j_1},\cdots ,i_{j_s},i}\rangle _{{\mathcal {A}}}$ and $|e_{i_{j_1},\cdots ,i_{j_s},i}\rangle _{{\mathcal {B}}}$ are defined as

$$\begin{aligned} \begin{array}{ccl} |e_{i_{j_1},\cdots ,i_{j_s},i}\rangle _{{\mathcal {A}}}:&{}=&{}\frac{1}{d^{(t-1)/2}}\displaystyle \sum _{\oplus _{x=s+1}^{s+t}i_{j_{x}}=i}|i_{j_1}\rangle _{A_{j_1}}\cdots |i_{j_s}\rangle _{A_{j_s}}( \otimes _{x=s+1}^{s+t}|i_{j_x}i_{j_x}\rangle _{ {A}_{j_x},\overline{A}_{j_x}}),\\ |e_{i_{j_1},\cdots ,i_{j_s},i}\rangle _{{\mathcal {B}}}\!:&{}=&{}\! \frac{1}{d^{(n-s-t)/2}}\displaystyle \sum _{i_{j_{s+t+1}},\cdots ,i_{j_{n}}=0}^{d-1} |i_{j_1}\rangle _{\overline{A}_{j_1}}\cdots |i_{j_s}\rangle _{\overline{A}_{j_s}}(\otimes _{y=s+t+1}^n|i_{j_y}i_{j_y}\rangle _{ {A}_{j_y},\overline{A}_{j_y}}) |\\ &{}&{}(\oplus _{z=1}^s i_{j_z})\oplus i\oplus (\oplus _{u=s+t+1}^n i_{j_u})\rangle _{B_1}. \end{array} \end{aligned}$$

One can check that the set $\{|e_{i_{j_1},\cdots ,i_{j_s},i}\rangle _{{\mathcal {A}}}\}_{i_{j_1},\cdots ,i_{j_s},i=0}^{d-1}$ and $\{|e_{i_{j_1},\cdots ,i_{j_s},i}\rangle _{{\mathcal {B}}}\}_{i_{j_1},\cdots ,i_{j_s},i=0}^{d-1}$ are both orthonormal sets. Therefore, by Eq. (A1), we have $S(|\Phi _o\rangle _{{\mathcal {A}}|{\mathcal {B}}})=(s+1)\log d.$ $\square$

Appendix: B the proof of Lemma 1

Step I Initializing a table of $(k+s)\times (k+s)$ as follows (See Table 3)

• (a) The coordinate $(r_i,c_j)$ is filled with j for integers i, j with conditions $1\le i\le (k+s)$ , $1\le j\le k$, and $(i-j) \notin \{1,2,\cdots , s\}.$

• (b) The coordinate $(r_i,c_{k+j})$ is filled with j for integer i, j with conditions $2\le i\le 1+s$, $1\le j\le s$, and $i\le j$.

One can see that each of the first seven rows are filled with k numbers $\{1,2,\cdots ,k\}$.

Table 3 The initial data of the Step I of the proof of Lemma 1

Step II We then recursively define the j-th coordinates ($j\ge k+1$) of the $(i+1)$-th row using the result of the i-th row when $s+1\le i\le k+s-1$. Assume that there are exactly k elements named $\{1,2,\cdots , k\}$ in the i-th row and the non-blank coordinates are $(r_i,c_j)$ with $1\le j\le i-(s+1)$ and $i\le j \le k+s$(this is true for $i=s+1$). One finds that the $(i+1)$-th row contains one more element than the i-th row at the left bottom triangle of the initialized table. In fact, that element is exactly $i-s$ at the coordinate $(r_{i+1},c_{i-s})$. As $\{1,2,\cdots , k\}$ are exactly the elements in the i-th row, there exists some x such that $V (r_i,c_x)=i-s$. Moreover, as $V (r_i,c_j)=j$ for $1\le j \le i-(s+1)$, so $V (r_i,c_i)\ge i-s$. We will leave the coordinate $(r_{i+1},c_i)$ to be blank.

• (1) If $V (r_i,c_i)$ happens to be $i-s$, then we set $V (r_{i+1},c_j)= V (r_{i},c_j)$ for $j\ge i+1$. In this setting, we have $V (r_{i+1},c_j)= V (r_i,c_j)$ for $1\le j\le i-(s+1)$ or $i+1\le j\le k+s$. In addition, we also have $V (r_{i+1},c_{i-s})= V (r_{i },c_{i})=i-s.$ Therefore, there are also exactly k elements named $\{1,2,\cdots , k\}$ in the $(i+1)$-th row and the non-blank coordinates are $(r_{i+1},c_j)$ with $1\le j\le (i+1)-(s+1)$ or $i+1\le j \le k+s$.

• (2) If the element of the coordinate ($r_i,c_i$) do not equal to $i-s$, i.e., $V (r_i,c_i)>i-s$, one may find that $x\ge i+1$ and $x\in \{k+1,k+2,\cdots ,k+s\}$ (otherwise $V (r_i,c_x)=x=i-s$, hence $i-x=s$ which is contradicted with the condition (a) of step I). Then we set

  $$\begin{aligned} \ \ \ \ \ \ \ V (r_{i+1},c_j)=\left\{ \begin{array}{ll} V (r_{i},c_i), &{} j=x\\ V (r_{i},c_j),&{} j\ge i+1 \text { and } j\ne x. \end{array} \right. \end{aligned}$$

  In this setting, we have $V (r_{i+1},c_j)= V (r_i,c_j)$ for $1\le j\le i-(s+1)$ or $i+1\le j\le k+s$ but $j\ne x$. In addition, we have $V (r_{i+1},c_{i-s})= V (r_{i },c_{x})=i-s$ and $V (r_{i+1},c_{x})= V (r_{i },c_{i}).$ Therefore, there are also exactly k elements named $\{1,2,\cdots , k\}$ in the $(i+1)$-th row and the non-blank coordinates are $(r_{i+1},c_j)$ with $1\le j\le (i+1)-(s+1)$ or $i+1\le j \le k+s$. Note that

  $$\begin{aligned} V (r_{i+1},c_{x})= V (r_{i },c_{i})>i-s= V (r_{i},c_{x}). \end{aligned}$$

  (B1)

Note that for any fixed integer $j\in [k+1, k+s]$, the elements in the j-th column are in a nondecreasing order from top to bottom, i.e., $V (r_{i+1},c_{j})\ge V (r_{i},c_{j})$ whenever both elements are non-blank. If $V (r_{i_2},c_{j})$ is strictly larger than $V (r_{i_1},c_{j})$, we call $V (r_{i_1},c_j)$ a predecessor of $V (r_{i_2},c_j)$ in the j-th column and $V (r_{i_2},c_j)$ a successor of $V (r_{i_1},c_j)$ in the j-th column. Denote ${\mathcal {P}}_j( V (r_{i},c_j))$ (resp. ${\mathcal {S}}_j( V (r_{i},c_j))$) to be the set of all predecessors (resp. successors) of $V (r_{i},c_j)$ in the j-th column. Fixed $s+2\le i+1\le k+s$, the predecessors of $V (r_{i+1},c_j)$ in the j-th column ($k+1\le j\le k+s$) are contained in the set $\{1,\cdots ,i-s\}$. This statement can be followed by the two facts. Fact 1: there is no predecessor at all of $V (r_{s+1},c_j)$ in the j-th column. Fact 2: by step II and Eq. (B1), at most one more predecessor (say $i-s$) would be generated to one of the element in $(i+1)$-th row for the recursive definition from i-th row to $(i+1)$-th row.

Step III Read out of the non-blank elements for each column. For $j\in \{1,2,\cdots ,k+s\}$, set

$$\begin{aligned} {\mathcal {I}}_j:=\{ V (r_i,c_j) | V (r_i,c_j) \text { is non-blank }, 1\le i\le k+s \}. \end{aligned}$$

We define a $(k+s)$-tuple of maps $(f_1,f_2,\cdots ,f_{k+s})$ by $f_j:=\oplus _{i\in {\mathcal {I}}_j } e_i$ (here and the following $e_i$ denotes the i-th coordinate map from $\mathbb {Z}_d^{k}$ to $\mathbb {Z}_d$). One finds that ${\mathcal {I}}_j=\{j\}$ for $1\le j\le k$. Therefore, $f_j=e_j$ for $1\le j\le k$.

We claim that the $(f_1,f_2,\cdots ,f_{k+s})$ defined above is indeed a canonical circle block of dimensional d. We need to check that any k adjacent maps $(f_i,f_{i+1},\cdots , f_{i+k-1})$ (where $1\le i\le k+s$. If the subscript $i+j$ is larger than $k+s$, we replace the corresponding subscript $i+j$ by $i+j-(k+s)$) is a bijective map from $\mathbb {Z}_d^{k}$ to itself. It sufficient to show that for any ${\varvec{i}}:=(i_1,i_2,\cdots ,i_{k}),$ ${\varvec{i}}':=(i_1',i_2',\cdots ,i_{k}')$ in $\mathbb {Z}_d^{k},$ $(f_i({\varvec{i}}),f_{i+1}({\varvec{i}}),\cdots , f_{i+k-1}({\varvec{i}}))$ equals to $(f_i({\varvec{i}}'),f_{i+1}({\varvec{i}}'),\cdots , f_{i+k-1}({\varvec{i}}'))$ implies ${\varvec{i}}={\varvec{i}}'$. Firstly, we define

$$\begin{aligned} \begin{array}{rcl} {\mathcal {E}}_i:&{}=&{}\{l | V (r_i,c_l) \text { is non-blank }, 1\le l\le k \},\\ {\mathcal {J}}_i:&{}=&{}\{l | V (r_i,c_l) \text { is non-blank }, 1\le l\le k+s \}. \end{array} \end{aligned}$$

Under the above replacement, the set of subscripts in $(f_i,f_{i+1},\cdots , f_{i+k})$ is the same with the set ${\mathcal {J}}_i$. We separate the argument into three cases.

• (1) $1\le i\le s+1$. For $l\in {\mathcal {E}}_i$, ${\mathcal {I}}_l=\{l\}$, therefore $f_l=e_l$. Hence $i_l=i_l'$ for such l. And for any $l\in \{1,2,\cdots , k\} \setminus {\mathcal {E}}_i$, there is exactly one j such that $V (r_i,c_j)=l$. Moreover, there is no predecessor of l in the j-th column and the successors of l in the j-th column are just the set ${\mathcal {I}}_j\setminus \{l\}$ whose elements are all greater than or equal to $s+1$. Hence we have $l\in {\mathcal {I}}_j$ and ${\mathcal {I}}_j\setminus \{l\} \subseteq {\mathcal {E}}_i$. As $f_j=\oplus _{i\in {\mathcal {I}}_j}e_i= e_l\oplus (\oplus _{i\in {\mathcal {I}}_j\setminus \{l\}}e_i)$, so $f_j({\varvec{i}})=f_j({\varvec{i}}')$ implies that $i_l=i_l'$. From these, we can conclude that ${\varvec{i}}={\varvec{i}}'$.

• (2) $s+2\le i\le k$. For $l\in {\mathcal {E}}_i$, ${\mathcal {I}}_l=\{l\}$, therefore $f_l=e_l$. Hence $i_l=i_l'$ for such l. Moreover, one finds that

  $$\begin{aligned} \{1,2,\cdots ,k\}\setminus {\mathcal {E}}_i=\{i-s, \cdots , i-1\}. \end{aligned}$$

  For $l=i-1$, there exists exactly one $j\in [k+1,k+s]$ such that $V (r_i,c_j)=l$. We have noted that the predecessors of $V (r_i,c_j)$ in the j-th column are in the set $\{1,\cdots , i-(s+1)\}\subseteq {\mathcal {E}}_i$. As the nondecreasing property of the column, the successors of $i-1$ of the l column can only be in $\{i,\cdots ,k+s\}\subseteq {\mathcal {E}}_i$. In the expression $f_l$, the $e_l$ is the only one undetermined variable. Hence $i_l=i_l'$. Now for $l=i-2$, there is also exactly one $j\in [k+1,k+s]$ such that $V (r_i,c_j)=l$. We have ${\mathcal {P}}_j(l)\subseteq \{1,\cdots , i-(s+1)\}\subseteq {\mathcal {E}}_i$. Moreover, as the nondecreasing property of each column, ${\mathcal {S}}_j(l)\subseteq \{i-1,i,\cdots ,k+s\}$. The equality $f_{j}({\varvec{i}})=f_{j}({\varvec{i}}')$ can be expressed as

  $$\begin{aligned} \ \ \ \ \ i_l \oplus (\oplus _{x\in {\mathcal {P}}_j(l)\cup {\mathcal {S}}_j(l)} i_x ) =i_l' \oplus (\oplus _{x\in {\mathcal {P}}_j(l)\cup {\mathcal {S}}_j(l)} i_x '). \end{aligned}$$

  As we already have $i_x=i_x'$ for all $x\in {\mathcal {P}}_j(l)\cup {\mathcal {S}}_j(l)$, hence $i_l=i_l'$. This argument is similar for the other undetermined coordinates. Finally, we would also obtain ${\varvec{i}}={\varvec{i}}'$.

• (3) $k+1\le i\le k+s$. For these cases, ${\mathcal {E}}_i=\{1,2,\cdots , i-(s+1)\}$. So $e_1,\cdots ,e_{i-(s+1)}$ are among the list of $(f_i,f_{i+1},\cdots , f_{i+k-1})$. So we always have $i_l=i_l'$ for $1\le l\le i-(s+1)$. One finds that

  $$\begin{aligned} \{1,2,\cdots ,k\}\setminus {\mathcal {E}}_i=\{i-s, \cdots , k\}. \end{aligned}$$

  Let $l=k$, there exists some $j\ge k+1$ such that $V(r_i,c_j)=l$. We have ${\mathcal {P}}_j(l)\subseteq {\mathcal {E}}_i$ and ${\mathcal {S}}_j(l)=\emptyset$. Then $f_j({\varvec{i}})=f_j({\varvec{i}}')$ implies that $i_{k}=i_{k}'$. For $l=k-1$, there is also exactly one $j\in [k+1,k+s]$ such that $V (r_i,c_j)=l$. We have ${\mathcal {P}}_j(l) \subseteq {\mathcal {E}}_i$. Moreover, as the nondecreasing property of each column, ${\mathcal {S}}_j(l)\subseteq \{k\}$. The equality $f_{j}({\varvec{i}})=f_{j}({\varvec{i}}')$ can be expressed as

  $$\begin{aligned} \ \ \ \ \ i_l \oplus (\oplus _{x\in {\mathcal {P}}_j(l)\cup {\mathcal {S}}_j(l)} i_x ) =i_l' \oplus (\oplus _{x\in {\mathcal {P}}_j(l)\cup {\mathcal {S}}_j(l)} i_x '). \end{aligned}$$

  As we already have $i_x=i_x'$ for all $x\in {\mathcal {P}}_j(l)\cup {\mathcal {S}}_j(l)$, hence $i_l=i_l'$. This argument is similar for the other undetermined coordinates. Finally, we would also obtain ${\varvec{i}}={\varvec{i}}'$.