1 Introduction

Time evolving neutrinos [35] and their oscillation focus and stimulate research from various perspectives. Dynamic properties of neutrino oscillations [10, 11, 44] initially studied in the most natural particle physics [35] context become equipped and extended by multitude of various and seemingly far investigations concerning decoherence [8, 9, 11, 24, 31, 41, 47] or various aspects of quantum information [5, 6, 10, 18, 33, 49] to mention but a few. Such a broad interest seems to be at least partially motivated not only by natural applicability in the domain of particle physics methods and computational techniques borrowed from quantum information processing but also by recent attempts of information transfer as a resource utilizing neutrinos [52] or gravitational waves [1] reflecting an everlasting human dream of interstellar communication [25]. One can divide the quantum-information-based neutrino research into two overlapping classes: the first, focused on quantum properties of evolving neutrino—with an entanglement or contextuality as examples—and relating them to fundamental properties of these fascinating particles; the second, seemingly more exotic, motivated by neutrino-based quantum information processing. However, history of science shows that an effective feedback coupling between fundamentals and applications is a sine qua non condition of progress [22].

In this paper, we consider one of fundamental features of neutrino oscillation analysed as a quantum dynamical process and, after short review of neutrino time-evolution in a qutrit approximation, we discuss geometric quantum speed limit [29] of neutrino oscillation. Quantum speed limits (QSL) or quantum limit of evolution time reviewed in Ref. [28] can be studied form various context-dependent perspectives [7, 21, 27, 30, 34, 55]: quantum control, quantum information or metrology. There were various motivations diving these investigations. The first approaches [42, 43] were unified [40] and further developed in very various, sometimes divergent directions [28]. Some of them focus practical role of speed limit as a natural bound for control strategies, the other emphasize fundamental relation between various speed limits and intrinsic time scales of quantum systems [28]. In particular, contrary to recent operational approaches [21, 53], geometric QSL proposed in Ref. [29] allows to identify a class of fundamental statistical and informational properties of quantum dynamics since it constitutes an upper bound for time-dependent changes of a shortest (geodesic) path qualified by the Fisher–Rao statistical distance [13] between states. With this interpretation geometric speed limit of Deffner and Lutz [29] allows to identify how a rate of information, given by a change of statistical distance, relates to dynamical properties of quantum dynamical systems governed by a very general class of equations of motion. Following [10, 12], we neglect non-Markovian effects in neutrino time evolution and describe it in a qutrit approximation (i.e. as an effective qutrit using three dimensional flavour F space) in terms of Gorini–Kossakowski–Sudarshan–Lindblad Markovian master equation (\(\hbar =1\)) [4, 20]:

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t} \rho _{F}(t) = \mathbb {L}[\rho _{F}(t)], \end{aligned}$$
(1)

where \(\rho _{F}(t)\in \mathcal {B}(\mathbb {C}^3)\) is a neutrino state. The generator \(\mathbb {L}[\cdot ]\) consisting of Hamiltonian and Lindbladian (decohering) parts is specified in the following section. For a time-evolving quantum system Eq. (1), its geometric QSL reads [29] as follows:

$$\begin{aligned} \nu _\mathrm{QSL}(t)= & {} \frac{\Vert \mathbb {L}[\rho _F(t)] \Vert }{2\cos (l(t))\sin (l(t))} \end{aligned}$$
(2)

where the operator norm \(\Vert \cdot \Vert \) is given by \(\Vert \mathbb {L} \Vert = \sigma _{\max }\) with \(\sigma _{\max }\) the largest singular value of \(\mathbb {L}[\rho _F(t)]\) and the Bures distance

$$\begin{aligned} l(t)= & {} \arccos (\sqrt{F(\rho _F(0),\rho _F(t))}) \end{aligned}$$
(3)

related to fidelity F [13]. The notion of QSL is based on suitably defined bound of time derivative of the Fisher–Rao metric [29]. For pure initial states \(\rho _F(0)\) Eq. (2) is derived [28, 29] using \(2\cos (l)\sin (l)\dot{l}\le |\text{ Tr }[\dot{\rho }_F(t)\rho _F(0)]|\le \Vert \mathbb {L}[\rho _F(t)] \Vert = \sigma _{\max }\) where the operator norm in a last inequality provides sharpest bound in comparison with trace norm or Hilbert–Schmidt [28]. The equality which relates QSL to a largest singular value \(\sigma _{\max }\) of \(\mathbb {L}[\rho _F(t)]\) is for pure initial states \(\rho _F(0)\) granted. Let us emphasize that QSL, which is a time-dependent quantity, characterizes quantum dynamics at a given instant contrary to other often very different operational approaches to quantum speed limits such as e.g. [53].

In this work, we investigate relations between properties of the neutrino QSL and conditions affecting neutrino oscillation: (i) interaction with normal matter’ (electrons or neutrons) induced by forward elastic scattering (in Sect. 2), (ii) an effect of decoherence resulting in nonunitary damping of neutrino oscillation (in Sect. 3). Motivated by recent experiments [54] indicating possible violation of CP (charge conjugation parity) symmetry for neutrinos we investigate (iii) the effect of CP violation relating this fundamental feature to the geometric QSL in Sect. 4. We show that the CP-violation is a highly non-trivial feature affecting QSL of neutrino oscillation being a candidate for a hallmark of CP-violation in neutrino systems. Finally, we discuss and summarize our results.

2 Neutrino as a qutrit

As the discovery of the neutrino oscillations, originating from mixing of three neutrino fields, was a first evidence in favor of a beyond the standard model physics attracting attention of particle community [14]. Following it, neutrino studies from a perspective of quantum information and communication are naturally supported by an effective description of neutrino’s flavour in terms of a qutrit approximation. It is known [35] that a neutrino of a given flavour \(\alpha \in \{e,\mu ,\tau \}\) evolves in time and can be measured in a different flavour state. This phenomenon is an essence of neutrino oscillation and originates from a fundamental non-correspondence between neutrino’s flavour \(\{\nu _{e},\nu _{\mu },\nu _{\tau }\}\) and massive states \(\{\nu _{1},\nu _{2},\nu _{3}\}\). These two sets of orthogonal states are unitarily related by Pontecorvo–Maki–Nakagawa–Sakata mixing matrix \(U_\mathrm{PMNS}\):

$$\begin{aligned} \left( \begin{array}{c}\nu _{e} \\ \nu _{\mu } \\ \nu _{\tau }\end{array}\right) = U_\mathrm{PMNS}\left( \begin{array}{c}\nu _{1}\\ \nu _{2} \\ \nu _{3}\end{array}\right) , \end{aligned}$$
(4)

parameterized by three mixing angles \(\theta _{12},\;\theta _{23},\;\theta _{13}\) and one CP-violating phase \(\delta \) [35]:

$$\begin{aligned} U_\mathrm{PMNS} = \left( \begin{array}{ccc} c_{12}c_{13} &{}\quad s_{12}c_{13} &{}\quad s_{13}e^{-i\delta } \\ -s_{12}c_{23}-c_{12}s_{23}s_{13}e^{i\delta } &{}\quad c_{12}c_{23}-s_{12}s_{23}s_{13}e^{i\delta } &{}\quad s_{23}c_{13}\\ s_{12}s_{23}-c_{12}c_{23}s_{13}e^{i\delta } &{}\quad -c_{12}s_{23}-s_{12}c_{23}s_{13}e^{i\delta } &{}\quad c_{23}c_{13} \end{array}\right) \end{aligned}$$
(5)

with \(c_{ij}=\cos (\theta _{ij})\) and \(s_{ij}=\sin (\theta _{ij})\) (following Ref. [23] we set \(s_{12}^2=0.307\), \(s_{13}^2=0.021\) and \(s_{23}^2=0.5\)) and \(\delta \) being the CP-violating phase. The phase \(\delta \) according to the most recent experiments  [54] can be non-vanishing indicating necessity of reformulation of most fundamental aspects of the universe at (almost) all scales. The symmetry between matter and antimatter, charge-conjugation parity-reversal CP symmetry, seemed to be a perfect symmetry of nature. However, it was proposed by Sakharov in Ref. [51] that CP violation is one of the necessary conditions for known and observed imbalance of matter and anti-matter abundance in the universe. As the CP violation known for quarks is too small to be sufficient the CP symmetry and its potential violation remains a central topic of many investigations in particle physics. In particular, results of the above mentioned experiment [54] motivate searching consequences of the neutrinos’ CP violation in various areas of natural science.

Neutrino oscillations are customarily approximated in a framework of unitary evolving closed quantum systems. However, as every physical system coupled to a matter, neutrino is also subjected to decoherence effects [10, 12] originating from interaction with the environment and resulting in non-unitary corrections to its time-evolution [20]. Decoherence effects not only serve as a possible explanation of certain experimental data [8, 9, 31, 32, 41, 47]—cf. Ref. [24] for a summary of a recent progress on that topic—but also significantly modify dynamic properties of the oscillation. It is since in a presence of decoherence any system becomes open and its evolution is determined by a reduced (with respect to its environment) density matrix [4]. Description of a time evolution of an open system cannot be arbitrary—complete positivity [4, 12, 20] together with a semi-group property are two of the best known requirements.

Neutrino oscillation in a qutrit approximation Eq. (1) is given by a solution of a master equation

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t} \rho _{F} = - i[\mathcal {H}_{\mathcal {F}},\rho _{F}] + L[\rho _{F}], \end{aligned}$$
(6)

where initially we assume neutrino in a particular flavour state \(\rho _F(0)=|\varPsi _F\rangle \langle \varPsi _F|\) which in our case chosen to be electron, i.e. \(|\varPsi _F\rangle =|\nu _e\rangle \). Neutrino oscillation can be quantified in a most natural way by considering an overlap between a flavour state solving Eq. (6) and a state of well-defined flavour \(\rho (0)=|\nu _e\rangle \langle \nu _e|\) initializing oscillation Eq. (6). The corresponding probability

$$\begin{aligned} P_0= & {} \text{ Tr }[\rho _F(0)\rho _F(t)] \end{aligned}$$
(7)

serves in the following discussion as natural reference (benchmark) for QSL dynamics which properties are compared. Let us notice that for a neutrino initially in a pure state \(\rho _F(0)\), the overlap \(P_0\) in Eq. (7) is related to the fidelity of states [13]. The terms \([\mathcal {H}_{\mathcal {F}},\cdot ]\) and \(L[\cdot ]\) are responsible for unitary (Hamiltonian generated) and dissipative (Lindbladian) part of time evolution Eq. (6), respectively. The Hamiltonian \(\mathcal {H}_{\mathcal {F}}\) [19, 26, 35, 50]:

$$\begin{aligned} \mathcal {H}_{\mathcal {F}}= H_\mathrm{kin} + H_\mathrm{pot}, \end{aligned}$$
(8)

includes the kinetic \(H_\mathrm{kin}\) and the potential \(H_\mathrm{pot}\) part, the latter resulting from neutrino interaction with normal matter. The Lindbladian L in Eq. (6) describes decoherence and a discussion of its influence on the QSL is postponed to the next Sections. In the absence of decoherence the time evolution of the neutrino, Eq. (6) reduces to the Schrödinger equation. Operating at an ultrarelativistic limit for the neutrinos (with neutrino’s eigenenergies \(E_{k} = E + \frac{m_{k}^{2}}{2E}\) and momentum \( p \sim E \))—the kinetic part of the Hamiltonian \(\mathcal {H}_{\mathcal {F}}\) in the flavour basis reads:

$$\begin{aligned} H_\mathrm{kin} = \frac{1}{2E}U_\mathrm{PMNS}\left( \begin{array}{ccc} 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad \varDelta m_{21} ^{2} &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad \varDelta m_{31} ^2 \end{array}\right) U_\mathrm{PMNS}^{\dag }, \end{aligned}$$
(9)

where \(\varDelta m_{ij} ^{2} = m_{i}^2-m_j^2\) is the difference between the masses of two oscillating neutrinos. In the following numerical calculations, we set \(\varDelta m_{12} ^{2}=7.37\cdot 10^{-5}\,\mathrm{eV}^2\) and \(\varDelta m_{31} ^{2}=2.52\cdot 10^{-3}\,\mathrm{eV}^2\) [23]. The main contribution to the potential part \(H_\mathrm{pot}\) originates from neutrino’s interaction due to coherent forward elastic scattering (and for negligible non-coherent effects) with the matter’s electrons or neutrons generating charged-current potential \(V_{CC}\). The potential part of the Hamiltonian takes then the following form:

$$\begin{aligned} H_\mathrm{pot} = \left( \begin{array}{ccc} V_{C} &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \end{array}\right) . \end{aligned}$$
(10)

The charged-current potential \(V_{C}\) is related to the electron’s density in the matter \(V_{C}=\sqrt{2} G_{F}n_e\) with the Fermi coupling constant \(G_{F}\) and the electron number density \(n_e\).

Fig. 1
figure 1

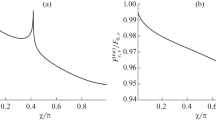
Upper panel: decoherence-free neutrino oscillation qualified by \(P_0\) Eq. (7) as a function of time for various values of the charge-current potential \(V_C\). Lower panel: geometric quantum speed limit of decoherence-free neutrino oscillation \(\nu _\mathrm{QSL}\) Eq. (2) (for clarity of presentation truncated to \(\nu _\mathrm{QSL}<4\)) as a function of time for various values of the charge-current potential \(V_C\). The CP violating phase \(\delta =0\)

Full size image

3 Results

Quantum speed limit of neutrino oscillation is analysed by means of numerical solution of Eq. (6) obtained using QuTip [38, 39], a Python-based toolbox dedicated to dynamics and control of open quantum systems. We present results in three steps: first including normal matter, the second including decoherence effects and finally presenting our central results concerning QSL for CP-violating system. We investigate numerical solution of Eq. (6) with Hamiltonian and Lindbladian parts given in Eq. (8) and (introduced below) Eq. (11), respectively. We utilize QuTiP master equation solver qutip.mesolve (both for unitary and dissipative evolution) for a neutrino initially in the electron flavour. In calculation of quantum speed limit Eq. (2), we utilize qutip.bures_angle for Bures distance and scipy.linalg.svdvals to compute singular values of \(\mathbb {L}[\rho _F(t)]\) in Eq. (2).

3.1 Normal matter

The charged-current potential \(V_C\) is the first quantity which significantly affects neutrino oscillation modifying its period as presented in an upper panel of Fig. 1. The modification is present also in the geometric QSL as presented in lower panel of Fig. 1. Let us notice that in an absence of normal matter i.e. for \(V_C=0\) maximal values \(P_0=1\) correspond to discontinuities of \(\nu _\mathrm{QSL}\rightarrow \infty \) what is in agreement with interpretation of geometric QSL as a speed of changes of statistical distance between states [28, 29]. Due to the discontinuities (vertical asymptotes) a range of \(\nu _\mathrm{QSL}\) for \(V_C=0\) presented in Fig. 1 is truncated. Increase in \(V_C\) results in changes of periodicity of oscillation and, as a consequence of interaction with normal matter, discontinuities in \(\nu _\mathrm{QSL}\) disappear cf. Fig. 1 replaced by sharp but continuous peaks. As in the absence of decoherence quantum finite-dimensional systems are periodic or quasi-periodic, one obtains large values of \(\nu _\mathrm{QSL}\) provided that \(P_0\approx 1\), i.e. the time-evolving systems returns in a neighbourhood of its starting point. Inclusion of interaction with matter allows to abandon an artefact of discontinuous QSL time characteristics clearly absent in real systems.

3.2 Decoherence

One of peculiarities of neutrino as a fundamental particle is its extremely weak interaction with almost everything existing in the Universe. However, omnipresent decoherence is unavoidable and can serve as one of possible mechanisms [8, 9, 11, 24, 31, 41, 47] affecting unusual properties of a neutrino. We consider the simplest Markovian model of decoherence based on natural requirement of complete positivity of time evolution [4] leading to a Master equation Eq. (6) with a (non-Hamiltonian) Lindbladian part

$$\begin{aligned} L[\rho _{F}] = \sum _{i,j=0} ^{N^{2}-1}c_{ij} \left( F_{i}\rho _{F}F_{j}^{\dag }-\frac{1}{2}\left\{ F_{j}^{\dag }F_{i},\rho _{F}\right\} \right) \end{aligned}$$
(11)

being responsible for the non-standard effects connected with dissipation and decoherence. Here, \(N=3\) denotes the dimension of the system, \(\{\cdot ,\cdot \}\) is an anti-commutator, the matrices \(F_{n}\) stand for the generators of SU(3). In the standard representation, they are given by the celebrated Gell–Mann matrices \(F_{n} = \frac{\lambda _{n}}{2}\), where \(\lambda _{n}\) [37]:

$$\begin{aligned} \lambda _{0}= & {} \mathbb {I}_{3},\; \lambda _{1} = \left( \begin{array}{ccc}0 &{}\quad 1 &{}\quad 0 \\ 1 &{}\quad 0 &{} \quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \end{array}\right) ,\; \lambda _{2}= \left( \begin{array}{ccc}0 &{}\quad -i &{}\quad 0 \\ i &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \end{array}\right) ,\\\nonumber \lambda _{3}= & {} \left( \begin{array}{ccc}1 &{}\quad 0 &{}\quad 0 \\ 0 &{} \quad -1 &{} \quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \end{array}\right) ,\;\lambda _{4}= \left( \begin{array}{ccc}0 &{}\quad 0 &{}\quad 1 \\ 0 &{}\quad 0 &{}\quad 0 \\ 1 &{}\quad 0 &{}\quad 0 \end{array}\right) ,\\\nonumber \lambda _{5}= & {} \left( \begin{array}{ccc}0 &{}\quad 0 &{}\quad -i \\ 0 &{}\quad 0 &{}\quad 0 \\ i &{}\quad 0 &{}\quad 0 \end{array}\right) ,\; \lambda _{6} =\left( \begin{array}{ccc}0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 \\ 0 &{}\quad 1 &{}\quad 0 \end{array}\right) ,\\\nonumber \lambda _{7}= & {} \left( \begin{array}{ccc}0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad -i \\ 0 &{}\quad i &{}\quad 0 \end{array}\right) ,\; \lambda _{8} = \frac{1}{\sqrt{3}}\left( \begin{array}{ccc}1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad -2 \end{array}\right) . \end{aligned}$$
(12)

The coefficients \(c_{ij}\) in Eq. (11) satisfy the set of inequalities granting complete positivity [11, 12]):

$$\begin{aligned} |c_{ij}|\le \frac{1}{2} (c_{ii} + c_{jj}). \end{aligned}$$
(13)

In our analysis, we make one more simplifying step and we limit our consideration to diagonal decoherence with \(c_{ii}=\kappa \) and \(c_{i\ne j}=0\). In Fig. 2, we present simultaneous effect of decoherence and very weak interaction with normal matter with \(V_C=0.03\) in order to avoid artificial discontinuities in \(\nu _\mathrm{QSL}\) present in ideal noise-less systems. Let us notice that a range of \(\nu _\mathrm{QSL}\) presented in Fig. 2 for a noise-less case, \(\kappa =0\) is (as irrelevant for further discussion) truncated. Let us also notice initially asymptotic value of \(\nu _\mathrm{QSL}\) as \(t\rightarrow 0^+\) due to a definition (and its geometric interpretation) of the geometric speed limit Eq. (2). Markovian decoherence, contrary to previously discussed interaction with normal matter, does not influence periodicity of neutrino oscillation but rather effects in amplitude damping as it can be inferred from an upper panel of Fig. 2. Non-vanishing decoherence removes discontinuities present in a noise-less time evolution of \(\nu _\mathrm{QSL}\) but does not affect position of peaks since decoherence of any amplitude \(\kappa \) does not alter positions of extreme values in QSL compared to the noise-less oscillations. For sufficiently large values of \(\kappa \), there is a qualitative change in the QSL characteristics which, as it is presented in the lower panel of Fig. 2, starts to be monotonically decreasing function of time.

Fig. 2
figure 2

Neutrino oscillation quantified by \(P_0\) Eq. (7) (upper panel) and neutrino QSL quantified by \(\nu _\mathrm{QSL}\) Eq. (2) for clarity of presentation truncated to \(\nu _\mathrm{QSL}<0.5\) (lower panel) for different amplitudes of decoherence \(c_{ii}=\kappa \) in a presence of normal matter \(V_C=0.03\) and no CP-violation \(\delta =0\)

Full size image

3.3 CP-violation

An influence of the CP symmetry and its potential violation is visible both in decoherence-affected neutrino oscillation and geometric QSL as presented in upper and (respectively) lower panel of Fig. 3. For a better visualization of results, a range of \(\nu _\mathrm{QSL}\) is in the lower panel of Fig. 3 truncated. Let us emphasize the presence of initially asymptotic value of \(\nu _\mathrm{QSL}\) as \(t\rightarrow 0^+\). Contrary to previously discussed cases of modification via decoherence only affecting height of \(P_0\) graph, non-vanishing CP phase \(\delta \) results in increase in \(P_0\) depth which becomes maximal for \(\delta =\pi \). In other words, neutrino oscillates with the same (quasi)period but in a presence of CP-violation it wanders off further (in a sense of decreasing fidelity) than it does for \(\delta =0\). Resulting behaviour of \(\nu _\mathrm{QSL}\) suggests possibility of using geometric QSL to quantify the CP-violation if one utilizes relation between amplitude of \(\nu _\mathrm{QSL}\) and a value of \(\delta \). However, let us emphasize an existence of time windows where both \(P_0\) and \(\nu _\mathrm{QSL}\) become indistinguishable with respect to different \(\delta \) limiting potential applicability of QSL as a hallmark of violation of the CP symmetry. Let us notice that the effect of CP-symmetry is even stronger if one considers \(\nu _\mathrm{QSL}\) cf. lower panel of Fig. 3. First, the non-vanishing \(\delta \) enhances peaks of which otherwise are damped by decoherence. As a result, geometric QSL quantifies a potential CP violation provided that we remember the above mentioned time windows where both \(P_0\) and \(\nu _\mathrm{QSL}\) for all values of \(\delta \) are identical. It occurs close to local maxima of \(P_0\), i.e. at time instance when the neutrino returns close to its initial state.

Fig. 3
figure 3

Neutrino oscillation quantified by \(P_0\) Eq. (7) (upper panel) and neutrino QSL quantified by \(\nu _\mathrm{QSL}\) Eq. (2) for clarity of presentation truncated to \(\nu _\mathrm{QSL}<0.4\) (lower panel) for different values of CP-violating phase \(\delta \) in the presence of decoherence with \(\kappa =0.03\) in Eq. (11) and in the presence of normal matter \(V_C=0.03\)

Full size image

4 Discussion

Neutrinos belong to a class of objects allowing for ’complementary’ studies. The most common approaches of particle physics community become often successfully augmented by results concerning quantum informational properties studied from seemingly different perspective.

Our work belongs to a part of investigations indicating possibility of utilizing quantum informational perspective for better understanding the nature of neutrino. We considered geometric quantum speed limit and we showed its potential applicability as a hallmark for the CP-violation. First, we presented how QSL as a function of time becomes modified by interaction of neutrino with normal matter formed by matter’s electrons or neutrons and generating the charge-current correction \(V_C\) in the Hamiltonian Eq. (8). Removal of artificial discontinuities in the QSL-time characteristics is the main effect of this interaction. Infinite peaks in \(\nu _\mathrm{QSL}\) typical for an ideal decoherence-free system become shifted and lowered by \(V_C\) and, for sufficiently large values of \(V_C\) lose their direct connection to the position of extremal values of \(P_0\) Eq. (7). These results after inclusion of decoherence effect become supplemented by damping of oscillations of \(\nu _\mathrm{QSL}\) which, for sufficiently high decoherence (given by an amplitude \(\kappa \) of Lindblad dissipators Eq. (11). Although we used purely phenomenological model of decoherence guided solely by the requirement of complete positivity, the results are generic for Markovian open quantum systems.

The most significant results allow to relate geometric QSL to a very hot topic of hypothetical violation of the CP symmetry for neutrinos [54]. We infer that such a violation indicated by non-vanishing \(\delta \) in the Pontecorvo–Maki–Nakagawa–Sakata mixing matrix Eq. (5) results in an enhancement of \(\nu _\mathrm{QSL}\) amplitude and effective separation of time characteristics of geometric QSL of systems with different \(\delta \). We also identified time windows of geometric QSL where this effect becomes either particularly visible or vanishes making time characteristics almost \(\delta \)-independent.

Fig. 4
figure 4

Quantum speed limit time \(\tau _\mathrm{QSL}\) Eq. (14) as a function of time: (i) upper panel: for various values of the charge-current potential \(V_C\) in the absence of decoherence \(\kappa =0\) and with CP violating phase \(\delta =0\). (ii) Central panel: for different amplitudes of decoherence \(c_{ii}=\kappa \) in the presence of normal matter \(V_C=0.03\) and no CP-violation \(\delta =0\). (iii) Bottom panel: for different values of CP-violating phase \(\delta \) in the presence of decoherence with \(\kappa =0.03\) in Eq. (11) and in a presence of normal matter \(V_C=0.03\)

Full size image

Geometric quantum speed limit Eq. (2) quantifies informational (statistical) content of a time-local (calculated at a given time instant t) rate of change of neutrino state. There are three factors affecting this rate which are studied in this paper: interaction between neutrino and normal matter (for \(V_C\ne 0\)), Markovian decoherence (for \(\kappa \ne 0\) in Eq. (11) and potential violation of the CP symmetry (for \(\delta \ne 0\) in Eq. (5)). From a mathematical perspective, the changes in the geometric speed limit Eq. (2) reported here are due to a collective effect of collaboration of these three factors. In particular, the effect of \(\delta \) in \(\nu _\mathrm{QSL}\) starts to be visible provided that one allows for the presence of decoherence in a dynamical model of neutrino oscillation. It is due to an effective cancellation of the CP-violating phase both for the operator norm and the Bures distance l(t) (related to fidelity and for pure states given by their overlap) in the numerator and denominator of Eq. (2), respectively, for conservative model of neutrino oscillation with \(\kappa =0\). The numerator of QSL Eq. (2) is given by maximal singular value which, to be calculated, demands multiplication of an operator and its conjugate [28] resulting in the above-mentioned cancellation of phase. In the presence of decoherence resulting in an information loss due to non-unitary dynamics Eq. (11), the effect of \(\delta \) is present indicating limiting applicability of purely Hamiltonian models of a description of at least certain properties of neutrino oscillation in time. The QSL quantifying instantaneous rate of changes of neutrino state under non-unitary evolution is a quantity which allows to exhibit otherwise ’invisible’ effects related to characteristic time scale of neutrino dynamics. The phenomenon of neutrino oscillations in time and for decoherence-free Hamiltonian description is related to the Mandelstam–Tamm time-energy uncertainty relation [16]. Despite of the presence of certain controversial issues [3, 15], it allows to set a characteristic time interval required for a significant change of the flavour neutrino state, i.e. an intrinsic time scale of the inter-flavour passage [16]. Let us emphasize that in particular the Mössbauer neutrinos produced in two-body decays of nuclei embedded in a crystal lattice [2] can be utilized for justification and verification of this property [17]. Working beyond conservative dynamics approximation, as we do here, one can utilize QSL as a natural generalization of a (local in time) bound for a rate of neutrino oscillation. Moreover, the geometric quantum speed limit Eq. (2) is directly associated with a quantum speed limit time [28]

$$\begin{aligned} \tau _\mathrm{QSL}^{-1}(t)= & {} \frac{1}{t}\int _0^t \nu _\mathrm{QSL}(t') \mathrm{d}t' \end{aligned}$$
(14)

which thereafter can serve as a generalization of the characteristic time interval for a significant change of the flavour neutrino state in a very general, possibly non-Hamiltonian, systems. The quantum speed limit time Eq. (14) is directly related to geometric quantum speed limit QSL Eq. (2) and, by extension, it reflects the results reported in this work. The quantum speed limit time \(\tau _\mathrm{QSL}\) is presented in Fig. 4 for the same set of parameters as previously \(\nu _\mathrm{QSL}\). Let notice that although the results are qualitative only, one recognizes characteristic features of geometric speed limit Eq. (2) also present in the speed limit time Eq. (14). Following the interpretation given in Refs. [16, 17] of the time-energy uncertainty and a related time scale as being characteristic for duration of a neutrino inter-flavour passage, one observes both an interaction with normal matter of an amplitude \(V_C\) and Markovian decoherence quantified by \(\kappa \) in the model Eq. (11) significantly modifying the quantum speed limit time Eq. (14). In particular, the effect of \(V_C\) (as presented in the upper panel of Fig. 4 influences both a magnitude of \(\tau _\mathrm{QSL}\) and its periodicity as it was for geometric speed limit Eq. (2) in Fig. 1. Similar modification yet applied to an amplitude only is shared by geometric speed limit and its corresponding speed limit time under Markovian decoherence cf. Fig. 2 and the central panel of Fig. 4, respectively. The effect of CP violation, seemingly less ’spectacular’, is also present (bottom panel of Fig. 4 indicating an enhancement of the quantum speed limit time due to an increasing value of the CP-violating phase \(\delta \). We strongly emphasize that all the neutrino experiments such as the recent one reported in Ref. [54]) belong to the most sophisticated experiments performed so far and our predictions concerning QSL and the corresponding time are nothing but qualitative signatures of certain properties of neutrino oscillation.

5 Conclusions

Quantum information processing models  [46] such as circuit model [46], topological models, Zidan’s model of quantum computing proposed in Refs. [56, 57] or quantum communication protocols [36, 45, 48] can—in principle—be realized using neutrinos  [52]. However, despite recent experiments [52], such implementations, together with models using gravitational waves [1] as resource, still remain in a domain of science fiction [25] rather than reality. Nevertheless, investigations of fundamental properties of neutrino with an emphasis given on CP-violation [51] inspire researchers of various branches of science. In our work, we provided one more quantifier, the geometric QSL, of dynamic properties of neutrino oscillations. Formal similarity of dynamical model governing neutrino oscillation and qutrit dynamics, which we utilize, is a starting point of many investigations concerning properties of neutrino conducted from a perspective of quantum information. However, expecting all the predictions of quantum information to be directly applicable or translatable to a language of neutrino physics can be due to their redundancy unjustifiable. Dynamics of neutrino oscillation even simplified to a qutrit model remains confined and limited by our (current) knowledge of neutrino’s physics. As we currently know, neutrinos are massive and are affected—via charged-current potential \(V_{CC}\), cf. Eq. (8)—by normal matter. We also expect that neutrinos undergo decoherence Eq. (11) which (for hardly interacting neutrinos) can safely be assumed Markovian. Moreover, most recent experiments [54] remove at least a part of these limitations due to a possible non-preservation of the CP symmetry. Extension of the domain of studies to geometric quantum speed limit Eq. (2) of CP-violating oscillation models in a presence of decoherence and normal matter, allowed to identify regimes where the QSL, being essentially dynamical property, becomes modified by changes of equations of motion Eq. (6) induced by all the three above mentioned factors, i.e. normal matter, decoherence and CP-violation. We recognized tailored range of time where the effect of modifications becomes most significant not only indicating an opportunity of using QSL as a diagnostic tool for neutrino properties, e.g. as a hallmark of the CP violation, but also expressing quantum informational content of neutrino oscillation in terms of its geometric quantum speed limit.