Context-aware quantum simulation of a matrix stored in quantum memory

Abstract

In this paper, a storage method and a context-aware circuit simulation idea are presented for the sum of block diagonal matrices. Using the design technique for a generalized circuit for the Hamiltonian dynamics through the truncated series, we generalize the idea to (0–1) matrices and discuss the generalization for the real matrices. The presented circuit requires O(n) number of quantum gates and yields the correct output with the success probability depending on the number of elements: For matrices with poly(n), the success probability is 1 / poly(n). Since the operations on the circuit are controlled by the data itself, the circuit can be considered as a context-aware computing gadget. In addition, it can be used in variational quantum eigensolver and in the simulation of molecular Hamiltonians.

Appendices

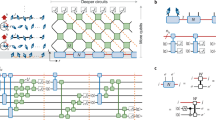
Appendix A: Validation of the circuit in Fig. 1

The controlled gate set in the circuit has the following matrix form:

$$\begin{aligned} \left( \begin{matrix} I^{\otimes 2n-2} \otimes X &{}&{}&{}\\ &{} I^{\otimes 2n-2} \otimes Z &{}&{}\\ &{}&{} \ddots &{}\\ &{}&{}&{} I^{\otimes 2n-2} \otimes I \end{matrix}\right) \end{aligned}$$

(A1)

We can represent the whole circuit more concisely by using the direct sum of matrices:

$$\begin{aligned} \left( H^{\otimes 3}\otimes I^{\otimes 2n-1}\right) \left( \bigoplus _{j=0}^{N/2}X \oplus \bigoplus _{j=0}^{N/2}Z \oplus \bigoplus _{j=0}^{N/2}-Z \oplus \dots \bigoplus _{j=0}^{N/2}I\right) \end{aligned}$$

(A2)

To illustrate the action of the circuit, we will use the example matrix $Q_i = Z\oplus XZ$ which leads to the following $\left| g_{ik}\right\rangle \left| k\right\rangle \hbox {s}$:

$$\begin{aligned} \left| g_{i0}\right\rangle \left| 0\right\rangle = \left| \mathbf 1\right\rangle \left| 0\right\rangle \text { and } \left| g_{i1}\right\rangle \left| 1\right\rangle = \left| \mathbf 3\right\rangle \left| 1\right\rangle . \end{aligned}$$

(A3)

Then, we form the following 6-qubit initial state:

$$\begin{aligned} \left| g_i\right\rangle \left| \psi \right\rangle = \frac{1}{\sqrt{2}} \left( \left| \mathbf 1\right\rangle \left| 0\right\rangle \left| \psi \right\rangle + \left| \mathbf 3\right\rangle \left| 1\right\rangle \left| \psi \right\rangle \right) . \end{aligned}$$

(A4)

After applying the controlled gates (CG) to the initial state, we obtain:

$$\begin{aligned} CG \left| g_i\right\rangle \left| \psi \right\rangle = \frac{1}{\sqrt{2}} \left( \left| \mathbf 1\right\rangle \left| 0\right\rangle (Z\otimes Z)\left| \psi \right\rangle + \left| \mathbf 3\right\rangle \left| 1\right\rangle (XZ\otimes XZ)\left| \psi \right\rangle \right) . \end{aligned}$$

(A5)

Applying the Hadamard gates to the first three qubits produces the following final state:

$$\begin{aligned}&\frac{1}{4} \bigg (\big ( \left| 000\right\rangle - \left| 001\right\rangle +\left| 010\right\rangle -\left| 011\right\rangle +\left| 100\right\rangle - \left| 101\right\rangle \nonumber \\&\qquad \qquad +\left| 110\right\rangle -\left| 111\right\rangle \big ) \left| 0\right\rangle (Z\otimes Z)\left| \psi \right\rangle \nonumber \\&\quad + \big ( \left| 000\right\rangle - \left| 001\right\rangle -\left| 010\right\rangle +\left| 011\right\rangle +\left| 100\right\rangle - \left| 101\right\rangle \nonumber \\&\qquad \qquad -\left| 110\right\rangle +\left| 111\right\rangle \big )\left| 1\right\rangle (XZ\otimes XZ)\left| \psi \right\rangle \bigg ). \end{aligned}$$

(A6)

Here, the states where the first three qubits are in $\left| 000\right\rangle$ includes the expected output which are:

$$\begin{aligned} \frac{1}{4} \big ( \left| 000\right\rangle \left| 0\right\rangle (Z\otimes Z)\left| \psi \right\rangle +\left| 000\right\rangle \left| 1\right\rangle (XZ\otimes XZ)\left| \psi \right\rangle \big ). \end{aligned}$$

(A7)

The equivalent of $Q_i\left| \psi \right\rangle$ is produced on the amplitudes of the states:

$$\begin{aligned} \{\left| 000000\right\rangle , \left| 000001\right\rangle , \left| 000110\right\rangle , \left| 000111\right\rangle \}. \end{aligned}$$

(A8)

Appendix B: Validations of the circuits in Figs. 2 and 3

In the circuit in Fig. 2, we have the superpositioned input state $\left| g\right\rangle$. Before the Hadamard gates on the first register of the circuit, for different $\left| i\right\rangle$ on the output we have normalized $Q_i \left| \psi \right\rangle$ on the same states as given in (A7) and (A8). That means for $\left| \mathbf 0\right\rangle$ on the first register we have normalized $Q_0 \left| \psi \right\rangle$ on the chosen states, and for $\left| \mathbf 1\right\rangle$ we have $Q_1 \left| \psi \right\rangle$, and so on. By applying the Hadamard gates to the first register, for $\left| i\right\rangle = \left| \mathbf 0\right\rangle$, we generate the normalized summation $\sum _i Q_i \left| \psi \right\rangle$ on the same chosen states.

Figure 3 is just the generalization of Fig. 2 and acts the same way.

Appendix C: A larger Hamiltonian divided into submatrices

$$\begin{aligned} \mathcal {H}= \left( \begin{matrix} H_{00}&{} H_{10}&{} H_{20}&{}H_{30}&{}H_{40}&{} H_{50}&{} H_{60}&{}H_{70}\\ H_{11}&{} H_{01}&{} H_{31}&{}H_{21}&{}H_{51}&{} H_{41}&{} H_{71}&{}H_{61}\\ H_{22}&{} H_{32}&{} H_{02}&{}H_{12}&{}H_{62}&{} H_{72}&{} H_{42}&{}H_{52}\\ H_{33}&{} H_{23}&{} H_{13}&{}H_{03}&{}H_{73}&{} H_{63}&{} H_{53}&{}H_{43}\\ H_{44}&{} H_{54}&{} H_{64}&{}H_{70}&{}H_{04}&{} H_{14}&{} H_{24}&{}H_{34}\\ H_{55}&{} H_{45}&{} H_{75}&{}H_{61}&{}H_{15}&{} H_{05}&{} H_{35}&{}H_{25}\\ H_{66}&{} H_{76}&{} H_{46}&{}H_{52}&{}H_{26}&{} H_{36}&{} H_{06}&{}H_{16}\\ H_{77}&{} H_{67}&{} H_{57}&{}H_{43}&{}H_{37}&{} H_{27}&{} H_{17}&{}H_{07}\\ \end{matrix}\right) _{16\times 16}. \end{aligned}$$

(C1)