Quantum path computing: computing architecture with propagation paths in multiple plane diffraction of classical sources of fermion and boson particles

Abstract

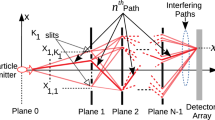
Quantum computing (QC) architectures utilizing classical or coherent resources with Gaussian transformations are classically simulable as an indicator of the lack of QC power. Simple optical setups utilizing wave-particle duality and interferometers achieve QC speed-up with the cost of exponential complexity of resources in time, space or energy. However, linear optical networks composed of single-photon inputs and photon number measurements such as boson sampling achieve solving problems which are not efficiently solvable by classical computers while emphasizing the power of linear optics. In this article, quantum path computing (QPC) setup is introduced as the simplest optical QC satisfying five fundamental properties all-in-one: exploiting only the coherent sources being either fermion or boson, i.e., Gaussian wave packet of standard laser, simple setup of multiple plane diffraction (MPD) with multiple slits by creating distinct propagation paths, standard intensity measurement on the detector, energy-efficient design and practical problem solving capability. MPD is unique with non-Gaussian transformations by realizing an exponentially increasing number of highly interfering propagation paths while making classical simulation significantly hard. It does not require single-photon resources or number resolving detection mechanisms making the experimental implementation of QC significantly low complexity. QPC setup is utilized for the solutions of specific instances of two practical and hard number theoretical problems: partial sum of Riemann theta function and period finding to solve Diophantine approximation. Quantumness of MPD with negative volume of Wigner function is numerically analyzed, and open issues for the best utilization of QPC are discussed.

Appendices

Iterative formulation of path integrals

Throughout the appendices, various formulations are listed in Table 5. In the following, all the calculations are performed for the specific nth path assuming the corresponding slit width parameters are given by the values of $\beta _j$ on jth plane for $j \in [1, N-1]$. Therefore, all the following parameters depend on the path index n without explicitly showing, e.g., $A_{j}$ and $B_{j}$ should be replaced with $A_{j,{n}}$ and $B_{j,{n}}$, respectively, for the specific nth path. The same is valid for the remaining parameters except the local parameters $C_{j,n}$, $D_{j,n}$ and $\chi _{j,n}$. They depend directly on the slit positions and accordingly on n such that they are denoted by including the path index n for jth plane as $C_{j,n}$, $D_{j,n}$ and $\chi _{j,n}$. Similarly, $\overrightarrow{c}_{N-1}$ and $\overrightarrow{d}_{N-1}$ should be replaced by $\overrightarrow{c}_{N-1, n}$ and $\overrightarrow{d}_{N-1, n}$, respectively. The final resulting matrix ${\mathbf {H}}$ utilized in (13) should be replaced with ${\mathbf {H}}_{N-1, n}$ as in (14). Only the parameters $A_0$, $B_0$ and $\chi _0$ are path independent. Therefore, the corresponding numerical results of the expressions for varying slit widths on each path are obtained by changing $\beta _j$ on jth plane for the corresponding path. After integration in (12), the following is obtained:

$$\begin{aligned} \begin{aligned} \varPsi _{n,j}(x) \, = \,&\chi _{0} \, \left( \prod _{k=1}^{j-1} \chi _{k,n} \right) \, e^{(A_{j-1} \,+ \, \imath \, B_{j-1})\, x^2 \,+ \, (C_{j-1,n} \,+ \, \imath \, D_{j-1,n})\, x} \end{aligned} \end{aligned}$$

(36)

where $j \in [1, N]$, x corresponds to the position in x-axis on jth plane and iterative variables $\chi _{j,n}$, $A_{j}$, $B_{j}$, $C_{j,n}$ and $D_{j,n}$ are defined in Table 5. The first integration is obtained with $\varPsi _0(x)$ by free propagation until the first slit plane resulting in $A_0$, $B_0$, $\chi _0$ while $C_0= D_0 = 0$. The second LCT results in $A_1$, $B_1$, $C_{1,n}$, $D_{1,n}$, $\chi _{1,n}$, where $p_{1, j}$, $\varsigma _j$, $\xi _{j}$, $\varrho _j$, $\zeta _j$, $\zeta _{j,c}$ and $\zeta _{j,d}$ are defined for $j \in [1, N-1]$. Then, the iterations for $A_j$, $B_j$, $C_{j,n}$, $D_{j,n}$, $\chi _{j,n}$, $p_{2,j}$, $p_{3,j}$, $p_{4,j}$, $p_{5,j}$ and $\chi _{T,j} { \, \equiv \, \chi _{0} \prod _{k=1}^{j} \chi _{k,n}}$ are obtained for $j \in [2, N-1]$. An iterative relation is obtained as follows:

$$\begin{aligned} \left[ \begin{array}{c} C_{j,n} \\ D_{j,n} \end{array} \right] = \left[ \begin{array}{c} \zeta _{j,c} \\ \zeta _{j,d} \end{array} \right] X_{j,s_{n,j}} + \left[ \begin{array}{cc} p_{4,j}&{}\quad p_{5,j} \\ -\,p_{5,j}&{}\quad p_{4,j} \end{array} \right] \left[ \begin{array}{c} C_{j-1,n} \\ D_{j-1,n} \end{array} \right] \end{aligned}$$

(37)

Performing iterations results in $C_{N-1,n} = \overrightarrow{c}_{N-1}^\mathrm{T} \overrightarrow{x}_{N-1,n}$ and $D_{N-1,n} = \overrightarrow{d}_{N-1}^\mathrm{T} \overrightarrow{x}_{N-1,n}$, where jth element of the vector $\overrightarrow{x}_{N-1,n}$ of the length $N-1$ is defined as $X_{j,s_{n,j}}$, and the row vectors $\overrightarrow{c}_{j}^\mathrm{T}$ and $\overrightarrow{d}_{j}^\mathrm{T}$ are defined as follows:

$$\begin{aligned} \left[ \begin{array}{c} \overrightarrow{c}_{j}^\mathrm{T} \\ \overrightarrow{d}_{j}^\mathrm{T} \end{array} \right] = \left[ \begin{array}{cccc} \overrightarrow{v}_{0,j}&\overrightarrow{v}_{1,j}&\ldots&\overrightarrow{v}_{j-1,j} \end{array} \right] \end{aligned}$$

(38)

where $\overrightarrow{v}_{k, j}$ for $k \in [0, j-1]$, utilized to obtain $C_{j,n} = \overrightarrow{c}_{j}^\mathrm{T} \overrightarrow{x}_{j, n}$ and $D_{j, n} = \overrightarrow{d}_{j}^\mathrm{T} \overrightarrow{x}_{j, n}$, is given as follows:

$$\begin{aligned} \overrightarrow{v}_{k, j} \, \equiv \, \left( \prod _{i=1}^{j-1-k} \left[ \begin{array}{cc} p_{4,j+1-i} &{} p_{5,j+1-i} \\ -p_{5,j+1-i} &{} p_{4,j+1-i} \end{array} \right] \right) \left[ \begin{array}{c} \zeta _{k+1,c} \\ \zeta _{k+1,d} \end{array} \right] \end{aligned}$$

(39)

and the matrix multiplication symbol $\prod _{i=1}^{k} {\mathbf {U}}_i$ denotes ${\mathbf {U}}_1 \, {\mathbf {U}}_2 \ldots {\mathbf {U}}_k$ for any matrix ${\mathbf {U}}_i$ for $i \in [1,k]$. The following is obtained after inserting the resulting expressions of $C_{N-1,n}$ and $D_{N-1,n}$ into $\chi _{T,{N-1}}$:

$$\begin{aligned} \chi _{T,N-1}&\equiv \, \chi _0 \left( \prod _{j=1}^{N-1} \sqrt{\xi _{j}} \right) \, e^{ \overrightarrow{p}_1^\mathrm{T} \big ( \overrightarrow{x}_{N-1, n} \odot \overrightarrow{x}_{N-1,n} \big ) } \times \, e^{ \overrightarrow{p }_2^\mathrm{T}\big ( \big ({\mathbf {G}} \, \overrightarrow{x}_{N-1, n} \big ) \odot \big ({\mathbf {G}} \, \overrightarrow{x}_{N-1, n} \big ) \big ) }\nonumber \\&\quad \times \, e^{\overrightarrow{p}_3^\mathrm{T} \big ( \big ({\mathbf {G}} \, \overrightarrow{x}_{N-1, n} \big ) \odot \big ( {\mathbf {E}}_{1}\, \overrightarrow{x}_{N-1, n} \big ) \big ) } \end{aligned}$$

(40)

where $\odot$ denotes the point-wise product, ${\mathbf {G}}$ and $\mathbf {E_1}$ are defined as follows:

$$\begin{aligned} {\mathbf {G}} \equiv \left[ \begin{array}{cc} {\mathbf {E}}_{2} {{\mathbf {V}}_{L}} &{}\quad {\mathbf {0_{N-2}}} \\ {\mathbf {0^\mathrm{T}_{N-2}}} &{} \quad 0 \end{array} \right] ; \, \, {\mathbf {E_1}} \equiv \left[ \begin{array}{cc} {\mathbf {0_{N-2}}} &{}\quad {\mathbf {I_{N-2}}} \\ 0 &{}\quad {\mathbf {0^\mathrm{T}_{N-2}}} \end{array} \right] \end{aligned}$$

(41)

while ${\mathbf {E}}_{2}$ has jth row as $\left[ \begin{array}{cccc} {\mathbf {0^\mathrm{T}_{2(j-1)}}}&1&\imath&{\mathbf {0^\mathrm{T}_{2(N-2-j)}}} \end{array} \right]$, ${\mathbf {V}}_{L}$ is the matrix whose jth column is given by $\left[ \begin{array}{cccc} {\mathbf {0^\mathrm{T}_{2(j-1)}}}&\overrightarrow{v}_{j-1,j}^\mathrm{T}&\ldots&\overrightarrow{v}_{j-1,N-2}^\mathrm{T} \end{array} \right] ^\mathrm{T}$, ${\mathbf {0_{k}}}$ is the column vector of zeros of length k, the sizes of ${{\mathbf {E}}_{2}}$ and ${{\mathbf {V}}_{L}}$ are $(N - 2) \times (2 N - 4)$ and $(2 N - 4) \times (N - 2)$, respectively, and ${\mathbf {G}}$ and ${\mathbf {E}}_1$ are $(N - 1) \times (N - 1)$. Then, the resulting wave function $\varPsi _{n,N}(x)$ is given by the following:

$$\begin{aligned} \begin{aligned} \varPsi _{n,N}(x)&= \,{\varUpsilon _{N}}\, e^{\sum _{k = 1}^3 \overrightarrow{p}_k^\mathrm{T} \bigg ( \big ({\mathbf {M}}_{1,k} \, \overrightarrow{x}_{N-1, n} \big ) \odot \big ({\mathbf {M}}_{2,k} \, \overrightarrow{x}_{N-1, n} \big ) \bigg ) } \\&\quad \times \, e^{(A_{N-1} \, + \, \imath \, B_{N-1}) \, x^2 \, + \, (\overrightarrow{c}_{N-1}^\mathrm{T} \, + \, \imath \, \overrightarrow{d}_{N-1}^\mathrm{T}) \, \overrightarrow{x}_{N-1, n} \, x } \, \, \, \, \, \, \, \end{aligned} \end{aligned}$$

(42)

where $\varUpsilon _{j} = \chi _0 \, \big ( \prod _{i=1}^{j-1} \sqrt{\xi _{i}} \big )$, ${\mathbf {M}}_{1,1} = {\mathbf {M}}_{2,1} = \mathbf {I_{N-1}}$, ${\mathbf {M}}_{1,2} = {\mathbf {M}}_{2,2} = {\mathbf {G}}$, ${\mathbf {M}}_{1,3} = {\mathbf {G}}$, ${\mathbf {M}}_{2,3} = {\mathbf {E}}_{1}$, ${\mathbf {I_{k}}}$ is identity matrix of size k, complex-valued column vectors $\overrightarrow{p}_{k}$ for $k \in [1, 3]$, real-valued iterative variables $A_j$ and $B_j$, and complex-valued iterative variable $\xi _j$ are defined in Table 5, and $\overrightarrow{x}_{{N-1}, n} \equiv [X_{1,s_{n,1}} \, X_{2,s_{n,2}} \, \ldots \, X_{N-1,s_{n, N-1}} ]^\mathrm{T}$. Intensity distribution on screen is $I_N(x) \!=\! \big \vert \varPsi _{N}(x) \big \vert ^2$ which is equal to $\big \vert \sum _{n=0}^{N_p-1} \, e^{ (A_{N-1} \, {+\, \imath \, B_{N-1} })\, x^2 }$ ${\varUpsilon _N} \, e^{r \lbrace \overrightarrow{x}_{n}\rbrace } \,e^{\overrightarrow{c}^\mathrm{T} \overrightarrow{x}_{n} \, x} \,e^{\imath \, \overrightarrow{d}^\mathrm{T} \overrightarrow{x}_{n} \, x} \big \vert ^2$ where $I_j(x) = \big \vert \varPsi _{j}(x) \big \vert ^2$ denotes the intensity or the probability of detection on jth plane for $j \in [0, N]$, $I_0(x) \equiv \vert \varPsi _{0}(x)\vert ^2$, the subscript $N - 1$ is dropped from the vectors to simplify the notation, e.g., $r\lbrace \overrightarrow{x}_{n} \rbrace \, \equiv \, \sum _{k = 1}^3 \overrightarrow{p}_k^\mathrm{T} \big ( ({\mathbf {M}}_{1,k} \, \overrightarrow{x}_{n} ) \odot ({\mathbf {M}}_{2,k} \,\overrightarrow{x}_{n} ) \big )$, $\overrightarrow{x}_{n} \equiv \overrightarrow{x}_{N-1, n}$, $\overrightarrow{c} \equiv \overrightarrow{c}_{N-1}$ and $\overrightarrow{d} \equiv \overrightarrow{d}_{N-1}$. It can be easily shown that $r \lbrace \overrightarrow{x}_{n}\rbrace$ is equal to $\overrightarrow{x}_{n}^\mathrm{T} \, {\mathbf {H}} \, \overrightarrow{x}_{n}$ where the proof is in “Appendix B” and the matrix ${\mathbf {H}}$ is given as ${\mathbf {H}} = \sum _{k=1}^{3} {\mathbf {M}}_{2,k}^\mathrm{T} \, \hbox {diag}\lbrace \overrightarrow{p}_k \rbrace \, {\mathbf {M}}_{1,k}$, where $\hbox {diag}\lbrace \overrightarrow{y} \rbrace$ is the operator creating a diagonal matrix with the elements composed of the vector $\overrightarrow{y}$.

Generation of the H-matrix

$\sum _{k = 1}^3 \overrightarrow{p}_k^\mathrm{T} \big ( ({\mathbf {M}}_{1,k} \overrightarrow{x}_{n} ) \odot ({\mathbf {M}}_{2,k} \overrightarrow{x}_{n} ) \big )$ is transformed to four different equalities. Firstly, it equals to $\overset{1}{=} \sum _{k = 1}^3$ $\mathbf {Tr} \big \lbrace \hbox {diag}\lbrace \overrightarrow{p}_k \rbrace$ ${\mathbf {M}}_{1,k}$ $\overrightarrow{x}_{n} \overrightarrow{x}_{n}^\mathrm{T}$ ${\mathbf {M}}_{2,k}^\mathrm{T} \big \rbrace$, where the equality is obtained by transforming the inner and point-wise product combination into a trace. Then, $\overset{2}{=}$ $\sum _{k = 1}^3 \mathbf {Tr}$ $\big \lbrace {\mathbf {M}}_{2,k}^\mathrm{T} \, \hbox {diag}\lbrace \overrightarrow{p}_k \rbrace \, {\mathbf {M}}_{1,k} \, \overrightarrow{x}_{n} \, \overrightarrow{x}_{n}^\mathrm{T} \big \rbrace$ and $\overset{3}{=}$ $\mathbf {Tr}$ $\big \lbrace$ $\big ( \sum _{k = 1}^3 {\mathbf {M}}_{2,k}^\mathrm{T}$ $\hbox {diag}\lbrace \overrightarrow{p}_k \rbrace$ ${\mathbf {M}}_{1,k} \big )$ $\overrightarrow{x}_{n} \, \overrightarrow{x}_{n}^\mathrm{T} \big \rbrace$ are obtained due to the permutation and the addition properties of the trace, respectively. Finally, $\overset{4}{=}$ $\mathbf {Tr} \big \lbrace$ $\overrightarrow{x}_{n}^\mathrm{T}$ $\big ( \sum _{k = 1}^3 {\mathbf {M}}_{2,k}^\mathrm{T} \, \hbox {diag}\lbrace \overrightarrow{p}_k \rbrace \, {\mathbf {M}}_{1,k} \big )$ $\overrightarrow{x}_{n} \, \big \rbrace$ is obtained with the permutation property. Then, the quadratic form is obtained.

Proof of Theorem 1

The intensity at ${\widetilde{k}} - k$ for $k \in [1, {\widetilde{k}}]$ is given as follows due to the definition in (21) and the first condition in Theorem 1:

$$\begin{aligned} {\widetilde{I}}[{\widetilde{k}} - k] \overset{1}{ = } \left| \sum _{n = 0}^{N_p - 1} g_3[n] \, (g_1[n])^{{\widetilde{k}} - k} \, e^{ - \imath \, 2 \, \pi \, {\widetilde{G}}_2[n] \, k / {\widetilde{k}} } \right| ^2 = \vert H[{ {\widetilde{k}} \, - \, }k,{\widetilde{G}}_2] \vert ^2 \end{aligned}$$

(43)

Then, ${\widetilde{I}}[{\widetilde{k}} - k]$ $\overset{2}{ < }$ $\left| \sum _{n = 0}^{N_p - 1} g_3[n] \, (g_1[n])^{{\widetilde{k}} - k} \right| ^2 \, \overset{3}{ < }$ ${\widetilde{I}}[{\widetilde{k}}] = \left| \sum _{n = 0}^{N_p - 1} g_3[n] \, (g_1[n])^{{\widetilde{k}}} \right| ^2$ are obtained with the second condition in Theorem 1.

Proof of Theorem 2

The conditional probability for the sample at $k_p$ is given by the following:

$$\begin{aligned} p(I^{*}_n[k_p] \big \vert {\widetilde{k}}) = (2 \, \pi \, {\widetilde{\sigma }}^2_p)^{-1/2} e^{- (I^{*}_n[k_p] - I^{*}[k_p])^2 / (2 \, {\widetilde{\sigma }}^2_p)} \end{aligned}$$

(44)

where ${\widetilde{\sigma }}_p \equiv \sigma ^{*}[k_p]$. Then, denoting the noisy and noise-free intensity vectors by $\overrightarrow{I}^{*}_n = [I^{*}_n[k_0] \ldots I^{*}_n[k_{M-1}]]^\mathrm{T}$ and $\overrightarrow{I}^{*} = [I^{*}[k_0] \ldots I^{*}[k_{M-1}]]^\mathrm{T}$, respectively, the log likelihood function is given as $\hbox {log}\big ( p(\overrightarrow{I }^{*}_n \big \vert {\widetilde{k}}) \big ) = - \frac{M}{2} \, \hbox {log}(2 \, \pi ) \, - \, \frac{1}{2} \sum _{p = 0}^{M-1} \hbox {log}({\widetilde{\sigma }}_p^2) \, - \, (\overrightarrow{I}^{*}_{n, {\widetilde{\sigma }}} - \overrightarrow{I}^{*}_{{\widetilde{\sigma }}})^\mathrm{T} \cdot (\overrightarrow{I}^{*}_{n, {\widetilde{\sigma }}} - \overrightarrow{I}^{*}_{{\widetilde{\sigma }}})$, where $I^{*}_{n, {\widetilde{\sigma }}}[k_p] \equiv I^{*}_n[k_p] / ({\widetilde{\sigma }}_p \, \sqrt{2})$ and $I^{*}_{{\widetilde{\sigma }}}[k_p] \equiv I^{*}[k_p] / ( {\widetilde{\sigma }}_p\, \sqrt{2})$. Fisher information matrix is given as follows:

$$\begin{aligned} I_F[{\widetilde{k}}]\equiv E \bigg \lbrace \bigg (\delta \, \hbox {log}\big ( p(\overrightarrow{I}^{*}_n \big \vert {\widetilde{k}}) \big ) \,/\,\delta {\widetilde{k}} \bigg )^2 \bigg \rbrace \,= \,- \,E \lbrace \delta ^2 \hbox {log}\big ( p(\overrightarrow{I}^{*}_n \big \vert {\widetilde{k}}) \big ) \, / \,\delta {\widetilde{k}}^2 \rbrace \end{aligned}$$

(45)

where $\delta (.) / \delta {\widetilde{k}}$ denotes the partial derivative of (.) with respect to ${\widetilde{k}}$. If the zero mean random variable is assumed at each sample point, then $I_F[{\widetilde{k}}]$ is obtained after simple calculations as $I_F[{\widetilde{k}}] = \sum _{p=0}^{M-1} {\widetilde{\sigma }}_p^{-2}$ $\big ( \delta I^{*}[k_p] / \delta \, {\widetilde{k}}\big )^2$ which depends on the square of the derivative of the intensity on the period ${\widetilde{k}}$. Then, assuming an estimation method denoted by ${\widehat{k}}$ has a bias $b({\widehat{k}}) \equiv E \lbrace {\widehat{k}} \rbrace - {\widetilde{k}}$, the Cramer–Rao Bound, i.e., $\hbox {CR}({\widetilde{k}})$, satisfies $\hbox {Var}({\widehat{k}}) \, \ge \, \hbox {CR}({\widetilde{k}})$ for the variance of estimation where $\hbox {CR}({\widetilde{k}})$ is given by the following:

$$\begin{aligned} \hbox {CR}({\widetilde{k}}) \, \equiv \, (1 \, + \, \delta b({\widehat{k}}) / \delta {{\widetilde{k}}})^2 / I_F[{\widetilde{k}}] \, = \, (1 \, + \, \delta b({\widehat{k}}) / \delta {{\widetilde{k}}})^2 \left( \sum _{p=0}^{M-1} {\widetilde{\sigma }}_p^{-2} \big ( \delta I^{*}[k_p] \, / \, \delta \, {\widetilde{k}} \big )^2 \right) ^{-1} \end{aligned}$$

(46)

Furthermore, assuming ${\widetilde{\sigma }}_p^2 \le {\widetilde{\sigma }}_\mathrm{max}^2$, the maximum of the minimum variance bound is given by the following:

$$\begin{aligned} \hbox {CR}({\widetilde{k}}) \le {\widetilde{\sigma }}_\mathrm{max}^2 \, (1 \, + \, \delta b({\widehat{k}}) / \delta {{\widetilde{k}}})^2 \left( \sum _{p=0}^{M-1} \big ( \delta I^{*}[k_p] / \delta \, {\widetilde{k}}\big )^2 \right) ^{-1} \end{aligned}$$

(47)

while with $\Delta G_2[n, l] \equiv {\widetilde{G}}_2[l]\,-\,{\widetilde{G}}_2[n]$, $\delta I^{*}[k_p] / \delta \, {\widetilde{k}}$ becomes as follows for $I^{*}[k_p] \equiv {I}^G[k_p]$:

$$\begin{aligned} \sum _{n = 0}^{N_p - 1} \sum _{l = 0}^{N_p - 1} g_{3,*}[n,l] \, g_{1,*}^{k_p}[n,l] \, g_{4,*}^{k_p^2}[n,l] e^{ -\Delta G_2[n, l] \, \imath \, \, 2 \, \pi \, k_p / {\widetilde{k}} } \big (\Delta G_2[n, l] \, \imath \, 2 \, \pi \, k_p / {\widetilde{k}}^2 \big ) \end{aligned}$$

(48)

and it is represented as follows for the normalized wave function $I^{*}[k_p] \equiv e^{- 2\, A_{N-1} \, (k_p\,T_\mathrm{s})^2} I[k_p]$:

$$\begin{aligned} \sum _{n = 0}^{N_p - 1} \sum _{l = 0}^{N_p - 1} g_{3,*}[n,l] \, g_{1,*}^{k_p}[n,l] e^{ -\Delta G_2[n, l] \, \imath \, \, 2 \, \pi \, k_p / {\widetilde{k}} } \big (\Delta G_2[n, l] \, \imath \, 2 \, \pi \, k_p / {\widetilde{k}}^2 \big ) \end{aligned}$$

(49)

Path integral with exotic paths

The evolution of the wave function in nth path after the non-classical travels of k slits with $k \in [1, N_E]$ as shown in Fig. 3 is given as $\varPsi _{n,j,k}^E(x^E_{j,k}) = \int _{x_j} f^E_{n,k}(x^E_{j,k}, x_{j}) \, \varPsi _{n,j,0}^E(x^E_{j,0}) \, \mathrm {d}x_j$ where $\varPsi _{n,j,0}^E(x^E_{j,0}) \equiv G_{n,j}(x_{j} - X_{j, s_{n,j}}) \, \varPsi _{n, j}(x_j)$, $x_{j, 0}^E \equiv x_j$, $f^E_{n,1}(x^E_{j,1}, x_{j}) \equiv K(x^E_{j,1}, t^E_{j,1}; x_{j}, t_{j})$ and $f^E_{n,k}(x^E_{j,k}, x_{j})$ for $k \ge 2$ is defined as follows:

$$\begin{aligned}&\int _{\overrightarrow{x}^E_{j, k}} \mathrm {d}\overrightarrow{x}^E_{j, k} \, K(x^E_{j,1}, t^E_{j,1}; x_{j}, t_{j}) \prod _{p = 2}^{k} K(x^E_{j,p}, t^E_{j,p}; x^E_{j,p-1}, t^E_{j,p-1}) \nonumber \\&\qquad \times \,G_{n,j}(x^E_{j,p-1} - X_{j, s_{n,j,p-1}}) \end{aligned}$$

(50)

while $k = 0$ case corresponds to the wave function evolution without any non-classical path, i.e., $\varPsi _{n,j,0}^E(x^E_{j,0})$, $t^E_{j,k} \equiv \sum _{p = 1}^{k} t_{p-1,p}^E(j) \, + \, t_j$ is the time after visiting kth slit on jth plane, $t_j$ corresponds to the time at the beginning of the non-classical movements and $\overrightarrow{x}^E_{j, k} \equiv [ x_{j, 1}^E \, \, x_{j,2}^E \, \, \ldots \, \, x_{j, k-1}^E ]$. If it is assumed that the nth path performs $k \ge 1$ consecutive visits to the slits on jth plane while the entrance slit is $X_{j, s_{n,j}}$ and the wave function at the position $x_j$ is $\varPsi _{n, j}(x_j)$, then the wave function on the next plane, i.e., $\varPsi _{n,j+1}(x_{j+1})$, is calculated as follows:

$$\begin{aligned} \int K(x_{j+1}, t^E_{j,k} + \, t_{j,j+1}; x^E_{j,k}, t^E_{j,k}) \, G_{n,j}(x^E_{j,k} - X_{j, s_{n,j,k}}) \, \varPsi _{n,j,k}^E(x^E_{j,k}) \, \mathrm {d}x^E_{j,k} \end{aligned}$$

(51)