Abstract
We study selected aspects of non-classical correlations of arbitrary states from the stochastic local operations and classical communication orbit of rank-deficient two-qubit states. In particular, we find explicitly entanglement of formation and quantum discord for these states. Moreover, we determine and analyze the Einstein–Podolsky–Rosen steering ellipsoids corresponding to these states.
Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.Avoid common mistakes on your manuscript.
1 Introduction
Quantum state transformations of the form
play a special role in quantum information theory. Such transformations preserve the tensor product structure of the space of states \(\mathscr {H}=\mathscr {H}_A \otimes \mathscr {H}_B\). In this work we consider two-qubit states. In this case, a density matrix can be written as
where \(\sigma _0=I\), \(\sigma _i\), \(i=1,2,3\), are Pauli matrices, and \(4\times 4\) matrix R fulfills conditions guaranteeing hermicity, positive semidefiniteness and proper normalization of \(\rho \). For two-qubit states transformations (1) take the form
The above transformation corresponds to the following transformation of R [compare (2)]:
where \(\Lambda _1\) and \(\Lambda _2\) are Lorentz transformations (images of A and B in the canonical homomorphism from SL\((2,\mathbb {C})\) group onto proper orthochronous Lorentz group \(L_{+}^{\uparrow }\)).
Transformations of the form (3) are related to the so-called stochastic local operations and classical communication (SLOCC) [1]. Classification of all two-qubit states into orbits with respect to transformations (3), so-called SLOCC orbits, was considered in [2]. In our previous work [3] we have refined this classification. In [2, 3] it was shown that each of two-qubit states can be generated from one of the following distinct states:
-
(i)
Three-parameter family of Bell-diagonal states,
-
(ii)
Two-parameter family of rank-deficient states,
-
(iii)
One of three fixed states.
In this work we restrict our attention to the SLOCC orbit of rank-deficient states [case (ii) from the above list]. As it was shown in [3], this orbit is generated via (3) from
where
with \(0\le \tilde{x}<1\), \(0<\tilde{y}<1-\tilde{x}\).
In particular, we study different aspects of non-classical correlations present in an arbitrary two-qubit state from the SLOCC orbit generated by the state (5). Although various notions of quantumness of correlations exist in the literature (for review see, e.g., [4,5,6,7]), we consider here quantum entanglement (as quantified by entanglement of formation), quantum discord and Einstein–Podolsky–Rosen steering.
Note that the two-qubit states from the SLOCC orbit generated by the state (5) are the X states for which quantum discord has been studied [8,9,10,11,12,13,14,15,16,17,18,19,20]. However, for a considered here restricted class we are able to find analytic formulas for quantum discord in the form of piecewise function together with the regions of validity of each of the branches. For a general X state we have to take for the quantum discord the lesser of two values because there is no prescription which branch should be chosen for the given set of parameters defining the state. Therefore, our results in this aspect are new.
Note also that EPR steering ellipsoid for general two-qubit state is well known. Nevertheless, our result that two-qubit states from the deficient-rank class lead to the EPR steering ellipsoids with some definite properties, and vice versa, so that this class could be characterized by the properties of EPR steering ellipsoid is, to our best knowledge, new and original.
2 The orbit of rank-deficient states
The density matrix corresponding to \(\Sigma \) given by Eq. (6) has the following form
where \(0\le \tilde{x}<1\), \(0<\tilde{y}< 1-\tilde{x}\). This is a mixed state.
Now, an arbitrary Lorentz transformation can be obtained as a composition of a pure Lorentz boost in a given direction and rotation. Therefore, we can write
where \(O_1,O_2\in \text {SO}(3)\) and \(B_3(\beta )\) denote boost in the z-axis direction with the velocity \(\beta \in (-1,1)\). Consequently, the most general state can be generated from \(\Sigma \) via the following transformation
A direct but tedious calculation shows that for \(O_1=O_2=I\) we get
with
and
Note that we admit here negative values of x, contrary to positive values of \(\tilde{x}\), as x parametrizes states from the whole orbit, while \(\tilde{x}\) parametrizes generating states, and therefore we are interested in restricting the domain of \(\tilde{x}\) as much as possible. In Fig. 1 we have depicted the region described by inequalities (11).
The parameter space described by inequalities (11) (interior of the cone)
The corresponding density matrix reads
Now, taking into account Eq. (9), we see that each state on the considered SLOCC orbit of rank-deficient states can be obtained from (13) via local unitary transformation
That is why our analysis will be restricted mainly to the states of the form (13).
3 Quantum entanglement
In quantum information science one of the most important problems is quantification of non-classical correlations present in quantum states [4, 5]. In this regard, the most significant progress has been made in the case of bipartite quantum systems which have been studied initially in the framework of the entanglement-separability paradigm in which the correlations present in a quantum state can be classified as either classical or quantum, where the latter ones are identified with quantum entanglement [4]. Although quantum entanglement of a bipartite state \(\rho \) can be quantified by a variety of entanglement measures, in this work we restrict our attention to entanglement of formation [21] being the first measure of quantum entanglement for mixed bipartite states.
Entanglement of formation of a bipartite quantum state \(\rho \) is defined by
where the minimum is taken over all possible ensembles of states \(|\psi _{i}\rangle \) with probabilities \(p_{i}\) such that \(\rho = \sum _{i} p_{i} |\psi _{i}\rangle \langle \psi _{i}|\), and \(S(\sigma ) = -\text {Tr}(\sigma \log _{2} \sigma )\) is the von Neumann entropy.
The optimization procedure involved in the above definition is what it makes entanglement of formation intractable in the general case. However, for a two-qubit state \(\rho \) entanglement of formation can be expressed in terms of concurrence [22]
where \(h(x) = - x\log _{2} x - (1-x)\log _{2}(1-x)\) is the binary entropy function, and concurrence of \(\rho \) is given by
where the \(\lambda _{i}\)’s are the square roots of the eigenvalues of \(\rho (\sigma _2\otimes \sigma _2) \rho ^{*} (\sigma _2\otimes \sigma _2)\) in decreasing order, with \(\rho ^{*}\) being the complex conjugation of \(\rho \).
Now, using the above formulas, one can verify that concurrence of the states (7) and (13) is given by
Therefore, for these states entanglement of formation has the following form
It is known that concurrence is invariant under local unitary transformations [4]. Therefore, Eq. (14) implies that we have explicitly determined concurrence for all states from the SLOCC orbit of rank-deficient two-qubit states.
4 Quantum discord
The separability-entanglement paradigm has been replaced by the information-theoretic one as it has become clear that quantum entanglement cannot be regarded as the only kind of non-classical correlations present in quantum systems [4,5,6,7]. Although non-classical correlations beyond quantum entanglement present in a bipartite state \(\rho \) can be quantified by a variety of information-theoretic measures, in this work we consider quantum discord [23] being the first information-theoretic measure of non-classical correlations, and then Einstein–Podolsky–Rosen steering [24, 25].
In quantum information science the quantum mutual information
quantifies the total correlations present in a bipartite quantum state \(\rho \), where \(\rho _{A(B)} = \text {Tr}_{B(A)} (\rho )\) is the state of system A(B). Note here that the quantum mutual information can be rewritten as \(I(\rho ) = S(\rho _{A}) - S(\rho _{A|B})\), where \(S(\rho _{A|B}) = S(\rho ) - S(\rho _{B})\) is the quantum conditional entropy. The fact that the quantum conditional entropy quantifies the ignorance about the system A that remains if a measurement is performed on the system B allows one to find alternative expressions for the quantum conditional entropy and the quantum mutual information.
Note that if the von Neumann projective measurement described by a complete set of rank-one orthogonal projectors \(\{\Pi _{i}^{B}\}\) is performed, then the post-measurement state of the system A is given by
where \(p_{i}^{B} = \text {Tr}[(I \otimes \Pi _{i}^{B}) \rho ]\). The von Neumann entropies \(S(\rho _{A|i})\) weighted by probabilities \(p_{i}^{B}\) yield to an alternative expression for the quantum conditional entropy of the system A when the von Neumann projective measurement is performed on the system B
and thereby the measurement-induced quantum mutual information is defined by
The measurement-independent quantum mutual information
quantifies classical correlations present in a bipartite state \(\rho \) [23, 26], and quantum discord being the difference between the total correlations (22) and the classical correlations (26) is a measure of quantum correlations present in a bipartite state \(\rho \) [23]
Note that in general quantum discord (27) is not symmetric under exchange of the systems A and B, unless \(S(\rho _{A}) = S(\rho _{B})\) [27]. Therefore, in a similar way one can define
where now the von Neumann projective measurement described by a complete set of rank-one orthogonal projectors \(\{\Pi _{i}^{A}\}\) is performed on the system A, and the post-measurement state of the system B is given by
where \(p_{i}^{A} = \text {Tr}[(\Pi _{i}^{A} \otimes I) \rho ]\).
Since in general evaluation of quantum discord is an NP-complete problem [28], the analytic expressions for quantum discord are known only for a limited number of quantum states [5, 6], mostly belonging to certain subclasses of five-parameter two-qubit X states [8,9,10,11,12,13,14,15,16,17,18,19,20]. Although the states from the orbit of rank-deficient states (13) form a three-parameter subclass of two-qubit X states (as the density matrix (13) has only nonzero diagonal and off-diagonal elements), this family of states has not yet been considered explicitly in the literature in the context of quantum discord.
To find a closed analytic formula for quantum discord of the state (13) note first that
and
In the following we determine both quantum discords D(A : B) and D(B : A) because in general they are different, except the case when \(z=0\).
Note that the von Neumann projective measurement being performed on the qubit A(B) is described by the complete set of rank-one projectors of the form \(\Pi _{\pm }^{A(B)} = \frac{1}{2} (I \pm \mathbf {n} \cdot \mathbf {\sigma })\), where \(\mathbf {n} = (n_{1}, n_{2}, n_{3})\) is a real three-dimensional unit vector and \(\mathbf {\sigma } = (\sigma _{1}, \sigma _{2}, \sigma _{3})\).
In [14] with
the general prescription for calculating quantum discord in qubit–qudit extended X states was given. Therefore, applying the procedure given in [14] or performing direct calculation one finds that for the state (13) the quantum conditional entropy of the system A when the von Neumann projective measurement is performed on the system B, i.e., \(\sum _{i} p_{i}^{B} S(\rho _{A|i})\), is given by
while the quantum conditional entropy of the system B when the von Neumann projective measurement is performed on the system A, i.e., \(\sum _{i} p_{i}^{A} S(\rho _{B|i})\), is given by
In the above formulas
and eigenvalues of \(\rho _{A|+}\) and \(\rho _{B|+}\) are given by
respectively.
Therefore, to minimize \(\sum _{i} p_{i}^{A} S(\rho _{B|i})\) and \(\sum _{i} p_{i}^{B} S(\rho _{A|i})\) over the von Neumann projective measurements performed on the system A and B, respectively, for a given state (13), one has to minimize functions \(S_{A}(n_3)\) and \(S_{B}(n_3)\) with respect to \(n_3 \in [-1,1]\) for a given x, y and z fulfilling the inequalities (11).
It can be verified that, depending on the choice of state (13), the minimal value of functions \(S_{A}(n_3)\) and \(S_{B}(n_3)\) can be achieved only for \(n_3=0\) or for \(n_3 = \pm 1\). This coincides with the observation made in [14] that the extreme value is usually attained at the end-point values of the variable \(n_3\). Thus, for \(S_A(n_3)\), as well as for \(S_B(n_3)\), the parameter space described by inequalities (11) is divided into two subregions. In the first subregion the minimal value is achieved for \(n_3=0\), while in the second one it is achieved for \(n_3=\pm 1\). Furthermore, in the case of function \(S_A(n_3)\) the border between these two subregions is described by equation
while in the case of function \(S_B(n_3)\) by equation
Although we determine both quantum discords D(A : B) and D(B : A) for the state (13), we focus our attention only on D(A : B). Thus, in Fig. 2 we present the subregions in the parameter space described by inequalities (11) where minimal values of \(S_B(n_3)\) are achieved for \(n_3=0\) and \(n_3=\pm 1\), respectively.
Subregions in the parameter space described by inequalities (11) where minimal values of the function \(S_B(n_3)\) are achieved for \(n_3=0\) and \(n_3=\pm 1\), respectively. The subregion where the minimal value is achieved for \(n_3=0\) (the subregion I) is more transparent
Note that in the subregions I and II the minimal values of functions \(S_{A}(n_3)\) and \(S_{B}(n_3)\) are given by
Now, substituting Eqs. (30), (31b) and (40) into Eq. (27), and Eqs. (30), (31a) and (39) into Eq. (28) one can determine quantum discords D(A : B) and D(B : A) for the state (13) in the subregions I and II
In Fig. 4 we have depicted D(A : B) at different sections of the parameter space described by inequalities (11), while the sections corresponding to respective plots in Fig. 4 are shown in Fig. 3.
Quantum discord D(A : B) given by Eq. (41) at different sections of the parameter space described by inequalities (11). The corresponding sections are shown in Fig. 3. Here \(r=\sqrt{x^2+z^2}\), dashed line represents the border between the subregions I and II, solid lines are lines of constant quantum discord. Note that in (a) the quantum discord is equal to zero in the whole region
It is known that quantum discord is invariant under local unitary transformations [5]. Therefore, taking into account Eq. (14), we have explicitly determined the both quantum discords D(A : B) and D(B : A) for all states from the SLOCC orbit of rank-deficient two-qubit states.
5 Einstein–Podolsky–Rosen steering
Beside quantum entanglement and quantum discord other aspects of non-classical correlations have been also considered in quantum information science (for review see, e.g., [6, 7]), where one of the most prominent example is Einstein–Podolsky–Rosen steering [24, 25]. The idea of EPR steering is very simple: consider a bipartite quantum state shared by Alice and Bob. Quantum steering refers to the fact that the local measurement performed by Bob on his system can change the reduced state of Alice’s system. Thus, Bob can influence Alice’s system without having access to it, but Alice cannot learn the possible influence unless Bob informs her about the measurement he performed, as well as the measurement outcome.
A particularly intuitive approach to quantum steering is based on quantum steering ellipsoid picture [29]. Let us briefly recall this approach. Following notation used in [29], the matrix R corresponding to a two-qubit state \(\rho \) (compare (2)) can be written as
where \(\mathbf {a}\), \(\mathbf {b}\) are the Bloch vectors of the reduced states \(\rho _A\) and \(\rho _B\), respectively, while T is a \(3\times 3\) matrix. Now, performing on Bob’s side the local measurement \(I\otimes \Pi _{\mathbf {n}}\) where \(\Pi _{\mathbf {n}} = \tfrac{1}{2}(I+\mathbf {n}\cdot \mathbf {\sigma })\) with \(\mathbf {n}^2=1\), one steers the reduced Alice’s state to
where
The state (44) is obtained with probability \(\tfrac{1}{2}(1+\mathbf {b}\cdot \mathbf {n})\). From the geometrical point of view, the end of the vector \(\mathbf {A}\) is located on an ellipsoid \(\mathscr {E}_A\) contained in the Alice’s Bloch sphere and centered at
with orientation and semiaxes lengths \(s_i=\sqrt{q_i}\) given by the eigenvectors and eigenvalues \(q_i\) of the matrix
where \(b^2=\mathbf {b}^2\) (for derivation see [29], we follow the notation used there). The steering ellipsoid encodes a lot of information on the two-qubit state including estimation of quantum discord and quantum entanglement [29, 30].
Notice also that under the transformation (3) performed only on Bob’s side, i.e.,
the steering ellipsoid \(\mathscr {E}_A\) stays unchanged [29]. Furthermore, under local rotation performed on Alice’s side
the steering ellipsoid \(\mathscr {E}_A\) becomes rotated by the orthogonal matrix \(O_1\), corresponding to U in the standard homomorphism \(\mathrm {SU}(2)\rightarrow \mathrm {SO}(3)\).
Using the above formulas we can determine the steering ellipsoid \(\tilde{\mathscr {E}}_A\) corresponding to the state (13) with the R matrix given in (10). After rather straightforward calculation we obtain for the ellipsoid \(\tilde{\mathscr {E}}_A\):
and
Semiaxes of this ellipsoid are given by
and they are oriented in the directions of coordinate axes. Thus, we see that \(\tilde{\mathscr {E}}_A\) is an ellipsoid of revolution (invariant under rotations around z-axis). One can also easily check that for the above ellipsoid it holds
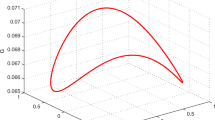
i. e., \(\tilde{\mathscr {E}}_A\) is tangent to the Alice’s Bloch sphere at the north pole. Moreover, in this case \(\tilde{\mathbf {a}}\parallel \tilde{\mathbf {c}}_A\). We have depicted such an ellipsoid in Fig. 5.
Alice’s steering ellipsoid \(\tilde{\mathscr {E}}_A\) described by Eqs. (50–51) [corresponding to the state (13)]. \(\tilde{\mathscr {E}}_A\) is an ellipsoid of revolution (invariant under rotations around z-axis), and it is tangent to the Alice’s Bloch sphere at the north pole and \(\tilde{\mathbf {a}}\parallel \tilde{\mathbf {c}}_A\)
As we have stated previously, Eq. (9) implies that each state on the considered SLOCC orbit of rank-deficient states can be obtained from (13) via local unitary transformation given in (14). Thus, Alice’s steering ellipsoid for arbitrary state from this orbit is obtained from \(\tilde{\mathscr {E}}_A\) by rotation \(O_1\), where \(O_1\) corresponds to \(U_1\) in the standard homomorphism \(\mathrm {SU}(2)\rightarrow \mathrm {SO}(3)\) [compare the considerations after Eqs. (48) and (49)]. The vector \(\mathbf {a}\) undergoes the same rotation. Therefore, we arrived at the following conclusion: for each state from the orbit generated by the state \(\Sigma \) given by Eq. (6), Alice’s steering ellipsoid \(\mathscr {E}_A\) has the following properties:
-
(i)
\(\mathscr {E}_A\) is an ellipsoid of revolution,
-
(ii)
\(\mathscr {E}_A\) is tangent to the Alice’s Bloch sphere,
-
(iii)
Bloch vector of Alice’s reduced state is parallel to a vector determining the center of \(\mathscr {E}_A\) and both of these vectors are parallel to the axis of revolution of the ellipsoid (see Fig. 6).
Alice’s steering ellipsoid \(\mathscr {E}_A\) for a general state from the orbit of rank-deficient states. \(\mathscr {E}_A\) is an ellipsoid of revolution, and it is tangent to the Alice’s Bloch sphere. Moreover, Bloch vector of Alice’s reduced state is parallel to a vector determining the center of \(\mathscr {E}_A\) and both of these vectors are parallel to the axis of revolution of the ellipsoid
Now, we can easily check that the converse statement also holds. That is, if Alice’s steering ellipsoid of certain two-qubit state \(\rho \) fulfills the conditions (i)–(iii) listed above then the state \(\rho \) belongs to the orbit of rank-deficient states generated from the state (13). Indeed, in [29] the explicit formulas for determining the state from the steering ellipsoid are given. One can show that applying these formulas to the ellipsoid fulfilling the conditions (i)–(iii) one obtains a state from the orbit of rank-deficient states.
Note that according to Eq. (41) quantum discord \(D(A:B)=0\) iff \(x=0\) (see also Fig. 4). But Eq. (52) implies that for \(x=0\) the ellipsoid \(\tilde{\mathscr {E}}_A\) reduces to radial line segment. This observation is consistent with the general theorem, proved in [29], stating that for arbitrary two-qubit state quantum discord D(A : B) is equal to zero iff Alice’s steering ellipsoid is a radial line segment.
It is also worth noting that concurrence of the considered state vanishes for \(x=0\) [compare Eq. (19)].
6 Conclusions
We have discussed different aspects of non-classical correlations of states from the SLOCC orbit of rank-deficient two-qubit states. We have extended an introductory analysis of this orbit given in [3]. In particular, we have explicitly calculated entanglement of formation and quantum discord for all states from the considered SLOCC orbit of rank-deficient two-qubit states. We have also completely characterized the EPR steering ellipsoids corresponding to these states and discussed relation between quantum discord and geometrical parameters of these ellipsoids.
References
Avron, J.E., Bisker, G., Kenneth, O.: Visualizing two qubits. J. Math. Phys. 48, 102107 (2007)
Verstraete, F., Dehaene, J., DeMoor, B.: Local filtering operations on two qubits. Phys. Rev. A 64, 010101(R) (2001)
Caban, P., Rembieliński, J., Smoliński, K.A., Walczak, Z.: Classification of two-qubit states. Quantum Inf. Process. 14, 4665 (2015)
Horodecki, R., Horodecki, P., Horodecki, M., Horodecki, K.: Quantum entanglement. Rev. Mod. Phys. 81, 865 (2009)
Modi, K., Brodutch, A., Cable, H., Paterek, T., Vedral, V.: The classical-quantum boundary for correlations: Discord and related measures. Rev. Mod. Phys. 84, 1655 (2012)
Adesso, G., Bromley, T.R., Cianciaruso, M.: Measures and applications of quantum correlations. J. Phys. A 49, 473001 (2016)
Cavalcanti, D., Skrzypczyk, P.: Quantum steering: a review with focus on semidefinite programming. Rep. Prog. Phys. 80, 024001 (2017)
Luo, S.: Quantum discord for two-qubit systems. Phys. Rev. A 77, 042303 (2008)
Ali, M., Rau, A.R.P., Alber, G.: Quantum discord for two-qubit X states. Phys. Rev. A 81, 042105 (2010)
Fanchini, F.F., Werlang, T., Brasil, C.A., Arruda, L.G.E., Caldeira, A.O.: Non-Markovian dynamics of quantum discord. Phys. Rev. A 81, 052107 (2010)
Li, B., Wang, Z.X., Fei, S.M.: Quantum discord and geometry for a class of two-qubit states. Phys. Rev. A 83, 022321 (2011)
Chen, Q., Zhang, C., Yu, S., Yi, X.X., Oh, C.H.: Quantum discord of two-qubit X states. Phys. Rev. A 84, 042313 (2011)
Shi, M., Yang, W., Jiang, F., Du, J.: Quantum discord of two-qubit rank-2 states. J. Phys. A 44, 415304 (2011)
Vinjanampathy, S., Rau, A.R.P.: Quantum discord for qubit-qudit systems. J. Phys. A 45, 095303 (2012)
Huang, Y.: Quantum discord for two-qubit X states: analytical formula with very small worst-case error. Phys. Rev. A 88, 014302 (2013)
Maldonado-Trapp, A., Hu, A., Roa, L.: Analytical solutions and criteria for the quantum discord of two-qubit X-states. Quantum Inf. Process. 14, 1947 (2015)
Wu, X., Zhou, T.: Quantum discord for the general two-qubit case. Quantum Inf. Process. 14, 1959 (2015)
Yurischev, M.A.: On the quantum discord of general X states. Quantum Inf. Process. 14, 3399 (2015)
Jing, N., Yu, B.: Quantum discord of X-states as optimization of a one variable function. J. Phys. A 49, 385302 (2016)
Rau, A.R.P.: Calculation of quantum discord in arbitrary dimensions, especially for X- and other specialized states (2017). ArXiv: 1701.05922
Bennett, C.H., DiVincenzo, D.P., Smolin, J.A., Wootters, W.K.: Mixed-state entanglement and quantum error correction. Phys. Rev. A 54, 3824 (1996)
Wootters, W.K.: Entanglement of formation of an arbitrary state of two qubits. Phys. Rev. Lett 80, 2245 (1998)
Olivier, H., Zurek, W.H.: Quantum discord: a measure of the quantumness of correlations. Phys. Rev. Lett. 88, 017901 (2001)
Schrödinger, E.: Discussion of probability relations between separated systems. Proc. Camb. Phil. Soc. 31, 555 (1935)
Wiseman, H.M., Jones, S.J., Doherty, A.C.: Steering, entanglement, nonlocality, and Einstein–Podolsky–Rosen paradox. Phys. Rev. Lett. 98, 140402 (2007)
Henderson, L., Vedral, V.: Classical, quantum and total correlations. J. Phys. A 34, 6899 (2001)
Vedral, V.: Classical correlations and entanglement in quantum measurements. Phys. Rev. Lett. 90, 050401 (2003)
Huang, Y.: Computing quantum discord is NP-complete. New J. Phys. 16, 033027 (2014)
Jevtic, S., Pusey, M., Jennings, D., Rudolph, T.: Quantum steering ellipsoids. Phys. Rev. Lett. 113, 020402 (2014)
Milne, A., Jevtic, S., Jennings, D., Wiseman, H., Rudolph, T.: Quantum steering ellipsoids, extremal physical states and monogamy. New J. Phys. 16, 083017 (2014)
Author information
Authors and Affiliations
Corresponding author
Additional information
This work has been supported by the Polish National Science Centre under the contract 2014/15/B/ST2/00117 and by the University of Lodz.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Caban, P., Rembieliński, J., Smoliński, K.A. et al. SLOCC orbit of rank-deficient two-qubit states: quantum entanglement, quantum discord and EPR steering. Quantum Inf Process 16, 178 (2017). https://doi.org/10.1007/s11128-017-1626-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11128-017-1626-7