Abstract
In this work, we present a method of decomposition of arbitrary unitary matrix \(U\in \mathbf {U}(2^k)\) into a product of single-qubit negator and controlled-\(\sqrt{\text{ NOT }}\) gates. Since the product results with negator matrix, which can be treated as complex analogue of bistochastic matrix, our method can be seen as complex analogue of Sinkhorn–Knopp algorithm, where diagonal matrices are replaced by adding and removing an one-qubit ancilla. The decomposition can be found constructively, and resulting circuit consists of \(O(4^k)\) entangling gates, which is proved to be optimal. An example of such transformation is presented.
Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.Avoid common mistakes on your manuscript.
1 Introduction
Scaling a real matrix O with non-negative entries means finding diagonal matrices \(D_1, D_2\) such that \(B=D_1OD_2\) is bistochastic. Sinkhorn theorem presents a necessary and sufficient condition for existence of the decomposition of a matrix. Moreover, the iterative Sinkhorn–Knopp algorithm finds the bistochastic matrix B [1]. Such decomposition can be used for ranking web pages [2], preconditioning sparse matrices [3] and understanding traffic circulation [4].
Since unitary matrices are complex analogue of orthogonal matrices, it is natural to ask whether there exist a counterpart of Sinkhorn theorem for them. De Vos and De Baerdemacker considered whether it is possible, that for arbitrary unitary matrix \(U\in \mathbf {U}(n)\), there exist two unitary diagonal matrices \(U_1, U_2\) such, that matrix \(U_1UU_2\) has all lines sums equal to 1. Such decomposition exists for arbitrary unitary matrix, and an algorithm for finding it approximately was presented [5]. Matrices called negators were treated as quantum counterpart of bistochastic matrices and form a group \(\mathbf {XU}(n)\) under multiplication. Idel and Wolf propose an application of the quantum scaling in quantum optics [6].
Algorithm converges for arbitrary unitary matrix U [7]. Similar decomposition of unitary matrices \(U\in \mathbf {U}(2m)\) called bZbXbZ decomposition was presented [8]. They show that there always exist matrices \(A, B, C, D\in \mathbf {U}(m)\) such that
where \({I}\) is identity matrix. Matrix in the middle is a block-negator matrix (which is also a negator matrix), while left and right matrices are block diagonal matrices. In [9], an algorithm of finding such decomposition was presented.
Group \(\mathbf {XU}(2^n)\) is isomorphic to \(\mathbf { U}(2^n-1)\) and can be generated by single-qubit negator and controlled-\(\sqrt{\text{ NOT }}\) gates [10]. However, the proof is non-constructive since a decomposition designed for generating random matrices was used [11]. Although it is proved that it exists for any unitary matrix, obtaining such a decomposition is a very complex task. Therefore, another approach is needed for efficient decomposition procedure.
In this article, using similar method presented by de Vos and de Baerdemacker [10], we demonstrate an implementation of arbitrary k-qubit unitary operation using one-qubit ancilla with controlled-\( \sqrt{\text {NOT}}\) and single-qubit negator gates. Since product of these basic negator gates is still a negator matrix, our result can be seen as quantum analogue of scaling matrix. More precisely, we prove that for arbitrary matrix \(U\in \mathbf {U}(2^k)\), which is performed on system \(\mathcal {H}\), there exist a negator \(N\in \mathbf {XU}(2^{k+1})\) such that for arbitrary state \(| \psi \rangle \in \mathcal {H}\), we have
Here, \(\Phi \) denotes the operation of extending the system with an ancilla register in \(| - \rangle \) state and \(\Psi \) denotes partial trace over the ancilla system. Since after performing operations \(\Phi \) and N the state is of the form \(| - \rangle \otimes U| \psi \rangle \), the partial trace is simply removing the ancilla system giving a pure state \(U| \psi \rangle \). We describe an efficient algorithm that for given U returns explicit and exact form of N with decomposition into a sequence of single-qubit negator and controlled-\(\sqrt{\text {NOT}}\) gates only in contrast to results of de Vos and de Baerdemacker [9, 10].
In Sect. 2, we recall basic facts. In Sect. 3, we show how to perform such transformation efficiently and demonstrate the cost in terms of controlled-\( \sqrt{\text {NOT}}\) gates.
To illustrate the transformation method, a transformation of Grover’s search algorithm is presented step by step in Sect. 4.
2 Basic facts
Negator gates of dimension 2 were introduced by de Vos and de Baerdemacker [10] as unitary matrices \(N\in \mathbf {U}(2)\) which are also a convex combination of identity matrix and NOT gate. Simple calculation shows that they are of the form
where \(\theta \in [0,2\pi )\). Negators form a subgroup of single-qubit unitary operations, i.e., \(N(\phi )N(\psi )=N(\phi +\psi )\) for any values of \(\phi \) and \(\psi \). In the following, we will also use a 2-qubit negator operation controlled-\(\sqrt{\text {NOT}}\) gate (which is also controlled-\(N(\frac{\pi }{2})\) gate)
As these gates are used as basic operators, we will use a simplified notation in circuit, respectively

These two kinds of unitary matrices will be called NCN gates (Negators-Controlled-Negator).
In Sect. 3, decomposition of single-qubit unitary gates will be needed. Every unitary matrix \(U\in \mathbf {U}(2)\) can be presented as a product of global phase, two z-rotators and one y-rotator [12]
Since global phase is not measurable, we can simplify this representation without loss of information
where ‘\(\cong \)’ means equality up to a global phase. The same applies in the case of global phase change on one of the registers of a bigger system
Using these two facts, we can say that in any situation, we can ignore global phase change on any register.
While it may lead to a conclusion that our transformation is mainly applied to group \(\mathbf {SU}(n)\), we decided to stay with the unitary matrices formalism, since negator gates are not special unitary matrices. The result may be written using the special matrices; however, then the negators gates column and row sums will equal \(e^{i\theta }\) in general.
3 Circuit transformation method
In this section, we provide complete description of the transformation method. We recall a sketch of a proof of universality theorem between quantum gates and negator gates from the work of de Vos and de Baerdemacker [10]. Next, we present transformation method of arbitrary single-qubit gate into NCN product. Then, we provide a method of decomposition for arbitrary k-qubit circuit, based on the single-qubit case. Finally, we analyze the cost of presented transformation.
3.1 Universality theorem
De Vos and de Baerdemacker proved a universality theorem: Group \(\mathbf {XU}(2^k)\) generated by negators and controlled-\( \sqrt{\text {NOT}}\) is isomorphic to \(\mathbf {U}(2^k-1)\) [10]. The proof consists of several steps:
-
1.
Every matrix \(U\in \mathbf {U}(2^k-1)\) can be decomposed into a product of m gates \(U_1U_2\cdots U_m\), where matrices \(U_i\in \mathbf {U}(2^k-1)\) are of some special forms [11].
-
2.
Group \(\mathbf {U}(2^k-1)\) is isomorphic to group
$$\begin{aligned} \mathbf {^{1}U}(2^k) = \left\{ \begin{bmatrix} 1&\quad \mathbf 0 ^T\\ \mathbf 0&\quad U\end{bmatrix}: U\in \mathbf {U}(2^k-1) \right\} , \end{aligned}$$(6)because of the isomorphism \(h: \mathbf {U}(2^k-1) \rightarrow \mathbf {^{1}U}(2^k) \)
$$\begin{aligned} h(U) = \begin{bmatrix} 1&\quad \mathbf 0 \\ \mathbf 0&\quad U \end{bmatrix}. \end{aligned}$$(7) -
3.
Function \(f : \mathbf {^{1}U}(2^k) \rightarrow \mathbf {XU}(2^k)\) of the form \(f(U)=(H\otimes {I}_{2^k})U(H\otimes {I}_{2^k})\) is an isomorphism.
-
4.
Decomposition of every \(f(h(U_i))\) into a product of NCN gates is possible, where \(U_i\) comes from point 1.
The proof used the decomposition presented in the work of Poźniak et al. [11], because it is proven that the decomposition exists for any unitary matrix. However, obtaining such decomposition is a very complex task. Therefore, we need to choose a different decomposition in order to find an efficient decomposition procedure.
Obviously, group \(\mathbf {U}(2^k)\) is isomorphic to some subgroup of \(\mathbf {XU}(2^{k+1})\). In other words, with ancilla (one additional qubit), every unitary matrix can be replaced with a sequence of NCN gates. For our purpose, we choose function \(g:\mathbf {U}(2^k) \rightarrow \mathbf {XU}(2^{k+1})\)
Using the function g, every gate U changes into controlled-U. Using circuit notation, we can present this fact as

Note that if we assume that the first qubit is set to \(| - \rangle \), the control qubit does not influence the result (the condition is always ‘true’).
3.2 Single-qubit gate transformation
Now, we aim at decomposition of arbitrary single-qubit gate into NCN gates. With Eq. (4) for any \((U \in {\mathbf {U}}(2))\), there exist real parameters \(\alpha ,\beta ,\gamma \) such that
Therefore, after applying function g, we have

We change the rotators with neighboring Hadamard gates into NCN gates as shown in Fig. 1

Let us note that the symbols of controlled-NOT, controlled-\(\sqrt{\text {NOT}}^\dagger \) and controlled-negator used in the decomposed circuit do not mean that these gates cannot be transformed. We use these symbols as a simplified notation for its decomposition with use of controlled-\(\sqrt{\text {NOT}}\) gates as shown in Fig. 2.
Decomposition of controlled-y-rotator, controlled-z-rotator and Toffoli gate. Decompositions use the simplified notation from Fig. 2
Decomposition of controlled-NOT, controlled-\( \sqrt{\text {NOT}}^\dagger \) gates and controlled-negator [10]
3.3 General transformation method
Now, we consider transformation of arbitrary k-qubit circuit. Let us assume that we have a circuit which consists of unitary operation \( (U \in {\mathbf {U}}(2^k))\), generalized measurement \(\mathbf M = \{M_a\in {L}(\mathbb {C}^{2^k}):a\in \Sigma \}\), where \(\Sigma \) is a set of classical outputs of measurement, and starting state \(| \phi _0 \rangle \)

In order to construct a decomposition of unitary U into a sequence of negator gates, we begin with obtaining a decomposition of U into controlled-NOT and single-qubit gates

here denoted by a sequence of gates \(U=V_m\cdots V_1\). Contrary to the decomposition presented in the work of Poźniak, Życzkowski and Kuś, there exist efficient methods for constructing such circuit [13]. Next, we need to add an additional qubit, transform \(V_i\) gates into controlled-\(V_i\) gates and add Hadamard gates as below (since \(HH={I}\))

Let us note that product \(H\cdot \text {controlled-}V_j\cdot H\) is an image of homomorphism presented in Eq. (8) on \(V_j\). Next, we replace the product with the sequence of NCN gates (here denoted by \(\mathbf N_j\)) as in previous subsection (if \(V_j\) is controlled-NOT, then we choose Toffoli gate transformation from Fig. 1)

For the sake of simplicity, we may change the starting state and resulting state on the first wire

Now, we have an equivalent circuit which consists of negators and controlled-\( \sqrt{\text {NOT}}\) gates only.
3.4 Transformation cost
Now, we consider upper bound of cost of decomposition into negator circuit. Two kinds will be discussed: memory complexity and number of single- and two-qubit gates. In the first case for arbitrary k-qubit circuit transformation requires one additional qubit.
Let \(c_{\text {CNOT}}(k) \) and \(c_s(k)\) denote upper bound of the number of, respectively, controlled-NOT and single-qubit gates needed for the implementation of an arbitrary k-qubit circuit. Using the operation presented above, we need \(17c_{\text {CNOT}}(k) + 64c_s(k)\) controlled-\( \sqrt{\text {NOT}}\) gates and \(11c_{\text {CNOT}}(k)+34c_s(k)\) negators to implement an equivalent circuit (up to global phase).
Any circuit which consists of controlled-NOT and single-qubit gates can be simplified in such a way that \(c_s(k)\le 2c_{\text {CNOT}}(k)+k\). This estimation is based on the worst case, when there are two single-qubit gates between every controlled-NOT gate. Taking this into account, we can express the previous result in terms of \(c_{\text {CNOT}}\) only, because only \(17c_{\text {CNOT}}(k)+ 64c_s(k) \le 145 c_{\text {CNOT}}(k)+64k\) controlled-\( \sqrt{\text {NOT}}\) gates are needed. In fact, if \(c_{\text {CNOT}} = O(4^k)\), then so is the number of controlled-\( \sqrt{\text {NOT}}\) gates.
4 Step-by-step transformation example
To illustrate the introduced decomposition, we will present Grover’s algorithm for \(k=2\) qubits as NCN circuit. The original circuit for this algorithm is presented in Fig. 3, where \(\omega \) denotes the searched state.
Original Grover’s search algorithm circuit in case \(k=2\). G is Grover diffusion operator, \(U_\omega \) is quantum black box and we perform measurement M. Algorithm comes from [14]
Grover’s search algorithm decomposition. Unnecessary Hadamard gates have already been removed (a) \(| 1 \rangle \) changes into \(| - \rangle \); (b) measurement \(\mathbf {M}\) does not change, on first wire we end with \(| - \rangle \) state; (c) subcircuit simplification; (d) subcircuit transforming into NCN gates. Any other transformation left can be done similarly, except the \(U_\omega \) case
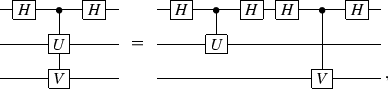
As in the previous section, we will add one qubit, change every H and G gate into controlled-H and controlled-G, respectively, and add Hadamard gates on the ancilla register. Former steps of the decomposition are explicitly presented in Fig. 4. The following facts were used
-
the decomposition of Hadamard gate is \(H\cong R_z(\pi )R_y(\frac{\pi }{2})R_z(0)=R_z(\pi )R_y(\frac{\pi }{2})\),
-
the decomposition of NOT gate is \(\text{ NOT }\cong R_z(\pi )R_y(\pi )R_z(0)=R_z(\pi )R_y(\pi )\),
-
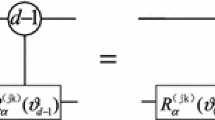
for any \((U, V \in {\mathbf {U}}(2))\), we have
-
Grover’s diffusion operator can be decomposed in the following way

Decomposition of \(U_\omega \) depends strictly on the value of \(\omega \); therefore, it is not presented in the example. The full decomposition is presented in Fig. 4.
5 Concluding remarks
In the presented work, we provide a constructive method of scaling arbitrary unitary matrices \(U\in \mathbf {U}(2^k)\). More precisely, we proved that for arbitrary unitary matrix \(U\in \mathbf {U}(2^k)\), there exists unitary negator matrix \(N\in \mathbf {XU}(2^{k+1})\) such that for arbitrary state \(| \psi \rangle \), we have
Here, \(\Phi \) denotes the operation of extending the system with an ancilla register in \(| - \rangle \) state and \(\Psi \) denotes partial trace over the ancilla system. We described efficient algorithm of decomposing N into product of single-qubit negator and controlled-\(\sqrt{\text{ NOT }}\) gates. Our decomposition consists of \(O(4^k)\) entangling gates which is proved to be optimal and needs one-qubit ancilla.
Our result can be seen as complex analogue of Sinkhorn–Knopp algorithm, which is known to have wide applications. The result is in contrast to the previous results [10], which could be only used to prove the existence of such decomposition. Moreover, our transformation is exact and can be found constructively. In contrast to [9], our transformation consists only of negator gates. The main difference is that transformation needs one-qubit ancilla.
References
Sinkhorn, R., Knopp, P.: Concerning nonnegative matrices and doubly stochastic matrices. Pac. J. Math. 21(2), 343–348 (1967)
Knight, P.A.: The Sinkhorn–Knopp algorithm: convergence and applications. SIAM J. Matrix Anal. Appl. 30(1), 261–275 (2008)
Livne, O.E., Golub, G.H.: Scaling by binormalization. Numer. Algorithms 35(1), 97–120 (2004)
Knight, P.A., Ruiz, D.: A fast algorithm for matrix balancing. IMA J. Numer Anal. 33(3), 1029–1047 (2013)
De Vos, A., De Baerdemacker, S.: Scaling a unitary matrix. Open Syst. Inf. Dyn. 21(04), 1450013 (2014)
Idel, M., Wolf, M.M.: Sinkhorn normal form for unitary matrices. Linear Algebra Appl. 471, 76–84 (2015)
De Vos, A., De Baerdemacker, S.: On two subgroups of U(n), useful for quantum computing. In: Journal of Physics: Conference Series, vol. 597, p. 012030. IOP Publishing (2015)
Führ, H., Rzeszotnik, Z.: On biunimodular vectors for unitary matrices. Linear Algebra Appl. 484, 86–129 (2015)
De Vos, A., De Baerdemacker, S.: Sinkhorn-based synthesis of an arbitrary quantum circuit. arXiv preprint arXiv:1512.07240 (2015)
De Vos, A., De Baerdemacker, S.: The NEGATOR as a basic building block for quantum circuits. Open Syst. Inf. Dyn. 20(01), 1350004 (2013)
Poźniak, M., Życzkowski, K., Kuś, M.: Composed ensembles of random unitary matrices. J. Phys. A Math. Gen. 31(3), 1059 (1998)
Nielsen, M.A., Chuang, I.L.: Quantum Computation and Quantum Information. Cambridge University Press, Cambridge (2010)
Möttönen, M., Vartiainen, J.J., Bergholm, V., Salomaa, M.M.: Quantum circuits for general multiqubit gates. Phys. Rev. Lett. 93(13), 130502 (2004)
Lavor, C., Manssur, L., Portugal, R.: Grover’s algorithm: quantum database search. arXiv preprint arXiv:quantum-ph/0301079 (2008)
Acknowledgments
The work was supported by the Polish National Science Center: A. Glos under the research Project Number DEC-2011/03/D/ST6/00413, P. Sadowski under the research Project Number 2013/11/N/ST6/03030.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Glos, A., Sadowski, P. Constructive quantum scaling of unitary matrices. Quantum Inf Process 15, 5145–5154 (2016). https://doi.org/10.1007/s11128-016-1448-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11128-016-1448-z