Abstract
This paper presents a quantum version of the Monty Hall problem based upon the quantum inferring acausal structures, which can be identified with generalization of Bayesian networks. Considered structures are expressed in formalism of quantum information theory, where density operators are identified with quantum generalization of probability distributions. Conditional relations between quantum counterpart of random variables are described by quantum conditional operators. Presented quantum inferring structures are used to construct a model inspired by scenario of well-known Monty Hall game, where we show the differences between classical and quantum Bayesian reasoning.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Probability theory has a lot of applications in many areas of science and engineering. In particular probabilistic modelling has strong impact in development of artificial intelligence, providing tools for knowledge representation, knowledge management and reasoning [1]. Many problems related to computer vision, speech recognition, extraction of information or diagnosis of diseases can be modelled by probabilistic graphical models which structures describe conditional dependencies between random variables [2]. This kind of models is indirectly related with Bayesian reasoning, which is a method of statistical inference based on Bayes’ theorem. Bayesian reasoning gives a possibility of decision making under uncertainty, which leads to updating of beliefs in light of new information. The Bayesian approach to reasoning can be used in the well-known Monty Hall problem, which can be considered as a counterintuitive two-step decision problem. The probabilistic analysis of this problem develops an intuition about updating a prior belief as new evidence becomes, which gives a deeper understanding of Bayesian methods used in the artificial intelligence. Consequently, we use the Monty Hall problem as an illustration of quantum Bayesian reasoning based on quantum information theory and quantum inferring acausal structures.
Cerf and Adami [3, 4] introduced a quantum conditional amplitude operator as an extension of conditional probability distribution. This approach allowed to complement of relationship between Shannon conditional entropy and von Neumann conditional entropy. In this context, quantum conditional operators are considered as a generalization of classical conditional probability distributions.
Definition of conditional states was extended in the context of quantum channel by Leifer [5]. He connected classical conditional probabilities and bipartite density operators with variant of well-known Jamiołkowski isomorphism. Subsequently, Leifer with Spekkens [6, 7] presented formalism of quantum inferring structures based on quantum conditional states. They described two cases of structures: causal (one system at two times) and acausal (two systems at a single time).
Quantum inferring structures based on quantum probability theory allow for a novel causal interpretation and generalization of the results of quantum mechanics. Recently, in many scientific disciplines, the inferring causal and acausal relations from observed correlations are relevant problems. The framework of quantum conditional operators was used by Brunker [8] to investigate quantum causality. The author assumed, that indefinite causal structures could provide methodological tools in quantum theories of gravity. In [9], the authors used the quantum conditional operators as causal maps to consideration of the problem of causal inference for quantum variables. They introduced the concept of causal tomography, which unifies conventional quantum tomography schemes and provides a complete solution of the causal inference problem using a quantum analogue of a randomized trial.
2 Quantum conditional operators
In [6, 7], Leifer and Spekkens introduced a definition of elementary region as a quantum system at fixed point in time. By them, the relations between regions were described in two contexts. In the first case, elementary regions A, B are causally related. It means that there is casual inference from A to B, e.g. it can be a single system at two times. In the second case, the A, B are acausally related, it means that elementary regions represent two distinct systems at a fixed time. In this paper, the emphasis is put on the elementary regions acausally related.
Let \(\mathcal {L}(\mathcal {H})\) be the set of linear operators on complex Hilbert space \(\mathcal {H}\). The classical probability distribution can be generalized by density operator \(\rho _A\in \mathcal {L}{(\mathcal {H}_A)}\) (\(\rho _A=\rho ^\dagger \), \(\rho _A\ge 0\), \(\mathrm {Tr}(\rho _A)=1\)). The analogue of joint probability distribution for quantum systems AB is a density operator \(\rho _{AB}\in \mathcal {L}(\mathcal {H}_{A}\otimes \mathcal {H}_{B})\). Moreover, the analogue of marginalization over a joint distribution is the partial trace of quantum state, i.e. \(\rho _A=\mathrm {Tr}_B(\rho _{AB})\). An acausal conditional state [10] for B given A is a positive operator \(\rho _{B|A}\in \mathcal {L}(\mathcal {H}_{AB})\) that satisfies
where \(\mathrm {I}_A\) is the identity operator from \(\mathcal {L}(\mathcal {H}_{A})\). Conditional operators can be defined by the usage of \(\star \) product [6], where \(\star : \mathcal {L}(\mathcal {H})\rightarrow \mathcal {L}(\mathcal {H})\) and
for \(\sigma _A,\sigma _B\in \mathcal {L}(\mathcal {H})\). Hence, the conditional operator is expressed as
where \((\cdot )^{-1}\) denotes the Moore-Penrose pseudoinverse. Similarly as in classical probability theory, the following equation holds true
The occurrence of the event \(| b \rangle \langle b |\) on the subsystem B causes the transformation of \(\rho _{AB}\) into
The comma in index of \(\rho _{A,B=b}\) is used only for readability. The marginal probability distribution acting on subsystem A after the transformation is given as
Summing up, given an initial \(\rho _A\) one can compute an updated \(\rho _{A}^{B=b}\) by first computing \(\rho _{AB}\) using \(\rho _{B|A}\) and Eq. (4) and the following Eqs. (5) and (6).
3 Inferring acausal structures
The graphical model is defined as a probabilistic model for which the conditional dependence between random variables are defined by a graph. It can be used for statistical inference under a set of random variables. Replacing classical random variables by their quantum counterparts gives a class of quantum structures, which can be used for inferring amongst a set of quantum states.
Let us consider operators \(\rho _{B|A}\in \mathcal {L}(\mathcal {H}_{AB})\) and \(\rho _A\in \mathcal {L}(\mathcal {H}_{A})\). The state \(\rho _{B|A}\) characterizes conditional relationship between systems A and B. In this case, the state of system B can be expressed as
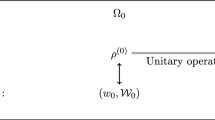
In classical probability theory, this formula is called the law of total probability. Figure 1 illustrates graphical interpretation of reasoning over \(\rho _{B|A}\) and \(\rho _A\), what can be considered as simple Bayesian network.
The conditional relationship associated with graphical structure of the network allows to rewrite the joint state of A and B as follows
Consider the structure given in Fig. 2 described by state \(\rho _A\) and conditional states \(\rho _{B|A}\) and \(\rho _{C|A}\). To obtain joint state of A and B or A and C, we use formulas
The join state of A, B and C can be obtained by using the formula
Acausal relations between quantum states can be described by quantum Bayesian networks [10] defined as a pair \((\mathbb {G}, \mathbb {D})\) where
-
\(\mathbb {G}=(\mathbf{X}, \mathbf{E})\) is a directed acyclic graph, where each vertex \(X_i\in \mathbf{X}\) is associated to a quantum system with space \(\mathcal {L}(\mathcal {H}_{i})\).
-
\(\mathbb {D}=\{\rho _{{X_i}|\Pi _{X_i}}:1\le i \le N\}\) is the set of the conditional operators between node \(X_i\) and its parents \(\Pi _{X_i}\).
The quantum Bayesian network can be interpreted as a quantum system associated with space \(\mathcal {L}(\mathcal {H}_{1}\otimes \cdots \otimes \mathcal {H}_{N})\). The conditional independence relationship associated with a graphical structure of Bayesian network allows to rewrite the generalized joint distribution of \(\mathbf{X}\) as follows
where \(\big (\bigstar \big )_{i=1}^N \rho _{{X_i}|\Pi _{X_i}}=\rho _{{X_1}|\Pi _{X_1}} \star \cdots \star \rho _{{X_N}|\Pi _{\mathcal {X}_N}}\). In Eq. (11), each factor \(\rho _{{X_i}|\Pi _{X_i}}\) should be expressed as \(\mathrm {I}\otimes \rho _{{X_i}|\Pi _{X_i}}\otimes \mathrm {I}\), but we drop identity operators and Kronecker products for simplicity.
Leifer and Poulin [10] emphasize the fact, that quantum graphical models have significant applications in quantum error corrections and the simulation of many-body quantum systems.
4 Acausal structure in Monty Hall game
In this section, we present the usage of the quantum inferring structures in modelling a quantum system inspired by a well-known Monty Hall problem based on the popular game show Let’s Make a Deal. The problem was first described by Selvin in [11, 12]. Subsequently, the Monty Hall problem has been considered as a subject of many investigations, i.e. this issue is modelled through a formal application of Bayes’ rule [13, 14]. In [15], the Monty Hall game was generalized to the quantum domain. The paper shows that fair zero-sum game can be realized if the quantum measurement strategy is permitted. A more detailed discussion about quantum Monty Hall can be found at [16, 17], where authors consider many scenarios. In [18, 19], the effect of decoherence on results of the game was analysed.
Classical scenario of the Monty Hall game is as follows. There are two participants of the game: host and player. Assume that three doors labelled 0, 1 and 2 are closed. A car is behind one of the doors, while the goats are behind the other two. The host knows which of the three doors hides the car, but the player does not know where the main prize is hidden. The player picks a door and subsequently, the host opens one of the remaining doors, revealing a goat. Finally, the player selects one of the remaining doors. The question is: should the player stick to his/her original choice or pick the other door?
4.1 Classical case
The Monty Hall game can be modelled as a simple Bayesian network with three random variables \(X_A,X_B,X_C\), whose graph is presented in Fig. 3. The variable \(X_A\) represents the player’s information about which door contains the prize. Initially, the player do not have any knowledge about this, and thus we assume that probability distribution P(X) is uniform and is given by (1 / 3, 1 / 3, 1 / 3). The \(X_B\) describes the first choice of the player and we also assume that the probability distribution of \(X_B\) is (1 / 3, 1 / 3, 1 / 3). The random variable \(X_C\) depends on the \(X_A,X_B\) and describes selected door by the host. The probability distribution \(P(X_C|X_A,X_B)\) is given in Table 1.
Now, given the computational basis \(\{| ijk \rangle \}\) for \(0\le i,j,k\le 2\), we create an analogous quantum Bayesian network, where the random distributions \(P(X_A)\), \(P(X_B)\), \(P(X_C|X_A,X_B)\) are replaced by
Next, we determine
which describes the state of composite quantum system ABC identified with graph in Fig. 3. Note that \(\star \) product is non-associative in general but when the factors in the product commute it is associative. Thus, taking into account given diagonal matrices \(\rho _A\), \(\rho _B\) and \(\rho _{C|AB}\), obtained state (13) can be expressed in form \({\rho _{ABC} =\frac{1}{9}\rho _{C|AB}}\).
Let us assume that the player chooses b-th door, where doors are labelled by 0, 1 and 2. Hence, we assume that measurement labelled by b is performed on subsystem B and the state \(\rho _{AB}\) is transformed into
Afterwards, the host opens the c-th door. Similarly, the measurement labelled by c is performed on subsystem C and we get
After performed measurements, state of subsystem A is given by
State \(\rho _A\) has encoded a priori information about position of prize, which is updated under observed evidences. Thus, state \(\rho _A^{B= b,C= c}\) represents updated player’s knowledge about doors which can contain the prize, with assumption that firstly the player chose door b and the host opened door c.
Since, the host knows where the car is hidden, we assume that \(b \not = c\). Suppose, that player chooses 0-th door and the host opens 1-st door. Hence, using Eqs. (13)-(16) we get
The solution obtained above corresponds to optimal player’s strategy in classical Monty Hall game. According to the probability distribution (17), the player should change his/her first decision. In general, for any \(a,b,c\in \{0,1,2\}\) such that \(a \not = b\), \(b \not = c\) and \(a \not = c\) equality \(\langle a | \rho _A^{B= b,C= c} | a \rangle =\frac{2}{3}\) holds. It means that, if the player changes his/her first choice, then the probability of winning the car is \(\frac{2}{3}\) .
4.2 Non-classical case
In the non-classical case, we assume, that systems A describing the prize position and B describing the first choice of the player are entangled. The state \(\rho _{AB}\) must satisfy following conditions:
-
1.
\(\langle k |\mathrm {Tr}_A (\rho _{AB})| k \rangle = \langle k |\mathrm {Tr}_B (\rho _{AB}) | k \rangle = \frac{1}{3}\) for \(k\in \{0,1,2\}\),
-
2.
\(\langle c |\rho _{A}^{B=b,C=c} | c \rangle =0\) for all \(b,c\in \{0,1,2\}\) such that \(b\ne c\).
The second condition implies, that the host cannot open the door with the prize behind it. In our considerations, the behaviour of player and host is similar like in classical case. It means that the player do not have access to quantum strategies. However, we assume that quantum effects occur between position of prize and player’s first decision but participants of the game don’t know about it.
Suppose that system is in state
After tracing-out this state we get
Thus \(\tilde{\rho }_A\) and \(\tilde{\rho }_B\) are maximally mixed and given reduced states correspond to the states from the previous section. Since states of systems A and B are entangled, we describe a inferring structure of this scenario according to Fig. 4.
Let us notice, that \(\tilde{\rho }_{AB}\) is a pure state, hence the equations \(\tilde{\rho }_{AB}^{\frac{1}{2}}=\tilde{\rho }_{AB}\) and \(\tilde{\rho }_{ABC}=\rho _{C|AB}\star (\tilde{\rho }_{AB}\otimes \mathrm {I}_C)= (\tilde{\rho }_{AB}\otimes \mathrm {I}_C)\rho _{C|AB}(\tilde{\rho }_{AB}\otimes \mathrm {I}_C)\) hold true. Using the same state \(\rho _{C|AB}\) as in (12) and proceeding similarly like in (13)–(17) we get for \(b=0\) and \(c=1\) following results
Note that \(\langle 0 |\tilde{\rho }_A^{B= 0,C= 1}| 0 \rangle =1\). In general, the equality \(\langle b | \tilde{\rho }_A^{B= b,C= c} | b \rangle =1\) holds for any \(b,c\in \{0,1,2\}\) such that \(b\ne c\). It means, that if player don’t change his/her first choice, then he/she always win a prize.
Similar case in quantum Monty Hall game was considered by Flitney and Abbott in [17], where the authors assumed that the players are permitted to select quantum strategies. As a result, if both players have access to quantum strategies, then there is a Nash equilibrium amongst mixed quantum strategies. We will show that there exist initial quantum state \(\rho _{AB}\) for which the game is fair without permission to quantum strategies of the players.
Now consider another quantum state
Here we achieved opposite results. For any \(a,b,c\in \{0,1,2\}\) such that \( a\ne b\), \(b\ne c\) and \(a\ne c\) we have \(\langle a | \hat{\rho }_A^{B= b,C= c} | a \rangle =1\). Hence, in this case, if the player behaves like in classical scenario, then his/her probability of winning is equal to 1.
Subsequently, let us consider convex combination of \(\tilde{\rho }_{AB}\) and \(\hat{\rho }_{AB}\)
For all \(\lambda \in [0,1]\) the state \(\rho _{AB}\) satisfies conditions specified at the beginning of this section. The probability of winning the prize by the player, under assumption that the player’s first decision remains unchanged, is shown in Fig. 5. Moreover, for \(\lambda =0.6\) and \(a,b,c\in \{0,1,2\}\), where \( a\ne b\) and \(b\ne c\) we get \(\langle a |\bar{\rho }_A^{B= b,C= c} | a \rangle =\frac{1}{2}\). Thus, the player and the host win with equal probability and the game is fair.
Last example is very unintuitive. Consider following state
As a result we have
Above results show that the player shouldn’t change his first decision b only if the \(c=(b+2)(\!\!\mod 3)\)-th door has been opened. However, the host can minimize the player’s chance to \(\frac{3}{4}\) by opening the \(c=(b+1)(\!\!\mod 3)\)-th door.
5 Conclusions
In this paper, we showed the approach based on quantum inferring acausal structures to reasoning in quantum information theory. Considered structures can be identified with a generalization of Bayesian networks, which concept is based on investigations of Leifer and Poulin [10]. Proposed methodology was used to construct quantum model inspired by scenario of Monty Hall game.
The model was investigated both in classical and quantum case, whereby we showed that the entanglement of quantum states has influence on results of reasoning. We show that there exist quantum state for which Monty Hall game is fair under assumption that the player and the host do not have access to quantum strategies.
References
Bishop, C.M.: Pattern Recognition and Machine Learning. Springer, New York (2006)
Koller, D., Friedman, N.: Probabilistic Graphical Models: Principles and Techniques. MIT Press, Cambridge (2009)
Cerf, N.J., Adami, C.: Negative entropy and information in quantum mechanics. Phys. Rev. Lett. 79(26), 5194–5197 (1997)
Cerf, N.J., Adami, C.: Quantum extension of conditional probability. Phys. Rev. A 60(2), 893–897 (1999)
Leifer, M.S.: Quantum dynamics as an analog of conditional probability. Phys. Rev. A 74(4), 042310 (2006)
Leifer, M.S., Spekkens, R.W.: Towards a formulation of quantum theory as a causally neutral theory of bayesian inference. Phys. Rev. A 88(5), 052130 (2013)
Leifer, M.S., Spekkens, R.W.: A bayesian approach to compatibility, improvement, and pooling of quantum states. J. Phys. A Math. Theor. 47(27), 275301 (2014)
Brukner, Č.: Quantum causality. Nat. Phys. 10(4), 259–263 (2014)
Ried, K., Agnew, M., Vermeyden, L., Janzing, D., Spekkens, R.W., Resch, K.J.: A quantum advantage for inferring causal structure. Nat. Phys. 11(5), 414–420 (2015)
Leifer, M.S., Poulin, D.: Quantum graphical models and belief propagation. Ann. Phys. 323(8), 1899–1946 (2008)
Selvin, S.: A problem in probability (letter to the editor). Am. Stat. 29(1), 67–71 (1975)
Selvin, S.: On the monty hall problem (letter to the editor). Am. Stat. 29(3), 131–134 (1975)
Fenton, N., Neil, M.: Risk Assessment and Decision Analysis with Bayesian Networks. CRC Press, Boca Raton (2012)
Gill, J.: Bayesian Methods: A Social and Behavioral Sciences Approach, vol. 20. CRC Press, Boca Raton (2014)
Li, C., Zhang, Y., Huang, Y., Guo, G.: Quantum strategies of quantum measurements. Phys. Lett. A 280(5), 257–260 (2001)
D’Ariano, G.M., Gill, R.D., Keyl, M., Kuemmerer, B., Maassen, H., Werner, R.F.: The quantum monty hall problem. Quantum Inf. Comput. 2(5), 355–366 (2002)
Flitney, A.P., Abbott, D.: Quantum version of the monty hall problem. Phys. Rev. A 65(6), 062318 (2002)
Gawron, P.: Noisy quantum Monty Hall game. Fluct. Noise Lett. 9(1), 9–18 (2010)
Khan, S., Ramzan, M., Khan, M.K.: Quantum Monty Hall problem under decoherence. Commun. Theor. Phys. 54(1), 47–54 (2010)
Acknowledgments
This work was supported by the Polish National Science Centre: D. Kurzyk under the research project number UMO-2013/11/N/ST6/03090, A. Glos under the research project number DEC-2011/03/D/ST6/00413.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kurzyk, D., Glos, A. Quantum inferring acausal structures and the Monty Hall problem. Quantum Inf Process 15, 4927–4937 (2016). https://doi.org/10.1007/s11128-016-1431-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11128-016-1431-8