Multi-boson correlation sampling

Abstract

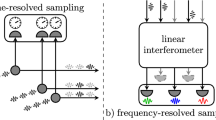
We give a full description of the problem of multi-boson correlation sampling (MBCS) at the output of a random interferometer for single input photons in arbitrary multi-mode pure states. The MBCS problem is the task of sampling at the interferometer output from the probability distribution associated with polarization- and time-resolved detections. We discuss the richness of the physics and the complexity of the MBCS problem for non-identical input photons. We also compare the MBCS problem with the standard boson sampling problem, where the input photons are assumed to be identical and the system is “classically” averaging over the detection times and polarizations.

Appendices

Appendix 1: Correlation functions as expectation values of permanents of operator matrices

We derive the expression in Eq. (8) of the correlation function $G^{(\mathscr {D},\mathscr {S})}_{\{t_j,{\varvec{p}}_j\}}$ for multi-mode single-photon states. Inserting Eq. (5) into Eq. (6), we obtain

$$\begin{aligned} G^{(\mathscr {D},\mathscr {S})}_{\{t_j,{\varvec{p}}_j\}}&= \langle \mathscr {S} \vert \prod _{j=1}^N \Big [ \sum _{i'=1}^N \big ( \mathscr {U}^{(\mathscr {D},\mathscr {S})}_{j,i'}\big )^{*} \Big ( {\varvec{p}}_j^{*} \cdot {\hat{{\varvec{E}}}}_{i'}^{(-)}(t_j -\Delta t) \Big ) \Big ]\\&\quad \times \Big [ \sum _{i=1}^N \mathscr {U}^{(\mathscr {D},\mathscr {S})}_{j,i} \Big ( {\varvec{p}}_j \cdot {\hat{{\varvec{E}}}}_{i}^{(+)}(t_j -\Delta t) \Big ) \Big ] \vert \mathscr {S} \rangle , \end{aligned}$$

which, after interchanging the order of the product and the two summations, becomes

$$\begin{aligned} G^{(\mathscr {D},\mathscr {S})}_{\{t_j,{\varvec{p}}_j\}}= & {} \sum _{ \{ i_j, i_j' \}_{j=1,\ldots ,N} }\,\, \prod _{j=1}^N \big ( \mathscr {U}^{(\mathscr {D},\mathscr {S})}_{j,i_j'} \big )^{*} \mathscr {U}^{(\mathscr {D},\mathscr {S})}_{j,i_j}\nonumber \\&\times \langle \mathscr {S} \vert \prod _{j=1}^N \Big ( {\varvec{p}}^{*}_j \cdot {\hat{{\varvec{E}}}}^{(-)}_{i_j'}(t_j - \Delta t) \Big ) \prod _{j=1}^N \Big ( {\varvec{p}}_j \cdot {\hat{{\varvec{E}}}}^{(+)}_{i_j}(t_j - \Delta t) \Big ) \vert \mathscr {S} \rangle . \end{aligned}$$

(27)

Here, the summation over the 2N indices $\{i_j,i_j'\}_{j=1,\ldots ,N}$ covers all possible ways the N sources contribute to the product of 2N field operators in the expectation value in Eq. (6), independently of the input state.

Equation (27) can be simplified by recalling that the input state is the product of single-photon states in each of the input ports. Thus, since each source can at most contribute one photon, the expression $\prod _{j=1}^N \big ( {\varvec{p}}_j \cdot {\hat{{\varvec{E}}}}^{(+)}_{i_j}(t_j-\Delta t) \big ) \vert {\mathscr {S}}\rangle$ is non-vanishing only if the indices $i_j\ (j=1,\ldots ,N)$ take pairwise different values. Introducing the symmetric group $\varSigma _N$ of all permutations $\sigma$ of N elements, we find that in the non-vanishing cases, the indices take the values $i_j = \sigma (j)$, with $\sigma \in \varSigma _N$. The same argument can also be made for the possible values of the indices $i_j'$. Therefore, the correlation function in Eq. (27) reduces to

$$\begin{aligned} G^{(\mathscr {D},\mathscr {S})}_{\{t_j,{\varvec{p}}_j\}}&= \sum _{\sigma ,\sigma '\in \varSigma _N} \prod _{j=1}^N \big ( \mathscr {U}^{(\mathscr {D},\mathscr {S})}_{j,\sigma '(j)} \big )^{*} \mathscr {U}^{(\mathscr {D},\mathscr {S})}_{j,\sigma (j)}\nonumber \\&\quad \times \langle \mathscr {S} \vert \prod _{j=1}^N \Big ( {\varvec{p}}^{*}_j \cdot {\hat{{\varvec{E}}}}^{(-)}_{\sigma '(j)}(t_j - \Delta t) \Big ) \Big ( {\varvec{p}}_j \cdot {\hat{{\varvec{E}}}}^{(+)}_{\sigma (j)}(t_j - \Delta t) \Big ) \vert \mathscr {S} \rangle , \end{aligned}$$

(28)

which, with the definition of the operator matrix ${\hat{\mathscr {M}}}_{\{t_j,{\varvec{p}}_j\}}^{(\mathscr {D},\mathscr {S})}$ in Eq. (7), becomes

$$\begin{aligned} G^{(\mathscr {D},\mathscr {S})}_{\{t_j,{\varvec{p}}_j\}}&= \langle \mathscr {S} \vert \Big [ \sum _{\sigma '\in \varSigma _N} \prod _{j=1}^N \big ( \mathscr {U}^{(\mathscr {D},\mathscr {S})}_{j,\sigma '(j)} \big )^{*} \Big ( {\varvec{p}}^{*}_j \cdot {\hat{{\varvec{E}}}}^{(-)}_{\sigma '(j)}(t_j - \Delta t) \Big ) \Big ] \\&\quad \times \Big [ \sum _{\sigma \in \varSigma _N} \prod _{j=1}^N \mathscr {U}^{(\mathscr {D},\mathscr {S})}_{j,\sigma (j)} \Big ( {\varvec{p}}_j \cdot {\hat{{\varvec{E}}}}^{(+)}_{\sigma (j)}(t_j - \Delta t) \Big ) \Big ] \vert \mathscr {S} \rangle \\&= \langle \mathscr {S} \vert \Big ({\text {perm}}{\hat{\mathscr {M}}}^{(\mathscr {D},\mathscr {S})}_{\{t_j,{\varvec{p}}_j\}}\Big )^{\dagger } \Big ( {\text {perm}}{\hat{\mathscr {M}}}^{(\mathscr {D},\mathscr {S})}_{\{t_j,{\varvec{p}}_j\}} \Big ) \vert \mathscr {S} \rangle . \end{aligned}$$

Appendix 2: Correlation functions for multi-mode single-photon states

We demonstrate here the expression for the correlation function for multi-mode single-photon states, found in Eq. (11). From the definition of the input state in Eq. (1), we find the expression

$$\begin{aligned} \prod _{j=1}^N \Big ( {\varvec{p}}_j \cdot {\hat{{\varvec{E}}}}^{(+)}_{\sigma (j)} (t_j - \Delta t) \Big ) \vert {\mathscr {S}}\rangle&= \prod _{j=1}^N \Big ( {\varvec{p}}_j \cdot {\hat{{\varvec{E}}}}^{(+)}_{\sigma (j)} (t_j - \Delta t) \Big ) \bigotimes _{i=1}^N \vert {1[{\varvec{\xi }}_i]}\rangle _{s_i} \bigotimes _{s\notin \mathscr {S}} \vert {0}\rangle _s\nonumber \\&= \bigotimes _{j=1}^N \Big [ \Big ( {\varvec{p}}_j \cdot {\hat{{\varvec{E}}}}^{(+)}_{\sigma (j)} (t_j - \Delta t) \Big ) \vert {1[{\varvec{\xi }}_{\sigma (j)}]}\rangle _{s_{\sigma (j)}} \Big ] \bigotimes _{s\notin \mathscr {S}} \vert {0}\rangle _s \end{aligned}$$

(29)

for the terms in Eq. (28). By using the definition of the single-photon states in Eq. (2) and the field operators

$$\begin{aligned} {\hat{{\varvec{E}}}}^{(+)}_i (t) = \frac{1}{\sqrt{2\pi }} \sum _{\lambda =1,2} {\varvec{e}}_{\lambda } \int \limits _0^{\infty } {\hbox {d}}{\omega }\,{\text {e}}^{-\mathrm {i}\omega t} \hat{a}_{i,\lambda }(\omega ) \end{aligned}$$

in the narrow bandwidth approximation, we obtain

$$\begin{aligned}&\Big ( {\varvec{p}}_j \cdot {\hat{{\varvec{E}}}}^{(+)}_i (t_j- \Delta t) \Big ) \vert {1[{\varvec{\xi }}_i]}\rangle _{s_i}\\&\quad = \frac{1}{\sqrt{2\pi }} \sum _{\lambda =1,2} ({\varvec{p}}_j \cdot {\varvec{e}}_{\lambda }) \int \limits _0^{\infty } {\hbox {d}}{\omega } {\text {e}}^{-\mathrm {i}\omega (t_j-\Delta t)} \hat{a}_{i,\lambda }(\omega ) \sum _{\lambda '=1,2} \int \limits _0^{\infty } {\hbox {d}}{\omega '} ( {\varvec{e}}_{\lambda '} \cdot {\varvec{\xi }}_{i}(\omega ') ) \hat{a}^{\dagger }_{i,\lambda '}(\omega ') \vert {0}\rangle _{s_i}\\&\quad = \frac{1}{\sqrt{2\pi }} \sum _{\lambda ,\lambda '=1,2} \int \limits _0^{\infty } {\hbox {d}}{\omega } \int \limits _0^{\infty } {\hbox {d}}{\omega '} ({\varvec{p}}_j \cdot {\varvec{e}}_{\lambda }) {\text {e}}^{-\mathrm {i}\omega (t_j-\Delta t)}\big ( {\varvec{e}}_{\lambda '} \cdot {\varvec{\xi }}_{i}(\omega ') \big ) \hat{a}_{i,\lambda }(\omega ) \hat{a}^{\dagger }_{i,\lambda '}(\omega ') \vert {0}\rangle _{s_i}\\&\quad = \frac{1}{\sqrt{2\pi }} \sum _{\lambda ,\lambda '=1,2} \int \limits _0^{\infty } {\hbox {d}}{\omega } \int \limits _0^{\infty } {\hbox {d}}{\omega '} ({\varvec{p}}_j \cdot {\varvec{e}}_{\lambda }) {\text {e}}^{-\mathrm {i}\omega (t_j-\Delta t)}\big ( {\varvec{e}}_{\lambda '} \cdot {\varvec{\xi }}_{i}(\omega ') \big )\\&\qquad \times \big [ \hat{a}^{\dagger }_{i,\lambda '}(\omega ')\hat{a}_{i,\lambda }(\omega ) + \delta _{\lambda ,\lambda '} \delta (\omega - \omega ') \big ] \vert {0}\rangle _{s_i}\\&\quad = \frac{1}{\sqrt{2\pi }} \sum _{\lambda =1,2} \int \limits _0^{\infty } {\hbox {d}}{\omega } ({\varvec{p}}_j \cdot {\varvec{e}}_{\lambda }) {\text {e}}^{-\mathrm {i}\omega (t_j-\Delta t)}\big ( {\varvec{e}}_{\lambda } \cdot {\varvec{\xi }}_{i}(\omega ) \big ) \vert {0}\rangle _{s_i}\\&\quad = \frac{1}{\sqrt{2\pi }} \int \limits _0^{\infty } {\hbox {d}}{\omega } \big ({\varvec{p}}_j \cdot {\varvec{\xi }}_i(\omega )\big ) {\text {e}}^{-\mathrm {i}\omega (t_j-\Delta t)} \vert {0}\rangle _{s_i}. \end{aligned}$$

In the narrow bandwidth approximation, we can approximately expand the integration over $\omega$ to the complete real axis. By using the definition of a Fourier transform

$$\begin{aligned} \mathscr {F}[f](t) :=\frac{1}{\sqrt{2\pi }} \int \limits _{-\infty }^{\infty } {\hbox {d}}{\omega } f(\omega ) {\text {e}}^{-\mathrm {i}\omega t} \end{aligned}$$

we then find

$$\begin{aligned} \Big ( {\varvec{p}}_j \cdot {\hat{{\varvec{E}}}}^{(+)}_i (t_j- \Delta t) \Big ) \vert {1[{\varvec{\xi }}_i]}\rangle _{s_i}&\approx \frac{1}{\sqrt{2\pi }} \int \limits _{-\infty }^{\infty } {\hbox {d}}{\omega } \big ({\varvec{p}}_j \cdot {\varvec{\xi }}_i(\omega )\big ) {\text {e}}^{-\mathrm {i}\omega (t_j-\Delta t)} \vert {0}\rangle _{s_i}\\&= \big ( {\varvec{p}}_j \cdot \mathscr {F}[{\varvec{\xi }}_i](t_j-\Delta t) \big ) \vert {0}\rangle _{s_i} = \big ( {\varvec{p}}_j \cdot {\varvec{\chi }}_s(t_j) \big ) \vert {0}\rangle _{s_i}. \end{aligned}$$

By substituting this result together with Eq. (29), Eq. (28) reduces to the expression

$$\begin{aligned} G^{(\mathscr {D},\mathscr {S})}_{\{t_j,{\varvec{p}}_j\}}&= \sum _{\sigma ,\sigma '\in \varSigma _N} \prod _{j=1}^N \big ( \mathscr {U}^{(\mathscr {D},\mathscr {S})}_{j,\sigma '(j)} \big )^{*} \mathscr {U}^{(\mathscr {D},\mathscr {S})}_{j,\sigma (j)} \big ( {\varvec{p}}_j \cdot {\varvec{\chi }}_{\sigma '(j)}(t_j) \big )^{*} \big ( {\varvec{p}}_j \cdot {\varvec{\chi }}_{\sigma (j)}(t_j) \big )\nonumber \\&= \Big |\sum _{\sigma \in \varSigma _N} \prod _{j=1}^N \mathscr {U}^{(\mathscr {D},\mathscr {S})}_{j,\sigma (j)} \big ({\varvec{p}}_j \cdot {\varvec{\chi }}_{\sigma (j)}(t_j) \big ) \Big |^2 = \left|{{\text {perm}}\mathscr {T}^{(\mathscr {D},\mathscr {S})}_{\{t_j,{\varvec{p}}_j\}}}\right|^2 \end{aligned}$$

(30)

in Eq. (11).

Appendix 3: Probabilities for non-resolved detections

1.1 Accounting for photon bunching

We now derive the probabilities (18) in the case of non-resolved detections in time and polarization. Toward this end, we have to take into account that the correlation function in Eq. (6) is symmetric under permutation of the arguments $\{t_j,{\varvec{p}}_j\}$ and $\{t_{j'},{\varvec{p}}_{j'}\}$ if both corresponding photons are detected in the same output port, i.e., if $d_j = d_{j'}$.

For example, in the case of $N=2$ and with both photons detected in the same output port d ($\mathscr {D}=\{d,d\}$), the correlation function

$$\begin{aligned} G^{(\{d,d\},\mathscr {S})}_{\{t_1,{\varvec{p}}_1;t_2,{\varvec{p}}_2\}} = \langle \mathscr {S} \vert \Big ( {\varvec{p}}^{*}_1 \cdot {\hat{{\varvec{E}}}}^{(-)}_d(t_1) \Big )\Big ( {\varvec{p}}^{*}_2 \cdot {\hat{{\varvec{E}}}}^{(-)}_d(t_2) \Big )\Big ( {\varvec{p}}_2 \cdot {\hat{{\varvec{E}}}}^{(+)}_d(t_2) \Big )\Big ( {\varvec{p}}_1 \cdot {\hat{{\varvec{E}}}}^{(+)}_d(t_1) \Big ) \vert \mathscr {S} \rangle \end{aligned}$$

is symmetric with respect to the two possible detection times and respective polarizations $\{t_1,{\varvec{p}}_1\}$ and $\{t_2,{\varvec{p}}_2\}$: $G^{(\{d,d\},\mathscr {S})}_{\{t_1,{\varvec{p}}_1;t_2,{\varvec{p}}_2\}} = G^{(\{d,d\},\mathscr {S})}_{\{t_2,{\varvec{p}}_2;t_1,{\varvec{p}}_1\}}$. This reflects the fact that both expressions describe the same probability rate of two photons being detected in the output port d, one at time $t_1$ and with polarization ${\varvec{p}}_1$ and the other at time $t_2$ and with polarization ${\varvec{p}}_2$.

Therefore, the corresponding probability

$$\begin{aligned} P_{\text {av}}(\{d,d\};\mathscr {S}) =\frac{1}{2!} \sum _{{\varvec{p}}_1,{\varvec{p}}_2 \in \{{\varvec{e}}_1,{\varvec{e}}_2\}}\int \limits _{-\infty }^{\infty } {\hbox {d}}{t_1} \int \limits _{-\infty }^{\infty }{\hbox {d}}{t_2} G^{(\mathscr {D},\mathscr {S})}_{\{t_1,{\varvec{p}}_1;t_2,{\varvec{p}}_2\}} \end{aligned}$$

for non-resolved detections contains the additional factor 1 / 2! in order to avoid double counting.

Generalizing to the case of arbitrary samples $\mathscr {D}$ in a 2M-port interferometer, where d is contained $n_d$ times in $\mathscr {D}$ ($\sum _{d=1}^{M} n_d = N$), we find the time- and polarization-averaged probabilities

$$\begin{aligned} P_{\text {av}}(\mathscr {D};\mathscr {S}) = \frac{1}{\prod _{d=1}^{M} n_d!} \sum _{\{{\varvec{p}}_j\}\in \{{\varvec{e}}_1,{\varvec{e}}_2\}^{N}} \int \limits _{-\infty }^{\infty } \Big ( \prod _{j=1}^{N} {\hbox {d}}{t_j} \Big ) G^{(\mathscr {D},\mathscr {S})}_{\{t_j,{\varvec{p}}_j\}} \end{aligned}$$

in Eq. (18).

1.2 Integrated probabilities

We derive now Eq. (24) from the general expression of the probability $P_{\text {av}}(\mathscr {D};\mathscr {S})$ in Eq. (18) for non-resolved detections. We first substitute in Eq. (18) the value for the correlation function in Eq. (30), yielding

$$\begin{aligned} P_{\text {av}}(\mathscr {D};\mathscr {S})&= \frac{1}{\prod _{d=1}^{M} n_d!} \sum _{\{{\varvec{p}}_j\}\in \{{\varvec{e}}_1,{\varvec{e}}_2\}^{N}} \int \limits _{-\infty }^{\infty }\Big (\prod _{j=1}^N {\hbox {d}}{t_j} \Big )\nonumber \\&\quad \times \sum _{\sigma ,\sigma '\in \varSigma _N} \prod _{j=1}^N \big ( \mathscr {U}^{(\mathscr {D},\mathscr {S})}_{j,\sigma (j)} \big )^{*} \mathscr {U}^{(\mathscr {D},\mathscr {S})}_{j,\sigma '(j)}\big ({\varvec{p}}_j \cdot {\varvec{\chi }}_{\sigma (j)}(t_j) \big )^{*} \big ( {\varvec{p}}_j \cdot {\varvec{\chi }}_{\sigma '(j)}(t_j) \big )\nonumber \\&= \frac{1}{\prod _{d=1}^{M} n_d!} \sum _{\sigma ,\sigma '\in \varSigma _N} \prod _{j=1}^N \big ( \mathscr {U}^{(\mathscr {D},\mathscr {S})}_{j,\sigma (j)} \big )^{*} \mathscr {U}^{(\mathscr {D},\mathscr {S})}_{j,\sigma '(j)}\nonumber \\&\quad \times \Bigg [ \sum _{{\varvec{p}}_j \in \{{\varvec{e}}_1, {\varvec{e}}_2\}} \int \limits _{-\infty }^{\infty } {\hbox {d}}{t_j} \big ({\varvec{p}}_j \cdot {\varvec{\chi }}_{\sigma (j)}(t_j) \big )^{*} \big ( {\varvec{p}}_j \cdot {\varvec{\chi }}_{\sigma '(j)}(t_j) \big ) \Bigg ]\nonumber \\&= \frac{1}{\prod _{d=1}^{M} n_d!} \sum _{\sigma ,\sigma '\in \varSigma _N} \prod _{j=1}^N \big ( \mathscr {U}^{(\mathscr {D},\mathscr {S})}_{j,\sigma (j)} \big )^{*} \mathscr {U}^{(\mathscr {D},\mathscr {S})}_{j,\sigma '(j)}\nonumber \\&\quad \times \Bigg [ \int \limits _{-\infty }^{\infty } {\hbox {d}}{t} {\varvec{\chi }}_{\sigma (j)}(t) \cdot {\varvec{\chi }}_{\sigma '(j)}(t)\Bigg ]. \end{aligned}$$

(31)

With the substitution $\sigma ' \rightarrow \rho \circ \sigma$, where $\rho \in \varSigma _N$, Eq. (31) becomes

$$\begin{aligned} P_{\text {av}}(\mathscr {D};\mathscr {S})&=\frac{1}{\prod _{d=1}^{M} n_d!} \sum _{\rho \in \varSigma _N} \sum _{\sigma \in \varSigma _N} \Bigg [\prod _{j=1}^N \big ( \mathscr {U}^{(\mathscr {D},\mathscr {S})}_{j,\sigma (j)} \big )^{*} \mathscr {U}^{(\mathscr {D},\mathscr {S})}_{j,\rho (\sigma (j))} \Bigg ]\\&\quad \times \Bigg [\prod _{j=1}^N \int \limits _{-\infty }^{\infty } {\hbox {d}}{t} {\varvec{\chi }}_{\sigma (j)}(t) \cdot {\varvec{\chi }}_{\rho (\sigma (j))}(t) \Bigg ]. \end{aligned}$$

Here, the second product can be written as a product over $i=\sigma (j)$ instead of j since $\sigma$ is bijective, rendering this expression independent of the permutation $\sigma$:

$$\begin{aligned} P_{\text {av}}(\mathscr {D};\mathscr {S})&= \frac{1}{\prod _{d=1}^{M} n_d!} \sum _{\rho \in \varSigma _N} \Bigg [ \prod _{i=1}^N \int \limits _{-\infty }^{\infty } {\hbox {d}}{t} {\varvec{\chi }}_{i}(t) \cdot {\varvec{\chi }}_{\rho (i)}(t) \Bigg ]\nonumber \\&\quad \times \sum _{\sigma \in \varSigma _N} \Bigg [\prod _{j=1}^N \big ( \mathscr {U}^{(\mathscr {D},\mathscr {S})}_{j,\sigma (j)} \big )^{*} \mathscr {U}^{(\mathscr {D},\mathscr {S})}_{j,\rho (\sigma (j))} \Bigg ]. \end{aligned}$$

(32)

By using the definitions of $f_{\rho }(\mathscr {S})$ and $\mathscr {A}_{\rho }^{(\mathscr {D},\mathscr {S})}$ in Eqs. (20) and (23), Eq. (32) finally reduces to the expression

$$\begin{aligned} P_{\text {av}}(\mathscr {D};\mathscr {S}) = \frac{1}{\prod _{d=1}^{M} n_d!} \sum _{\rho \in \varSigma _N} f_{\rho }(\mathscr {S}) {\text {perm}}A_{\rho }^{(\mathscr {D},\mathscr {S})} \end{aligned}$$

in Eq. (24).

Appendix 4: Two-photon indistinguishability factors for Gaussian spectral distributions

We derive the two-photon indistinguishability factors for Gaussian spectral distributions in Eq. (22). By inserting Eq. (21) into Eq. (19), we obtain the Gaussian integral

$$\begin{aligned} g(i,i')&=\big ( {\varvec{v}}_i \cdot {\varvec{v}}_{i'} \big ) \frac{1}{(2\pi \Delta \omega _i\Delta \omega _{i'})^{1/2}} \\&\quad \times \int \limits _{-\infty }^{\infty } {\hbox {d}}{\omega } \exp \left[ -\frac{(\omega -\omega _{0i})^2}{4(\Delta \omega _i)^2} - \mathrm {i}\omega \, t_{0i} \right] \exp \left[ -\frac{(\omega -\omega _{0i'})^2}{4(\Delta \omega _{i'})^2} + \mathrm {i}\omega \, t_{0i'} \right] , \end{aligned}$$

which, using the well-known relation $\int \limits _{-\infty }^{\infty }dx \exp (-a x^2 + bx +c) = \sqrt{\pi /a} \,\exp (b^2/(4a) + c)$, can be evaluated as

$$\begin{aligned} g(i,i')&= \big ( {\varvec{v}}_i \cdot {\varvec{v}}_{i'} \big ) \sqrt{\frac{2\Delta \omega _i \Delta \omega _{i'}}{(\Delta \omega _i)^2+(\Delta \omega _{i'})^2}} \exp \left[ -\frac{(\omega _{0i}-\omega _{0i'})^2}{4((\Delta \omega _i)^2 +(\Delta \omega _{i'})^2)}\right] \\&\quad \times \exp \left[ -\frac{(\Delta \omega _i)^2 (\Delta \omega _{i'})^2}{(\Delta \omega _i)^2+(\Delta \omega _{i'})^2} (t_{0i}-t_{0i'})^2\right] \\&\quad \times \exp \left[ -\mathrm {i}\frac{\omega _{0i}(\Delta \omega _{i'})^2 + \omega _{0i'}(\Delta \omega _i)^2}{(\Delta \omega _i)^2 + (\Delta \omega _{i'})^2} (t_{0i}- t_{0i'}) \right] . \end{aligned}$$