Skip to main content
SpringerLink
Log in

Entanglement of four-qubit rank-2 mixed states

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

It is known that there are three maximally entangled states \(|\varPhi _1 \rangle = (|0000 \rangle + |1111 \rangle ) / \sqrt{2}\), \(|\varPhi _2 \rangle = (\sqrt{2} |1111 \rangle + |1000 \rangle + |0100 \rangle + |0010 \rangle + |0001 \rangle ) / \sqrt{6}\), and \(|\varPhi _3 \rangle = (|1111 \rangle + |1100 \rangle + |0010 \rangle + |0001 \rangle ) / 2\) in four-qubit system. It is also known that there are three independent measures \(\mathcal{F}^{(4)}_j (j=1,2,3)\) for true four-way quantum entanglement in the same system. In this paper, we compute \(\mathcal{F}^{(4)}_j\) and their corresponding linear monotones \(\mathcal{G}^{(4)}_j\) for three rank-two mixed states \(\rho _j = p |\varPhi _j \rangle \langle \varPhi _j | + (1 - p) |\text{ W }_4 \rangle \langle \text{ W }_4 |\), where \(|\text{ W }_4 \rangle = (|0111 \rangle + |1011 \rangle + |1101 \rangle + |1110 \rangle ) / 2\). We discuss the possible applications of our results briefly.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

Notes

  1. The current status of quantum computer technology was reviewed in Ref. [8].

  2. For complete proof on the connection between SLOCC and local operations, see Appendix A of Ref. [27].

  3. In this paper, we will call \(\tau _3\) three-tangle and \(\tau _3^2\) residual entanglement.

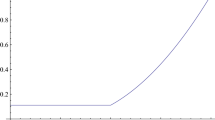
  4. The parameter \(p_1\) is obtained by an equation \(6 p_1 (4 p_1 - 3)^2 = (1 - p_1) (1 + 2 p_1)^2\).

References

  1. Nielsen, M.A., Chuang, I.L.: Quantum computation and quantum information. Cambridge University Press, Cambridge, (2000)

    MATH  Google Scholar 

  2. Horodecki, R., Horodecki, P., Horodecki, M., Horodecki, K.: Quantum entanglement. Rev. Mod. Phys. 81, 865 (2009). quant-ph/0702225 and references therein

    Article  MATH  MathSciNet  ADS  Google Scholar 

  3. Bennett, C.H., Brassard, G., Crepeau, C., Jozsa, R., Peres, A., Wootters, W.K.: Teleporting an unknown quantum state via dual classical and Einstein–Podolsky–Rosen channles. Phys. Rev. Lett. 70, 1895 (1993)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  4. Bennett, C.H., Wiesner, S.J.: Communication via one- and two-particle operators on Einstein–Podolsky–Rosen states. Phys. Rev. Lett. 69, 2881 (1992)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  5. Scarani, V., Lblisdir, S., Gisin, N., Acin, A.: Quantum cloning. Rev. Mod. Phys. 77, 1225 (2005). quant-ph/0511088 and references therein

    Article  MATH  ADS  Google Scholar 

  6. Ekert, A.K.: Quantum cryptography based on bells theorem. Phys. Rev. Lett. 67, 661 (1991)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  7. Kollmitzer, C., Pivk, M.: Applied Quantum Cryptography. Springer, Heidelberg, (2010)

    Book  MATH  Google Scholar 

  8. Ladd, T.D., Jelezko, F., Laflamme, R., Nakamura, Y., Monroe, C., O’Brien, J.L.: Quantum computers. Nature 464, 45 (2010). arXiv:1009.2267 (quant-ph)

    Article  ADS  Google Scholar 

  9. Vidal, G.: Efficient classical simulation of slightly entangled quantum computations. Phys. Rev. Lett. 91, 147902 (2003). quant-ph/0301063

    Article  ADS  Google Scholar 

  10. Bennett, C.H., DiVincenzo, D.P., Smokin, J.A., Wootters, W.K.: Mixed-state entanglement and quantum error correction. Phys. Rev. A 54, 3824 (1996). quant-ph/9604024

    Article  MathSciNet  ADS  Google Scholar 

  11. Vedral, V., Plenio, M.B., Rippin, M.A., Knight, P.L.: Quantifying entanglement. Phys. Rev. Lett. 78, 2275 (1997). quant-ph/9702027

    Article  MATH  MathSciNet  ADS  Google Scholar 

  12. Vedral, V., Plenio, M.B.: Entanglement measures and purification procedures. Phys. Rev. 57, 1619 (1998). quant-ph/9707035

    Article  ADS  Google Scholar 

  13. Smolin, J.A.: Four-party unlockable bound entangled state. Phys. Rev. A. 63, 032306 (2001). quant-ph/0001001

    Article  MathSciNet  ADS  Google Scholar 

  14. Ghosh, S., Kar, G., Roy, A., Sen(De), A., Sen, U.: Distinguishability of bell states. Phys. Rev. Lett. 87, 277902 (2001). quant-ph/0106148

    Article  MathSciNet  ADS  Google Scholar 

  15. Chen, Y.X., Jin, J.S., Yang, D.: Distillation of multiple copies of bell states. Phys. Rev. A. 67, 014302 (2003)

    Article  ADS  Google Scholar 

  16. Yang, D., Chen, Y.X.: Mixture of multiple copies of maximally entangled states is quasipure. Phys. Rev. A 69, 024302 (2004)

    Article  ADS  Google Scholar 

  17. Miranowicz, A., Ishizaka, S.: Closed formula for the relative entropy of entanglement. Phys. Rev. A 78, 032310 (2008). arXiv:0805.3134 (quant-ph)

    Article  MathSciNet  ADS  Google Scholar 

  18. Kim, H., Hwang, M.R., Jung, E., Park, D.K.: Difficulties in analytic computation for relative entropy of entanglement. ibid. A 81, 052325 (2010). arXiv:1002.4695 (quant-ph)

  19. Park, D.K.: Relative entropy of entanglement for two-qubit state with \(z\)-directional Bloch vectors. Int. J. Quantum. Inf. 8, 869 (2010). arXiv:1005.4777 (quant-ph)

    Article  MATH  Google Scholar 

  20. Friedland, S., Gour, G.: Closed formula for the relative entropy of entanglement in all dimensions. J. Math. Phys. 52, 052201 (2011). arXiv:1007.4544 (quant-ph)

    Article  MathSciNet  ADS  Google Scholar 

  21. M. W. Girard, G. Gour, and S. Friedland, On convex optimization problems in quantum information theory. arXiv:1402.0034 (quant-ph)

  22. Jung, E., Park, D.K.: REE From EOF. Quantum. Inf. Process. 14, 531 (2015). arXiv:1404.7708 (quant-ph)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  23. Uhlmann, A.: Fidelity and concurrence of conjugate states. Phys. Rev. 62, 032307 (2000). quant-ph/9909060

    Article  MathSciNet  ADS  Google Scholar 

  24. Hill, S., Wootters, W.K.: Entanglement of a pair of quantum bits. Phys. Rev. Lett. 78, 5022 (1997). quant-ph/9703041

    Article  ADS  Google Scholar 

  25. W. K. Wootters, Entanglement of formation of an arbitrary state of two qubits. ibid. 80 2245 (1998) quant-ph/9709029

  26. Bennett, C.H., Popescu, S., Rohrlich, D., Smolin, J.A., Thapliyal, A.V.: Exact and asymptotic measures of multipartite pure-state entanglement. Phys. Rev. 63, 012307 (2000). quant-ph/9908073

    Article  Google Scholar 

  27. Dür, W., Vidal, G., Cirac, J.I.: Three qubits can be entangled in two inequivalent ways. Phys. Rev. A 62, 062314 (2000). quant-ph/0005115

    Article  MathSciNet  ADS  Google Scholar 

  28. Acín, A., Bruß, D., Lewenstein, M., Sanpera, A.: Classification of mixed three-qubit states. Phys. Rev. Lett. 87, 040401 (2001). quant-ph/0103025

    Article  MathSciNet  ADS  Google Scholar 

  29. Verstraete, F., Dehaene, J., De Moor, D.: Normal forms and entanglement measures for multipartite quantum states. Phys. Rev. A 68, 012103 (2003). quant-ph/0105090

    Article  MathSciNet  ADS  Google Scholar 

  30. Coffman, V., Kundu, J., Wootters, W.K.: Distributed entanglement. Phys. Rev. A 61, 052306 (2000). quant-ph/9907047

    Article  ADS  Google Scholar 

  31. Lohmayer, R., Osterloh, A., Siewert, j, Uhlmann, A.: Entangled three-qubit states without concurrence and three-tangle. Phys. Rev. Lett. 97, 260502 (2006). quant-ph/0606071

    Article  MathSciNet  ADS  Google Scholar 

  32. Eltschka, C., Osterloh, A., Siewert, J., Uhlmann, A.: Three-tangle for mixtures of generalized GHZ and generalized W states. New J. Phys. 10, 043014 (2008). arXiv:0711.4477 (quant-ph)

    Article  ADS  Google Scholar 

  33. Jung, E., Hwang, M.R., Park, D.K., Son, J.W.: Three-tangle for rank-3 mixed states: mixture of Greenberger–Horne–Zeilinger, W and flipped W states. Phys. Rev. A 79, 024306 (2009). arXiv:0810.5403 (quant-ph)

    Article  ADS  Google Scholar 

  34. Jung, E., Park, D.K., Son, J.W.: Three-tangle does not properly quantify tripartite entanglement for Greenberger–Horne–Zeilinger-type state. Phys. Rev. A 80, 010301(R) (2009). arXiv:0901.2620 (quant-ph)

    Article  MathSciNet  ADS  Google Scholar 

  35. Jung, E., Hwang, M.R., Park, D.K., Tamaryan, S.: Three-party entanglement in tripartite teleportation scheme through noisy channels. Quantum Inf. Comput. 10, 0377 (2010). arXiv:0904.2807 (quant-ph)

    MathSciNet  Google Scholar 

  36. Eltschka, C., Siewert, J.: Entanglement of three-qubit Greenberger–Horne–Zeilinger-symmetric states. Phys. Rev. Lett. 108, 020502 (2012). arXiv:1304.6095 (quant-ph)

    Article  ADS  Google Scholar 

  37. Siewert, J., Eltschka, C.: Quantifying tripartite entanglement of three-qubit generalized werner states. Phys. Rev. Lett. 108, 230502 (2012)

    Article  ADS  Google Scholar 

  38. Osterloh, A., Siewert, J.: Constructing N-qubit entanglement monotones from antilinear operators. Phys. Rev. A 72, 012337 (2005). quant-ph/0410102

    Article  ADS  Google Scholar 

  39. Doković, D.Ž., Osterloh, A.: On polynomial invariants of several qubits. J. Math. Phys. 50, 033509 (2009). arXiv:0804.1661 (quant-ph)

    Article  MathSciNet  ADS  Google Scholar 

  40. Osterloh, A., Siewert, J.: The invariant-comb approach and its relation to the balancedness of multiple entangled states. New J. Phys. 12, 075025 (2010). arXiv:0908.3818 (quant-ph)

    Article  ADS  Google Scholar 

  41. Osterloh, A., Siewert, J.: Entanglement monotones and maximally entangled states in multipartite qubit systems. Inf. Comput. 4, 0531 (2006). quant-ph/0506073

    Google Scholar 

  42. Verstraete, F., Dehaene, J., De Moor, B., Verschelde, H.: Four qubits can be entangled in nine different ways. Phys. Rev. A 65, 052112 (2002)

    Article  MathSciNet  ADS  Google Scholar 

  43. Osterloh, A., Siewert, J., Uhlmann, A.: Tangles of superpositions and the convex-roof extension. Phys. Rev. A 77, 032310 (2008). arXiv:0710.5909 (quant-ph)

    Article  ADS  Google Scholar 

  44. Hiriart-Urruty, J.-B., Lemaréchal, C.L.: Convex Analysis and Minimization Algorithms. Springer, Berlin, (1996)

    Google Scholar 

  45. C. Eltschka and J. Siewert, Monogamy equalities for qubit entanglement from Lorentz invariance. arXiv:1407.8195 (quant-ph)

Download references

Acknowledgments

This research was supported by the Basic Science Research Program through the National Research Foundation of Korea(NRF) funded by the Ministry of Education, Science and Technology(2011-0011971).

Author information

Authors and Affiliations

  1. Department of Electronic Engineering, Kyungnam University, Changwon, 631-701, Korea

    Eylee Jung & DaeKil Park

  2. Department of Physics, Kyungnam University, Changwon, 631-701, Korea

    DaeKil Park

Authors
  1. Eylee Jung
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. DaeKil Park
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to DaeKil Park.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jung, E., Park, D. Entanglement of four-qubit rank-2 mixed states. Quantum Inf Process 14, 3317–3333 (2015). https://doi.org/10.1007/s11128-015-1039-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11128-015-1039-4

Keywords

Search

Navigation