Asymmetric “4+2” protocol for quantum key distribution with finite resources

Abstract

In this paper, we present an asymmetric “4+2” protocol for quantum key distribution with finite photon pulses. The main work of this paper focuses on the composable security proof for this protocol in a finite-key scenario. Based on the essence security basis of the original “4+2” protocol proposed by Huttner et al. (Phys Rev A 51(3):1863–1869, 1995), we first develop the squashing model for this protocol with the quantum non-demolition measure theory. From this model, against the collective photon-number-splitting attack, we then provide the security proof (formulas of finite-key security bounds) for this protocol. The expected performance of this protocol are also evaluated on a priori reasonable expected values of parameters. Our work shows that the performance we derived is the lower one and it can cover long distances in the lossy channel.

Appendix

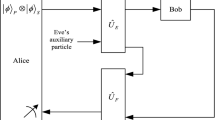
As shown in Fig. 1, the process of coherent pulses preparation (by Alice) and measurement (by Bob) states the following: The relatively strong coherent pulse $\left| {\hbox {e}^{i\theta _0 }\sqrt{3\mu _1 }} \right\rangle$ in the path 0 is described by a field operator $a_0^\dagger$. The transformation for $a_0^\dagger$ in terms of the creation operators $a_1^\dagger$ and $a_2^\dagger$ of the upper and lower paths (labeled by 1 and 2, respectively) is

$$\begin{aligned} a_0^\dagger \rightarrow ^{BS_1 }\hbox {e}^{i\theta _1 }\frac{\sqrt{3}}{3}a_1^\dagger +\frac{\sqrt{6}}{3}a_2^\dagger . \end{aligned}$$

(19)

The transformation for $a_2^\dagger$ in terms of the creation operators $a_3^\dagger$ and $a_4^\dagger$ (operators of BS$_{2}$ for the paths 3 and 4) is

$$\begin{aligned} a_2^\dagger \rightarrow ^{BS_2 }\hbox {e}^{i\theta _2 }\frac{1}{\sqrt{2}}a_3^\dagger +\frac{1}{\sqrt{2}}a_4^\dagger . \end{aligned}$$

(20)

While the transformations for the operators $a_1^\dagger$ and $a_3^\dagger$ in terms of the creation operators $a_5^\dagger$ and $a_6^\dagger$ (operators of the BS3 for the paths 5 and 6) is, respectively, given by

$$\begin{aligned} a_1^\dagger \rightarrow ^{BS_3 }\hbox {e}^{i\theta _3} \frac{1}{\sqrt{2}}a_5^\dagger +\frac{1}{\sqrt{2}}a_6^\dagger . \end{aligned}$$

(21)

$$\begin{aligned} a_3^\dagger \rightarrow ^{BS_3 }\frac{1}{\sqrt{2}}a_5^\dagger -\hbox {e}^{-i\theta _3 }\frac{1}{\sqrt{2}}a_6^\dagger . \end{aligned}$$

(22)

Where $\theta _1, \theta _2, \theta _3$ represent, respectively, the phase shift due to beam splitter reflection (for simplicity, another term of phase shift due to path length and the transmission in beam splitters are neglected). From the above discussion, we obtain the transformation operator of the QKD system:

$$\begin{aligned} \frac{1}{\sqrt{2}}\left[ \hbox {e}^{i(\theta _1 +\theta _3 +\phi _A )}+\hbox {e}^{i(\theta _2 +\phi _B )}\right] a_5^\dagger +\frac{1}{\sqrt{2}}[\hbox {e}^{i(\theta _1 +\phi _A )}-\hbox {e}^{i(\theta _2 -\theta 3+\phi _B )}]a_6^\dagger , \end{aligned}$$

(23)

where beam splitters are chosen such that the phase shift in the upper path compensates the phase shift in the lower path($\theta _1 +\theta _3 =\theta _2 )$. Then, if Alice prepares the state $\left| {\hbox {e}^{i\theta _0 }\sqrt{3\mu _1 }} \right\rangle$ in the path 0, the outgoing state $\left| {\psi _{lj}^{\prime } } \right\rangle$ in the paths 5 and 6 is given by

$$\begin{aligned}&\left| {\psi _{lj}^{\prime } } \right\rangle =\left| {\frac{1}{\sqrt{2}}\left[ \hbox {e}^{i(\theta _1 +\theta _3 +\phi _{A_j } )}+\hbox {e}^{i(\theta _2 +\phi _{B_j } )}\right] \sqrt{\mu _1 }} \right\rangle _5 \nonumber \\&\left| {\frac{1}{\sqrt{2}}[\hbox {e}^{i(\theta _1 +\phi _{A_j } )}-\hbox {e}^{i(\theta _2 -\theta _3 +\phi _{B_j } )}]\sqrt{\mu _1 }} \right\rangle _6, \end{aligned}$$

(24)

where $\phi _{A_j }$ and $\phi _{B_j}$ represents, respectively, the encoding phase modulation (used by Alice) and the decoding phase modulation (used by Bob). The outgoing state can also be written in the form

$$\begin{aligned}&\left| {\psi _{lj}^{\prime } } \right\rangle =\left| {\hbox {e}^{i\left( \frac{\theta _1 +\theta _2 +\theta _3 +\phi _{A_j } +\phi _{B_j } }{2}\right) }\cos \left( \frac{\Delta \phi }{2}\right) \sqrt{2\mu _1 }} \right\rangle _5,\end{aligned}$$

(25)

$$\begin{aligned}&\left| {\psi _{lj}^{\prime } } \right\rangle =\left| {\hbox {e}^{i\left( \frac{\theta _1 +\theta _2 -\theta _3 +\phi _{A_j } +\phi _{B_j } }{2}\right) }\sin \left( \frac{\Delta \phi }{2}\right) \sqrt{2\mu _1 }} \right\rangle _6, \end{aligned}$$

(26)

where $\Delta \phi =\phi _{A_j } -\phi _{B_j }$ means the inner phase shift of two-beam interference. The state of the RP that enters D(2) is $\left| {\hbox {e}^{i\theta _0 }\sqrt{\mu _1 }} \right\rangle$. It is easy to figure out that clicks will occur in detector D(0) if $\phi _{A_j } =0, \phi _{B_j } =0$ or $\phi _{A_j } =\pi /2, \phi _{B_j} =\pi /2$ and other results can be similarly obtained, while there will be random clicks in D(0) or D(1) with equal probability for the cases that unmatched phases for decoding are used by Bob and the corresponding bits will be discarded in key sifting procedures. From the above discussion, the specific form of the POVM elements for both the full optical measurement and the equivalent squashing model can be obtained.