Affirmative action in large population tullock contests

Abstract

We compare equal treatment and affirmative action policies in Tullock contests. Equal treatment means that agents who exert equal effort have an equal probability of success. In affirmative action, agents who incur an equal cost of effort have an equal probability of success. Finite player contests with non-linearities in impact and cost functions cannot be solved in closed form. Instead, we approximate them with large population contests with measure zero agents. Affirmative action reduces aggregate effort in such contests, which can be solved. However, it ensures equality without any significant loss of aggregate welfare. We verify these findings for finite player contests through numerical simulations. For a sufficiently large number of players, the numerical simulations support the results of the large population analysis.

Appendix

1.1 Proofs

Proof of Proposition 3.2

Both parts follow from (11). Recall from (5) and (7) respectively that under equal treatment, the bias parameters are $\theta _p=1$ and under affirmative action, $\theta _p=k_p^{\frac{r}{\gamma }}$. Hence, for part (1), we apply $\theta _p=1$ while for part (2), we apply $\theta _p=k_p^{\frac{r}{\gamma }}$. $\square$

Proof of Corollary 4.1

The fact that ${\hat{\alpha }}_p^{*}>\alpha _p^{*}$ if and only if $k_p>{\bar{k}}$ follows from a direct comparison of (12) and (13). Furthermore, $k_1<k_2<\cdots <k_n$, $r<\gamma$ and $\sum _{q\in \mathcal {P}}m_q=1$ imply that $k_1<{\bar{k}}<k_n$. Hence, it must be that ${\hat{\alpha }}_1^{*}<\alpha _1^{*}$ and ${\hat{\alpha }}_n^{*}>\alpha _n^{*}$. $\square$

Proof of Proposition 4.2

Comparing (15) and (16), it is evident that (17) will be proven if we can show that

$$\begin{aligned} \frac{\sum _{p\in \mathcal {P}}m_pk_p^{\frac{1}{r-\gamma }}}{\left( \sum _{q\in \mathcal {P}}m_qk_q^{\frac{r}{r-\gamma }}\right) ^{\frac{1}{\gamma }}}>\left( \sum _{p\in \mathcal {P}}\frac{m_p}{k_p^{\frac{1}{\gamma }}}\right) . \end{aligned}$$

(27)

Note that if $r=0$, the two sides of (27) are equal. Moreover, the RHS of (27) is independent of r. Hence, to establish this inequality, it suffices to show that the LHS of (27) is strictly increasing in r.

For this purpose, recall our assumption that $k_1<k_2<\cdots <k_n$. Through some tedious algebra, we then calculate

$$\begin{aligned}&\frac{\partial }{\partial r}\left( \frac{\sum _{p\in \mathcal {P}}m_pk_p^{\frac{1}{r-\gamma }}}{\left( \sum _{q\in \mathcal {P}}m_qk_q^{\frac{r}{r-\gamma }}\right) ^{\frac{1}{\gamma }}}\right) \nonumber \\ =&\frac{\left( \sum _pm_pk_p^{\frac{r}{r-\gamma }}\right) ^{\frac{-1}{\gamma }}\sum _p\sum _{q>p}\left( m_pm_q(\log k_q-\log k_p)k_p^{\frac{r}{r-\gamma }}k_q^{\frac{r}{r-\gamma }}\right) \left( k_p^{\frac{1-r}{r-\gamma }}-k_q^{\frac{1-r}{r-\gamma }}\right) }{(\gamma -r)^2\sum _pm_pk_p^{\frac{r}{r-\gamma }}}>0, \end{aligned}$$

given our assumptions that $k_p<k_q$ if $p<q$ and $r<\gamma$. Thus, (27) holds for all $r\in (0,1]$ and $\gamma \ge 1$ with the additional restriction that both r and $\gamma$ are not equal to 1. $\square$

Proof of Proposition 4.3

• 1. The Nash equilibrium effort level $\alpha _p^{*}$ under equal treatment is given by (12). Every agent of type p exerts this effort level. Further, $\theta _p=1$ at this Nash equilibrium. Hence, the aggregate impact (3) at the corresponding Nash equilibrium $\mu ^{*}$ is

  $$\begin{aligned} A(\mu ^{*})=\sum _{p\in \mathcal {P}}m_p(\alpha _p^{*})^r=\left( \frac{rV}{\gamma }\right) ^\frac{r}{\gamma }\left( \sum _{p\in \mathcal {P}}m_pk_p^{\frac{r}{r-\gamma }}\right) ^{1-\frac{r}{\gamma }}. \end{aligned}$$

  (28)

  Therefore, the CSF at $\mu ^{*}$ for a type p agent is $\frac{(\alpha _p^{*})^r}{A(\mu ^{*})}=\frac{k_p^{\frac{r}{r-\gamma }}}{\sum _{q\in \mathcal {P}}m_qk_q^{\frac{r}{r-\gamma }}}$. The equilibrium cost of effort is

  $$\begin{aligned} k_p(\alpha _p^{*})^{\gamma }=\frac{rV}{\gamma }\frac{k_p^{\frac{r}{r-\gamma }}}{\sum _{q\in \mathcal {P}}k_q^{\frac{r}{r-\gamma }}}. \end{aligned}$$

  (29)

  The equilibrium payoff $F_{\alpha ^{*}_p,p}(\mu _p^{*})$ then follows from the definition of F in (5). For aggregate payoff, we apply (18) to $\mu ^{*}$. From (29), we obtain the aggregate cost

  $$\begin{aligned} \sum _p\int _{\mathcal {S}}k_px^{\gamma }\mu _p^{*}(dx)=\sum _p m_pk_p(\alpha _p^{*})^{\gamma }=\frac{rV}{\gamma }. \end{aligned}$$

  (30)

  Hence, aggregate payoff at $\mu ^{*}$ is

  $$\begin{aligned}{\bar{F}}(\mu ^{*})=V-\sum _p\int _{\mathcal {S}}k_px^{\gamma }\mu _p^{*}(dx)=V-\frac{rV}{\gamma }=V\left( 1-\frac{r}{\gamma }\right) .\end{aligned}$$

• 2. The Nash equilibrium effort level ${\hat{\alpha }}_p^{*}$ under affirmative action is given by (13). Every agent of type p exerts this effort level. Hence, the aggregate impact (3) at the corresponding Nash equilibrium ${\hat{\mu }}^{*}$ is given by

  $$\begin{aligned} A({\hat{\mu }}^{*})=\sum _{p}m_pk_p^{\frac{r}{\gamma }}k_p^{\frac{-r}{\gamma }}\left( \frac{rV}{\gamma }\right) ^{\frac{r}{\gamma }}=\left( \frac{rV}{\gamma }\right) ^{\frac{r}{\gamma }} \end{aligned}$$

  (31)

  Therefore, the CSF at $\mu ^{*}$ for a type p agent is $\frac{k_p^{\frac{r}{\gamma }}({\hat{\alpha }}_p^{*})^r}{A({\hat{\mu }}^{*})}=1$. The equilibrium cost of effort is

  $$\begin{aligned} k_p{\hat{\alpha }}_p^{*\gamma }=\frac{rV}{\gamma }. \end{aligned}$$

  (32)

  The equilibrium payoff ${\hat{F}}_{{\hat{\alpha }}^{*}_p,p}({\hat{\mu }}_p^{*})$ then follows from the definition of ${\hat{F}}$ in (7). For aggregate payoff, we apply (18) to ${\hat{\mu }}^{*}$. From (32), we obtain the aggregate cost

  $$\begin{aligned} \sum _p\int _{\mathcal {S}}k_px^{\gamma }{\hat{\mu }}_p^{*}(dx)=\sum _p m_pk_p({\hat{\alpha }}_p^{*})^\gamma =\frac{rV}{\gamma }. \end{aligned}$$

  (33)

  Hence, aggregate payoff at ${\hat{\mu }}^{*}$ is

  $$\begin{aligned} {\bar{F}}({\hat{\mu }}^{*})=V-\sum _p\int _{\mathcal {S}}k_px^{\gamma }{\hat{\mu }}_p^{*}(dx)=V-\frac{rV}{\gamma }=V\left( 1-\frac{r}{\gamma }\right) .\end{aligned}$$

The fact that ${\hat{F}}_{{\hat{\alpha }}_p^{*},p}({\hat{\mu }}^{*})>F_{\alpha _p^{*},p}(\mu ^{*})$ if and only if $k_p>{\bar{k}}$ then follows from direct comparison of (19) and (21). $\square$

Proof of Proposition 6.1

If $\gamma =1$, then $r<1$ in (12) and (13). Then, (24) follows from (13) by taking $\gamma =1$ and $r\rightarrow 1$.

To establish (23), we note that we can write (12) as

$$\begin{aligned} \alpha _p^{*}=\left( \frac{rV}{\sum _{q\in \mathcal {P}}\frac{m_q}{k_q^{\frac{r}{1-r}}}}\right) k_p^{\frac{-1}{1-r}}. \end{aligned}$$

(34)

If r is close to 1, then $\sum _{q\in \mathcal {P}}\frac{m_q}{k_q^{\frac{r}{1-r}}}\approx \frac{m_1}{k_1^{\frac{r}{1-r}}}$ due to $k_1<k_2<\cdots <k_n$. Hence, for r close to 1, (34) approximates

$$\begin{aligned} rV\frac{k_1^{\frac{r}{1-r}}}{m_1}\frac{1}{k_p^{\frac{1}{1-r}}}. \end{aligned}$$

(35)

If $p=1$, then (35) equals $\frac{rV}{m_1k_1}$. Hence, as $r\rightarrow 1$, $\alpha _1^{*}\rightarrow \frac{V}{m_1k_1}$. On the other hand, if $p>1$, then by (35), $\alpha _p^{*}\rightarrow 0$ due to $k_1<k_p$. This establishes (23).

We now verify that the effort levels characterized in (23) and (24) constitute a Nash equilibrium in F and ${\hat{F}}$ respectively when $r=\gamma =1$. First, consider (23) and note from the first payoff in (5) that at the corresponding Nash equilibrium $\mu ^{*}$ in the equal treatment contest, $\sum _{q\in \mathcal {P}}\int _{\mathcal {S}}x^r\mu _q^{*}(dx)=m_1\frac{V}{m_1k_1}=\frac{V}{k_1}$. This is due to $\alpha _p^{*}=0$ for all $p>1$. Straightforward calculation using (5) then shows that $F_{x,1}(\mu ^{*})=0$ for all $x\in \mathcal {S}$. For $p>1$, $F_{x,p}(\mu ^{*})=(k_1-k_p)x$, which is maximized at $x=0$ due to $k_1<k_p$. Therefore, at $\mu ^{*}$, when all agents exert effort levels (23), they play a payoff maximizer in F when $r=\gamma =1$.

Now consider (24) and note from the first payoff in (7) that at the corresponding Nash equilibrium ${\hat{\mu }}^{*}$ in the affirmative action contest, $\sum _{q\in \mathcal {P}}\int _{\mathcal {S}}k_q^{\frac{r}{\gamma }}x^r{\hat{\mu }}_q^{*}(dx)=\sum _{q\in \mathcal {P}}m_qk_q\frac{V}{k_q}=V$. We then obtain from (7) that for all $p\in \mathcal {P}$, ${\hat{F}}_{x,p}({\hat{\mu }}^{*})=0$. Hence, for all $p\in \mathcal {P}$, the effort levels (24) constitute a payoff maximizer in ${\hat{F}}$ when $r=\gamma =1$. $\square$

Proof of Proposition 6.2

Given (25) and (26), we need to show

$$\begin{aligned} \frac{V}{k_1}>V\sum _{p\in \mathcal {P}}\frac{m_p}{k_p}&\Leftrightarrow \frac{1}{k_1}>\sum _{p\in \mathcal {P}}\frac{m_p}{k_p}\\&\Leftrightarrow \sum _{p\in \mathcal {P}}\frac{m_p}{k_1}>\sum _{p\in \mathcal {P}}\frac{m_p}{k_p}, \end{aligned}$$

which is true because $k_1<k_2<\cdots <k_n$. $\square$

1.2 Numerical calculations

Consider the general finite player contest (1). Let $N_q$ be the number of type q agents. A symmetry argument implies that at the unique Nash equilibrium of (1), every agent of a type q will play the identical effort level ${\tilde{x}}_q^{*}$. The n first-order conditions that determine the Nash equilibrium effort levels are then

$$\begin{aligned} \frac{\theta _prV{\tilde{x}}_p^{r-1}}{\sum _{q\in \mathcal {P}}N_q\theta _q{\tilde{x}}_q^r}-\frac{\theta _p^2rV{\tilde{x}}_p^{2r-1}}{\left( \sum _{q\in \mathcal {P}}N_q\theta _q{\tilde{x}}_q^r\right) ^2}=\kappa _p\gamma {\tilde{x}}_p^{\gamma -1}. \end{aligned}$$

(36)

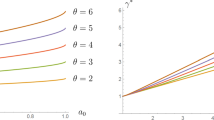
In Sect. 5, we have three types with $N_1=N_2=N_3$ and $N=N_1+N_2+N_3$. Further, the parameter values are $\{V,r,\gamma \}=\{100,0.8,1.2\}$ and $\{\kappa _1,\kappa _2,\kappa _3\}=\{1,2,3\}$. In the equal treatment contest (6), $\theta _p=1$ for all $p\in \mathcal {P}$ while in the affirmative action contest (9), $\theta _p=\kappa _p^{\frac{r}{\gamma }}$ (see (8)). Hence, under affirmative equation, $\{\theta _1,\theta _2,\theta _3\}=\{0.8637, 1.3711, 1.7966\}$. With these parameter values, we can solve the system of FOCs (36) to obtain the Nash equilibrium effort levels under both equal treatment and affirmative action in the finite player contests. Applying those effort levels to (6) and (9) would then give us the equilibrium type–specific payoffs under equal treatment and affirmative action, respectively.

We specify those equilibrium levels of effort and payoff below for the different values of N considered in Tables 1 and 2. We denote by $x^{*}_p$ and ${\hat{x}}^{*}_p$ the Nash equilibrium effort level of a type p agent under equal treatment and affirmative action respectively. Similarly, we denote by $\pi ^{*}_p$ and ${\hat{\pi }}^{*}_p$ the Nash equilibrium effort level of a type p agent under equal treatment and affirmative action, respectively. Aggregate effort in the two finite player contests are then respectively $\sum _{q\in \mathcal {P}}N_q x^{*}_q$ and $\sum _{q\in \mathcal {P}}N_q{\hat{x}}^{*}_q$ (Table 1) while aggregate payoffs are $\sum _{q\in \mathcal {P}}N_q\pi ^{*}_q$ and $\sum _{q\in \mathcal {P}}N_q{\hat{\pi }}^{*}_q$ (Table 2).

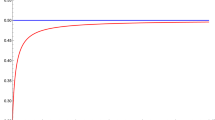
Also recall that for the large population contests, the cost parameters are $k_p=\frac{\kappa _p}{N^{\gamma -1}}$ and that the type distribution is $(m_1,m_2,m_3)=\left( \frac{1}{3},\frac{1}{3},\frac{1}{3}\right)$. By (19), equilibrium payoffs of the three types in the large population equal treatment contest are $(F_1^{*},F_2^{*},F_3^{*})=(73.4694, 18.3673, 8.1633)$. By (21), the equilibrium payoff of all agents of all types in the large population affirmative action contest is $V\left( 1-\frac{r}{\gamma }\right) =33.3333$. Hence, by Proposition 4.3, the aggregate payoff in both large population contests is $V\left( 1-\frac{r}{\gamma }\right) =33.3333$.

• 1. $N_1=N_2=N_3=1$. Under equal treatment, $(x^{*}_1,x^{*}_2,x^{*}_3)=(10.4014,5.0161,2.6691)$ and $(\pi _1^{*},\pi _2^{*},\pi _3^{*})=(36.1602, 15.5972, 8.0322)$. Hence, aggregate effort is $\sum _{q\in \mathcal {P}}N_q x^{*}_q=18.0866$, while aggregate payoff is $\sum _{q\in \mathcal {P}}N_q\pi ^{*}_q=59.7896$. Under affirmative action, $({\hat{x}}^{*}_1,{\hat{x}}^{*}_2,{\hat{x}}^{*}_3)=(9.4532, 5.3054, 3.7842)$. Equilibrium payoff is ${\hat{\pi }}_p^{*}=18.5185$ for all $p\in \mathcal {P}$. Hence, aggregate effort is $\sum _{q\in \mathcal {P}}N_q {\hat{x}}^{*}_q=18.5429$ while aggregate payoff is $\sum _{q\in \mathcal {P}}N_q{\hat{\pi }}^{*}_q=55.5556$. Note that $N=N_1+N_2+N_3=3$. Therefore, for the large population contests, $(k_1,k_2,k_3)=\left( \frac{\kappa _1}{N^{\gamma -1}},\frac{\kappa _2}{N^{\gamma -1}},\frac{\kappa _3}{N^{\gamma -1}}\right) =(0.8027, 1.6055, 2.4082)$. Hence, applying (12), we obtain $(\alpha _1^{*},\alpha _2^{*},\alpha _3^{*})=(76.8187, 13.5798, 4.9279)$, the large population Nash equilibrium levels of effort under equal treatment. The aggregate effort level is then $\sum _{p\in \mathcal {P}}m_p\alpha _p^{*}=31.7755$. Applying (13), we obtain $({\hat{\alpha }}_1^{*},{\hat{\alpha }}_2^{*},{\hat{\alpha }}_3^{*})=(39.7598, 22.3144, 15.9163)$, the large population Nash equilibrium levels of effort under affirmative action. The aggregate effort level is then $\sum _{p\in \mathcal {P}}m_p{\hat{\alpha }}_p^{*}=25.9969$.

• 2. $N_1=N_2=N_3=10$. Under equal treatment, $(x^{*}_1,x^{*}_2,x^{*}_3)=(3.4421,0.6961,0.2596)$ and $(\pi _1^{*},\pi _2^{*},\pi _3^{*})=(2.7104, 0.6868, 0.3055)$. Hence, aggregate effort is $\sum _{q\in \mathcal {P}}N_q x^{*}_q=43.9793$ while aggregate payoff is $\sum _{q\in \mathcal {P}}N_q\pi ^{*}_q=37.0269$. Under affirmative action, $({\hat{x}}^{*}_1,{\hat{x}}^{*}_2,{\hat{x}}^{*}_3)=(1.8911, 1.0614, 0.757)$. Equilibrium payoff is ${\hat{\pi }}_p^{*}=1.1852$ for all $p\in \mathcal {P}$. Hence, aggregate effort is $\sum _{q\in \mathcal {P}}N_q {\hat{x}}^{*}_q=37.0952$, while aggregate payoff is $\sum _{q\in \mathcal {P}}N_q{\hat{\pi }}^{*}_q=35.5556$. Note that $N=N_1+N_2+N_3=30$. Therefore, for the large population contests, $(k_1,k_2,k_3)=\left( \frac{\kappa _1}{N^{\gamma -1}},\frac{\kappa _2}{N^{\gamma -1}},\frac{\kappa _3}{N^{\gamma -1}}\right) =(0.5065, 1.013, 1.5195)$. Hence, applying (12), we obtain $(\alpha _1^{*},\alpha _2^{*},\alpha _3^{*})=(112.755, 19.9324, 7.2332)$, the large population Nash equilibrium levels of effort under equal treatment. The aggregate effort level is then $\sum _{p\in \mathcal {P}}m_p\alpha _p^{*}=46.64$. Applying (13), we obtain $({\hat{\alpha }}_1^{*},{\hat{\alpha }}_2^{*},{\hat{\alpha }}_3^{*})=(58.3594, 32.7531, 23.362)$, the large population Nash equilibrium levels of effort under affirmative action. The aggregate effort level is then $\sum _{p\in \mathcal {P}}m_p{\hat{\alpha }}_p^{*}=38.1582$.

• 3. $N_1=N_2=N_3=50$. Under equal treatment, $(x^{*}_1,x^{*}_2,x^{*}_3)=(0.966, 0.1755, 0.064)$ and $(\pi _1^{*},\pi _2^{*},\pi _3^{*})=(0.501, 0.1253, 0.0557)$. Hence, aggregate effort is $\sum _{q\in \mathcal {P}}N_q x^{*}_q=60.2752$, while aggregate payoff is $\sum _{q\in \mathcal {P}}N_q\pi ^{*}_q=34.0998$. Under affirmative action, $({\hat{x}}^{*}_1,{\hat{x}}^{*}_2,{\hat{x}}^{*}_3)=(0.5059, 0.2839, 0.2025)$. Equilibrium payoff is ${\hat{\pi }}_p^{*}=0.2252$ for all $p\in \mathcal {P}$. Hence, aggregate effort is $\sum _{q\in \mathcal {P}}N_q {\hat{x}}^{*}_q=49.6206$, while aggregate payoff is $\sum _{q\in \mathcal {P}}N_q{\hat{\pi }}^{*}_q=33.7778$. Note that $N=N_1+N_2+N_3=150$. Therefore, for the large population contests, $(k_1,k_2,k_3)=\left( \frac{\kappa _1}{N^{\gamma -1}},\frac{\kappa _2}{N^{\gamma -1}},\frac{\kappa _3}{N^{\gamma -1}}\right) =(0.3671, 0.7342, 1.1013)$. Hence, applying (12), we obtain $(\alpha _1^{*},\alpha _2^{*},\alpha _3^{*})=(147.445, 26.0648, 9.4586)$, the large population Nash equilibrium levels of effort under equal treatment. The aggregate effort level is then $\sum _{p\in \mathcal {P}}m_p\alpha _p^{*}=60.9893$. Applying (13), we obtain $({\hat{\alpha }}_1^{*},{\hat{\alpha }}_2^{*},{\hat{\alpha }}_3^{*})=(76.3143, 42.8299, 30.5495)$, the large population Nash equilibrium levels of effort under affirmative action. The aggregate effort level is then $\sum _{p\in \mathcal {P}}m_p{\hat{\alpha }}_p^{*}=49.8979$.

• 4. $N_1=N_2=N_3=100$. Under equal treatment, $(x^{*}_1,x^{*}_2,x^{*}_3)=(0.5469, 0.098, 0.0357)$ and $(\pi _1^{*},\pi _2^{*},\pi _3^{*})=(0.2477, 0.0619, 0.0275)$. Hence, aggregate effort is $\sum _{q\in \mathcal {P}}N_q x^{*}_q=68.0562$, while aggregate payoff is $\sum _{q\in \mathcal {P}}N_q\pi ^{*}_q=33.7183$. Under affirmative action, $({\hat{x}}^{*}_1,{\hat{x}}^{*}_2,{\hat{x}}^{*}_3)=(0.2847, 0.1598, 0.114)$. Equilibrium payoff is ${\hat{\pi }}_p^{*}=0.1119$ for all $p\in \mathcal {P}$. Hence, aggregate effort is $\sum _{q\in \mathcal {P}}N_q {\hat{x}}^{*}_q=55.8529$, while aggregate payoff is $\sum _{q\in \mathcal {P}}N_q{\hat{\pi }}^{*}_q=33.5556$. Note that $N=N_1+N_2+N_3=300$. Therefore, for the large population contests, $(k_1,k_2,k_3)=\left( \frac{\kappa _1}{N^{\gamma -1}},\frac{\kappa _2}{N^{\gamma -1}},\frac{\kappa _3}{N^{\gamma -1}}\right) =(0.3196, 0.6392, 0.9587)$. Hence, applying (12), we obtain $(\alpha _1^{*},\alpha _2^{*},\alpha _3^{*})=(165.501, 29.2567, 10.6169)$, the large population Nash equilibrium levels of effort under equal treatment. The aggregate effort level is then $\sum _{p\in \mathcal {P}}m_p\alpha _p^{*}=68.4582$. Applying (13), we obtain $({\hat{\alpha }}_1^{*},{\hat{\alpha }}_2^{*},{\hat{\alpha }}_3^{*})=(85.6599, 48.075, 34.2907)$, the large population Nash equilibrium levels of effort under affirmative action. The aggregate effort level is then $\sum _{p\in \mathcal {P}}m_p{\hat{\alpha }}_p^{*}=56.0085$.

• 5. $N_1=N_2=N_3=200$. Under equal treatment, $(x^{*}_1,x^{*}_2,x^{*}_3)=(0.3083, 0.0549, 0.0199)$ and $(\pi _1^{*},\pi _2^{*},\pi _3^{*})=(0.1232, 0.0308, 0.0137)$. Hence, aggregate effort is $\sum _{q\in \mathcal {P}}N_q x^{*}_q=76.6157$, while aggregate payoff is $\sum _{q\in \mathcal {P}}N_q\pi ^{*}_q=33.5263$. Under affirmative action, $({\hat{x}}^{*}_1,{\hat{x}}^{*}_2,{\hat{x}}^{*}_3)=(0.16, 0.0898, 0.064)$. Equilibrium payoff is ${\hat{\pi }}_p^{*}=0.0557$ for all $p\in \mathcal {P}$. Hence, aggregate effort is $\sum _{q\in \mathcal {P}}N_q {\hat{x}}^{*}_q=62.7801$, while aggregate payoff is $\sum _{q\in \mathcal {P}}N_q{\hat{\pi }}^{*}_q=33.4444$. Note that $N=N_1+N_2+N_3=600$. Therefore, for the large population contests, $(k_1,k_2,k_3)=\left( \frac{\kappa _1}{N^{\gamma -1}},\frac{\kappa _2}{N^{\gamma -1}},\frac{\kappa _3}{N^{\gamma -1}}\right) =(0.2782, 0.5564, 0.8346)$. Hence, applying (12), we obtain $(\alpha _1^{*},\alpha _2^{*},\alpha _3^{*})=(185.769, 32.8396, 11.9171)$, the large population Nash equilibrium levels of effort under equal treatment. The aggregate effort level is then $\sum _{p\in \mathcal {P}}m_p\alpha _p^{*}=76.8417$. Applying (13), we obtain $({\hat{\alpha }}_1^{*},{\hat{\alpha }}_2^{*},{\hat{\alpha }}_3^{*})=(96.15, 53.9623, 38.49)$, the large population Nash equilibrium levels of effort under affirmative action. The aggregate effort level is then $\sum _{p\in \mathcal {P}}m_p{\hat{\alpha }}_p^{*}=62.8674$.

• 6. $N_1=N_2=N_3=500$. Under equal treatment, $(x^{*}_1,x^{*}_2,x^{*}_3)=(0.144, 0.0255, 0.0093)$ and $(\pi _1^{*},\pi _2^{*},\pi _3^{*})=(0.0491, 0.0123, 0.0054)$. Hence, aggregate effort is $\sum _{q\in \mathcal {P}}N_q x^{*}_q=89.4147$, while aggregate payoff is $\sum _{q\in \mathcal {P}}N_q\pi ^{*}_q=33.4106$. Under affirmative action, $({\hat{x}}^{*}_1,{\hat{x}}^{*}_2,{\hat{x}}^{*}_3)=(0.0746, 0.04189, 0.02988)$. Equilibrium payoff is ${\hat{\pi }}_p^{*}=0.0223$ for all $p\in \mathcal {P}$. Hence, aggregate effort is $\sum _{q\in \mathcal {P}}N_q {\hat{x}}^{*}_q=73.1994$, while aggregate payoff is $\sum _{q\in \mathcal {P}}N_q{\hat{\pi }}^{*}_q=33.3778$. Note that $N=N_1+N_2+N_3=1500$. Therefore, for the large population contests, $(k_1,k_2,k_3)=\left( \frac{\kappa _1}{N^{\gamma -1}},\frac{\kappa _2}{N^{\gamma -1}},\frac{\kappa _3}{N^{\gamma -1}}\right) =(0.2316, 0.4632, 0.6949)$. Hence, applying (12), we obtain $(\alpha _1^{*},\alpha _2^{*},\alpha _3^{*})=(216.419, 38.2579, 13.8833)$, the large population Nash equilibrium levels of effort under equal treatment. The aggregate effort level is then $\sum _{p\in \mathcal {P}}m_p\alpha _p^{*}=89.5201$. Applying (13), we obtain $({\hat{\alpha }}_1^{*},{\hat{\alpha }}_2^{*},{\hat{\alpha }}_3^{*})=(112.014, 62.8658, 44.8406)$, the large population Nash equilibrium levels of effort under affirmative action. The aggregate effort level is then $\sum _{p\in \mathcal {P}}m_p{\hat{\alpha }}_p^{*}=73.2401$.

• 7. $N_1=N_2=N_3=800$. Under equal treatment, $(x^{*}_1,x^{*}_2,x^{*}_3)=(0.097, 0.0173, 0.0063)$ and $(\pi _1^{*},\pi _2^{*},\pi _3^{*})=(0.03066, 0.0077, 0.0034)$. Hence, aggregate effort is $\sum _{q\in \mathcal {P}}N_q x^{*}_q=96.7432$, while aggregate payoff is $\sum _{q\in \mathcal {P}}N_q\pi ^{*}_q=33.3817$. Under affirmative action, $({\hat{x}}^{*}_1,{\hat{x}}^{*}_2,{\hat{x}}^{*}_3)=(0.0505, 0.0283, 0.0202)$. Equilibrium payoff is ${\hat{\pi }}_p^{*}=0.0139$ for all $p\in \mathcal {P}$. Hence, aggregate effort is $\sum _{q\in \mathcal {P}}N_q {\hat{x}}^{*}_q=79.1805$, while aggregate payoff is $\sum _{q\in \mathcal {P}}N_q{\hat{\pi }}^{*}_q=33.3611$. Note that $N=N_1+N_2+N_3=2400$. Therefore, for the large population contests, $(k_1,k_2,k_3)=\left( \frac{\kappa _1}{N^{\gamma -1}},\frac{\kappa _2}{N^{\gamma -1}},\frac{\kappa _3}{N^{\gamma -1}}\right) =(0.2108, 0.4217, 0.6326)$. Hence, applying (12), we obtain $(\alpha _1^{*},\alpha _2^{*},\alpha _3^{*})=(234.054, 41.3752, 15.0146)$, the large population Nash equilibrium levels of effort under equal treatment. The aggregate effort level is then $\sum _{p\in \mathcal {P}}m_p\alpha _p^{*}=96.8145$. Applying (13), we obtain $({\hat{\alpha }}_1^{*},{\hat{\alpha }}_2^{*},{\hat{\alpha }}_3^{*})=(121.141, 67.9883, 48.4944)$, the large population Nash equilibrium levels of effort under affirmative action. The aggregate effort level is then $\sum _{p\in \mathcal {P}}m_p{\hat{\alpha }}_p^{*}=79.208$.

• 8. $N_1=N_2=N_3=1000$. Under equal treatment, $(x^{*}_1,x^{*}_2,x^{*}_3)=(0.0809, 0.0143, 0.0052)$ and $(\pi _1^{*},\pi _2^{*},\pi _3^{*})=(0.0245, 0.0061, 0.0027)$. Hence, aggregate effort is $\sum _{q\in \mathcal {P}}N_q x^{*}_q=100.424$, while aggregate payoff is $\sum _{q\in \mathcal {P}}N_q\pi ^{*}_q=33.372$. Under affirmative action, $({\hat{x}}^{*}_1,{\hat{x}}^{*}_2,{\hat{x}}^{*}_3)=(0.0419, 0.0235, 0.0168)$. Equilibrium payoff is ${\hat{\pi }}_p^{*}=0.0111$ for all $p\in \mathcal {P}$. Hence, aggregate effort is $\sum _{q\in \mathcal {P}}N_q {\hat{x}}^{*}_q=82.1864$, while aggregate payoff is $\sum _{q\in \mathcal {P}}N_q{\hat{\pi }}^{*}_q=33.3556$. Note that $N=N_1+N_2+N_3=3000$. Therefore, for the large population contests, $(k_1,k_2,k_3)=\left( \frac{\kappa _1}{N^{\gamma -1}},\frac{\kappa _2}{N^{\gamma -1}},\frac{\kappa _3}{N^{\gamma -1}}\right) =(0.2016, 0.4033, 0.6049)$. Hence, applying (12), we obtain $(\alpha _1^{*},\alpha _2^{*},\alpha _3^{*})=(242.922, 42.943, 15.5835)$, the large population Nash equilibrium levels of effort under equal treatment. The aggregate effort level is then $\sum _{p\in \mathcal {P}}m_p\alpha _p^{*}=100.483$. Applying (13), we obtain $({\hat{\alpha }}_1^{*},{\hat{\alpha }}_2^{*},{\hat{\alpha }}_3^{*})=(125.732, 70.5644, 50.3319)$, the large population Nash equilibrium levels of effort under affirmative action. The aggregate effort level is then $\sum _{p\in \mathcal {P}}m_p{\hat{\alpha }}_p^{*}=82.2093$.