Abstract
In random voting, the committee chair, whose vote decides in the case of a draw, is more often decisive than ordinary voters. Therefore, in the power indices literature, the committee chair is said to be more powerful. Players with a veto right are even more powerful still. Similarly, the production of threshold public goods may involve “tie-breaking players” (with more effective contributions) and “veto players” (specialists or larger players) whose contributions are necessary. We pose the question of whether power is beneficial for an individual. Except in the equilibrium where no player contributes, veto players are disadvantaged while tie-breaking players can be advantaged. In experiments with otherwise symmetric players, about 80% of the veto players contribute, but tie-breaking players also contribute almost as frequently as veto players, and significantly more frequently than ordinary players. Even with three times the costs of ordinary players, veto players stick to their behavior, while tie-breaking players reduce their contributions below those of ordinary players. Overall, powerful players always are worse off than ordinary players; thus, power seems not to pay off herein.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In the literature on public goods, symmetric games are the predominant focus, with only rare cases of asymmetry concerning contribution cost \(c_{i}\) and benefits from the production of the public good \(G_{i}\). We investigate another form of asymmetry, namely the individual importance of player i’s contribution to the production of a public good. Typically, only the sum of public good provision is important, but in most cases of cooperation, specialists can be critical for reaching the necessary threshold. For example, when building a house, you hire a predefined team of specialists (bricklayers, carpenters, plumbers, electricians, and so on) and cannot substitute one with another (e.g., an electrician with an additional bricklayer). If the possible set of players \(N=\{1,2,\ldots ,n\}\) contains only one electrician, it is crucial for the project that that person is on board (i.e., contributes).
Differential importance of contributions for the realization of a public good has been investigated in the field of voting. Player asymmetries concerning the outcome of a vote are interpreted as differences in power. Often, the committee chair has tie-breaking power in the case of a draw. Even more powerful are members with a veto right to block a majority vote.Footnote 1 Determining such power by power indices (Holler et al. 2001) is largely based on criteria that determine the likelihood of being included in more (minimal) winning coalitions than the other players. A tie-breaking player participates in more winning coalitions and a veto player participates in all of them. Power indices deliberately neglect structural components as well as personal preferences. They are meaningful in binary threshold public good games (BTPG) wherein players produce a public good if “large enough coalitions” contribute. Here, “meaningful” does not necessarily lead to the conclusion that greater power implies a comparative advantage for the powerful individual; we might as well argue that greater power comes with greater responsibility and therefore turns out to be a relative disadvantage. Responsibility implies the acceptance of one’s important role in the community and can mean more frequent costly contributions. Power having a negative downside is easy to joke about; however, specialized expertise as a strong indicator of power clearly raises expectations in most coalitions.
From a theoretical and a behavioral point of view, it is a non-trivial question whether the more powerful players profit or suffer from having greater power. The theoretical investigations of our experimental BTPG show counterintuitive attributes of equilibria and result in mixed predictions: in one case, more powerful players can be advantaged; in another case, they certainly are not. Our experimental results show that more powerful players always are disadvantaged.
1.1 Background literature
Theoretical and experimental work on BTPG (and related games) is concerned almost exclusively with symmetric games. Most studies concentrate on two extreme cases: the volunteer’s dilemma (Diekmann 1985), in which one contribution is sufficient for the production of the public good, and the stag hunt game (Rousseau 1762), in which all players must contribute. Experimental results for the volunteer’s dilemma (Diekmann 1985, 1993) reject theoretical predictions about success probabilities (which increase instead of decrease with group size) and about the order of contribution frequency (low-cost players theoretically should contribute less, but actually contribute more often than high-cost players). Those results are broadly confirmed (Franzen 1995; Goeree 2017; Przepiorka and Diekmann 2013; Diekmann and Przepiorka 2015).
All players are veto players when voting under the unanimity rule. That is an extreme case of BTPG, namely the stag hunt game, introduced by Rousseau (1762) as a group of players who can hunt down a stag if and only if they all participate. The value of the share of the stag which each hunter i receives is \(G_{i}\). The opportunity costs \(c_{i}<G_{i}\) are the value of a hare that a hunter can alternatively capture alone without the help of others. The stag hunt game is paradigmatic for the problem of cooperation by coordination, and it is used to investigate two principles of equilibrium selection, namely payoff dominance versus risk dominance (Carlsson and Van Damme 1993). Almost all results in the literature are from 2 × 2 games (for an overview, see Spiller and Bolle 2017). BTPG experiments with intermediate thresholds can require contributions in a small group subset (i.e., two out of three players) or a large group subset (i.e., six out of ten). Palfrey et al. (1991) experimentally investigate incomplete information about payoffs and emphasize the importance of communication. All other BTPG experiments include full payoff information. The importance of information about other players’ previous behavior is stressed (Erev and Rapoport 1990), and the influence of refunding insufficient contributions or punishing successful free riding is highlighted (Dawes et al. 1986). The most consistent experimental result is (assumed) player pivotality. Player pivotality clearly increases the contribution frequency in sequential games (Erev and Rapoport 1990; Chen et al. 1996; McEvoy 2010), while Bartling et al. (2015) find responsibility attribution through pivotal positions with corresponding strategies. Falk et al. (2020) show that the expectation of being pivotal (i.e., the strategic consideration) is the main driver of contributions to a public good and not (expressed) moral motives. However, Tyran et al. (2019) find mixed evidence of expressive (low-cost) voting where pivotality is of minor importance. Spiller and Bolle (2017) investigate simultaneous-move BTPG under sixteen different experimental treatments and stress that public good contributions increase with the height of the threshold, but decline with contribution costs. Once more, pivotality influences the contribution frequency, as being a pivot player in the previous round increases current contributions in this repeated rematching stranger design. Essentially, however, behavior is static and can be described successfully by a finite mixture model of both strategically and morally acting populations (Bolle and Spiller 2021).
BTPG experiments with differently powerful players are reported by Goren et al. (2003) and Kagel et al. (2010). Goren et al. (2003) investigate contributions with five players having different weights (5, 10, 15, 20, 25) and a threshold that requires the sum of weighted contribution to be at least 30. Here, sequential contributions lead to more efficient outcomes than contributing simultaneously. Kagel et al. (2010) introduce veto power in a stylized negotiation process model (Baron et al. 1989), which differs considerably from a standard BTPG, and in which introducing a veto player reduces efficiency. Our simultaneous BTPG experiment delivers the opposite result, namely increasing contributions to the public good with power asymmetry by introducing tie-breaking players and furthermore veto players.
1.2 Research questions
Our basic BTPG resembles a four-player majority vote; i.e., it takes three contributions (voting “Yes”) for the production of a public good (acceptance of a proposal). The two variations of that basic game are first, making one of the players a tie-breaking player, and second, including one veto player in the game. Power and costs are varied experimentally in five different experimental treatments. We investigate contribution behavior in those variants of the game theoretically and experimentally.
Games with and without powerful players generate a large number of equilibria. Therefore, clear theoretical predictions require equilibrium selection. Two frequently adopted equilibrium selection theories are applied: first, payoff dominance, and second, limits of quantal response equilibria (McKelvey et al. 1995). Third, equilibrium selection will be based on fairness considerations (criterion: minimal income differences but non-zero incomes for all), and fourth, the assumption that powerful players act responsibly (contribute with certainty). The performance of equilibrium predictions by these four particular selection principles are tested experimentally. In addition, the following implications of non-formal derivations for responsible behavior of powerful players are evaluated:
Hypothesis 1
More powerful players are worse off than less powerful players.
Hypothesis 2
The provision of public goods is more frequent in a group with powerful players than in a group of homogeneous players.
In Sect. 2, BTPG equilibria are determined and principles for equilibrium selection are applied. Section 3 describes the experimental procedure. Section 4 reports results based on non-parametric tests and regression analyses. Section 5 concludes with a discussion of the obtained results.
2 BTPG equilibria
A set of n players \(N=\{1,\ldots ,n\}\) can contribute to the production of a public good. If a threshold of contributions is reached, the public good is produced. For the production of public goods, complementary or substitutive relationships may arise between the possibly heterogeneous contributions of the players.Footnote 2
-
1.
Threshold \(\mathcal {H}\) designates the set of all subsets of N whose contributions suffice to produce the public good. It has the following properties: The empty set \(\phi \notin \mathcal {H}\), \(N\in \mathcal {H}\). If \(S\subset S'\subset N\) and \(S'\subset \mathcal {H}\) then also \(S\in \mathcal {H}\).
-
2.
We call \(S\in \mathcal {H}\) a minimal supporting set if no strict subset of S is contained in \(\mathcal {H}\).
-
3.
For \(k\in N\), \(\mathcal {H}=\{S:|S|\ge k\}\), i.e., all subsets of N with at least k players describe an equal weight game.
-
4.
A player i is called a veto player if \(i\in S\) for every \(S\in \mathcal {H}\).
-
5.
Player j is said to be replaceable by i if, for every \(S\subset N-\{i,j\}\) with \(S\notin \mathcal {H}\) and \(S\cup \{j\}\in \mathcal {H}\), \(S\cup \{i\}\in \mathcal {H}\) also applies. If j is replaceable by i but not i by j, then i is deemed more powerful than j.
1 to 5 describe simple cooperative or voting games in which the characteristic function takes binary values. Isbell (1958) introduces replaceability as “i being at least as desirable as j.” In the literature on power indices, replaceability/desirability is adopted to characterize local monotonicity, i.e., if i is at least as desirable as j, then i’s power index is not lower than j’s index. Local monotonicity applies for the Shapley-Shubik index, the Banzhaf index, and other power indices (Freixas and Gambarelli 1997). Not all power indices are locally monotone (Holler et al. 1983), but we interpret the technical attribute “one-sided replaceability” as “more powerful”. Players in an equal weight game all are mutually replaceable and thus equally powerful.Footnote 3 A veto player and a chair with tie-breaking power cannot be replaced by other players. Therefore, they are more powerful than the other players. Our BTPG, however, is a non-cooperative game.
Definition 1
In a BTPG game, all players simultaneously contribute to the production of the public good (with costs \(c_{i}>0\)) or do not contribute (with no costs). If the set of contributing players is in \(\mathcal {H}\), then every player i enjoys the benefit \(G_{i}>c_{i}\); otherwise, the benefit is zero.
In general BTPG, namely voting games, positive and negative \(c_{i}\) as well as \(G_{i}\) are possible (Bolle 2019; Bolle and Otto 2020).
2.1 Pure and mixed strategy equilibria
Pure strategy equilibria Every minimal supporting set S designates a pure strategy equilibrium in which the players from S contribute and all others do not. If no minimal supporting set is a singleton, then a pure strategy equilibrium exists wherein no player contributes. Those are the only pure strategy equilibria. Coordination on one of several pure strategy equilibria may be difficult. Therefore, in many cases, mixed strategy equilibria are more plausible, particularly if they show symmetries and can be selected according to payoff dominance.
Mixed strategy equilibria Now assume that the players’ contribution probabilities are \(p=(p_{i})_{i=1,\ldots ,n}\). \(Q=Q(p)\) denotes the probability of success, i.e., that players from a set \(S\in \mathcal {H}\) contribute to the production of the public good. Let \(Q_{+i}\) and \(Q_{-i}\) denote the probability of success if i contributes or does not contribute, respectively; those probabilities depend on \(p_{j}\), where \(j\ne i\). Then \(Q(p)=p_{i}Q_{+i}+(1-p_{i})Q_{-i}\). The probability \(q_{i}=Q_{+i}-Q_{-i}\) is the probability that i’s contribution is decisive for the production of the public good. Player i’s expected return is defined by
A mixed strategy equilibrium with \(0<p_{i}<1\) requires that \(R_{i}\) is independent of \(p_{i}\) with
This requirement is derived informally by Downs (1957, p. 244) for the binary decision of voting or not voting. If \(G_{i}q_{i}-c_{i}<(>)0\), then player i contributes with \(p_{i}=0\) (1). Inserting \(q_{i}\) from Eq. 2 into Eq. 1 provides the equilibrium payoff which i expects if she plays a mixed strategy.
Attributes of equilibria:
-
1.
if i plays a strictly mixed strategy, then \(q_{i}=r_{i}:=c_{i}/G_{i}\)
-
2.
\(q_{i}>r_{i}\) implies \(p_{i}=1\) and \(q_{i}<r_{i}\) implies \(p_{i}=0\)
-
3.
an equilibrium with \(p_{i}=1\) requires \(Q\ge r_{i}\)
-
4.
\(R_{i}=G_{i}Q_{+i}-c_{i}\) and \(Q_{+i}\ge r_{i}\) apply for \(p_{i}>0\)
-
5.
\(R_{i}=G_{i}Q_{-i}\) and \(Q_{-i}\le 1-r_{i}\) apply for \(p_{i}<1\)
1 to 5 follow directly from Eq. 1, Eg. 2, and Eq. 3. Because \(Q_{-i}=0\) for veto players, in a mixed strategy equilibrium, they earn \(R_{i}=0\). If \(\{i\}\in \mathcal {H}\) then \(Q_{+i}=1\) and \(R_{i}=G_{i}-c_{i}\); i.e., player i earns as much as when contributing with certainty.
Remarks on intuition: Games in which one contribution by some player is sufficient for the production of the public good are called volunteers’ dilemmas (Diekmann 1985, 1993). Such games have, at most, one strictly mixed strategy equilibrium and in such an equilibrium, players with larger cost/benefit ratios contribute with higher probabilities than players with lower cost/benefit ratios. In Bolle (2019), it is shown for general BTPG that the same relationship applies if contributions are strategic substitutes; the intuitive conjecture that larger cost/benefit ratios cause lower contribution probabilities applies for strategic complements. Diekmann (1993) confirm intuition experimentally, but not theoretically.
Another intuition is that increasing the set of successful coalitions, i.e., substituting \(\mathcal {H}\) by \(\mathcal {H}'\) with \(\mathcal {H}\subset \mathcal {H}'\) (while keeping the cost/benefit ratios unchanged), will increase the probability of success. According to that assumption, the introduction of a tie-breaking player should be beneficial because it enlarges \(\mathcal {H}\), and the introduction of a veto player should be harmful because it reduces \(\mathcal {H}\). That rationale certainly would apply under random decision-making, but fully neglects strategic implications. We will see that the assumed effects of those changes are rejected not only theoretically but also on empirical grounds.
Equilibrium selection BTPG suffer from a plethora of equilibria. In our experimental cases, however, after excluding asymmetric strategies for symmetric players, the principle of payoff dominance selects a unique equilibrium. Income vector x payoff-dominates y if and only if \(x\ge y\) and \(x_{i}>y_{i}\) for at least one i. An equilibrium is efficient if it has the largest sum of expected incomes.
Definition 2
An equilibrium is achievable if symmetric players use the same strategy. An achievable equilibrium is payoff-dominant if, in binary comparisons, it payoff-dominates all other achievable equilibria.
If asymmetric equilibrium strategies for symmetric players exist, then other equilibria always exist with a permutation of the symmetric players. In a game where three of four players are necessary for the production of the public good, four pure strategy equilibria with the production of the public good exist, but the players have no possibility of coordinating on one of those efficient equilibria.
Another method of equilibrium selection was suggested by McKelvey et al. (1995) as a limit of quantal response equilibria (QRE), which assumes all strategies (from a finite set) to be played with probabilities that are ordered according to the utility a strategy gains against the strategies of the other players. When random deviations from the best response vanish, QRE converges to a Nash equilibrium.
The expected utilities after contributing and not contributing are \(Q_{+i}G_{i}-c_{i}\) and \(Q_{-i}G_{i}\), respectively. In a logistic QRE, player i’s probability of contributing is
The precision parameter \(\lambda \) characterizes the magnitude of deviations from best responses. If all \(G_{i}\) are equal, as in our experiments, we cannot disentangle the influence of \(G_{i}\) and \(\lambda \). The solution of Eq. 4 is the QRE with \(\lambda \), denoted as \(\hbox {QRE}(\lambda )\). For \(\lambda =0\), \(p=0.5\) for all i, and for \(\lambda \rightarrow \infty \), \(\hbox {QRE}(\lambda )\) converges to a Nash equilibrium as shown by McKelvey et al. (1995). Generically, a unique continuous path from \(\hbox {QRE}(0)\) to \(\hbox {QRE}(\infty )\) exists.
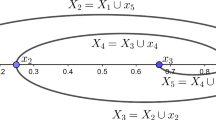
The limits of equilibria \(\hbox {QRE}(\infty )\) is determined numerically. We use \(\lambda (i)=0.002\times 1.001^{i},i=1,\ldots ,10000\), which results in \(\lambda \) values from 0.002 to 43.8 (\(\lambda G_{i}\) between 0.01 and 2192). The equilibrium with \(\lambda (i)\) is used as the starting value for the numerical computation of the equilibrium with \(\lambda (i+1)\). Figure 1 shows equilibrium selection in our five experimental treatments.

Note The paths of the experimental treatments TA, TS, VA, VS, and ES (with T for tie-breaking powers, V for veto powers, and S(A) for (a)symmetric costs) are shown in Table 1. All paths start at \(\hbox {QRE}(0)=(0.5,0.5,0.5,0.5)\). The probabilities of the ordinary players (\(p_{\mathrm{ord}}\)) are the same for all three equal players. Probabilities for the powerful players (\(p_{\mathrm{pow}}\)) are respectively for the veto or the tie-breaking player. For TA and TS, the probabilities converge to the equilibrium where the tie-breaking player contributes with certainty and the remaining three players play a volunteer’s dilemma, i.e resulting from Eq. 2 or attributes of equilibria with \(n=3\) and \(k=1\). The points ta, ts, va, vs, and es correspond to empirical contribution frequencies
\(\hbox {QRE}(\infty )\) selection.
2.2 Equilibrium selection in experimental games
The five treatments of the experimental games are described in Table 1. Achievable equilibria for each treatment are listed (together with the associated returns) in Table 2 if they are at least as efficient as the most efficient strictly mixed strategy equilibrium Eq. 3. Italic indicates the (achievable and) payoff-dominant equilibria. The requirement of achievability excludes all pure strategy equilibria except \(p=(0,0,0,0)\) and equilibria with different strictly mixed strategies played by symmetric players. Only the tie-breaking and veto players can have different strategies than the other players. Thus, it is not only the powerful position that makes them different, but power means distinctness, which makes equilibria Eq. 1 and Eq. 2 achievable.
The unique payoff-dominant equilibrium in the experimental treatments with tie-breaking power (TS with symmetric and TA with asymmetric costs depicted as Equil. ??) requires the tie-breaking player to be contributing with a probability of zero. As a consequence, he or she is advantaged. The unique payoff-dominant equilibrium in the experimental treatments with veto power (VS with symmetric and VA with asymmetric costs depicted as Equil. 2) requires the veto player to be contributing with a probability of one. As a consequence, veto players are strongly disadvantaged. The second most efficient equilibrium not only is payoff-dominated, but also reduces efficiency by a minimum of 80%. Equil. 1 and Equil. 2 cause efficiency losses of 28% to 33%. Those equilibria favor ordinary members. \(\hbox {QRE}(\infty )\) always selects less efficient equilibria than payoff dominance, namely Equil. 2 in TS and TA and \(p=(0,0,0,0)\) otherwise (see Fig. 1). Below, we comment on the relation between observed frequency and the paths to \(\hbox {QRE}(\infty )\).
Concerning social preferences, we know that efficiency (with and without payoff dominance) is an important influence in experimental games (Kritikos and Bolle 2001; Engelmann and Strobel 2004), but fairness in the sense of income equality likewise can be important (Bolton and Ockenfels 2000), possibly with an emphasis on own disadvantage (Fehr and Schmidt 1999). In TS, TA, and VA, the completely mixed strategy equilibrium is connected with the smallest income differences, so players with sufficient inequality aversion may favor Equil. 3.Footnote 4 The main empirical question here, however, is not easily expressed by social preferences: Does power lead to more responsibility? Equil. 2 best supports such a stance, with powerful players contributing with certainty. The four competing theoretical predictions for our experimental results are payoff dominance, \(\hbox {QRE}(\infty )\), responsibility (Equil. 2), and fairness (Equil. 3).
3 BTPG experiment
Four players interacted in repeated simultaneous-move games, always beginning the period with an endowment of 30 eurocents, and they decided between “contributing” or “not contributing” to a public good. The player’s costs for contributing are given in Table 1. If a sufficient combination of players contributed (including the veto player or for draws including the tie-breaking player), then each player received \(G_{i}=50\) eurocents. Participants kept their player number (1, 2, 3, or 4) throughout the experiment and took part in four games with eight repetitions each. Decisions were made under either cost symmetry in treatments ES, TS, and VS, or under cost asymmetry in TA and VA.Footnote 5 The order of experimental games was randomized over the sessions so that each game was played at least three times in the first, second, third, and fourth blocks. Subjects were not informed about the order of the games in advance, but were informed when the threshold changed.
In both the symmetric and the asymmetric condition, 13 sessions took place. Each session included eight subjects (each player number twice) who were, in each period, divided randomly into two groups of players, constituting a re-matching stranger design with \(2^{4}=16\) different possible matchings. Over the course of eight rounds with the two groups, always different combinations were formed; i.e., players never met all of the same co-players from any previous round, but met two of them with a probability of 3/7. The experiment took place in a standard laboratory using z-tree (Fischbacher 2007). At the beginning, participants received printed instructions with a general description of all of the games and an overview of the procedure (see Appendix 1). Once all participants understood the task, an example calculation appeared on the screen. Then, six comprehension questions had to be answered, including an example of the resulting profit distribution for each threshold variant of the game. Participants who did not understand the instructions received personal advice until the task was understood fully.
Directly after each round, subjects were told which of the players contributed. From the player numbers, they could infer whether powerful players (if present) contributed and whether their own contribution had (or would have) been decisive for the production of the public good, i.e., whether they had been a pivot player. Although implied in the information about contributing players, they also were informed about whether the public good had been produced and what profit they had earned in this round. In addition, they were required to evaluate that result in terms of “satisfaction”, “fairness”, and “anger” on a five-point scale. After the last period, a questionnaire had to be completed, which asked empathy and demographic questions. A session lasted on average about one hour. The aggregate net payoff from the 32 periods was between €10.00 and €19.90 (€15.50 on average).
4 Results
The decisions of 208 subjects are evaluated. In ES we have 104 times 8 (subjects, time periods) decisions; in the other treatments we have 26 times 8 decisions by powerful and 78 times 8 decisions by ordinary players. Comparisons are made by Mann-Whitney and Wilcoxon matched-pairs tests concerning the averages of the 13 independent sessions of all treatments. We compare powerful with ordinary players, treatments TS and VS with ES, TS with TA, and VS with VA. Table 3 provides average contribution frequencies and distances to the theoretical predictions. The comparison of the experimental frequencies with our four predictions shows that, for every prediction, non-negligible deviations are evident. According to the distance measure as the sum of differences between predicted and observed probabilities, responsibility as Equil. 2 prevails over the three other predictions. The two formal equilibrium selection theories perform the worst. In the case of QRE selection, the empirical frequencies are different not only from \(\hbox {QRE}(\infty )\), but also from the path to \(\hbox {QRE}(\infty )\); i.e., it would not help to substitute \(\lambda =\infty \) by a finite \(\lambda \) (see Fig. 1).
When costs are equal, powerful players contribute with significantly higher frequency than ordinary players (Table 3). The transition from VS to VA diminishes only slightly the veto players’ readiness to contribute, although their costs are three times the costs of ordinary players. Shares of “almost fully” contributing veto players (see Table 4) actually increase under cost asymmetry. That is not the case for tie-breaking players, with fewer fully contributing players and smaller contributions under cost asymmetry. Powerful players are significantly disadvantaged, with generally lower payoffs, which is particularly important for the symmetric cost games. In the asymmetric cases, the disadvantage of powerful players crucially is caused by their higher costs. It is important to note that they did not reduce their contribution probabilities so far that incomes were equal, although they could have done so. Giving one of the four players more power improves the payoffs of the three ordinary players, making them significantly better off than the powerful player. Also, success and efficiency (R) are improved, although significantly only on a rather lower level when switching games from ES to TS. Comparisons of success rates and average payoffs R between ES and TA and VA are difficult to interpret. Altogether, the non-parametric tests strongly support Hypothesis 1 and weakly support Hypothesis 2.
A regression analysis of individual contribution decisions controls for further influences on contribution behavior. In addition to the impact of power, dynamic components of behavior are investigated. The evidence is mixed concerning separate or joint regressions concerning the game variants. According to AIC and likelihood ratio tests, the joint regression of the two asymmetric games is preferable; the joint regression of symmetric games or of all games seems to neglect systematic differences. According to BIC, however, all joint regressions are justified. For the sake of simplicity, we follow the latter advice and interpret mainly the joint regression (ALL) in Table 5.
Contributions decline over the eight repetitions of a game (rounds). That steady trend is illustrated in Fig. 2 and shows no end-of-play effect. The position of a game in the sequence of the games (stage) does not have a significant influence. Having been a pivot player in the previous round increases the likelihood of contributing in the current round. A player is a pivot player if, given the contributions of the other players, his contribution is decisive. Being a powerful player has a significant positive effect on contribution frequency, and costs have a significant negative effect.
A player’s mood can have an effect on the contribution levels, which is here measured by the elicited scores of “fairness”, “satisfaction”, and “anger” at the end of each round. The latter two have an important influence on contribution behavior. It is plausible to assume that emotions mirror a player’s evaluation of the previous rounds of the game, including the effect of a player’s previous pivot position, and may explain the downward trend of contribution probabilities. An accordingly extended regression is reported in Appendix 2. Demographic attributes and measured empathy show no significant influences there.
5 Conclusions
In the binary threshold public good games (BTPG) with powerful players, several equilibria can be identified, which differ in rankings (efficiency: a payoff-dominant equilibrium always exists among the achievable equilibria) and income spreads (fairness). With two types of players (tie-breaking and veto players) having more power than the other players according to power indices, the central question was whether or not power is exploited to increase individual benefits. Experimental investigations have shown that “power comes with responsibility” (Bolle and Vogel 2011; Hamman et al. 2011; Fleiß and Palan 2013; Otto et al. 2016). Here, we add responsibility as a third equilibrium selection principle along with fairness and payoff dominance. It simply requires powerful players to contribute with certainty. As a fourth principle, we add equilibrium selection according to the limit of quantal response equilibria, \(\hbox {QRE}(\infty )\). Whether the introduction of a powerful player leads to payoff improvements depends on the equilibrium selection principle and the type of power (tie-breaking or veto). Except for the selection under the fairness principle, giving one player power always increases efficiency (sum of all incomes). \(\hbox {QRE}(\infty )\) shows advantages and disadvantages for powerful players. Responsible behavior always provides a powerful individual with less income than ordinary players.
All four theoretical model predictions show non-negligible deviations from experimental behavior, but according to a distance measure, responsibility is clearly winning the comparison, thus supporting Hypothesis 1. Responsibility is the flipside of power and it comes with extra costs for the powerful players. In all games, powerful players earned significantly less than ordinary players. Efficiency always increases after the introduction of a powerful player, which is in line with Hypothesis 2. In addition, Hypothesis 1 is strongly and Hypothesis 2 weakly supported by non-parametric tests.
Furthermore, our experimental results reveal dynamics that cannot be captured by static theories. Pivotality in the previous round increased a player’s contribution probability in the next round. The same effect has been reported in experiments with sequential decisions (Erev and Rapoport 1990; Chen et al. 1996; McEvoy 2010), with the elicitation of beliefs in simultaneous decisions (Falk et al. 2020), and over repeated rounds in simultaneous decisions (Spiller and Bolle 2017). The importance of pivotality for simultaneous decisions appears surprising because pivotality is simply hypothetical in a stranger rematching design.Footnote 6
Powerful players show responsibility, which confirms previous experimental results. That does not mean that power makes people fully forget their own interests. Responsible behavior is limited by material and opportunity costs. Specific player types may allow exploitation of their power up to different degrees. Therefore, our result showing that powerful players are worse off than ordinary players is probably not a general phenomenon and is restricted to a specific class of games. For example, an upfront bargaining stage with side payments may influence decisions and incomes in the experimental games presented here.
In a liberal and individualistic society more generally, differences in the amounts or specificity of resources are inevitable; however, the power resulting from such inequality need not always be disadvantageous. Pessimistic expectations such as, for example, the assumption by Tsebelis (1995) that efficiency deteriorates with an increase in the number of veto players in a society, need not be necessarily true. The flipside of power, responsibility, can predominate behavior in a largely interdependent and cooperative world.
Data policy
The generated experimental data analyzed in the current study are available from the corresponding author on reasonable request.
Notes
For example, the permanent members of the UN Security Council are veto players. All member countries can vote Yes, No, or Abstain. A proposal is passed if nine of all fifteen members vote Yes AND none of the five permanent members votes No.
Examples of complex threshold structures in voting include different weights of the players and multiple majorities necessary for the passing of a proposal, as in assemblies of business or condominium owners, as well as decision-making in international organizations (compare Posner and Sykes 2014).
In simple cooperative games, mutually replaceable players are called symmetric; in BTPG games they can be asymmetric because of differing costs and benefits.
The mixed strategy equilibria in Table 2 apply if every player expects the other players to be payoff maximizers. If all know the social preferences of the others, then the mixture probabilities change.
Further experimental games varying the form of possible coalitions were played, but are analyzed in a separate investigation. The two additional games had minimal supporting sets 1,2 and 3,4 and either costs of 20 for all players (symmetric treatment) or 30 for players 1 and 4 and 10 for players 2 and 3 (asymmetric treatment).
In sequential games, a player’s contribution is pivotal if it may be or is decisive for the production of a threshold public good. In a sequence of games with simultaneous decisions, a player’s decision in the previous round has been pivotal only if, given her co-players’ contributions, it had been decisive for the production of the public good, independent of whether the player had contributed or not.
References
Baron, D. P., & John, A. F. (1989). Bargaining in legislatures. American Political Science Review, 83(4), 1181–1206.
Bartling, B., Fischbacher, U., & Schudy, S. (2015). Pivotality and responsibility attribution in sequential voting. Journal of Public Economics, 128, 133–139.
Bolle, F. (2019). When will party whips succeed? Evidence from almost symmetric voting games. Mathematical Social Sciences, 102, 24–34.
Bolle, F., & Otto, P. E. (2020). Voting games: An experimental investigation. Journal of Institutional and Theoretical Economics (JITE), pp. 496525.
Bolle, F., & Spiller, J. (2021). Cooperation against all predictions, Economic Inquiry, 59(3), 904–924.
Bolle, F., & Vogel, C. (2011). Power comes with responsibility-or does it? Public Choice, 148(3–4), 459–470.
Bolton, G. E., & Ockenfels, A. (2000). ERC: A theory of equity, reciprocity, and competition. American Economic Review, 90(1), 166–193.
Carlsson, H., & Van Damme, E. (1993). 12 equilibrium selection in stag hunt games. Frontiers of Game Theory, p. 237.
Chen, X.-P., Wing, T. A., & Komorita, S. S. (1996). Sequential choice in a step-level public goods dilemmad: The effects of criticality and uncertainty. Organizational Behavior and Human Decision Processes, 65(1), 37–47.
Dawes, R. M., Orbell, J. M., Simmons, R. T., & Van De Kragt, A. J. C. (1986). Organizing groups for collective action. American Political Science Review, 80(4), 1171–1185.
Diekmann, A. (1985). Volunteer’s dilemma. Journal of Conflict Resolution, 29(4), 605–610.
Diekmann, A. (1993). Cooperation in an asymmetric volunteer’s dilemma game: Theory and experimental evidence. International Journal of Game Theory, 22(1), 75–85.
Diekmann, A., & Przepiorka, W. (2015). Punitive preferences, monetary incentives and tacit coordination in the punishment of defectors promote cooperation in humans. Scientific Reports, 5, 10321.
Downs, A. (1957). An economic theory of democracy. New York: Harper.
Engelmann, D., & Strobel, M. (2004). Inequality aversion, efficiency, and maximin preferences in simple distribution experiments. American Economic Review, 94(4), 857–869.
Erev, I., & Rapoport, A. (1990). Provision of step-level public goods: The sequential contribution mechanism. Journal of Conflict Resolution, 34(3), 401–425.
Falk, A., Neuber, T., & Szech, N. (2020). Diffusion of being pivotal and immoral outcomes. The Review of Economic Studies, 87(5), 2205–2229.
Faul, F., Erdfelder, E., Lang, A.-G., & Buchner, A. (2007). G* Power 3: A flexible statistical power analysis program for the social, behavioral, and biomedical sciences. Behavior Research Methods, 39(2), 175–191.
Fehr, E., & Schmidt, K. M. (1999). A theory of fairness, competition, and cooperation. Quarterly Journal of Economics, 114(3), 817–868.
Fischbacher, U. (2007). z-Tree: Zurich toolbox for ready-made economic experiments. Experimental Economics, 10(2), 171–178.
Fleiß, J., & Palan, S. (2013). Of coordinators and dictators: A public goods experiment. Games, 4(4), 584–607.
Franzen, A. (1995). Group size and one-shot collective action. Rationality and Society, 7(2), 183–200.
Freixas, J., & Gambarelli, G. (1997). Common internal properties among power indices. Control and Cybernetics, 26, 591–604.
Goeree, J. K., Holt, C. A.., & Smith, A. M. (2017). An experimental examination of the volunteer’s dilemma. Games and Economic Behavior, 102, 303–315.
Goren, H., Kurzban, R., & Rapoport, A. (2003). Social loafing versus social enhancement: Public goods provisioning in real-time with irrevocable commitments. Organizational Behavior and Human Decision processes, 90(2), 277–290.
Hamman, J. R., Weber, R. A., & Woon, J. (2011). An experimental investigation of electoral delegation and the provision of public goods. American Journal of Political Science, 55(4), 738–752.
Holler, M. J., & Edward, W. P. (1983). Power, luck and the right index. Zeitschrift fur Nationalokonomie, 43(1), 21–29.
Holler, M. J., Edward, W. P., & Guillermo, O. (2001). Why power indices and coalition formation? In Power indices and coalition formation. Springer (pp. 1–13).
Isbell, J. R. (1958). A class of simple games. Duke Mathematical Journal, 25(3), 423–439.
Kagel, J. H., Sung, H., & Winter, E. (2010). Veto power in committees: An experimental study. Experimental Economics, 13(2), 167–188.
Kritikos, A., & Bolle, F. (2001). Distributional concerns: Equity-or efficiency-oriented? Economics Letters, 73(3), 333–338.
Laërtius, D. (1901). The lives and opinions of eminent philosophers. G. Bell & sons.
McEvoy, D. M. (2010). Not it: Opting out of voluntary coalitions that provide a public good. Public Choice, 142(1—-2), 9.
McKelvey, R. D., & Thomas, R. P. (1995). Quantal response equilibria for normal form games. Games and Economic Behavior, 10(1), 6–38.
Otto, P. E., & Bolle, F. (2016). The advantage of hierarchy: Inducing responsibility and selecting ability journal of behavioral and Experimental. Economics, 65, 49–57.
Palfrey, T. R., & Rosenthal, H. (1991). Testing for effects of cheap talk in a public goods game with private information. Games and Economic Behavior, 3(2), 183–220.
Posner, E. A., & Sykes, A. O. (2014). Voting rules in international organizations. Chicago Journal of International Law, 15, 195–228.
Przepiorka, W., & Diekmann, A. (2013). Individual heterogeneity and costly punishment: a volunteer’s dilemma. Proceedings of the Royal Society B: Biological Sciences, 280(1759), 0247.
Rousseau, J. J. (1762). The Social contract’and other later political writings. Cambridge University Press, 1762. 1997 English translation by Gourevitch of the 1762 original.
Spiller, J., & Bolle, F. (2017). Experimental investigations of binary threshold public good games. Discussion Paper: Technical Report.
Tsebelis, G. (1995). Decision making in political systems: Veto players in presidentialism, parliamentarism, multicameralism and multipartyism. British Journal of Political Science, 25(3), 289–325.
Tyran, J. R., & Alexander, K. W. (2019). Experimental evidence on expressive voting. In Voigt, S., Congleton, R. D., & Grofman, B. N. (Eds.) The Oxford handbook of public choice, Vol. 2. Oxford University Press, chapter 45 (pp. 928–940).
Funding
Open Access funding enabled and organized by Projekt DEAL. This study was funded by the German Science Foundation (#BO747/14-1).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendices
Appendix 1: General experimental instructions
These general instructions, here shown for symmetric costs as in ES, TS, VS, were handed out on a sheet of paper which was kept by the participants throughout the experiment. The general instructions were supplemented by on screen examples of all thresholds and questions asking which individual payments would result for various decisions of the players. The experiment started only after every player had understood the effects of the different thresholds and answered all test examples correctly.
Welcome and many thanks for participating in this study on group behavior. The session will last about one hour. Your payment will depend on your and your co-players’ decisions.
Please switch off your mobile phones and similar devices. The experiment is fully computerized. Please do not speak or otherwise communicate with your co-players during the experiment.
Following is a brief overview of the procedure. Please read this carefully. In the case of questions, please directly consult the investigator. After this introduction, you will have to answer some comprehension questions.
-
1.
In this experiment, you have to make decisions in several rounds.
-
2.
In every round, groups of four players are formed randomly. You always remain the same player. You are either player 1, player 2, player 3, or player 4. Your player number is shown on the screen.
-
3.
In every round, each player receives 30 eurocents.
-
4.
Each player can choose either action A or action B.
-
5.
Action B is costless.
-
6.
Action A costs this player 20 eurocents.
-
7.
If sufficient players have chosen action A, then all players receive 50 eurocents in addition.
-
8.
The condition describing the meaning of sufficient players changes every 8 rounds. For example, a minimum number of players have to choose A or certain combinations of players have to choose A. The exact conditions for the additional payment will be explained in detail on the screen before the eight rounds begin.
The eurocents you earned are computed for every round according to the above rules and added up over all rounds. The final sum is your payment for your participation in this experiment, which you will receive individually directly after the experiment.
We start when everybody is ready.
Appendix 2: Extended regression analysis
In extended regressions, we test the influence of combinations of emotions (end of previous period), of demographic variables (age, sex, semester, German or Polish nationality, business or law student, resident of Berlin or Frankfurt (Oder)), and empathy questionnaire answers (agreement on a five-level scale). Emotions are highly significant, and the other 27 variables are insignificant with one exception (see Table 6). The last model is identical to ALL in Table 5 for comparison purposes. Model expansions concern the selective inclusion of the measured emotions, demographic variables, and empathy variables. The estimated coefficients of the main variables are stable over these model expansions.
The inclusion of emotions improves the fit of the regression considerably, but the interpretation of their influence needs further elaboration—preferably in a model which allows non-trivial interactions of decisions and emotions. Surprisingly, anger has a positive influence on the contribution probability. This may be explained by reversed causality, namely the conjecture that those who permanently (and even so after continued disappointments) contribute with high probability are particularly angry.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bolle, F., Otto, P.E. The flip side of power. Public Choice 190, 75–92 (2022). https://doi.org/10.1007/s11127-021-00916-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11127-021-00916-8


 (power shows the man)
(power shows the man)