Abstract
In this paper, we incorporate spatial analysis to estimate industry-level productivity in the presence of inter-sectoral linkages. Since each industry plays a role in providing intermediate goods to other sectors, the interdependence of economic activities across industries is inevitable. We exploit the linkage patterns from the input-output relationship to define cross-industry dependencies in economic space. We propose a spatial stochastic frontier model, which extends the stochastic frontier model to a spatially dependent specification. The models are estimated using quasi-maximum likelihood methods. Applying the approach to U.S. industry-level data from 1947 to 2010, we find that sectoral dependencies are the consequences of indirect effects via the supply chain network of industries resulting in larger output elasticities as well as scale effects for the networked production processes. However, productivity growth is estimated comparably across different spatial and non-spatial model specifications.







Similar content being viewed by others
Notes
For a summary of the Network DEA model, see Färe et al. (2007).
A referee suggested using the model of Filippini and Greene (2016) to distinguish possible unobserved, time-invariant heterogeneity from unobserved productivity (efficiency). It would be interesting to pursue this in a different study as a complement to our approach.
The observations stacked with t being the fast-running index and i the slow-running index, i.e., \(y={({y}_{11},{y}_{12},\cdots ,{y}_{1T},\cdots ,{y}_{N1},\cdots ,{y}_{NT})}^{{\prime} }\). The order of observations is very important for writing correct software codes. In typical spatial analysis literature, the slower index is over time, the faster index is over individuals.
Different spatial correlation structures for dependent variable and independent variables are possible. In the present paper, we use the same dependence structure for both variables.
As pointed out by a referee there is an issue of endogeneity of the spatial weights matrix when using a measure of economic distance to specify spatial weights, such as trade flows, as proxies of economic distance. However, as also pointed out by many studies of spatial production econometrics (see, for example, Ertur and Koch, 2007) direct L and K inputs are assumed to be exogenous, which implies that the input/output coefficients and thus the weights on which they are based also can be taken to be exogenous. Endogenous network formation and the strategy games engaged by players in such a network is beyond the scope of this contribution. We are thus assuming that when deciding on current input choice the firm does not believe its actions will impact the supply chain network at that point in time and is thus predetermined to the firm.
The diagonals of the symmetrized MPM, \({m}_{ii}^{E}\), are not necessarily the largest element. We need to set the wii to be zero to satisfy the regularity assumption A1.
A similar set of expressions for the SDM will be provided on request.
There was minimal variation in the I-O patterns of US industries over our sample period, so we used averaged data for the spatial weighting matrix. Technically, adjusting for time-varying weights proved challenging, especially for the parameter η, which was estimated through cross-validation. Our merged data cover the period 1995–2011 and 1947–2011, which may have missed earlier industry linkages prior to 1995. However, we did not want to lose the substantial information contained in the relatively long period for which the KLEMS data are complete. We experimented with annual changes in the weight matrix, but these didn’t significantly affect our final elasticities. Our spatial models require sufficient data; attempts at utilizing the shortened time-series for 1995-2011 data led to economically meaningless results.
We used ’fminbnd’ of Matlab function, which is based on Brent’s method. It should be noted that this is a possible approach out of various numerical search algorithms, such as Newton-Raphson, Quasi-Newton or other methods.
δi can be estimated by regressing the residuals (\({y}_{it}-{\hat{\rho }}_{within}\mathop{\sum }\nolimits_{j = 1}^{N}{w}_{ij}{y}_{jt}-x^{\prime}_{it}{\hat{\beta }}_{within}\)) on a constant, time and time-squared (\(R^{\prime}_{t}\)). (Cornwell et al. 1990).
Hence, the relative efficiency score can be written as \({\widehat{EFF}}_{it}={e}^{-{\hat{u}}_{it}}\).
The databases are open-sources on the following web pages: http://www.worldklems.net/, and http://www.wiod.org/.
In addition, each country’s national accounts system is based on a different international classification, and it is difficult to maintain consistency among them.
However, the two databases have slightly different industry definitions. That is, Textiles, Leather and Footwear and Transport and Storage industries are finely defined in World Input–Output Database, which requires us to aggregate the finer industries to meet the number of industries of datasets.
The complete industry classifications and the excluded industries can be found in Appendix D.
As we have pointed out above, we only have the I-O data from 1995 to 2011 and thus the assumption of a time-invariant I-O structure is needed. We found the over-time variation of input–output structure to be rather low. For example, the share of output produced by a specific industry as an intermediate input for each industry (say input cost share) is almost unchanged. The correlation coefficient between the input cost shares in 1995 and 2011 is about 0.984.
The estimation results using the value-added as a dependent variable are given in Appendix B.
We can also choose between SARCSS and SDMCSS by comparing the AIC values. For within-estimation, the AICs in SARCSS and SDMCSS are −3919.86 and −3928.42, respectively. For GLS-estimation, the AICs in SARCSS and SDMCSS are −3845.26 and −3853.96, respectively. For both within and GLS, the spatial Durbin model provides the better model fit. In addition, the ratio of the indirect to direct marginal effects differs across variables, which is more realistic. On the basis of these criteria, one can choose the spatial Durbin model over the spatial autoregressive model.
The indirect effect estimate of intermediate inputs is statistically insignificant at the 5% significance level.
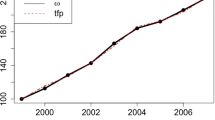
Note that TFPs are calculated using TFP growth rates obtained from the growth accounting approach, which set the TFP level of the reference year to be 1. The growth accounting approach applies the methodology to a dataset from each industry independently. Hence, the comparison of TFP levels across industries is not provided. Because the approach sets the TFP level of the reference year (2005) as one, we may have the period average TFP that is greater than one depending on the fluctuations in TFP levels.
The rank correlation between the non-spatial CSSW and the SARCSSW and the SDMCSSW is 0.9684 and 0.9733, respectively. The rank correlation between the non-spatial CSSG and the SARCSSG and the SDMCSSG is 0.9674 and 0.9684, respectively.
Note that the variables in Z do not vary over time. Hence γ cannot be identified because MQZ = 0.
Q need to be a full column rank matrix for estimation of the individual δi.
References
Acemoglu D, Carvalho VM, Ozdaglar A, Tahbaz-Salehi A (2012) The network origins of aggregate fluctuations. Econometrica 80(5):1977–2016
Areal F, Balcombe K, Tiffin R (2012) Integrating spatial dependence into stochastic frontier analysis. Aust J Agric Resour Econ 56(4):521–541
Areal FJ, Pede VO (2021) Modeling spatial interaction in stochastic frontier analysis. Front Sustain Food Syst 5:673039
Behrens K, Ertur C, Koch W (2012) ’Dual’ gravity: Using spatial econometrics to control for multilateral resistance. J Appl Econom 27:773–794
Brunsdon C, Fortheringham AS, Charlton ME (1996) Geographically weighted regression: a method for exploring spatial nonstationarity. Geogr Anal 28(4):281–298
Carvalho A (2018) Efficiency spillovers in Bayesian stochastic frontier models: application to electricity distribution in New Zealand. Spatial Econ Anal 13(2):171–190
Chudik A, Pesaran MH (2015) Large panel data models with cross-sectional dependence: a survey, In: Baltagi BH (ed.) The Oxford handbook on panel data, New York: Oxford University Press, p 3–45
Cobb CW, Douglas PH (1928) A theory of production. Am Econ Rev 18(1):139–165
Coelli TJ, Rao D, Prasada O, Battese GE (2005) An introduction to efficiency and productivity analysis. New York, NY: Springer
Cornwell C, Schmidt P, Sickles RC (1990) Production frontiers with cross-sectional and time-series variation in efficiency levels. J Econom 46(1):185–200
Diewert WE (1976) Exact and superlative index numbers. J Econom 4(2):115–145
Diewert WE (1978) Superlative index numbers and consistency in aggregation. Econometrica 46(4):883–900
Druska V, Horrace WC (2004) Generalized moments estimation for spatial panel data: Indonesian rice farming. Am J Agric Econ 86(1):185–198
Elhorst JP (2014) Spatial econometrics: from cross-sectional data to spatial panels. Berlin, Heidelberg: Springer
Elhorst JP, Halleck Vega S (2017) The SLX model: Extensions and the sensitivity of spatial spillovers to W. Papeles Econ Espanola 152:34–50
Ertur C, Koch W (2007) Growth, technological interdependence and spatial externalities: theory and evidence. J Appl Econom 22(6):1033–1062
Färe R, Grosskopf S, Whittaker G (2007) Network DEA. In: Zhu J and Cook WD (eds.) Modeling data irregularities and structural complexities in data envelopment analysis, Boston, MA: Springer US, p 209–240
Filippini M, Greene W (2016) Persistent and transient productive inefficiency: a maximum simulated likelihood approach. J Prod Anal 45:187–196
Getis A, Aldstadt J (2004) Constructing the spatial weights matrix using a local statistic. Geogr Anal 36(2):90–104
Glass AJ, Kenjegalieva K, Paez-Farrell J (2013) Productivity growth decomposition using a spatial autoregressive frontier model. Econ Lett 119(3):291–295
Glass AJ, Kenjegalieva K, Sickles RC (2016a) Returns to scale and curvature in the presence of spillovers: evidence from European countries. Oxford Econ Pap 68(1):40–63
Glass AJ, Kenjegalieva K, Sickles RC (2016b) A spatial autoregressive stochastic frontier model for panel data with asymmetric efficiency spillovers. J Econom 190(2):289–300
Gong B, Sickles RC (2021) Resource allocation in multi-divitional multi-product firms. J Prod Ana 55:47–70
Griliches Z (1960) Estimates of the aggregate U.S. farm supply function. J Farm Econ 42(2):282–293
Halleck Vega S, Elhorst JP (2015) The SLX model. J Reg Sci 55(3):339–363
Han J, Ryu D, Sickles RC (2016a) How to measure spillover effects of public capital stock: a spatial autoregressive stochastic frontier model, In: Blatagi BH, Lesage JP, Pace RK (eds) Spatial econometrics: qualitative and limited dependent variables (Advances in Econometrics, Vol 37), Emerald Group Publishing Limited, p 259–294
Han J, Ryu D, Sickles RC (2016b) Spillover effects of public capital stock using spatial frontier analyses: a first look at the data. In: Greene WH, Sickles R, Khalaf L, Veall M and Voia M-C (Eds.), Productivity and efficiency analysis: proceedings from the 2014 North American Productivity Workshop, New York, Springer Publishing, p 83–97
Hulten CR (2001) Total factor productivity: a short biography, In: Hulten CR, Dean ER and Harper MJ (eds.) New developments in productivity analysis, National Bureau of Economic Research, Inc., p 1–54
Jones CI (2013) Misallocation, economic growth, and input-output economics, In: Acemoglu, D., Arellano M and Dekel E (eds.) Advances in economics and econometrics: Tenth World Congress, eds. Cambridge: Cambridge University Press, p 419–456
Jorgenson DW, Gollop FM and Fraumeni BM (1987) Productivity and U.S. economic growth. Cambridge, MA: Harvard University Press
Jorgenson DW, Griliches Z (1967) The explanation of productivity change. Rev Econ Stud 34(3):249–283
Jorgenson DW, Ho MS, Samuels JD (2012) A prototype industry-level production account for the United States, 1947–2010. Paper presented at the second world KLEMS conference, Harvard University, Cambridge, Massachusetts
Kumbhakar SC, Hung-Pin L (2022) Recent advances in the panel stochastic frontier models: heterogeneity, endogeneity and dependence. Int J Empir Econ 1(1):1–38
Lai HP, Tran K (2022) Persistent and transient inefficiency in a spatial autoregressive panel stochastic frontier model. J Prod Anal 58:1–13
Lee LF (2004) Asymptotic distributions of quasi-maximum likelihood estimators for spatial autoregressive models. Econometrica 72(6):1899–1925
LeSage JP, Pace RK (2009) Introduction to spatial econometrics. Boca Raton, Florida: Chapman & Hall/CRC
McMillen DP (2003) Identifying sub-centres using contiguity matrices. Urban Stud 40(1):57–69
Orea L, Alvarez IC (2019) A new stochastic frontier model with cross-sectional effects in both noise and inefficiency terms. J Econom 213(2):556–577
Pede VO, Areal FJ, Singbo A, McKinley J, Kajisa K (2018) Spatial dependency and technical efficiency: an application of a Bayesian stochastic frontier model to irrigated and rainfed rice farmers in Bohol, Philippines. Agric Econ 49(3):301–312
Phillips PCB, Sul D (2003) Dynamic panel estimation and homogeneity testing under cross section dependence. Econom J 6(1):217–259
Schmidt AM, Moreira ARB, Helfand SM, Fonseca TCO (2008) Spatial stochastic frontier models: accounting for unobserved local determinants of inefficiency. J Prod Anal 31:101–112
Schmidt P, Sickles RC (1984) Production frontiers and panel data. J Bus Econ Stat 2(4):367–374
Solow RM (1957) Technical change and the aggregate production function. Rev Econ Stat 39(3):312–320
Sonis M, Hewings GJD (1999) Economic landscapes: multiplier product matrix analysis for multiregional Input-Output systems. Hitotsubashi J Econ 40(1):59–74
Timmer M, Ye X (2018) Productivity and substitution patterns in global value chains, In: Tatje EG, Lovell CAK and Sickles RC (eds.) The Oxford handbook of productivity analysis, New York: Oxford University Press, p 10–13
Timmer MP, Dietzenbacher E, Los B, Stehrer R, de Vries GJ (2015) An illustrated user guide to the world input-output database: the case of global automotive production. Rev Int Econ 23(3):575–605
Timmer MP, Erumban AA, Los B, Stehrer R, de Vries GJ (2014) Slicing up global value chains. J Econ Perspect 28(2):99–118
Ward JHJ (1963) Hierarchical grouping to optimize an objective function. J Am Stat Assoc 58(301):236–244
Yang Z (2013) Quasi-maximum likelihood estimation for spatial panel data regressions. Research Collection School of Economics, Available at https://ink.library.smu.edu.sg/soe_research/1575
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Conflict of interest
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: QML estimators for SARCSS
In Appendix A, we provide a detailed procedure of QML estimation for SARCSSW and SARCSSG.
Let \(\psi ={(\beta ,\gamma ,\rho ,{\sigma }_{v}^{2})}^{{\prime} }\). The log-likelihood function of Eq. (4) is:
The first order condition of maximizing Eq. (A1) with respect to δi is
By solving for (A2), we can obtain
Substituting (A3) into the log-likelihood function, (A1), we obtain the concentrated likelihood function
where \(\tilde{V}={M}_{Q}y-\rho {M}_{Q}({W}_{N}\otimes {I}_{T})y-{M}_{Q}X\beta\), and \({M}_{Q}={I}_{NT}-Q{({Q}^{{\prime} }Q)}^{-1}{Q}^{{\prime} }\)Footnote 22.
1.1 Within estimator
Assuming T ≥ L, the projections onto the column space of Q and the null space of Q are denoted by \({P}_{Q}=Q{({Q}^{{\prime} }Q)}^{-1}{Q}^{{\prime} }\) and MQ = INT − PQ, respectively.Footnote 23 Let’s suppose the true value of ρ is known, say ρ*. By pre-multiplying MQ on (5), we have the within-transformed model
And the estimates of β(ρ*) and of \({\sigma }_{v}^{2}({\rho }^{* })\) are derived by
respectively, where \(e({\rho }^{* })=y-{\rho }^{* }({W}_{N}\otimes {I}_{T})y-X{\hat{\beta }}_{W}({\rho }^{* })\). By substituting the closed form solutions for the parameters β(ρ*) and \({\sigma }_{v}^{2}({\rho }^{* })\) to Eq. (A4), we can concentrate out β and \({\sigma }_{v}^{2}\), and the concentrated log-likelihood function with single parameter ρ is of the form:
where C is a constant term that is not a function of ρ. By maximizing the concentrated log-likelihood function Eq. (A8) with respect to ρ, we can obtain the optimal solution for ρ. Even if there is no closed-form solution for ρ, we can find a numerical solution because the equation is concave in ρ. Finally, the estimators for β and σ2 can be calculated by plugging \({\rho }^{* }=\hat{\rho }\) in Eq. (A6) and Eq. (A7).
The asymptotic variance-covariance matrix of parameters (β, ρ, σ2) is given by:
where \(\tilde{X}={M}_{Q}X\) and \({W}^{* }=W{({I}_{N}-\rho W)}^{-1}\).
1.2 Generalized least squares estimator
Alternatively, we can estimate Eq. (5) by generalized least squares(GLS). Denote the variance-covariance matrix of the composite error ε = QU + V as cov(ε) = Ω.
The GLS estimator is the SAR estimator applied to the following transformed equation:
where ε = QU + V, \({{\Omega }}=cov(\varepsilon )={\sigma }_{v}^{2}{I}_{NT}+Q({I}_{N}\otimes {{\Delta }}){Q}^{{\prime} }\). The estimation procedure of Eq. (A10) is same as the procedure for within-estimation. Let η = (β, γ, δ0). Assuming we know the true value of ρ = ρ*, the GLS estimators of η(ρ*) are
Hence, the GLS estimators of η can be represented as a difference of OLS estimators of regressing \(\widetilde{y}\) on \((\widetilde{X},\widetilde{{{{\boldsymbol{Z}}}}},\widetilde{{{{\boldsymbol{R}}}}})\) and regressing \(\widetilde{({W}_{N}\otimes {I}_{T})y}\) on \((\widetilde{X},\widetilde{{{{\boldsymbol{Z}}}}},\widetilde{{{{\boldsymbol{R}}}}})\) premultiplied by the spatial autoregressive coefficient ρ*, where tilde represents GLS transformation. Ω can be estimated by:
Following Cornwell et al. (1990), Δ can be estimated as
where \({e}_{i}={M}_{R}y-{\rho }^{* }{M}_{R}({W}_{N}\otimes {I}_{T})y-{M}_{R}X{\hat{\beta }}_{W}({\rho }^{* }){| }_{i}\), which represents the IV residuals for individual i, and \({M}_{R}={{{\boldsymbol{R}}}}{({{{{\boldsymbol{R}}}}}^{{\prime} }{{{\boldsymbol{R}}}})}^{-1}{{{{\boldsymbol{R}}}}}^{{\prime} }\) is the projection onto the column space of R.
Consider the likelihood function of Eq. (A10). Since σvΩ−1/2ε has mean zero and variance \({\sigma }_{v}^{2}\), the likelihood function is written in the form of
where ε = y − ρ(WN ⊗ IT)y − Xβ − Zγ − Rδ0. Substitution of Eq. (A11) and Eq. (A12) into Eq. (A14) gives a concentrated likelihood function as follows:
where \(e(\rho )={\hat{\sigma }}_{v}\hat{{{\Omega }}}{(\rho )}^{-1/2}y-\rho {\hat{\sigma }}_{v}\hat{{{\Omega }}}{(\rho )}^{-1/2}({W}_{N}\otimes {I}_{T})y-{\hat{\sigma }}_{v}\hat{{{\Omega }}}{(\rho )}^{-1/2}X\hat{\beta }-{\hat{\sigma }}_{v}\hat{{{\Omega }}}{(\rho )}^{-1/2}{{{\boldsymbol{Z}}}}\hat{\gamma }-{\hat{\sigma }}_{v}{\hat{{{\Omega }}(\rho )}}^{-1/2}{{{\boldsymbol{R}}}}\hat{{\delta }_{0}}\), and C is a constant term that is not a function of ρ. Finally, as is the case of within estimator, we can obtain the estimators for η and Ω using the estimate of ρ from Eq. (A15).
1.3 Implementation
For the implementation, we combine the procedure suggested by Elhorst (2014) and a typical two-stage approach of FGLS. In this section we discuss the implementation of within estimator and then turn to the implementation of the GLS estimator. The implementation consists of the following steps.
1.3.1 [Within Estimator]
From Eq. (A6), it is easy to show that \({\hat{\beta }}_{W}={b}_{0}-{\rho }^{* }{b}_{1}\), where b0 and b1 are the OLS estimators of regressing MQy and MQ(WN ⊗ IT)y on MQX, respectively. Similarly, the estimated residuals from Eq. (A5), e(ρ*), can be expressed as e(ρ*) = e0 − ρ*e1, where e0 and e1 are the associated OLS residuals to b0 and b1, respectively. Hence the first step is obtaining b0, b1, e0, and e1. Second, we maximize Eq. (A8) with respect to ρ after replacing e(ρ) = e0 − ρe1, i.e.,
Third, by replacing \({\rho }^{* }=\hat{\rho }\) in Eq. (A6) and (A7) gives the within estimator, \({\hat{\beta }}_{W}\), and the estimated variance, \({\hat{\sigma }}^{2}\). Finally, the asymptotic variance-covariance matrix of parameters \(({\hat{\beta }}_{W},\hat{\rho },{\hat{\sigma }}_{v})\) can be calculated by Eq. (A9).
1.3.2 [GLS Estimator]
Unlike the within estimator case, we are unable to find the separate OLS estimators of regressing σvΩ−1/2y and σvΩ−1/2(WN ⊗ IT)y on σvΩ−1/2(X, Z, R) in advance of having \(\hat{\rho }\), although Eq. (A11) is expressed as a subtraction of two terms. This is because the feasible Ω is obtainable only after we have a value for ρ. Instead of following the steps of within estimator, we can obtain \(\hat{\rho }\) by simply maximizing the concentrated log-likelihood function (A15). Once we have \(\hat{\rho }\), Eq. (A13), Eq. (A12), Eq. (A11) give \({{\Delta }}(\hat{\rho })\), \({{\Omega }}\hat{\rho }\), and \({\eta }_{G}(\hat{\rho })\) in order.
Appendix B: Estimation results with value-added dependent variable
Appendix C: Sensitivity analyses
Appendix D: Industry classifications and ISIC Rev.3 codes
Table 14
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Han, J., Sickles, R.C. Estimation of industry-level productivity with cross-sectional dependence by using spatial analysis. J Prod Anal (2024). https://doi.org/10.1007/s11123-023-00718-8
Accepted:
Published:
DOI: https://doi.org/10.1007/s11123-023-00718-8