Proper modelling of industrial production systems with unintended outputs: a different perspective

Abstract

The question of how to properly model production systems with unintended outputs has proven both controversial and of particular interest to the productivity and efficiency community. The paper explains why some of the arguments put forward in these controversies are hardly convincing for industrial and other processes. Among other things, there is a lack of clear conceptual labelling of the different types of joint production, especially coupled production, which is the main source of undesirable and other unintended outputs, unless neglected. It is largely ignored that the desirability of such by-products may depend on the quantity produced. This is also true for reduction processes such as waste incineration or end-of-life vehicle dismantling, which in turn generate new unintended outputs. As a rule, industrial material and energy balances are modelled implicitly. Koopmans’ activity analysis is the standard approach in modelling production systems with undesirable outputs in the literature of business economics on sustainable production and supply chain management. With data envelopment analysis (DEA), instead of entire production possibilities, it is sufficient to know only certain local properties in the relevant range of input and output quantities of the observed activities. This lowers the challenge to verify their empirical validity.

1 Introduction

In May 2021, a special-topic issue on Proper modelling of production systems that produce both desirable and undesirable outputs was published in this journal. It includes an article on “Performance measurement and joint production of intended and unintended outputs” by Førsund (2021a), three comments on this article by Färe and Grosskopf (2021), Murty and Russell (2021), and Ang and Dakpo (2021) as well as rejoinders to the comments by Førsund (2021b). The special issue is anticipated to be the first of an irregular series on symposia sponsored by the journal. In their overview, the editors state: “The intent of the series is to give leading scholars in the productivity and efficiency community the chance to exchange ideas on topics that have proven both controversial and of particular interest to the community” (Greene et al. 2021).

To complement the exchange of ideas in the first special issue, I would like to share insights and experiences from several decades of research and teaching in sustainable industrial production and controlling by commenting on the topic in general and the statements of the five papers in particular. I hope that this will shed better light on some facts and help to further clarify some controversies. The following statements summarise several (differently important) conclusions of my paper:

• a. In general, material and energy balances are not explicated in production models. How to systematically decide which types of inputs and outputs should be taken account of and distinguished seems to be an open question that has not yet been satisfactorily answered by the productivity and efficiency literature.

• b. Quite a few industries are characterised by unintended outputs (by-products) which may nevertheless be desirable. On the contrary, even intended outputs (main products) – i.e., outputs where the process is established or perpetuated by the purpose of obtaining certain quantities of them – can be undesirable if they are produced in abundance, in which case their excess quantities are superfluous or waste.

• c. Reality shows that multi-output production exists in various manifestations, which are often not clearly defined and delineated in the literature, leading to misunderstandings. This is especially true for different types of joint production. In order to capture the important phenomena that are the main cause for producing undesirable outputs, the notion of ‘coupled production’ is proposed here.

• d. A coupled output is defined as an output – and a co-product in particular as a main product – that is taken account of and unavoidably emerges with a main product and is of a different type (otherwise, it would be an excess quantity).¹ A production system is characterised by coupled production if at least one type of coupled output or co-product is considered (to be relevant).

• e. The purpose of a system that transforms inputs into outputs may also be to eliminate a particular type of undesirable objects (bads). They form the intended input of so-called reduction processes that reduce, convert, abort, or destroy this input, such as the treatment of wastewater and incineration of solid waste or the dismantling of end-of-life vehicles, old buildings, and nuclear power plants. Reduction processes inevitably generate new kinds of different outputs (which are often themselves more or less undesirable), so that they are strongly coupled with the elimination of the bad.

• f. To measure the relative performance of production or reduction activities of decision-making units (DMUs) with non-parametric methods such as data envelopment analysis (DEA), it is not necessary to know the properties of the actual entire real technology in this respect. One only needs to know the feasibility and (validity of the) properties of the efficient ‘best practice’ frontier determined by the envelopment of the measured data points via the chosen method.

These statements will now be explained and extended, referring to the topic and papers of the special issue. Section 2 discusses general aspects of proper modelling of production systems with unintended or undesirable outputs, and Section 3 specifically respective models for industrial processes. Both sections focus in particular on performance measurement by DEA. Section 4 concludes with comments on future research perspectives.

2 Modelling of productions systems in general

Section 2.1 is concerned with the neglection and desirability of inputs and outputs and with the purpose of a production system, Section 2.2 with coupled production as important phenomenon that is the cause for the emergence of undesirable outputs, Section 2.3 with the knowledge and assumptions regarding possible production activities sufficient for an efficiency measurement with DEA, and Section 2.4 with properties of the data envelopment in case of undesirable outputs.

2.1 Neglection, desirability, and purpose

Many types of input and output objects, although actually involved in a production process to be analysed, are usually not taken account of by the corresponding models of production economics but are completely ignored. As a rule, more – and more detailed – types of material inputs and outputs are considered in production models with environmental or engineering issues than in those with purely economic issues. Which types of (input or output) objects are distinguished or else considered to be of the same kind is not given a priori but a decision of the model designer with regard to the empirical facts and the purpose of modelling.

Mass and energy conservation laws of physics enforce material and energy balances, but only if all types of material objects and forms of energy affected by the analysed process are considered in the production model and only if all their input and output quantities are correctly measured. Indeed, mass balances, such as in formula (1) of Førsund (2021a), can in principle be stated not only for the total mass of all inputs and outputs and also for each chemical compound, like water (H₂O), if no chemical reactions occur during the production process, but even for the content of each natural element, such as hydrogen (H) and oxygen (O), if there is no nuclear fission or fusion. In environmental management it is common to use such material and energy balances as accounting equations for documentation and evaluation purposes, e.g. in a life cycle assessment of products. However, the efficiency of production is usually evaluated in the sense of a plausibility check, only, e.g. when analysing the inventory of inputs and outputs of a production process in a certain period of time. A balance gap between the total output and the total input of such an element or compound may then indicate an inefficiency of the empirical process, e.g., due to an unknown underground water leakage.

In fact, any production technology obeys the laws of physics, such as energy conservation and non-decreasing entropy, referred to as the First and Second Law of thermodynamics (Baumgärtner et al. 2006). However, I do not recommend explicitly implementing such theoretical information in general formal models designed to measure production performance in a meaningful way in practice. Insufficient knowledge of the production system in question, improper modelling of system boundaries, measurement errors, inefficiencies and other things can unpredictably disturb accounting equations based on mass and energy balances. Therefore, it is not a good idea to use material balances in general as an explicit part of production models in performance measurement (cf. Førsund (2021a, p. 159) and (2021b, p. 196 f)). I agree with Murty & Russell’s observation (2021, p. 177 f) “that, while in theory the production relations governing emission generation should reflect the two laws of thermodynamics, in practice it might be impossible for the researchers to spell out completely the material-balance conditions.” To further explain this view, they add in particular (p. 178): “It is also the case that some types of residuals might be omitted from a model of pollution generation because they are relatively harmless and therefore of little relevance to policy making. Hence, although representations of many technologies may appear to be incomplete because they do not explicitly incorporate material-balance conditions, it does not follow that they violate these conditions.” Production models in business economics and operations research generally ignore many types of inputs and outputs but have nonetheless been used successfully in most industries since the 1960s, especially for planning and accounting of production systems that jointly produce both desirable and undesirable outputs.

On the one hand, production models must be rich enough to capture and explain the relevant phenomena, on the other hand, they should be constructed as parsimoniously as possible.² Generally speaking, Ragnar Frisch (1965, p. 14) – certainly “one of the giants of economics” (Førsund 2021b, p. 197) – concluded with respect to the countless number of things which are part of a production process or influence it: “No analysis, however completely it is carried out, can include all these things at once. In undertaking a production analysis we must therefore select certain factors whose effect we wish to consider more closely.”

In his pioneering multi-equation approach to modelling multi-input and multi-output technologies (Murty and Russell 2021, p. 178), Frisch (1965, p. 8 and 346) defined production in the economic sense as “the attempt to create a product which is more highly valued than the original input elements”. Because of the unintended outputs he ignored in his analysis, I define production as a human-directed and controlled process of value creation that uses and transforms selected objects and services (as input) with the intention that certain new objects or services shall emerge (as output) from the process, whereby the total advantages generated shall outweigh the total disadvantages of the transformation. Disadvantages result from the consumption of goods and from the emergence of bads.

Therefore, any economic theory of production must be decision-based by taking account of the perceptions, intentions and preferences of the human beings who direct and control the transformation process (Dyckhoff 2006). In market environments without externalities, economic theory usually assumes that the preference of the producer(s) is in the interests of the shareholders by seeking to maximise profits. With the increasing importance of ecological damage, this becomes more complicated. Hence, how to properly model a production system is much more than merely a question of pure technological possibilities; in particular: how to decide whether an output is a main product or a by-product, or whether it is desirable or undesirable, or whether it is neglected at all, or whether two different outputs are classified as of the same quality (type) or not.

A by-product can often be qualitatively almost indistinguishable from a main product, e.g., when cutting pieces from a log. Some of the wooden offcuts may be valuable, so it can be difficult to formally discriminate intended from unintended outputs in a rigorous manner. An external observer does not easily recognise the purpose of a production system with multiple outputs (except perhaps from legal declarations by the owner of the company in question). However, this difficulty also applies to distinguishing outputs into those that are either desired or undesired by producers in the absence of objective criteria such as market prices.³

Furthermore, the price of a by-product can change its sign with the quantity produced. For example, the value of flue-gas desulphurisation gypsum (which emerges as coupled output of filtering out sulphur dioxide (SO₂) from the emissions of a lignite-fired power plant) is often ambiguous and either positive or negative depending on actual local market conditions. In their historical review of the economics of joint production, Baumgärtner et al. (2006, p. 142) detect as one of two major gaps⁴ “the lack [of] a general and encompassing theory of joint production that does not simply assume, or impose, the character of the outputs as positively or negatively valued, but endogenously derives this character.” Converting a waste stream into a useful and saleable by-product may create an operational synergy between two jointly produced outputs. It can lead to counterintuitive profit-maximising strategies such as increasing the amount of waste generated, and thus increasing the quantity of original product above the business-as-usual production volume (Lee 2012). Whether an output is desired or undesired, is not given per se, but depends on the economic circumstances which change over time (Kronenberg and Winkler 2009), as already Frisch (1965, p. 11) remarked: “A change in the price situation may result in the bi-product [by-product; H.D.] or even the waste product being elevated to the status of main product.” The fact that intangible by-products can also have positive and negative impacts is addressed by Ang and Dakpo (2021, p. 187) in their comments to Førsund (2021a).

The distinction between intended and unintended outputs according to the purpose pursued is of paramount importance when investing in and building a new production system. It may be of less importance for the short-term performance measurement of an on-going system, where, for the given purpose, specific productivity and efficiency questions arise whether and to what extent the generated advantages actually outweigh the disadvantages of the transformation process. Nevertheless, the terms ‘unintended’ (regarding purpose) and ‘undesirable’ (regarding preference) should be distinguished in principle and not used synonymously, as was done in the special issue. Purpose is decisive for assessing the effectivity – in addition to the efficiency – of production.⁵

2.2 Coupled production as causal phenomenon for undesirable outputs

The Entropy Law states that any (energy) transformation process, be it production, reduction, or consumption, inevitably generates some kind of unintended output (Georgescu-Roegen (1971); cf. Baumgärtner et al. (2001)). From a purely thermodynamical point of view, every production would thus be coupled production. The notion defined in the introduction is nevertheless useful because most by-products, including entropy, are neglected in economic studies, even in usual ecological ones. I prefer the term ‘coupled production’⁶ because the term ‘joint production’ is often imprecisely defined and ambiguously used in the international literature (Dyckhoff and Souren 2023).

Førsund (2021a, p. 163) defines ‘joint production’ in a broader sense⁷ and distinguishes three subtypes. His terminology differs from that of Frisch (1965, pp. 11, 269–281)⁸ and the one used here:

• Rigid coupling of certain outputs:⁹ The quantities of these outputs cannot be changed if the quantity of one of them is fixed, regardless of any variations of actual inputs; then, they are complementary and form a “product bundle” (Stackelberg 1932).

• Flexible coupling of certain outputs:¹⁰ A restricted, but not complete substitution between these outputs is possible.

• Alternative (or assorted) outputs: Each of these outputs can be produced solely or combined with others by the same (scarce) unit(s) of the production system within the considered period.¹¹

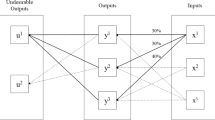
The first two types represent coupled production, the last not. They are consistent with Frisch’s (1965) use of the term ‘coupling’. However, his definitions are only concerned with main products, ignoring undesirable outputs. Figure 1 illustrates the three types.

Fig. 1

Types of joint production: rigid and flexible coupled production; alternative production

In alternative production, the products are not coupled but connected, so that complete substitution is possible. It is the limiting case of extremely flexible coupled production. Both flexibly coupled and alternative production form two kinds of rival production¹² where the main products compete for (efficient) production possibilities if the capacity or availability of inputs is limited.

Almost at the same time of Frisch (1965), Danø (1966, p. 166f) stated: “[S]ome justification of the predominance of single-output models in the theory of production may be sought in the fact that it is often possible to decompose a multi-product model into separate models for the respective products, […] [S]uch cases will be treated as alternative processes and only the non-decomposable models will be referred to as cases of truly joint production (multi-product processes).” He adds in a footnote (p. 167): “This fundamental distinction will usually but not always coincide with the criterion whether or not it is possible (though not necessarily economical) to produce each output without making any of the others. Limiting cases are conceivable where solutions on the boundary of the range of product substitution are possible even though the joint process cannot be decomposed.” Thus, ‘truly joint products’ in the Danø sense, while not obligatorily unavoidable, will usually be produced together to make better use of scarce resources or to achieve other synergistic effects. For example, bread and cakes can be baked (separately) one after the other in the same oven, but also together when appropriate to use its free capacity.¹³

The last example illustrates that simultaneity of production is not the defining characteristic for the emergence of (undesirable) coupled outputs. This is often erroneously written, also by the remark of Dakpo and Ang (2019, p. 604) that “Baumgärtner et al. (2001) used the term of ‘joint production’ to describe economic systems that simultaneously produce desirable and undesirable goods.” Indeed, ‘simultaneous’ means something other than ‘necessary’, ‘unavoidable’, or ‘inevitable’. Simultaneity in generating outputs is neither sufficient nor necessary for coupled production, as demonstrated by the classical examples of (first) wool and (then) mutton from a sheep, or (first) milk and (then) meat and hide from a cow, used by Førsund (2021a, p. 164). This kind of imprecise definition and use of the term ‘joint production’ has led to many misunderstandings.¹⁴

In contrast to Førsund (2021a),¹⁵ Baumgärtner et al. (2006) basically use the term ‘joint production’ as synonym for the notion of coupled production defined here. However, in their Chapter 6 “Joint Production in the History of Economic Thought” they do not make a clear distinction between coupled and other forms of joint production. This matches with the historical review by Kurz (1986) who gives no definition of joint production and seems to use the term synonymously with “multiple-product processes”. Nonetheless, most of the examples of the classical economists for joint production mentioned by Kurz (1986) represent special cases of coupled production.¹⁶ He points out that joint production was a main subject of essays and intensive discussions by influential classical and early neoclassical economists, even before the 19^th century, and that it played a significant role in the evolution of economic thought during the 19^th century.

2.3 Envelopment of production data and local empirical relevance

Before discussing specific approaches for modelling production systems with unintended outputs in the next sections, I pose a more fundamental question that is generally of crucial importance, also in cases without undesirable outputs: What properties of the unknown technology or production possibility set (PPS) underlying the observed data need to be known (or assumed) in the first place for an empirically sound performance measurement? This paper cannot fully answer the question. Nevertheless, I will offer some reasoning, especially for a performance measurement that applies the usual models of data envelopment analysis (DEA). Figure 2 illustrates my main argument, which I then explain more generally.

Fig. 2

Attainable efficient frontier of convexly enveloped eight data points (Dyckhoff 2006, p. 178)

The diagram of Fig. 2 shows the observed activities of eight decision making units (DMUs) as points (z₁, z₂) = (−x, y) of the real-valued input-output space. Here, the non-negative input quantity x is placed on the negative horizontal axis. In a first interpretation of Fig. 2, both object types of input x and output y are assumed to represent (desirable) goods of a two-dimensional technology.

The dark shaded hexagon is generated as convex hull (‘envelopment’) T^env of the eight data points, with points #3 and #5 in its interior. All DEA models commonly used in applications suppose a PPS that contains at least such a convex hull of the observed activities – whose efficiencies are to be analysed – and usually more activities as well. The usual DEA models assume moreover that the entire PPS itself is convex,¹⁷ contrary to the example of Fig. 2 where the usually unknown, admissible production activities are depicted by the light-shaded non-convex area. It illustrates a PPS with a north-east frontier that may represent a classic production function with first increasing and then decreasing returns.

The black triangle north-east of #5, i.e. the intersection of its dominance cone with the convex envelopment of all observed data, contains all those points of the hexagon that dominate activity #5 by using less input or producing more output. Thus, #5 is inefficient with respect to the convex hull. The bold traverse line in the north-east of the hexagon, connecting points #2, #4, #6, and #8, shows all (relatively) efficient convex combinations, called efficient frontier. It represents the ‘best-practice production function’ regarding the hexagon as an approximation of the relevant part of the unknown real (here non-convex) PPS. DEA models determine a performance measure for DMU #5 by projecting it to a proper reference or ‘target point’ on the intersection of its (black) dominance cone with the efficient frontier. The (radial, additive, or directional) distance metric of the chosen DEA model determines the respective target point and efficiency score of DMU #5, whereas those DMUs on the efficient frontier the activities of which are combined to define the target point form the so-called ‘benchmarking partners’ of DMU #5, in this case DMUs #4 and #6.

If this common DEA procedure should provide valid empirical information in practice, some specific questions must first be answered, and corresponding decisions made, e.g. regarding the homogeneity of the DMUs or the selection of inputs and outputs. Then it must be clarified which DEA model is suitable. This includes the question of whether the target points of the inefficient DMUs are actually attainable. Otherwise, they cannot provide useful indications for a performance evaluation. A necessary condition is that at least the relevant parts of the calculated efficient frontier and a certain neighbourhood are contained in the (generally unknown) real PPS. In Fig. 2, the convex hull of the eight observed activities is even fully embedded in the PPS, although the PPS itself is not convex.

Figure 2 demonstrates that it is not necessary to know the entire real PPS and all its technological properties. It is sufficient to know certain locally empirically valid properties of the PPS in the relevant range of input and output quantities of the observed and analysed activities. Thus, if e.g. the basic radial DEA model for variable returns to scale, well-known as “BCC model”, is applied, it is enough to know that the PPS contains the convex hull of the observed activities, i.e. the hexagon in case of Fig. 2. Moreover, it would even be sufficient that only the relevant activities on the efficient best-practice frontier are elements of the PPS. For example, an output-oriented BCC model projects activity #7 of Fig. 2 upwards to that point of the hexagon that produces maximum output with at most the input quantity of #7 (and not categorically with the identical input), leading to activity #8 as target point of #7. Hence, it is not necessary to assume further properties of the PPS concerned with activities outside the range of input and output quantities relevant for the performance evaluation. In particular, it is dispensable to postulate strong or free disposability (Dyckhoff 2019).

The above statements, illustrated by the example of Fig. 2, are obviously true in general, especially for undesirable outputs. The fact that only local properties in the range of the observed DMUs are of interest allows for an easier distinction of outputs into desirable and undesirable ones than possibly on the macro level of the entire underlying PPS, particularly in cases where the classification of a by-product depends on the quantity produced.¹⁸

In a different (second) interpretation of Fig. 2, it may display the two-dimensional part of a more-dimensional technology where the horizontal axis now represents the output y₁ of a bad instead of the input x of a good, i.e. (z₁, z₂) = (−y₁, y₂), whereas object type #2 is still desirable, at least with output quantities smaller than z₂ = 8, while larger quantities might be undesirable. In any case, the efficiency assessment of activity #5 is not influenced by a negative price of output #2 if more than eight quantity units are produced, i.e. when excess quantities of the second object type become undesirable.

2.4 Properties of the data envelopment in cases of undesirable outputs

Since the term ‘joint production’ is not clearly defined in the literature, Førsund had to reiterate and emphasise the fact in his rejoinders that his paper shall “capture joint production of the type that production of bads is unavoidable” and that certain model approaches of his commentators are “not compatible with what I define as joint production” (2021b, p. 195 f).¹⁹ In fact, motivated by the question how to calculate efficiency measures when undesirable outputs are unavoidably produced, he focuses on a specific type of coupled production described by certain multi-equation models (which Frisch (1965) originally called “factorially determined multi-ware production”). He notably criticises the Shephard-inspired approach, defended by Färe and Grosskopf (2021).

I will not discuss these approaches in detail. However, if one accepts the conclusion of the last section that it is sufficient to know or presume only local properties of the PPS in the relevant range of the observed activities of DMUs, then the traditional Shephard-inspired axiomatic approaches concerned with the entire technology do not (or no longer) play an important role for performance measurement by DEA. Nevertheless, instead of considering the entire real PPS T, which usually is unknown in practice, one can ask which of the usual axioms may be assumed to construct the set T^env of enveloped observed data, although they might eventually not be empirically valid in a strict sense.

It is preferable but not necessary that T^env⊂T. Because, as noted before, it is merely essential that the relevant activities on the efficient best-practice frontier of T^env and possibly those in a certain neighbourhood, too, are actually admissible. Indeed, not all parts of the efficient frontier of T^env need to be elements of the real PPS T. For example, in case that the quantities of a certain type of input or output are defined as integer values only, the assumption of convexity of T^env is wrong from a strictly empirical point of view but may nonetheless be acceptable under certain circumstances where the distance of the calculated convex solution on the efficient frontier of T^env to an admissible integer valued point in the neighbourhood is relatively small, implying a minor error only. Furthermore, although assuming an (unbounded) linear T^env is empirically wrong in any case because all real PPS on planet Earth exhibit finite boundaries, it may anyway lead to good results of a performance analysis.

Let (x, y) denote a multi-dimensional activity with non-negative quantities of inputs x and outputs y, and let $({\boldsymbol{x}}^{j}, \,{\boldsymbol{y}}^{j}), {j} = {1},\, \ldots , n$, be the observed activities.²⁰ The specific kind of data envelopment considered in the last section was their convex hull, which displays variable returns to scale (VRS):

$${{{\mathbf{T}}}}^{{{{\mathrm{vrs}}}}} = \left\{ \begin{array}{l}\left( {{{{\boldsymbol{x}}}},{{{\boldsymbol{y}}}}} \right)\left| {\left( {{{{\boldsymbol{x}}}},{{{\boldsymbol{y}}}}} \right)} \right. = \mathop {\sum}\limits_{j = 1}^n {\lambda ^j \cdot \left( {{{{\boldsymbol{x}}}}^j,{{{\boldsymbol{y}}}}^j} \right)} ;\\ \mathop {\sum}\limits_{j = 1}^n {\lambda ^j = 1;\lambda ^j \ge 0,j = 1, \ldots ,n} \end{array} \right\}$$

(1)

Clearly, this convex set is bounded, closed, and non-empty. In general, the other standard axioms of Shephard (1970), namely feasibility of inactivity, strong disposability of inputs, and weak disposability of outputs (Färe and Grosskopf 2021, p. 190), are not satisfied. In particular, assuming feasibility of inactivity, i.e. (x, y) = (0,0) ∈ T^env, in addition to convexity, would lead to a data envelopment with non-increasing or decreasing returns to scale (DRS):

$${{{\mathbf{T}}}}^{{{{\mathrm{drs}}}}} = \left\{ \begin{array}{l}\left( {{{{\boldsymbol{x}}}},{{{\boldsymbol{y}}}}} \right)\left| {\left( {{{{\boldsymbol{x}}}},{{{\boldsymbol{y}}}}} \right)} \right. = \mathop {\sum}\limits_{j = 1}^n {\lambda ^j \cdot \left( {{{{\boldsymbol{x}}}}^j,{{{\boldsymbol{y}}}}^j} \right)} ;\\ \mathop {\sum}\limits_{j = 1}^n {\lambda ^j \le 1;\lambda ^j \ge 0,j = 1, \ldots ,n} \end{array} \right\}$$

(2)

which reveals a weaker version of the well-known ‘weak disposability’ property.²¹ With y = (y_G, y_B) distinguished into good outputs y_G and bad outputs y_B where appropriate (at least for all relevant output vectors), I define this more realistic weaker (output) disposability for a set T as follows:

• For each activity (x, y)∈T and each 0 ≤ λ ≤ 1 there exists a bundle $\widetilde {{{\boldsymbol{x}}}}$ of input quantities (‘factor combination’) such that $\left( {\widetilde {{{\boldsymbol{x}}}},\lambda {{{\boldsymbol{y}}}}} \right) \in {{{\mathbf{T}}}}$.

The discrepancy with the neo-classical ‘weak disposability’ property is that the input vector x is fixed in Shephard’s (1970, p. 187) definition when all outputs are radially contracted. This has led to severe criticism with regard to material balances. This criticism does not apply to the weaker disposability property defined here. In fact, the convex envelopment T^drs with feasible inactivity satisfies this property with an input: $\widetilde {{{\boldsymbol{x}}}} = \lambda {{{\boldsymbol{x}}}}$ that shrinks proportionately with the outputs. T^drs is also bounded, closed and non-empty. However, inputs are not strongly disposable.

Färe and Grosskopf (2021, p. 191) defend their additional axiom of null-joint production as a property that “captures the unavoidability of producing good output without simultaneously producing some bad output” (which actually means coupled production). Both above types of convex data envelopment with variable or non-increasing returns to scale, T^vrs and T^drs, fulfil this assumption if none of the observed activities (x, y^j) itself allows to produce desirable outputs without undesirable ones, i.e. if ${{{\boldsymbol{y}}}}_B^j = 0$ implies ${{{\boldsymbol{y}}}}_G^j = 0$. That is, both types of data envelopment exhibit coupled production if each enveloped DMU already does (and no strong disposability of inputs or outputs is assumed additionally).

It can be shown that this is also true for a linear envelopment; it displays constant returns to scale (CRS):

$${{{\mathbf{T}}}}^{{{{\mathrm{crs}}}}} = \left\{ {\left( {{{{\boldsymbol{x}}}},{{{\boldsymbol{y}}}}} \right)\left| {\left( {{{{\boldsymbol{x}}}},{{{\boldsymbol{y}}}}} \right)} \right. = \mathop {\sum}\nolimits_{j = 1}^n {\lambda ^j \cdot \left( {{{{\boldsymbol{x}}}}^j,{{{\boldsymbol{y}}}}^j} \right)} ;\lambda ^j \ge 0,j = 1, \ldots ,n} \right\}$$

(3)

This cone-technology is closed, non-empty, and exhibits weaker disposability. Although not bounded itself, its output possibility sets P(x): = {y|(x; y)∈T} are bounded for given input x.

Regarding the two-dimensional example of Fig. 2, it is obvious that – because of its non-linear and even non-convex frontier – none of the two data envelopments T^crs and T^drs are subsets of the underlying PPS. However, an output-oriented DEA model would project all DMUs to attainable target points on the respective efficient frontier, except for DMU #7 in case of T^crs (the “CCR model”).

3 Modelling of industrial processes with unintended outputs

In contrast to other areas of economics, the production theory of Ronald Shephard (1970) with its axioms based on input or output possibility sets has not found much interest in business sciences, neither in the theory of business economics nor in research and teaching on production and operations management. This is in stark contrast to the alternative approach of Activity Analysis of Production and Allocation, documented in the proceedings of a conference edited by Tjalling Koopmans in 1951. In this book, the foundations of linear programming (LP) as well as of efficiency analysis were laid by several authors, in particular by Dantzig (1951) and by Koopmans (1951) himself. To date, numerous mathematical models and methods based on this origin have been developed to deal with economic planning, scheduling, and accounting problems. For example, LP models have been used regularly for oil refining since the 1950s. The use of such models and methods is common practice in larger companies of industries that are heavily affected by coupled production, such as the chemical or iron and steel industries. In addition, activity analysis has been a standard approach in modelling undesirable outputs in the literature of sustainable production and supply chain management since the 1990s (Thies et al. 2021).

3.1 Activity analytic modelling of production systems with undesirable outputs

Murty and Russell (2021, p. 180) emphasise that “the key to correct modelling of an emission-generating technology lies in a proper formulation of its disposability properties.” In his essay on the Analysis of production as an efficient combination of activities, Koopmans (1951) does not make use of any general disposability assumption, but instead allows for the inclusion of separate disposal activities, e.g. to dispose of waste produced, which is thus explicitly treated as an intermediate product. His analysis deals with convex polyhedral cones generated by a finite set of basic activities.

If $({\boldsymbol{x}}^{j}, {\boldsymbol{y}}^{j})$ denotes the input and output quantities of the considered basic activities j $({j} = {1}, \ldots, n )$ the set T^crs, defined in (3), represents such cones (except for the negative sign of the inputs that Koopmans uses in his notation²²), but only of those technologies that do not explicitly take account of intermediate objects, be it goods or bads. (Nonetheless, purely intermediate objects may exist that are consumed in exactly the same amount as produced within the production system, thus showing a net output/input of zero.) In realistic applications, T^crs fulfils Koopmans’ (1951, pp. 48–52) main postulates that (A) production is irreversible, (B) there is no output without input (“impossibility of the Land of Cockaigne”), and (C) production of output is possible.

Koopmans (1951) excludes undesirable outputs from his explicit analysis by specifying a further restriction on final commodities, adding following footnote (p. 38f): “Such a restriction disregards the fact that certain effects or conditions of production are negatively valued, such as smoke pollution. We could easily allow for this circumstance and still maintain the formal applicability […] by introducing these effects as negative outputs (i.e., inputs) of ‘desired’ commodities, of which the algebraic increase (i.e., the absolute reduction) is deemed desirable. Since setting such a category of commodities would complicate the notations rather than the reasoning in what follows, we have refrained from doing it.”

Since unintended outputs are the main topic of this paper, I will use his recommendation to simplify the notation of preference relations between activities, but with a different reasoning. For any PPS T with bad outputs, define a corresponding multi-dimensional value (possibility) set by

$${{{\mathbf{V}}}} = {{{\boldsymbol{v}}}}\left( {{{\mathbf{T}}}} \right) = \left\{ {{{{\boldsymbol{v}}}}: = \left( { - {{{\boldsymbol{x}}}};{{{\boldsymbol{y}}}}_G, - {{{\boldsymbol{y}}}}_B} \right)\left| {\left( {{{{\boldsymbol{x}}}};{{{\boldsymbol{y}}}}_G,{{{\boldsymbol{y}}}}_B} \right)\, {{\in}} \,{{{\mathbf{T}}}}} \right.} \right\}$$

(4)

Then, an activity #2 dominates an activity #1 (weakly) when v² ≥ v¹. Thus, the determination of the efficient frontier of PPS T, consisting of its non-dominated activities, is equivalent to the solution of the vector-maximisation problem “max v ∈ V” regarding the relevant values, well-known from multi-criteria decision analysis (Dyckhoff and Allen 2001, p. 320f).

This kind of notation is a matter of better handling in the first place, and by no means implies that bad outputs are inputs – as presumed by Dakpo et al. (2016, p. 357) and other authors when criticising the approach to measure environmental efficiency by Dyckhoff and Allen (2001, p. 315). Although good inputs and bad outputs are treated in the same way, this is meant syntactically (mathematically) only – and in no way semantically (interpretive) –, namely with the purpose to take into account that the non-negative quantities of both are to be minimised, contrary to those of good outputs and bad inputs whose maximisation is preferred (Dyckhoff and Souren 2022, p. 811).

In this kind of interpretation, the horizontal axis to the left of Fig. 2 may also represent the negative value v₁ = −y₁ of the positive output y₁ of a bad (instead of the positive input x₁ of a good: v₁ = −x₁), as discussed at the end of Section 2.3. Then, the convex hexagon derived from T^vrs would show possible bundles of the good output #2 and the bad output #1, which are flexibly coupled within the range of observed activities. Whereas the underlying real (light-shaded) PPS in Fig. 2 would not allow to produce the good without the bad, the converse would be possible (different from the middle diagram of Fig. 1).

3.2 Basic types of industrial productions systems with unintended outputs

This section presents different realistic basic types of industrial production systems with unintended outputs in order to demonstrate the usefulness of the activity analytic approach, thereby (partly implicitly) commenting on several issues discussed in the papers mentioned in the introduction. In particular, it is shown that it is the process in the first place which is causal for the emergence of undesirable outputs,²³ while the material input used or the joint main product connected with this process are of secondary importance, only. It may help to clarify the discussion about the different approaches for a proper modelling of pollution-generating technologies.

3.2.1 Block-unit heating power plant as rigidly coupled production

Different sets T may show the same value set V, as in the following example of a four-dimensional ray

$${{{\mathbf{V}}}} = \left\{ {{{{\boldsymbol{v}}}} = \left( { - 1.11\lambda ,\, - 52.3\lambda ,\,0.47\lambda ,\,0.53\lambda } \right)\left| {\lambda \ge 0} \right.} \right\}$$

(5)

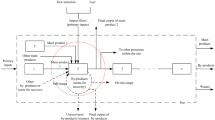
In fact, on the one hand, V is the image of the realistic ‘blue-print technology’ of a block-unit heating power plant (BHPP) described as input-output graph by the basic activity of Fig. 3.

Fig. 3

Input-output graph of a block unit heating power plant (Dyckhoff et al. 2012)

A total of one megawatt-hour (MWh) electrical and thermal energy is produced as two rigidly coupled main products (cf. the left diagram of Fig. 1) from the input of 1.11 MWh natural gas, i.e. with an energy conversion efficiency of 1/1.11 = 90%. Process costs arising from production are modelled as a second input, measured in currency units.²⁴ Assuming constant returns-to-scale, by choosing a certain amount of natural gas input x₁ all other inputs and outputs are fixed by the following linear equations:²⁵

$$\begin{array}{*{20}{c}} {y_1 = 0.423 \cdot x_1} \\ {y_2 = 0.477 \cdot x_1} \\ {x_2 = 47.07 \cdot x_1} \end{array}$$

(6)

On the other hand, if one ignores process costs x₂ in a purely environmental analysis and instead considers an undesirable output y₃ – like carbon dioxide (CO₂) –, measured in suitable units, the value set V in (5) can furthermore be the image of a different linear representation of the same BHPP technology, namely of the special case of a “factorially determined” multi-output (coupled) production of the type analysed by Frisch (1965) and Førsund (2021a):

$$\begin{array}{*{20}{c}} {y_1 = 0.423 \cdot x_1} \\ {y_2 = 0.477 \cdot x_1} \\ {y_3 = 47.07 \cdot x_1} \end{array}$$

(7)

Because Fig. 3 and the corresponding formulae (5)-(7) represent a blue-print technology, real BHPPs will not achieve the theoretical energy conversion efficiency of 90% (cf. Førsund (2021a), p. 171). The produced amounts of thermal and electrical energy of BHPPs observed in practice will be smaller than calculated from (6) and (7), as a rule, while the process costs or the undesirable output may be larger. That is, the BHPPs are usually inefficient with respect to the blue-print technology.

If the real PPS that is based on the considered blue-print technology is not known, DEA and other efficiency measurement methods – like Stochastic Frontier Analysis (SFA) and Stochastic Non-smooth Envelopment of Data (StoNED) if generalised for multiple outputs (Schaefer and Clermont 2018) – allow to determine those BHPPs that are efficient relative to others as well as to calculate an (in-) efficiency score for each BHPP (considered as DMU). By assuming convexity and constant returns-to-scale, the efficient best-practice frontier of the data envelopment T^crs defined by (3) – whereby (x^j, y^j) denotes the total input and output quantities of BHPP j (j = 1, …, n) observed in practice – may form a good approximation of the real efficient frontier of the unknown PPS in the neighbourhood of the considered DMUs.²⁶

3.2.2 Leontief-type production system with by-product

It is crucial to categorically distinguish between the two types of convex polyhedral cones T^crs that are used in the last section: (1) on the one hand, the fictitious or real technology or PPS T that is generated by certain basic activities as ‘blue-prints’ of realisable elementary processes, (2) on the other hand, the data envelopment T^env as local approximation of the real PPS T that is generated by the observed activities as complex processes realised by the considered DMUs. In the special case of Fig. 3, T is generated by a single elementary process (depicted by the rectangle) with two inputs and two outputs, only. In general, however, a variety of different technologies may be generated by using several suitable basic activities, even including multi-stage processes with recycling (Dyckhoff 1994).

In many industries, the demand for the main products is exogenously determined (at least in the short term) so that the quantities of considered and controllable inputs and undesirable by-products are to be minimised and those of desirable by-products to be maximised (as long as preferences for the by-products do not change with increasing quantity). Figure 4 shows a further special case of a basic type of industrial processes, now with two elementary processes #1 and #2 (squares) that transform three types of inputs into three types of outputs (circles). Object type #4 (= output #1) is produced solely by process #1, and object type #5 (= output #2) solely by process #2. The respective basic activities are:

$$\left( {{{{\boldsymbol{x}}}}^1,{{{\boldsymbol{y}}}}^1} \right) = \left( {50;40;0.15;1;0;30} \right)$$

$$\left( {{{{\boldsymbol{x}}}}^2,{{{\boldsymbol{y}}}}^2} \right) = \left( {50;15;0.4;0;1;25} \right)$$

Fig. 4

Leontief-type production system determined by objects #4 and #5 (Dyckhoff 2006, p. 90)

Assuming that objects #4 and #5 are the main products, while object type #6 is a by-product (= output #3), implies that the linear technology generated by these two activities is completely determined if the quantities of both main products are fixed, e.g. by a given demand of customers. This blue-print technology is described by four equations, three for the inputs

$$\begin{array}{{l}} {x_1 = 50 \cdot y_1 + 50 \cdot y_2} \\ {x_2 = 40 \cdot y_1 + 15 \cdot y_2} \\ {x_3 = 0.15 \cdot y_1 + 0.4 \cdot y_2} \end{array}$$

(8)

and one for the by-product:

$$y_3 = 30 \cdot y_1 + 25 \cdot y_2$$

(9)

The numerical example may represent the production of shoes (y₁) and bags (y₂) from leather (x₃) as material input with trim loss (y₃) by using the service of labour (x₁) and a sewing machine (x₂).

Both main products can be produced alternatively, i.e. without the other one, but not without some trim loss as coupled output of each of the two. Without free disposability, the amount of trim loss is uniquely determined by the assortment of both main products calculated from equality (9). Although the input x₃ of leather for the production of shoes and bags is the physical source of its residual y₃ in this interpretation of the numerical example, it does not determine its emerging quantity uniquely. For example, with an input of x₃ = 30 it would be possible to produce either y₁ = 200 pairs of shoes with trim loss y₃ = 6000 or y₂ = 75 bags with trim loss y₃ = 1875, supposed that enough capacity of labour and sewing machine are available. This is in contrast to the blue-print BHPP technology of the last section where the input of natural gas uniquely determines all outputs, in particular also the resulting carbon dioxide if considered. It is questionable how the technology described by Fig. 4 could be modelled as a ‘factorially determined’ technology, as used by Førsund (2021a), or as a by-production technology, proposed by Murty et al. (2012).

For such a Leontief-type technology with limitational inputs and coupled by-product, an output possibility set P(x) or an input possibility set L(y), known from Shephard’s (1970) production theory, make sense only if some disposability of inputs and outputs can be assumed. Otherwise, Eqs. (8) and (9) have in general no feasible solution for a given x or y. On the other hand, in real production contexts, most inputs are available in limited quantities only, i.e. x ≤ c, be it the capacity of an existing machine or the material in stock. This defines a (possibly short term) output possibility set P(c) which, in the current example, may be described e.g. by following inequalities

$$\begin{array}{*{20}{c}} {x_1 = 50 \cdot y_1 + 50 \cdot y_2 \le 5000 = c_1} \\ {x_2 = 40 \cdot y_1 + 15 \cdot y_2 \le 3000 = c_2} \\ {x_3 = 0.15 \cdot y_1 + 0.4 \cdot y_2 \le 30 = c_3} \end{array}$$

(10)

That is, there are two categories of input quantities that must be distinguished, on the one hand the quantities x actually used within the process, and, on the other hand, the quantities c available for processing within the considered production period. This distinction is seldom made clear in the productivity and efficiency literature (except e.g. for a short remark of Ray et al. (2018) in their introduction). Regarding performance measurement, however, the question must be answered to what extent the (economic or ecological) costs are fixed or are variable, at least in the short term, namely how much they depend on the available capacity or the used quantity of an input. Unused quantities of a stock of raw material may be used in a later period, contrary to the potential of an unused machine or labour force. For example, the feasible activity

$$\left( {{{{\boldsymbol{x}}}},{{{\boldsymbol{y}}}}} \right) = \left( {5000;2500;30;40;60;2700} \right)$$

leaves 3000 – 2500 = 500 units of sewing machine time unused when producing 40 pairs of shoes and 60 bags while the available capacities of the other two inputs are exhausted. However, because of a mistake one bag may be damaged such that only 59 saleable bags have been produced actually, with a larger amount of leather residuals. Thus, real production activities may deviate from those calculated by the blue-print technology defined by the two basic activities of Fig. 4. The inefficiencies of a set of such complex activities can be calculated e.g. by a DEA model of CCR type that minimises the quantities of all inputs and of the by-product if it is undesirable.²⁷

3.2.3 Cutting stock processes with trim loss

Regarding the basic technologies of the last two sections one may argue that the by-product carbon dioxide is factorially determined by the input of natural gas and that leather trim loss is a coupled output of each of the two main products shoes and bags. Though, it is the performing of an elementary process that causes the production of output quantities as well as the consumption of input quantities.

In case of the previous BHPP technology, it is the process of burning natural gas that leads to carbon dioxide and heat the last of which is then used to generate power. In case of the Leontief technology, it is the cutting and sewing process that needs leather combined with labour and machine time to produce either a pair of shoes or a bag, with some residuals of leather. In both cases, however, there is a relation of an input or an output with only one elementary process in the respective production network of the Figs. 3 and 4, shown as single arrow from a circle as input to a square node or as single arrow to a circle as output from a square node. In case of Fig. 3, the single arrow from natural gas to the burning process allows to identify gas as cause of the process and therefore of the coupled outputs, too. In case of Fig. 4, it is the single arrow to the shoes – or alternatively to the bags – from ‘their’ elementary process which allows to interpret the output of a pair of shoes or of a bag as individual cause for this process and consequently also for the residual leather as well as the consumed inputs by this basic activity. However, in the example of Fig. 5 no such single arrow from a circle or to a circle exists in the input-output graph. Each circle is connected with at least two elementary processes.

Fig. 5

Cutting two types of items from two types of larger objects by five patterns (Dyckhoff 2006, p. 167)

The figure illustrates a production system with five elementary processes and four relevant object types, two being inputs and two outputs, respectively. It may represent a simple example of a special type of joint production which is essential for a variety of industries and well-known from cutting stock or trim loss problems (cf. Dyckhoff et al. (1985) and Dyckhoff (1990)). Steel tubes of a uniform diameter of the two standard lengths 210 cm (#1) and 270 cm (#2) are cut into shorter tubes of the order lengths 129 cm (#3) and 36 cm (#4). Here, remaining pieces of other lengths are classified as valueless by-products by the producer and are not explicitly considered. For the first standard length two and for the second three cutting patterns are considered as basic activities. They comprise all possible patterns with a residual length of less than 36 cm as trim loss. Each pattern describes how many tubes in the order lengths are obtained from one tube in standard length. Pattern #4 is dotted in Fig. 5 because it is dominated by an equally weighted convex combination of patterns # 3 and #5 if a linear (or convex) technology can be assumed. The corresponding production model reads as follows:

$$\begin{array}{l}\begin{array}{{l}} {x_1 = \lambda _1 + \lambda _2} \\ {x_2 = \lambda _1 + \lambda _2 + \lambda _3} \\ {\lambda _1 + 2\lambda _3 + \lambda _4 = y_1} \end{array}\\ 2\lambda _1 + 5\lambda _2 + 3\lambda _4 + 7\lambda _5 = y_2\end{array}$$

(11)

All variables are non-negative, and λ_j denotes the activity levels of the five elementary processes, i.e. the frequency of applying the cutting patterns.²⁸ If the by-products should not be ignored the following equation sums up the lengths of all residual tubes as trim loss:

$$9\lambda _1 + 30\lambda _2 + 12\lambda _3 + 33\lambda _4 + 18\lambda _5 = y_3$$

(12)

With this additional equation, the production model would take the material balance of steel tubes into account.²⁹ Since the demand for the order lengths r = 1 and r = 2 is given in most practical instances of cutting stock problems and has to be fulfilled exactly, i.e. y_r = d_r, minimising the total trim loss length y₃ is equivalent with minimising the total lengths of used standard lengths: 210x₁ + 270x₂. Thus, the additional Eq. (12) is unnecessary for maximising the productivity of used steel as single relevant material.

Production model (11) – regardless of taking the trim loss explicitly into account or not, i.e. with (12) in addition where appropriate – cannot be reformulated as an explicit production function where all output quantities are either ‘factorially determined’: y = f(x), i.e., uniquely determined by all input quantities, as used by Førsund (2021a), or the other way round: x = g(y), as known from Leontief functions. The example falsifies Førsund’s (2021b, p. 195) statement “that the Frisch inspired factorially determined multi output production function is […] sufficient to capture joint production of the type that production of bads is unavoidable.” It shows that it is the transformation process which is the cause for the inputs used as well as the outputs generated. It is questionable to what extent the by-production approach, which “distinguishes between emission-generating and non-emission-generating inputs” (Murty and Russell 2021, p. 180), will be a proper model for this type of joint production of intended and unintended outputs.³⁰

Moreover, a theory or methodology for ‘proper modelling of production systems that produce both desirable and undesirable outputs’, i.e. for the topic of the special issue of this journal mentioned in the introduction, should not exclude – at least conceptually – cases where the quantity of an input or output or an activity level can only be measured by integers. Then, excess quantities of desirable outputs become still more relevant. For example, a demand for eight tubes of order length #4 and zero for the other one (y₁ = 0, y₂ = 8), could be fulfilled by applying each cutting pattern #2 and #4 once which, however, additionally leads to two unintended tubes of the other order length. Alternatively, pattern #2 could be applied twice which implies an excess of two tubes of this order length in addition to the eight actually demanded. What is the better solution or performance?

To answer this question one must know more about the value of excess quantities of order lengths, but also that of other potential residuals. Can they be sold or used otherwise in this or a later period? If they can be stored for a later demand, then further cutting patterns become relevant which allow for larger residuals (Dyckhoff 1981). For example, the above demand for eight tubes of order lengths #4 can also be satisfied by first applying pattern #5 once, yielding seven tubes of this order length and a residual tube of length 18 cm, and then applying a new (sixth) pattern once that cuts only one, namely the eighth tube of this order length 36 cm (#4) from the same standard length of 270 cm, now with a residual of length 234 cm which can possibly be better used for unknown further demand and then taken from inventory. In my view, the topics of excess quantities of desirable types of outputs as well as that of by-products with an ambiguous value should find much more attention in the economic and performance evaluation literature.

3.3 The intended input of undesirable factors

By now, the Web of Science lists more than thousand papers with the undesirable output of bads as topic, most of them concerned with aspects or applications of performance measurement methods, usually DEA. In contrast, a systematic literature review by Wojcik et al. (2017) reveals only 22 DEA articles which explicitly address the opposite phenomenon, i.e. the desirable input of bads (as original undesirable factors entering the first stage of a single- or multi-stage process). Only four of these papers deal with real applications, namely waste-water treatment. There seems to be a large gap in the productivity and efficiency literature with respect to this topic, even though the utilisation and disposal of bads is of eminent practical importance in a ‘full world’ where the ecological impact of economic activities is reaching the physical limits of planet Earth. Contrary to production, which provides society with goods for consumption, reduction (as defined in the introduction)³¹ serves to rid society of undesirable residues of production and consumption through recycling, recovery, and disposal processes, forming the third phase of a circular economy (Dyckhoff 2000). Bad objects thus generally initially emerge as the unintended output of production and consumption, but later form the intended input of reduction processes.

A bad constitutes the opposite of a good from the perspective of the preferences of the decision maker or evaluator. While a good is an object that people would like to have access to and possession of, people seek to rid themselves of a bad and remove it from their sphere of responsibility and disposition, whether due to environmental regulation or individual motivation. A bad is characterised by the fact that it cannot be disposed of easily, but its removal is not costless because it requires the use of additional goods. Otherwise, one would adopt an indifferent (neutral) attitude towards this object and simply ignore it (Dyckhoff and Allen 2001). A bad is thus an undesirable, negatively valued object that is not freely disposable, as a rule, and whose production is also undesirable. While its generation incurs economic, social, or ecological costs, its targeted utilisation or disposal through elimination or conversion as input in reduction processes represents a benefit. In this sense, bads as input into a transformation process represent undesirable (production or reduction) factors of this process, of which more input is preferred to less, ceteris paribus (Wojcik et al. 2017).

To cope with such undesirable factors we differentiate the input and output quantities into those of goods (G), of bads (B), and of neutral objects (N) and extend correspondingly the multi-dimensional value (possibility) set for a PPS T, defined in (4), by

$${{{\mathbf{V}}}} = {{{\boldsymbol{v}}}}\left( {{{\mathbf{T}}}} \right) = \left\{ {{{{\boldsymbol{v}}}}: = \left( { - {{{\boldsymbol{x}}}}_G,{{{\boldsymbol{x}}}}_B;{{{\boldsymbol{y}}}}_G, - {{{\boldsymbol{y}}}}_B} \right)\left| {\left( {{{{\boldsymbol{x}}}}_G,{{{\boldsymbol{x}}}}_B,{{{\boldsymbol{x}}}}_N;{{{\boldsymbol{y}}}}_G,{{{\boldsymbol{y}}}}_B,{{{\boldsymbol{y}}}}_N} \right) \in {{{\mathbf{T}}}}} \right.} \right\}$$

(13)

This may be illustrated by the following activity of combined waste incineration and power generation:

$$\left( {{{{\boldsymbol{x}}}},{{{\boldsymbol{y}}}}} \right) = \left( {800;1000;6000;470;5000;330;1860} \right)$$

Here, 1000 kg of waste as intended input are reduced together with 800 l water and 6000 m³ air, resulting in following outputs: 470 kWh power, 5000 m³ greenhouse gas emissions, 330 kg cinder, and 1860 kWh lost heat. Assume that waste and greenhouse gas emissions are bads, water and power goods, whereas air, lost heat, and cinder are classified as neutral. Then, the non-zero values created and destroyed by this activity and measured by their incommensurable physical quantities are

$${{{\boldsymbol{v}}}}\left( {{{{\boldsymbol{x}}}},{{{\boldsymbol{y}}}}} \right) = \left( { - 800;1000;470; - 5000} \right)$$

Costs (in terms of disadvantages) are the consumption of 800 l water and the emission of 5000 m³ greenhouse gases, benefits (advantages) 1000 kg less waste and 470 kWh power generated. If the performance of a number of such waste incineration plants is to be measured as DMUs generating electricity at the same time, in principle the well-known mathematical methods of DEA can be used, but conceptually in terms of such non-monetary (physically measured) costs and benefits instead of ‘inputs’ and ‘outputs’ as is usually the case (cf. Dyckhoff and Souren (2022), Section 5.2.3).

4 Conclusions

Clarity, precision, and consistency of basic concepts and terms are crucial for the quality of any theory and methodology. Properly modelling production systems that jointly generate both desirable and undesirable outputs is a topic “proven both controversial and of particular interest to the [productivity and efficiency] community” (Greene et al. 2021). As a business economist with a particular focus on production theory and industrial sustainability control who has worked with engineers at my university, my paper uses relevant insights and experience to shed new light on some of these controversies. Corresponding conclusions (a)–(f) are already stated in the introduction of my paper. Whereas (a), (c), and (d) may be of secondary or even tertiary importance, the other three statements concerning excess quantities, reduction processes, and empirically valid local approximations of the real production possibility set are in my view of main interest for future research on the productivity and efficiency analysis of production systems with unintended outputs and intended inputs. In this regard, I conclude with a few remarks, which I believe should be addressed more intensely in future research and application.

Murty and Russell’s (2021, p. 180) assertion that “the key to correct modelling of an emission-generating technology lies in a proper formulation of its disposability properties” falls short, in my opinion. The assertion is true for a so-called clean technology where the prevention, abatement, and disposal of the bad outputs generated is an integral part of the production technology that generates them. In case of an end-of-pipe technology, however, it is more appropriate to explicitly model the disposal of afore emerged undesirable outputs as a separate activity of a multi-stage production and reduction system. Koopman’s activity analysis offers a suitable approach for this.

In the past decades, various alternative disposability assumptions were proposed and used in applications. They were reviewed and criticized e.g. by Dakpo et al. (2016) and Dakpo and Ang (2019) who are in favour of structural representations with multiple equations. Dakpo and Ang (2019, p. 640) remark that the by-production approach “is typical for engineering science and is appealing for economists. [It] opens the black box by making the technical relationships between all inputs and outputs explicit. This increase in accuracy does, however, require appropriate knowledge of the production system …” Indeed, disposability assumptions in applications should be carefully justified by technological reasons related to the physical production process in question (Dyckhoff 2019). To this end, the designer of the production model must have a deep understanding of the realm of reality concerned. I agree with Rodseth (2014, p. 211) “that the popular production models that incorporate undesirable outputs may not be applicable to all cases involving pollution production and that more emphasis on appropriate empirical specifications is needed.”

The challenge of how to verify the empirical validity of assumptions about production characteristics has not really been resolved to date. In my experience, such verifications must necessarily be specific to the application area addressed, which means that generic guidelines and assumptions alone will not suffice. However, as Section 2.3 has demonstrated in case of DEA applications, it is sufficient to know only certain local properties of the PPS in the relevant range of input and output quantities of the observed and analysed activities.