Abstract
This paper investigates the efficiency of Italian hospitals and how their performances have changed over the years 2007–2016, characterized by the great economic recession and budget constraints. We apply the Benefit of Doubt (BoD) approach to determine a composite index that considers the multi-dimensionality of the hospital outcome to be used as main output in a metafrontier production function based on a stochastic frontier framework. The efficiency score distribution is then used to construct a Theil index in order to compare, over time, the inequality of the estimated efficiency between hospitals, both within and between regions. The main findings show that the primary source of inefficiency comes from managerial inefficiency especially for hospitals located in southern regions. A clear and persistent North-South gap in efficiency performances of hospitals has been found along with an increase in the inequality in terms of efficiency between the areas of the country mostly determined by between region inequality.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The Italian National Health Service (NHS), introduced in 1978, is a universal health care system providing comprehensive health insurance coverage and uniform health benefits to the whole population. It is inspired by the two fundamental pillars enshrined in Article 32 of the Italian Constitution: universality and equality. While the principle of universality has never been questioned, the principle of equality, especially if broken down into terms of equality of services in the local territories, has been repeatedly overlooked in recent years. The last decade has been characterized by the profound financial crisis, exacerbating the economic differences between North and South (see about this aspect Lagravinese (2015)) with inevitable effects also on the demand and supply of health. Indeed, inequalities have started to increase again with evident effects on available healthcare resources, on the quality of uneven healthcare services, and on the living conditions of citizens.
Since its introduction, and as in other European countries (see Costa-Font and Greer (2013)), the Italian NHS has undergone important reforms to decentralize health management and policy responsibilities to the sub-layers of government (Turati, 2013). As a result of a federal reform (Legislative Decree 56/2000), each region is in charge of organizing the health system, following the general guidelines defined by the central government that is responsible for setting the Essential Levels of Health Services (LEA, Livelli Essenziali di Assistenza).Footnote 1 However, the separation of financing from expenditure responsibilities in the provision of LEA, and before LEA in the provision of uniform levels of service, has provided a non-negligible incentive to the uncontrolled growth of Italian health expenditures and has historically contributed to creating bailing out expectations in regional behavior (Liberati, 2003), especially in a context of often inadequate regional health governance and accountability (Carinci et al., 2012).
The public policies concerning a reduction in beds, in medical and nursing staff, hospital mergers and acquisitions as well as lower investments in infrastructure are now subject to revaluation in many countries. Even the decentralized organization itself is questioned and, in many cases, possible scenarios of re-centralization of the health system are well thought-out (Mosca, 2007). In this respect, Italy is among the western countries that have significantly reduced healthcare spending by reshaping its hospital organization and decentralizing management at regional level. The effects of these policies are still controversial to this day, but what is undoubtedly an established fact is that the inequalities between the regional systems in these 20 years have not diminished. Furthermore, the recovery plans imposed by the central government in 2007 for the regions with high deficitsFootnote 2 have certainly favored the reduction of healthcare expenditures and have proved to be an effective mechanism for eliminating sub-national governments deficits (Bordignon et al., 2020). Nevertheless, there is still no clear consensus in the literature whether these plans, and in general the decentralization process, have also had an impact on increasing health inequalities between or within regions. Our work attempts to enrich this literature looking at how hospital efficiency (one of the pillar of health services restructuring by the regions) has changed over the last decade within and across regions.
The economic literature has so far produced a rich and consolidated series of works to study hospital efficiency. As far as Italy is concerned, most of them have investigated if the efficiency has changed either with the introduction of new accounting systems, such as the use of the diagnostic-related groups (Barbetta et al., 2007, Cavalieri et al., 2018), or due to the ownership of hospitals (Cellini et al., 2000, Colombi et al., 2017, Daidone and D’Amico, 2009). To the best of our knowledge, there are no studies that measure in a more holistic way how efficiency has changed over the years and whether the regional policies have actually reduced the differences in hospitals between and within regions. This paper attempts to fill this gap. In particular, the aim of the present study is threefold.
The first contribution of the paper regards the methodology used to measure the efficiency of hospitals. Indeed, health performances are usually averaged across several dimensions to obtain a composite indicator useful for ranking and comparisons. However, the obtained average score can hide contrasting attitudes and specialisations, being a crucial issue the definition of a proper set of weights to aggregate different subjects.Footnote 3 We apply the benefit of doubt (BoD) approach to determine a composite index that considers the multi-dimensionality of the hospital outcome. As far as we know, the BoD has received scarce attention so far in the health care sector. Nonetheless, in the absence of information about value judgments, as it is the case of hospitals, the BoD methodology can be an useful tool to account for the complexity of the health care system (Matos et al., 2021). The BoD aggregates linearly quantitative performance sub-indicators into a single composite one using the combination of weights that is the most convenient for the evaluated hospital (Cherchye et al., 2007). This is done by implicitly assigning less (more) weight to those sub-indicators or aspects of performance that the particular hospital is relatively weak (strong) when compared with all others in the sample (Karagiannis and Paschalidou, 2017).Footnote 4 The high flexibility in terms of exogenous assumptions for setting weights, makes the BoD an appropriate approach to account for the specializations of individual hospitals.
Secondly, the composite indicator generated by the BoD is then used as output in a metafrontier production function based on a stochastic frontier framework.Footnote 5 More specifically, we apply a two-step stochastic frontier approach recently developed by Huang et al. (2014), based on the idea that hospitals have access, potentially, to distinct production technologies in different time periods, being conditioned by several factors such as, for instance, environmental characteristics, regulation and the availability of resources. The analysis is carried out using hospital data over almost one decade: in 2007, the year before the great recession and when, with the introduction of the recovery plans, a number of regions had to substantially reconsider their offer on the territory and in 2016, the last year for which the data are available in detail for all Italian healthcare facilities. To account for the change in efficiency between the two years, the metafrontier has been used. To the best of our knowledge, this is the first work that applies this methodology to the Italian hospital context. The main findings show that the primary source of inefficiency comes from managerial inefficiency especially for hospitals located in southern regions.
The final contribution of the paper is an attempt to link the literature on the hospitals’ efficiency and inequality in the healthcare services at local level. The efficiency score distribution is employed to compute the Theil index (Theil, 1967), a perfect decomposable inequality index, to compare over time the inequality of the estimated efficiency between hospitals in the same region and between different regions. The results of this analysis allow us to make some more general considerations regarding the evolution of the healthcare services in Italy. The findings show a clear and persistent North-South gap in efficiency performances of hospitals along with an increase in the inequality in terms of efficiency between the areas of the country mostly determined by between region inequality. The empirical evidence provides helpful recommendations for policy makers regarding whether local level provision of hospital services need to be improved or whether the regional policies implemented in these years must be reconsidered in order to favor a convergence process.
The rest of the paper is organized as follows. The next section describes the methodology employed, Section 3 presents the data and provides some descriptive statistics, Section 4 discusses the results both in the metafrontier and inequality analyses and finally, Section 5 concludes and offers some policy implications.
2 Methodology
2.1 Efficiency of hospitals
We calculate the hospital’s relative efficiency at converting inputs into a production set while maximizing outputs. In the literature of productive efficiency analysis and frontier estimation, hospital efficiency has been estimated by two main alternative methods such as data envelopment analysis - DEA (Charnes et al., 1978, Farrell, 1957) and stochastic frontier analysis—SFA (Aigner et al., 1977, Meeusen and van den Broeck, 1977). The main advantage of the former method is the non-parametric treatment of the frontier that does not require the underlying production function to belong to any specific functional form.Footnote 6 Although its underlying assumptions provide a way to economize on data requirements, making efficiency analysis possible even when other methods of estimation would not be applicable (Patrizii and Resce, 2013), it ignores any stochastic noise in the data. The advantage of the SFA, instead, is in its stochastic treatment of these deviations.Footnote 7 However, the data used in these analyses may be relatively noisy, so that the deterministic approach (such as the DEA) seems to be inappropriate. Moreover, the units analyzed may apply different production technologies making also the parametric approach (such as the SFA) inappropriate. To incorporate the benefits of both approaches and to bridge the gap between SFA and DEA, several solutions have been proposed in the literature. For a recent and comprehensive view of the theoretical and empirical methods approaches to productivity and efficiency analysis, see Sickles and Zelenyuk (2019).
To comply with the characteristics of the hospital sector and to better understand the differences in average health costs and productivity among hospitals operating in the same environment, more standard techniques along with alternative approaches are used. An extension of the stochastic frontier is applied to estimate the determinants of persistent (long-run) and transient (short-run) inefficiencies (Colombi et al., 2017). With the aim of measuring the impact of environmental characteristics on hospitals’ technical efficiency, the conditional-efficiency approach (Cordero et al., 2015, Halkos and Tzeremes, 2011, Mastromarco et al., 2019, Varabyova et al., 2017) as well as a two-stage semiparametric bootstrap-based approach are applied (Cavalieri et al., 2018, Chowdhury and Zelenyuk, 2016). The importance of the spatial dependent heterogeneity in hospital technical efficiency is also underlined, through a spatial stochastic frontier, to separate spatial issues from the effects of geographical institutional factors (Auteri et al., 2019, Cavalieri et al., 2020). Stochastic input and output distance functions are also employed (Daidone and D’Amico, 2009, Jiang and Andrews, 2020) to model multiple input and output technologies. However, although extensive, the literature has not reached a clear consensus on which method should be adopted to measure the efficiency of healthcare provision institutions. For a comprehensive view, see Jacobs et al. (2009).
In our opinion, the stochastic frontier model is particularly well-suitable for the analysis of health facilities. It allows for stochastic errors, results cannot be severely affected by the presence of outliers, statistical inferences can be drawn, and the estimated parameters (which significance can be tested) can provide potentially useful information in terms of policy implications. Moreover, since operating in more advantageous (more disadvantageous) environments may increase (decrease) a hospital’s efficiency, such factors should be taken into account in the efficiency estimation. We recognize merits of the SFA in integrating the environmental factors in a one-step approach avoiding collinearity issues between the error term and the efficiency scores. Potential limits in handling a multi-output and multi-input environment are solved through the use of a single composite outcome (BoD approach).
2.2 The stochastic frontier analysis
To estimate hospital technical efficiency, we rely on a parametric approach, such as the SFA, through which a frontier is estimated on the relation between inputs and outputs. This can be, for example, a linear function, a quadratic function or a translog function. We use a more general functional form, that is the transcendental logarithmic or “translog” (see Barbetta et al. (2007), Colombi et al. (2017)). It may be preferred to the Cobb-Douglas form to overcome the latter restrictive elasticity of substitution and scale properties, and to allow for non-linear causalities. This method has become a common technique to assess production and inefficiencies in the production of good and services in several contexts, such as economics, health, education, and energy sectors. The methodology employed in this paper is developed by Huang et al. (2014). In a general canonical form, the stochastic frontier model is described by the following set of equations:
where Y denotes the output of the ith hospital at time t, xi is 1 × k vector of input of the ith hospital at time t, β is k × 1 vector of unknown parameters to be estimated, ϵit is the random error, with uit denoting the short-term inefficiency distributed by each unit as half normal, and νit is the stochastic component, distributed independently and identically as \(N(0,{\sigma }_{\nu }^{2})\).
The model described in the system of Eqs. (1–4) is estimated by means of maximum-likelihood methods.Footnote 8 The technical efficiency is calculated as the ratio of the observed output and the maximum feasible output on the production frontier. Formally:
where \({\hat{Y}}_{it}\) is the maximum feasible output that lies on the production frontier.
2.3 Metafrontier model
We follow the procedure proposed by Huang et al. (2014), apply a two-stage parametric approach and estimate a metafrontier production function based on a stochastic frontier framework. We calculate technical efficiency scores for hospitals in separate groups adopting different technologies as we expect hospitals in 2007 and in 2016 not generated from a single production frontier. This procedure allows us to assess both the group-specific frontiers (hospitals in 2007 and hospitals in 2016) and the metafrontier (for both periods).
As in Battese et al. (2004) and O’Donnell et al. (2008), the comparable technical efficiency measures can be decomposed in technical efficiency scores specific to the two groups and technology gap ratios. The main difference between the method proposed by Huang et al. (2014) is that the latter’s second-step estimation of the metafrontier is still based on the stochastic frontier framework, rather than on a mathematical programming technique. Indeed, the two-step method applied by Battese et al. (2004) and O’Donnell et al. (2008) combines the stochastic frontier regression (used in the first step) to estimate the frontier of the separate groups with mathematical programming technique (in the second step) to obtain the metafrontier.Footnote 9 The second-step estimation proposed by Huang et al. (2014) is still based on the stochastic frontier configuration, such that the metafrontier estimation is a stochastic metafrontier (SMF) regression method, with some important computational advantages. First, the usual statistical inferences can be performed without relying on simulations or bootstrap methods, as opposed to mathematical programming techniques.Footnote 10 Second, the metafrontier makes possible to directly estimate the technology gaps by treating them as a conventional one-sided error term. This strategy allows us to separate the random shocks from the technology gaps.
The procedure is based on two stages. In the first stage, the group-specific frontiers (i.e. hospitals in 2007 and 2016) are estimated by means of a stochastic frontier model as in the system of Eqs. (1–4) for each hospital. The estimated parameter β associated to the pooled stochastic frontier model changes to βj for each group j. In the second stage, a metafrontier is enveloped over the frontiers associated to each year (see for more details about the metafrontier optimization (O’Donnell et al., 2008)).
We calculate the technical efficiency (TE) associated to the metafrontier in order to compare the efficiency scores of the hospitals across different technology sets (frontiers). Formally:
where \({Y}_{it}^{* }\) denotes the output on the metafrontier, β* defines the parameters associated to the metafrontier function for all groups j, while \(T{E}_{it(j)}^{* }\) represents the ratio of the observed output of hospital i in group j to the metafrontier output over time t.
The technology gap ratio ratio (TGR), described by the ratio of the output of the production function for hospital i over time t relative to the potential output of the metafrontier for a given set of input variables, is as follows:
In particular, a technology gap exists due to the chosen technology depending on both economic and non-economic production environments. More specifically, TGR captures the difference between the productivity of the group and the metatechnology (i.e. the technology available to all hospitals) (see for more details the geographical representation associated to metafrontier in O’Donnell et al. (2008)).
Finally, the two previous terms can be also used to calculate the hospital technical efficiency with respect to the metafrontier production technology as opposed to the hospital’s technical efficiency with respect to the group-j production technology (MTE), as follows:
2.4 Inequality in efficiencies scores over time
In order to investigate inequality in terms of efficiency scores, we use the results of MTE. The distribution in the two periods is then computed disentangling between and within regions inequality using the Theil index (Theil, 1967), which is a perfectly decomposable inequality index, as follows:
where fit is the group of hospital i at time t, τit is the efficiency index of the hospital i at time t and μ is the average of efficiency scores obtained from the full sample.
The index in Eq. (9) can be decomposed into a between and within group component as follows:
where j refers to the sub-group, gjt is the share of group j and TIjt is the inequality in group j at time t. The between component of inequality is captured by the first term, i.e., the level of inequality if everyone within each group j had efficiency level μj at time t, the second term gives the within component of inequality (Cowell, 2000, Elbers et al., 2005).
3 Data
3.1 Inputs and outputs
The data were collected by the Ministry of Health. The dataset for 2016 can be consulted directly by downloading it from the government website whereas for the 2007 data, the Archive Internet Wayback Machine on the Ministry of Health website was used.
Data include information on different inputs and outputs usually considered in the studies on hospital efficiency (see, for instance, Barbetta et al. (2007), Cavalieri et al. (2018), Colombi et al. (2017), Jiang and Andrews (2020), Mastromarco et al. (2019)) with regard to 403 hospitals followed in two years (more specifically, we collect data on 29 accredited, 42 private and 332 public hospitals).
More specifically, five measures of inputs are included in the model. The first three measures reflect the number of personnel units: the number of physicians (Physicians), the number of nurses (Nurses) and the number of other personnel (Other). The fourth input refers to a measure of capital such as the number of available beds (Beds). The fifth input is the number of magnetic resonance imaging scans (MRI scans)Footnote 11 per one thousand population at province level as a medical input to acknowledge the growth and importance of healthcare technology.Footnote 12 With regard to the output side, three measures of outputs are included in the model: the number of discharged patients (Discharged Patients), the number of inpatient days (Inpatient Days), and the number of emergency room treatments (Emergency Room Treatments).
Weighting outputs according to case-mix has been acknowledged as vital, particularly when the sample consists of hospitals of different sizes, or university hospitals together with other acute hospitals, to minimize intra-hospital as well as inter-hospital differences and therefore account for the different cost of hospital services (Chowdhury and Zelenyuk, 2016, Chowdhury et al., 2014, Mastromarco et al., 2019). To take heed of the complexity and different characteristics of the health services, following Colombi et al. (2017), we weight the three outputs using a weighted annual output of hospital i in year t, using the diagnosis-related group weight.
3.2 Variability of (in)efficiency
It seems inappropriate to assume that efficiency will vary for each hospital in the same way. Institutions can react in very different ways to the contexts they operate in. To take into account the effects of factors that affect the performance of hospitals, we include a vector of exogenous variables in the variance of the inefficiency term (see Colombi et al. (2017)).
First of all, we reckon with the impact of ownership on hospital performances. In general, private ownership characterized by the presence of residual claimants should represent a powerful incentive to economic efficiency and cost reduction; on the contrary, public ownership and/or the absence of any claimant of residual earnings may induce shirking and could decrease effort, consequently reducing efficiency (Barbetta et al., 2007). We use a dummy variable taking the value of 1 in case the hospital has a private/accredited private health care (Private) ownership, and 0 otherwise.
Second, we also deal with the fact that, in some Italian regions, region-specific recovery plans, called “Piani di Rientro”, have been implemented since 2007 in order to recover from the budget deficit related to health care expenditures.Footnote 13 Although part of the literature agrees on the fact that being included in such plans helps to contained costs (Atella et al., 2019), the consequences in terms of health outcomes are less clear.Footnote 14 A dummy variable is therefore included: 1 if the hospital is located in a region included in the recovery plan (Recovery Plans), and 0 otherwise.
Finally, a macro-area dummy is also included to control for geographical area effects (North) taking the value of 1 in case the hospital is located in a region in the North of Italy, and 0 otherwise (Centre-South as reference group).
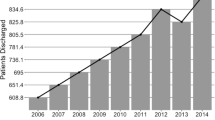
Table 1 contains the descriptive statistics of the variables used in the production set. Table 2 specifies the outputs, inputs and the exogenous factor combinations in the empirical models. Hospitals in the southern regions have, on average, a lower number of personnel (both physicians and nurses) and beds available than those in the northern regions. Hospitals located in northern regions also have, on average, a higher number of discharged patients and emergency room treatments, as well as a higher number of inpatient days, compared to the hospitals in central and southern regions. See Figs. 1 and 2 for a graphical representation of the inputs and outputs at regional level, respectively.
3.3 Composite index of efficiency: benefit of doubt approach
Hospitals exhibit a wide variation in the quality of the product and its characteristics being particularly relevant on the output sides. To control for these differences, we construct a composite index consisting of the three output variables described above. The main aim is to avoid common subjectivity on the weight selection by proposing an endogenous weighting mechanism. Therefore, variables in which hospitals have a comparative advantage are more heavily weighted than those in which hospitals have a lower comparative advantage, or even a comparative disadvantage. Since the strengths of hospitals differ, the weights on the performances should differ as well. For example, hospital X may perform relatively poorly with regard to the number of discharged patients. Therefore, in an endogenous weighting, the output ‘number of discharged patients’ will be assigned a lower weight. In contrast, outputs where the hospitals perform relatively well, for instance, the number of emergency room treatments, will obtain a higher weight. In a similar model the weights are observation-specific, diverging from the previous literature and practices. The idea corresponds to the BoD model, a concept that was first developed by Melyn and Moesen (1991).Footnote 15 Using BoD, each hospital gains its own weights that maximize (or minimize) the impact of the criteria in which the hospital performs relatively well (or poorly) compared to others.Footnote 16 The BoD scores are used as composite output to measure the efficiency of hospitals.
4 Results
This section is divided into two sub-sections. First, we examine the results of the hospitals’ metafrontier production function based on a stochastic frontier framework (§4.1). The results of the analysis of the inequality in hospital efficiency are then presented and discussed (§4.2).
4.1 The hospitals’ metafrontier production function
Following the approach suggested by Huang et al. (2014), we apply the likelihood ratio test for the null hypothesis that the production frontiers are the same for the two groups of hospitals (those operating in 2007 and 2016) and find that the null hypothesis is rejected supporting the idea that the sample hospitals are operating, over a distance of almost a decade, using heterogeneous technologies. Therefore, the existence of a potential production technology gap justifies the estimation of the metafrontier production function in hospital performance/efficiency.
Table 3 reports the hospitals’ stochastic frontier estimates. Columns 1 and 2 report the estimates of the hospital group-specific stochastic frontiers for both years 2007 and 2016, respectively. The ratio of the group-specific production frontier to the metafrontier is reported in Column 3. All input variables have a positive and statistically significant effect on the outcomes of the hospitals (BoD composite index of efficiency). Being located in a region which is included in the recovery plan is negatively correlated with the technical level of inefficiency. This evidence suggests that being included in such plans not only helps to contain costs, but also seems to have positive consequences on the efficiency of the hospitals (Bordignon et al., 2020, Di Novi et al., 2019). Private hospitals outperform public hospitals. Finally, operating in more economically developed areas (North area of the country) is associated, on average, with higher efficiency. Given the gap in economic development between northern and southern Italy, this result raises serious social issues under the equity profile. Indeed, all else equal, hospitals that operate in southern Italy are required to provide extra effort to produce the same level of output. To deal with multiple outputs in the stochastic frontier framework, we also use as robustness analysis a distance function approach, still assuming a translog functional form. The results, reported in Table 7 in the Appendix, corroborate our results implying that the functional form does not invalidate the findings of the analysis.Footnote 17
Table 4 reports the summary statistics of various efficiency scores, at regional level, for the two groups of regions (in 2007 and 2016)Footnote 18 while Fig. 3 reports a graphical representation of the hospitals’ efficiency scores at regional level. All regions in 2016 (with the exception of Lazio, Puglia, Sardegna, Sicilia and Toscana) seem to be more technically efficient (average TE = 0.7839) with respect to their own peer group in 2007 (average TE = 0.7781). Hospitals operating in 2016 seem to be highly more efficient (average TGR = 0.9876) compared to those in 2007 (average TGR = 0.9630) in adopting the best available hospital-operating technology as measured in the technology gap ratio. The hospitals in 2007 are less technically efficient (average MTE = 0.7614) with respect to the same hospitals in 2016 (average MTE of 0.7838) as measured by the metafrontier technical efficiency. Overall, on average the TGR scores play a more important role in the determination of the ranking in MTE, suggesting that sources of inefficiency for hospitals operating in 2007 come especially from the technology used rather than from managerial inefficiency.
An interesting heterogeneity is present when single regions are taken into account. Indeed, the TE scores play a more important role in the determination of the lowering (or not notable increasing) MTE ranking in 2016 with respect to 2007 for Lazio, Puglia, Sardegna, Sicilia and Toscana, suggesting that the primary source of inefficiency come from (lower) managerial efficiency rather than the technology undertaken. On the other hand, the TE scores play a more important role in the determination of the ranking in MTE for Emilia-Romagna, Friuli-Venezia Giulia, Liguria, Lombardia, Trentino (P.A. Bolzano and P.A. Trento), Piemonte and Veneto, suggesting that the primary source of efficiency in 2016 comes from (higher) managerial efficiency rather than the technology undertaken (that remain quite constant, although very high). Finally, although Basilicata, Calabria, Marche and Umbria in year 2016 outperform year 2007, the TGR scores play a more important role in determining the ranking in MTE, suggesting that for hospitals located in those regions the main source of efficiency come especially from the technology undertaken rather than managerial efficiency. The opposite is true, instead, for Molise for which the main source of efficiency for hospitals operating in 2016 seems to come from managerial efficiency rather than the technology used. Finally, both TE and TGR scores play an important role in determining the increasing ranking in MTE for Abruzzo and Campania, suggesting that sources of efficiency in 2016 are both (higher) managerial efficiency and the technology undertaken.
4.2 Rising Inequality in Hospital Efficiencies
To analyze the distribution over time of the ‘more efficient and ‘less efficient’ hospitals, we divide the rank distribution of the hospitals’ scores into 5 percentiles. The graphical representation of the rank distribution is represented in Fig. 4 (the blue, brown, green, orange and red lines illustrate, for each region and for years 2007 and 2016, the share of hospitals that falls in the 20th, 40th, 60th, 80th and 100th rank percentile) and shows a clear and persistent North-South gap in the efficiency performances of hospitals. Indeed, in all the northern regions (Piemonte, Valle d’Aosta, Liguria, Lombardia, Trentino-Alto Adige, Veneto, Friuli-Venezia Giulia, Emilia-Romagna) the hospitals’ efficiency scores reached the highest 61th–80th and 81th–100th percentiles. The gap between the central-northern and southern regions did not change substantially between 2007 and 2016. A clear pattern emerges: none of the southern hospitals reach the highest percentile both in 2007 and 2016. More specifically, in the southern regions and in the two periods analyzed, the distribution of efficiency never reaches the highest percentiles in Basilicata, Calabria and Sardegna.
In line with the previous literature, the findings highlight that in the last decades no process of convergence between the southern regions and those in the north has been observed (Lagravinese et al., 2019). The neglect inefficiencies are still evident between the two macro areas (north-south) and in 2016 the best hospital in the south never reaches the results of the northern hospitals. This result may explain how health mobility between northern and southern regions has increased in recent years, posing serious problems of inequality due to the fact that only individuals with higher incomes can afford to be treated outside their own region (Balia et al., 2018, 2020).
The rank distribution can then be further decomposed to estimate the variability between and within regions according to Eq. (10). To this purpose, Table 5 reports the Theil index for hospital’ performances, with two components: the between regions (estimated within 20 regions) and the within regions. Table 5 shows that between 2007 and 2016, the total inequality of the country increased from 0.022 to 0.025, suggesting that the differences between areas of the country have remained almost unchanged. Much of this inequality is determined by between inequality (around 63.9% of the total). In both years 2007 and 2016, the between inequality increased from 0.014 to 0.015 and the within inequality slightly increased from 0.008 to 0.009.
Additionally, we also calculate the Theil index for each region to further examine how the within inequality has changed in the single regions. The results, summarized in Table 6, show that in general, as was to be expected, inequality in the regions is not as high. This is explained by the fact that by now the regions have outlined the distribution of the service on the local territory where all the hospitals follow guidelines and homogeneous protocols in the regional territory. However, some differences can be seen. In the central-northern regions (net of the regions of Umbria and especially Lazio), it is generally observed that the differences in the same region are minimal with values very close to zero, while the differences are greater among the hospitals in the southern regions. Between 2007 and 2016, an increase in the within inequality occurred especially in Calabria and Sardegna.
5 Concluding remarks and policy implications
5.1 Conclusion
This paper investigates the efficiency of Italian hospitals and how their performances have changed over the period 2007–2016. We apply the BoD approach to determine a composite index that considers the multi-dimensionality of the hospital outcome to be used as main output in a metafrontier production function based on a stochastic frontier framework. This procedure disentangles the group-specific frontiers and the metafrontier, further decomposing the efficiency scores of various groups of hospitals into technical efficiency scores and technology gaps.
The main findings show that almost all regions in 2016 (with some exceptions) seem to be more technically efficient than their own peer group in 2007, being, on average, also more efficient in adopting the best available hospital-operating technology. More heterogeneity is found when looking at the single regions. Indeed, managerial efficiency rather than the efficiency in adopting the best available technology seems to be more important (or not important) in determining the lowering (increasing) in the metafrontier technical efficiency ranking, especially for hospitals located in southern regions. Furthermore, with a closer look at the distribution of the efficiency scores across time, the empirical evidence shows a clear and persistent North-South gap in the efficiency performances of hospitals that did not change substantially between 2007 and 2016. Finally, when we further decomposed the rank distribution in order to estimate the variability between and within regions, the results show an increase in the inequality in terms of efficiency between the areas of the country mostly determined by between region inequality. An increase in within region inequality is also found, especially for the southern regions.
A possible shortcoming of our empirical strategy is worthy to be further discussed. We apply the BoD methodology using the typical construction of the meta-frontier which is estimated under the assumption that the metaset is convex. Violating this assumption could make the estimates biased (see Kerstens et al. (2019) for a discussion). The convexity assumption is usually justified using a time divisibility argument (Hackman, 2008, Shephard, 1970) according to which if production processes are time divisible, then a (hospital) manager could use, in some cases, an input to produce a specific output, and then use a second input to produce a further specific output the rest of the time. Our knowledge of hospital organization leads us to believe that this is not the case for the groups of hospitals operating in 2007 and 2016 suggesting that the technology-specific production possibilities sets may not be convex (i.e., possible differences in the methods that are available to transform inputs into outputs or in production environments).
Finally, given the data constraints and unavailability, more dimensions of inputs and outputs could not be used in the empirical analysis. However, besides labour and capital (represented by number of beds), the consumable (e.g., supplies in medical, drugs, and surgical, etc.) is also an important aspect to be accounted in as the inputs (see, for an example, Chowdhury and Zelenyuk (2016)). Moreover, the number of employees is used as the inputs for labour, even though the full-time equivalent staff is also widely accepted as an important variable in hospital efficiency analysis (see for comprehensive reviews Hollingsworth (2008), O’Neill et al. (2008), Worthington (2004)). These more thorough variables should be taken into account for empirical models and studies in the future.
5.2 Policy implications
Several implications can also be derived from our analysis.
The findings highlight the still unresolved social-economic dualism between the northern and southern regions of the country. Indeed, a persistent territorial divide in the regional health care in Italy has been seen to be, at least partially, the possible cause of a large heterogeneity of mortality rates among regions (Arcà et al., 2020, Lagravinese et al., 2019). We find that the gap between the central-northern and southern regions not only did not change substantially between 2007 and 2016, but also that none of the central-southern hospitals reach the highest percentile in both periods, confirming that in the last decades no process of convergence between the southern regions and those in the north has been observed.
Although, there is evidence of the general positive effect of decentralization on health performance in Italy (Atella et al., 2019, Bordignon et al., 2020, Di Novi et al., 2019), our study, along with some recent literature (Arcà et al., 2020, Depalo, 2019, Lagravinese et al., 2019), provides evidence that such improvements may not involve all the health dimensions and all the regions, and, more importantly, may not solve, even partially, the increasing gap between northern and southern regions. The decentralization process therefore does not seem to have helped bridging the gap between hospitals in the north and those in the south. Indeed, the differences have also (albeit slightly) worsened over the years. Certainly, further analyses are needed in the future to more carefully indicate whether the efficiency changes are the result of such policies in filling up the gap, given that also other social-economic factors changed in the study period (e.g., the demography changes in different regions). However, in the next few years, also in light of the critical issues on regional organization revealed by the recent pandemic due to the COVID-19 virus, national policies will have to be implemented to bridge the infrastructural and economic gap in the southern regions.
Change history
18 July 2022
The original online version of this article was revised: Missing Open Access funding information has been added in the Funding Note.
Notes
LEA is a list of health care services that the central government requires to be guaranteed in all regions, being recently updated by a ministerial decree in 2017.
Some regions were subject to specific recovery plans, called “Piani di Rientro”, implemented to recover from budget deficit related to health expenditures.
To address shortcomings associated with multiple outputs and avoid limitations arising from the use of simple arithmetic or geometric averages, a few solutions have been proposed such as the multi-directional efficiency analysis approach (Tziogkidis et al., 2020). With regard to an application in the health sector, Castelli et al. (2015) impose an explicit set of weights with which to combine diverse outputs into a single index.
For this reason, decision makers should not be worried about unfair weighting schemes since each hospital is put in its most favorable condition, since any other weighting scheme would generate a lower composite index (Cherchye et al., 2007).
The use of a single composite outcome allows us to take into account the complexity of the hospitals in the production function, avoiding a limit of the Stochastic Frontier Analysis, for example, the use of a single output for each production function.
It relies on the general regularity properties such as free disposability, convexity, and assumptions concerning the returns to scale and it does not require any assumption on the error term either, because it assumes that any deviation from frontier is due to inefficiency.
It requires an ex-ante assumption of a functional form for the underlying production function (that may however violate the monotonicity, concavity/convexity and homogeneity conditions).
Alternative estimation methods of stochastic frontier models are also available such as the local likelihood estimation method introduced by Kumbhakar et al. (2007) and the extended methods based on it, such as Park et al. (2015), allowing for categorical variables in the local likelihood method, and Simar et al. (2017), using local least squares method instead of the local likelihood method.
Due to the fact that the second step estimation is a linear programming algebraic calculation, the resulting metafrontier has no statistical properties. Moreover, the characteristic of the environment in which the unit analyzed operate cannot be incorporated.
Indeed, it applies the conventional maximum likelihood method to estimating the parameters of the SMF regression.
The linear homogeneity is ensured by dividing all inputs by one input (in our case the number of other personnel) and symmetry conditions are also imposed.
Plans were signed in February 2007. To date, three waves of Piani di Rientro have been concluded. The first round of plans formally ended in 2009; afterwards, regions were allowed to sign new plans over the periods of 2010–2012 and 2013–2015. Ten regions underwent the program: Lazio was the first in February 2007; Abruzzo, Campania, Liguria, Molise and Sardegna joined the plan in March of the same year; Sicilia joined the plan in July of the same year. Of these regions, Liguria met requirements at the end of the first round (in 2010 instead of 2009) and left the program, whereas all of the other regions signed a new plan for 2010–12. For the second round, Calabria also signed a plan in December 2009 and Piemonte and Puglia signed a plan in 2010.
Therefore, for each hospital, the BoD procedure searches for weights that maximize the impact of the strengths and minimize the influence of the relative weaknesses. This means that in absence of any other detailed information on the true weights, the BoD procedure assumes that representative weights can be inferred from looking at the relative strengths and weaknesses.
We use the number of inpatient days for the normalization of the outcome variable (O’Donnell and Coelli, 2005). Although the choice of the normalizing the outcome variable is innocuous when using stochastic frontier models as they are mathematically equivalent, for robustness, we also conduct a sensitivity analysis normalizing by the number of discharged patients and by the number of emergency room treatments (results on the different normalization are similar and available on request).
The efficiency scores are obtained using data at individual hospital level and then summed up at regional level. The individual hospital efficiency scores are available on request.
References
Afonso A, St Aubyn, M (2006) Relative Efficiency of Health Provision: A DEA Approach with Non-Discretionary Inputs. European Economics: Political Economy & Public Economics eJournal, 1–32
Aigner D, Lovell CAK, Schmidt P (1977) Formulation and estimation of stochastic frontier production function models. J Econom 6:21–37
Arcà E, Principe F, Van Doorslaer E (2020) Death by austerity? the impact of cost containment on avoidable mortality in italy. Health Econ 29:1500–1516
Atella V et al. (2019) How health policy shapes healthcare sector productivity? evidence from italy and uk. Health Policy 123:27–36
Auteri M, Guccio C, Pammolli F, Pignataro G, Vidoli F (2019) Spatial heterogeneity in non-parametric efficiency: An application to italian hospitals. Soc Sci Med 239:1–11
Balia S, Brau R, Marrocu E (2018) Interregional patient mobility in a decentralized healthcare system. Reg Stud 52:388–402
Balia S, Brau R, Moro D (2020) Choice of hospital and long-distances: Evidence from italy. Reg Sci Urban Econ 81:103–502
Barbetta GP, Turati G, Zago AM (2007) Behavioral differences between public and private not-for-profit hospitals in the italian national health service. Health Econ 16:75–96
Battese GE, Rao DSP, O’Donnell CJ (2004) A metafrontier production function for estimation of technical efficiencies and technology gaps for firms operating under different technologies. J Product Anal 21:91–103
Bordignon M, Coretti S, Piacenza M, Turati G (2020) Hardening subnational budget constraints via administrative subordination: The italian experience of recovery plans in regional health services. Health Econ 29:1378–1399
Carinci F, Caracci G, Di Stanislao F, Moirano F (2012) Performance measurement in response to the tallinn charter: experiences from the decentralized italian framework. Health Policy 108:60–66
Castelli A, Street A, Verzulli R, Ward P (2015) Examining variations in hospital productivity in the english nhs. Eur J Health Econ 16:243–254
Cavalieri M, Di Caro P, Guccio C, Lisi D (2020) Does neighbours’ grass matter? testing spatial dependent heterogeneity in technical efficiency of italian hospitals. Soc Sci Med 265:1–13
Cavalieri M, Guccio C, Lisi D, Pignataro G (2018) Does the extent of per case payment system affect hospital efficiency? evidence from the italian nhs. Public Financ Rev 46:117–149
Cellini R, Pignataro G, Rizzo I (2000) Competition and efficiency in health care: an analysis of the italian case. Int Tax Public Financ 7:503–519
Charnes A, Cooper WW, Rhodes E (1978) Measuring the efficiency of decision making units. Eur J Oper Res 2:429–444
Cherchye L, Moesen W, Rogge N, Van Puyenbroeck T (2007) An introduction to ‘benefit of the doubt’composite indicators. Soc Indicators Res 82:111–145
Chowdhury H, Zelenyuk V (2016) Performance of hospital services in ontario: Dea with truncated regression approach. Omega 63:111–122
Chowdhury H, Zelenyuk V, Laporte A, Wodchis WP (2014) Analysis of productivity, efficiency and technological changes in hospital services in ontario: How does case-mix matter? Int J Product Econ 150:74–82
Coco G, Lagravinese R, Resce G (2020) Beyond the weights: a multicriteria approach to evaluate inequality in education. J Econ Inequal 18:469–489
Colombi R, Martini G, Vittadini G (2017) Determinants of transient and persistent hospital efficiency: The case of italy. Health Econ 26:5–22
Cordero JM, Alonso-Morán E, Nuño Solinis R, Orueta JF, Arce RS (2015) Efficiency assessment of primary care providers: A conditional nonparametric approach. Eur J Oper Res 240:235–244
Costa-Font J, Greer SL. (2013) Territory and Health: Perspectives from Economics and Political Science. In: Federalism and Decentralization in European Health and Social Care. Palgrave Macmillan, London
Cowell F (2000) Measurement of inequality. In: Atkinson AB, Bourguignon F (eds) Handbook of income distribution. Chapter 2, North-Holland, pp 87–166
Daidone S, D’Amico F (2009) Technical efficiency, specialization and ownership form: evidences from a pooling of italian hospitals. J Product Anal 32:203–216
De Witte K, Hudrlikova L (2013) What about excellence in teaching? a benevolent ranking of universities. Scientometrics 96:337–364
De Witte K, Rogge N (2011) Accounting for exogenous influences in performance evaluations of teachers. Econ Educ Rev 30:641–653
Depalo D (2019) The side effects on health of a recovery plan in italy: A nonparametric bounding approach. Reg Sci Urban Econ 78:1–22
Di Novi C, Piacenza M, Robone S, Turati G (2019) Does fiscal decentralization affect regional disparities in health? quasi-experimental evidence from italy. Reg Sci Urban Econ 78:103–465
Elbers C, Lanjouw P, Mistiaen JA, Ozler B (2008) Reinterpreting between-group inequality. J Econ Inequal 6:231–245.
Farrell MJ (1957) The measurement of productive efficiency. J R Stat Soc 120:253–290
Hackman S (2008) Production economics: integrating the microeconomic and engineering perspectives. Springer, Berlin
Halkos GE, Tzeremes NG (2011) A conditional nonparametric ana- lysis for measuring the efficiency of regional public healthcare delivery: An application to greek prefectures. Health Policy 103:73–82
Hollingsworth B (2008) The measurement of efficiency and productivity of health care delivery. Health Econ 17:1107–1128
Huang CJ, Huang TH, Liu NH (2014) A new approach to estimating the metafrontier production function based on a stochastic frontier framework. J Product Anal 42:241–254
Jacobs R, Smith PC, Street A (2009) Measuring Efficiency in Health Care - Analytic Techniques and Health Policy. Cambridge University Press, Cambridge
Jiang N, Andrews A (2020) Efficiency of new zealand’s district health boards at providing hospital services: A stochastic frontier analysis. J Product Anal 53:53–68
Karagiannis G, Paschalidou G (2017) Assessing research effectiveness: a comparison of alternative nonparametric models. J Oper Res Soc 68:456–468
Kerstens K, O’Donnell C, Van de Woestyne I (2019) Metatechnology frontier and convexity: A restatement. Eur J Oper Res 275:780–792
Kumbhakar SC, Park BU, Simar L, Tsionas EG (2007) Nonparametric stochastic frontiers: A local maximum likelihood approach. J Econ 137:1–27
Lagravinese R (2015) Economic crisis and rising gaps north–south: evidence from the italian regions. Camb J Reg Econ Soc 8:331–342
Lagravinese R, Liberati P, Resce G (2019) Exploring health outcomes by stochastic multicriteria acceptability analysis: An application to italian regions. Eur J Oper Res 274:1168–1179
Liberati P (2003) Fiscal federalism and national health standards in Italy: implications for redistribution. I sistemi di welfare tra decentramento regionale e integrazione europea (Franco Angeli).
Mastromarco C, Stastna L, Votapkova J (2019) Efficiency of hospitals in the czech republic: Conditional efficiency approach. J Product Anal 51:73–89
Matos R, Ferreira D, Pedro MI (2021) Economic analysis of portuguese public hospitals through the construction of quality, efficiency, access, and financial related composite indicators. Soc Indic Rese 157:361–392.
Meeusen W, van den Broeck J (1977) Efficiency estimation from cobb-douglas production function with composed error. Int Econ Rev 8:435–444
Melyn W, Moesen W (1991) Towards a synthetic indicator of macroeconomic performance: unequal weighting when limited information is available. Public Economics Research Paper No. 17, Katholieke Universiteit Leuven. Leuven, Belgium
Mosca I (2007) Decentralization as a determinant of health care expenditure: empirical analysis for oecd countries. Appl Econ Lett 14:511–515
O’Donnell C, Coelli T (2005) A bayesian approach to imposing curvature on distance functions. J Econ 126:493–523
O’Donnell CJ, Rao DSP, Battese GE (2008) Metafrontier frameworks for the study of firm-level efficiencies and technology ratios. Empir Econ 34:231–255
O’Neill L, Rauner M, Heidenberger K, Kraus M (2008) A cross-national comparison and taxonomy of dea-based hospital efficiency studies. Socio-Econ Plan Sci 42:158–189
Park BU, Simar L, Zelenyuk V (2015) Categorical data in local maximum likelihood: theory and applications to productivity analysis. J Product Anal 43:199–214
Patrizii V, Resce G (2013) Municipal police costs and efficiency. Economia dei Servizi 3:221–238
Retzlaff-Roberts D, Chang C, Rubin R (2004) Technical efficiency in the use of health care resources: a comparison of oecd countries. Health Policy 69:55–72
Shephard R (1970) The theory of cost and production functions. Princeton University Press, Princeton
Sickles RC, Zelenyuk V (2019) Measurement of Productivity and Efficiency—Theory and Practice. Cambridge University Press, Cambridge
Simar L, Van Keilegom I, Zelenyuk V (2017) Nonparametric least squares meth- ods for stochastic frontier models. J Product Anal 47:189–204
Theil H (1967) Economics and Information Theory. North-Holland, Amsterdam
Turati G (2013) The Italian Servizio Sanitario Nazionale: a renewing tale of lost promises. Palgrave Macmillan, London
Tziogkidis P, Philippas D, Leontitsis A, Sickles RC (2020) A data envelopment analysis and local partial least squares approach for identifying the optimal innovation policy direction. Eur J Oper Res 285:1011–1024
Varabyova Y, Blankart C, Torbica A, Schreyögg J (2017) Comparing the efficiency of hospitals in italy and germany: Non-parametric conditional approach based on partial frontier. Health Care Manag Sci 20:379–394
Worthington AC (2004) Frontier efficiency measurement in health care: a review of empirical techniques and selected applications. Med Care Res Rev 61:135–170
Acknowledgements
The author wishes to thank Giuliano Resce and the participants of the Summer School in Political Science: Next Generation EU, Unimolise, Campobasso 13–16 September 2021 for the useful comments and suggestions. We also would like to thank three anonymous referees and Associated Editor for their insightful comments.
Funding
Open access funding provided by Università degli Studi di Bari Aldo Moro within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Barra, C., Lagravinese, R. & Zotti, R. Exploring hospital efficiency within and between Italian regions: new empirical evidence. J Prod Anal 57, 269–284 (2022). https://doi.org/10.1007/s11123-022-00633-4
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11123-022-00633-4