Technical efficiency and firm heterogeneity in stochastic frontier models: application to smallholder maize farms in Ethiopia

Abstract

This study estimates the technical efficiency measures of maize producing farm households in Ethiopia using stochastic frontier (SF) panel models that take different approaches to model firm heterogeneity. The efficiency measures are found to vary depending on how the estimation model treats both unobserved and observed firm heterogeneity. Estimates from the ‘true’ random effects (TRE) models that treat firm effects as heterogeneity are found to be identical to those from pooled SF models. Those results differ from the ones generated from the basic random effects (RE) models that treat firm effects as part of overall technical inefficiency. The more flexible generalised ‘true’ random effects (GTRE) model that splits the error term into firm effects, persistent inefficiency, transient inefficiency, and a random noise component indicates the presence of higher levels of persistent inefficiency than transient inefficiency. The basic truncated-normal RE model and heteroscedastic RE model yields similar efficiency estimates. The GTRE model predict persistent efficiency measures similar to those from the basic RE and flexible RE model with environmental variables incorporated in the variance function as well as in the deterministic production frontier. These results imply that the RE and GTRE panel models provide reliable efficiency estimates for our data compared to the TRE models. All the estimated SF models generate comparable production function parameters in terms of magnitude and sign. Overall, the results underscore the importance of scrutinising stochastic frontier models for their reliability of analytical results before drawing policy inferences.

1 Introduction

The specification and estimation of stochastic frontier production function models, first introduced by Aigner et al. (1977) and Meeusen and van den Broeck (1977), has evolved rapidly during the last decades. A range of cross-sectional and panel data stochastic frontier (SF) models have emerged that are commonly applied in empirical research to estimate technical efficiency. The abundance of choices of SF models and their underling different assumptions often makes it empirically challenging for policy analysts to select the most appropriate model to suit their data and this has implications for the estimated technical efficiency scores as well as model production function parameters. Given the interest in technical efficiency measures in policy discussions, there is a need to examine the robustness of results generated from competing SF models under varying production contexts while accounting for firm heterogeneity (Abdulai and Tietje 2007; Kumbhakar et al. 2014; Van Nguyen et al. 2021). In this paper, we focus on analysing the technical efficiency of smallholder farmers in a developing country production context.

Analysis of smallholder farm efficiency can provide economic insights on how well available resources are used to produce food crops in developing countries. High levels of technical efficiency may imply best use of inputs to produce outputs that are close to what is technically possible given the prevailing production technology. Farms that are technically efficient are the ones that fully utilise the available production know how. Thus, efficiency measures offer useful insights into the competitiveness of farm households (Abdulai and Tietje 2007; Coelli et al. 2005; Kumbhakar et al. 2015). Such insights are vital for designing effective policy programmes to reduce resource wastage and increase enterprise output and productivity.

Stochastic frontier (SF) models have been widely used to measure the technical efficiency of farm households. The stochastic production frontier model has two parts, the deterministic production function part and the stochastic part with technical inefficiency and random noise¹. Technical efficiency estimates are sensitive to assumptions implied by different SF models and how firm heterogeneity is treated (Caudill and Ford 1993; Caudill et al. 1995; Kumbhakar and Lovell 2000; Kumbhakar et al. 2014). Consequently, different SF models can produce inconsistent technical efficiency estimates. When estimating SF models with panel data, disentangling firm heterogeneity from inefficiency is crucial for accurate efficiency estimate but challenging in practice because of the complexity of distinguishing the two (Greene 2004, 2005a).

Stochastic² frontier panel models can be used to separate firm effects from inefficiency measures that otherwise would be confounded in cross-sectional³ models. In the literature, two types of stochastic frontier panel models that differ in how they treat firm effects have been advanced. The first type of models treats firm effects as part of overall inefficiency with two components, the persistent (time-invariant/long-run) inefficiency and transient (time-variant/short-run) inefficiency (Battese 1992; Kumbhakar and Hjalmarsson 1993, 1995; Kumbhakar 1990; Kumbhakar and Heshmati 1995). The second type of models treat firm effects as firm heterogeneity (Greene 2005a, b; Kumbhakar and Wang 2005; Wang and Ho 2010) and assume only transient inefficiency⁴.

Models that lump firm effects with inefficiency might produce an upward bias in inefficiency estimates (Abdulai and Tietje 2007; Colombi et al. 2014; Filippini and Greene 2016; Greene 2004, 2005b; Kumbhakar et al. 2014; Tsionas and Kumbhakar 2014). This bias can be severe if firm effects are related to the structure of the production technology but not to the inefficiency component (Colombi et al. 2014). However, if firm effects are related to inefficiency and not to the structure of the production technology, the models can adequately capture firm effects as persistent inefficiency in addition to the transient inefficiency. Hence, these models are adequate in estimating overall inefficiency. The second type of models only assume transient inefficiency by treating all firm effects as firm heterogeneity and are likely to produce inefficiency estimates that are downward biased. The downward bias can be severe if persistent technical inefficiency exists but is erroneously attributed to firm heterogeneity (Colombi et al. 2014).

The objective of this paper is to examine the variability in technical efficiency estimates computed using stochastic frontier panel models that take different approaches to account for firm heterogeneity in the deterministic production function and the inefficiency effect component. The focus of the empirical analysis is on maize producing smallholder farms in Ethiopia. The goal is not to give a comprehensive review of stochastic frontier panel models or to recommend a particular ‘winning’ model. Instead, we apply a selection of competing SF models to a single data set to illustrate how technical efficiency estimates may differ depending on how the model used treats both observed and unobserved firm heterogeneity and how this might affect policy inferences that can be drawn from such measures. Empirical studies that evaluate a broad set of stochastic frontier models in the agricultural production sector are rare. Two notable exceptions are Kumbhakar et al. (2014) for the Norwegian grain farms and Abdulai and Tietje (2007) for Germany dairy farms. We contribute to this line of literature with an application of stochastic frontier panel models to maize producing smallholder households in Ethiopia. Thus, the contribution of this paper is twofold. First, the paper empirically addresses the long-standing subject of estimating technical efficiency of smallholder farmers in a developing country context. Second, the paper investigates the sensitivity of technical efficiency estimates across competing SF models, particularly in the assumptions of the error term accounting for inefficiency. There is more heterogeneity across farm households in sub-Saharan Africa compared to farms in developed countries such as Norway and Germany due to diverse agro-ecological, climatic, socio-economic, and institutional factors, which makes such an empirical application particularly appropriate. This study is the first application in a developing country in sub-Saharan Africa. We apply the models to a nationally representative panel data set collected in 2009/2010 and 2012/2013 across 39 districts, and 183 kebeles⁵.

Our analysis reveals that estimated technical efficiency are sensitive to the way both unobserved and observed heterogeneity (measured environmental variables) are treated in estimation as well as to the distributional assumptions made about inefficiency. The results show that random effects (RE) panel models that treat firm effects as part of overall inefficiency to provide reliable efficiency estimates in contrast to ‘true’ random effects (TRE) panel models that treat these firm effects as firm heterogeneity. Further, the estimates from TRE models mimic the simple pooled SF models that ignore firm effects and do not distinguish between persistent and transient efficiency. The GTRE model reveals evidence of differences in persistent inefficiency and transient inefficiency across farm households, a pattern that is picked by the RE models but not by the TRE models or the simpler pooled frontier models. Incorporating observed heterogeneity (measured as environmental variables) in the variance rather than in the mean specification for the RE model inefficiency term, or both in the mean and the variance specifications, produces coefficient estimates that are consistent⁶ with those from the basic truncated-normal RE model where both the mean and the variance of the inefficiency term are assumed constant. Likewise, controlling for environmental factors which are beyond the control of farm operators in the deterministic production function provides consistent technical efficiency estimates across RE models. All the estimated models yield consistent production function parameters (i.e., output elasticity, marginal productivity of inputs, input interaction effects and returns to scale)⁷. The results suggest that the way heterogeneity is treated in the SF models manifests itself more in the measured technical inefficiency scores rather than in the estimates of the production function.

The empirical results underscore the importance of considering the underlying assumptions of SF models under varying contexts before drawing any policy inferences. For example, practitioners may choose models that control for environmental factors affecting production but are beyond the control of the farm operator (e.g., rainfall, temperature etc.) in the deterministic production function. However, the factors under the control of the farm operator should be controlled for in the inefficiency effect component. Following this approach appears to greatly improve model consistency as different SF models predict similar efficiency levels and partial effects for exogenous factors.

The rest of the paper is organised as follows. The next section presents the methodology with a description of empirical models and estimation strategies. These are followed by a brief description of the data and variables used for the analysis. We present and discuss results in the third section. The article then concludes by drawing some empirical insights.

2 Methodology

We assume that maize producers use the prevailing production technology to maximise output given a set of inputs in a heterogeneous production environment. Thus, farmers with identical input bundles may produce different output levels and differ in their technical efficiency levels. The efficiency differences could be attributed to differences in environmental factors (such as weather, land topography, and soil types) and institutional factors (like access to credit and extension services, and managerial factors like the age, skills, aptitudes, and gender of farm operators). When proxies are used to measure these environmental factors, they can be included in SF models as observed firm heterogeneity, for example, as covariates in the technical inefficiency effect component. The omission of such observed heterogeneity in SF models has been found to bias estimates of technology parameters as well as technical efficiency measures (Abdulai and Tietje 2007; Okike et al. 2004; Rahman and Hasan 2008; Sherlund et al. 2002). Even when these environmental variables are observed and controlled for in the analysis, efficiency estimates can still be biased due to misspecification of production function form and statistical errors (Alvarez et al. 2006; Greene 2008; Kumbhakar et al. 2015; Simar et al. 1994).

In this paper, we investigate the effects of both unobserved and observed heterogeneity on efficiency measures. Those effects can be time-invariant or time-variant (Greene 2008). For example, time-invariant factors include farm location and the gender of the farm operator. Time-variant factors include rainfall and farm management techniques. Heterogeneity can be related to the structure⁸ of the deterministic production function or the technical inefficiency component although the latter has been the focus of most research. For our case study, we assume (based on our understanding of the production and institutional environment) that smallholder maize producers have access to the same production technology but operate under varied environmental production conditions.

2.1 Empirical models

For our empirical application, we adopt stochastic frontier (SF) panel data models that assume time-variant inefficiency in production. The time-variant SF approach is appropriate for our production context as it accounts for the stochastic and seasonal nature of agricultural production (Abdulai and Tietje 2007; Bravo-Ureta and Pinheiro 1993; Coelli 1995). In the efficiency literature, SF panel models can be classified into two types depending on whether the time-variant stochastic feature is fully maintained or not. The first type of models are the random effects panel SF models that accommodate the stochastic nature of the production function by imposing distributional assumptions about inefficiency and the random error term (Battese and Coelli 1992; Greene 2005a; Kumbhakar 1990). The second type of models are models in which the time-variant inefficiency term is not fully stochastic (Cornwell et al. 1990; Lee and Schmidt 1993). These models do not require distributional assumptions of the error terms for the estimation of inefficiency. However, two features warrant further investigation of the second type of models as pointed out by Greene (2005b) and Filippini and Greene (2016). First, the time-invariant heterogeneity that is not inefficiency cannot be accounted for; and second, producers are ranked relative to the “best firm” in the sample, which is an estimate that is subject to statistical error.

Therefore, we follow the random effects SF panel models for our empirical application. We consider two groups of SF panel models. The first group of models are random effects (hereafter RE) models that treat time-invariant firm effects as part of overall inefficiency (Battese 1992; Kumbhakar and Hjalmarsson 1993, 1995; Kumbhakar 1990; Kumbhakar and Heshmati 1995). The second group of models are Greene’s “true” random effects (hereafter TRE) models which treat all time-invariant firm effects as heterogeneity, not as inefficiency (Greene 2005a, b). These two competing groups of models have become popular in empirical applications (Parmeter and Kumbhakar 2014).

Kumbhakar et al. (2014) suggested a general ‘true’ random effects (GTRE) model which has both the RE and TRE model features. The GTRE model makes a distinction between four components: firm effects, persistent inefficiency, transient inefficiency, and random noise. In the next section, we specify these competing panel models in the context of the Ethiopian smallholder agricultural production sector.

2.1.1 Battese and Coelli model

Among the basic RE panel models, the model proposed by Battese and Coelli (1992)⁹ is mostly applied in the agricultural production literature¹⁰. The basic half-normal model can be specified as:

$$\begin{array}{l}\ln y_{it} = \alpha + \ln f\left( {x_{it};\beta } \right) + v_{it} - u_{it},\\ v_{it} \sim N\left( {0,\sigma _v^2} \right),\\ u_{it} = \exp \left[ {\left( { - \eta \left( {t - T_i} \right)} \right.} \right] \times u_i,u_i \sim N^ + \left( {0,\sigma _u^2} \right)\\ \varepsilon _{it} = v_{it} - u_{it}\end{array}$$

(1)

where y_it is the logarithm of output for farm household i in period t; x_it is a matrix of the logarithms of productive inputs (land, seed, labour, nitrogen, oxen draught power, and pesticide); v_it is a random error that is normally distributed with mean zero and a variance of $\sigma _v^2$; u_it is a non-negative inefficiency term that changes over time exponentially with additional scaled parameter η and t indicates current production period; T_i is the terminal period; ε_it is a composite error term; and α is a common intercept for all the productive units and β are technology parameters to be estimated. The term u_i is the individual stochastic component. This model is labelled as BC92HN (Model 1). The model in Eq. (1) can allow the individual stochastic component u_i to be distributed truncated-normal as $u_i \sim N^ + \left( {\mu ,\sigma _u^2} \right)$. The truncated–normal model is identified as BC92TN (Model 2). The models do not distinguish between inefficiency and firm-specific heterogeneity.

2.1.2 Greene’s ‘true’ random effects (TRE) model

Unlike the RE model in Eq. (1), Greene’s TRE model (Greene 2005a, b) introduces firm-specific intercepts in the panel structure to account for unobserved firm heterogeneity. Greene’s TRE model has the following form:

$$\begin{array}{l}\ln y_{it} = \left( {\alpha + w_i} \right) + \ln f\left( {x_{it};\beta } \right) + v_{it} - u_{it},\\ v_{it} \sim N\left( {0,\sigma _v^2} \right),\\ w_i \sim N\left( {0,\sigma _w^2} \right),\\ u_{it} \sim N^ + \left( {0,\sigma _u^2} \right),\\ \varepsilon _{it} = v_{it} - u_{it}\end{array}$$

(2)

where v_it, u_it, α, β and ε_it are as defined earlier. The term w_i is a random term that is time-invariant and normally distributed with mean zero and variance of $\sigma _w^2$; it captures unobserved firm heterogeneity, not inefficiency. In this model, the one-sided inefficiency term varies freely across time and firms. Any time-invariant firm effects that could reflect persistent inefficiency are assumed away. This model produces a downward bias in the estimated overall inefficiency as it fails to accommodate any persistent inefficiency (Kumbhakar et al. 2014; Tsionas and Kumbhakar 2014). Persistent inefficiency is expected in panel data with a short time span, such as our data. It reflects the effect of inputs that vary across firms but not time. For example, in our case land quality and innate ability of farm operators may vary across farm households but do not change over a short time span. We estimated this model under both a half-normal assumption, labelled as TREHN (Model 3) and an exponential-normal assumption, labelled as TREEN (Model 4).

2.1.3 General ‘true’ random effects (GTRE) model

The GTRE model distinguishes between persistent and transient inefficiency as well as firm-heterogeneity and noise. A practical concern about this model is whether these four error components can be precisely estimated (Badunenko and Kumbhakar 2016). The GTRE model is specified as:

$$\begin{array}{l}\ln y_{it} = \alpha + \ln f\left( {x_{it};\beta } \right) + \left( {w_i - h_i} \right) + v_{it} - u_{it},\\ v_{it} \sim N\left( {0,\sigma _v^2} \right),\\ w_i \sim N\left( {0,\sigma _w^2} \right),\\ h_i \sim N^ + \left( {0,\sigma _h^2} \right),\\ u_{it} \sim N^ + \left( {0,\sigma _u^2} \right),\\ \varepsilon _{it} = v_{it} - u_{it}\\ \phi _i = w_i - h_i\end{array}$$

(3)

where v_it, u_it, α, β, ε_it and w_i are as defined earlier and h_i is a term that captures persistent technical inefficiency; it is half-normally distributed with a variance of $\sigma _h^2$. The terms ε_it = (v_it = u_it) and ϕ_i = (w_i−h_i) follow a skew-normal distribution (Filippini and Greene 2016; Kumbhakar et al. 2014). The model is labelled as GTRE (Model 5).

In some circumstances, unmeasured heterogeneity might correlate with inputs and could bias estimates of technology parameters. In such cases, the Mundlak auxiliary equation has been proposed for the random effects linear regression model. However, this approach is based on the normality assumption that does not strictly apply to non-linear stochastic frontier models that follow asymmetric composite error distribution (Filippini and Greene 2016).

2.1.4 Random effects models with environmental variables

Inefficiency can be modelled as a function of environmental variables E_it that capture firm heterogeneity. The environmental variables (E_it) include sub-components of environmental factors z_it, sustainable agricultural practices s_it¹¹ and managerial related socio-economic factors m_it. According to Greene (2005b), the model in Eq. (1) can accommodate variations with firm-specific covariates (measured environmental variables) E_it. The model can be specified as:

$$\begin{array}{l}y_{it} = \alpha + f\left( {x_{it};\beta } \right) + v_{it} - u\left( E \right)_{it},\,E_{it}\,{{{\mathrm{include}}}}\,{{{\mathrm{z}}}}_{it},s_{it},m_{it}\\ v_{it} \sim N\left( {0,\sigma _v^2} \right),\\ u_{it} \sim N^ + \left( {0,\sigma _u^2\left( {E_{it}} \right)} \right),\\ u_{it} = \exp \left( {\delta ^\prime E_{it}} \right) \times u_i,u_i \sim N^ + \left( {0,\sigma _u^2} \right)\\ \varepsilon _{it} = v_{it} - u_{it}\end{array}$$

(4)

where v_it, u_it, α, β and ε_it are as defined earlier and E_it are the environmental variables with an unknown vector of parameters δ and u_i is a time-invariant half-normally distributed inefficiency term. This model has two attractive features for empirical applications. First, its multiplicative formulation/scaling function does not change the shape of the underlying basic inefficiency distribution u_i (Alvarez et al. 2006; Parmeter and Kumbhakar 2014). Second, the model corrects for heteroscedasticity in the variance of inefficiency through measured environmental variables (Greene 2016; Kumbhakar et al. 2015). This model is labelled as BC92G (Model 6).

Battese and Coelli (1995) also proposed an inefficiency effects model with environmental variables for panel data with an additive formulation¹² that cannot be decomposed into independent parts. The model assumes that the mean of inefficiency distribution μ_it is a linear function of environmental variables E_it and a vector of parameters δ under a constant variance $\sigma _u^2$. The model has the following form:

$$\begin{array}{l}\ln y_{it} = \alpha + \ln f\left( {x_{it};\beta } \right) + v_{it} - u\left( {E_{it}} \right),\,E_{it}\,{{{\mathrm{include}}}}\,{{{\mathrm{z}}}}_{it},s_{it},m_{it}\\ v_{it} \sim N\left( {0,\sigma _v^2} \right),\\ u_{it} \sim N^ + \left( {\mu _{it},\sigma _u^2} \right),\\ \mu _{it} = \delta _0 + \delta ^\prime E_{it},\\ \varepsilon _{it} = v_{it} - u_{it}\end{array}$$

(5)

This model is widely applied in the agricultural economics literature despite some shortcomings. The assumption of a homoscedastic inefficiency variance is too strong for decision-making units operating in more heterogeneous production environments, such as our case study. Furthermore, as pointed out by Alvarez et al. (2006), the model’s assumption of independence¹³ of the inefficiency over time with the function of the environmental variables is also widely recognised as unrealistic. Treating a farm observed in two periods as two different farms can lead to intrinsic estimation bias due to misspecification and statistical error. The model is identified as BC95 (Model 7).

Wang (2002) proposed a general model in which the same set of environmental variables can simultaneously be incorporated into the mean and the variance of inefficiency with different vectors of parameters δ and η, respectively. The model has the following form:

$$\begin{array}{l}\ln y_{it} = \alpha + \ln f\left( {x_{it};\beta } \right) + v_{it} - u\left( {E_{it}} \right),\,E_{it}\,{{{\mathrm{include}}}}\,{{{\mathrm{z}}}}_{it},s_{it},m_{it}\\ v_{it} \sim N\left( {0,\sigma _v^2} \right),\\ u_{it} \sim N^ + ( {\mu _{it},\sigma _{u_{it}}^2} ),\\ \mu _{it} = \delta _0 + \delta ^\prime E_{it},\\ \sigma _{u_{it}}^2 = \exp \left( {\eta ^\prime E_{it}} \right),\\ \varepsilon _{it} = v_{it} - u_{it}\end{array}$$

(6)

This model assumes independence of inefficiency over time as the Battese and Coelli (1995) model. The model may be subject to misspecification and statistical error because of the simultaneous placement of environmental variables on the mean and the variance of inefficiency. The model in Eq. (6) confounds the effects of environmental variables on inefficiency measures as the mean and the variance are related statistics (Saastamoinen 2013). Like the other models already discussed, any time-invariant unobserved heterogeneity is pushed into the inefficiency term. This general specification is included in the present study for comparison purposes. The model is labelled as GEN (Model 8).

However, environmental factors are beyond the control of farm operators and may not directly affect technical efficiency (Kumbhakar and Lovell 2000; Sherlund et al. 2002). Instead, they directly affect the production function¹⁴. Therefore, environmental factors z_it are incorporated directly in the deterministic production function in models 6, 7 and 8. Those models are labelled as BC92GE (Model 6A), BC95E (Model 7A) and GENE (Model 8A). The basic structure of the models is $y_{it} = \alpha + f\left( {x_{it},{{{\mathrm{z}}}}_{it};\beta } \right) + v_{it} - u_{it}\left( {s_{it},m_{it}} \right)$. Sustainable agricultural practices s_it¹⁵ and managerial related socio-economic factors m_it are incorporated in the inefficiency effect component of the models and their associated paramaters are as defined earlier.

We also estimated, for comparison purposes, simple pooled SF models that ignore the panel nature of the data. The simple pooled models treat data for a farm observed in two periods as two separate farms, which is unrealistic as argued earlier. The simple pooled frontier model has the form:

$$\begin{array}{l}\ln y_i = \alpha + \ln f\left( {x_i;\beta } \right) + v_i - u_i,\\ v_i \sim \left( {0,\sigma _v^2} \right),\\ \varepsilon _i = v_i - u_i\end{array}$$

(7)

It should be noted that simple pooled models ignore any commonalities or panel data effects. Consequently, the models lump any firm heterogeneity with the inefficiency measure. Because of these limitations, panel data SF models are preferred to pooled cross-sectional SF models when panel data are available (Kumbhakar and Lovell 2000; Kumbhakar et al. 2015). The simple pooled models¹⁶ can be estimated under alternative assumptions of inefficiency distribution. These are half-normal $u_i\,{\sim }\,N^ + \left( {0,\sigma _u^2} \right)$, labelled as HN (Model 9); truncated-normal $u_i\,{\sim}\,N^ + \left( {\mu ,\sigma _u^2} \right)$, labelled as TN (Model 10); exponential-normal $u_i\,{\sim}\,\theta \exp \left( { - \theta u_i} \right),u_i \ge 0$, labelled as EN (Model 11); and gamma-normal $u_i\,{\sim }\,{gamma}\left( {\theta ,P} \right)$, labelled as GN (Model 12).

Overall, we investigated variants of the popular Battese and Coelli RE models with and without environmental variables in the inefficiency effect component, Greene’s TRE model, the recently suggested general TRE (GTRE) model, and simple pooled models for comparison. A summary of the 12 investigated models is presented in Table 1.

Table 1 Key characteristics of the stochastic frontier models investigated

2.2 Estimation procedure

The different forms of the RE panel models can be estimated using maximum likelihood (ML) methods under the assumption that inefficiency is half-normal or truncated-normal distributed. The RE panel models that incorporate environmental variables can be estimated using ML methods in a single-stage approach (Wang and Schmidt 2002). The TRE model and the GTRE model can be estimated by the maximum simulated likelihood (MSL) method following the recent literature (Filippini and Greene 2016; Greene 2016).

The estimated parameters are used to calculate firm-specific estimates of technical efficiency (TE) using the conditional expectation predictor (Jondrow et al. 1982) $TE_{it} = E\left[ {\exp \left( { - u_{it}} \right)\left| {\varepsilon _{it}} \right.} \right]$. It should be noted that the Jondrow et al. estimator is not consistent for cross-sectional models because E[u_it|ε_it] does not approach zero for each firm as the cross-section sample increases (Kumbhakar and Lovell 2000, Kumbhakar et al. 2014). Hence, efficiency estimates from pooled data could be less reliable than panel data. Similarly, persistent technical efficiency from the GTRE model is estimated as $PGTRE_{it} = E\left[ {\exp \left( { - h_{it}} \right)\left| {\varepsilon _{it}} \right.} \right]$ and transient technical efficiency as $TGTRE_{it} = E\left[ {\exp - \left( {u_{it}} \right)\left| {\varepsilon _{it}} \right.} \right]$. The overall technical efficiency (OTE) is calculated as a product of the persistent and transient technical efficiencies, i.e., OTE_it = PGTRE_it × TGTRE_it (Kumbhakar et al. 2014).

We chose a translog¹⁷ functional form to approximate the production function for our empirical analysis because of its flexibility (Christensen et al. 1973). The input and output variables were scaled by their arithmetic means prior to transformation into logarithm values. As a result, the first-order coefficients of the estimated production function can be interpreted as elasticities of output evaluated at the sample mean. The stochastic frontier models are estimated using the econometric software LIMDEP Version 11 (Greene 2016). The exponential form of the TRE model (Model 4) is estimated using the sfpanel package for Stata (Belotti et al. 2013)¹⁸.

2.3 Data

We use farm household survey data collected from maize growing areas of Ethiopia. The data were collected in 2009/2010 and 2012/2013 by the Ethiopian Institute of Agricultural Research (EIAR) and the International Maize and Wheat Improvement Centre (CIMMYT). The data contained an unbalanced panel with 4471 farm household observations; 2339 households were surveyed in the first wave and 2132 in the second wave. The panel data were three years apart, and the short duration of data did not compromise the comparison of SF models about inefficiency and heterogeneity for smallholder maize farmers whose production is highly variable because of the unpredictable weather and socio-economic conditions. The data were comprehensive and included detailed information about production activities. The sample households were randomly selected from study kebeles drawn using a multistage random sampling procedure. Production inputs and output were collected at the plot level¹⁹. We analysed the data at the farm (household) level because households change the size and type of plots they allocate to maize production over seasons. Thus, we aggregate the plot-level inputs and outputs data for maize into a household level data. A number of empirical studies have used a similar approach (Alem et al. 2010; Bezabih and Sarr 2012; Ndlovu et al. 2014).

Table 2 provides the descriptive statistics of the production inputs and output. The dependent variable used is the quantity of maize produced in kilograms. The average land acreage under maize crop in the sample was 0.81 hectares, which illustrates the smallness of household farms. Land includes both owned and rented that the household put under maize production. Labour data are measured in person-days and include both family and hired workers disaggregated by gender and age²⁰. Inorganic nitrogen fertiliser is measured in kilograms. Oxen draught power is measured in oxen-days for ploughing. Ethiopian farmers have used traditional oxen-drawn traction systems for millennia. Pesticide represents the quantity index²¹ of key herbicides such as 2, 4-D and Roundup measured in liters. Ethiopian farmers apply insignificant quantities of these pesticides/herbicides for maize production. These pesticides/herbicides were applied by only a small proportion of farmers in the sample (16%) across a few localities that practice conservation tillage. However, we included this input for completeness in the analysis.

Table 2 Descriptive statistics

The standard deviations of the output and the inputs indicate the variability in the production system. Environmental variables that are used to represent observed firm heterogeneity in the production function and inefficiency effect are presented in Table 2. These environmental variables include three sub-components. The first sub-component denotes environmental factors such as climate, biophysical conditions, and stress incidence in production. The second sub-component refers to farmers’ adaptive managerial response proxies of sustainable agricultural practices to improve land productivity. The third sub-component includes socio-economic factors such as age, education, credit access, and savings. These environmental variables and other unobserved factors can influence farmers’ production decisions and hence explain differences in inefficiency levels among farmers.

3 Results and discussion

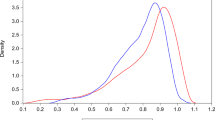
The estimates of the basic SF panel models are presented in Table 3, and those models with environmental variables determining the inefficiency effect are shown in Tables 4 and 8. We present the results of the simple pooled stochastic frontier models for comparison (see Table 5). The models are estimated under alternative assumptions of inefficiency distribution (see Fig. 4). For our data, technical efficiency estimates generated from the half-normal assumption are different from those of the truncated, exponential and gamma assumptions. The truncated and exponential assumptions have striking consistency and either of the two distributional assumptions can be used for comparing the models²².

Table 3 Parameter estimates of translog stochastic production frontier panel models

Table 4 Estimates of the parameters of production frontier for models with environmental variables

Table 5 Parameter estimates of the translog stochastic production frontier simple pooled models

3.1 Heterogeneity and estimated production frontiers

We find estimated production function coefficients to be insensitive to model specifications. The technology parameters as indicated by the coefficients of the first order, second order and input interactions are similar in magnitude and direction across all models (see Tables 3–5 and 8). Because the input-output data are scaled by their mean before taking the logarithms, the first order, second order and the interaction terms are interpreted as output elasticities, marginal productivity of inputs and input interaction effects, respectively. The sum of the output elasticities (first order terms) is interpreted as the average returns to scale which are also consistent across the estimated models. These results are consistent with the existing production frontier literature (Coelli et al. 2005; Greene 2008; Kumbhakar et al. 2015). However, Abdulai and Tietje (2007) found inconsistent estimates on the production frontier parameters possibly because firm-specific effects are related to the structure of the production technology for their dairy farms. Their analyis revealed that output elasticities from the Battese and Coelli (1995) model and simple pooled models were inconsistent from the rest of the models. These insights suggest that production frontier estimates from different SF models depend on how firm heterogeneity is treated and type of data applied (Kumbhakar et al. 2014).

Our results show that output is more responsive to cropping acreage relative to other inputs evaluated at the sample mean. Oxen power has a negative effect²³ on output at the mean value. The negative effect is associated with the overuse of traditional oxen-power due to repeated ploughings (Temesgen 2007; Temesgen et al. 2008, 2009). In certain production environments, some inputs can be weakly disposable (Coelli et al. 2005). Farmers appear to face diminishing marginal returns for the use of labour and seed but increasing returns for the use of nitrogen. We observe significant positive interaction effects between some inputs (e.g., seed and labour, oxen and labour, land and pesticide) but negative interaction effects between others (e.g., seed and pesticide, nitrogen and labour). The average returns to scale is one indicating that most farm operations are operating at constant returns to scale when evaluated at sample mean.

While the production function coefficients are consistent across all models, frontier intercepts (constants) are not. Some models have relatively higher frontier intercepts than others (e.g. Models 3, 5, 7, 8 and 9). In particular, the highest frontier intercept is associated with the general model (Model 8). On the other hand, Model 2 (BC92TN) and Model 6 (BC92G) have relatively lower intercepts relative to the other models²⁴. The remaining models fall in between these two extremes. Differences in the levels of frontier intercept may indicate the extent of heterogeneity affecting estimated inefficiency (Greene 2008; Kumbhakar et al. 2015), an issue we now explore in detail.

3.2 Technical efficiency estimates and firm heterogeneity

Table 6 presents the summary statistics of technical efficiency estimates of the models. Mean technical efficiencies range from 47% in the general Wang (2002) model (Model 8 or GEN) to 78% in the basic Battese and Coelli (1992) model with the truncated-normal specification (Model 2 or BC92TN). Note that the general model (Model 8 or GEN) incorporates the same set of environmental variables in the mean and the variance of inefficiency. Mean technical efficiencies for five models stand at 71% or 72%. The mean efficiency estimate for the Battese and Coelli (1992) model with environmental variables in the variance of inefficiency measure (Model 6) is 75%. Note that this model (Model 6 or BC92G) corrects for heterogeneity by addressing the heteroscedasticity problem in the variance of inefficiency using measured environmental variables. The simple pooled half-normal model (Model 9 or HN), Greene’s TRE half-normal model (Model 3 or TREHN) and Battese and Coelli (1995) with environmental variables in the mean function (Model 7 or BC95) have a mean efficiency of just over 61%. However, the RE panel models incorporating environmental factors in the deterministic production function produce comparable and consistent technical efficiency estimates (see Table 9 and Figs. 7 and 8).

Table 6 Summary statistics of technical efficiency for the estimated stochastic frontier models

The GTRE model provides estimates of the persistent (PGTRE) and transient (TGTRE) component of technical efficiency. The mean persistent technical efficiency is 76% while the mean residual (transient) technical efficiency is 87%. From Fig. 3, the spread of efficiency is higher for the persistent component than for the residual component. These results suggest that persistent technical inefficiency is a prominent problem than residual technical inefficiency for smallholder maize farms in Ethiopia. A greater persistent inefficiency gap of 32% or [((1 − 0.76)/0.76) × 100] than transient inefficiency gap of 15% or [((1 − 0.87)/0.87) × 100] underscores the need for addressing structural inefficiency drivers in maize production²⁵. The high levels of persistent inefficiency in maize production in Ethiopia also suggest that farm households could benefit greatly from changes in policy and management aimed at reducing lasting barriers to the diffusion of desirable crop management practices.

Kumbhakar et al. (2014) found similar results for the Norwegian grain farms in which persistent technical inefficiency was higher than residual technical inefficiency. The mean persistent technical efficiency was 71% and residual efficiency was 89%. Similarly, Kumbhakar and Heshmati (1995) found higher persistent technical efficiency than residual technical efficiency for dairy farms in Sweden for the period 1976–1988. The high degree of persistent technical inefficiency could reflect long-run problems of farms that require policy intervention. Nonetheless, differences in efficiency estimates among the different competing groups of SF models demonstrate the difficulty in correctly measuring technical efficiency estimates, as also demonstrated by Kumbhakar et al. (2014) and Abdulai and Tietje (2007).

Controlling for measured environmental factors in the deterministic production function produces consistent technical efficiency estimates (see Table 9 and Figs. 7 and 8)²⁶. The technical efficiency estimates and the shape of the technical efficiency distributions for Model 6 (BC92G) vs. Model 6A (BC92GE) are highly consistent but those of Model 7 (BC95) vs. Model 7A (BC95E) and Model 8 (GEN) vs. Model 8A (GENE) are not (see Fig. 7). These results demonstrate the importance of evaluating how environmental variables are incorporated in different SF models to minimise the impact of heterogeneity bias and ensure empirical consistency of estimated efficiency scores.

We observe an inverse relationship between frontier intercept levels and mean technical efficiency estimates. Models with higher frontier intercepts (e.g., Model 3 (TREHN), Model 5 (OTE), Model 7 (BC95), Model 8 (GEN) and Model 9 or HN) are associated with lower mean efficiency scores and vice versa (see Fig. 1). In particular, the general model (Model 8 or GEN) has the highest intercept and the lowest mean efficiency inference. Such an inverse relationship appears to be an important indicator of heterogeneity bias that appears as inefficiency. Based on a simulation study, Caudill and Ford (1993) revealed that neglected heterogeneity in the variance of inefficiency (heteroscedasticity/misspecification) could lead to overestimation of frontier intercept and inefficiency measure. This implies an underestimation of technical efficiency. Likewise, the results from the general model (Model 8 or GEN) seems to support this conjecture. The Battese and Coelli (1995) inefficiency effects model (Model 7 or BC95), the half-normal TRE model (Model 3 or TREHN) and the half-normal simple pooled models (Model 9 or HN) show a similar trend. By contrast, Model 2 (BC92TN) and Model 6 (BC92G) have relatively lower frontier intercepts and higher mean efficiency estimates²⁷. This observation implies that these models seem to be less impacted by the bias compared to other models. It appears that both observed and unobserved heterogeneity leads to higher frontier intercepts and understated efficiency estimates if neglected in the analysis. Some empirical studies have reported a greater effect of neglected heterogeneity/heteroscedasticity on technical efficiency estimates (Caudill and Ford 1993; Caudill et al. 1995; Kumbhakar et al. 2014).

Fig. 1

Plots of mean technical efficiency (TE) and frontier intercept for stochastic frontier models. The figure shows that the higher mean efficiency the lower is frontier intercept. Greene’s TRE models (Models 3 and 4) are very close to pooled Models 9 and 10. The truncated-normal basic panel model (Model 2) is very close to the model with environmental variables in the variance of inefficiency measure (Model 6). The general model in which the same set of environmental variables is incorporated in the mean and variance of inefficiency (Model 8) has highest intercept and the lowest mean efficiency estimate of all the models. A similar trend is observed for the half-normal TRE (Model 3), the half-normal pooled (Model 9) and the BC95 inefficiency effects model (Model 7)

Abdulai and Tietje (2007) found inconsistent estimates of both the production function and inefficiency measure in their application of the German dairy farms. They also found evidence of correlation between firm effects and measured heterogeneity (explanatory variables) in the production structure. This situation could lead to inconsistent estimates of production frontier and technical efficiency due to omitted variables bias. Previous research has shown that any omitted heterogeneity in the production function can show up in the inefficiency measure/the stochastic component (Sherlund et al. 2002; Greene 2008). Our results show that omitting measured environmental factors in the production function can greatly distort estimates of technical efficiency especially for RE models with mean truncation.

For our case study, the way observed heterogeneity is treated in SF models appears to be the major source of bias in the inefficiency measure. In this paper, we control for environmental variables in the inefficiency component as well as the deterministic production function²⁸. The model with environmental variables incorporated in the variance of inefficiency (Model 6 or BC92G) is close to Model 2 (BC92TN). On the other hand, the Battese and Coelli (1995) model (Model 7) with environmental variables incorporated in the mean function yielded mean efficiency estimates that are very close to the simple pooled model (Model 9 or HN) and the Greene’s TRE model (Model 3 or TREHN). The ‘general’ model (Model 8 or GEN) in which the same set of environmental variables are simultaneously incorporated in the mean and the variance of inefficiency had the lowest mean efficiency estimate (47%). Using the other results as a benchmark, the mean efficiency estimate from the ‘general’²⁹ model (Model 8 or GEN) appears implausible. Efficiency estimates from Models 7 and 8 appear to be understated relative to the estimates of the other models (see lower panel of Fig. 5 and upper panel of Fig. 6). However, controlling for environmental factors in the deterministic production function can produce similar (consistent) technical efficiency estimates and significantly reduce heterogeneity bias in the RE models (see Table 9 and Fig. 8). The impact of omission of environmental factors in the production function on technical efficiency measure appears substantial for the Battese and Coelli (1995) (Model 7 or BC95) and the general model (Model 8 or GEN) but not for Model 6 (BC92G) (see Fig. 7)³⁰.

The results appear to support the prior conjecture that RE models that incorporate environmental variables in the mean function of the inefficiency measure could lead to biased efficiency estimates due to misspecification and statistical error as argued in the literature (Alvarez et al. 2006; Kumbhakar and Lovell 2000; Simar et al. 1994)³¹. Furthermore, the simultaneous placement of the same set of environmental variables in both the mean and the variance of inefficiency measure as in Wang (2002) could distort efficiency estimates due to potential confounding effects because the mean and variance statistics are not unrelated. However, the shape of distribution of efficiency observed in Model 6 (BC92G) appears stable and this stability could be related to its scaling property³² unlike the location transformation or the truncation of the mean function by environmental variables in Model 7 (BC95) and Model 8 (GEN).

Efficiency estimates also depend on the distributional assumptions of inefficiency. For example, the mean technical efficiency estimates of the half-normal RE model (Model 1 or BC92HN) is 71% while that of the truncated-normal RE model (Model 2 or BC92TN) is 78%. Since these models are nested within each other, they can be compared using the likelihood ratio test. In our case, the test rejected Model 1 in favour of Model 2 at 1% level of significance. The mean technical efficiency estimates for the half-normal and exponential-normal TRE model are 61% and 72%, respectively. The overall TE from the GTRE model is 66% and appears to be affected by the half-normality of the inefficiency distribution. These results support the notion that efficiency estimates are sensitive to distributional assumptions of the inefficiency term (Coelli et al. 2005; Kumbhakar et al. 2015; Nguyen et al. 2021).

Furthermore, the efficiency estimates of TRE models (Models 3 and 4) which treat all firm effects as heterogeneity are much closer to the simple pooled models than to the basic RE models (Models 1 and 2). Greene (2005b) found a similar result using a banking application in which the TRE model had similar estimates as the simple SF pooled model. Note that the RE models treat unobserved firm effects as overall technical inefficiency. Figure 2 shows pairwise scatter plots for the SF panel models with and without environmental variables. The graphical illustration clearly shows the differences in efficiency estimates across the models. The scatter plots show that the efficiency estimates from the TRE models are closer to those of the simple pooled half-normal or exponential–normal models than to the basic RE models. The kernel density distribution of technical efficiency confirms the striking consistency of Greene’s TRE models with the simple pooled frontier models than to the Battese and Coelli RE models (see Fig. 5). We also observe that the RE models are close to the persistent efficiency (PGTRE) while the TRE models are close to residual efficiency (TGTRE). Similarly, the RE models with environmental variables are closer to the persistent efficiency than to the transient efficiency³³. These observations are consistent irrespective of the assumptions of inefficiency distribution.

Fig. 2

Scatter plot matrices of pairwise technical efficiency estimates of the alternative models. Technical efficiency levels for each scatter plot are shown on both the horizontal and vertical axes for each pair-wise comparison. The transient and persistent efficiency are included for comparison. The figure shows that the TRE models (TREHN and TREEN) have a relatively a higher correlation with the simple pooled models than the RE models (BC92HN and BC92TN). The RE models with environmental variables are closer to the persistent (PGTRE) than to the transient efficiency (TGTRE)

Technical efficiency from RE and TRE models depends on the way heterogeneity is treated rather than the assumptions of inefficiency distribution. The GTRE model (Model 5) reveals substantial persistent technical inefficiency which is captured by the RE models but not by the TRE models (see Fig. 3). We observe that both the persistent and transient efficiency scores are closer to the RE models than to the TRE model (see Fig. 6). Thus, the TRE models that mimic the simple pooled models (lump all heterogeneity with inefficiency) appear not supported for our data. Likewise, efficiency estimates from simple pooled models are less likely to be correct (Kumbhakar and Lovell 2000).

Fig. 3

Distribution of persistent, transient and overall technical efficiency from the GTRE model

3.3 Ranking of farm households and heterogeneity

Ranking of farm households based on their efficiency scores is also interesting for policy purposes. If different frontier models rank farm households differently, then policy inference may be fragile and inconsistent as noted by Abdulai and Tietje (2007). Table 7 provides the Spearman rank correlation coefficients for the technical efficiency scores generated from the estimated stochastic frontier models. The coefficients show the close rankings of farm households based on their efficiency scores. The results suggest that Greene’s TRE models (Models 3 and 4) have strong ranking correlations (0.97) with the simple pooled models (Models 9 and 10). On the other hand, the basic RE Battese and Coelli models (Models 1 and 2) have relatively weaker ranking correlations with the TRE models or the simple pooled models. This result suggests that the RE and TRE panel models show quite inconsistent efficiency patterns and hence inconsistent rankings. We observe that the ranking correlations between the TRE models (Models 3 and 4) are consistent with the transient efficiency (TGTRE). Conversely, the basic RE models (Models 1 and 2) are close to the persistent efficiency (PTGRE). Ranking correlations between PGTRE and TGTRE are positive but weak (0.39); and one would not expect these two estimates to be highly correlated. The result could indicate some overlap in estimating these two types of inefficiencies (see Fig. 3). Based on a simulation experiment and real data, Badunenko and Kumbhakar (2016) showed that the GTRE model might not separate the four error components reliably and the model may not outperform the preceding simpler panel models. According to the authors, either the persistent or the transient inefficiency is estimated reliably at any one time but not simultaneously. Among the extensions of RE modes, incorporating environmental variables (measured heterogeneity) in the variance of inefficiency (Model 6) appears to provide closer ranking of technical efficiency to the basic RE models (Models 1 and 2) and persistent efficiency (PGTRE) than incorporating in the mean (Model 7) and in both the mean and the variance simultaneously (Model 8). These models (Models 6, 7 and 8) also show weak ranking correlations with the TRE modes (Models 3 and 4) and the transient efficiency (TGTRE). However, incorporating environmental factors in the deterministic production function resulted in technical efficiency estimates that are consistent to those from the basic RE model (see Fig. 9) and persistent efficiency (PGTRE) (see Fig. 10).

Table 7 Spearman rank correlation between efficiency estimates of the frontier models

These results reveal substantial persistent inefficiency which is picked up by the RE and GTRE models but not by the TRE or the simple pooled models. We argue that the TRE model’s core assumption that technical efficiency is only transient could be inappropriate for agricultural production environments such as ours (see Fig. 3). Persistent inefficiency could be a result of some rigidity in the production structure and managerial capabilities in the production process (Filippini and Greene 2016; Kumbhakar and Heshmati 1995; Kumbhakar et al. 2014). Factors such as gender of the farm manager, work motivation, traditional farm power, and agroecology as well as soil types and quality could lead to persistent inefficiency for our production context.

Overall, our results underscore the importance of scrutinising stochastic frontier models for their ability to generate comparable and reliable analytical results in the context of specific institutional and production environments. Among the panel models that address unmeasured heterogeneity (environmental variables are not controlled for) but are assumed to be constant for each firm, the mean efficiency estimate (78%) from the basic truncated-normal Battese and Coelli (1992) model (Model 2 or BC92TN) appears to be less biased. However, when differences in production environments are measured, the mean efficiency estimate (75%) from the RE model (Model 6 or BC92G) that incorporates environmental variables into the variance of inefficiency (Greene 2005b) appears to be less biased³⁴ than the panel models which incorporate into the mean or both the mean and variance of inefficiency. Likewise, when environmental factors are included in the deterministic production function because these are beyond the control of farms, the mean technical efficiency estimates appear to be highly similar (consistent) and less biased. The mean technical efficiency estimates for Models 6A (BC92GE), 7A (BC95E) and 8A (GENE) are 77%, 75% and 75%, respectively. The five RE models produced consistent and robust estimates of technical efficiency for our data. These efficiency estimates (the average from the above five consistent models, 76%) are also comparable with efficiency estimates from Ethiopia and elsewhere in Africa. For example, based on meta-regression analysis, Bravo-Ureta et al. (2007) found average technical efficiency for maize production to be about 75% and average technical efficiency for the African region to be about 74%. The key insight from our analysis is that policy inferences on how to improve production should be based on evaluating the empirical results of different SF models. Indeed, policy inference should be based on results from multiple models with consistent or robust estimates. Technical efficiency estimates from an inappropriately chosen SF model could lead to erroneous policy inferences on how to diffuse agricultural innovations and narrow the productivity gap (Sherlund et al. 2002; Abdulai and Tietje 2007; Bravo-Ureta et al. 2007).

4 Concluding remarks

We estimated technical efficiency of maize producing farm households in Ethiopia using stochastic production frontier models that take different approaches to address observed and unobserved firm heterogeneity. The first type of models are random effects (RE) panel models which treat unobserved firm effects as part of overall inefficiency. The second type of models include ‘true’ random effects (TRE) panel models which treat all unobserved firm effects as heterogeneity rather than inefficiency. We estimate the general model (GTRE) that decompose overall technical efficiency into persistent and transient components. We estimated RE models with environmental variables (observed heterogeneity) incorporated into the mean inefficiency function. We also controlled for environmental factors in the deterministic production function while allowing managerial related variables, including sustainable agronomic practices and socio-economic factors, in the inefficiency effect function. Simple pooled models (without heterogeneity) were estimated for comparison.

We found technical efficiency estimates are sensitive to how unobserved and observed heterogeneity is treated in SF models and the assumptions made about the distribution of inefficiency. The mean technical efficiency estimates from the investigated models range from 47% to 78%. All the SF models produced consistent estimates of the production function parameters.

These results have two key insights for researchers and policymakers. First, policy inferences based on estimated technology parameters from competing SF models are easier to draw as they tend to be consistent across models. Second, policy inferences about technical efficiency measures requires more caution as different SF models can yield varying results. For example, inference based on average estimates from Model 8 would imply high levels of inefficiency in the production process (47%) compared to estimates from Model 2 (78%).

We can draw three methodological insights from this case study. First, the TRE panel models generate results that are strikingly close to those from the simple pooled models. This result contrasts with the RE models. Given the apparent advantage of stochastic frontier panel models over cross-sectional models (Kumbhakar and Lovell 2000), the RE models that treat firm effects as part of overall technical inefficiency would appear to be more appropriate than the TRE models that have no allowance for persistent inefficiency for our data. The GTRE model indicates substantial levels of persistent inefficiency (mean of 32%) which is also supported by the RE models but ignored by the TRE models.

Second, incorporating environmental variables (observed heterogeneity) in the specification of the variance function of inefficiency in the RE model (Model 6) appears to provide efficiency estimates that are similar with those from the basic truncated-normal RE model (Model 2), but not with the RE models that incorporate the variables in the mean function (Model 7) or both the mean and the variance function of inefficiency simultaneously (Model 8). Likewise, the efficiency estimates from the RE models (Model 2 and Model 6) are correlated with the persistent efficiency (PGTRE) estimates predicted by the GTRE model (Model 5). Efficiency estimates from a ‘general’ model (Model 8) that allows the same set of environmental variables in the mean and the variance function of the inefficiency term appears less reliable compared to the other results. However, controlling for environmental factors in the deterministic production function (Models 6A, 7A and 8A) provides consistent technical efficiency estimates and significantly reduce heterogeneity bias for the RE models. These insights underscore the importance of evaluating stochastic frontier models for their empirical consistency before making policy prescriptions about how to reduce or eliminate mistakes in production.

Third, technical efficiency estimates depend on the assumed distribution assumption. We observed that SF model that assumes the inefficiency term follows a half-normal distribution yields mean efficiency estimates that are not consistent to those models that assume a truncated, exponential, or gamma-normal distributions. This is worrying given that the half-normal distribution is the most frequently used assumption in practice. These results underscore the importance of choosing a distributional assumption of the inefficiency term that is appropriate for a given production environments. The choice of type of SF model to estimate should not be a matter of computational convenience (e.g., due to software availability) as pointed out by Coelli et al. (2005). For our data, the half-normal assumption of inefficiency distribution is rejected in favour of the flexible truncated-normal. The technical efficiency estimates from SF models that assume the inefficiency follow the truncated-normal, exponential-normal and gamma-normal distributions are highly consistent for our data. Therefore, evaluating and testing alternative inefficiency distributions for a particular data set appears critical to ensure robust estimates and draw valid policy prescriptions when heterogeneity is not controlled but assumed to be constant for each farm.

Because economic theory does not provide any guidance on how to choose a SF model for a particular data set (Huang and Lai 2012; Parmeter et al. 2019; Van Nguyen et al. 2021), a step-by-step evaluation of competing SF models is important in ensuring the reliability of analytical results. Some studies have suggested the use of statistical selection criteria (e.g., likelihood ratio test) by formulating a ‘general model’ assumed to nest other simpler models (Alvarez et al. 2006; Colombi et al. 2014; Liu and Myers 2009). However, Lai and Huang (2010) argue that such model selection criteria can be unsatisfactory because the ‘general model’ itself is subject to specification error. Likewise, the assumed distribution assumptions about the inefficiency term have no basis in economic theory.

However, this study demonstrated that a step-by-step evaluation of a broad set of stochastic frontier models could help researchers to narrow the range of possible models to consider for a particular case study in a specific production and institutional environment. Here, the researchers would be looking for models that generate results that are comparable in terms of summary statistics, distribution, and rank correlation after considering practical, methodological and data implications. As noted by Kumbhakar et al. (2014), no one model can be considered an adequate representation of the “true” efficiency estimates that are unobserved. Kumbhakar et al. (2014) stress that when choosing a SF model to use, one should consider the specific institutional and environmental production conditions where the firms operate.

With adequate sample size, one could explore group frontier approaches to address potential technology heterogeneity that might affect the estimated efficiency measure. Farm households might also self-select in the choice of technologies and addressing self-selection bias could help practitioners obtain robust estimates of technical efficiency in SF models. These are left for further research. Further research could also consider the application of SF panel models with four-error components to accommodate heterogeneity as well as both persistent and transient inefficiency, possibly with environmental variables incorporated in both the persistent and transient efficiency modelling (e.g., Badunenko and Kumbhakar 2017; Lai and Kumbhakar 2018), as well as allowing for potentially endogenous environmental variables that may correlate with the basic inefficiency distribution values (e.g., Amsler et al. 2017). ‘Model averaging’ approaches (e.g., Parmeter et al. 2019) could also be explored as an alternative to a step-by-step evaluation of SF models considering both technology parameters and efficiency scores.

Appendix

Figures 4–11 and Tables 8–11

Fig. 4

Kernel density estimates of technical efficiency for simple pooled stochastic frontier models. The figure shows that technical efficiency estimates from the pooled truncated-normal, exponential-normal and gamma-normal distributions are highly consistent but the half-normal distribution is quite different from them. The truncated-normal and the exponential-normal distributions have a striking agreement

Fig. 5

Kernel density estimates of technical efficiency under half-normal (upper panel) and under truncated normal distributional assumptions of inefficiency (lower panel). The figure shows that TRE models are very close to the simple pooled model (HN) than to other models. The Battese and Coelli (1995) inefficiency effects model and the general model (GEN) are quite different from the benchmark simple pooled models (TN) or the basic panel frontier models (TREEN or BC92TN). The general model greatly underestimates efficiency scores

Fig. 6

Technical efficiency scatter plots from panel models relative to the efficiency score from the simple pooled truncated-normal (TN) model (upper panel) and the half-normal (HN) model (lower panel). The figures show that the efficiency score of the TRE models highly correlate with the simple pooled models as shown by the linear trend. The persistent and transient efficiency scores are closer to the BC92G than to the TREHN model. The BC95 inefficiency effects model and the general model (GEN) underestimate efficiency inference in comparison to other panel models

Fig. 7

Kernel density estimates of technical efficiency for a pair of models with and without the environmental factors incorporated in the deterministic production function. The figure shows that the model which incorporates all environmental variables in the variance function (BC92G) is still consistent when environmental factors are included in its deterministic part (BC92GE). However, the Battese and Coelli (1995) model and the general model (GEN) appear quite inconsistent when the environmental factors are incorporated in their deterministic frontier function (BC95E or GENE)

Fig. 8

Kernel density estimates of technical efficiency when all environmental variables are included in the inefficiency part (upper panel) and when certain environmental factors are included in the deterministic production frontier part (lower panel). The figure shows that incorporating environmental factors which are beyond the control of farms in the deterministic production function part yields consistent technical efficiency estimates rather than incorporating all the environmental variables in the inefficiency measure

Fig. 9

Kernel density estimates of technical efficiency of empirical consistent random effects (RE) models. The figure shows that the basic RE model (BC92TN) and its various extensions with environmental factors included in the deterministic part and managerial related variables included in the mean (BC95E), variance (BC92GE) and both mean and variance (GENE) yield consistent or robust technical efficiency estimates

Fig. 10

Scatter plot matrices of pairwise technical efficiency estimates of sub-group of models. Technical efficiency levels for each scatter plot are shown on both the horizontal and vertical axes for each pair-wise comparison. The figure shows that RE models with environmental factors included in the deterministic production function are closer to the persistent (PGTRE) than to the transient efficiency (TGTRE)

Fig. 11

Kernel density estimates of technical efficiency from full sample and midland zone (upper panel) and lowland and highland zones (lower panel). The figure shows that technical efficiency from separate production frontier estimation of full sample and midland agroecology zone are highly consistent. The technical efficiency estimates from the lowland and highland agroecology zones appear similar but concentrated around the extremes of the distribution

Table 8 Estimates of the parameters of production frontier for models with environmental factors in the deterministic production frontier

Table 9 Summary statistics of technical efficiency for panel models with environmental variables

Table 10 Mean technical efficiency and deterministic production frontier intercepts

Table 11 Summary of technical efficiency estimates from separate translog frontiers