Latent heterogeneity to evaluate the effect of human capital on world technology frontier

Abstract

Although human capital has been recognized as playing important role in spurring productivity growth, its empirical effect remains ambiguous due to the possibility of latent heterogeneity. To reveal the impact of this important driver of economic growth, we propose an alternative empirical methodology, robust frontier in non parametric location-scale models for accommodating simultaneously the problem of model specification uncertainty, latent heterogeneity and cross-section dependence in modelling technical efficiency. We estimate a nonparametric frontier model to define the world technology frontier of 40 countries over the period 1970–2007. Conditional versions of the frontier enables us to investigate the effect of external factors on the production process. One of these factors will allow to measure the openness of the economy of the country and the second will be this latent factor of heterogeneity linked to the absorptive capability and hence to human capital of the country. We have to adjust the methodology to take into account the panel structure of our data set, i.e., handling the time dimension and the cross-sectional dependence affecting the process. Our findings prove that human capital plays an important role in accelerating the technological catch-up (increase in the efficiency) but not on the technological changes (shifts in the frontier). This result seems to confirm the theoretical hypothesis that countries benefit from new technology (technological catch-up) only when they have the ability to exploit it, hence only when they have high level of absorptive capability.

1 Introduction

US economic slowdown in the second half of the nineties and the slowdown following 2001—more marked in Europe than in US—, leading many to question the recipe for endogenous self-sustained growth. The understanding of the sources of growth may mirror the larger debate between the neoclassical and new growth theories, but economists generally agree that this recent economic decline has largely been caused by the weak growth in TFP (total factor productivity), i.e., that part of the rise in economic growth which is neither due to the increase in capital nor to the rise in the labour. Productivity growth is the net change in output due to changes in efficiency and technical change. The main advantage of the frontier approach, used here, is that it allows this important distinction. In a macroeconomics context, as the one used in this paper, production inefficiency can be identified as the distance of the individual production from the frontier, estimated by the maximum output of the reference country, regarded as the empirical counterpart of an optimal boundary of the production set. Inefficiencies generally reflect a sluggish adoption of new technologies, and thus efficiency improvement will represent productivity catch-up via technology diffusion.¹

The “new” growth theory of Lucas (1988), Romer (1990a) and Barro (1990) and Barro (1997) has human capital playing an important role in productivity growth because human capital can help in explaining an economy’s capacity to absorb new technologies (Abromovitz, 1986, Cohen and Levinthal, 1989, Kneller, 2005, Kneller and Stevens, 2006). For example, Benhabib and Spiegel (1994), in their empirical study, suggest that human capital plays a role in economic growth by helping the adoption of technology from abroad and to develop the appropriate domestic technology. Guellec and van Pottelsberghe de la Potterie (2004) provide macroeconomic evidence that high absorptive capability enhances the positive effect of foreign knowledge on the domestic economy. Eaton and Kortum (2001) and Caselli and Coleman (2006) convey that only a few research and development (R&D) intensive countries produce most of the world’s capital; the rest of the world just acquires embodied technologies from world technological leaders. Consequently, a country’s productivity depends on its access to new technology and ability to use it. Hence, according to these studies, human capital is the most important force behind economic growth of countries. Our paper contributes to this literature by proposing an empirical model ables to identify “absorptive capability” as the main driver of productivity growth.

Moreover, in response to the question of how technology diffusion affects economic growth, there has been an emerging empirical literature examining the nexus between the technology diffusion and human capital in promoting economic growth. The evidence on this issue is mixed (Delgado et al., 2014, Miller and Upadhyay, 2000, 2002, Olofsdotter, 1998). However, a consistent feature of all the empirical studies on this issue is the use of parametric cross-country regression framework on a sample of developed and developing countries. The parametric approach suffers from misspecification problems when the data-generating process is unknown, as usual in the applied studies, and nonparametric methods often give the most reliable results. Furthermore, the effect of this important growth factor—human capital—on economic growth remains ambiguous due to the possibility of latent heterogeneity, which can arise, for example, from the different institutions (e.g., different property right systems) in the various countries.

Starting with Färe et al. (1994), efficiency frontier econometric studies on macroeconomic data using nonparametric approaches (like FDH or DEA) are not new (see, for example, (Henderson and Russell, 2005, Henderson and Zelenyuk, 2007, Kumar and Russell, 2002, Mallick et al., 2016)). The purpose of this paper is to provide fully nonparametric estimators of production frontiers and time-variant technical efficiency in a dynamic framework which allows spatial dependence and both observed and latent factors to affect technical efficiency.

We will consider, in a nonparametric setup, a frontier model to define the world technology frontier, and due to extreme values and outliers we will focus on a robust version of the frontier, see Cazals et al. (2002). Conditional versions of the frontier (Cazals et al., 2002, Daraio and Simar, 2005) will be important to investigate the effect of external factors on the production process. One of these factors will allow to measure the openness of the economy of the country and the second will be this latent factor of heterogeneity linked to the absorptive capability of the country. The latter will be identified by some nonparametric nonseparable model, see e.g., Matzkin (2003).

Particularly, an exact dynamic mechanism as to how technology efficiency and human capital relate each other remains ambiguous. Particularly the focus of theoretical debates is how best to model dynamic adjustments. Hence, the inclusion of the short-run dynamics in a stochastic frontier approach is likely to be relevant (Ahn and Sickles, 2000, Tsionas, 2006). We propose an nonparametric approach to take into account unobserved heterogeneity and cross section dependence due to common factors attributable to global shocks in a dynamic framework.

Since we will estimate the global frontier of 40 countries over the period 1970–2007, we have to extend the methodology proposed in Cazals et al. (2002) and Simar et al. (2016) to take into account the panel structure of our data set, i.e., handling the time dimension and the Cross-Sectional Dependence (CSD) affecting the process. More fundamentally, we propose a robust method which simultaneously addresses the problem of model specification uncertainty, latent heterogeneity and spatial dependence in the analysis of productivity. It also accounts for heteroskedasticity.

Specifically our methodology allows us to isolate the channel through which human capital affects productivity convergence toward the technological frontier. Indeed our approach reveals “the capability to use new technology” as the main force behind the technological convergence process.

The paper is organized as follows. In the next section we describe the Data Generating Process (DGP) and the underlying assumptions we consider to define our basic model. Section 3 gives the main ideas of the chosen methodology to reach our objective. Then Section 4 will provide the technical econometric details for estimating the pieces of our model. Section 5 describes our data set and the empirical results we obtain in our application. Section 6 concludes and summarizes our main findings.

2 The basic model

We acknowledge the endogenous growth models of Lucas (1988) and Romer (1990a) that use a theoretical framework where persistent economic growth is conditional on the accumulation of human capital. The new endogenous growth theories (Aghion and Howitt, 1992, Romer, 1990a) describe human capital as the engine of growth through innovation. Grossman and Helpman (1991) show that the skill composition of the labor force matters for the amount of innovation in the economy. In particular, they obtain that an increase in the stock of skilled labor is growth-enhancing while an increase in the stock of unskilled labor can be growth-depressing. Benhabib and Spiegel (1994), Tallman and Wang (1994) find that the channel through which human capital positively affects output is through the efficiency enhancing effect. Recent contributions emphasize the different roles that different types of human capital may play in either backward or advanced economies ((Caselli and Coleman, 2006)), and the distinction between innovation activities and adoption of existing technologies from the (world) technology frontier (Acemoglu et al., 2006). In this context, low-skilled human capital appears better suited to the adoption of technology in low-income countries, while skilled human capital has a growth enhancing impact which increases with the level of development (Caselli and Coleman, 2006, Vandenbussche et al., 2006).

To analyze the productivity performances of the countries, we use nonparametric frontier models where the traditional inputs Capital-X_K and Labor-X_L are considered along with Human Capital-X_H, measured as an index based on the average years of schooling. So the latter may be interpreted as the “cognitive” part of human capital. These inputs produce the output Y, the GDP of the country. The production frontier is the maximal amount of output a country can reach for a given value of its inputs. The frontier can thus be seen as the upper boundary of the support of the input-output variables (X,Y) where X = (X_K,X_L,X_H). The basic DGP is thus an appropriate probability space on (X,Y) with a joint density f_X,Y(x,y); the support of this density is the attainable set. Therefore, see e.g., Cazals et al. (2002), the technology frontier function can be defined as

$$\tau (x)=\sup \{y| {S}_{Y| X}(y| X\,\le \,x)\,> \,0\},$$

(2.1)

where the survival function ${S}_{Y| X}(y| X\,\le \,x)={\mathbb{P}}(Y\,\ge \,y| X\,\le \,x)$. So we can write

$$Y=\tau (X)-\widetilde{U},where\,{\widetilde{U}}\ge 0.$$

(2.2)

In this presentation, $\widetilde{U}$ represents inefficiency: its distribution may depend on X but its support (≥0) does not. This model is appropriate if the technology is well described by the attainable set in the input-output space.

However, we know that in some cases, we have to take into account some external factors (often called “environmental” factors), that are not under the direct control of the units but that may influence the production process, and so the efficiency analysis. They can affect the process either (i) only through the support of the input-output variables or (ii) only through the conditional distribution of (X,Y) given these external factors (affecting the probability of approaching the optimal boundary), or (iii) through both channels. In general, we do not know in advance what will be the picture and if these factors behave, e.g., as free disposal inputs (being favorable to the production process) of as undesirable outputs, etc. So these factors introduce heterogeneity among the countries and if they affect the boundary of the attainable set of values (X,Y), any analysis neglecting these factors will introduce endogeneity issues (see Simar et al. (2016) and see below).

In our setup here we will consider two of such external factors. First we consider Z = FDI, Foreign Direct Investment, which may be viewed as the most important openness channel of technology diffusion. FDI leads to increases in productivity by spurring competition and transferring technology. New foreign competition arrivals provide domestic firms an incentive to use existing resources more efficiently which increases their productivity. Consequently, foreign firms have to invest even more in order to keep up with their technological advantage (Glass and Saggi, 1998). FDI can also increase productivity through the transfer of technology. This occurs with the adoption of new technology brought by foreign multinational companies, imports of high- technology inputs, and the skills acquired by the local labour force as they are educated and trained by the foreign firms (see (Mastromarco and Simar, 2015), for the empirical evidence on the effect of FDI on productivity).²

Second we would like to consider a factor, V, measuring the “absorptive capability” of a country that was mentioned in the Introduction above. This factor V is not directly observed so it can be viewed as a latent factor of heterogeneity which is linked to Human Capital, X_H (see e.g., (Abromovitz, 1986, Benhabib and Spiegel, 1994, Cohen and Levinthal, 1989, Kneller, 2005, Kneller and Stevens, 2006)). The fact that it affects the production process and under which channel is an open empirical issue we address in this paper. We model its link with X_H with the help of an auxiliary variable W through a nonparametric nonseparable model X_H = ϕ(W, V), where the auxiliary variable W is Life Expectancy. This model has been studied e.g., in Matzkin (2003) and in a frontier set-up in Simar et al. (2016). We give more details on this model in Sections 3 and 4, but roughly V is identified as the part of X_H which is not explained by W. The methodology will produce predicted values of V for each country. In our model, human capital X_H impacts directly the productivity of a country. However, there may exist unobserved characteristics of the countries that may influence both the existing level of education and the productivity, as the ability to innovate. To take into account this latent heterogeneity we use life expectancy as auxiliary variable. The resulting identified factor V—independent on our auxiliary variable—will be interpreted as absorptive capability or as some measures of “innovation” in the country, defined as the potential to master new knowledge embodied in innovation, which we expect would act as a free disposal input. The innovation has similar attributes as a public good, indeed it is non rival and non exclusive. Given these features, there exists the problem to protect the property rights of innovations which would guarantee profits to the innovators and stimulate new efforts to innovate. Hence, it is very likely that, this unobservable factor is capturing the difference in property rights systems among countries (e.g., very high in US, very low in Mexico) and the ability to innovate. We will see in our data set how these potential interpretations receive some empirical evidences, by looking to the links of the estimated versions of V with some appropriate indicators.

To investigate the effects of these external factors on the production process, we consider an augmented DGP concerning now the variables (X,Y,Z,V) defined on an appropriate probability space and having some joint distribution. Now, for a given value of (z,v), the attainable set of values in the input-output space is the support of the conditional density f_XY∣ZV(x, y∣z, v). We thus have to analyze the conditional technology frontiers defined for any (z,v) as (see (Cazals et al., 2002, Daraio and Simar, 2005)

$$\tau (x| z,v)=\sup \{y| {S}_{Y| X,Z,V}(y| X\le x,Z=z,V=v)\,> \,0\},$$

(2.3)

where the survival function ${S}_{Y| X,Z,V}(y| X\le x,Z=z,V=v)={\mathbb{P}}(Y\ge y| X\le x,Z=z,V=v)$. As pointed in Simar et al. (2016), replacing the unobserved values of V by the predicted values they suggest, does not affect the asymptotic properties of the frontier estimators. Now we can write

$$Y=\tau (X| Z,V)-U,{\rm{where}}U\ge 0.$$

(2.4)

Again U represents inefficiency, its distribution may depend on (X, Z, V) and its support does not (U ≥ 0). This is the concept of partial exogeneity of (X,Z,V) introduced by Cazals et al. (2016), where it is shown that there is no severe consequence for the estimation of the conditional frontier by traditional methods (like conditional FDH/DEA): we keep consistency and the same rates of convergence. But if we ignore any of these conditioning variables (suppose we ignore both) and use τ(X) as frontier model we have endogeneity issues. Indeed we have $Y=\tau (X)-\widetilde{U}$ but now $\widetilde{U}=\tau (X)-\tau (X| Z,V)+U$ and we loose the partial exogeneity condition for $\widetilde{U}$, unless τ(X) = τ(X∣Z, V) with probability one. The latter is a reformulation of the separability condition for (Z,V) introduced by Simar and Wilson (2007).

So our main research questions are: (i) identify the factor V and check if our strategy (choice of model and auxiliary variable for identifying V) produces indeed a factor that can be interpreted as “absorptive capability” or “measure of innovation” for a country and (ii) analyze the effect of this new factor on the production process. For the latter we will compare the results obtained by using the simple conditional frontier τ(x∣z) where we condition on FDI with those obtained by using τ(x∣z, v) where we condition on both Z and V.

Finally, we have to take into account the panel structure of our data set: 40 countries over 1970–2007. For handling the time dimension and the cross sectional dependence (CSD) due to the influence of globalization factors (e.g., technological shocks and financial crises) on the economic performance of countries under analysis, we envelop the effect of CSD on the production process. For doing so, we assume that the production process is function of some unobserved time-varying factors. We follow here Pesaran (2006) and Bai (2009) and we consider F_t = (t, X_•t, Y_•t) as proxy for the unobserved time-varying factors.³ We will therefore analyze production frontier that are also conditional to these time-varying factors F_t in addition to the factors (Z, V) described above.⁴

Of course the analysis of the resulting efficiency scores will also allow to study the channels under which the identified heterogeneity factor V, linked to human capital, affects the production process and its components: impact on the attainable production set (input-output space), and the impact on the distribution of efficiencies. We use a flexible nonparametric two-step approach on conditional efficiencies to eliminate the dependence of production inputs/outputs on common and external factors, as suggested by Florens et al. (2014). We emphasize the usefulness of “pre-whitened” inputs/outputs introduced in Florens et al. (2014) to eliminate cross-section dependence and observed heterogeneity and to obtain more reliable measure of productivity and efficiency to better investigate the impact of our identified latent factor V on the catching-up productivity process. Methodological details and estimation techniques are described in the two next sections.

3 The methodology

We consider a production process that involves the production of an output $Y\in {{\mathbb{R}}}_{+}$ (the level of production) by using inputs $X\in {{\mathbb{R}}}_{+}^{p}$ (the factors of production). The optimal level of production is given by a global frontier, which is defined as the maximum attainable level of outputs that can be reached by using a level X of the factors. The efficiency of each observation can then be measured by its distance to its corresponding (optimal) frontier point.

As introduced above, a simple (but naive) way to investigate the production process, and the performance of each observation, would be to analyze how far are the observations from a simple unconditional frontier, locus of optimal level of production y for a given level of the input factors x. This unconditional frontier function was defined in (2.1). So τ(x) is the upper support for Y among units (countries) using less input factors than x.⁵ This probability formulation allows also to define a less extreme benchmark than the full frontier for providing robust versions of the frontier that will be less sensible to extreme or outlying data. We select here the order-m frontier introduced by Cazals et al. (2002), where for a given value of m, we have

$${\tau }_{m}(x)={\mathbb{E}}[\max ({Y}_{1},\ldots ,{Y}_{m})| X\le x]$$

(3.1)

where Y₁, …, Y_m are m independent copies of Y drawn in the conditional population of units with X ≤ x, i.e., using less that x input factors. So we have (when Y is univariate)

$$\begin{array}{lll}{\tau }_{m}(x)=\displaystyle{\int \nolimits_{0}^{\infty }}[1-{({F}_{Y| X}(y| X\le x))}^{m}]dy\\ =\tau (x)-\displaystyle{\int\nolimits_{0}^{\tau (x)}}{F}_{Y| X}^{m}(y| X\le x)dy\end{array}$$

(3.2)

since F_Y∣X = 1 − S_Y∣X, the conditional cdf of Y given X ≤ x, is equal to 1 when y ≥ τ(x).⁶ It is known that when m → ∞, the order-m frontier converges to the full frontier τ(x). But for finite m it is a less extreme benchmark frontier, since it involves an expectation. In practice we will use large values of m to provide robust estimates of the production frontier (see (Daouia et al., 2012), for the theoretical justifications and see below how to fix m in practice). We can also look at the case m = 1 for exploring the average production level for units using less than x inputs.

Nonparametric estimators of τ(x) are then obtained by plugging in (2.1) an empirical version of the survival function providing the FDH estimators introduced in Deprins et al. (1984). The statistical properties have been derived in Park et al. (2000) and Daouia et al. (2010). To summarize, under wide regularity conditions, the asymptotic distribution is linked to the Weibull but suffers from the “curse of dimensionality” with rates of convergence n^1/(p+q) depending on the number of variables: p inputs and q outputs (in our case, p + q = 4).

Nonparametric estimates of τ_m(x) are obtained in the same way by plugging the empirical survival in Eq. (3.1). These order-m share interesting properties. The main advantage is that they have better asymptotic properties, a parametric $\sqrt{n}$-rate of convergence and an asymptotic normal distribution but also they are much more robust to extreme or outlying data points as discussed in details in Cazals et al. (2002) and Daraio and Simar (2005). See also Daouia and Gijbels (2011) for the analysis of these estimators from a theory of robustness perspective. Simar and Wilson (2015) offer a recent survey on all these concepts with a detailed description of the statistical properties of the most popular nonparametric estimators.

In the presence of a panel data, and due to our particular macroeconomic set-up, we have to adapt these concepts by extending conditional frontiers as developed in Cazals et al. (2002), Daraio and Simar (2005) and more recently by Florens et al. (2014). As explained above, for handling the time dimension and the CSD we consider F_t = (t, X_•t, Y_•t) as proxy for the unobserved time-varying factors. We will therefore analyze production frontiers that are conditional to these time-varying factors F_t and in a first stage conditional to the observed environmental factors Z (FDI which allows for controlling the effect of openness of the economy on productivity).

To summarize we will first estimate for any value of (x, y, f, z) the conditional production frontier as the maximal achievable output level y for a country using inputs X ≤ x and confronted to the time-varying factors F = f and to the observable environmental conditions Z = z (FDI). From the literature on conditional frontier models (see (Cazals et al., 2002, Daraio and Simar, 2005)) this frontier is defined as

$$\tau (x| f\!,z)=\sup \{y| {S}_{Y| X,F,Z}(y| x,f,z)\,> \,0\},$$

(3.3)

thus the frontier level, given a value of (x,z,f), is the upper support point of the following conditional survival function

$${S}_{Y| X,F,Z}(y| x,f,z)={\mathbb{P}}(Y\ge y| X\le x,F=f,Z=z).$$

(3.4)

We remark that τ(x∣f,z) is a function of (x,f,z) since Y is univariate.⁷ We note also, as explained in Cazals et al. (2002), that the conditioning on X is through an inequality (to insure monotonicity of the frontier in the input level) but conditioning on the other factors is, as in usual conditional models, through equalities. Once we have the conditional frontier, we can define the performance (efficiency) of a unit operating at level (x, y) and confronted to conditions (f, z) by its distance to the frontier. We can use an additive directional measure of inefficiency in the output direction defined as

$$\delta (x,y| f,z)=\sup \{\delta\, > \,0| {S}_{Y| X,F,Z}(y(1+\delta)| x,f,z)\,> \,0\}=\tau (x| f,z)-y,$$

(3.5)

where we see this unit (x, y) is efficient if δ(x, y∣f, z) = 0. Here, for projecting a current value (x, y) on the frontier, we use the directional vector d_x = 0 for the inputs and d_y = y for the output (see for basic definitions, e.g., (Färe and Grosskopf, 2000, Simar and Vanhems, 2012), for the probabilistic characterization we use here).

For estimating the conditional frontiers, conditional to (F, Z), we will follow the strategy of Florens et al. (2014) that use in a first step a flexible nonparametric location scale model to whiten the inputs X and the output Y from the effect of business cycles and globalization shocks (proxied by the common factors F) and from the effect of FDI, Z. The technical details are given in the next section, but the idea is to build “pure” inputs ε_x and “pure” output ε_y, cleaned from these effects. The efficient frontier in these new units is given by

$$\varphi ({e}_{x})=\sup \{{e}_{y}| {S}_{{\varepsilon}_{y}| {\varepsilon}_{x}}({e}_{y}| {e}_{x})={\mathbb{P}}({\varepsilon}_{y}\ge {e}_{y}| {\varepsilon}_{x}\le {e}_{x})\,> \,0\},$$

(3.6)

gives the optimal level in the pure units. As in Florens et al. (2014) we define a measure of pure inefficiency for a unit with current values (e_x, e_y) by using the directional output distance between this point and its projection to the efficient frontier (e_x, φ(e_x))

$$\rho ({e}_{x},{e}_{y})=\varphi ({e}_{x})-{e}_{y}.$$

(3.7)

The main advantage is that this measure of inefficiency has been cleaned from the effect of (F, Z) and allows a more fair comparison of the performance of each country. We will show in the next section that from these “pure” objects, we can recover, if wanted, the frontier τ(x∣f, z) and the conditional inefficiency δ(x, y∣f, z) in the original units for all values of (x, y, f, z).

Now we have to identify our latent factor V linked to Human Capital. As introduced above, we model its link with X_H with the help of an auxiliary variable W through a nonparametric nonseparable model X_H = ϕ(W, V), where the auxiliary variable W is Life Expectancy ((Imbens and Newey, 2009)). So we use the following model

$${X}_{H}=\phi (W,V),$$

(3.8)

which is nonseparable in V. Here, W has to be correlated to X_H but is independent of V. As explained in details in Simar et al. (2016), the unobserved variable V can be viewed as the part of the X_H which is independent of W. We also impose a classical assumption of monotonicity of ϕ with respect to V and we assume, without loss of generality, that V is uniformly distributed on [0, 1]. Under these assumptions V is identified by the conditional distribution of X_H given W:

$$V={F}_{{X}_{H}| W}.$$

(3.9)

It is useful to notice that ϕ is unknown and since V is uniform on [0, 1], ϕ can be interpreted as a quantile function. The choice of a uniform distribution for V is just a matter of scaling V, so this assumption has no effect on the analysis.

As explained in the preceding section, we have to estimate the conditional frontier where in addition to the former variables (F, Z), we condition on the identified latent factor V. This is defined in (2.3) and as above, conditioning now on (F, Z, V), the measure of inefficiency of a unit operating at level (x, y) is given by

$$\delta (x,y| f,z,v)=\tau (x| f,z,v)-y,$$

(3.10)

to be compared with (3.5).

For the estimation here, we have to be coherent with all the above assumptions, including the location-scale model to whiten the inputs and output. We explain below that this can be achieved by assuming a similar model for V, in other words, we will also whiten V from the effects of business cycles and globalization shocks and from the effect of FDI. This provide ε_v, the “pure” version of the latent factor V. Now using the methodology suggested by Simar et al. (2016) we can easily determine the conditional frontier in the pure inputs/output space (ε_x, ε_y), conditionally on ε_v = e_v:

$$\varphi ({e}_{x}| {e}_{v})=\sup \{{e}_{y}| {S}_{{\varepsilon }_{y}| {\varepsilon }_{x},{\varepsilon }_{v}}({e}_{y}| {e}_{x},{e}_{v})\,> \,0\},$$

(3.11)

and ${S}_{{\varepsilon }_{y}| {\varepsilon }_{x},{\varepsilon }_{v}}({e}_{y}| {e}_{x},{e}_{v})={\mathbb{P}}({\varepsilon }_{y}\ge {e}_{y}| {\varepsilon }_{x}\le {e}_{x},{\varepsilon }_{v}={e}_{v})$ is the conditional survival of ε_y given that ε_x ≤ e_x and that ε_v = e_v. Accordingly, a pure measure of inefficiency for a unit with current values (e_x, e_y) and facing the value of the pure latent factor e_v is given by

$$\rho ({e}_{x},{e}_{y}| {e}_{v})=\varphi ({e}_{x}| {e}_{v})-{e}_{y}.$$

(3.12)

Again, we will show in the next section that if corresponding values of τ(x∣f, z, v) and δ(x, y∣f, z, v) in the original units are wanted, they can be immediately derived from φ(e_x∣e_v) and ρ(e_x∣e_v), respectively.

It is the comparison of the estimators of these two conditional frontiers in “pure” units, φ(e_x) and φ(e_x∣e_v) (or of their corresponding “pure” efficiency measures ρ(e_x) and ρ(e_x∣e_v)) that will allow to explore the effect of V on the production process. We will choose and adapt the methodology suggested by Bădin et al. (2012), and Daraio and Simar (2014), as described in details in the next section.

Finally, we know that some extreme values (or outliers) in the data may influence the estimation of the frontier and may hide the real effect of ε_v on the frontier levels (see Figs. 5.3 and 5.4 in (Daraio and Simar, 2007), for some classroom examples). So we will, as in Florens et al. (2014) and as in Simar et al. (2016) use the robust, order-m versions of the conditional frontiers. We will first evaluate the order-m frontier in the “pure” inputs and output units cleaned from the effect of (F, Z). To summarize

$${\varphi }_{m}({e}_{x})={\mathbb{E}}[\max ({\varepsilon }_{y,1},\ldots ,{\varepsilon }_{y,m})| {\varepsilon }_{x}\le {e}_{x}],$$

(3.13)

is the simple order-m frontier of ε_y given that ε_x ≤ e_x and ε_y,1, …, ε_y,m are m iid copies of ε_y. Its computation goes along the lines of (3.1)–(3.2) by using the survival function ${S}_{{\varepsilon }_{y}| {\varepsilon }_{x}}$ defined in (3.6). Here again, a measure of pure order-m inefficiency for a unit with current value in pure units (e_x, e_y) is given by the distance

$${\rho }_{m}({e}_{x},{e}_{y})={\varphi }_{m}({e}_{x})-{e}_{y}.$$

(3.14)

Note that here the values of ρ_m(e_x, e_y) are not restricted to be positive, since the current value (e_x, e_y) can be above the order-m frontier.

Now for conditioning on the “pure” latent ε_v = e_v we have for the conditional order-m frontier

$${\varphi }_{m}({e}_{x}| {e}_{v})={\mathbb{E}}[\max ({\varepsilon }_{y,1},\ldots ,{\varepsilon }_{y,m})| {\varepsilon }_{x}\le {e}_{x},{\varepsilon }_{v}={e}_{v}].$$

(3.15)

Here, its computation can be done along the lines of (3.2), using the conditional survival function ${S}_{{\varepsilon }_{y}| {\varepsilon }_{x},{\varepsilon }_{v}}$ defined above in (3.11). Accordingly, the conditional pure inefficiency measure of order-m is given by

$${\rho }_{m}({e}_{x},{e}_{y}| {e}_{v})={\varphi }_{m}({e}_{x}| {e}_{v})-{e}_{y}.$$

(3.16)

The way to estimate these measures and the asymptotic properties of the resulting estimators are described in Florens et al. (2014) and Simar et al. (2016) when conditioning on the latent factor. We summarize these details in the next section and show also how the corresponding measures can, if wanted, be easily derived in the original units of (X, Y) and V (e.g., to recover τ_m(x∣f, z) and τ_m(x∣f, z, v) and the corresponding inefficiencies).

As explained above for large values of m we have robust estimator of the full frontier, we will use these with large values of m to get insight on the role of V on the location of the frontier (check if V may influence the production set). We explain below how to select appropriate value of m in order to eliminate potential outliers. Then, as suggested in Bădin et al. (2012), we also estimate order-m frontier with small values of m, e.g., m = 1 to explore the effect of V on the position of the center of the distribution of the efficiencies, since m = 1 gives the conditional average of the production levels. All technical details for the estimation are presented in the next section.

4 The estimation strategy

In this section, we summarize the concepts and notations introduced in Florens et al. (2014) and Simar et al. (2016) and how we adapt to panel data and extend them to include time, global factors and heterogeneity factors. This is needed for applying the methodology summarized above that is used in the empirical application. Given our DGP, we have data on (X_it, Y_it, F_t, Z_it, W_it) for i = 1, …, n and t = 1, …, s where a generic X = (X_K, X_L, X_H). Our model assumes also that a latent factor of heterogeneity V, linked to Human Capital, might affect the production process. From the observations (X_H,it, W_it) we will predict the values ${\widehat{V}}_{it}$. Then we will first estimate for any value of (x, y, f, z) the conditional production frontier as the maximal achievable output level y for a country using inputs X ≤ x and confronted to the time-varying factors F = f and to the observable environmental conditions Z = z (FDI) and then we will do the analog when conditioning on V, for any value of (x, y, f, z, v).

4.1 Predicted values of the latent factor and endogeneity issues

As explained above under the nonseparable model (3.8) which link X_H to the latent factor by the way of the auxiliary variable W, V is identified by (3.9). So, given the data (X_H,it, W_it) the predicted values of V for each observation point is given by ${\widehat{F}}_{{X}_{H}| W}({X}_{H,it}| {W}_{it})$. A natural nonparametric estimator, as the one proposed by Simar et al. (2016) is defined for i = 1, …, n and t = 1, …, s by

$${\widehat{V}}_{it}={\widehat{F}}_{{X}_{H}| W}({X}_{H,it}| {W}_{it})=\frac{\mathop{\sum }\nolimits_{j = 1,u = 1}^{n,s}{\mathbb{1}}\left(\right.{X}_{H,ju}\le {X}_{H,it}\left)\right.{K}_{{h}_{w}}\left(\right.{W}_{ju}-{W}_{it}\left)\right.}{\mathop{\sum }\nolimits_{j = 1,u = 1}^{n,s}{K}_{{h}_{w}}\left(\right.{W}_{ju}-{W}_{it}\left)\right.},$$

(4.1)

where ${K}_{{h}_{w}}(\zeta)=(1/{h}_{w})K(\zeta /{h}_{w})$ and K(•) is a kernel with compact support on [−1, +1], like e.g., Epanechnikov and h_w is a bandwidth. In practice this bandwidth can be determined by Least-Squares Cross Validation (LSCV) techniques that are now standard in nonparametric estimation (see e.g., (Li et al., 2013)).

As explained above, if we ignore this latent factor when evaluating the performances of the countries we may create endogeneity problems unless τ(X∣F, Z) ≡ τ(X∣F, Z, V) with probability one (the “separability condition” for V introduced in Simar and Wilson (2007)).

4.2 Nonparametric estimation of the conditional frontier τ(x∣f, z)

The conditional frontier τ(x∣f, z) has been defined in (3.3) and a natural nonparametric estimator is obtained by plugging a nonparametric estimator of the conditional survival function S_Y∣X,F,Z(y∣x, f, z) given in (3.4). This requires some smoothing relative to the conditioning variables (F, Z) but not for X since the condition on X is an equality and so empirical conditional cdf can be used when only X is concerned. These estimators have been analyzed in Cazals et al. (2002) and Daraio and Simar (2005) and we have

$${\widehat{S}}_{Y| X,F,Z}(y| x,f,z)=\frac{{\sum }_{it}{\mathbb{1}}({X}_{it}\le x,{Y}_{it}\ge y){K}_{{h}_{f}}({F}_{t}-f){K}_{{h}_{z}}({Z}_{it}-z)}{{\sum }_{it}{\mathbb{1}}({X}_{it}\le x){K}_{{h}_{f}}({F}_{t}-f){K}_{{h}_{z}}({Z}_{it}-z)},$$

with the ${K}_{{h}_{u}}(\zeta)=(1/{h}_{u})K(\zeta /{h}_{u})$ where K(•) are traditional kernels (when needed multivariate kernels (like e.g., product kernels) with compact support and bandwidths vector h_u, with the usual notational convention that division by vectors is element-wise. We will not follow this route since Florens et al. (2014) have shown the advantage of using an alternate approach based on a flexible nonparametric location-scale models for “cleaning” the input Y and the outputs X from their dependence of (F, Z).

The approach can be seen as follows. Suppose the vector (X, Y, F, Z) follows the location-scale regression model:

$$\begin{array}{r}\left\{\begin{array}{lll}{X}_{it}&=&{\mu }_{x}({F}_{t},{Z}_{it})+{\sigma }_{x}({F}_{t},{Z}_{it}){\varepsilon }_{x,it}\\ {Y}_{it}&=&{\mu }_{y}({F}_{t},{Z}_{it})+{\sigma }_{y}({F}_{t},{Z}_{it}){\varepsilon }_{y,it}\end{array}\right.,\end{array}$$

(4.2)

where μ_x, σ_x and ε_x have each 3 components (in our setup we have 3 input factors) and, for ease of notations, the product of vectors is component-wise. So the first equation in (4.2) represents 3 relations. Here ${\mu }_{x}(F,Z)={\mathbb{E}}(X| F,Z)$ and element by element, ${\sigma }_{x}^{2}(F,Z)={\mathbb{V}}(X| F,Z)$ and the same for Y, ${\mu }_{y}(F,Z)={\mathbb{E}}(Y| F,Z)$ and ${\sigma }_{y}^{2}(F,Z)={\mathbb{V}}(Y| F,Z)$. The location-scale model assume that (ε_x, ε_y) is asymptotically independent of (F, Z). The approach suggested by Florens et al. (2014) is to estimate the full frontier ρ(e_x), and their robust versions ρ_m(e_x) and their corresponding inefficiency measures ρ(e_x, e_y) and ρ_m(e_x, e_y) without being affected by (F, Z). In other words, under model (4.2), comparison and ranking of observation units is legitimate, since the effect of the variables (F, Z) has been eliminated.

But if wanted we can recover the conditional frontier τ(x∣f, z) and the inefficiency measures δ(x, y∣f, z) as follows. Under the model assumptions, we have indeed from (3.3) and (3.4)

$$\begin{array}{lll}\tau (x| f,z)=\sup \left\{y| {\mathbb{P}}\left(\frac{Y-{\mu }_{y}(F,Z)}{{\sigma }_{y}(F,Z)}\ge \frac{y-{\mu }_{y}(f,z)}{{\sigma }_{y}(f,z)}\left|\right.X\le x,F=f,Z=z\right)\,> \,0\right\}\\ ={\mu }_{y}(f,z)+\sup \left\{{e}_{y}| {\mathbb{P}}\left({\varepsilon }_{y}\ge {e}_{y}\left|\right.{\varepsilon }_{x}\le \frac{x-{\mu }_{x}(f,z)}{{\sigma }_{x}(f,z)}\right)\,> \,0\right\}{\sigma }_{y}(f,z)\\ ={\mu }_{y}(f,z)+\varphi \left(\frac{x-{\mu }_{x}(f,z)}{{\sigma }_{x}(f,z)}\right){\sigma }_{y}(f,z),\end{array}$$

(4.3)

where φ(e_x) is defined in the pure units space, see (3.6). In other words (4.3) indicates that the frontier function in the original units is a simple transformation of the frontier obtained in the new units. For the distance function, it is easy to verify that

$$\delta (x,y| f,z)={\sigma }_{y}(f,z)\rho ({e}_{x},{e}_{y}),$$

(4.4)

which interestingly indicates that the distance in original units may be highly dependent of the variables (F, Z) through a scaling factor. This again advocate our approach of using “pure” measures of inefficiency.

The advantage is also from an estimation perspective: we only need estimators of the functions μ_ℓ(f, z) and σ_ℓ(f, z) (ℓ = x, y) to obtain an estimate of τ(x∣f, z) which require only smoothing in the center of the data. The fact that we avoid smoothing at the frontier is important, as in general, data are more sparse there and estimators can be sensitive to outliers. In addition, as pointed in Bădin et al. (2019), no easy ways are available to derive optimal bandwidths for estimating the support of a conditional distribution like S_Y∣X,F,Z(y∣x, f, z). Note that in some applications, the practitioner may also analyze these additional tools like, e.g., μ_ℓ(f, z) to appreciate marginally the mean behavior of inputs and output as a function of (f, z).

We can also derive the link between the order-m conditional frontier and its analog in the “pure” units space:

$${\tau }_{m}(x| f,z)={\mu }_{y}(f,z)+{\varphi }_{m}\left(\frac{x-{\mu }_{x}(f,z)}{{\sigma }_{x}(f,z)}\right){\sigma }_{y}(f,z),$$

(4.5)

where φ_m(e_x) was defined in (3.13). Similarly it is easy to show that

$${\delta }_{m}(x,y| f,z)={\sigma }_{y}(f,z){\rho }_{m}({\varepsilon }_{x},{\varepsilon }_{y}),$$

(4.6)

where ρ_m was defined in (3.14). We observe the same scaling factor as for the full frontier above.

In practice the estimation steps go as follows. We first clean the inputs and the output by estimating the models (4.2). We use local-linear models for estimating the functions μ_x and the function μ_y. From the squared residuals regressed on (F, Z) by a local constant estimator (to avoid negative variances) we derived the estimator of σ_ℓ, ℓ = x, y. Finally the estimates of the “pure” inputs and output are obtained as

$${\widehat{\varepsilon }}_{x,it}=\frac{{X}_{it}-{\widehat{\mu }}_{x}({F}_{t},{Z}_{it})}{{\widehat{\sigma }}_{x}({F}_{t},{Z}_{it})},$$

(4.7)

$${\widehat{\varepsilon }}_{y,it}=\frac{{Y}_{it}-{\widehat{\mu }}_{y}({F}_{t},{Z}_{it})}{{\widehat{\sigma }}_{y}({F}_{t},{Z}_{it})},$$

(4.8)

where as before, for ease of notation, a ratio of two vectors has to be understood component wise.

We only need an estimator of the survival function ${S}_{{\varepsilon }_{y}| {\varepsilon }_{x}}({e}_{y}| {e}_{x})$ for obtaining estimators of the frontier and of the inefficiencies in the pure units, but this does not require any smoothing and can be obtained at parametric $\sqrt{N}$-rates (see Corollary 2,(i) in (Florens et al., 2014)) where N = ns is the total number of observations. The empirical version of this survival is given by

$${\widehat{S}}_{{\varepsilon }_{y}| {\varepsilon }_{x}}({e}_{y}| {e}_{x})=\frac{{\sum }_{it}{\mathbb{1}}({\widehat{\varepsilon }}_{x,it}\le {e}_{x},{\widehat{\varepsilon }}_{y,it}\ge {e}_{y})}{{\sum }_{it}{\mathbb{1}}({\widehat{\varepsilon }}_{x,it}\le {e}_{x})}$$

(4.9)

Algorithms for computing ${\widehat{\varphi }}_{m}({e}_{x})$ or ${\widehat{\rho }}_{m}({e}_{x},{e}_{y})$ are described in Simar and Vanhems (2012) and Daraio and Simar (2014).

As proven in Florens et al. (2014) under wide regularity conditions (smoothness of the μ_ℓ and σ_ℓ functions, ℓ = x, y), the resulting estimators of the full-frontier and of the order-m conditional frontiers obtained through the location-scale models (and through their estimates), are similar to the one that we would obtain by using ${\widehat{S}}_{Y| X,F,Z}(y| x,f,z)$. Here and below we are mostly interested to the robust order-m version and it can be proven that under wide regularity conditions, we have $\sqrt{N}$-rates of convergence and an asymptotic normal distribution (see Corollary 2,(ii) in (Florens et al., 2014)). This will be enough for what we need in our application for exploring the effect of V on the production process.

4.3 Nonparametric estimation of the conditional frontier τ(x∣f, z, v)

We might be willing to use the same attractive approach of the location-scale models to whiten also the output and the inputs from the influence of V. However the non-separable assumption defining V is not compatible with a location-scale model in V. So, here we have no choice and we follow the approach suggested in Simar et al. (2016). As shown below if we want to use the results of the preceding section and working in the “pure” inputs and output space, we need to whiten the latent factor V from the influence of (F, Z) and we will also a flexible location-scale model. So we add to the system (4.2) a new equation defining a “pure” version of the latent factor ε_v whitened from the influence of (F, Z):

$${V}_{it}={\mu }_{v}({F}_{t},{Z}_{it})+{\sigma }_{v}({F}_{t},{Z}_{it}){\varepsilon }_{v,it}$$

(4.10)

where now the independence assumption is that (ε_x, ε_y, ε_v) are jointly independent of (F, Z). The estimation of ε_v goes along the same lines as for ε_x and ε_y described above.⁸

We can now easily determine the conditional frontier in the pure units space, conditionally on ε_v = e_v:

$$\varphi ({e}_{x}| {e}_{v})=\sup \{{e}_{y}| {S}_{{\varepsilon }_{y}| {\varepsilon }_{x},{\varepsilon }_{v}}({e}_{y}| {e}_{x},{e}_{v})\,> \,0\},$$

(4.11)

and ${S}_{{\varepsilon }_{y}| {\varepsilon }_{x},{\varepsilon }_{v}}({e}_{y}| {e}_{x},{e}_{v})={\mathbb{P}}({\varepsilon }_{y}\ge {e}_{y}| {\varepsilon }_{x}\le {e}_{x},{\varepsilon }_{v}={e}_{v})$ is the conditional survival of ε_y given that ε_x ≤ e_x and that ε_v = e_v.

It is easy to prove that the knowledge of φ(e_x∣e_v) allows to recover τ(x∣f, z, v). Indeed we can write from (2.3)

$$\begin{array}{lll}\tau (x| f,z,v)=\sup \{y| {\mathbb{P}}(Y\ge y| X\le x,F=f,Z=z,V=v)\,> \,0\}\\ =\sup \left\{y| {\mathbb{P}}\left(\frac{Y-{\mu }_{y}(F,Z)}{{\sigma }_{y}(F,Z)}\ge \frac{y-{\mu }_{y}(f,z)}{{\sigma }_{y}(f,z)}\left|\right.X\le x,F=f,Z=z,V=v\right)\,> \,0\right\}\\ ={\mu }_{y}(f,z)+\sup \left\{{e}_{y}| {\mathbb{P}}\left({\varepsilon }_{y}\ge {e}_{y}\left|\right.{\varepsilon }_{x}\le \frac{x-{\mu }_{x}(f,z)}{{\sigma }_{x}(f,z)},F=f,Z=z,V=v\right)\,> \,0\right\}{\sigma }_{y}(f,z)\\ ={\mu }_{y}(f,z)+\sup \left\{{e}_{y}| {\mathbb{P}}\left({\varepsilon }_{y}\ge {e}_{y}\left|\right.{\varepsilon }_{x}\le \frac{x-{\mu }_{x}(f,z)}{{\sigma }_{x}(f,z)},{\varepsilon }_{v}=\frac{v-{\mu }_{v}(f,z)}{{\sigma }_{v}(f,z)}\right)\,> \,0\right\}{\sigma }_{y}(f,z).\end{array}$$

where the last equality is obtained because we assume ε_v is independent of (F,Z). Then we have the relation

$$\tau (x| f,z,v)={\mu }_{y}(f,z)+\varphi \left(\frac{x-{\mu }_{x}(f,z)}{{\sigma }_{x}(f,z)}{\Bigg|}\frac{v-{\mu }_{v}(f,z)}{{\sigma }_{v}(f,z)}\right){\sigma }_{y}(f,z).$$

(4.12)

We thus immediately obtain

$$\delta (x,y| f,z,v)={\sigma }_{y}(f,z)\rho ({e}_{x},{e}_{y}| {e}_{v})$$

(4.13)

where the pure measure of conditional inefficiency ρ(e_x, e_y∣e_v) is defined in (3.12).

The robust order-m versions follow the same scheme. To summarize we have

$${\tau }_{m}(x| f,z,v)={\mu }_{y}(f,z)+{\varphi }_{m}\left(\frac{x-{\mu }_{x}(f,z)}{{\sigma }_{x}(f,z)}{\Bigg|}\frac{v-{\mu }_{v}(f,z)}{{\sigma }_{v}(f,z)}\right){\sigma }_{y}(f,z),$$

(4.14)

and similarly

$${\delta }_{m}(x,y| f,z,v)={\sigma }_{y}(f,z){\rho }_{m}({e}_{x},{e}_{y}| {e}_{v}).$$

(4.15)

Due to our objectives described above, we are mainly interested in the measures in the pure units space. The needed quantities will be estimated, as above, by plugging a nonparametric estimator of the survival function ${S}_{{\varepsilon }_{y}| {\varepsilon }_{x},{\varepsilon }_{v}}$ obtained from the estimates $\{({\widehat{\varepsilon }}_{y,it},{\widehat{\varepsilon }}_{x,it},{\widehat{\varepsilon }}_{v,it})\}$, i = 1, …, n and t = 1, …, s. Note that here the nonparametric estimator of this conditional survival involves smoothing in the variable ε_v, and requires bandwidth selections. Simar et al. (2016) notice that we obtain better properties of the resulting estimator of the conditional frontier by determining the optimal bandwidth for estimating the joint conditional probabilities ${H}_{{\varepsilon }_{y},{\varepsilon }_{x}| {\varepsilon }_{v}}({e}_{y},{e}_{x}| {e}_{v})={\mathbb{P}}\left({\varepsilon }_{y}\ge {e}_{y},{\varepsilon }_{x}\le {e}_{x}| {\varepsilon }_{v}={e}_{v}\right)$, i.e., where we only condition in ε_v. With this approach, there is also only one bandwidth to determine (and not one value for each value of e_x); see Appendix A in Simar et al. (2016) for the details and arguments. To be specific we have to compute the following estimator

$${\widehat{H}}_{{\varepsilon }_{y},{\varepsilon }_{x}| {\varepsilon }_{v}}({e}_{y},{e}_{x}| {e}_{v})=\frac{{\sum }_{it}{\mathbb{1}}({\widehat{\varepsilon }}_{y,it}\ge {e}_{y},{\widehat{\varepsilon }}_{x,it}\le {e}_{x}){K}_{{h}_{v}}({\widehat{\varepsilon }}_{v,it}-{e}_{v})}{{\sum }_{it}{K}_{{h}_{v}}({\widehat{\varepsilon }}_{v,it}-{e}_{v})},$$

(4.16)

with the standard notation for the kernel ${K}_{{h}_{v}}$ already introduced above and the bandwidth h_v determined by LSCV (see (Li et al., 2013), for details). Then ${\widehat{S}}_{{\varepsilon }_{y}| {\varepsilon }_{x},{\varepsilon }_{v}}$ may be obtained as

$${\widehat{S}}_{{\varepsilon }_{y}| {\varepsilon }_{x},{\varepsilon }_{v}}({e}_{y}| {e}_{x},{e}_{v})=\frac{{\widehat{H}}_{{\varepsilon }_{y},{\varepsilon }_{x}| {\varepsilon }_{v}}({e}_{y},{e}_{x}| {e}_{v})}{{\widehat{H}}_{{\varepsilon }_{y},{\varepsilon }_{x}| {\varepsilon }_{v}}(-\infty ,{e}_{x}| {e}_{v})}.$$

(4.17)

The practical computations for obtaining the estimators $\widehat{\rho }({e}_{x},{e}_{y}| {e}_{v})$ and ${\widehat{\rho }}_{m}({e}_{x},{e}_{y}| {e}_{v})$ are described in Daraio and Simar (2014).

Compared to the estimator of the preceding section, due to the smoothing in ε_v we loose the parametric $\sqrt{N}$ rate of convergence but it may be proven (see (Cazals et al., 2002)) that by conditioning on ε_v, the rate of convergence is now $\sqrt{N{h}_{v}}$. Since the optimal bandwidths obtained by LSCV are order of ${h}_{v}=O\left(\right.{N}^{-1/5}\left)\right.$ this gives a rate of convergence for the conditional order-m estimators ${\widehat{\varphi }}_{m}({e}_{x}| {e}_{v})$ or ${\widehat{\rho }}_{m}({e}_{x},{e}_{y}| {e}_{v})$ of the order $\sqrt{{N}^{4/5}}$ which is a bit lower than the rate $\sqrt{N}$ obtained for the unconditional objects ${\widehat{\varphi }}_{m}({e}_{x})$ or ${\widehat{\rho }}_{m}({e}_{x},{e}_{y})$. As shown in Simar et al. (2016) the rates and the asymptotic normality are preserved when replacing the unobserved ε_v,it by their estimates ${\widehat{\varepsilon }}_{v,it}$.

4.4 Exploring the effect of the latent factor on the production process

Updating the ideas of Daraio and Simar (2005) and Florens et al. (2014) to our framework here, the analysis of the global effect of the factor V (measured by its cleaned version ε_v) on the production process can be captured by the analysis of the differences (remember that here Y and so ε_y are univariate)

$$\begin{array}{rcl}D({\varepsilon }_{x},{\varepsilon }_{v})\,=\,\varphi ({\varepsilon }_{x})-\varphi ({\varepsilon }_{x}| {\varepsilon }_{v}),\,\qquad\\ =\,\rho ({\varepsilon }_{x},{\varepsilon }_{y})-\rho ({\varepsilon }_{x},{\varepsilon }_{y}| {\varepsilon }_{v})\end{array}$$

as a function of ε_v, at various fixed levels of the inputs ε_x. For the output orientation we have here, D(ε_x, ε_v) ≥ 0 but a global tendency of these differences to decrease with ε_v indicates a positive effect, the conditional frontier φ(ε_x∣ε_v) moves up to unconditional one φ(ε_x) when ε_v increases, so ε_v acts as a freely disposable input. On the contrary, if the differences increase with ε_v indicates a negative effect of ε_v on the production process, the conditional frontier φ(ε_x∣ε_v) moves away from the unconditional one φ(ε_x), so ε_v acts as an undesirable output.

As explained above we prefer to do the analysis on the robust order-m frontiers, i.e., To be specific define the following random variable

$$\begin{array}{lll}{D}_{m}({\varepsilon }_{x},{\varepsilon }_{v})\,=\,{\varphi }_{m}({\varepsilon }_{x})-{\varphi }_{m}({\varepsilon }_{x}| {\varepsilon }_{v}),\\ \qquad\qquad\quad=\,{\rho }_{m}({\varepsilon }_{x},{\varepsilon }_{y})-{\rho }_{m}({\varepsilon }_{x},{\varepsilon }_{y}| {\varepsilon }_{v}).\end{array}$$

(4.18)

When the effect of the frontier of the production set is wanted we will choose large m to have a robust estimate of the frontier (in our empirical application we took m = 900 to let the most extreme 1% of data points outside the order-m frontier, we see below how to justify this choice). Then, as suggested in Bădin et al. (2012), we will choose small m for looking to the effect of ε_v on the center of the distribution of the efficiencies; e.g., with m = 1 we look to the average production level. Some potential shifts already observed for large m (robust frontier estimates) could be enhanced (or reduced) when looking to the difference in the center (with m = 1).

In our empirical analysis, we will fix the level of the inputs X_K and X_L jointly to their three quartile values to look to the effect of V on the differences D_m(ε_x, ε_v) for three levels of these two factors of production: those with low level of both X_K and X_L, those with joint median level and finally those with joint high level. This is done of course on the pure units for Capital and Labor. To be specific, when fixing these level, we select for each of the three analysis, the data points such that ${\varepsilon }_{x}=Median({\varepsilon }_{x})\pm {h}_{{\varepsilon }_{x}}$, where ${h}_{{\varepsilon }_{x}}$ is a bandwidth given by the normal reference rule and ε_x is only considered for Capital and Labor. Then we can analyze the corresponding nonparametric (local linear) regression of D_m(ε_x, ε_v) on ε_v, for these subsamples.

We can also provide a marginal analysis, i.e., neglecting the effect of ε_x, and looking to the differences D_m(ε_x, ε_v) as a function of ε_v only. Of course by doing so, we may hide some local effect or some interaction between ε_x and ε_v. We will illustrate these approaches in the empirical application below.

5 Empirical application

5.1 The data and the variables

The dataset is collected over the period, 1970–2007 (38 years) for a total of 40 countries using data from the Penn; 26 are developed OECD countries (Australia, Austria, Belgium, Canada, Chile, Hong Kong, Denmark, Finland, France, Germany, Greece, Ireland, Israel, Italy, Japan, Korea, Mexico, Netherlands, New Zealand, Norway, Portugal, Spain, Sweden, Turkey, the United Kingdom and the United States) and 14 are developing countries (Argentina, Bolivia, Côte d’Ivoire, Dominican Republic, Honduras, Jamaica, Kenya, Malawi, Morocco, Philippines, Thailand, Venezuela, Zambia, Zimbabwe).⁹

We use data from the Penn World Tables (version 9) where output is the real gross domestic product RGDP measured in million US dollars at 2005 constant prices. For labor input, we use the number of workers EMP. Capital stock which is our chosen input is then measured in million US dollars at 2005 constant prices. All three variables are transformed in logarithms and then rescaled to get a standard deviation of 1 before estimation.

For human capital we use a measure from the PWT 9.0 which is measured as an index based on the average years of schooling from Barro and Lee (2012) and an assumed rate of return to education, based on Mincer equation estimates around the world ((Psacharopoulos, 1994)). The empirical growth literature emphasizes the latent heterogeneity of human capital in the economic process, due to unobserved characteristics, which may impact both the level of education and the level of output. This problem leads often to ambiguous empirical results due to the difficulty to properly assess the impact of this important economic growth driver on country’s output. Indeed, many empirical papers find not significant or even negative impact of human capital on economic growth.¹⁰ To take into account the unobserved heterogeneity of human capital we use life expectancy as an auxiliary variable which enables us to isolate the effect of human capital independent on this factor. This variable (from World Bank Indicators) is measured as “life expectancy at birth indicates the number of years a newborn infant would live if prevailing patterns of mortality at the time of its birth were to stay the same throughout its life”.

For globalization factor we identify one of the most important channels: FDI inflows, measured as net inflows of foreign direct investment, which are then transformed as a ratio to GDP.¹¹ This external variable FDI might suffer from endogeneity bias. The endogeneity caused by reverse causality is still an open issue in the empirical studies investigating the relationship between total factor productivity (TFP) and FDI. We explicitly address this issue by eliminating in the first stage the dependence of the FDI on the production process. Furthermore, the global economy becomes increasingly integrated, all the individual countries are likely to be exposed more to global shocks. As explained above we follow Pesaran (2006) and Bai (2009) and consider F_t = (t, X_⋅t, Y_⋅t) as proxy for these common factors.

5.2 Effect of human capital on the production process

In our framework we consider that there is an unobserved heterogeneity, as different absorptive capability among countries, which determines the level of innovation and, hence, affects our production data generation process. We assume that this latent heterogeneity is linked to one of our production factor and, specifically, to human capital variable. By following Simar et al. (2016) we use life expectancy as an auxiliary variable W to identify the latent factor. We calculate the predicted value $\widehat{V}$ for each observation given by Eq. (4.1) as explained in section 2. We then estimate the conditional output-oriented efficiency, conditional on observed and non-observed factors.

The latent factor $\widehat{V}$ proxies for the aggregate effect of human capital not explained by life expectation - our auxiliary variable W -. In our macroeconomic context, this component would be related, for example, to the influence of institutions as difference in property rights systems or absorptive capability, defined as the potential to master new knowledge, among countries. Figure 1 shows the distributions and Table 1 summarizes descriptive statistics for the latent factor for 40 countries. The highest values over the sample period are registered by USA, New Zealand and Australia, whereas France, Portugal, Italy and Spain stand at the bottom of the ranking. These low values are mainly due to the fact that, in these countries, the life expectancy is very high. We may infer that these countries benefit from the increase in human capital more in terms of highest life expectancy than in capacity to innovate.

Fig. 1

Distribution of latent factor $\widehat{V}$ for the countries under analysis

Table 1 Estimated latent factor $\widehat{V}$ of 40 countries over 1970 till 2007: mean and standard deviation over time and change in % from 1970 to 2007

To explore if our predicted latent variable are somehow linked to absorptive capability, defined as the potential to master new knowledge and, hence, to the level of innovation in a country, in Table 2 we report the correlations between $\widehat{V}$ and R&D (expenditure in R&D as %of GDP) and with “The Worldwide Governance Indicators (WGI)” from the Wold Bank for the available countries and periods: voice and accountability, political stability and absence of violence, government effectiveness, regulatory quality, rule of law, and control of corruption.¹² High values of these government indicators denote good governance, which provides better property rights system and creates incentives to innovate.

Table 2 Correlation between $\hat{V}$ and R&D, the government quality indicators = Accountability, Political Stability, Government Effectiveness, Regulatory Quality, Rule of Law, Control of Corruption. P values for testing the hypothesis of no correlation in parentheses

As Table 2 exhibits the correlations are all positive and significant, and unveils that our estimated unobserved factor is significantly positive correlated with R&D expenditure (as % of GDP) and with these governance indicators, especially with Political Stability, Rule of Law and Control of Corruption. Our estimated unobserved factor captures heterogeneity in political stability or rule of law between, for example, U.S. and Australia (ranked first as latent factor value) and Italy or Spain which, indeed, register very low level of unobserved factor.

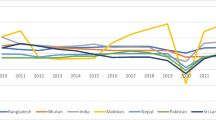
This evidence seems to confirm that our latent variable is somehow connected to the level of innovation. To give a visual impression of the change in latent factor over time, average value for each year is displayed in Fig. 2 for United States, New Zealand, Australia, Morocco, Spain, Belgium and Italy.¹³

Fig. 2

Evolution over time of latent factor $\widehat{V}$ for Australia (AUS), Belgium (BEL), Italy (ITA), Morocco (MAR), New Zealand (NZL), Spain (ESP) and United States (USA). Note also that we use the Hodrick and Prescott (1997) filter to smooth the time paths with a smoothing weight equal to 100

To take into account the impact on the production process of observed and non-observed common factors, we follow the two-stage estimation procedure described above which enables us, in the first stage, to better capture the impacts of global shocks (such as FDI, trade policy and cycle fluctuations) and, hence, CSD on the world production frontier and technical efficiency. By applying the estimation of the models (4.2) to our transformed data, we obtain by Eqs. (4.7) and (4.8) the “pure” versions of our inputs, ${\widehat{\epsilon }}_{x}$ (capital, labour and human capital) and of the output ${\widehat{\epsilon }}_{y}$ (GDP). Before looking for frontier estimates we have to verify if our assumption of asymptotic independence between the “pure” inputs-output (ε_x, ε_y) and the conditioning variables (F_t, Z) is reasonable. Table 3 reports the correlations between ε_x, ε_y and time factors F_t = (t, X_⋅t, Y_⋅t) and FDI. They are very small and the p values denote that we cannot reject the null of no-correlation, indicating that our first stage location-scale model has cleaned most of the effects of these variables and confirming that the influence of FDI and the cross section dependence has been removed from our data.

Table 3 Correlation between ε_L, ε_K, ε_H, ε_Y, ε_V and the factor F_t = t, L_⋅t, K_⋅t, H_⋅t, Y_⋅t and FDI. P values for testing the hypothesis of no correlation in parentheses

The estimation of the world production frontier then follows in the second stage. The full frontier estimate is the FDH of the preceding cloud of points and was defined above as $\widehat{\varphi }({e}_{x}| {\widehat{\varepsilon }}_{v})$. For a robust version of the frontier we have to specify a value for m. We compute the order-m frontier for several values of m and look to the corresponding percentage of data points staying above the resulting ${\widehat{\varphi }}_{m}({e}_{x})$ (see e.g., (Daraio and Simar, 2007, Simar, 2003)). We know that this percentage decreases when m increases, converging to 0 when m → ∞ since at a moment, for very large value of m we will observe ${\widehat{\varphi }}_{m}\equiv \widehat{\varphi }$, i.e., the FDH estimate. This percentage of points outside the frontier (with values ${\widehat{\varepsilon }}_{y,it}\,> \,{\widehat{\varphi }}_{m}({e}_{x}| {\widehat{\varepsilon }}_{v})$) as a function of m is shown in Fig. 3. We see that as expected for small values of m this percentage decreases rapidly but around values near 900, the value of m has to increase a lot to get the remaining points outside the frontier at this stage, under the frontier. So the points that are outside the frontier for m = 900 are rather extreme and may be outlying relative to the rest of the clouds. In fact the “elbow” effect just described is more precisely identified near m = 900. So for the robust version of the full frontier, we select m = 900 (this leaves 1% of data points above the corresponding order-m frontier).

Fig. 3

Percent of points outside the m-frontier at each value of m

Table 4 summarizes descriptive statistics for the conditional pure efficiency Eq. (3.16) for the 40 countries. We find that the most efficient countries conditioned on latent factor of human capital, and cleaned by the effect of economic cycle and other globalized factor, as FDI, over the sample period, are Germany, Israel and Spain, while the least efficient are Finland, New Zealand and Zimbabwe.

Table 4 Mean, standard deviation and percentage change of pure conditional mean efficiency; see Eq. (3.16)

To assess the influence of cleaned latent variable ${\widehat{\varepsilon }}_{v}$ defined as “the part of the human capital which is not related to the life expectancy” on the production process, we investigates the differences of conditional and unconditional efficiency measures for full and partial frontier as discussed in Section 4.4. The results of the potential effects of the latent variable ${\widehat{\varepsilon }}_{v}$ are shown in Fig. 4 for the differences Eq. (4.18) for m = 900 (robust version of the full differences) and for m = 1 to assess the influence of ${\widehat{\varepsilon }}_{v}$ on the average of the inefficient distribution.

Fig. 4

Estimated differences of marginal and conditional efficiency of order-m = 900 frontier (left panel) and order-m = 1 frontier (right panel). The sample size n = 1520

The main messages of these pictures is as follows. To investigate the effect of ${\widehat{\varepsilon }}_{v}$ on the shift of the frontier, we have to analyze the differences for robust version (Fig. 4 left panel) of the full frontier. We see for the left panel a nonlinear shape with the level of the differences very low and near to zero that, in our setup, we can interpret that we have not shifts of the frontiers when human capital increases. So, ${\widehat{\varepsilon }}_{v}$ does not act on the shift of the boundary. Hence, from this evidence, ${\widehat{\varepsilon }}_{v}$ appears not to play an important role in accelerating the technological change (shifts in the frontier).

The Fig. 4 (right panel) allows to identify some changes in the distribution of the inefficiencies due to ${\widehat{\varepsilon }}_{v}$. Globally, we can see some changes in the shape of the clouds of points and we observe a clear decreasing trend of differences with respect to ${\widehat{\varepsilon }}_{v}$. The level of these differences is different from zero. Combining this result with the previous on the shift of the technology, we could interpret as the fact that ${\widehat{\varepsilon }}_{v}$, which captures absorptive capacity, thus the capability to assimilate innovations, induces catching-up to the production frontier, but not necessarily shifts of it. This seems to suggest that countries benefit from new technology only when they have the ability to exploit it. Countries can switch to a better technology if they accumulate the technology-specific expertize ((Greenwood and Jovanovic, 2001, Helpman and Rangel, 1999)).

In addition, since there may be some interaction with the values of the inputs, in Fig. 5 we fix the values of Labor and Capital simultaneously at their three univariate quartiles, looking to the effect of human capital on the production process for small, medium and large countries, in term of these inputs.¹⁴ To facilitate the interpretation of the pictures we computed as usual in this kind of analysis the nonparametric regression line of the differences on ${\widehat{\varepsilon }}_{v}$. The main messages of these pictures is as follows. To investigate the effect of ${\widehat{\varepsilon }}_{v}$ on the shift of the frontier, we have to analyze the differences for the robust version of the full frontier. First, we see for left and right panels an inverted-U shaped of the regression lines for small and medium countries, and a more linear shape for the large sized countries. Second and importantly, the level of the differences is changing with the size of the countries: high level, for the small, degreasing for medium and very low, for large countries (near the values zero). In our setup this can be interpreted as follows. We might have some shift of the frontier when human capital increases. So, human capital accumulation acts on the shift of the boundary. Hence, from this evidence, human capital appears to play an important role in accelerating the technological change (shifts in the frontier). This is particularly true for small and medium countries (large values of differences). The bottom panels of Fig. 5 deserve also some comments, they allow, when compared to the top panels, to identify some changes in the distribution of the inefficiencies due to ${\widehat{\varepsilon }}_{v}$. Globally, we can see changes in the shape of the clouds of points and of the regression lines. Now the level of the differences are similar for small, medium and large countries. So the shift of the technology we have identified above, is compensated by the fact that for small, medium and large size countries, there is much less dispersion, ending up with similar values for the average production levels. This could be interpreted as the fact that human capital induces some shift of the production frontier, but mainly acts as driven factor of technology catching-up process.

Fig. 5

The first three top panels represent the estimated differences of marginal and conditional efficiency of order-m = 900 as a function of ${\widehat{\varepsilon }}_{V}$ with the two inputs (labour and capital) fixed at their three quartiles, from left to right, Q_0.25, Q_0.50, Q_0.75;, the bottom panels are for m = 1

Efficiency is the most important growth component for convergence analysis of countries that are below the technological frontier because it reflects “the process of imitation and transmission of existing knowledge” ((Romer, 1986)). Quah (1997), Mankiw et al. (1992), Barro and Sala-i-Martin (1995) argue that slow convergence in the level of output per worker is caused by slow technological catch-up. This latent variable which captures the part of human capital not linked to life expectancy, i.e., might capture absorptive capability, might increase efficiency and, hence, convergence. This occurs with the adoption of foreign technology through technology licensing or technology purchase, imports of high technology capital goods, and the skills acquired by the local labour force ((Borensztein et al., 1998, De Mello, 1999, Xu, 2000)).

Our findings support the convergence evolution of output among countries with respect to human capital. Our latent variable which captures the part of human capital not linked to life expectancy, i.e., might measure absorptive capability of a country, thus the capability to assimilate innovations, influences efficiency distribution and it acts as a transmission channel to diffuse technology. Hence, it induces catching-up to the production frontier, but not necessarily shifts of it.

It is worth noting that our results show that efficiency and technology are correlated with human capital and they might suffer from endogeneity caused by reserve causality. The difficulty of establishing a causal link between human capital and productivity is still an open issue in empirical studies (Delgado et al., 2014, Peri, 2012). However, as long as endogeneity is caused by omitted variables this is of minimal concern as differences in unobservables are absorbed by our estimated unobserved factor.

6 Conclusion

The recent economic slowdown first in USA during late nineties and then in Europe in 2001 leads the economists to question the recipe for endogenous self-sustained economic growth. Economic growth literature emphasizes the importance of human capital in spurring productivity growth. Moreover, the productivity analysis recognizes the importance of considering the spillover effects of global shocks and business cycles due to increasing globalization and interconnection among countries.

So far all studies analyzing effect of human capital on productivity of countries have produced ambiguous empirical results due to endogeneity and latent heterogeneity. Many empirical studies have been on the stream of parametric modelling which suffers of misspecification problems when the data generating process is unknown, as usual in the applied studies.

In order to avoid the pitfalls of these parametric cross-regression studies we propose an alternative empirical methodology, robust frontier in non parametric location-scale models for accommodating simultaneously the problem of model specification uncertainty, potential endogeneity and cross-section dependence in modelling technical efficiency in frontier models.

The neglect of a latent factor, or unobserved global factors or an observed one will cause an endogeneity problem ((Simar et al., 2016)). By adapting to panel data we combine two different methodology, the two-step procedure advanced by Florens et al. (2014), which enables us to deal with both observed heterogeneity and cross section dependence by combining location scale model and conditional efficiency estimation and Simar et al. (2016) which handles the endogeneity due to latent heterogeneity.

Our non parametric approach to estimate conditional efficiency does not require any parametric assumption regarding technology or efficiency term. Moreover, the assumption of complete homogeneity of considered units is not needed. Therefore the economic units under investigation, can potentially consist of different groups of population governed by different distributional laws of the generation of input-output mix and on efficiency. This is an advantage in our sample formed by developed and developing countries which most likely have different distributions of efficiency scores.

Moreover our frontier model enables us to see whether the effect of environmental/global variables on productivity occurs via technology change or efficiency. We can then quantify the impact of environmental/global factors on efficiency levels and make inferences about the contributions of these variables in affecting efficiency.

The “new” growth theory of Romer (1990a), Lucas (1988) and Barro (1997) has human capital playing an important role in growth because human capital can help in explaining an economy’s capacity to absorb new technologies ((Abromovitz, 1986, Cohen and Levinthal, 1989, Kneller, 2005, Kneller and Stevens, 2006, Mastromarco and Ghosh, 2009)). Our paper extends previous studies on similar topics by investigating this channel in full nonparametric framework which avoids some restrictive and often unverifiable prior assumptions on functional relationships and distributions.

We focus on the effect of human capital on economic performance of 40 countries over the period 1970–2007. In a cross-country framework, production inefficiencies can be identified as the distance of the individual country’s production from the frontier as proxied by the maximum output of the reference country (regarded as an empirical counterpart of an optimal production boundary). Hence, efficiency improvement will represent productivity catch-up via technology diffusion because inefficiencies generally reflect a sluggish adoption of new technologies (Ahn and Sickles, 2000).

We show that our estimated latent factor is positively and significantly correlated with policy indicators denoting good governance which provides better property rights system and creates incentives to innovate.

Furthermore, our findings prove that ‘absorptive capability’ plays an important role in accelerating the technological catch-up (increase in the efficiency) but not on the technological changes (shifts in the frontier). This result seems to confirm the theoretical hypothesis that countries benefit from new technology (technological catch-up) only when they have the ability to exploit it, hence only when they have high level of absorptive capability. Countries can switch to a better technology if they accumulate the technology-specific expertize (Greenwood and Jovanovic, 2001, Helpman and Rangel, 1999).