Abstract
This paper examines the scale and scope economies of higher education institutions in Japan assuming the presence of productive inefficiency. The standard approach to testing the scope economies is to apply the cost function. However, the cost function approach often entails the difficulty of obtaining reliable data on input prices, especially the input prices of capital for higher education institutions. This paper proposes a duality approach based on the input distance function. The scope economies are tested under a necessary and sufficient condition by retrieving the costs of joint and separate production from the input distance function. We apply the testing procedure to data pertaining to 218 Japanese private universities in 1999 and 2004. The results indicate the scale economies and the scope diseconomies.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
This paper examines the scale and scope economies of higher education institutions in Japan assuming the presence of productive inefficiency. For this purpose, we propose a duality approach that enables us to locally retrieve the cost function from the input distance function. A higher education institution is a multi-product organization that is generally subject to public regulation and unmotivated by profit maximization. With weak market competition, managerial inefficiency is likely to cause the observed pair of inputs and outputs to deviate from the production frontier. Because the scale and scope economies are defined on the production frontier, an analytical model is needed to filter the inefficiency out of the observations so that the production frontier or its dual cost frontier can be identified. Consequently, the stochastic cost frontier model is a straightforward technique to accomplish this goal.
However, this model may not be appropriate for higher education institutions because input price data, especially the input price of capital, are difficult to obtain. The widely employed user’s cost of capital is an irrelevant indicator of the input price of capital because a higher education institution does not invest in capital according to profit-maximizing criteria. Thus, this paper estimates an input distance function for analyzing the cost structure of Japanese private universities without requiring input prices. The degrees of ray economies of scale, product-specific economies of scale, global economies of scope, and product-specific economies of scope are measured for university production in education and research outputs.
The duality relationships between the input distance function and the cost function are presented in Hajargasht et al. (2006). Utilizing these relationships, Hajargasht et al. (2008) proposed to examine the sign of the second-order cross derivatives of the cost function with respect to the outputs recovered from the input distance function. If the sign is negative, the production technology exhibits cost complementarity, a sufficient condition for the scope economies. Compared to the Hajargasht et al. (2008) approach, this paper presents a more direct test for scope economies. Rather than focusing on the second-order derivatives, we recover the cost function value at a relevant point from the input distance function. It is then possible to evaluate the costs of both joint and separate productions so that the scope economies are testable under a necessary and sufficient condition. Furthermore, because the average incremental costs are measurable in a similar way, our procedure provides a test for the product-specific scope economies.
Another advantage of the input distance function approach is that it explicitly treats non-cost minimizing behavior; the reciprocal of the input distance function serves as a technical efficiency measure. However, it is not well known whether both technical inefficiency and allocative inefficiency can be addressed with the input distance function. As shown in this paper, by evaluating the input distance function at the shadow prices of inputs, the scope economies can be tested even if allocative inefficiency exists. This ability is a notable advantage of the input distance function approach over the cost function approach assuming cost minimization.
By definition, the cost function determines the minimum costs to produce a certain amount of outputs for given input prices. Thus, the cost function will not allow non-cost minimization if the domain of input prices over which the cost function is defined is restricted to within actual prices. To allow productive inefficiency, the cost function must be evaluated at virtual input prices. The duality approach can be used to do this by retrieving the cost evaluated at the shadow prices (marginal products) of inputs from the input distance function. In this sense, production is inefficient as long as the shadow prices do not coincide with the actual prices. Our paper is structured based on these assertions.
The studies on empirical economics in higher education reveal many examinations of scale and scope economies: Cohn et al. (1989), de Groot et al. (1991, Dundar and Lewis (1995), Koshal and Koshal (1999) and Koshal et al. (2001) for the US universities; Lloyd et al. (1993) and Worthington and Higgs (2011) for the Australian universities; Izadi et al. (2002), Stevens (2005), Johnes and Johnes (2009) and Thanassaoulis et al. (2011) for the UK universities; Johnes and Salas-Velasco (2007) for the Spanish universities; Lewis and Dundar (1995) for the Turkish universities, Fu et al. (2008) for the Taiwanese universities; and Hau et al. (2009) for the Chinese universities. For Japanese universities, Hashimoto and Cohn (1997) analyzed private universities and detected both scale and scope economies.
From a methodological perspective, all of the previous studies applied the cost function. Izadi et al. (2002), Johnes and Salas-Velasco (2007), Fu et al. (2008) and Johnes and Johnes (2009) allowed for non-cost minimizing behavior by employing the stochastic cost frontier model. All of these studies except Stevens (2005) and Fu et al. (2008) assume the constancy of the input prices over the observations to estimate the cost functions without the input prices. Stevens partially captures variations in the input prices by introducing the average staff cost into the cost function, but capital cost remains uncontrolled. Fu et al. (2008) controls the effects of the input prices on costs by implicitly calculating the input price of capital as residuals from the total costs given the prices of other inputs and the quantity of all inputs. While this method potentially circumvents the limitation of data availability, the calculated input price of capital is heavily influenced by the measurement errors in costs.
The input distance function approach proposed in this paper provides a direct testing procedure for scale and scope economies in the presence of inefficiency without requiring data on the input prices. We apply this procedure to Japanese private universities in 1999 and 2004. The cost structure of the universities has received increasing attention in Japan in relation to the managerial aspects of universities facing rapid declines in the under-20 population.
The rest of the paper is organized as follows. Section 2 provides an overview of the background of the empirical study of Japanese private universities. Section 3 presents an analytical model of the input distance function along with details concerning the duality approach. Section 4 explains the empirical model and dataset. Section 5 presents the empirical results on scale and scope economies as well as measurements of technical efficiency. Section 6 concludes the paper and makes recommendations for future research.
2 Background of the empirical study
Higher education institutions in Japan are confronted with the serious managerial problem of a rapid decline in the college-age population. As seen in Fig. 1, the number of 18-year-olds in Japan was 1.22 million in 2010, compared with 2.03 million in 1990, a 34 % decrease. On the other hand, this decrease is partially mitigated by a shift toward higher education demands. Figure 2 shows the number of students enrolled in public and private universities from 1990 to 2010. Enrollment at all universities increased from 2.13 million in 1990 to 2.89 million in 2010. Private universities accounted for about three-fourths of students, and this remained stable throughout the period. A total of 1.55 million students attended private universities in 1990, and 2.12 million students attended in 2010.
However, a substantial increase in the supply of higher education far outweighs the rising rate of student enrollment. Figure 3 shows the number of public and private universities from 1990 to 2010. The number of universities increased from 507 in 1990 to 778 in 2010. Although the number of national universities decreased from 96 to 86, the increase in the number of private universities and local public universities was so large that the share of private universities rose to 76.7 % in 2010 from 73.4 % in 1990. During this period, many private junior and community colleges were reformed and upgraded to universities. This structural change is due to a relaxation of regulations for university establishment standards by the Ministry of Education, Culture, Sports, Science, and Technology (henceforth MEXT) in 1991. Consequently, the excess supply of higher education makes the managerial environment surrounding private universities very competitive. The Promotion and Mutual Aid Corporation for Private Schools of Japan reports that 42.3 % of private universities failed to enroll the planned number of students in 2009; in the same year, almost 40 % of private universities generated budget deficits. Universities with smaller enrollments tend to be financially poorer than large universities. For universities with fewer than 3,000 students, revenue, even including subsidies from MEXT, is generally less than expenditures for universities, whereas for universities with more than 8,000 students revenue exceeds expenditures by 7 % on average. In Japan, MEXT regulates the establishment and operation of private and public universities. The managerial aspects of higher education are among the most important concerns for MEXT and university administrators. From a public policy perspective, the demand-supply imbalance of higher education may cause a considerable misallocation of social resources, although competitive pressure may enhance productivity. It is not surprising that university mergers have been considered as cost-saving instruments that could ease managerial difficulties. Therefore, scale and scope economies are now a crucial issue in Japanese higher education.
3 Methodology
3.1 Input distance function
Let \(x=(x_1,x_2, \ldots ,x_m)'\) and \(y=(y_1,y_2, \ldots ,y_n)'\) be an m × 1 input vector and an n × 1 output vector, respectively. The input distance function is defined as
where \(\Upgamma(y)\) is the input requirement set: \(\Upgamma(y)=\left\{ x\,\left|\,x\, can\, produce\, y\, \right.\right\}.\) Assume that \(\Upgamma(y)\) satisfies the regularity conditions including closedness, convexity, and monotonicity. Then, the input distance function is characterized by the properties that D I (x, y) is Footnote 1
-
(i)
Nondecreasing in x,
-
(ii)
Nonincreasing in y,
-
(iii)
Concave in x.
-
(iv)
Linearly homogeneous in x.
Furthermore, the input distance function by definition is
-
(iv)
Linearly homogeneous in x.
By definition, D I (x,y) ≥ 1 holds for the technologically feasible (x, y) and D I (x,y) = 1 if (x, y) is technically efficient. We approximate Eq. (1) by a second-order polynomial of logarithmic inputs and Box–Cox transformed outputs as:
where a ij = a ji for \(i,j=1,2, \ldots, m\) and b rs = b sr for \(r,s=1,2, \ldots, n.\) In the fourth line of Eq. (2), the dummy variables D k are appended to capture the effects of differences in the academic organization of a university. Details on dummy variables are explained in Sect. 4 The Box–Cox transformation is then defined as
where γ is the parameter to be estimated.
The terms associated with inputs and the left-hand-side of Eq. (2) are logarithmically transformed to make the input distance function linearly homogeneous in x by imposing parameter restrictions on Eq. (2):
The terms associated with outputs are taken by the Box–Cox transformation to allow for substituting zero for the outputs in testing the scope economies.
The concavity condition in inputs is globally imposed by the method based on the Cholesky factorization of the Hessian matrix. Footnote 2 In particular, the following restrictions are imposed on Eq. (2):
where λ ij = λ ji for \(i,j=1,2,\ldots, m\) and λ ii = 1 for \(i=1,2,\ldots, m.\) The input distance function is reparametrized with λ ij and δ i . The monotonicity conditions in inputs and outputs, (i) and (ii), are locally imposed at the means by the parameter restrictions: Footnote 3
To test scope economies, zero values are substituted for the outputs. The monotonicity condition in outputs (ii) is thereby imposed at points such as \(y_r=0, \, y_s=1, \, r\neq s, \, r=1,2,\ldots,n\). Footnote 4 The following parameter restrictions are formally imposed on Eq. (2):
Normally, the input-oriented technical efficiency is defined by the reciprocal of the input distance function. Letting \(\exp (-u)\) represent technical efficiency for u > 0, one can write
where the superscript or subscript “h” indicates the hth observation. From the linear homogeneity in inputs, Eq. (8) can be normalized as \(\ln|x^h|=-\ln D_I(x^h/|x^h|,y^h)+u_h,\) where |x h| is the Euclidean norm of x h. Substituting Eq. (2) into \(\ln D_I(x^h/|x^h|,y^h)\) after appending an approximation error v h to the right-hand-side of Eq. (2), and transforming x h/|x h| to the polar representation form, we obtain
where \(z_i(\theta)=\sin\theta_i \prod\nolimits_{l=0}^{i-1}\cos\theta_l,\) \(i=1,2,\ldots,m\) where \(\theta^h=(\theta_1^h, \theta_2^h, \ldots, \theta_{m-1}^h),\) \(0<\theta_1^h,\theta_2^h,\ldots,\theta_{m-1}^h<\pi/2,\) and θ h0 = 0, θ h m = π/2.
We employ standard assumptions of the stochastic frontier model on u h and v h , i.e., u h ∼ |N(0, σ 2 u )| and v h ∼ N(0, σ 2ν ). Based on Eq. (9), the likelihood function is formed by the further assumptions that u f , u h , v r , and v s for r ≠ s are independent of each other and that u h and v h are independent of y h and \(\theta_i^h, i=1,2,\ldots,m,\) for all observations.
3.2 Technical efficiency
Once the input distance function is estimated, its parameters can be used to measure technical efficiency. As an estimate of technical efficiency for the hth observation, the conditional expectation estimate of \(\exp (-u_h)\) proposed by Battesse and Coelli (1988) is employed. Formally, we estimate
where \(\epsilon_h = \ln D_I(x^h, y^h)\) and \(\sigma_* = \sigma_{\nu} \sigma_u / \sqrt{\sigma_{\nu}^2 + \sigma_u^2}.\) Eq. (10) is evaluated at the estimates of σ ν, σ u , x h, and y h.
3.3 Scale economies
The degree of ray scale economies is measured by a proportionate change in outputs on the frontier induced by a proportionate change in inputs. In terms of the input distance function, this is formally defined by \(d\ln \mu/ d\ln \lambda|_{\lambda=\mu=1},\) where D I (λ x, μ y) = 1. Denoting the degree of ray scale economies by R SCALE and taking the total derivative of the input distance function yields Footnote 5
Scale economies are deemed to be present if R SCALE ≥ 1, while diseconomies are present if R SCALE < 1. Assuming C(p, y) to be the cost function and p to be an input price vector, we can straightforwardly verify that R SCALE is equivalent to the reciprocal of the scale elasticity, \((\sum \partial \ln C(p,y)/ \partial \ln y_r)^{-1}\). Footnote 6
The degree of the product-specific scale economies is measured by the ratio of the average increment cost to the marginal cost. The average increment cost of y r is the additional unit cost resulting from the increasing production of the pth output from zero to y r , while the amount of other outputs is kept constant at y s for s ≠ r. Specifically,
where \(y_{\{n-r\}} = (y_1,\ldots, 0, \ldots, y_n)\) is a vector replacing the rth element of y with a zero. To obtain AIC r from the input distance function, the following proposition is useful.
Proposition 1
If the input requirement set is closed and convex for any x ≥ 0 and y ≥ 0, there exists p * ≥ 0 such that
If the input distance function is differentiable, p* is given by the relationship
The derivation for Eq. (14) is illustrated in Färe and Primont (1995, p. 55). It is easily seen that Eq. (13) results directly from Eq. (14) because of the linear homogeneity of the input distance function. The proof of Eq. (13) without assuming differentiability is presented in Färe and Primont (1995, p. 48). We present another proof of Eq. (13) in the Appendix.
To measure the average incremental cost, we need to find x * such that \( C(p^{*}, y_{ \{ n-r \} }) = p^{*\prime}x^{*}/D(x^{*}, y_{ \{ n-r \} })\). The average incremental cost is then obtainable from the input distance function as \( p^{*\prime} \{ D^{-1} (p^{*}, y)x - D^{-1} (p^{*}, y_{ \{ n-r \} })x^{*} \} / y_{r} \) using Eq. (13). However, as subsequently shown, x * = x follows if the input distance function is multiplicatively separable in inputs and outputs; that is, the input distance function takes the form of D(x, y) = d(x)/g(y), where d(x) and g(y) are nondecreasing functions of x and y, respectively. This property of the input distance function is referred to as the input homotheticity.Footnote 7 As can be seen, the present input distance function Eq. (2) is input homothetic if \(\sum\nolimits_{r=1}^{n}c_{ir}=0,\) for all i and r.
Under the input homothetic technology, it follows from Eq. (14) that
Solving Eq. (15) for x yields x *. However, because Eq. (15) is independent of y, x * is invariant over the outputs. As a consequence, the input distance function can always be evaluated at the observed x to measure the cost for producing any output vector. Eventually, the degree of the product-specific scale economies defined by the ratio of AIC r to the corresponding marginal cost becomes
after some manipulation if the production technology exhibits the input homotheticity. The product-specific scale economies are indicated by P r SCALE > 1, while the diseconomies are indicated by P r SCALE < 1.
3.4 Scope economies
Scope economies are benefits that arise from joint production in multi-product technology. If joint production is less expensive than separate production, scope economies exist. To test this, let \(y_{\{r\}}=(0,\ldots,y_r,\ldots,0)\) be an output vector solely producing the rth output y r . The global scope economies exist at y if and only if
Given input homotheticity, Eq. (13) is applied to examine whether this inequality holds on the basis of the input distance function. The degree of the global scope economies, G SCOPE , is defined as:
Global scope economies are deemed to exist if G SCOPE > 0, while global scope diseconomies exist if G SCOPE < 0.
As is well known, cost complementarity provides a sufficient condition for global scope economies. The cost function is cost complementary at y r if
which is sufficient for global scope economies. The derivatives of the cost function can be recovered from the input distance function by the duality relationship derived in Hajargasht et al. (2006) as
We apply Eq. (20) to examine the cost complementarity as an alternative test of the global scope economies to a more direct test based on Eq. (18).
Product-specific scope economies are the economies that arise from the cost reduction caused by the joint production of a specific output with other outputs. The product-specific scope economies for the rth output exist if and only if
Similar to the construction of G SCOPE , the degree of product-specific scope economies based on the input distance function, P r SCOPE , is obtained from Eq. (13) as
Product-specific scope economies exist if P r SCOPE > 0, while the diseconomies exist if P r SCOPE < 0.
4 Empirical model and data
We assume that private universities employ three inputs—faculty, nonfaculty staff, and capital—in order to produce the outputs of education and research. Following the previous studies of higher education in Japan, we assume that private universities produce three outputs: undergraduates, graduates, and research. The three inputs are measured by the number of faculty and nonfaculty staff as well as by the tangible fixed assets as a proxy for capital stock.
Nonfaculty staff are measured in terms of full-time-equivalent (FTE) positions; part-time staff are counted as half of an FTE. The number of faculty are also counted in terms of FTE, where a part-time faculty member is counted as a fraction of an FTE based on the average ratio of classes taught by the parttime faculty members. Moreover, a physical measure is considered superior as a proxy for capital over tangible fixed assets in historical costs. However, a physical measure of capital stock, such as floor space or site area, fails to capture the effects of equipment and library collections on research and education. The tangible fixed assets can provide a better approximation of capital inputs covering land, building, equipment, and other physical resources of a university.
The education output is measured by the number of enrolled students. We divided the education output into two distinct outputs: that of undergraduate programs and that of graduate programs, measured by the numbers of enrolled undergraduate and graduate students, respectively. Research output is measured by the number of research grant awards, as a proxy.
In the literature, most studies choose the value of research grants, rather than the number of them, as a research output. An output is sometimes measured by its production cost when the market value is unavailable. The value of research grants has been widely accepted as a research output reflecting the costs of conducting research projects. Such a choice is rational in the context of the cost function approach, in which the total cost is a monotonic increasing function of outputs given input prices. However, this is not necessarily true in the estimation of the production function or distance function. In the input–output space, the reverse causality may be compounded by the use of the research grants as an output, because research grants are used to pay for hiring faculty and nonfaculty staff members as well as to purchase equipment. The reverse causality not only causes biased estimates but also raises an identifiability problem of inputs and outputs. In fact, the estimated input distance function with our data set fails to satisfy the monotonic decreasingness of research output if it is measured by the value of research grants, despite the imposed local monotonicity condition. Thus, we employ the number of research grants, instead of their value, as a research output.
Another problem in measuring research output is how quality aspects of research are considered. In the literature, several indicators are used to control for the quality of research output, including the number of publications, the number of citations, the number of patents, and patent fee income. Unfortunately, those indicators are not available in the present analysis. In our data set, almost 70 % of the research grants are provided by the Japanese Society for the Promotion of Science (JSPS), an independent agency of the Japanese government. Footnote 8 The JSPS is the largest research funding source in Japan and covers all fields of the natural and social sciences and the humanities. A peer-review screening process is conducted to select grant recipients, and the award rate is not more than 25 %. Final and intermediate research reports are obligatory and publically accessible via the JSPS website. Those features imply that research projects receiving funding from the JSPS can be regarded as qualified enough to produce some research output. The other 30 % of the research grants come from science foundations funded by the private sector and directly from private companies. Although it is unclear whether all grants meet standards comparable to those of the JSPS, a widely utilized competitive screening process, similar to that used by the JSPS, is expected to rule out inferior research projects. As a consequence, the number of research grants can be an acceptable proxy for research output. In addition, research output counts not only the number of newly awarded projects but also continuing projects awarded in the past, implying that the research output includes works in progress. We assume that research projects proceed gradually and that knowledge is produced through the project periods. The final report of a project is not the only output of research.
Further, some previous papers, such as Koshal and Koshal (1999), emphasize the importance of controlling for differences in student quality. For Japanese universities, scores on the national center tests for university admission for entering freshmen are possible indicators of student quality. Unfortunately, these scores are inapplicable to our data set in which an individual university is anonymous and thus unidentifiable. We thereby cannot adjust for student quality among universities.
On the other hand, we can reasonably assume that the number of enrollments well approximates the number of students completing their education. Most undergraduates in Japan complete their degree in the standard four years, and only a few students drop out. Although the completion rate is not available in our data set, another survey conducted by Yomiuri Shimbun, the largest newspaper publisher in Japan, reported on graduation rates at 98 universities from 128 in a cross-section sample taken in 2004. The average graduation rate at those 98 universities was 91.1 %. At 90 out of 98 of these institutions, the completion rate was not lower than 85 % and the lowest rate was 78 % indicating that most university students in Japan successfully graduate.
Further, the ratio of undergraduates exceeding the standard length of study in total enrollment was not more than 4 % in 2007 (Statistical Abstract 2008, MEXT). Thus, undergraduate students have rather uniform graduation rates, indicating that the number of enrollments provides a good proxy for the output of undergraduate education. Similar uniformity is observed among graduate students. The completion rates for master’s programs in the standard length of study ranged from 0.93 to 0.95 for 20 cohorts of new entrants during the period 1989–2008, and the rates for doctoral programs ranged from 0.83 to 0.93 (Statistical Abstract 2011, MEXT). Footnote 9 Although the performance of doctoral programs is relatively unstable, the number of students enrolled in master’s programs has been four to five times larger than the number enrolled in doctoral programs. As a whole, the intensity of work in graduate programs is considered uniform among students. It is thus reasonable to assume that the number of graduate students also well approximates the output of graduate education.
All data were taken from the White Paper on Private Colleges and Universities of Japan published by the National Association of Faculties of Private Colleges and Universities for Affairs Concerning Government Subsidies. This comprehensive survey of private higher education institutions in Japan has been issued almost every four years since 1976. This paper uses the 7th and 8th surveys from 1999 and 2004. The White Paper on Private Colleges and Universities of Japan reports the survey results for 135 universities in 1999 and 128 in 2004. To detect outliers, we apply the following three criteria: there exist neither graduate nor undergraduate students; there exist neither faculty nor nonfaculty staff; there exist no tangible fixed assets. Any observation that meets any of those criteria is considered an outlier and is removed from the data set.
The resulting data set comprises 110 universities from 1999 and 108 universities from 2004. Unfortunately, we could not compile a panel because the surveys were anonymous. The input distance function is then estimated by pooling these 218 universities. However, pooling cross-section data may induce a non-iid structure, thus biasing the maximum likelihood estimates. Footnote 10 We also use a single cross-section to confirm the analytical results.
As illustrated in Fig. 4, all 218 universities provide undergraduate education. In addition, 165 universities provide graduate programs, and 193 universities generate research outputs. Approximately two-thirds of the universities in the sample, (i.e., 154 universities) jointly produce all three outputs, while 14 universities produce only the undergraduate education output.
To consider the diversity of the organization of a university, we introduced five dummy variables. The first dummy, D G , is defined as follows: D G = 1 if a university provides a graduate program and D G = 0 otherwise. The second to fifth dummies are defined by whether or not a university includes those schools categorized as natural sciences and engineering, D S ; social sciences and humanities, D L ; medical and health sciences, D M ; and arts, music, and other fields, D O . Footnote 11
If a university includes the corresponding schools, then D k = 1; otherwise, D k = 0, for k = S, L, M, O. By definition, the coefficient of each subject dummy captures additional effects on the input distance induced by having the corresponding school as part of the university. Since those dummies are not linearly dependent, none of them are omitted from the estimation equation. We also added a dummy variable, D Y , taking unity for observations in 2004 and zero for observations in 1999.
Table 1 summarizes the descriptive statistics of the inputs and the outputs as well as the dummy variables. On average, a university has 192 faculty members and 168 nonfaculty staff to provide programs that enroll 4,939 undergraduate students and 198 graduate students. Because the mean is larger than the median for all inputs and outputs, their distributions are positively skewed with a relatively small number of large universities and a long tail of smaller universities. In particular, there are a few medical science universities that obtain an exceptionally large number of research grants. The majority of the private universities are education-oriented. Their programs are based more on humanities and social sciences than on natural sciences. Seventy percent of the total observations include schools of humanities and/or social sciences, while 30 % include schools of natural sciences. Universities with a medical school comprise half of those with schools of natural sciences. This composition is not surprising because private universities in Japan are differentiated from national universities, which act primarily as leading universities with advanced research facilities, especially in the natural sciences.
5 Empirical results
Using the data set discussed above, we estimate the input distance function by applying the maximum likelihood method. We omit interaction terms of inputs and outputs from Eq. (3) because the estimated coefficients of those terms were very unstable and it was sometimes hard to compute the standard errors. As a result, the input distance function becomes input homothetic.
Table 2 displays the estimated results of the input distance function with three outputs and three inputs. As seen, the parameter estimates are in general statistically significant. The variance of inefficiency is larger than that of the statistical noise, implying that ignorance of inefficiency leads to misspecification and biased estimates of scale and scope economies. The coefficients of the dummy variables indicate that the production frontier is higher if the university has a school of natural sciences than if it does not. Conversely, any school other than natural sciences lowers the production frontier. Regarding the time dummy, the frontier in 1999 was higher than that in 2004.
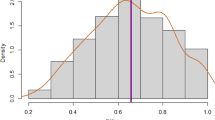
Figure 5 shows the distribution of measured technical efficiency in the histogram. Almost half of the technical efficiency ranges from 0.6 to 0.8. The lower quartile, median, and upper quartile of technical efficiency are 0.53, 0.67, and 0.77, respectively. For the median observation, the 95 % confidence interval is from 0.51 to 0.87, implying that 13–49 % of the total costs were potentially reducible by managerial efforts. Given the broad confidence interval, we conclude that the universities in the sample are rather uniform in efficiency. In particular, a university at the median is statistically no different in its efficiency from approximately 90 % of the entire set of observations.
Table 3 presents the measurement results of the scale economies for 12 selected universities that correspond to the quartiles of three outputs and to the Euclidean norm of the output vector. Footnote 12 In the first column, the measurements of R SCALE larger than unity indicate ray scale economies for all 12 universities; 10 of them were statistically significant in ray scale economies. Product-specific scale economies were present for the three outputs. Although there is no significant evidence for the product-specific scale diseconomies, smaller universities seem to exhibit constant returns to specific products. The most insignificant product-specific scale economies are found in the universities at the lower quartiles of output measures.
Table 4 presents the number of universities exhibiting the scale economies, the scale diseconomies, or the constant returns to scale with a 5 % significance level. Footnote 13 In addition to the measurement results from the full sample of 218 universities, the results based on the single cross-section data of 110 universities in 1999 are shown in parentheses. When estimating the input distance function with the sample of the cross-section in 2004 the numerical solution of the maximum likelihood problem is difficult to obtain, and thus the results from the cross-section in 2004 are omitted. In an overall view of the scale economies, the results show similar patterns between the samples. Ray scale economies and the product-specific scale economies prevail in Japanese private universities; Ray scale economies significantly exist in two-thirds of those universities. Similarly, two-thirds and more than two-thirds of the universities significantly exhibit product-specific scale economies in graduate education and research, respectively. Furthermore, product-specific scale economies in undergraduate education are evidenced for half of the universities.
Figures 6 and 7 plot the measures of the degree of ray scale economies, R SCALE , against the sizes of the outputs measured by the Euclidean norm of the output vector. The plotted R SCALE values are measured from the full sample in Fig. 6 and from the cross-section sample in 1999 in Fig. 7. Scale economies are evidently seen over the sizes of the outputs. Because the three outputs are centered on their means, the size of the outputs is 1.73 for a university that provides the mean level of outputs. While the degrees of scale economies range roughly from 1 to 1.5 for universities larger than the mean, stronger ray scale economies are observed in the smaller universities, especially in Fig. 6. Consequently, an increase in size is more beneficial for smaller universities.
Table 5 shows the measurement results of scope economies for the same 12 universities in Table 3. The global scope diseconomies are indicated for all 12 universities when the G SCOPE measurements are less than zero. The local scope diseconomies are also evidenced for the three outputs, except that the product-specific scope economies could exist in the research output for smaller universities. The product-specific scope economies for the research output are not surprising because it is unlikely that universities can afford research activity alone without education, especially in smaller universities.
Table 6 counts the number of universities for which measurements indicate significant scope economies, significant scope diseconomies, or neither. Footnote 14 The measured results from the full sample are compared to the results from the cross-section sample in 1999, presented in parentheses. The results for both samples suggest that the scope diseconomies are dominant over the scope economies in both the global and product-specific senses. In fact, no significant scope economies are indicated in Table 6 except for the research-specific scope economies.
In the first row, the global diseconomies are significant in 72 % of observations in the full sample and in 45 % of those in the cross-section sample in 1999. This result is very similar to the product-specific scope economies in undergraduate education. For the graduate-specific scope economies, the same ratio is slightly lower in the full sample and is higher in the cross-section sample in 1999. Unlike the above results, the results in the fourth row indicate significant research-specific scope economies. Almost 20 % of observations indicate significant research-specific scope economies, while approximately 45 % of the observations exhibit significant diseconomies. The differences between the samples are negligible for this result.
These results imply that segmentation of education and research is favorable from a cost perspective. Possibly related to this observation is that a majority of the private universities in Japan are undergraduate education-oriented universities, whereas national universities focus on research or graduate-level education. By implication, the undergraduate focus of private universities makes it costly to include a graduate school or advanced research institutes. On the other hand, significant evidence for the research-specific scope economies at 20 % of the sample suggests that some private universities participate in advanced research.
Figures 8 and 9 plot the measures of the degree of global scope economies, G SCOPE , against the Euclidean norm of the output vector. The plots in Figs. 8 and 9 are, respectively, measurements from the full sample and the cross-section sample in 1999. In these figures, some plots are above the horizontal axis, suggesting that some universities exhibit global scope economies besides statistical significance. Those universities are larger in size than the Euclidean norm of 10. Some large private universities in Japan are distinguishable by their comprehensiveness, in the sense that they have diversified schools at both the undergraduate and graduate levels and research-oriented faculty members. By implication, they potentially hold resources that could be efficiently exploited in the joint production of education and research, although the statistical evidence of global scope economies is currently unclear.
Examining cost complementarity using Eqs. (18) and (19), we obtain consistent but uninformative results. There are no observations for which all the cross cost derivatives are significantly negative, implying that global scope economies are not detected. Because the cost complementarity only provides a sufficient condition for the global scope economies, it is difficult to use this approach to further investigate whether global scope economies exist.
The findings of scale economies and scope diseconomies in this paper contrast with the results of a previous study of Japanese private universities by Hashimoto and Cohn (1997). They obtain evidence for the scale and scope economies by using the 1991 issue of the same survey data that we used (for 1999 and 2004). A possible reconciliation is obtained from the difference in when the data were collected. Because Hashimoto and Cohn use data before the deregulation of the university establishment standard in 1991, the universities in their sample were strictly restricted in their ability to exploit opportunities to benefit from scale and scope economies. On the other hand, our study is based on data obtained from 1999 and 2004, more than a decade after the deregulation. If the private universities had exhausted such opportunities in the 1990s, it is plausible that the scope diseconomies would be found in our study.
The discrepancy may also result from assumptions made in the analytical models. Hashimoto and Cohn use the quadratic cost function with an assumption of fully efficient production. In addition, they imperfectly control input prices. The capital cost is not included in the cost function because of the lack of reliable data. The input distance function approach taken in this paper is free from those limitations and robust for technical inefficiency and capital costs.
Scale economies of higher education have been widely detected by empirical studies outside Japan. Most of the previous studies, including Hau et al. (2009), Fu et al. (2008), Johnes and Salas-Velasco (2007), Izadi et al. (2002) and Koshal and Koshal (1999), reach a consensus on the existence of ray scale economies in higher education institutions. Footnote 15 Our results also agree with this consensus.
In contrast, the results on scope economies are mixed and more controversial. While Hau et al. (2009), Fu et al. (2008) and Koshal and Koshal (1999) evidence, respectively, the global scope economies for Chinese, Taiwanese, and US universities, Johnes and Johnes (2009), Izadi et al. (2002) and Johnes and Salas-Velasco (2007) show the global scope diseconomies for UK and Spanish universities. Our results favor the existence of scope diseconomies.
It is not easy to provide a consistent interpretation of these opposing results. One possibility is that some studies in the literature separate the outputs by subject area, whereas the present study employs the aggregate number of students as outputs. Among the previous studies above, Johnes and Johnes (2009), Johnes and Salas-Velasco (2007) and Izadi et al. (2002) disaggregate the number of undergraduate students into science and nonscience subjects. To examine the robustness of the scope diseconomies, we estimate the input distance function with four outputs: graduate education, research, and two disaggregated undergraduate outputs that are measured by the number of undergraduate students enrolled in natural-science-oriented programs and in the other programs, respectively. Natural-science-oriented programs here include engineering and medical sciences as well as natural sciences in a narrow sense. If the full sample is employed, the results indicate that 48 out of 154 universities exhibit significant global scope economies, in contrast to no significant scope economies in Table 6. Footnote 16 This casts some doubt on the robustness of the present analysis.
However, the estimated input distance function with the four outputs fails to satisfy the monotonicity conditions at the 69 % of the sample that is substantially higher than the corresponding rate of 32 % in the input distance function based on the three outputs. Footnote 17 Since disaggregating outputs in the translog form increase the number of parameters in a quadratic order, it becomes much more difficult for the input distance function to identify the production and cost structure of a university. Therefore, we do not proceed further with the four outputs in this paper. However, the possibility of different results on scope economies for a different mix of subject categories must be noted. Future studies are necessary to scrutinize the effects of the specification of outputs on scope economies using richer data; for example, a long panel data covering diverse higher education institutions.
6 Conclusions
This paper examines the scale and scope economies of private universities in Japan by estimating the stochastic frontier model of the input distance function. An advantage of this approach is that it avoids the use of unreliable data on input prices, unlike a cost function approach. The costs of joint and separate productions are retrievable from the duality relationship between the cost function and the input distance function, enabling us to directly test scope economies under the necessary and sufficient condition. The input distance function provides a further advantage in that it allows for technical inefficiency in production.
On the basis of the empirical results, we find that scale economies exist uniformly regardless of a university’s size, and that scope diseconomies exist even though very large universities may potentially have scope economies. As a consequence, a straightforward implication for the management of private universities is that they should first become larger by taking advantage of scale economies. However, because global scope economies do not exist, an increase in size should be accompanied by the concentration of outputs. In this regard, it is beneficial for universities with no product-specific scope economies to merge with each other so as to make larger and more specialized universities, especially in either undergraduate or graduate education. On the other hand, some universities exhibit research-specific scope economies. These universities can enhance cost efficiency by providing an education program with research activity, implying that a merger of those universities with education-oriented universities is also beneficial. Our results further suggest that the degree of global scope economies tends to increase with an increase in university size. Potentially, some large universities may become comprehensive universities, though the statistical significance of such growth is unclear.
It is, however, necessary to emphasize that the applicability of the previous implications is confined to private universities. In Japan, national universities differ from private universities in many aspects. Most national universities are comprehensive and are the leading universities in the region, suggesting they are more likely to have scale and scope economies than are private universities. The next step for the study is to investigate national universities and compare them with private universities.
Notes
Quasi-concavity in y may be added to the list of regularity conditions of the input distance function. However, unlike concavity in x, this condition is derived from the convexity of the producible output set and not from the convexity of the input requirement set unless the production technology exhibits constant returns to scale. An implicit fundamental assumption in this paper is the convexity of the input requirement set, while the convexity of the producible output set is not necessarily assumed. We thereby do not adopt a quasi-concavity condition in y in this estimation.
This method was first applied to the translog cost function by Jorgenson and Fraumeni (1981).
The inputs and outputs are centered on their means in the estimation. Thus Eq. (6) restricts the first derivatives of the input distance function at y = 1 and x = 1.
As noted in the previous footnote, y r = 1 indicates the mean values of y r .
Scale economies are defined along the frontier. The marginal cost is evaluated at D I (x/D I (x, y), y) and not D I (x, y).
More precisely, the JSPS’s share was 70.2 % in 1999 and 65.4 % in 2004.
Graduate study in Japan consists of 2-year master’s programs and 3-year doctoral programs.
The list of universities available in the White Paper on Colleges and Universities implies that at most 68 universities are observed twice in the full sample.
Here, natural science and technology cover the physical and mathematical sciences, biological and agricultural sciences, and all fields of engineering and technology. Medical and health sciences include nursing, pharmaceutical sciences, and veterinary medicine as well as medicine and health sciences. These definitions simply follow the standard classification of university schools in Japan. The rationale for such a classification can be provided from a cost perspective. A school of natural sciences and engineering requires costly experimental facilities, whereas a building containing faculty rooms, lecture halls, seminar rooms, and a library is almost sufficient for a school of social sciences and humanities. A school of medical and health sciences normally has one or more affiliated hospitals that have large budgets that are independent of university administration.
The full results on the degree of scale and scope economies for 218 universities are available from the authors on request.
If an output is zero, the input distance function is not differentiable with respect to the output. We thus omit universities when at least one of the three outputs is zero because the standard errors of the measures of scale economies cannot be obtained by the delta method.
Again, footnote 13 applies here.
The only exception is found in Johnes and Johnes (2009). They report scale diseconomies for UK universities by using a stochastic frontier model with random parameters.
We cannot find the maximum likelihood estimates if single cross section are used.
The curvature condition is ex ante imposed on the input distance function.
References
Balk BM (1998) Industrial price, quantity, and productivity indices. Kluwer, Dordrecht
Battesse G, Coelli T (1988) Prediction of firm-level technical efficiencies with a generalized frontier production function and panel data. J Econ 38:387–399
Cohn E, Rhine SLW, Santos MC (1989) Institutions of higher education as multi-product firms: economies of scale and scope. Rev Econ Stat 71:284–290
deGroot H, McMahon W, Volkin J (1991) The cost structure of American research universities. Rev Econ Stat 73:423–431
Dundar H, Lewis D (1995) Departmental productivity in American universities: economies of scale and scope. Econ Educ Rev 14:119–144
Färe R, Primont D (1995) Multi-output production and duality: theory and applications. Kluwer, Dordrecht
Fu T, Huang CJ, Tien F (2008) University cost structure in Taiwan. Contemp Econ Policy 26:651–662
Hajargasht G, Coelli T, Rao P (2006) A dual measure of economies of scope. Working paper series 03/2006. Center for efficiency and productivity analysis, University of Queensland
Hajargasht G, Coelli T, Rao DSP (2008) A dual measure of economies of scope. Econ Lett 100:185–188
Hashimoto K, Cohn E (1997) Economies of scale and scope in Japanese private universities. Educ Econ 5:107–115
Hau L, Li F, Min W (2009) Multi-product total cost functions for higher education: the case of Chinese research universities. Econ Educ Rev 28:505–511
Izadi H, Johnes G, Oskrochi R, Crouchley R (2002) Stochastic frontier estimation of a CES cost function: the case of higher education in Britain. Econ Educ Rev 21:63–71
Johnes G, Johnes J (2009) Higher education institutions’ costs and efficiency: taking the decomposition a further step. Econ Educ Rev 28:107–113
Johnes G, Salas-Velasco M (2007) The determinants of costs and efficiencies where producers are heterogeneous: the case of Spanish universities. Econ Bull 4:1–9
Jorgenson DW, Fraumeni BM (1981) Relative prices and technical change. In: Berndt ER, Field BC (eds) Modeling and measuring natural resources substitution, MIT Press, Cambridge, MA
Koshal RK, Koshal M (1999) Economies of scale and scope in higher education: a case of comprehensive universities. Econ Educ Rev 18:269–277
Koshal RK, Koshal M, Gupta A (2001) Multi-product total cost function for higher education: a case of bible colleges. Econ Educ Rev 20:297–303
Lewis D, Dundar H (1995) Economies of scale and scope in Turkish universities. Educ Econ 3:133–158
Lloyd P, Morgan M, Williams R (1993) Amalgamations of universities: are there economies of scale and scope?. Appl Econ 25:1081–1092
Shephard RW (1970) Theory of cost and production functions. Princeton University Press, Princeton
Stevens PA (2005) A stochastic frontier analysis of English and Welsh universities. Educ Econ 13:355–374
Thanassoulis E, Kortelainen M, Johnes G, Johnes J (2011) Costs and efficiency of higher education institutions in England: a DEA analysis. J Oper Res Soc 62:1282–1297
Worthington AC, Higgs H (2011) Economies of scale and scope in Australian higher education. High Educ 61:387–414
Author information
Authors and Affiliations
Corresponding author
Appendix: A proof of proposition 1
Appendix: A proof of proposition 1
Proof
Letting x * = x/D I (x, y) for any x ≥ 0, we have D I (x *, y) = 1, which implies that \((x^*,y)\in\partial \Upgamma(y)\) where \(\partial \Upgamma(y)\) is the boundary set of \(\Upgamma(y)\). Because \(\Upgamma(y)\) is closed and convex, it follows from the supporting hyperplane theorem that for any nonnegative \(x \in \Upgamma(y),\) there exists a normal direction p * ≥ 0 such that the supporting hyperplane of \(\Upgamma(y)\) with contact at x * can be written as
It is clear that C(p *, y) = p *′ x * is the cost function. Let p * be normalized to \(\hat{p}=p^*/C(p^*,y)\) then \(C(\hat{p},y)=\hat{p}'x^* = 1\) by construction. By the definition of x *, we have \(\hat{p}'x^* = p^{*'}x / \{ C(p^*,y)D(x,y) \}=1,\) which proves Proposition 1. \(\square\)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Nemoto, J., Furumatsu, N. Scale and scope economies of Japanese private universities revisited with an input distance function approach. J Prod Anal 41, 213–226 (2014). https://doi.org/10.1007/s11123-013-0378-3
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11123-013-0378-3