Abstract
The field of productive efficiency analysis is currently divided between two main paradigms: the deterministic, nonparametric Data Envelopment Analysis (DEA) and the parametric Stochastic Frontier Analysis (SFA). This paper examines an encompassing semiparametric frontier model that combines the DEA-type nonparametric frontier, which satisfies monotonicity and concavity, with the SFA-style stochastic homoskedastic composite error term. To estimate this model, a new two-stage method is proposed, referred to as Stochastic Non-smooth Envelopment of Data (StoNED). The first stage of the StoNED method applies convex nonparametric least squares (CNLS) to estimate the shape of the frontier without any assumptions about its functional form or smoothness. In the second stage, the conditional expectations of inefficiency are estimated based on the CNLS residuals, using the method of moments or pseudolikelihood techniques. Although in a cross-sectional setting distinguishing inefficiency from noise in general requires distributional assumptions, we also show how these can be relaxed in our approach if panel data are available. Performance of the StoNED method is examined using Monte Carlo simulations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The literature of productive efficiency analysis and frontier estimation is large and growing, consisting of several thousands of studies in the fields of applied economics, econometrics, operations research, and statistics (see e.g., Fried et al. 2008, for an up-to-date introduction and literature review). This field is currently dominated by two approaches: the nonparametric data envelopment analysis (DEA: Farrell 1957; Charnes et al. 1978) and the parametric stochastic frontier analysis (SFA: Aigner et al. 1977; Meeusen and van den Broeck 1977). The main appeal of DEA lies in its axiomatic, nonparametric treatment of the frontier, which does not assume a particular functional form but relies on the general regularity properties such as free disposability, convexity, and assumptions concerning the returns to scale. However, the conventional DEA attributes all deviations from the frontier to inefficiency, and ignores any stochastic noise in the data. The key advantage of SFA is its stochastic treatment of these deviations, which are decomposed into a non-negative inefficiency term and a random disturbance term that accounts for measurement errors and other random noise. However, SFA builds on the parametric regression techniques, which require an ex ante specification of the functional form. Since the economic theory rarely justifies a particular functional form, the flexible functional forms, such as the translog or generalized McFadden are frequently used. In contrast to DEA, the flexible functional forms often violate the monotonicity, concavity/convexity and homogeneity conditions. Further, imposing these conditions can sacrifice the flexibility (see e.g., Sauer 2006). In summary, it is generally accepted that the virtues of DEA lie in its general, nonparametric treatment of the frontier, while the virtues of SFA lie in its stochastic, probabilistic treatment of inefficiency and noise.
Bridging the gap between SFA and DEA has been recognized as one of the most important research objectives in this field, and contributions to this end have accumulated since the early 1990s. The emerging literature on semi/nonparametric stochastic frontier estimation has thus far mainly departed from the SFA side, replacing the parametric frontier function by a nonparametric specification that can be estimated by kernel regression or local maximum likelihood (ML) techniques. Fan et al. (1996) and Kneip and Simar (1996) were among the first to apply kernel regression to frontier estimation in the cross-sectional and panel data contexts, respectively. Fan et al. (1996) proposed a two-step method where the shape of the frontier is first estimated by kernel regression, and the conditional expected inefficiency is subsequently estimated based on the residuals, imposing the same distributional assumptions as in standard SFA. Kneip and Simar (1996) similarly use kernel regression for estimating the frontier, but they make use of panel data to avoid the distributional assumptions. Other semi/nonparametric panel data approaches include Park et al. (1998, 2003, 2006) and Henderson and Simar (2005), among others. Recently, Kumbhakar et al. (2007) proposed a more flexible SFA method based on local polynomial ML estimation. While the model is parametrized in a similar way to the standard SFA models, all model parameters are approximated by local polynomials. Simar and Zelenyuk (2008) have further extended the local polynomial ML method to multi-output technologies, building upon results by Hall and Simar (2002) and Simar (2007). Interestingly, Simar and Zelenyuk (2008) also apply DEA to the fitted values of the Kumbhakar et al. (2007) method in order to impose monotonicity and concavity.
Departing from the DEA side, Banker and Maindiratta (1992) were the first to consider ML estimation of the stochastic frontier model subject to the global free disposability and convexity axioms adopted from the DEA literature. While their theoretical model combines the essential features of the classic DEA and SFA models, solving the resulting ML problem has proved extremely difficult, if not impossible in practical applications. We are not aware of any reported empirical applications of the Banker and Maindiratta’s constrained ML method.
While the earlier semi/nonparametric developments come a long way in bridging the gap between DEA and SFA approaches, further elaboration of the interface between these two paradigms is clearly desirable. Since conventional DEA literature emphasizes the fundamental philosophical difference between DEA and the regression techniques (e.g., Cooper et al. 2004), the intimate links between DEA and regression analysis may not have attracted sufficient attention. In this respect, the recent studies Kuosmanen (2008) and Kuosmanen and Johnson (2010) have shown that DEA can be understood as a constrained special case of nonparametric least squares subject to shape constraints. More specifically, Kuosmanen and Johnson (2010) prove formally that the classic output-oriented DEA estimator can be computed in the single-output case by solving the convex nonparametric least squares (CNLS) problem (Hildreth 1954; Hanson and Pledger 1976; Groeneboom et al. 2001a,b; Kuosmanen 2008) subject to monotonicity and concavity constraints that characterize the frontier, and a sign constraint on the regression residuals. Thus, DEA can be naturally viewed as a nonparametric counterpart to the parametric programming approach of Aigner and Chu (1968). Building on this analogue, Kuosmanen and Johnson (2010) propose a nonparametric counterpart to the classic COLS method (Greene 1980), which has generally a higher discriminatory power than the conventional DEA in the deterministic setting. However, the deterministic frontier shifting method of Kuosmanen and Johnson (2010) is more sensitive to stochastic noise than the conventional DEA.
Departing from Kuosmanen and Johnson (2010), this paper introduces a stochastic noise term explicitly into the theoretical model to be estimated, and takes it into account in the estimation. In the spirit of Banker and Maindiratta (1992), we examine an encompassing semiparametric frontier model that includes the classic SFA and DEA models as its constrained special cases. More specifically, we assume that the observed data deviates from a nonparametric, DEA-style piecewise linear frontier production function due to a stochastic SFA-style composite error term, consisting of homoskedastic noise and inefficiency components. To estimate this theoretical model, we develop a new two-stage method, referred to as stochastic non-smooth envelopment of data (StoNED).Footnote 1 In line with Kuosmanen and Johnson (2010), we first estimate the shape of the frontier by applying the CNLS regression, which does not assume a priori any particular functional form for the regression function. CNLS identifies the function that best fits the data from the family of continuous, monotonic increasing, concave functions that can be non-differentiable. In the second stage, we estimate the variance parameters of the stochastic inefficiency and noise terms based on the skewness of the CNLS residuals. The noise term is assumed to be symmetric, so the skewness of the regression residuals is attributed to the inefficiency term. Given the parametric distributional assumptions of the inefficiency and the noise terms, we can estimate the variance parameters by using the method of moments (Aigner et al. 1977) or pseudolikelihood (Fan et al. 1996) techniques. The conditional expected value of the inefficiency term can obtained by using the results of Jondrow et al. (1982).
The proposed StoNED method differs from the parametric and semi/nonparametric SFA treatments in that we do not make any assumptions about the functional form or its smoothness, but build upon the global shape constraints (monotonicity, concavity). These shape constraints are equivalent to the free disposability and convexity axioms of DEA. Compared to DEA, the StoNED method differs in its probabilistic treatment of inefficiency and noise. Whereas the DEA frontier is typically spanned by a small number of influential observations, which makes it sensitive to outliers and noise, the StoNED method uses information contained in the entire sample of observations for estimating the frontier, and infers the expected value of inefficiency in a probabilistic fashion.
While this paper focuses on the cross-sectional model, we will also briefly suggest how the approach could be extended to the panel data setting. In that case, the time-invariant inefficiency components can be estimated in a fully nonparametric fashion by resorting the standard fixed effects treatment analogous to Schmidt and Sickles (1984). In the cross-sectional setting, imposing some distributional assumptions seems necessary, otherwise inefficiency cannot be distinguished from noise. However, the parametric distributional assumptions should not be taken as the main limitation. While the absolute levels of our frontier and the inefficiency estimates critically depend on the distributional assumptions, the shape of the estimated frontier and the relative rankings of the evaluated units are not affected by these assumptions. In contrast, the classic homoskedastic inefficiency term must be recognized as a more critical assumption. Indeed, even the shape of the frontier and the efficiency rankings tend to be biased if the homoskedasticity assumption is violated (see Sect. 4.5 for a more detailed discussion of this point). Dealing with heteroskedastic inefficiency is left as an interesting and important issue to be addressed in the future research.Footnote 2
The remainder of the paper is organized as follows. Section 2 introduces the semiparametric model of frontier production function that encompasses the classic DEA and SFA models as its special cases. Section 3 introduces the two-stage estimation strategy of the StoNED method: Sect. 3.2 elaborates the first stage consisting of nonparametric estimation of the production function by employing CNLS regression. Based on the CNLS residuals, we estimate the inefficiency and noise terms by means of method of moments and pseudolikelihood techniques, as described in Sect. 3.3. Section 4 discusses some useful extensions to the proposed approach. Section 5 examines how the proposed techniques perform in a controlled environment of Monte Carlo simulations. Finally, Sect. 6 makes concluding remarks. An illustrative example is presented in the “Appendix”. Further supplementary material such as graphical illustrations, example applications, and computational codes are available in the working papers Kuosmanen (2006), Kuosmanen and Kortelainen (2007), and the website: http://www.nomepre.net/stoned/.
2 Encompassing frontier model
This section introduces the theoretical model of frontier production functions to be estimated and the assumptions that will be maintained throughout the paper, except for Sect. 4.1 where a panel data model will be considered. Even in the cross-sectional setting we will later introduce more specific assumptions as they become necessary. To maintain direct contact with SFA, we describe the model for the single-output multiple input case. The m-dimensional input vector is denoted by \( {\mathbf x} \in \Re_{ + }^{m} \) and the scalar output by \( y \in \Re_{ + }^{{}} \). The production technology is represented by the frontier production function \( f:\Re_{ + }^{m} \to \Re_{ + }^{{}} \) that indicates the maximum output that can be produced with the given inputs. Following the classic DEA approach, we assume that function f belongs to the class of continuous, monotonic increasing and globally concave functions that can be nondifferentiable. In what follows, this class of functions will be denoted by F 2. In contrast to the traditional SFA literature, no specific functional form for f is assumed a priori; our specification of the production function proceeds along the nonparametric lines of the DEA literature.
The observed output y i of firm i may differ from f(x i ) due to inefficiency and noise. We follow the SFA literature and introduce a composite error term ε i = v i − u i , which consists of the inefficiency term u i > 0 and the random disturbance term v i , formally,
Terms u i and v i (i = 1,…,n) are assumed to be statistically independent of each other as well as of inputs x i . It will be assumed throughout the paper that the disturbance terms v i have a symmetric distribution with zero mean and a constant, finite variance \( \sigma_{v}^{2} \). The inefficiency terms u i have an asymmetric distribution with a positive expected value μ and a finite variance \( \sigma_{u}^{2} \). More specific distributional assumptions on u i and v i will be introduced as they become necessary (Sect. 3.3).
In model (1), the deterministic part (i.e., production function f) is defined analogous to DEA, while the stochastic part (i.e., composite error term \( \varepsilon_{i} \)) is defined similar to SFA. As a result, model (1) encompasses the classic SFA and DEA models as its constrained special cases. Specifically, if f is restricted to some specific functional form (instead of the class F 2), model (1) boils down to the classic SFA model by Aigner et al. (1977). On the other hand, if we impose the parameter restriction \( \sigma_{v}^{2} = 0 \), we obtain the single-output DEA model with an additive output-inefficiency, first considered by Afriat (1972) [see also Banker (1993)]. In this sense, the classic SFA and DEA models can both be seen as constrained special cases of the encompassing model (1).
Although the encompassing frontier model (1) described above is considerably more general than the classic DEA and SFA models, it does impose a number of assumptions that may be viewed as restrictive. From the perspective of DEA, assuming the single-output case is clearly restrictive. The multi-output technology could be modeled by using distance functions, but this is left as a topic for future research.Footnote 3 Further, the assumption of global concavity has been subject to debate, but we here restrict to the standard DEA specification.Footnote 4 From the econometric perspective, the additive structure of the composite error term and its components may be restrictive; a more standard multiplicative model will be examined in Sect. 4.3. Finally, assuming homoskedastic inefficiency and noise terms (i.e., \( \sigma_{v}^{2} \) and \( \sigma_{u}^{2} \) are constant across firms) can be very restrictive, as noted in the introduction. Extending the theoretical model to the heteroskedastic setting would be straightforward, but the methods developed in this paper assume the homoskedastic model. We will briefly discuss the possible consequences of the violations of this assumption in Sect. 4.5.
3 Stochastic non-smooth envelopment of data (StoNED) approach
3.1 Two-stage estimation strategy
It is not difficult to write a theoretical model like (1); developing an operational estimator proves more challenging. In this section we outline a new two-stage estimation strategy for estimating the encompassing model of the previous section, referred to as stochastic non-smooth envelopment of data (StoNED). Our objective is to estimate the deterministic part of the model in a nonparametric fashion imposing a minimal set of assumptions, in the spirit of DEA. We estimate the shape of the frontier by exploiting the standard axioms of DEA (i.e., monotonicity and concavity of f), free of any distributional assumptions or assumptions about the functional form of f or its smoothness. However, in the cross-sectional setting it is impossible to distinguish between inefficiency and noise without imposing some distributional assumptions (see Hall and Simar 2002, for a detailed analysis). Having estimated the shape of function f, we introduce parametric distributional assumptions adopted from the SFA literature to estimate the expected location of the frontier f, and the firm-specific conditional expected values for the inefficiency term. In summary, the StoNED method consists of two-stages:
-
Stage 1: Estimate the shape of function f by Convex Nonparametric Least Squares (CNLS) regression.
-
Stage 2: Imposing additional distributional assumptions, estimate the variance parameters \( \sigma_{u}^{2} ,\sigma_{v}^{2} \) based on the skewness of the CNLS residuals obtained in Stage 1, using the method of moments or pseudolikelihood techniques. Given estimates of parameters \( \sigma_{u}^{2} ,\sigma_{v}^{2} \), compute the conditional expected values of inefficiency.
We elaborate the implementation of Steps 1 and 2 in Sects. 3.2 and 3.3, respectively.
Our two-step estimation strategy parallels the modified OLS (MOLS) approach to estimating parametric SFA models, originating from Aigner et al. (1977).Footnote 5 Although SFA models are commonly estimated by maximum likelihood (ML) techniques, MOLS provides a consistent method for estimating the SFA model. While the ML estimators are known to be asymptotically efficient, provided that the distributional assumptions are correct, the MOLS estimators tend to be more robust to violations of the distributional assumptions about inefficiency terms u i and noise v i . Note that in MOLS the distributional assumptions about the composite error term do not influence the slope coefficients of f estimated in Step 1. We consider this relative robustness of MOLS with respect to ML as an attractive property, keeping in mind the present semiparametric setting. As mentioned in the introduction, Fan et al. (1996) have earlier explored a parallel two-stage approach in the context of kernel estimation.
3.2 Stage 1: CNLS estimation
The main obstacle in the least squares estimation of model (1) is that the expected value of the composite error term is negative due to the inefficiency term
Thus, the composite error term violates the Gauss-Markov assumptions. However, the Gauss-Markov properties can be restored by rephrasing the model as
where \( g({\mathbf x}) \equiv f({\mathbf x}) - \mu \) can be interpreted as an “average-practice” production function (in contrast to the “best-practice” frontier production function f), and \( \upsilon_{i} \equiv \varepsilon_{i} + \mu ,\quad i = 1, \ldots ,n \), is a modified composite error term. It is easy to verify that function g inherits the monotonicity and concavity properties of f since μ is a constant. Further, the modified errors \( \upsilon_{i} \) satisfy the Gauss-Markov conditions under the maintained assumptions of model (1). Thus, the average-practice production function g can be meaningfully estimated by nonparametric regression techniques.
The CNLS estimator for function g is obtained as the optimal solution to the problem
In words, the CNLS estimator of g is a monotonic increasing and concave function that minimizes the L 2-norm of the residuals. Note that the CNLS problem (4) does not restrict the functional form of g, but searches for the best-fit function from the family F 2, which includes an infinite number of functions. This makes problem (4) generally hard to solve.
In the univariate setting (m = 1), where input vector \( {\mathbf x} \in \Re_{ + }^{m} \) reduces to a scalar \( x \in \Re_{ + } \), the CNLS problem can be solved by sorting the data in ascending order according to the scalar-valued input (x 1 ≤ x 2 ≤ ⋯ ≤ x n ), and “parametrizing” problem (4) using the fitted values \( \hat{y}_{i} = \hat{g}({\mathbf x}_{i} ) \) as
Hanson and Pledger (1976) proposed this estimator, and proved its consistency. Groeneboom et al. (2001a, b) present a thorough and rigorous investigation of the statistical properties, showing that the fitted values \( \hat{y}_{i} \) converge to g(x i ) at rate n −2/5, and that the limit behavior of the estimator can be characterized by a canonical stochastic process that can be associated with the integrated Brownian motion. Other related work in statistics include Nemirovski et al. (1985), Mammen (1991), and Mammen and Thomas-Agnen (1999).
The univariate, single-input estimator is obviously too restrictive for the purposes of productive efficiency analysis. Earlier known computational algorithms for the CNLS estimator all relate to the univariate setting where the scalar-valued input data can be sorted to ensure g(x i ) ≥ g(x i−1). However, the input vector \( {\mathbf x} \in \Re_{ + }^{m} \) cannot be sorted prior to the estimation such that g(x i ) ≥ g(x i−1), i = 2,…,n. To resolve this challenge, Kuosmanen (2008) has shown that the infinite dimensional CNLS problem (4) has an equivalent finite dimensional representation, which can be stated as the following quadratic programming (QP) problem
The rationale of this formulation is the following. The first constraint of problem (6) can be interpreted as the regression equation. Note that coefficients α i , β i are specific to each observation i:i = 1,…,n, which reveals a technical similarity to the random parameters SFA models (e.g., Greene 2005). In the present setting, however, the coefficients α i , β i are not parameters of the estimated function g, but rather, they characterize tangent hyperplanes to the unknown function g at point x i . The inequality constraints in (6) can be interpreted as a system of Afriat inequalities (compare with Afriat 1967, 1972; and Varian 1984). When all inequalities of (6) are satisfied, we can employ the Afriat’s Theorem to show that there exist a continuous, monotonic increasing and concave function \( \hat{g} \) that satisfies \( y_{i} = \hat{g}({\mathbf x}_{i} ) + \upsilon_{i} \) for all i = 1,…,n. As Kuosmanen (2008) emphasizes, the Afriat inequalities are the key to modeling the concavity axiom in the general multiple regression setting where there is no unambiguous way of sorting input vectors x.
For estimating the shape of the production function, the coefficients (α i ,β i ) have a compelling economic interpretation: vector β i can be interpreted as the subgradient vector \( \nabla g({\mathbf x}_{i} ) \), and thus it represents the vector of marginal products of inputs at point x i . Thus, coefficients β i could be used for nonparametric estimation of substitution and scale elasticities. Note that equation \( y = \alpha_{i} + {\varvec{\upbeta^{\prime}}}_{i} {\mathbf{x}} \) can be interpreted as the tangent hyperplane to the estimated function g at point x i . Therefore, the coefficients of the QP problem (6) provide a local first-order Taylor series approximation to any arbitrary function g in the neighborhood of the observed points x i . In contrast to the flexible functional forms that can be interpreted as second-order Taylor approximations around a single, unknown expansion point, the CNLS estimator uses all n observations as expansion points for the local linear approximation.
The CNLS problems (4) and (6) are equivalent in the following sense (see Kuosmanen 2008, “Appendix”, for a formal proof).
Theorem 3.1
Denote the optimal solution to the infinite dimensional CNLS problem (4) by \( s_{CNLS}^{2} \) and the optimal solution to the finite quadratic programming problem (6) by \( s_{QP}^{2} \) . Then for any arbitrary data, \( s_{CNLS}^{2} = s_{QP}^{2} \) .
This result shows that the CNLS estimator can be computed in the general multivariate setting. Indeed, it is easy to verify that the univariate CNLS formulation (5) by Hanson and Pledger (1976) is obtained as a special case of (6) when m = 1. We would conjecture that the known statistical properties of the univariate CNLS estimator (consistency, rate of convergence) carry over to the multivariate setting, but this remains to be formally shown. Regarding the rates of convergence, Stone (1980, 1982) has established n −2d/(2d+m) as the optimal rate of convergence for any arbitrary nonparametric regression estimator, where d equals the degree of differentiability of the true but unknown g. We note that the rate of convergence established by Groeneboom et al. (2001a, b) for the univariate CNLS estimator falls below this optimal rate. Although the rate of convergence for the multivariate CNLS estimator remains unknown, Stone’s general result can be viewed as the theoretical upper bound that the CNLS estimator cannot exceed even under ideal conditions. This is a useful reminder that the CNLS estimator is subject to the “curse of dimensionality”, similar to the conventional DEA estimators (see, e.g., Simar and Wilson 2000, for discussion). In practice, this means that the sample size n needs to be large and the number of inputs m must be sufficiently small for any meaningful estimation. It might be possible to improve the rate of convergence by imposing further restrictions on the third and higher order partial derivatives of g, but it is unclear how the higher derivatives could be utilized in the CNLS estimator. Further, it would be interesting to link the non-smooth CNLS estimator to the kernel regression and other nonparametric smoothing techniques (see e.g., Mammen and Thomas-Agnen 1999; Yatchew 2003). On the other hand, the non-smooth CNLS estimator is closely related to the classic DEA estimator, which is an appealing property for the purposes of the present paper.
Consider for a moment the deterministic case where \( \sigma_{v}^{2} = 0 \). In this setting, all deviations from the frontier can be attributed to the inefficiency term u. Hence, we could impose an additional sign-constraint \( \upsilon_{i} \le 0 \, \forall i = 1, \ldots ,n \) for the composite error terms of the QP problem (6), analogous to the classic parametric programming (PP) approach of Aigner and Chu (1968). Interestingly, Kuosmanen and Johnson (2010) have formally shown that the resulting sign-constrained CNLS problem is in fact equivalent to the classic variable returns to scale DEA estimator: the output oriented DEA efficiency estimates are directly obtained from the CNLS residuals. In light of these results, the classic DEA can be interpreted as a sign-constrained variant of the CNLS problem (6). Further, the results of Kuosmanen and Johnson (2010) reveal DEA as a nonparametric counterpart to Aigner and Chu’s PP method.
Returning to the stochastic setting, we next elaborate the connection between CNLS and DEA further. Note that Kuosmanen and Johnson (2010) consider the CNLS estimator \( \hat{y}_{i} = \hat{\alpha }_{i} + {\hat{\varvec{\upbeta^{\prime}}}}_{i} {\mathbf{x}}_{i} \) only at the observed input levels x i , i = 1,…,n. It can be shown that the QP problem (6) always has a unique optimum, and that the fitted values \( \hat{y}_{i} \) are unique. However, estimating the function g at unobserved input levels x proves more complicated.
It is well known in the DEA literature that the input–output weights (shadow prices) of the multiplier-side DEA problem are generally not unique. The same is true for the CNLS estimator: the coefficients \( \hat{\alpha }_{i} ,{\hat{\varvec{\upbeta }}}_{i} \) obtained as the optimal solution to (6) need not be unique, even though the fitted values \( \hat{y}_{i} \) are unique for the observed x i , i = 1,…,n. In general, there are many ways to fit a monotonic and concave function through the finite number of points \( ({\mathbf{x}}_{i} ,\hat{y}_{i} ) \). As Kuosmanen (2008) notes, even the original CNLS problem (4) does not generally have a unique solution: there generally exists a family of alternate optima \( F_{2}^{ * } \).
To address the non-uniqueness issue, Kuosmanen (2008) has established the following lower and upper bounds for the alternate optima within \( F_{2}^{ * } \):
More specifically, Kuosmanen (2008, Theorem 4.1) shows that function \( \hat{g}_{\min } \) is the tightest possible lower bound for the family of functions \( F_{2}^{ * } \) (i.e., \( \hat{g}_{\min } ({\mathbf{x}}) = \mathop {\min }\limits_{f} f({\mathbf{x}}) \, s.t. \, f \in F_{2}^{ * } \)), and \( \hat{g}_{\max } \) is the tightest possible upper bound (i.e., \( \hat{g}_{\max } ({\mathbf{x}}) = \mathop {\max }\limits_{f} f({\mathbf{x}}) \, s.t. \, f \in F_{2}^{ * } \)). Recall that for the observed points x i , the fitted values are always unique: \( g({\mathbf{x}}_{i} ) = \hat{g}_{\min } ({\mathbf{x}}_{i} ) = \hat{g}_{\max } ({\mathbf{x}}_{i} ) \, \forall i = 1, \ldots ,n. \)
Interestingly, the lower bound function \( \hat{g}_{\min } \) can be interpreted as the variable returns to scale DEA frontier applied to the predictions \( ({\mathbf{x}}_{i} ,\hat{y}_{i} ) \) of the CNLS estimator. Applying the duality theory of linear programming, we can prove the followingFootnote 6:
Theorem 3.2
The lower bound function \( \hat{g}_{\min } \) characterized by (7) is equivalent to the variable returns to scale DEA frontier estimator applied to the data \( ({\mathbf{x}}_{i} ,\hat{y}_{i} ) \). Specifically, for any input vector \( {\mathbf{x}} \in \Re_{ + }^{m} \),
In line with the classic DEA, we can resolve the non-uniqueness of the CNLS estimator by resorting to the minimum function \( \hat{g}_{\min } \), which is always unique. Based on Theorems 3.1 and 3.2, we can give function \( \hat{g}_{\min } \) the following minimum extrapolation interpretation (compare with Afriat 1972, and Banker et al. 1984): function \( \hat{g}_{\min } \) is the minimum function that satisfies the axioms of free disposability and concavity and minimizes the sample variance of deviations \( (y_{i} - \hat{g}_{\min } ({\mathbf{x}}_{i} )) \). Recall that the classic DEA estimator has a similar minimum extrapolation property, with the exception that the DEA frontier envelopes all observed data, whereas \( \hat{g}_{\min } \) does not. In the deterministic setting, enveloping all observed data can be desirable. In the stochastic setting, replacing the envelopment axiom by some other axiom seems preferable. Minimization of the sample variance of deviations \( (y_{i} - \hat{g}_{\min } ({\mathbf{x}}_{i} )) \) seems a natural candidate for such an axiom.
Theorem 3.2 is also important for establishing a formal connection between CNLS and DEA estimators for the unobserved input levels x, complementing the results of Kuosmanen and Johnson (2010). Not only do the CNLS and DEA share the same axioms, the DEA estimator has a compelling regression interpretation as a sign-constrained variant of CNLS. On the other hand, to interpolate the fitted values of the CNLS regression, the classic DEA estimator provides the tightest lower bound for the family of functions that solve the problem (4).
Despite these compelling links and interpretations, we must recall that the piece-wise linear lower bound \( \hat{g}_{\min } ({\mathbf{x}}) \) does not estimate the frontier f(x) but the average-practice production function g(x). In the present setting, the shape of the average-practice function g(x) is exactly the same as that of the frontier f(x), because the expected inefficiency μ was assumed to be constant across all firms and thus g(x) = f(x) − μ. In the next section we show how the expected inefficiency μ and the unknown variance parameters \( \sigma_{u}^{2} ,\sigma_{v}^{2} \) can be estimated based on the skewness of the CNLS residuals.
3.3 Efficiency estimation
Given the CNLS residuals \( {\hat{\upsilon }} \equiv (\hat{\upsilon }_{1} , \ldots ,\hat{\upsilon }_{n} ) \), the next challenge is to disentangle inefficiency from noise. At this point, more specific distributional assumptions must be imposed.Footnote 7 We will follow the classic SFA study by Aigner et al. (1977) and assume the half-normal inefficiency term and a normally distributed noise term: \( u_{i} \mathop \sim \limits_{i.i.d} \left| {N(0,\sigma_{u}^{2} )} \right| \) and \( v_{i} \mathop \sim \limits_{i.i.d} N(0,\sigma_{v}^{2} ) \). Other distributions such as gamma or exponential are also used for the inefficiency term u i (e.g., Kumbhakar and Lovell 2000), but in this paper we restrict to the half-normal specification.
Since the noise term has a symmetric distribution, the negative skewness of the CNLS residuals signals that an asymmetric inefficiency term is present. Of course, the residuals might be skewed in a small sample just by coincidence; it would be advisable to test whether the negative skewness is statistically significant prior to estimation (see, e.g., Kuosmanen and Fosgerau 2009). If skewness is significant, there are at least two possible approaches for estimating the variance parameters \( \sigma_{u}^{2} ,\sigma_{v}^{2} \): the method of moments and pseudolikelihood estimation. We next briefly describe both these approaches and adapt them for our purposes.
3.3.1 Method of moments
Originating from the seminal paper by Aigner et al. (1977), the method of moments (MM) is commonly used in the MOLS estimation of SFA models (e.g., Greene 2008). Under the maintained assumptions of half-normal inefficiency and normal noise, the second and third central moments of the composite error distribution are given by
These can be estimated based on the distribution of the CNLS residuals as
Note that the third moment (which represents the skewness of the distribution) only depends on the standard deviation parameter σ u of the inefficiency distribution. Thus, given the estimated \( \hat{M}_{3} \) (which should be negative), we can estimate σ u parameter by
Subsequently, the standard deviation of the error term σ v is estimated using Eq. 10 as
These MM estimators are unbiased and consistent (Aigner et al. 1977; Greene 2008), but not necessarily as efficient as the maximum likelihood estimators.
3.3.2 Pseudolikelihood estimation
An alternative way to estimate the standard deviations σ u , σ v is to apply the pseudolikelihood (PSL) method suggested by Fan et al. (1996). Compared to the MM, PSL is potentially more efficient, but is computationally somewhat more demanding.
Like in the MM approach, our starting point is the CNLS residuals \( {\hat{\varvec{\upsilon }}} \equiv (\hat{\upsilon }_{1} , \ldots ,\hat{\upsilon }_{n} ) \). In the PSL approach we set parameters \( \sigma \equiv \sigma_{u} + \sigma_{v} \) and \( \lambda \equiv \sigma_{u} /\sigma_{v} \) to maximize the concentrated log-likelihood function. One of the main contributions of Fan et al. (1996) was to show that the log-likelihood can be expressed as a function of a single parameter (λ) as,
Note that \( \hat{\varepsilon }_{i} \) and \( \hat{\sigma } \) cannot be computed from the CNLS residuals as they depend on the unknown parameter λ. In practice, we maximize the log-likelihood function (16) by enumerating over λ values, using a simple grid search or more sophisticated search algorithms. After the pseudolikelihood estimate \( \hat{\lambda } \) that maximizes (16) is found, estimates for ε i and σ are obtained from (17) and (18). Subsequently, we obtain \( \hat{\sigma }_{u} = \hat{\sigma }\hat{\lambda }/(1 + \hat{\lambda }) \) and \( \hat{\sigma }_{v} = \hat{\sigma }/(1 + \hat{\lambda }) \). Fan et al. (1996) show that estimators \( \hat{\lambda } \) and \( \hat{\sigma } \) converge to the true λ and σ at the standard parametric rate \( n^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} \).
3.3.3 Estimation of the inefficiency term
Given a consistent estimator \( \hat{\sigma }_{u}^{{}} \) (obtained by either MM or PSL), the frontier production function f can be consistently estimated as \( \hat{f}({\mathbf{x}}) = \hat{g}_{\min } ({\mathbf{x}}) + \hat{\sigma }_{u} \sqrt {2/\pi } \). In practice, this means that frontier is obtained by shifting the CNLS estimate of the average-practice production function upwards by the expected value of the inefficiency term, analogous to the MOLS approach.
Regardless of how σ u , σ v are estimated, the firm-specific inefficiency component u i must be inferred indirectly in the cross-sectional setting. Jondrow et al. (1982) have shown that the conditional distribution of inefficiency u i given ε i is a zero-truncated normal distribution with mean \( \mu_{ * } = - \varepsilon_{i}^{{}} \sigma_{u}^{2} /(\sigma_{u}^{2} + \sigma_{v}^{2} ) \) and variance \( \sigma_{ * }^{2} = \sigma_{u}^{2} \sigma_{v}^{2} /(\sigma_{u}^{2} + \sigma_{v}^{2} ) \). As a point estimator for u i , one can use the conditional mean
where ϕ is the standard normal density function, and Φ is the standard normal cumulative distribution function. Given the estimated \( \hat{\sigma }_{u} ,\hat{\sigma }_{v} \) parameters, the conditional expected value of inefficiency can be computed as
where \( \hat{\varepsilon }_{i} = \hat{\upsilon }_{i} - \hat{\sigma }_{u} \sqrt {2/\pi } \) is the estimator of the composite error term (compare with (17)), not the CNLS residual. The conditional expected value (20) is an unbiased but inconsistent estimator of u i : irrespective of the sample size n, we have only a single observation of the firm i (see, e.g., Greene 2008, Section 2.8.2, for further discussion).
4 Possible extensions
This section briefly outlines some potential extensions of the proposed method and suggests some interesting avenues for future research. While some extensions are readily implementable, we must emphasize that every topic discussed in this section deserves a more systematic and rigorous examination of its own.
4.1 Panel data model
Panel data enables us to relax the distributional assumptions, and estimate the model in a fully nonparametric fashion. In the following we describe the fixed effects approach to estimating time-invariant inefficiency. Alternative panel data approaches such as random effects modeling, time-varying inefficiency, and modeling technical progress are left as interesting topics for future research.
Assuming a balanced panel where each firm is observed over time periods t = 1,…,T, the frontier model with time-invariant inefficiency can be described as
where u i ≥ 0 is a time-invariant inefficiency term of firm i and v i,t is the stochastic noise term for firm i in period t. Production function f is assumed to be monotonic increasing and concave as before. We assume that the noise components v it are uncorrelated random variables with \( E(v_{i,t} ) = 0 \, \forall i,t,\;E(v_{i,t}^{2} ) = \sigma_{v}^{2} < \infty \, \forall i,t,\;{\text{and}}\;E(v_{j,s} v_{i,t} ) = 0 \, \forall j \ne i,s \ne t \). Importantly, no distributional assumptions are imposed: model (21) is fully nonparametric.
It might be tempting to leave the inefficiency terms in the composite error term, and estimate the model (21) analogous to the cross-sectional approach examined above. However, the time-invariant u i would make the composite error term heteroskedastic across firms and autocorrelated across time periods. To avoid the problems of heteroskedasticity and autocorrelation, we can eliminate the time-invariant inefficiency terms from the regression equation by rewriting the model (21) in terms of the first differences
We can take equality (22) as the regression equation to be estimated by CNLS. Specifically, the CNLS problem can be stated as
This is a quadratic programming problem with (nT)2 + 2nT − n linear constraints. As the number of constraints is a quadratic function of both n and T, the problem is computationally demanding. Developing efficient computational algorithms or heuristics must be recognized as one important challenge for further research.
Given the optimal solution to (23), we can compute the firm-specific “fixed effects” as
Following Schmidt and Sickles (1984), we can take the most efficient firm in the sample as the reference, and estimate the time-invariant inefficiency terms u i by using
In a finite sample, the estimator of Schmidt and Sickles (1984) is upward biased; the most efficient firm in the observed sample may be inefficient compared to the true but unobserved frontier. Consistency of this estimator requires that there is a strictly positive probability of observing a perfectly efficient firm with u i = 0. Park and Simar (1994) present a more detailed investigation of consistency and the rates of convergence of this estimator in the semiparametric setting.
To estimate the frontier, we can directly apply the DEA formulation of lower bound function presented in (9). Given this lower bound function, we can estimate the frontier as
4.2 Returns to scale
We have thus far left returns to scale (RTS) unrestricted. In many applications, it is meaningful to impose further structure on RTS or it is interesting to test for alternative RTS assumptions. Imposing RTS is straightforward in the QP problems (6) and (23). In problem (6) we can simply add the following constraints:
-
constant returns to scale (CRS): \( \alpha_{i} = 0 \, \forall i = 1, \ldots ,n \)
-
non-increasing returns to scale (NIRS): \( \alpha_{i} \ge 0 \, \forall i = 1, \ldots ,n \)
-
non-decreasing returns to scale (NDRS): \( \alpha_{i} \le 0 \, \forall i = 1, \ldots ,n \)
Rationale of these constraints is directly analogous to the standard multiplier-side DEA formulations where parallel constraints are employed for enforcing RTS assumptions.
While the CNLS regression is easily adapted to alternative RTS assumptions, the implications to the efficiency estimation are somewhat trickier. Specifically, if one estimates the average-practice technology g subject to CRS, and subsequently shifts the frontier upward by the estimated expected inefficiency, the resulting best-practice frontier does not generally satisfy CRS. This is due to the mismatch of the additive structure of the inefficiency and noise terms assumed in (1) and the multiplicative nature of the scale properties. If one imposes CRS, NIRS, or NDRS assumptions, it is logically consistent to employ the multiplicative specification of inefficiency and noise, to be discussed next.
4.3 Multiplicative model
Most SFA studies employ a multiplicative error model due to the log-transformations applied to the data (e.g., when the popular Cobb-Douglas or translog functional forms are used). As noted above, the CRS assumption requires a multiplicative error structure. Moreover, multiplicative error specification might help to alleviate heteroskedasticity from different scale sizes (cf. Caudill and Ford 1993).
Adhering to the standard multiplicative formulation from SFA, we can rephrase model (1) as
We maintain the same assumptions on production function f and the composite error term as in model (1). Applying the log-transformation to Eq. 27, we obtain
Note that the log-transformation is applied to function f, not directly to inputs x. Next, we may apply the decomposition presented in (3) to restore the Gauss-Markov conditions, rephrasing model (28) as
where μ is the expected inefficiency and g is the average-practice production function as before. To estimate g by CNLS, we may rephrase the QP problem (6) as
This yields a convex programming problem with a convex objective function and a system of linear inequality constraints. Note that the fitted values \( \hat{y}_{i} \) are model variables in (30): we cannot use data transformations to linearize this problem. The input–output data must be kept in the original units in order to use the Afriat inequalities for imposing concavity. Although the objective function involves logarithms of model variables, global convexity of the objective function of problem (30) presents an important advantage compared to the constrained ML problem suggested by Banker and Maindiratta (1992). With today’s computational capacity, convex programming problems are not considered less tractable than linear programming.
Given the composite residuals from model (30) (i.e., \( \upsilon_{i} = \ln y_{i} - \ln \hat{y}_{i} \)), the standard MM or PSL procedures can be applied, as described in Sect. 4. The log-transformation only concerns Step 1, and makes no difference in the estimation of Step 2. However, the interpretation of inefficiency term u i changes: exp(u i ) provides the Farrell output efficiency measure.
4.4 Cost functions
The duality theory has established that the production technology can be equivalently modeled by means of monetary representations, such as the cost function, which is formally defined as
Vector w represents the exogenously given input prices. The cost function indicates the minimum cost of producing a given target output at given input prices. Note that if data for the input and output quantities (x,y) are available, we could first estimate the production function f using the techniques developed in the previous sections, and simply apply the definition (31) to recover the cost function from the estimated production function f. This is a common approach in the DEA literature (see, e.g., Fried et al. 2008). In this section we briefly explore the more challenging case where the data of input quantities (or the cost shares of inputs) are not available, and we only observe the output y i , input prices w i , and the total cost C i for firms i = 1,…,n.
According to the microeconomic theory, the cost function C is non-negative and non-decreasing function of both input prices w and the output y. Further, the cost function is known to be continuous, concave and homogenous of degree one in input prices w (Shephard 1953). The known regularity properties of cost functions provide useful shape constraints that can be utilized in the semi- and nonparametric estimation.
If the production function f is concave, as assumed in DEA, then the cost function is a convex function of output y. In contrast, the cost function must be concave in input prices w. As a step towards resolving this mismatch between convexity in y and concavity in w, we note that the cost function can be factored as \( C(y,{\mathbf{w}}) = a({\mathbf{w}}) \cdot b(y) \) if and only if the technology satisfies the assumption of input homotheticity (Shephard 1953). If we impose a stronger assumption that production function f exhibits constant returns to scale (which implies input homotheticity), the cost function becomes separable in the following sense:
Note that the function \( a({\mathbf{w}}) = C(y,{\mathbf{w}})/y \) has a compelling interpretation as the average cost function. Further, this average cost function depends only on input prices w, and it inherits the concavity and homogeneity properties of the cost function C.
In the stochastic cost frontier models (e.g., Kumbhakar 1997), the observed costs C i (i = 1,…,n) are assumed to differ from the cost function due to a composite error term (ε i ) which is the sum of a non-negative inefficiency term (u i ) and a noise term (v i ). To ensure homogeneity of degree one in prices w, we postulate a multiplicative error term as in Sect. 4.3, that is,
Note the changed sign of the inefficiency term in (33). To estimate the cost frontier in the cross-sectional setting, we assume u i are half-normal and v i are normally distributed.
To estimate the average cost function a by CNLS, take logarithms of both sides of Eq. 33, and utilize the CRS assumption to rephrase the equation as
Parameter μ represents the expected value of cost inefficiency (compare with (3)). To obtain a least squares estimator for the average cost function, we formulate the CNLS problem as follows:
The fitted values \( \hat{a}_{i} \) for the average cost function are model variables: problem (35) is a convex programming problem with linear constraints, similar to problem (30). Coefficients β i indicate the marginal cost of input prices (which represent the input substitution possibilities). The second set of constraints is the system of Afriat inequalities that enforces concavity in input prices w. By excluding the intercept, we force the estimated average cost function to be homogenous of degree one in prices w, as required by the microeconomic theory. Importantly, this homogeneity property enables us to identify the parameter μ directly; we insert it to the objective function of the least squares problem (35) to obtain the least squares estimate. Given the half-normal specification of the inefficiency term, we can utilize the equation \( \mu = \sigma_{u} \sqrt {2/\pi } \) to estimate σ u directly based on the \( \hat{\mu } \) obtained from (35). The parameter σ v can be estimated based on the residuals using Eq. 15. The conditional expected values of cost inefficiency can be estimated using the result of Jondrow et al. (1982; as described in Sect. 4). Note the changed sign of the inefficiency component in the present setting.
The interpretation of the inefficiency term also changes from the production function setting: u i represents (overall) cost inefficiency that captures both technical and allocative aspects of inefficiency. If data of input quantities or cost shares is available, one could disentangle technical inefficiency from allocative inefficiency. Further, one could incorporate the share equations to the CNLS model (35) (see Kumbhakar 1997, for details). Incorporating the share equations, multiple outputs, and variable returns to scale to the CNLS formulation present interesting avenues for future research.
4.5 Heteroskedasticity
We have thus far assumed that standard deviations σ u , σ v are the same across all firms. This assumption is referred to as homoskedasticity, and it forms one of the maintained assumptions of the classic SFA model by Aigner et al. (1977). As Caudill and Ford (1993) and Florens and Simar (2005) demonstrate, violation of the homoskedasticity assumption leads to potentially serious problems in the context of parametric frontier estimation. Clearly, similar problems carry over to the present semiparametric setting as well. Thus, a brief discussion about robustness of the proposed method to heteroskedasticity is necessary, although more systematic and rigorous treatment of the topic is left for a separate study.
Firstly, we must distinguish between (1) heteroskedasticity of the noise term (i.e., parameter σ v varies across firms) and (2) heteroskedasticity of the inefficiency term (i.e., σ u varies across firms). Let us first consider heteroskedasticity of type (1). Of course, both types of heteroskedasticity may be present at the same time. However, their impacts on the StoNED estimators differ.
Note first that the expected inefficiency \( \mu = \sigma_{u} \sqrt {2/\pi } \) does not depend on σ v . Therefore, the shape of the average-practice production function g remains identical to that of the frontier f even if the noise terms are heteroskedastic. Hence, the proposed approach is not particularly sensitive to heteroskedasticity of type (1). Least squares estimators (incl. CNLS) are known to be unbiased and consistent under symmetric heteroskedasticity, even though more efficient estimators are possible if heteroskedasticity is modeled correctly. Given unbiased CNLS residuals, heteroskedastic σ v will likely increase variance of the parameter estimators \( \hat{\sigma }_{u} ,\hat{\sigma }_{v} \). However, since σ u is estimated based on the skewness of the residual distribution, and heteroskedasticity in the symmetric noise component does not affect skewness, the estimator \( \hat{\sigma }_{u} \) remains consistent. Thus, frontier f and expected inefficiency μ can be consistently estimated even under heteroskedasticity of type (1). The only problem is that the conditional expected value of inefficiency \( \hat{E}(u_{i} \left| {\hat{\varepsilon }_{i} } \right.) \) is a function of heteroskedastic \( \hat{\sigma }_{v} \). Thus, firm-specific efficiency scores and rankings can be affected by heteroskedasticity of type (1).
Heteroskedasticity of type (2) is a much more serious problem because σ u does directly influence the expected inefficiency E(u i ). When σ u is heteroskedastic, the expected inefficiency E(u i ) differs across firms, and thus the shape of the average-practice production function g is no longer identical to that of the frontier f. We stress that this problem arises only in case (2), not in case (1). Since the proposed StoNED method relies on consistent estimation of the average-practice production g in the step (1), the estimates can be sensitive to the violation of the homoskedasticity assumption for σ u (see the next section for some evidence from Monte Carlo simulations). Therefore, it is critically important to develop statistical tests of the homoskedasticity assumption and more general estimation methods that can deal with heteroskedastic inefficiency. Fortunately, such tests and methods have been developed for the least squares estimation in the context of the linear regression model (consider, e.g., the generalized least squares (GLS) method). The main challenge is to adapt and extend existing techniques from the linear regression analysis to the CNLS framework. This forms an important topic for future research.
4.6 Statistical inferences
Even though we impose parametric distributional assumption for the inefficiency and noise terms, the conventional methods of statistical inference do not directly apply to the present setting. For example, one might apply the likelihood ratio test for testing significance of two alternative hierarchically nested model variants, but the degrees of freedom are difficult to specify (see Meyer 2003, 2006, for discussion). One could also construct confidence intervals based on the known conditional distribution of the inefficiency term (see Horrace and Schmidt 1996, for details). However, such confidence intervals do not take into account the sampling distribution of the inefficiency estimators, and consequently, have poor coverage properties (Simar and Wilson 2010). In light of these complications, the parametric bootstrap method similar to Simar and Wilson (2010) would appear to be the best suited approach to statistical inference in the present context. Adapting the procedure to the present setting seems straightforward, but it is first important to ensure that the method is consistent and provides valid inferences even in finite samples. We leave this as an interesting research question for future research.
Related to the previous point, we should note that the least-squares residuals are often skewed in the wrong direction (\( \hat{M}_{3} > 0 \)). In the SFA literature, the usual approach is to set \( \hat{\sigma }_{u} = 0 \), which means that all firms are diagnosed as efficient. It may also occur that the skewness is so great that \( \hat{\sigma }_{u} > \hat{\sigma } \), and thus \( \hat{\sigma }_{v} \) becomes negative. In that case, the typical approach is to set \( \hat{\sigma }_{v} = 0 \) and attribute all observed variation to inefficiency (as in DEA). The “wrong skewness” is conventionally seen as a useful built-in diagnostic, which signals model misspecification or inappropriate data (Greene 2008). Indeed, inspecting the distribution of residuals might reveal some possible sources of model misspecification. However, evidence from several Monte Carlo studies shows that wrongly skewed residuals can arise even in correctly specified frontier models (e.g., Fan et al. 1996; Carree 2002; Simar and Wilson 2010). This is not only a problem for the method of moments, it equally affects the pseudolikelihood method. Interestingly, if Simar and Wilson’s (2010) bootstrap procedure is applicable in the present setting, it could alleviate the wrong skewness problem as well.
5 Monte Carlo simulations
In this section we examine performance of the StoNED method in the controlled environment of Monte Carlo simulations. Our objective is to compare performance of the StoNED method with the standard DEA and SFA under alternative conditions where the distributional assumptions of the StoNED model are violated.Footnote 8 The data generating processes used in the simulations has been adopted from Simar and Zelenyuk (2008). Systematic performance comparisons with other semi- and nonparametric methods is left as a topic for future research.Footnote 9
We consider performance in terms of the standard mean squared error (MSE) criterion, applying it to estimates of the frontier f and the inefficiency term u. For the frontier estimates, the MSE statistic is defined as
where \( \hat{f} \) denotes the estimated frontier function (estimated by DEA, SFA, or StoNED), and r = 1,…,R is the index of replications of a given scenario. Analogously, the MSE of the inefficiency estimates is defined as
For DEA, the standard output-oriented variable returns to scale (VRS) specification is used. Given the DEA efficiency score \( \theta = \hat{f}^{DEA} ({\mathbf{x}}_{i} )/y_{i} \), the DEA inefficiency estimator is obtained as \( \hat{u}_{i}^{DEA} = (\theta - 1)y_{i} \). For SFA, we use the Cobb-Douglas production function with the half-normal inefficiency term. The MOLS estimator is used to ensure comparability with the StoNED method. For the StoNED method, we assume the multiplicative specification (27) and the half-normal inefficiency distribution. Since the MC simulations are computationally intensive, we restrict to the simpler method of moment (MM) estimator in this section. In the MM estimation of SFA and StoNED models, we have dealt with the wrong skewness problem as follows. If \( \hat{M}_{3} \) is non-negative, we set \( \hat{M}_{3} \) = −0.0001. On the other hand, if \( \hat{\sigma }_{v} \) is negative, we set \( \hat{\sigma }_{v} \) = 0.0001. These settings ensure that the algorithm runs smoothly even in those scenarios where the DGP is inconsistent with the model assumptions (e.g., there are outliers or no inefficiency). Of course, the wrong skewness can be a signal of model misspecification (e.g., in scenarios involving outliers), but in these MC simulations we disregard this potentially useful information and force the postulated skewness to the estimated distributions of the composite error term.
5.1 Univariate Cobb-Douglas frontier
We start by replicating the first six scenarios of Simar and Zelenyuk (2008) as reported in their Section 3.1.1. The DGP is characterized by the univariate Cobb-Douglas model
where \( x_{i} \sim Uni[0,1],\;u_{i} \sim Exp[\mu = 1/6] \) with parameter μ representing the expected inefficiency, and \( v_{i} \sim N(0,\sigma_{v}^{2} ) \) where \( \sigma_{v} = \rho_{nts} \cdot \mu \) and parameter \( \rho_{nts} \) represents the noise-to-signal ratio. Using this DGP, Simar and Zelenyuk construct six alternative scenarios corresponding to different values of sample size n and parameter \( \rho_{nts} \). Before proceeding to the results, we note that the SFA estimator assumes the correct functional form for the frontier. However, both SFA and StoNED estimators assume a wrong distribution for the inefficiency term.
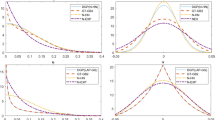
Table 1 describes the six scenarios and reports the average MSEs over 50 replications for the frontier estimates. We note first that the results for the DEA frontier estimator come reasonably close to those reported by Simar and Zelenyuk (2008). We see that the SFA estimator has a larger MSE than DEA in scenario (a) that does not involve any noise whatsoever, but it performs considerably better than DEA in other scenarios involving outliers or noise. Interestingly, the StoNED estimator has a lower MSE than the SFA estimator in all scenarios, even though the functional form of SFA is correct.
Table 2 reports the corresponding statistics for the inefficiency estimates. Interestingly, while the DEA estimator captures the frontier better than SFA or StoNED in scenario (a) that involves no noise, the DEA inefficiency estimator has a higher MSE than the two stochastic alternatives. While the SFA and StoNED estimators over-estimate the frontier when the true DGP has no noise, in the case of efficiency estimation, attributing a part of the total variance to the noise term will tend to offset the upward bias in the frontier estimation. This explains the better performance of SFA and StoNED in efficiency estimation in scenario (a). On the other hand, in the noisy scenarios, the advantages of SFA and StoNED are not so great in terms of inefficiency estimates as they are in the case of frontier estimation. Estimating inefficiency at the firm level in a cross-sectional setting is a notoriously challenging task when both the frontier and the evaluated input–output vector are subject to noise.
5.2 Trivariate Cobb-Douglas frontier
We next extend the previous six scenarios to the three-input case, characterized by the Cobb-Douglas model
where \( x_{j,i} \sim Uni[0,1],\;j = 1,2 \). The inefficiency and the noise terms are drawn in the identical manner to Section 6.1. The purpose of these scenarios is to examine how the curse of dimensionality might affect performances of alternative estimators.
Table 3 describes the six scenarios and reports the average MSEs over 50 replications for the frontier estimates. Table 4 presents the corresponding MSE statistics for the inefficiency estimates. We must emphasize that the MSEs reported in Tables 3 and 4 are not directly comparable with those of Tables 1 and 2 because the scale of output values is somewhat different. As expected, the DEA estimator performs best in scenarios (a) and (b) involving little or no noise. Its precision deteriorates dramatically when the noise to signal ratio increases. The MSEs of SFA and StoNED estimators are more stable across scenarios. StoNED performs better than SFA in most scenarios, except for (c) and (f) that involve the largest noise to signal ratios at given sample sizes.
5.3 Trivariate Cobb-Douglas frontier with heteroskedastic inefficiency
We next adapt the DGP of the previous section by introducing heteroskedasticity in the inefficiency term u. Following Simar and Zelenyuk (2008) Section 3.1.4, we draw inefficiency terms from the half-normal distribution as \( u_{i} \left| {\mathbf x}_{i} \right.\sim \left| {N(0,(\sigma_{u} (x_{1,i} + x_{2,i} )/2)^{2} )} \right| \), where σ u = 0.3. Note that variance of inefficiency distribution depends on inputs 1 and 2, which results as heteroskedasticity. The noise term is homoskedastic normal, \( v_{i} \sim N(0,\sigma_{v}^{2} ) \), where \( \sigma_{v} = \rho_{nts} \cdot \sigma_{u} \cdot \sqrt {(\pi - 2)/\pi } \). Parameter \( \rho_{nts} \) can be interpreted as the average noise to signal ratio, and it is varied across scenarios.
Table 5 reports the average MSEs over 50 replications for the frontier estimates. The MSEs reported in Tables 3 and 5 are comparable as we have used the same production function, the same sample sizes, and the same noise to signal ratios; the only difference is the heteroskedastic inefficiency term. Interestingly, although DEA is a distribution-free method, MSEs of the DEA estimator increase notably. This is because observations with large values of inputs 1 and 2 are likely to have larger inefficiencies. This will directly affect the local DEA approximation of the frontier in the region where x 1 and x 2 are greater than 0.5. By contrast, the MSEs of the SFA estimator decrease in all scenarios. The SFA frontier is more rigid by construction, and hence less sensitive to local heteroskedasticity. Moreover, the SFA benefits from the correct functional form of the (half-normal) inefficiency term, even though it fails to account for the heteroskedasticity. Performance of the StoNED estimator deteriorates for similar reasons to those noted in the case of DEA. While the StoNED estimator is more sensitive to local heteroskedasticity than SFA, its MSE remains lower than that of DEA in all noisy scenarios where the average noise to signal ratio is equal to one or higher.
For completeness, Table 6 presents the corresponding MSEs of the inefficiency estimates. Compared to Table 4, the MSEs of all three methods increase. In particular, performances of SFA and StoNED deteriorate in all scenarios, but especially in (a) and (b) involving little or no noise. Still, SFA and StoNED outperform DEA in those two scenarios. As the sample size and the noise to signal ratio increase, the StoNED estimator becomes more competitive in comparison to SFA.
In conclusion, the proposed StoNED estimator proved a competitive alternative to the conventional DEA and SFA estimators in the simulations adopted from Simar and Zelenuyk (2008). We should note that the distributional assumptions for the inefficiency term were incorrect in all scenarios that were considered. Despite this specification error, the StoNED estimator performed better than the distribution-free DEA estimator in many of the scenarios considered. This suggests it may often be preferable to model noise even at the risk of making a specification error in the distributional assumptions than assume away noise completely. The StoNED estimator also achieved a lower MSE than the corresponding SFA estimator in a majority of scenarios, even though the functional form of the frontier was correctly specified for the SFA estimator (the inefficiency term was wrongly specified, exactly the same way as for the StoNED estimator). It appears that the better empirical fit in the estimation of the frontier can also partly offset the possible specification errors in the estimation of the inefficiency distribution. Of course, evidence from any Monte Carlo study is limited, and the present comparison is restricted to the most basic variants of DEA and SFA. We recognize the need to compare the performance of the proposed method with other recently developed semiparametric and nonparametric approaches that were briefly reviewed in the Introduction, but we also realize that designing and implementing a comparison of many computationally intensive methods in a fair and objective manner is a daunting task that deserves a thorough investigation of its own.
6 Conclusions and discussion
We have developed a new encompassing framework for productive efficiency analysis, referred to as stochastic non-smooth envelopment of data (StoNED). One of our main objectives was to show how the StoNED method can be used to estimate a semiparametric frontier model that combines a nonparametric DEA-like frontier with a stochastic SFA-like inefficiency and noise terms. We also demonstrated that both classic DEA and SFA can be viewed as special cases of this encompassing model, obtainable by imposing some more restrictive assumptions to the model.
In our approach, we employed a two-stage estimation strategy that is commonly used in many areas of econometrics. In the first stage, the shape of the frontier is consistently estimated by using convex nonparametric least squares (CNLS), which does not assume any smoothing parameters, building upon the same shape constraints as DEA. In the second stage, we apply method of moments or pseudolikelihood techniques, adopted from the SFA literature, to disentangle the inefficiency and noise components from the CNLS residuals. Although this stepwise estimation strategy may not be as efficient as the constrained maximum likelihood, it has some important advantages, including the relative robustness of the CNLS estimator to distributional assumptions of inefficiency and noise terms, and substantially lower computational barriers (i.e., the constrained ML estimators are often computationally infeasible in the present setting).
This study has established further connections between CNLS regression and DEA, complementing the prior work of Kuosmanen (2008) and Kuosmanen and Johnson (2010). We find that DEA can be formulated as a constrained special case of the CNLS regression, and that CNLS has a minimum extrapolation interpretation analogous to that of the conventional DEA. While we mainly focused on the estimation of production functions under variable returns to scale, we also demonstrated how the method can be extended to the estimation of cost functions and to allow one to postulate for alternative specifications of returns to scale. Moreover, the performance of the approach was examined in the controlled environment of Monte Carlo simulations. The evidence from the simulations suggests the proposed method is a competitive alternative to standard DEA and SFA methods even when the distribution of the inefficiency term is wrongly specified.
The proposed StoNED approach shares many common features with SFA and DEA, being an amalgam of the two. Thus, many of the existing tools and techniques for SFA and DEA can be incorporated into the proposed framework. The hybrid nature of StoNED also implies that there are many important differences to both SFA and DEA, which should be kept in mind. For example, the interpretation of the StoNED input coefficients differs considerably from those of SFA coefficients. Moreover, in contrast to DEA, all observations influence the shape of the frontier. While the StoNED approach combines the appealing features of DEA and SFA, it also shares many of their limitations. Similar to DEA, the nonparametric orientation of StoNED can make it vulnerable to the curse of dimensionality, which means that the sample size needs to be very large when the number of input variables is high. On the other hand, the composite error term assumptions of SFA are rather restrictive, and might often be inappropriate. In this respect, we again emphasize that the focus of this paper has been on the development of an operational estimation strategy for an encompassing model that includes the classic DEA and SFA models as its special cases. Improving upon DEA and/or SFA aspects of the model is another challenge, which falls beyond the scope of the present study.
Further exploration of the connections established in this paper offers a number of interesting challenges for future research. We have identified and discussed a number of open research questions in the previous sections. To summarize, we consider the following twelve issues the most promising avenues for future research:
-
1.
Adapting the known econometric and statistical methods for dealing with heteroskedasticity, endogeneity, sample selection, and other potential sources of bias, to the context of CNLS and StoNED estimators.
-
2.
Extending the proposed approach to a multiple output setting.
-
3.
Extending the proposed approach to account for relaxed concavity assumptions (e.g., quasi-concavity).
-
4.
Developing more efficient computational algorithms or heuristics for solving the CNLS problem.
-
5.
Examining the statistical properties of the CNLS estimator, especially in the multivariate case.
-
6.
Investigating the axiomatic foundation of the CNLS and StoNED estimators.
-
7.
Implementing alternative distributional assumptions and estimating the distribution of the inefficiency term by semi- or nonparametric methods in the cross-sectional setting.
-
8.
Distinguishing time-invariant inefficiency from heterogeneity across firms, and identifying inter-temporal frontier shifts and catching up in panel data models.
-
9.
Extending the proposed approach to the estimation of cost, revenue, and profit functions as well as to distance functions.
-
10.
Developing a consistent bootstrap algorithm and/or other statistical inference methods.
-
11.
Conducting further Monte Carlo simulations to examine the performance of the proposed estimators under a wider range of conditions, and comparing the performance with other semi- and nonparametric frontier estimators.
-
12.
Applying the proposed method to empirical data, and adapting the method to better serve the needs of specific empirical applications.
These twelve points could be seen as limitations of the proposed approach, but also as an outline of a research program to address these challenges. We hope this study could inspire other researchers to join us in further theoretical and empirical work along the lines sketched above, and to expand our list of research questions further. Finally, we hope that this study could contribute to further cross-fertilization and unification of the parametric and nonparametric streams of productive efficiency analysis.
Notes
In earlier working papers Kuosmanen (2006) and Kuosmanen and Kortelainen (2007) the term “stochastic nonparametric envelopment of data” was used. However, as the Associate Editor and two anonymous reviewers of this journal correctly noted, the proposed method is actually semi-parametric due the parametric distributional assumptions imposed on the inefficiency and noise terms.
In the SFA literature, the problem of heteroskedasticity was recognized in the early 1990s (Caudill and Ford 1993; see also Florens and Simar 2005). The econometric literature provides many useful tools for dealing with heteroskedasticity, but suitability of these tools to the present setting deserves a thorough examination that falls beyond the scope of the present study.
Simar (2007) presents a formal description of a data generation process for a stochastic multi-output frontier model, which could be a useful starting point for multi-output extensions (see also Simar and Zelenyuk 2008). The working paper Kuosmanen (2006) suggests how the CNLS problem could be formulated in terms of the directional distance function.
MOLS should not be confused with the deterministic COLS (= corrected OLS) approach (Greene, 1980), where the frontier is shifted upward according to the largest OLS residual so as to envelop all observations.
The proof involves straightforward mechanical calculations and it is hence omitted. Details of the proof are available from the authors by request.
Since we replicate some of the simulations conducted by Simar and Zelenyuk (2008), an interested reader may compare our results with those reported by Simar and Zelenyuk for their local maximum likelihood estimator. However, it is worth noting that the synthetic data sets used in the different simulations are not exactly identical, but each random draw from the DGP yields unique data, which may have effect on the performance of estimators. The results reported here are averages over 50 replications of each scenario, whereas Simar and Zelenyuk (2008) report results of a single simulation run for each scenario.
References
Afriat SN (1967) The construction of a utility function from expenditure data. Int Econ Rev 8:67–77
Afriat S (1972) Efficiency estimation of production functions. Int Econ Rev 13:568–598
Aigner DJ, Chu S (1968) On estimating the industry production function. Am Econ Rev 58:826–839
Aigner DJ, Lovell CAK, Schmidt P (1977) Formulation and estimation of stochastic frontier models. J Econom 6:21–37
Banker RD (1993) Maximum-likelihood, consistency and data envelopment analysis—a statistical foundation. Manage Sci 39(10):1265–1273
Banker RD, Maindiratta A (1992) Maximum likelihood estimation of monotone and concave production frontiers. J Prod Anal 3:401–415
Banker RD, Charnes A, Cooper WW (1984) Some models for estimating technical and scale inefficiencies in data envelopment analysis. Manage Sci 30:1078–1092
Bogetoft P (1996) DEA on relaxed convexity assumptions. Manage Sci 42:457–465
Carree MA (2002) Technological inefficiency and the skewness of the error component in stochastic frontier analysis. Econ Lett 77:101–107
Caudill SB, Ford JM (1993) Biases in frontier estimation due to heteroscedasticity. Econ Lett 41(1):17–20
Charnes A, Cooper WW, Rhodes E (1978) Measuring the inefficiency of decision making units. Eur J Oper Res 2(6):429–444
Cooper WW, Seiford LM, Zhu J (2004) Data envelopment analysis: models and interpretations, ch. 1. In: Cooper WW, Seiford LM, Zhu J (eds) Handbook on data envelopment analysis. Kluwer Academic Publisher, Boston, pp 1–39
Deprins D, Simar L, Tulkens H (1984) Measuring labor efficiency in post offices. In: Marchand M, Pestieau P, Tulkens H (eds) The performance of public enterprises: concepts and measurements. North Holland, pp 243–267
Fan Y, Li Q, Weersink A (1996) Semiparametric estimation of stochastic production frontier models. J Bus Econ Stat 14(4):460–468
Farrell MJ (1957) The measurement of productive efficiency. J R Stat Soc A 120(3):253–282
Florens JP, Simar L (2005) Parametric approximations of nonparametric frontier. J Econom 124(1):91–116
Fried H, Lovell CAK, Schmidt S (2008) The measurement of productive efficiency and productivity change. Oxford University Press, New York
Greene W (1980) Maximum likelihood estimation of econometric frontier functions. J Econom 13:26–57
Greene WH (2005) Reconsidering heterogeneity in panel data estimators of the stochastic frontier model. J Econom 126:269–303
Greene WH (2008) The econometric approach to efficiency analysis, chapter 2. In: Fried H, Lovell K, Schmidt S (eds) The measurement of productive efficiency and productivity growth. Oxford University Press, New York
Groeneboom P, Jongbloed G, Wellner JA (2001a) A canonical process for estimation of convex functions: the “Invelope” of integrated brownian motion +t4. Ann Stat 29:1620–1652
Groeneboom P, Jongbloed G, Wellner JA (2001b) Estimation of a convex function: characterizations and asymptotic theory. Ann Stat 29:1653–1698
Hall P, Simar L (2002) Estimating a changepoint, boundary, or frontier in the presence of observation error. J Am Stat Assoc 97(458):523–534
Hanson DL, Pledger G (1976) Consistency in concave regression. Ann Stat 4(6):1038–1050
Henderson DJ, Simar L (2005) A fully nonparametric stochastic frontier model for panel data, Discussion Paper 0417, Institut de Statistique, Universite Catholique de Louvain
Hildreth C (1954) Point estimates of ordinates of concave functions. J Am Stat Assoc 49(267):598–619
Horrace WC, Schmidt P (1996) Confidence statements for efficiency estimates from stochastic frontier models. J Prod Anal 7:257–282
Jondrow J, Lovell CAK, Materov IS, Schmidt P (1982) On estimation of technical inefficiency in the stochastic frontier production function model. J Econom 19:233–238
Kneip A, Simar L (1996) A general framework for frontier estimation with panel data. J Prod Anal 7:187–212
Kumbhakar SC (1997) Modeling allocative inefficiency in a translog cost function and cost share equations: an exact relationship. J Econom 76(1–2):351–356
Kumbhakar SC, Lovell CAK (2000) Stochastic frontier analysis. Cambridge University Press, Cambridge
Kumbhakar SC, Park BU, Simar L, Tsionas EG (2007) Nonparametric stochastic frontiers: a local maximum likelihood approach. J Econom 137:1–27
Kuosmanen T (2001) DEA with efficiency classification preserving conditional convexity. Eur J Oper Res 132(2):326–342
Kuosmanen T (2006) Stochastic nonparametric envelopment of data: combining virtues of SFA and DEA in a unified framework, MTT Discussion Paper 3/2006
Kuosmanen T (2008) Representation theorem for convex nonparametric least squares. Econom J 11:308–325
Kuosmanen T, Fosgerau M (2009) Neoclassical versus frontier production models? Testing for the presence of inefficiencies in the regression residuals. Scand J Econ 111(2):317–333
Kuosmanen T, Johnson A (2010) Data envelopment analysis as nonparametric least squares regression. Oper Res 58(1):149–160
Kuosmanen T, Kortelainen M (2007) Stochastic nonparametric envelopment of data: cross-sectional frontier estimation subject to shape constraints. Univ. of Joensuu, Economics Discussion Paper No. 46
Mammen E (1991) Nonparametric regression under qualitative smoothness assumptions. Ann Stat 19:741–759
Mammen E, Thomas-Agnan C (1999) Smoothing splines and shape restrictions. Scand J Stat 26:239–252
Meeusen W, van den Broeck J (1977) Efficiency estimation from cobb-Douglas production function with composed error. Int Econ Rev 8:435–444
Meyer MC (2003) A test for linear vs. convex regression function using shape-restricted regression. Biometrika 90(1):223–232
Meyer MC (2006) Consistency and power in tests with shape-restricted alternatives. J Stat Plan Inference 136:3931–3947
Nemirovski AS, Polyak BT, Tsybakov AB (1985) Rates of convergence of nonparametric estimates of maximum likelihood type. Probl Inf Transmiss 21:258–271
Park B, Simar L (1994) Efficient semiparametric estimation in stochastic frontier models. J Am Stat Assoc 89:929–936
Park B, Sickles RC, Simar L (1998) Stochastic panel frontiers: a semiparametric approach. J Econom 84:273–301
Park B, Sickles RC, Simar L (2003) Semiparametric efficient estimation of AR(1) panel data models. J Econom 117:279–309
Park B, Sickles RC, Simar L (2006) Semiparametric efficient estimation of dynamic panel data models. J Econom 136:281–301
Petersen NC (1990) Data envelopment analysis on a relaxed set of assumptions. Manage Sci 36:305–314
Sauer J (2006) Economic theory and econometric practice: parametric efficiency analysis. Empir Econ 31:1061–1087
Schmidt P, Sickles R (1984) Production frontiers and panel data. J Bus Econ Stat 2:367–374
Shephard RW (1953) Cost and production functions. Princeton University Press, Princeton
Simar L (2007) How to improve the performances of DEA/FDH estimators in the presence of noise? J Prod Anal 28(3):183–201
Simar L, Wilson PW (2000) Statistical inference in nonparametric frontier models: the state of the art. J Prod Anal 13:49–78
Simar L, Wilson PW (2010) Estimation and inference in cross-sectional stochastic frontier models. Econom Rev 29(1):62–98
Simar L, Zelenyuk V (2008) Stochastic FDH/DEA estimators for frontier analysis. J Prod Anal. doi:10.1007/s11123-010-0170-6
Stone CJ (1980) Optimal rates of convergence for nonparametric estimators. Ann Stat 8(6):1348–1360
Stone CJ (1982) Optimal global rates of convergence for nonparametric regression. Ann Stat 10(4):1040–1053
Tulkens H (1993) On FDH analysis: some methodological issues and applications to retail banking, courts, and urban transit. J Prod Anal 4:183–210
Varian HR (1984) The nonparametric approach to production analysis. Econometrica 52:579–598
Yatchew A (2003) Semiparametric regression for the applied econometrician. Cambridge University Press, Cambridge
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Appendix 1: illustrative example
Appendix 1: illustrative example
The purpose of this “Appendix” is to illustrate the estimated StoNED frontiers graphically in a single-input single-output setting. Further examples and illustrations can be found in working papers Kuosmanen (2006) and Kuosmanen and Kortelainen (2007). Some computational codes for the GAMS and Matlab software are available at the website: http://www.nomepre.net/stoned/.
In the present example, the input data were randomly sampled from Uni[1,11] for a random sample of 100 firms, independently for each input and firm. The efficient output levels were calculated using the production function f(x i ) = ln(x i ) + 2. From the efficient output level, we subtracted a random inefficiency term \( u_{i} \mathop \sim \limits_{i.i.d} \left| {N(0,\sigma_{u}^{2} )} \right| \) and added a random error \( v_{i} \mathop \sim \limits_{i.i.d} N(0,\sigma_{v}^{2} ) \), to obtain the “observed” output data used in estimation as y i = ln(x i ) + 2 + v i − u i . The standard deviations of the inefficiency and noise terms are σ u = 0.6 and σ v = 0.3.
We applied the shape constrained CNLS method with additive error structure without restrictions on RTS to this simulated data, and subsequently computed the MM and PSL estimators using the CNLS residuals. Figure 1 illustrates the results by plotting a scatter of the sample data (points ×), the true frontier (thick black curve), the CNLS estimate of the average-practice production function (thick, grey, piece-wise linear curve), and the StoNED frontiers estimated by the MM (solid, thin, piece-wise linear curve) and PSL (broken, piece-wise linear curve), respectively. The CNLS curve consists of five different line segments (segments 3 and 4 are difficult to distinguish in Fig. 1). In this Scenario, the MM curve indicates slightly higher output levels than the PSL curve. Nevertheless, both curves closely approximate the true frontier.
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Kuosmanen, T., Kortelainen, M. Stochastic non-smooth envelopment of data: semi-parametric frontier estimation subject to shape constraints. J Prod Anal 38, 11–28 (2012). https://doi.org/10.1007/s11123-010-0201-3
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11123-010-0201-3
Keywords
- Data envelopment analysis (DEA)
- Frontier estimation
- Nonparametric least squares
- Productive efficiency analysis
- Stochastic frontier analysis (SFA)