Big and beautiful? On non-parametrically measuring scale economies in non-convex technologies

Abstract

Knowledge on the scale economies drives the incentives of regulators, governments and individual utilities to scale-up or scale-down the scale of operations. This paper considers the returns to scale (RTS) in non-convex frontier models. In particular, we evaluate RTS assumptions in a Free Disposal Hull model, which accounts for uncertainty and heterogeneity in the sample. Additionally, we provide a three-step framework to empirically analyze the existence and extent of RTS in real world applications. In a first step, the presence of scale (and scope) economies is verified. Secondly, RTS for individual observations are examined while in a third step we derive the optimal scale for a sector as a whole. The framework is applied to the Portuguese drinking water sector where we find the optimal scale to be situated around 7–10 million m³.

1 Introduction

Both academics and practitioners are interested in the optimal scale of operations. From the viewpoint of scholars, the scale of operations touches the debate on returns to scale (RTS) of the production frontier. RTS denotes the relation between a proportional change in inputs and the corresponding (proportional) change in outputs. Especially the introduction of different scale assumptions in non-convex frontier models (e.g. the Free Disposal Hull model, Deprins et al. 1984) recently attracted a significant amount of attention (e.g. Kerstens and Vanden Eeckaut 1999; Podinovski 2004a, c; Soleimani-damaneh and Reshadi 2007). On the other hand, practitioners are interested in insights on the optimal scale of operations as (1) they guide the individual utilities in their strategic decisions, (2) give direction to the government’s incentives, or (3) inspire merger commissions and regulators. This paper explores the concepts of RTS in non-convex models and provides a framework to employ them in real world applications where uncertainty and heterogeneity is accounted for in the data by using the robust and conditional efficiency estimates of, respectively, Cazals et al. (2002) and Daraio and Simar (2005, 2007).

The non-parametric literature has extensively discussed the use and existence of scale economies in convex frontier models as Data Envelopment Analysis (DEA) (e.g. Banker et al. 2004 and reference therein). However, the convexity assumption where DEA works with is sometimes difficult to argue in real world applications as it implies additivity and divisibility (see Cherchye et al. 2000a, b; Briec et al. 2004 and references therein). If in DEA the convexity assumption is dropped, one obtains the Free Disposal Hull (FDH) model (Deprins et al. 1984). Unfortunately, in the traditional FDH models scale economies are neglected as only variable returns to scale (VRS) are assumed. Only recently, Kerstens and Vanden Eeckaut (1999) integrated RTS assumptions in this non-convex model without invoking convexity (and thus without assuming convex combinations of utilities). Besides the opportunity to test the direction of the RTS, the inclusion of the relaxed convexity assumptions allows for an increased discrimination among the evaluated entities (Destefanis and Storti 2002). Indeed, in the traditional FDH formulation many observations are ‘efficient by default’ as frequently only few reference partners exist in a particular section of the production function. The RTS model accounts for this by enlarging the reference set to proportional replicas of observed variables (i.e. by imposing additional structure).

After having described the traditional non-convex FDH model, we outline how to include RTS assumptions in FDH. This model, as developed by Kerstens and Vanden Eeckaut (1999), is further described in Briec et al. (2004) and linearized to mixed integer linear programming models by Podinovski (2004a, c). Recently, less computationally intensive alternatives for the mixed integer linear programming models were proposed by Soleimani-damaneh and Reshadi (2007). This article contributes to this literature by extending the model in order to avoid two intricate issues in deterministic frontier models. On the one hand, we allow for noise in the data (arising from, e.g. outliers, a-typical observations and measurement errors) by considering the robust efficiency estimates of Cazals et al. (2002). On the other hand, we include heterogeneity in the sample by employing the conditional efficiency estimates of Daraio and Simar (2005, 2007).

In extending the non-convex RTS models, we develop three additional contributions. Firstly, we introduce a fully non-parametric and continuous presentation of the Most Productive Scale Size (MPSS) concept (Banker 1984). In particular, we suggest a graphical presentation of the minimal cost per unit of production in order to derive the optimal scale size for a sector as a whole. As such, this representation creates a convenient tool for practitioners.

Secondly, we provide a comprehensive and easy implementable framework to measure the existence and extent of scale economies. In this framework, which consists of three steps, we first interpret the conditional efficiency measures of Daraio and Simar (2005, 2007) to detect the existence of scale economies. This first step is also useful to detect scope economies. The latter are present if the simultaneous production of goods is less costly than the separate production. As scope economies are interrelated with the scale of operations (indeed, as argued by Baumol et al. (1988) a larger scope of operations induces a larger scale of the company as well), we disentangle the two effects in order to obtain the ‘pure’ scale economies. When examining RTS, the literature frequently ignores this first step and simply assumes the existence of RTS. We argue that one should first test for the presence of RTS before analyzing its direction. A second step derives the RTS for every individual observation. Following Podinovski (2004b), we distinguish local and global economies of scale such that the traditional constant, increasing and decreasing RTS are contrasted to sub-constant RTS (SCRS) (which indicates that an observation could obtain its MPSS by both scaling-up or scaling-down its operations). ¹ The third step of the framework examines the optimal scale of operations of the sector. The continuous version of the MPSS delivers rapid policy insights as it presents a visual representation of the minimal cost level.

A final contribution of the paper lies in its empirical application which considers the Portuguese drinking water utilities. Inspired by the current debate in the Portuguese water sector, in which both the regulator and the water utilities are doubting on the optimal scale of operations, we examine the economies of scale in the sector. In addition, this application suits the branch of the literature which detects economies of scale in drinking water utilities. For example Sabbioni (2007) for Brazil using a sample of 1,163 water utilities for the period 2000–2004 found the regional companies ere more scale efficient than local ones. In Canada, Renzetti (1999) reports the occurrence of substantial economies of scale for a sample of 77 utilities in Ontario for the period 1997–2000. For England and Wales, Ashton (2000) and Cubbin and Tzanifdakis (1998) using a translog cost function and DEA conclude by the existence of significant economies of scale. In Italy, Antonioli and Filippini 2001 took the same conclusions applying a Cobb-Douglas function for a sample of 32 water utilities between 1991 and 1995. Garcia and Thomas (2001) for France using translog specification for the variable cost function found short-run scale economies and for the long-run the absence of economies of scale. In the USA, Garcia et al. (2004) for the 171 water utilities of the State of Wisconsin found scale economies for the vertically integrated small utilities. They use as well a translogatithic specification form. Frequently, scale economies are found for small utilities (where the optimal scale obviously depends on the characteristic of a country) while diseconomies of scale are detected for larger companies. In Brazil, Ohira and Shirota (2005), employing a Cobb-Douglas for 179 water utilities, observe diseconomies of scale. Saal and Parker (2005), for England and Wales, using an input distance function (total cost) show that no scale economies exist for the average sized firm. Mizutani and Urakami (2001) in Japan for the year 1994 for Japan using different parametric functional form specification found diseconomies of scale at the sample mean. The optimal size corresponds to an water utility which supply 261 millions m³ per year, has 1,221 km of mains length and serves 766.000 inhabitants.

The remainder of the paper unfolds as follows. In Sect. 2, we present the robust and conditional FDH model. Section 3 introduces the scaling of operations in non-convex technologies. Section 4 provides a three step framework to analyze the existence and extent of scale economies. In Sect. 5, we show by an empirical application the merits of our framework. Finally, we conclude.

2 Conditional FDH estimates

Prior to defining the economies of scale in frontier models, we explain the traditional non-convex Free Disposal Hull model (Deprins et al. 1984). This approach is a generalization of the more popular Data Envelopment Analysis (DEA) model (Charnes et al. 1978). The FDH approach, in contrast to DEA, it does not assume convexity but only free disposability of the production set. The latter indicates that a particular input-output combination should also be producible by using more inputs, or alternatively, by producing less outputs (an assumption in both FDH and DEA). A convex combination (i.e. a linear combination in which the coefficients are nonnegative) implicates that a linear combination of two feasible observations should also be feasible. This in turn implies additivity and divisibility of inputs and outputs. Additionally FDH is always consistency (nevertheless with a lower rate of convergence than DEA), as the FDH estimator is shown to be consistent for both convex and non-convex production sets (whereas DEA is only consistent when the true production set is convex) (see, e.g., Cherchye et al. 2000; Daraio and Simar 2007). As a drawback, FDH assumes that linear combination of two efficient observations cannot be feasible. Thus, it can underestimate potential improvements in efficiencies.

Algebraically, the production frontier set Ψ is defined as the set of all feasible input ($x\in {\mathbb{R}} _{+}^{p}$) and output ($y\in {\mathbb{R}} _{+}^{q}$) combinations of the n observations in the sample: $\Psi =\left\{ (x,y):x\hbox{ can produce }y\right\} .$ The non-convex technology FDH relies only on the free disposability assumption (i.e. if (x, y) ∈ Ψ then $(x^{\prime },y^{\prime })\in \Psi$ for x′ ≥ x and y′ ≤ y). As such, the FDH estimator of the technology set Ψ is characterized by:

$$ \Psi _{\rm FDH}=\left\{ (x,y)\in {\mathbb{R}} _{+}^{p+q}|x\geq x_{i};y\leq y_{i};i=1,...,n\right\} . $$

(1)

This technology set is graphically represented by a step-wise function. Relative to this best practice technology set, the efficiency of an observation can be measured horizontally (i.e. input-oriented) by deducing the minimal input combination which is required to produce the given output set y. Alternatively, efficiency can be measured vertically (i.e. output-oriented) by searching the maximal feasible output production for a given input combination. In the remainder of this article, we focus on the input-orientation (as this is the most natural for our particular application). In its mixed integer linear programming formulation, the FDH input-oriented inefficiency estimate can be computed as:

$$ \theta (x,y)=\min \left\{ \theta |\theta x\geq \sum\limits_{i=1}^{n}\lambda _{i}x_{i};y\leq \sum\limits_{i=1}^{n}\lambda _{i}y_{i};\sum\limits_{i=1}^{n}\lambda _{i}=1;\lambda _{i}\in \left\{ 0,1\right\} ;i=1,...,n\right\} . $$

(2)

The binary value of the intensity vector λ, combined with the condition that $\sum_{i=1}^{n}\lambda _{i}=1$ ensures that the efficiency evaluation is only effected from actually observed entities (in contrast to a convex combination of entities in DEA). In an input-oriented model, the target inputs (i.e. the efficient quantity of inputs) can be radially (i.e. without considering slacks or input excesses) computed as $x^{\ast }=x^{\ast} \theta (x,y)$. The efficiency score θ(x, y) varies between 0 and 1, where a value of 1 denotes an efficient observation. The latter is a necessary, although not a sufficient, condition for Koopmans (1951) efficiency (i.e. an increase in any output requires a decrease in at least one other output, while a decrease in any input demands an increase in at least one other input). A sufficient condition for Koopmans efficiency is the absence of (nonradial) slacks (see infra).

As the evaluation of efficiency is a relative concept, it is extremely sensitive to outliers (caused by, e.g. measurement errors, a-typical observations or exogenous factors). Therefore, we adapt the traditional FDH model to the robust order-m estimates as suggested by Cazals et al. (2002). This approach, which mitigates the impact of outlying observations, evaluates the efficiency relative to a partial reference set D ^r (with the size of $\left\vert D^{r}\right\vert =$ m < n observations) rather than to the full reference set (where $\left\vert D\right\vert =$ n). By drawing with replacement the partial reference set of size m (among those x _i such that y ≤ y _i ) for every observation i R times, and by averaging these R efficiency evaluations, we obtain an efficiency estimate θ^m(x, y) which mitigates the impact of a-typical observations. Following Daraio and Simar (2007), we select m as the value from which on the number of super-efficient observations (i.e. θ^m(x,y) > 1) decreases only marginally with m. By setting R large, we obtain more stable results and a lower standard deviation around the estimates (which is important for the second step of the framework, see infra). The standard deviation can be used to, e.g., compute confidence intervals or significance levels.

As an extension to the robust order-m procedure, Daraio and Simar (2005, 2007) introduced a methodology to incorporate heterogeneity in the efficiency evaluation. As such, the efficiency estimates are corrected for the influence of an exogenous factor z. These so-called conditional efficiency estimates θ^m(x, y|z) boil down to evaluating the FDH efficiency relative to the reference set D ^r,z. In turn, D ^r,z adapts the reference set D ^r (of size m) by drawing with replacement only (1) among the x _i where y ≤ y _i and (2) such that the probability of drawing an observation corresponds to $K((z-z_{i})/h)/\sum \limits_{j=1}^{n}K((z-z_{j})/h)$, where K(.) denotes a Kernel function and h an appropriate bandwidth as estimated by the cross-validation principle. In its mixed integer linear programming formulation, the traditional FDH efficiency score is adapted to its robust and conditional variant as follows:

$$ \theta ^{m}(x,y|z)=\frac{1}{R}\sum\limits_{r=1}^{R}\left[ \min \left\{ \theta |\theta x\geq \sum\limits_{i=1}^{n}\lambda _{i}x_{i};y\leq \sum\limits_{i=1}^{n}\lambda _{i}y_{i};\sum\limits_{i=1}^{n}\lambda _{i}=1;\lambda _{i}\in \left\{ 0,1\right\} ;(x_{i},y_{i})\in D^{r,z}\right\} \right] . $$

(3)

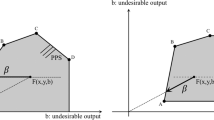
The traditional step-wise FDH frontier is represented graphically in the two-dimensional Fig. 1, with one input x on the horizontal and one output y on the vertical axis. The various input-output combinations, represented by the black dots, are observed and allow to estimate the true production technology set. The observations outside the technology frontier are outlying observations (e.g. due to measurement errors). In the order-m model the impact of these outlying observations is mitigated (although, the outlying observations are not removed from the analysis).

Fig. 1

The robust FDH model

3 Measuring scale economies

Within different intervals in the production set, different scaling of the operations could be present (Färe et al. 1994). The scaling represents the relation between a proportional change in the inputs and the resulting proportional change in the outputs. As these RTS are a characteristic of the shape of the frontier, different efficiency evaluation models can be deduced. By adding additional restrictions to the traditional FDH model, we are able to estimate the efficiency relative to different technologies (and thus different shapes) of the best practice frontier.² We start by exploring the RTS concepts, and subsequently demonstrate how to adapt the traditional FDH model to different RTS technologies.

3.1 The RTS concepts

The identification of the direction of RTS (see next section) requires the definition of three technologies (or assumptions on the shape of the best practice frontier). Firstly, in a Constant RTS (CRS) setting, a proportional increase in the inputs x delivers a proportional increase in the outputs y. Algebraically, the production set Ψ displays CRS if δΨ = Ψ for all δ > 0. A convenient characteristic of the CRS technology is that along the CRS frontier the average productivity (=y/x) remains constant. The observation with the highest average productivity is denoted as the Most Productive Scale Size (MPSS) (after Banker 1984). If efficiency is evaluated against the CRS frontier, the MPSS corresponds to the CRS-efficient observation. It is possible that several observations operate at the same average productivity such that each of them is an image of the MPSS (Banker and Thrall 1992). Secondly, the curvature of the frontier could exhibit Non Increasing RTS (NIRS) when a proportional increase in the inputs results in a less than proportional increase in the outputs. Formally, Ψ has NIRS if $\delta \Psi \subseteq \Psi$ for all 0 < δ ≤ 1. Thirdly, Non Decreasing RTS (NDRS) occurs if a proportional increase in the inputs creates a more than proportional increase in the outputs. Ψ displays NDRS if $\delta \Psi \subseteq \Psi$ for all 1 ≤ δ. The three technologies are interlinked as CRS is the union of the NIRS and NDRS: CRS = NIRS ∪ NDRS. Whereas in convex technologies (e.g. DEA) the Variable RTS (VRS) denotes the intersection between NIRS and NDRS (VRS = NIRS ∩ NDRS), in non-convex technologies VRS is only a subset of this intersection ($VRS\subseteq NIRS\cap NDRS$).

3.2 RTS in non-convex technologies

As in the traditional FDH model no particular assumptions are imposed on the intensity vector λ (besides summing to one), the traditional FDH model corresponds to VRS scenario. Under the VRS technology, no particular assumption on scaling is made so that VRS satisfies NDRS and NIRS in different intervals (see supra). Only recently, other assumptions on the frontier were proposed by Kerstens and Vanden Eeckaut (1999). Following the FDH principle of referring only to observed variables, their proposal adds additional structure to the step-wise frontier such that also proportional replicas of observed entities are included in the reference set. As such, it is possible to estimate FDH efficiency under CRS, NIRS and NDRS. As the former propose non-linear programming problems, Podinovski (2004a, c) suggests equivalent mixed integer linear programming problems. These in turn are further simplified (in terms of computational burden) by Soleimani-damaneh and Reshadi (2007). The dual representation is presented in Leleu (2006). We adapt the mixed integer linear programming formulation of Podinovski (2004a) to the conditional and robust efficiency estimates for, respectively, the CRS, the NIRS and the NDRS FDH frontier as follows:

$$ \begin{aligned} \theta ^{CRS,m}(x,y|z)=\min \left\{ \theta |\theta x\geq \sum\limits_{i=1}^{n}\lambda _{i}x_{i};y\leq \sum\limits_{i=1}^{n}\lambda _{i}y_{i};0\leq \lambda \leq Mb;\sum\limits_{i=1}^{n}b_{i}=1;b_{i}\in \left\{ 0,1\right\} ;(x_{i},y_{i})\in D^{r,z}\right\} ;\\ \theta ^{NIRS,m}(x,y|z)=\min \left\{ \theta |\theta x\geq \sum\limits_{i=1}^{n}\lambda _{i}x_{i};y\leq \sum\limits_{i=1}^{n}\lambda _{i}y_{i};0\leq \lambda \leq b;\sum\limits_{i=1}^{n}b_{i}=1;b_{i}\in \left\{ 0,1\right\} ;(x_{i},y_{i})\in D^{r,z}\right\} ;\\ \theta ^{NDRS,m}(x,y|z)=\min \left\{ \theta |\theta x\geq \sum\limits_{i=1}^{n}\lambda _{i}x_{i};y\leq \sum\limits_{i=1}^{n}\lambda _{i}y_{i};b\leq \lambda \leq Mb;\sum\limits_{i=1}^{n}b_{i}=1;b_{i}\in \left\{ 0,1\right\} ;(x_{i},y_{i})\in D^{r,z}\right\} \end{aligned} $$

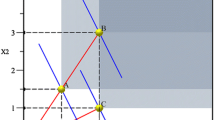
where M denotes the ratio of the largest element to the smallest (positive) element of x.³ In comparison to the traditional VRS-FDH model, the RTS assumption is imposed by adding a constraint, in particular a binary vector b which sums to one. Similar to the traditional VRS-FDH approach, this implies that every observation is evaluated against a single reference observation (x, y) although it could be rescaled by λ, which, by construction, can only be positive. In the CRS scenario, the scaling parameter λ is free (or more precisely, it is positive) such that every observation is evaluated against a proportional rescaling of the other observations. This is graphically represented in Fig. 2. Note that in the two-dimensional graph, the CRS-FDH frontier corresponds with the CRS-DEA frontier. In the CRS-FDH model, the inefficient observation Z ₁ is evaluated against a proportional decrease in activities of observation D, which is at MPSS. Observation Z ₁ could reach the same (maximal) average productivity as observation D if it could reduce its inputs to point $Z_{1}^{CRS}$. Assuming NIRS implies that the scaling parameter λ is constrained to non-larger proportional rescaling (i.e. 0 ≤ λ _i  ≤ 1) of a particular reference unit. Graphically, this corresponds for observation Z ₂ to a proportional decrease of reference observation G such that Z ₂ is evaluated in $Z_{2}^{NIRS}$. Similarly, for the NDRS, every inefficient observation is evaluated against non-smaller proportional rescaling (i.e. 1 ≤ λ _i ) of reference units. In the graphical example, observation Z ₁ is evaluated against a proportional increase of observation C in $Z_{1}^{NDRS}$. Remark that for observations which lie between two CRS efficient points (e.g. observation Z ₃) the CRS, NIRS and NDRS efficiency scores are equal (as the respective best practice frontiers overlap). Following the literature, we will label these observations in the next section as subconstant returns to scale.

Fig. 2

RTS in the robust FDH model

As Destefanis and Storti (2002) mention, the additional structure in terms of convexity which is imposed on the production set allows for a better discrimination among the observations. Indeed, frequently the VRS-FDH assumption was considered as too weak, as by construction many observations are considered as relatively efficient. Having defined the theoretical model on how to estimate RTS in a non-convex frontier model, we proceed by developing a three step framework.

4 A framework for empirical applications

In empirical applications, it is worthwhile to examine the economies of scale in three consecutive steps. In a first step, it is interesting to analyze whether the evaluated sector actually exhibits scale economies. As scale economies are often related to scope, we have to disentangle the two effects. In a second step, the direction of RTS has to be evaluated for each individual observation. Whereas the second step is an analysis on the micro level (the individual observation), the third step analyzes the macro level (the sector) by deriving the optimal scale of the operations for the sector as a whole.

4.1 Step 1: The existence of scale (and scope) economies

In a first step, we evaluate the very existence of scale economies. As shown by Baumol et al. (1988), the economies of scale are closely related to the economies of scope. Intuitively, if an observation produces several products (i.e. scope economies), this scope measure affects the scale of the operations as well. Therefore, in an analysis of scale economies, it could be useful to eliminate the interaction effect between scale and scope economies.

The existence of scale (and scope) economies is verified by an exploratory graphical tool, as introduced by Daraio and Simar (2005, 2007). The procedure requires a single scale (=z ₁) and scope (=z ₂) variable. Daraio and Simar suggest to compare the unconditioned robust VRS estimate θ^m(x, y) and conditioned θ^m(x, y|z) estimate by non-parametrically regressing (e.g. by the Nadaraya-Watson regression) the ratio $\theta ^{m}(x,y|z)/\theta ^{m}(x,y)$ against the conditioning variable z. In the obtained graph, an increasing regression line indicates a favorable effect to efficiency of the conditioned variable, while a decreasing regression denotes an unfavorable effect to efficiency from z. The absence of a graphical first order impact points to the absence of influence of z. Indeed, for a favorable variable (which can be considered as an unintended output) the conditional efficiency will be much lower than the unconditional efficiency for large values of z (implicating an increasing ratio between conditional and unconditional estimates with z). On the other hand, for an unfavorable variable (acts as an undesired input) the conditional efficiency will be significantly larger than the unconditioned estimates for larger values of z. In the multivariate framework, we non-parametrically regress the ratio of the partially conditioned efficiency scores (conditioned on only one environmental variable, say z ₁) to the fully conditioned efficiency scores (conditioned on both environmental variables, say z ₁ and z ₂) against the values of the conditioned variable (i.e. z ₂).

This exploratory tool has several advantages. Firstly, we can infer the effect of the ‘pure’ scale and scope economies. To evaluate the effect of scale economies while accounting for economies of scope; and vice versa, evaluating the ‘pure’ effect of scope economies (i.e. without scale economies), we decorrelate the scale and scope variables (e.g. by the use of a Mahalanobis transformation). Secondly, in contrast to many other studies in the literature, we measure the existence of scope economies without assuming a framework of different frontiers which are compared against each other (as, e.g. Färe et al. 1994; Kittelsen and Magnussen 2003; Arocena 2005), nor by requiring fully specialized units. These procedures are inconvenient as they introduce sample size bias (it is unlikely that the group of specialized units has the same size as diversified units) and require the existence of specialized units (which is rarely observed in reality). Finally, our approach does not involve the extrapolation and creation of hypothetical observations.

4.2 Step 2: RTS for individual observations

Several procedures to measure the direction of economies of scale have been proposed (although these are generally developed for the convex DEA model, the procedures apply for the non-convex FDH model as well) (for an overview see, e.g. Kerstens and Vanden Eeckaut 1999). The three most frequently used methodologies include the inspection of the sum of the intensity vector λ in a CRS model (Banker 1984), analyzing the convexity constraints in a VRS model (Banker et al. 1984; Banker and Thrall 1992) and comparing efficiency estimates for different scale assumptions (Färe et al. 1983). The equivalence of these basic procedures has been proved for DEA models by Banker et al. (1996) and Seiford and Zhu (1999). Among the many extensions for these methodologies, for the remainder of this article, we focus on a particular extension of the Färe et al. (1983) approach as introduced by Podinovski (2004b).

First consider the difference between local and global RTS. On the one hand, local economies of scale measure within a small neighborhood of the evaluated observation the change in outputs by a change of the inputs. As such, local RTS estimate the immediate gains in productivity of a small resizing in operation. It can be measured by looking at the ratio of marginal to average change in productivity. If this ratio, also called the scale elasticity (SE), is larger than one (i.e. marginal productivity is larger than average) the observation exhibits Increasing RTS. As such, a proportional increase in the inputs results for this particular observation in a larger percentage increase of the outputs. An observation with a SE smaller than one (i.e. larger average than marginal productivity) displays Decreasing RTS (DRS). Obviously, SE of 1 indicates CRS.⁴

On the other hand, the global RTS estimate the global (and long run) improvements in productivity. Therefore, the global RTS indicate the optimal productivity of an observation. In a convex setting the local and global RTS coincide (e.g. in the convex DEA model). However, if the assumption of convexity of the production set is relaxed (e.g. in FDH), different outcomes between local and global estimations are obtained. To account for this, Podinovski (2004b) introduced in addition to the traditional CRS, IRS and DRS, the sub-constant RTS (SCRS) which indicate that an observation can move towards its most productive scale (i.e. its long run CRS benchmark) by either reducing or increasing its scale. This becomes in particular relevant when several observations have the same maximal average productivity (=y/x) and hence, when multiple observations are at the MPSS. In this sense, the SCRS are an extension of the work of Banker and Thrall (1992) who considered the existence of multiple MPSS.

An observation exposes

• CRS $\iff \,\theta ^{VRS}(x,y)=\theta ^{NIRS}(x,y)=\theta ^{NDRS}(x,y);$

• IRS $\iff \,\theta ^{VRS}(x,y)\geq \theta ^{NIRS}(x,y)>\theta ^{NDRS}(x,y);$

• DRS $\iff \,\theta ^{VRS}(x,y)\geq \theta ^{NDRS}(x,y)>\theta ^{NIRS}(x,y);$

• SCRS $\iff \,\theta ^{VRS}(x,y)>\theta ^{NIRS}(x,y)=\theta ^{NDRS}(x,y).$

where CRS corresponds to the MPSS, IRS (DRS) occur if the observation is smaller (larger) than all MPSS. SCRS corresponds to the observations which produce between two MPSS sizes. In the outlined RTS detection procedure, we did not account for uncertainty and heterogeneity in the sample by the robust and conditional efficiency estimates. In examining robust efficiency, we use the same reference sets for each of the VRS, CRS, NIRS and NDRS efficiency evaluations (which is redone R times). Observations where $\theta ^{NIRS,m}(x,y|z)=\theta ^{CRS,m}(x,y|z)>\theta ^{NDRS,m}(x,y|z)$ undoubtly display IRS, observations where $\theta ^{NDRS,m}(x,y|z)=\theta ^{CRS,m}(x,y|z)>(=)\theta^{NIRS,m}(x,y|z)$ undoubtly exhibit DRS (CRS). However, due to the resampling, it is possible that the CRS estimate differs from both NIRS and NDRS estimate. To account for this deviation, we employ the Monte-Carlo confidence intervals around the CRS estimate (although the analysis would work around the NDRS and NIRS estimates as well). Denote $\tilde{\theta}^{CRS,m}(x,y|z)$ as the confidence interval of one standard deviation around θ^CRS,m(x, y|z) (i.e. if normality is assumed, θ^CRS,m(x, y|z) ± st.dev. of the estimate corresponds to the 68.3% confidence interval). An observation exhibits IRS if θ^NIRS,m(x, y|z) falls inside the $\tilde{\theta}^{CRS,m}(x,y|z)$ interval while θ^NDRS,m(x, y|z) does not (specifically, the NDRS score is lower than the CRS lower bound). Contrarily, DRS are observed if θ^NDRS,m(x, y|z) is part of the interval around the CRS estimate (denoted by $\theta ^{NDRS,m}(x,y|z)=\tilde{\theta}^{CRS,m}(x,y|z)$) while the NIRS score is larger than the CRS upper bound (denoted by $\theta ^{NIRS,m}(x,y|z)>\tilde{\theta}^{CRS,m}(x,y|z)$). SCRS occurs if both the NIRS and NDRS estimate belong to the $\tilde{\theta}^{CRS,m}(x,y|z)$. Summarizing, in a robust and conditional framework, we say that an observation exhibits:

• CRS $\iff \,\theta^{VRS,m}(x,y|z)=\theta^{NIRS,m}(x,y|z)=\theta^{NDRS,m}(x,y|z)=\tilde{\theta}^{CRS,m}(x,y|z);$

• IRS $\iff \,\theta ^{VRS,m}(x,y|z)\geq \theta ^{NIRS,m}(x,y|z)=\tilde{\theta}^{CRS,m}(x,y|z)>\theta ^{NDRS,m}(x,y|z);$

• DRS $\iff \,\theta ^{VRS,m}(x,y|z)\geq \theta ^{NDRS,m}(x,y|z)=\tilde{\theta}^{CRS,m}(x,y|z)>\theta ^{NIRS,m}(x,y|z);$

• SCRS $\iff \,\theta^{VRS,m}(x,y|z)>\theta^{NIRS,m}(x,y|z)=\theta^{NDRS,m}(x,y|z)=\tilde{\theta}^{CRS,m}(x,y|z).$

Observations exhibiting SCRS could obtain the MPSS by both increasing or decreasing the scale of operations. In the traditional (non-robust) model, no statement could be made on the optimal direction. In the robust framework, we exploit the difference, arising from redrawing, between the CRS, NIRS and NDRS efficiency estimates. An observation with SCRS should optimally increase (decrease) its scale of operations if the NIRS (NDRS) estimate is closer to the CRS estimate than the NDRS (NIRS) estimate. Formally, an observation satisfying SCRS exhibits:

• SCRS-IRS $\iff \,|\theta^{NIRS,m}(x,y|z)-\theta^{CRS,m}(x,y|z)|<|\theta ^{NDRS,m}(x,y|z)-\theta^{CRS,m}(x,y|z)|;$

• SCRS-DRS $\iff \,|\theta^{NIRS,m}(x,y|z)-\theta^{CRS,m}(x,y|z)|>|\theta ^{NDRS,m}(x,y|z)-\theta ^{CRS,m}(x,y|z)|$.

4.3 Step 3: Deriving the optimal scale size

In an empirical analysis, it is interesting for both the individual observation and the policy makers to verify the optimal scale of the operations. If cost (or price) variables are available, we can make a simple graphical analysis which exploits the idea of MPSS (i.e. the highest average productivity) and link it to the lowest cost per unit of production (the cost variables are needed to make a sensible aggregation of the heterogeneous inputs). In particular, we propose a continuous representation of the MPSS-concept. We suggest two assessments of the optimal scale, an ‘overall’ and a ‘specific’ optimum which, respectively, do and do not account for slacks in the inputs. Allowing for slacks could yield additional insights.

In both scenarios, we start from the observation that the MPSS corresponds to the CRS optimum (Banker 1984). In an input-oriented framework, when multiplying the input variables by the efficiency score θ^CRS,m(x, y|z) we obtain the minimum required inputs to produce the given amount of outputs (see supra). In the first scenario, the ‘overall’ optimum, we first assess the efficiency by considering all inputs x ($\in {\mathbb{R}} _{+}^{p}$) and all outputs y ($\in {\mathbb{R}} _{+}^{q}$) (i.e. compute θ^CRS,m(x, y|z)) and, second, multiply each of the inputs by this CRS efficiency score to obtain the efficient input quantity: $x^{\ast }=x\times \theta ^{CRS,m}(x,y|z).$ Thirdly, to obtain a minimal cost interpretation, the inputs are multiplied by their respective price vectors: ${\text{min}}_{{{\text{cost}}}} = x^{\ast} \times p.$ As in this scenario slacks are neglected, the obtained cost corresponds to the minimal overall cost to produce the given output (i.e. particular inputs will still contain some inefficiency). Finally, to infer the optimal scale, we divide the minimal cost by a one-dimensional measure for the production and non-parametrically regress this ratio against the production measure. In the obtained graph, the minimal overall cost can easily be recovered as the value with the lowest horizontal tangent.

The ‘specific’ optimum, i.e. the second scenario, accounts for slacks by estimating the linear programming problem for each input separately. In contrast to the first scenario, which computes the efficiency relative to all inputs and outputs, the specific optimum assesses in an input-oriented model the efficiency for every input x _P (P = 1, ..., p) separately against the outputs y ($\in{\mathbb{R}} _{+}^{q}$). As such, one obtains for each observation P (i.e., the number of inputs) conditional efficiency scores θ ^CRS,m _P (x _P , y|z).⁵ This approach allows us to account for slacks in the FDH model and consequently satisfies the necessary and sufficient condition for Koopmans efficiency. The minimal cost of this input is computed by multiplying $\theta _{P}^{CRS,m}(x_{P},y|z)\times x_{P}\times p_{P}$. Aggregating the minimal cost levels of the different inputs, we obtain a minimal specific cost which, once divided by a unit of production, delivers the minimal cost level.

The use of this graphical presentation provides a convenient tool for policy assessment. Remark that this optimal scale determination, although using input prices, still assesses technical efficiency and is not concerned with the allocative efficiency.

5 Empirical application

Drinking water provision in Portugal is performed by 300 small companies. Typically, a drinking water utility delivers water to 36,000 inhabitants (compare with, e.g. 1.5 million in the Netherlands, 2.6 million in England and Wales, 95,000 in Australia or 5,000 in Spain). The literature frequently indicates the presence of economies of scale for small utilities and the absence of scale economies for larger utilities (cfr. introduction). The current discussion in the Portuguese drinking water sector focuses on the extent and potential to obtain scale economies. Both the sector regulator (IRAR, Institute for the Regulation of Water and Waste) and the government are discussing the appropriate long term (i.e. global) scale of operations. To analyze the presence of scale and scope economies (about 80% of the companies provide both water and sewerage services, while about 20% of the utilities have also other revenues (mainly in transportation and solid waste)) and to determine the optimal scale, we apply the above sketched framework.

We obtained data from the annual accounts for the 63 largest drinking water utilities (corresponding to 60% of the total Portuguese drinking water sector). ⁶ The data correspond to observations for 2005. We selected three common input variables: cost of labor, cost of capital and other costs (all expressed in euro). The sum of these input variables delivers the total expenditures (TOPEX). Also the output variables are common in the literature: the volume of delivered water (m ³), the number of water customers and the number of sewerage customers. As exogenous environmental factor we selected the monthly peak factor. The latter denotes in a time span of a year the maximal ratio of monthly consumption to the yearly average. Therefore, higher deviations from one are extremely expensive for the utilities as large investments for water consumption are required during only a short peak period (e.g. utilities delivering water to holiday resorts have high peak factors). To capture scale economies (which is required in the first step of the framework) we use the sum of total revenues from water and sewerage (which is observed in the annual accounts). Scope economies are determined as the share of the revenues of non-drinking water delivery services (mainly sewerage, solid waste and transportation) in total revenues. We present the summary statistics in Table 1.

Table 1 Summary statistics

5.1 Step 1: The existence of scale and scope economies

After decorrelating the scale and scope variables, the robust (m = 30; R = 200) and conditional (on peak factor, scale and scope) efficiency estimates are explored. ⁷ We present the graphical analysis in Figs. 3 and 4. First consider Fig. 3 where the effect of the conditioning variable (the decorrelated scale variable which varies between −0.75 and 4.25) is drawn against the ratio of conditioned to unconditioned estimates. The graph reveals an upward slope with respect to the scale economies. As outlined before, the increasing regression line indicates the existence of scale economies for small utilities (note that we obtained very similar results for undecorrelated scale and scope estimates). This indicates that our results strengthen the literature on the existence of scale economies for small utilities. An intuitive reasoning for the absence of scale economies for large utilities can be found in the increasing complexity of the network and the subsequent difficulties in managing the complex network. From Fig. 4, we can derive the absence of scope economies (similar results for undecorrelated scale and scope proxies are obtained). These results are not in line with the literature which frequently finds economies of scope (e.g. Garcia et al. 2004; Torres and Morrison 2006 for USA; Garcia and Thomas 2001 for France; Ashton, 2000 for England and Wales). Intuitively, scope economies are unobserved because (similar to scale economies) they increase the complexity of organization which induces a larger bureaucratic burden. As we do not find scope economies, in the remainder of this empirical application we will neglect the scope economies and concentrate on the

Fig. 3

Effect on scale economies on the frontier

Fig. 4

Effect of scope economies on the frontier

5.2 Step 2: Measuring scale economies

In this second step, we compute for every particular observation the RTS (i.e. CRS, DRS, IRS or SCRS). The main conclusions are summarized in Table 2. ⁸ All model specifications are robust and conditional (with the peak factor as an exogenous variable). Without accounting for slacks, in the ‘overall’ model (with three inputs and three outputs) we count more than half of the observations which are, overall, producing at their MPSS. This can be attributed to the FDH model specification which allows for specialization in a particular input or output variable. However, the picture changes if slacks are considered (i.e. the ‘specific’ model). On the one hand, the specific model with labor cost as input suggests that about half of the utilities have excessive labor costs as they exhibit DRS in that variable. Also from the utilities operating under SCRS, the majority of the entities is advised to scale-down. On the other hand, the utilities could increase their average productivity by investing in capital as about a third of the utilities display IRS in that variable. Remark that about half of the utilities work under SCRS. Finally, also other costs are too high as a third of the utilities exhibits DRS in the cost variable. The difference between the overall and the specific model indicates the added value of analyzing more in detail the RTS.

Table 2 RTS for individual observations

5.3 Step 3: Deriving the optimal scale

In a final step, we try to provide some arguments in the discussion on the optimal scale in the Portuguese drinking water sector. Applying the previously outlined procedure, we derive the optimal scale in Fig. 5 for robust and conditional (on peak factor) estimates. We estimate production one-dimensionally by the volume of delivered drinking water (experiments with other production proxies (e.g. number of customers, total revenues) delivered very similar results). First consider the ‘overall’ optimal scale (without accounting for slacks in the input variables). According to the non-parametric regression, the lowest cost per customer corresponds to the largest observation (about 62 million m³ of water). However, this result is somewhat biased by the a-typical characteristics of Lisbon. Ignoring this largest observation, the overall optimum reveals about 10 million m³ of water delivery as an optimum. This minimal cost of production follows after a decreasing cost per m³ for the many small utilities in the sample and is proceeded by increasing costs per m³ for the larger (with exception for Lisbon). Secondly, consider in Fig. 6 the ‘specific’ scenario where each input variable is performing on its absolute minimal cost (i.e. even accounted for slacks). The optimal scale remains robust to the inclusion of slacks. The specific minimal cost is situated between 7 and 10 million m³ of water if the a-typical observation of Lisbon is neglected. Despite the similarity between the overall and specific optimal scale, we consider the specific optimum as superior. Indeed, the cost per m³ in the overall scenario hides the DRS for labor costs and the IRS for capital costs (see step 2). By considering the optimal input use for both labor, capital and other inputs, the specific optimal scale measure seems to be more reliable. This is in line with previous research for Portugal in particular (e.g. Martins et al. 2006) and the scale economies literature in general, as the results strengthen the natural monopoly idea.

Fig. 5

Optimal scale—overall scenario

Fig. 6

Optimal scale—specific scenario

6 Conclusion

In this paper, we analyzed the scale economies for non-convex frontier models, in particular the Free Disposal Hull (FDH) model. We adapted the model of Podinovski (2004a, c), which is a linearization of the model of Kerstens and Vanden Eeckaut (1999), to robust (i.e. allowing for uncertainty) and conditional (i.e. allowing for heterogeneity) efficiency estimates. Subsequently, we provided a framework to empirically analyze the economies of scale. After testing the existence of scale (and scope) economies, we derived, for both individual observations and the sector as a whole, the optimal scale. The framework is applied to the Portuguese drinking water sector. Our results indicate the existence of scale economies and the absence of scope economies. Further analyzing the RTS, we observe that, if all inputs are considered simultaneously, most utilities are performing at their MPSS. However, these results hide the inefficient scale for each of the input variables separately as, optimally, the utilities should decrease the labor and increase the capital expenditures. Examining the optimal scale, we find, for the sector as a whole, that the minimal costs are situated around 7–10 million m³. This denotes that Portugal optimally counts about 60 utilities (in contrast to the 300 utilities now).

Appendix

See Table 3.

Table 3 Portuguese utilities in 2005