Accurate photosynthetic parameter estimation at low stomatal conductance: effects of cuticular conductance and instrumental noise

Abstract

Accurate estimation of photosynthetic parameters is essential for understanding plant physiological limitations and responses to environmental factors from the leaf to the global scale. Gas exchange is a useful tool to measure responses of net CO₂ assimilation (A) to internal CO₂ concentration (C_i), a necessary step in estimating photosynthetic parameters including the maximum rate of carboxylation (V_cmax) and the electron transport rate (J_max). However, species and environmental conditions of low stomatal conductance (g_sw) reduce the signal-to-noise ratio of gas exchange, challenging estimations of C_i. Previous works showed that not considering cuticular conductance to water (g_cw) can lead to significant errors in estimating C_i, because it has a different effect on total conductance to CO₂ (g_tc) than does g_sw. Here we present a systematic assessment of the need for incorporating g_cw into C_i estimates. In this study we modeled the effect of g_cw and of instrumental noise and quantified these effects on photosynthetic parameters in the cases of four species with varying g_sw and g_cw, measured using steady-state and constant ramping techniques, like the rapid A/C_i response method. We show that not accounting for g_cw quantitatively influences C_i and the resulting V_cmax and J_max, particularly when g_cw exceeds 7% of the total conductance to water. The influence of g_cw was not limited to low g_sw species, highlighting the importance of species-specific knowledge before assessing A/C_i curves. Furthermore, at low g_sw instrumental noise can affect C_i estimation, but the effect of instrumental noise can be minimized using constant-ramping rather than steady-state techniques. By incorporating these considerations, more precise measurements and interpretations of photosynthetic parameters can be obtained in a broader range of species and environmental conditions.

Introduction

Gas exchange is a powerful tool in plant physiology that allows us to understand CO₂ and water relations in plants to compare plant performance in a range of environments (Stinziano and Way 2017; Vincent et al. 2017; Smith et al. 2020), to describe how plants cope with challenging environments (Kumarathunge et al. 2019; Zhu et al. 2020), and to model plant-environment interactions up to the global scale (Oleson et al. 2013; Rogers et al. 2017; Lombardozzi et al. 2018). However, gas exchange measurements require a sufficient signal-to-noise ratio to obtain high-quality data for inferences. This can be achieved by ensuring stomata are adequately open or by incorporating a model that accounts for cuticular conductance (g_cw) (Márquez et al. 2021). However, many lines of research specifically address either species or conditions that produce low stomatal conductance, including xerophytic species, conditions of water deficit, or high temperatures. A comprehensive understanding of the factors affecting gas exchange measurements, including stomatal conductance (g_sw) and g_cw, is crucial for obtaining accurate data and drawing sound conclusions (See Table 1 for a list of abbreviations and equations).

Table 1 Abbreviations, variables, and equations used to calculate conductances and estimate net assimilation and internal CO₂

Stomatal conductance is a vital process that has a direct impact on plant growth and productivity, as it constrains photosynthesis and water-use. Plant species present a wide variation in g_sw depending on leaf morphology, physiology, ecotype, and environment, with many exhibiting low conductance. Low g_sw presents a challenge to the estimation of photosynthesis, particularly in C3 species with maxima below 0.2 mol m⁻² s⁻¹ (Körner et al. 1986; Tezara et al. 1998), and rapid stomatal closure whenever conditions are not ideal (Radin et al. 1994) or at a particular time of day (Steppe et al. 2006). For example, in a survey of Citrus x sinensis (L.) and C. reticulata (Blanco), 35% of the mid-morning (9:00 am-11:00 am) gas exchange measurements exhibited total leaf conductance to water (g_lw) below 0.08 mol m⁻² s⁻¹ (Vincent et al., unpublished data). When g_lw is low, the signal-to-noise ratio in gas exchange measurements is also low. Additionally, it becomes difficult to obtain a sufficient range in intercellular CO₂ concentration (C_i) to characterize the response of net CO₂ assimilation (A) to C_i (A/C_i curves) (Stinziano et al. 2020). Further compounding the signal-to-noise challenge in the context of A/C_i curves, plants respond to elevated CO₂ by stomatal closure on an order of minutes.

Using A/C_i curves, we can apply the Farquhar-von Caemmerer-Berry model of photosynthesis (Farquhar et al. 1980) to estimate photosynthetic parameters for comparing plant performance (Way and Sage 2008), understanding photosynthetic acclimation (Kumarathunge et al. 2019), and modelling vegetative carbon uptake (Oleson et al. 2013). In species or conditions with low g_sw or stomata that close rapidly at high CO₂, such as those seen in evergreen broadleaved species, these responses are difficult to characterize (Lin et al. 2023). Stomatal limitations may further lead to incorrect conclusions on what is limiting photosynthesis. For example, it is possible to misinterpret a stomatal limitation as a constraint related to Rubisco carboxylation. The recent development of rapid A/C_i response (RACiR) curves (Stinziano et al. 2017, 2019a, b) and subsequently of the dynamic acclimation approach which allows more efficient use of constant-ramping methods (Saathoff and Welles 2021) may be sufficiently fast to circumvent the difficulties of stomatal closure in such species.

Although g_lw is often assumed equal to g_sw, this is not entirely accurate. Cuticular conductance (g_cw) is a component of g_lw and a key factor that impacts gas exchange measurements in plants, as it involves the diffusion of gases across the cuticle layer of leaves (Márquez et al. 2022). Although in practice it is usually not considered, g_cw can impact A/C_i measurement, because the ratio of conductance to H₂O and to CO₂ is dramatically different between stomata and cuticles. The diffusivity of H₂O and CO₂ through the stomata have a ratio of 1.6, which forms the basis of estimates of stomatal conductance to CO₂. However, the cuticle is a stronger barrier to CO₂ than H₂O where the diffusivity of H₂O is much higher than that of CO₂ with a ratio of 1:20–40 (Boyer et al. 1997; Boyer 2015b). In addition, overlooking g_cw can be problematic because, in certain cases, it can reach levels as high as 28% of g_lw (Holmgren et al. 1965; Boyer et al. 1997). Because estimates of C_i are based on total conductance to CO₂ (g_tc), assuming that g_lw = g_sw can lead to misestimating C_i (Table 1; Boyer 2015b). Variations in g_cw among plant species can significantly affect the accuracy of gas exchange measurements (Márquez et al. 2021; Boyer et al. 1997), particularly in low-conductance species (Márquez et al. 2022).

Previous studies have highlighted the impact of g_cw on gas exchange measurements and underscored the need for appropriate correction methods to ensure accurate measurements (Grassi and Magnani 2005; Tominaga et al. 2018). However, estimating g_cw separately from g_sw, which usually governs gas diffusion through the leaf surface under illuminated conditions, has been a major challenge. Consequently, it is often neglected in gas exchange calculations. In this regard, a recent study by Márquez et al. (2022) has proposed a new approach, called the red-light method, which estimates g_cw from gas exchange measurements and a known CO₂ concentration within the leaf during photosynthetic induction under red light. This novel method enables accurate estimation of g_cw, the inclusion of which can improve the precision of gas exchange measurements. Lamour et al. (2022) recently provided a theoretical reassessment of the impact of g_cw in the measurement of A/C_i curves and the parameters calculated from them, using real A/C_i curves and applying a range of hypothetical g_cw. In practice, many researchers face species or conditions of highly variable g_lw. Thus, knowledge of the impact of these factors and how to circumvent the resulting limitations in practice is essential, especially under low g_lw conditions.

In this work, our objective was to assess the impact of g_cw, g_sw, and other sources of error on the validity of estimates of photosynthetic parameters. To test the impacts of g_cw and g_sw we selected four species that vary in both. We used the red-light method of g_cw measurement and steady state and RACiR methods to estimate A/C_i-based parameters in these species with varying g_cw and g_sw. Although the RACiR method has been superseded by a dynamic assimilation technique (DAT; Tejera-Nieves et al. 2024), which eliminated the need for running empty-chamber curves, the utility of both RACiR and DAT in terms of the use of constant-ramping and frequent logging to assess A/C_i are interchangeable. We modeled the impact of g_lw and g_cw on C_i estimates and developed criteria to understand the impact of conductance on the reliability of A/C_i curves and the resulting parameters and provide this model for future work.

Materials and methods

Modeling the impact of stomatal and cuticular conductance on estimates of internal CO ₂

To estimate the impact of g_lw on the estimation of C_i we modeled the estimation of C_i in response to varying external CO₂ concentrations (C_a) and g_sw. To achieve this we used the Photosyn() command in the {plantecophys} package (Duursma 2015). This model allowed us to fix vapor pressure deficit (1.5 kPa) and C_a (100, 400, or 2000 ppm), along with temperature (25 °C) and maximum rates of carboxylation (50 µmol m⁻² s⁻¹) and electron transport (100 µmol m⁻² s⁻¹), which are the default values in the model. We considered a range of g_lw values from 0.001 to 1 mol m⁻² s⁻¹ in increments of 0.001 mol m⁻² s⁻¹ to cover the full range of expected values from medium to low conductance species. C_i was initially calculated according to the standard calculations of most gas exchange equipment. This calculation is based on von Caemmerer and Farquhar (1981) as:

$${C}_{i}=\frac{\left({g}_{tc}-\frac{E}{2}\right){C}_{a}-A}{\left({g}_{tc}+\frac{E}{2}\right)}$$

(1)

where g_tc is total conductance to CO₂, which was estimated as:

$${g}_{tc}=\frac{1}{\left(K+1\right)\frac{1.6}{{g}_{sw}}+\frac{1.37}{{g}_{bw}}}+\frac{K}{\left(K+1\right)\frac{1.6}{{g}_{sw}}+K\frac{1.37}{{g}_{bw}}}$$

(2)

where 1.6 and 1.37 are the ratios of diffusivity of CO₂ to H₂O in air (in stomata) and in the boundary layer. K is the ratio of stomatal resistance of the adaxial to abaxial sides of the leaf. For this consideration, we set K = 0, which is common for low conductance species, and boundary layer conductance to water (g_bw) as 2.23 mol m⁻² s⁻¹. These equations are standard for estimates in gas exchange. If K = 0 and g_bw is large enough to be ignored, as is expected in most gas exchange measurement contexts (Márquez et al. 2021), then Eq. 2 can be simplified as: ${g}_{tc}=\frac{{g}_{sw}}{1.6}$, which assumes that g_lw≈g_sw.

At high g_lw, this assumption may be roughly correct. However, as g_lw decreases relative to g_cw, the assumption is likely to become less tenable and increasingly impact estimates of C_i, because the cuticular conductance to CO₂ (g_cc) is expected to be approximately 0.05 g_cw (Márquez et al. 2022). Thus, we corrected the original g_lc by calculating:

$${g}_{sw}={g}_{lw}-{g}_{cw}$$

(3)

$${g}_{lc}=\frac{{g}_{sw}}{1.6}+\frac{{g}_{cw}}{20}$$

(4)

where 1:20 is the expected proportion of g_cw to g_cc (Boyer et al. 1997). Because the Photosynth() command assumes g_lw = g_sw and does not allow explicit parameterization of g_tc, but calculates g_tc = g_lw/1.6 (Duursma 2015), we recalculated a pseudo-g_lw to result in the corrected g_tc by multiplying the corrected g_tc by 1.6. C_i was then recalculated based on the new estimate of g_lc. We then calculated the proportional misestimation of C_i (C_{i mis}) when not accounting for g_cw as the difference between uncorrected C_i (C_{i uncorr}) and corrected C_i (C_{i cor}) as a proportion of C_i C_{i cor}:

$${C}_{i mis}=\frac{{C}_{i uncorr}{-C}_{i cor}}{{C}_{i cor}}$$

(5)

Plant material

Papaya (Carica papaya L.), bell pepper (Capsicum annuum L.), citrus (C. x sinensis cv. ‘Valencia’) and magnolia (Magnolia grandiflora L.) plants were grown in a greenhouse in Lake Alfred, FL 33850, USA (28.1021° N, 81.7121° W) in a natural diurnal cycle and daily maximum and minimum of ~ 25–34 °C. All plants were irrigated twice a week to ensure that the growing media 'Pro-mix BX' (Premier Tech Ltd, Quebec, Canada) remained adequately moist and were fertilized with 12-4-8 Miracle-Gro liquid fertilizer (The Scotts Company, LLC) every 2 weeks. SS and RACiR curves were performed on healthy and fully expanded leaves. In total, five plants each for bell pepper, magnolia, and papaya were measured, while 18 citrus plants were used.

Gas exchange measurements

Response curves were measured using a portable infrared gas analyzer (LI-6800, Li-COR Inc., Lincoln, NE, USA) (Console version: Bluestem v.1.4.02) equipped with a 3 × 3 cm leaf chamber (9 cm²). Leaf chamber settings were as follows: fan speed of 10,000 rpm, flow rate of 300 μmol s⁻¹ and 600 μmol s⁻¹ (for RACiR and SS, respectively), overpressure of 0.1 kPa, 24 mmol mol⁻¹ of H₂O in the reference cell producing between ~ 63% and 79% relative humidity (RH) in the leaf chamber, and producing a variation of ~ 2 to 3% in RH over the course of measurements, photosynthetically active radiation of 1200 µmol m⁻² s⁻¹ [90% red and 10% blue light], and chamber air temperature at 25 °C. We first measured paired standard RACiR and SS to compare parameter estimates from each. Each set of RACiR and SS curves was gathered on adjacent leaves of the same plant (not on the same leaf to avoid the effects of the first curve on the results of the second) on the same day.

Rapid A/C _i response (RACiR) curves

RACiR data were gathered beginning at a reference CO₂ concentration of 100 µmol mol⁻¹ with a ramping rate of 100 µmol mol⁻¹ min⁻¹, ending at 900 µmol mol⁻¹. After testing paired measurements, we gathered five additional RACiR curves from five plants each for all four species, this time the C_a range was 100 µmol mol⁻¹ to 2000 µmol mol⁻¹ with the same 100 µmol mol⁻¹ min⁻¹ ramping rate. Before each curve, the IRGA was matched to allow the system to stabilize in match mode. The empty chamber curves were determined in exactly the same way as the RACiR curves, except that the leaves were not clamped. Moreover, one empty chamber curve was used to calibrate the two leaf runs taken within 1 h. For all measurements, the leaf chamber was clamped on the leaf and allowed to acclimate to set environmental conditions until A reached a steady state before running the CO₂ response curves; however, the acclimation time was variable among species. The ‘Autolog’ program of LI-6800 was used to record data every 2 s (9 min and 19 min for RACiR when CO₂ concentration was set at 100–900 µmol mol⁻¹ and 100–2000 µmol mol⁻¹, respectively).

Steady-state A/C _i curves

The LI-6800 CO₂ response program was used for the steady-state (SS) A/C_i curves. Firstly, all environmental conditions were set the same as the RACiR curves except for the CO₂. Secondly, the sample CO₂ was set to 380 µmol mol⁻¹ CO₂. All leaves were acclimated to set environmental conditions until A reached a steady state before running the CO₂ response curves. SS curves were collected starting at a reference CO₂ concentration of 380 µmol mol⁻¹, then proceeding through the following progression conditions: 285, 190, 145, 100, 50, 380, 475, 570, 665, 760, 960, 1160, 1460, 1760, 1960 µmol mol⁻¹ CO₂ with minimum and maximum waiting times of 60 s and 120 s, respectively. The reference and sample IRGAs were matched before each measurement (Stinziano et al. 2017), and the measuring time for each SS A/C_i curve was approximately 30 min.

Measurement of cuticular conductance (g _cw )

The g_cw was estimated using the red-light technique introduced by Márquez et al. (2021). Briefly, the plants were dark-adapted for 12 h. A leaf was then placed in the darkened LI-6800 chamber and allowed to acclimate to 400 µmol mol⁻¹ CO₂, 25 °C, and 24 mmol mol⁻¹ of H₂O in the reference before recording dark respiration (R_dark). The dark-acclimated leaf was subsequently exposed to the same environmental conditions as those for R_dark measurements, except that 100 µmol m⁻² s⁻¹ red light was applied, and measurements were taken every 7 s during the light induction until the maximum A was achieved, and over 5 min at steady state.

To determine the rate of electron transport or the electron transport rate at a given CO₂ concentration (J_a) and gamma star (Γ*, represents the CO₂ photo-compensation point) during the experiment, a RACiR curve was performed under the same conditions as during the red-light induction, with the exception that stomatal opening is promoted using 100 µmol m⁻² s⁻¹ red-blue (40 µmol m⁻² s⁻¹ blue), and a CO₂ concentration ranging from 100 µmol mol⁻¹ to 1400 µmol mol⁻¹ with a 100 µmol mol⁻¹ min⁻¹ ramping rate. The leaf chamber was clamped onto the leaf and allowed to acclimate to the set environmental conditions until A reached a steady state before running the CO₂ response curves.

Analysis

Raw data obtained for each leaf sample were filtered and corrected using the empty chamber data as per the protocol for RACiR curve correction provided by Coursolle et al. (2019). RACiR data were calibrated using the {racir} R package (Stinziano et al. 2019a; Lawrence et al. 2019; Stinziano 2020). All curves were fit using the fitaci() command from the {plantecophys} package (Duursma 2015; Pilon et al. 2018) in R statistical software (R Core Team 2013), with options selected to fit triose phosphate utilization (TPU) limitation rate and with no temperature correction. We extracted the maximum Rubisco carboxylation capacity (V_cmax), maximum electron transport rate under saturating light (J₁₂₀₀), triose phosphate utilization (TPU), dark respiration (R_dark), the C_i at the CO₂ to RuBP transition (C_itrans1), and the C_i at RuBP to TPU transition (C_itrans2) for analysis. Subsequently, all A/C_i curves were fit with uncorrected and corrected g_sw values to assess the impact of g_cw on parameter estimates.

Statistics

The resulting parameters from the fit curves were subjected to analysis of variance and paired Student’s t-tests by using Statistix 8.1® software to test for differences between SS and RACiR curves. These tests were performed on A/C_i curves derived with uncorrected and corrected g_sw. Multiple comparisons were performed with Tukey’s honestly significant difference (Tukey’s HSD), and differences were significant when P < 0.05. Data in the figures were processed and analyzed with R (R version 4.1.1, 2021 "Kick Things").

Data and code

Data and code are available in supplementary files S1.

Results

At low g _sw , C _i estimates become unreasonable

There was a strong impact of g_lw on C_i. C_a also impacted the response dynamics, increasing the magnitude of C_i reduction in response to reduced g_lw (Fig. 1). The impact of g_lw at a C_a of 100 ppm was negligible, but its impact was strong at both 400 and 2000 ppm. This result indicated limits to the estimation of C_i at low g_lw, suggesting improvements in the accuracy of conductance estimates and C_i impact estimates of C_i to a greater degree at high C_a.

Fig. 1

C_i in response to g_lw, where g_lw is assumed to equal g_sw, under varying g_lw and scenarios of C_a = 100, 400, or 2000 µmol mol⁻¹. Proportional C_i values are proportional to the value when g_sw = 1 mol m⁻² s⁻¹. The light green ribbon shows the gap between the corrected and uncorrected C_i values, bounded on the bottom by the uncorrected C_i estimate (solid black line) and on the top by the corrected estimate (dashed black line). The correction accounts for the differential effect of g_cw in the estimation of g_cc and thus on C_i. The solid green line shows the proportional misestimation of C_i due to not accounting for g_cw proportional to the corrected value at the same g_sw. The dashed blue horizontal line denotes a proportion 0.05 (5% miscalculation or uncertainty). In all cases vapor pressure deficit was 1.5 kPa, temperature was 25 °C, maximum rate of carboxylation was 50 µmol m⁻² s⁻¹, electron transport was 100 µmol m⁻² s⁻¹, and g_cw was 0.0056 mol m⁻² s.⁻¹ (results for papaya, which fell toward the middle of the distribution among the four species)

Cuticular conductance impacts estimation of internal CO ₂ as a proportion of total leaf conductance

We modeled the impact of accounting for g_cw for a more accurate estimate of g_tc (Fig. 2), using 0.0056 mol m⁻² s⁻¹ estimate of g_cw from papaya as the case, because it fell toward the middle of the range of the four species assessed in this study (See below). As g_lw declined, the proportional misestimation of C_i increased exponentially (Fig. 1), this can be expressed as a proportion of g_cw: g_lw, resulting in a much greater alignment of the species tested and that the slope the response of misestimation due to the assumption that g_sw = g_lw is much slower than in response to g_lw alone. These results suggest that including g_cw in the calculation of C_i will be important in any context where g_cw is greater than 10% of g_lw. Additionally, even species with relatively high g_lw (eg. C. annuum and C. papaya) reached sufficiently high g_cw:g_lw to cause very large (> 50%) misestimations of C_i. The overall response of misestimation of C_i can be seen in Supplemental Fig. 1, where increasing g_cw:g_lw increases the misestimation of C_i with moderate impacts from A, E, and C_a.

Fig. 2

Miscalculation in estimates of leaf internal CO₂ (C_i) concentrations over a range of low leaf conductance to water (g_lw) values considering the impact of cuticular conductance to water (g_cw) in the estimation of g_sw and the resulting g_tc and C_i. Proportional C_i values are proportional to the value when g_sw = 1 mol m⁻² s⁻¹. A shows the impact of accounting for g_cw on the estimate of C_i, expressed as a proportion of the C_i estimate at g_lw = 1.0 mol H₂0 m⁻² s⁻¹. B shows the same values as a proportion of g_cw to g_lw. The light red, green, or blue ribbons show the gap between the corrected and uncorrected C_i values, bounded by the uncorrected C_i estimate (solid black line) and the corrected estimate (dashed black line) proportional to the corrected value at the same g_sw. The solid lines corresponding to the bands show the proportional misestimation of C_i due to not accounting for g_cw. The horizontal error bars show ± 1 standard deviation of maximum g_cw:g_lw in a series of five steady-state A/C_i curves for each species. Assumptions, in this case, are V_cmax = 50 µmol m⁻² s⁻¹, C_a = 400 µmol mol⁻¹, and VPD = 1.5 kPa

Noise in the measurement of leaf conductance to water impacts estimation of internal CO ₂ at low conductance

Noise is the random unexplained error associated with any measurement. Any instrument will have some noise associated with the estimation of any variable. We estimated the impact of noise on the IRGA instrument’s estimation of g_lw by summarizing the g_lw estimates across several empty-chamber rapid A/C_i curves, which had been gathered to calibrate the leaf-sample curves. Because an empty, sealed chamber with no sample is known to have a conductance of 0, we could then record the conductance to estimate the precision of the estimate of 0. The standard deviation of g_lw was 0.00415 mol m⁻² s⁻¹. Given that the true value of g_lw may easily be ± one standard deviation of the estimate at any given point, we added and subtracted this instrumental noise value from the g_lw estimate to provide a range of possible “true values” and re-calculated A and C_i. Instrumental noise in measuring g_lw greatly impacts estimates of C_i at low g_lw values and compounds the possible misestimation of C_i when not accounting for g_cw (Fig. 3).

Fig. 3

Uncertainty due to instrumental noise and miscalculation in estimates of leaf internal CO₂ (C_i) concentrations over a range of low leaf conductance to water (g_lw) values considering the impact of cuticular conductance to water (g_cw) and technical uncertainty in the estimation of g_lw. A shows C_i estimate and potential proportional miscalculation in response to g_lw. B shows the same variables in response to the ratio of g_cw to g_lw. C_i values are expressed as a proportion of the C_i estimate at g_lw = 1.0 mol H₂O m⁻² s⁻¹. Proportional error values are the difference between the uncorrected and the corrected values divided by the corrected value. Red indicates uncorrected estimates, and blue indicates corrected estimates. Dashed lines represent the estimate, while the ribbons indicate the range ± std. dev. Solid lines represent the proportional error in the C_i estimate. The purple line represents the maximum possible combined error from uncertainty in measuring g_lw and not accounting for g_cw. This scenario considers V_cmax = 50 µmol m⁻² s⁻¹, C_a = 400 µmol mol⁻¹, and VPD = 1.5 kPa. ambient CO₂, g_cw = 0.0056 µmol m⁻² s⁻¹, and the standard deviation of g_lw = 0.00415 mol m⁻² s⁻¹. The error in the g_lw is based on empty chamber measurements using an LI-6800 infrared gas analyzer (LI-COR Biosciences, Lincoln, NE). The dashed horizontal line denotes a proportion of 0.05 (5% miscalculation or uncertainty)

Considering cuticular conductance to water and instrumental noise alters A/C _i response estimates

We measured the g_cw of magnolia, papaya, citrus, and bell pepper, and found a wide range among these species from 0.0045 to 0.0076 mol m⁻² s⁻¹ (Table 2). Although the g_cw estimates were within the range of the standard deviation of any single measurement of g_lw, the standard deviation of the estimates of g_cw were between 0.0009 and 0.0024. The greater precision of the estimate of g_cw results from the approach to measuring g_cw which uses the average of g_lw over 5 min with measurements every 7 s Thus, each g_cw measurement resulted from the mean of 42 g_lw measurements. We considered the g_cw of each species, as well as possible instrumental noise, and applied these to the RACiR and SS A/C_i curves with the lowest observed conductance for each species (Fig. 4). The impact of accounting for g_cw and instrumental noise in the estimation of g_lw varied by species and by the A/C_i curve method, suggesting that in many cases constant-ramping (RACiR) curves are more precise than SS curves, and that under some conditions SS curves produced estimates within 1 standard deviation of g_lw of unrealistic A/C_i results.

Table 2 Mean leaf conductance to water (g_lw) and cuticular conductance to water (g_cw) of magnolia (Magnolia grandiflora), citrus (Citrus sinensis), bell pepper (Capsicum annuum), papaya (Carica papaya)

Fig. 4

Steady-state (SS) and rapid A/C_i (RACiR) curves for bell pepper (Capsicum annuum), citrus (Citrus x sinensis), magnolia (Magnolia grandiflora), and papaya (Carica papaya). Each panel shows a single A/C_i curve. The curves with the lowest leaf conductance to water (g_lw) for each method for each species were selected. Red lines represent an uncorrected curve in which g_lw is assumed to be equivalent to stomatal conductance to water. Solid black lines show the same curve after correcting C_i estimates accounting for the species-specific cuticular conductance. Dashed lines represent the range after accounting for instrumental noise in the measurement of stomatal conductance. The standard deviation of g_lw = 0.00415 mol m⁻² s⁻¹, based on empty chamber measurements in an LI-6800 infrared gas analyzer (LI-COR Biosciences, Inc., Lincoln, NE, USA)

RACiR versus steady-state A/C _i curves

Overall, results from SS and RACiR curves were similar (Table 3). Notable differences are the smaller R_dark estimates by SS than by RACiR and the small number of TPU estimates produced by RACiR, the latter was not surprising considering the lower pre-set range of C_a values for RACiR, which prompted us to gather a new data set to test whether consistent estimation of TPU was possible with RACiR (see below). In addition, for magnolia, V_cmax fitted to RACiR curves was lower than SS curves. In citrus, the value of g_sw was higher in RACiR than in SS, illustrating that stomatal attenuation in citrus is lesser when using constant ramping than SS methods, because there is less time for stomatal responses to high C_a.

Table 3 Comparison of photosynthetic parameters as measured by steady-state (SS) and rapid A/C_i response (RACiR) curves of magnolia (Magnolia grandiflora), citrus (Citrus sinensis), bell pepper (Capsicum annuum), papaya (Carica papaya) leaves with uncorrected g_sw or corrected g_sw, representing the mean value for all measurements of each curve

Correcting for g _cw impacts the estimation of photosynthetic parameters

To illustrate the effect of the g_cw on A/C_i-derived parameters, both the RACiR and SS A/C_i curves were recomputed with corrected g_sw. We then estimated the photosynthetic parameters from the recalculated A/C_i data (Table 3). For magnolia and citrus, correcting for g_cw affected V_cmax and J₁₂₀₀ estimates. In the case of SS curves, correcting for g_cw affected V_cmax estimates in all species except for magnolia. With corrected g_sw, no difference was found for R_dark regardless of A/C_i curve type, except for citrus, which had a greater R_dark value in RACiR with corrected g_sw. Interestingly, correcting g_sw decreased RACiR-derived C_itrans1 for all species. However, for SS, only citrus showed a difference between corrected and uncorrected g_sw-derived C_itrans1 and C_itrans2. The g_cw correction strongly decreased g_sw estimate in SS curves. However, for RACiR, only g_sw estimates in magnolia were affected by g_cw correction.

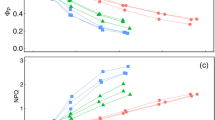
Stomatal limitations to gas exchange

Maximum and minimum g_sw and C_i differed among species (Fig. 5). Papaya had the greatest g_sw followed by bell pepper, citrus, and magnolia. The same trend was found for C_i. Each species’ g_sw responded differently to changing C_a in the RACiR curves, with some exhibiting reductions in A due to low g_sw. In magnolia, two curves decreased A noticeably as C_a exceeded 700 µmol mol⁻¹ (Fig. 5). Moreover, in all the RACiR curves in magnolia, g_sw decreased or remained low over time, regardless of C_i concentration. In bell pepper, g_sw increased from C_a of 380 µmol mol⁻¹ to 475 µmol mol⁻¹_, while higher C_a values decreased g_sw. In citrus, g_sw decreased as C_a increased above ~ 400 µmol mol⁻¹.

Fig. 5

Plots of net CO₂ assimilation (A) and stomatal conductance (g_sw) by intercellular CO₂ concentration (C_i), and distributions of maximum and minimum g_sw and C_i of leaves of magnolia (Magnolia grandiflora), citrus (Citrus sinensis), bell pepper (Capsicum annuum), papaya (Carica papaya) using RACiR method. P-values indicate the results of Tukey’s HSD test

RACiR curves with wide C _a range

To test the range of C_i attainable using constant-ramping, we performed separate curves with elevated C_a up to 2000 µmol mol⁻¹ (Table 4). Overall, the g_sw pattern among species was the same as for previous measurements. Moreover, TPU fitted by RACiR curves was observed for all species except for one curve in magnolia (Table 4 and Fig. 4). Correcting for g_cw increased the V_cmax estimate in all species, except citrus. J₁₂₀₀ was only impacted in magnolia. R_dark, TPU, and C_itrans2 were decreased in bell pepper and papaya while C_itrans1 and g_sw were decreased in all species by correcting for g_cw.

Table 4 Comparison of photosynthetic parameters as measured by rapid A/C_i response (RACiR) curves of magnolia (Magnolia grandiflora), citrus (Citrus sinensis), bell pepper (Capsicum annuum), papaya (Carica papaya) leaves with uncorrected and corrected g_sw

Discussion

Species-specific leaf conductance characteristics and their implications for A/C _i curves

Leaf conductance and stomatal behavior are known to vary across environmental conditions and species (Jones et al. 2009; Cabrerizo and Marañón 2022). Through the characterization of species-specific leaf conductance, researchers can gain valuable insights into the functional traits and adaptations that contribute to the successful adaptation of plants in diverse environments (Mott and Buckley 2000; Franks et al. 2009). For this study, we selected four plant species with distinct leaf conductance characteristics: bell pepper and papaya, exhibiting high g_lw, citrus with intermediate g_lw, and magnolia with the lowest g_lw. g_cw values were 1–2 orders of magnitude less than the g_lw (Table 2). g_cw:g_lw helped make species more comparable in terms of misestimation of C_i, and a ratio of only 0.1 was required to exceed 5% misestimation of C_i whenever C_a was 400 ppm or greater. This ratio could be used to assess the risk of large C_i misestimation, because the risk of misestimation could not be assessed using g_lw alone. The risk of misestimation of C_i increased with C_a, however, the 5% misestimation point is exceeded at approximately the same g_lw for C_a of both 400 and 2,000 ppm. This misestimation has implications for the interpretation of A/C_i curves, as demonstrated by the problematic nature of some of the uncorrected SS curves (Fig. 4). Our findings emphasize the necessity of accounting for g_cw in accurately estimating C_i and highlight the potential impact of misestimation on the interpretation of A/C_i responses.

Impact of accounting for g _cw on A/C _i fitted parameters

The cuticle has been known to impact the estimation of photosynthetic parameters by impacting estimates of C_i (Hanson et al. 2016). According to previous reports, g_cw influences the calculation of C_i (Boyer 2015a; Tominaga et al. 2018). In the present study, recalculated A/C_i curves (both SS and RACiR) using the g_cw values obtained from the red-light method (Márquez et al. 2021) indicate that considering g_cw does modify C_i estimates. The extent of the effect varies among species and is more pronounced when the g_cw:g_lw ratio is high or the g_sw is low, which results in a decrease in C_i. Lamour et al. (2022) proposed that the ratio of g_cw:g_lw could be important in predicting the misestimation of C_i. The present results support and extend that hypothesis by demonstrating that even high conductance species may have sufficiently high g_cw:g_lw ratios to have strong impacts on the misestimations of C_i. Papaya was the least affected on average, as it exhibited the highest g_sw during measurements, whereas magnolia, with low g_sw, showed significant changes in most photosynthetic parameters. These findings underscore the importance of g_cw in estimating photosynthetic traits, as ignoring g_cw can introduce a bias that incorrectly increases estimates of C_i. The data presented in Table 3 and Table 4 indicate a significant increase in V_cmax, J_max, R_dark, and C_itrans1 when the g_cw:g_sw ratio is high, which could occur in any of the species assessed when g_sw was low within the range for that species. Thus, plant conditions of water deficit, supra- or suboptimal temperatures, or other adverse growing conditions are likely to induce sufficiently low g_sw as to necessitate the estimation of g_cw to estimate accurate photosynthetic parameters.

Constant-ramping A/Ci method improves parameter resolution and avoids some stomatal limitations

In previous studies, comparisons between the RACiR and SS methods have indicated that the A/C_i fitted parameters, V_cmax and J_max, show no significant differences in a range of species (Stinziano et al. 2017, 2019b; Coursolle et al. 2019; Lawrence et al. 2019; Saathoff and Welles 2021; Lin et al. 2023). In our study, the results of A/C_i curves obtained using both the SS and RACiR methods were similar, with more precise estimates of C_itrans1 observed with the RACiR method, as seen in the smaller standard deviation in C_itrans1 in RACiR than SS for all species, with and without correction of C_i (Table 3). For example, the reductions in standard deviation represent a 16% decrease in the coefficient of variation (standard deviation/mean) for magnolia (the smallest change) and a 78% decrease in the coefficient of variation for bell pepper (the largest change). However, a notable difference was found in the g_sw values, where the SS curves showed a greater decrease in g_sw compared to the RACiR curves (Fig. 5). The likely reason for these differences is that the RACiR curves allowed less time for g_sw to decrease before reaching the critical threshold. SS curves are measured slowly relative to the time scale of leaf CO₂ attenuation of g_sw (Merilo et al. 2015). This leads to the reduction of g_sw in some curves below that required for reliable estimates of C_i. We do note, however, that the traditional approach to A/C_i curves—starting near atmospheric CO₂, going down, then up such as in Busch (2018) may not be the best option for maximizing g_sw during the SS. Starting at low CO₂ and monotonically increasing CO₂ may result in better A/C_i estimates (Sharkey 2019), though our initial attempts were not successful with this approach in terms of avoiding the g_sw crash in citrus and magnolia.

To assess the A/C_i relationship, it is ideal to achieve a wide range of C_i values. The RACiR method achieved as wide a range of C_i as the SS method, though low conductance magnolia limited the C_i range achieved (Fig. 2). These findings align with the results reported by Lin et al. (2023), who found that measuring SS A/C_i and RACiR curves in low conductance species posed challenges due to their low g_sw values. Consequently, driving C_i to a very high level is difficult or even impossible in these species. In the present study, at higher C_a values g_sw decreased (Fig. 5). In this case, the advantage of constant ramping lies in that its short time “beats” the speed of stomatal attenuation, affording the ability to avoid stomatal impacts on the shape of the A/C_i curve, making TPU estimation more feasible in low conductance species.

Stomatal attenuation can particularly affect the estimation of TPU, as it may induce changes in A at high C_i that are limited by g_sw, rather than by enzymatic limitations, despite the similarity in shape of the curve to the expected shape with TPU limitations, as is seen in Fig. 4 in papaya and bell pepper. Plants are not typically TPU-limited under ambient conditions (Sage and Sharkey 1987; Sharkey 2019; Ellsworth et al. 2015), and TPU limitation is most easily seen by elevating the rate of photosynthesis through increased light or CO₂ or decreased O₂ partial pressure (Sharkey et al. 1986) such that A is increased by 10% or 20% relative to ambient conditions (Kirschbaum 2011). Our initial comparison was between RACiR and SS fitted photosynthetic parameters with C_a maxima of 900 and 2000 µmol mol⁻¹, respectively. In this comparison, SS curves yielded a greater number of TPU estimates than RACiR curves. However, when RACiR was performed with a maximum C_a of 2000 µmol mol⁻¹, TPU estimates were achieved in all species (Table 4). Thus, constant-ramping methods can consistently estimate TPU when a sufficiently high maximum C_a are used.

In addition to its increased speed, the utilization of a constant ramping technique, such as RACiR, offers the advantage of improved resolution of parameter estimates. This improvement stems from the reduction in parameter uncertainty that can be achieved by having a larger amount of data available for curve fitting (Saathoff and Welles 2021). It has been observed that the accuracy of parameter estimation is directly influenced by both the number of data points and the accuracy of the gas exchange data used. When working with small and noisy data sets, obtaining robust parameter estimates can be particularly challenging (Sharkey et al. 2007; Wang et al. 2017). In our study, the SS A/C_i curve data consisted of only 16 data points, while the RACiR curves comprised significantly higher numbers (270 and 600 data points at 900 and 2000 µmol mol⁻¹ C_a, respectively). Our findings indicate the larger data set obtained by the RACiR technique reduced parameter uncertainty in comparison to SS.

The uncertainty of instrumental noise in g_lw estimates has the potential to further compound the challenges of low conductance. Accounting for g_cw can mitigate misestimation of C_i, and if g_cw is accounted for, the potential error due to instrumental noise only exceeds 5% at a g_cw: g_lw ratio of 0.13. However, constant-ramping methods ameliorate the impact of instrumental noise on the estimation of photosynthetic parameters due to the substantial number of measurements collected. While individual measurements of g_lw may deviate by approximately ± 0.00415 mol m⁻² s⁻¹ from the true value, the cumulative effect of numerous measurements diminishes the impact of the error on the overall results. With an increased number of measurements, the net effect tends toward zero, rendering the influence of instrumental noise inconsequential in the approach that employs the larger dataset. This is reflected in the very small impact of the error of g_lw on parameter estimates in RACiR relative to SS curves (Fig. 3). Thus, accounting for g_cw and utilizing constant-ramping methods significantly enhance the accuracy and reliability of A/C_i parameter estimates.

Conclusions

Low conductance presents a challenge to the estimation of photosynthetic parameters via gas exchange due to the misestimation of C_i. This work demonstrates that not accounting for g_cw can lead to a misestimation of C_i, which compounds to the estimation of parameters based on C_i, leading to underestimation of V_cmax and J_max. Instrumental noise can further compound errors when using a steady-state approach to A/C_i measurement. The ratio of g_cw:g_lw is useful in assessing the risk of misestimating C_i. Although this challenge was expected for low-conductance species, this work showed that high-conductance species, like C. papaya, can also exhibit high risk of overestimating C_i. Thus, practices to improve the estimation of C_i include using constant-ramping methods and measuring and accounting for g_cw on at least a species basis. Using these approaches will improve the accuracy of A/C_i-based photosynthetic parameter estimation, especially under conditions that reduce g_sw.