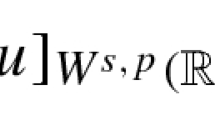Abstract
We extend the well-known result that any \(f \in W^{1,n}({\Omega }, \mathbb {R}^{n})\), \({\Omega } \subset \mathbb {R}^{n}\) with strictly positive Jacobian is actually continuous: it is also true for fractional Sobolev spaces \(W^{s,\frac {n}{s}}({\Omega })\) for any \(s \geq \frac {n}{n+1}\), where the sign condition on the Jacobian is understood in a distributional sense. Along the way we also obtain extensions to fractional Sobolev spaces \(W^{s,\frac {n}{s}}\) of the degree estimates known for W1,n-maps with positive or non-negative Jacobian, such as the sense-preserving property.
Similar content being viewed by others
References
Adams, R.A., Fournier, J.J.F.: Sobolev spaces, Volume 140 of Pure and Applied Mathematics (Amsterdam), 2nd edn. Elsevier/Academic Press, Amsterdam (2003)
Ball, J.M.: Convexity conditions and existence theorems in nonlinear elasticity. Arch. Rational Mech. Anal. 63(4), 337–403 (1976/77)
Bourgain, J., Brezis, H., Mironescu, P.: H1/2 maps with values into the circle: minimal connections, lifting, and the Ginzburg-Landau equation. Publ. Math. Inst. Hautes Études Sci. 99, 1–115 (2004)
Bourgain, J., Brezis, H., Mironescu, P.: Lifting, degree, and distributional Jacobian revisited. Comm. Pure Appl Math. 58(4), 529–551 (2005)
Brezis, H., Nguyen, H.: The Jacobian determinant revisited. Invent. Math. 185(1), 17–54 (2011)
Brezis, H., Nirenberg, L.: Degree theory and BMO. I. Compact manifolds without boundaries. Selecta Math. (N.S.) 1(2), 197–263 (1995)
Bui, H.-Q., Candy, T.: A characterization of the Besov-Lipschitz and Triebel-Lizorkin spaces using Poisson like kernels. In: Functional analysis, harmonic analysis, and image processing: a collection of papers in honor of Björn Jawerth, volume 693 of Contemp. Math., pp. 109–141. Amer. Math. Soc., Providence, RI (2017)
Chanillo, S.: Sobolev inequalities involving divergence free maps. Comm. Part. Differ. Eq. 16(12), 1969–1994 (1991)
Coifman, R., Lions, P.-L., Meyer, Y., Semmes, S.: Compensated compactness and Hardy spaces. J. Math. Pures Appl. (9) 72(3), 247–286 (1993)
Coifman, R.R., Jones, P.W., Semmes, S.: Two elementary proofs of the L2, boundedness of Cauchy integrals on Lipschitz curves. J. Amer. Math Soc. 2(3), 553–564 (1989)
Fonseca, I., Gangbo, W.: Degree Theory in Analysis and Applications, Volume 2 of Oxford Lecture Series in Mathematics and Its Applications. The Clarendon Press, Oxford University Press, New York (1995). Oxford Science Publications
Fonseca, I., Gangbo, W.: Local invertibility of Sobolev functions. SIAM J. Math. Anal. 26(2), 280–304 (1995)
Gladbach, P., Olbermann, H.: Coarea formulae and chain rules for the Jacobian determinant in fractional Sobolev spaces. J. Funct. Anal. 278(2), 108312, 21 (2020). 2
Goldstein, P., Hajłasz, P.: Modulus of continuity of orientation preserving approximately differentiable homeomorphisms with a.e. negative Jacobian. Ann. Acad. Sci. Fenn Math. 43(1), 147–170 (2018)
Goldstein, P., Hajłasz, P., Pakzad, M.R.: Finite distortion Sobolev mappings between manifolds are continuous. Int. Math. Res. Not. IMRN 14, 4370–4391 (2019)
Goldšteı̆n, V.M., Vodopyanov, S.K.: A test of the removability of sets for \({L^{1}_{p}}\) spaces of quasiconformal and quasi-isomorphic mappings. Sibirsk. Mat. Ž 18 (1), 48–68, 237 (1977)
Hajłasz, P., Malý, J.: Approximation in Sobolev spaces of nonlinear expressions involving the gradient. Ark. Mat. 40(2), 245–274 (2002)
Hang, F., Lin, F.: A remark on the Jacobians. Commun Contemp. Math. 2(1), 35–46 (2000)
Iwaniec, T., Martin, G.: Geometric Function Theory and Non-Linear Analysis. Oxford Mathematical Monographs. The Clarendon Press, Oxford University Press, New York (2001)
Jonsson, A., Wallin, H.: A Whitney extension theorem in Lp and Besov spaces. Ann. Inst. Fourier (Grenoble) 28(1), 139–192 (1978). vi
Lenzmann, E., Schikorra, A.: Sharp commutator estimates via harmonic extensions. Nonlinear Anal. 193, 111375 (2020)
Lewicka, M., Pakzad, M.R.: Convex integration for the Monge-A,mpère equation in two dimensions. Anal. PDE 10(3), 695–727 (2017)
Müller, S.: Higher integrability of determinants and weak convergence in L1. J. Reine Angew. Math. 412, 20–34 (1990)
Pakzad, M.R.: On the Sobolev space of isometric immersions. J. Differential Geom. 66(1), 47–69 (2004)
Rešetnjak, J.G.: The weak convergence of completely additive vector-valued set functions. Sibirsk. Mat. Z.̌, 9, 1386–1394 (1968)
Runst, T., Sickel, W.: Sobolev Spaces of Fractional Order, Nemytskij Operators, and Nonlinear Partial Differential Equations, Volume 3 of De Gruyter Series in Nonlinear Analysis and Applications. Walter de Gruyter & Co., Berlin (1996)
Schikorra, A., Van Schaftingen, J.: An estimate of the Hopf degree of fractional Sobolev mappings. Proc. Amer. Math Soc. 148(7), 2877–2891 (2020)
Sickel, W., Youssfi, A.: The characterisation of the regularity of the Jacobian determinant in the framework of potential spaces. J. London Math. Soc. (2) 59(1), 287–310 (1999)
Tartar, L.: Compensated compactness and applications to partial differential equations. In: Nonlinear analysis and mechanics: Heriot-Watt Symposium, Vol. IV, volume 39 of Res. Notes in Math., pp 136–212. Pitman, London (1979)
Tartar, L.: An introduction to Sobolev spaces and interpolation spaces, volume 3 of Lecture Notes of the Unione Matematica Italiana. Springer, Berlin (2007). UMI, Bologna
Šverák, V.: Regularity properties of deformations with finite energy. Arch. Rational Mech. Anal. 100(2), 105–127 (1988)
Wente, H.C.: An existence theorem for surfaces of constant mean curvature. J. Math. Anal. Appl. 26, 318–344 (1969)
Zhou, Y.: Fractional Sobolev extension and imbedding. Trans. Amer. Math. Soc. 367(2), 959–979 (2015)
Acknowledgments
This work has been done during SL’s stay as a CRM–ISM postdoctoral fellow at Centre de Recherches Mathématiques, Université de Montréal and Institut des Sciences Mathématiques. SL thanks these institutes for their hospitality. AS acknowledges funding by the Simons foundation, grant no 579261.
The authors would like to thank P. Hajłasz for helpful discussions; in particular he told us about Example 1.2 and Example 1.4. The authors also thank the anonymous referees for helpful suggestions on the presentation.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A: Fractional Sobolev spaces
Appendix A: Fractional Sobolev spaces
We recall results from fractional Sobolev spaces we employ here. Most of them are well-known to most experts.
We begin with proving Lemma 1.3. Lemma 1.3 was (essentially) proven in [28] as an extension of the ground-breaking paper [9], which showed that Jacobians of W1,n-maps can be tested with BMO-maps. The proof in [28] uses Littlewood-Paley theory and paraproducts. In [5] Brezis and Nguyen gave a simpler and more elegant proof of this result for \(s =\frac {n}{n+1}\). We present here the following slight adaptation of their argument from [21].
We restrict our attention to the a priori estimates, from which the claim follows easily due to multi-linearity.
Proof of 1.3 (a priori estimates)
Let \(\varphi \in C_{c}^{\infty }({\Omega })\) and \(f \in C^{\infty }(\overline {{\Omega }})\). Ω is an extension domain, [20, 33], so we may assume that \(f \in W^{s,\frac {n}{s}}(\mathbb {R}^{n}) \cap C^{1}(\mathbb {R}^{n})\). Then
Extend f and φ harmonically to \(\mathbb {R}^{n+1}_{+}\), say to F and Φ respectively. We write \((x,t) \in \mathbb {R}^{n} \times \mathbb {R}_{+} = \mathbb {R}^{n+1}_{+}\). By Stokes’ theorem and Hölder’s inequality,
If \(s \in (\frac {n-1}{n},1]\), then (1 − s)n ∈ (0, 1). Then, by trace estimates, see e.g. [21, Proposition 10.2], we have
and
Here we also used the fact that \([f]_{W^{s,\frac {n}{s}}(\mathbb {R}^{n})} \precsim [f]_{W^{s,\frac {n}{s}}({{\Omega })}}\). This is because Ω is an extension domain; see [20, 33]. We conclude, because we have shown
□
The ensuing result on trace operators will be useful for the subsequent developments. For detailed treatments we refer to [26, §2.4.2, Theorem 1], [1, Theorem 7.43, Remark 7.45] and [30, Lemma 36.1].
Lemma A.1 (Trace Theorem)
Let \({\Omega } \subset \mathbb {R}^{n}\) be either bounded or the complement of a bounded set, with smooth boundary. If s ∈ (0, 1), \(p \in (1,\infty )\) with \(s-\frac {1}{p} > 0\), then the trace operator on T = |∂Ω is a bounded, linear, surjective operator from Ws,p(Ω) to \(W^{s-\frac {1}{p},p}(\partial {\Omega })\). The harmonic extension is a bounded linear right-inverse of T.
The following is well-known for Sobolev functions in W1,p (it is essentially Fubini’s theorem):
Lemma A.2 (Restriction theorem)
For Ω a smooth, bounded domain let f ∈ Ws,p(Ω). Fix x0 ∈Ω. There exists a representative of f such that for \({\mathscr{L}}^{1}\)-almost every r ∈ (0,dist (x0, ∂Ω)) we have f ∈ Ws,p(∂B(x0, r)).
Moreover, for Ω = B(x0, R) we have
Proof
As Ω is an extension domain, see [20, 33], we may assume that \({\Omega } = \mathbb {R}^{n}\) and \(f \in W^{s,p}(\mathbb {R}^{n})\) with f ≡ 0 outside a compact set. Denote by \(F: \mathbb {R}^{n+1}_{+} \to \mathbb {R}\) the harmonic extension of f, and w.l.o.g. set x0 = 0. Then (see [21, Proposition 10.2])
By Fubini’s theorem, for \({\mathscr{L}}^{1}\)-almost every r > 0,
This implies that f ∈ Ws,p(∂B(r)) for almost every r > 0.
The last claim also follows from Fubini’s theorem in \(\mathbb {R}^{n+1}_{+}\):
□
Lemma A.3
Let \({\Omega } \subset \mathbb {R}^{n}\) be a bounded domain with smooth boundary. For s ∈ (0, 1), \(p \in (1,\infty )\) such that \(s-\frac {1}{p} > 0\):
-
(1)
If f ∈ Ws,p(Ω) and \(g \in W^{s,p}(\mathbb {R}^{n} \backslash {\Omega })\) with f = g on ∂Ω in the trace sense. Then
$$ h := \begin{cases} f \quad & \text{in} {\Omega}\\ g \quad &\text{in} \mathbb{R}^{n} \backslash {\Omega} \end{cases} $$belongs to the Sobolev space and
$$ [h]_{W^{s,p}(\mathbb{R}^{n})} \leq C({\Omega}) \left( [f]_{W^{s,p}({\Omega})} + [g]_{W^{s,p}(\mathbb{R}^{n}\setminus{\Omega})}\right). $$ -
(2)
In particular, if f ∈ Ws,p(Ω) satisfies f = 0 on ∂Ω in the trace sense, then \(f\in W^{s,p}_{0}({\Omega })\) and that
$$ h := \begin{cases} f \quad &\text{in} {\Omega}\\ 0 \quad &\text{in} \mathbb{R}^{n} \backslash {\Omega} \end{cases} $$belongs to \(W^{s,p}(\mathbb {R}^{n})\).
Lemma A.4
Let B(R) be a ball in \(\mathbb {R}^{n}\). Let \(f \in W^{s,\frac {n}{s}}(B(R))\) for some s ∈ (0, 1) and f|∂B(R) ∈ C0(∂B(R)). Then there exists an approximation \(f_{k} \in C^{\infty }_{c} (\mathbb {R}^{n})\) converging to f in \(W^{s,\frac {n}{s}}(B(R))\) and \(f_{k} \rightrightarrows f\) uniformly on ∂B(R).
Proof
W.l.o.g. B(R) = B := B(0, 1).
By the trace theorem, Lemma A.1, \(f \in W^{s-\frac {n}{s},\frac {n}{s}}(\partial B)\). Let g be the harmonic extension of f to \(\mathbb {R}^{n} \backslash B\). Then \(g \in W^{s,\frac {n}{s}}(\mathbb {R}^{n} \backslash B)\), again by Lemma A.1. Also, since f is continuous on ∂B, g is also continuous. Set
By Lemma A.3, \(h \in W^{s,\frac {n}{s}}(\mathbb {R}^{n})\) and h is locally uniformly continuous on \(\mathbb {R}^{n} \backslash B\). This last fact implies that
converges uniformly to h on ∂B as \(k \to \infty \), and also in \(W^{s,\frac {n}{s}}_{loc}(\mathbb {R}^{n})\).
Now let us consider the standard mollification fε := hk ∗ ηε. For ε small enough in comparison with \(\frac {1}{k}\), fε converges uniformly on ∂B to f and in \(W^{s,\frac {n}{s}}(B))\). This completes the proof. □
Rights and permissions
About this article
Cite this article
Li, S., Schikorra, A. \(W^{s,\frac {n}{s}}\)-maps with positive distributional Jacobians. Potential Anal 55, 403–417 (2021). https://doi.org/10.1007/s11118-020-09862-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11118-020-09862-4