The role of unpaid domestic work in explaining the gender gap in the (monetary) value of leisure

Abstract

The value of travel time savings (VTTS) representing the willingness to pay to reduce travel time, consists of two components: the value of liberating time [equal to the value of leisure (VoL)] and the value of time assigned to travel (VTAT), representing the travel conditions of a trip. Their relative values indicate which dimension to emphasize when investing in transport: speed or comfort. In this paper, we formulate and estimate a framework aimed at the improvement in the estimation of the VoL. By introducing a novel treatment of time assigned to domestic work, we consider that unpaid labor should be assigned a wage rate as a measure of the expenses avoided when assigning time to those chores. We use state-of-the-art data on time use and expenses as well as online data on gig workers collected in Austria, and apply the time-use and expenditure model of Jara-Diaz et al. (Transp Res Part B 42(10):946–957, 2008). The wage rates for paid and unpaid work were combined to re-formulate the budget constraint, which affected women more than men due to the higher involvement of the former in domestic activities. Compared against the original estimation, the VoL changed from €10/h for men and €6/h for women to €9/h for both genders, which in turn yields a larger average VTAT, which becomes positive for public transport. As a conclusion, the novel treatment of domestic labor contributes to closing the gap in the VoL between genders and highlights the power of unveiling the components behind the VTTS. The empirical findings imply that investments in travel time reductions rather than in comfort should be prioritized, given the very good conditions of public transport in Austria.

Introduction

The value of travel time savings (VTTS) has long been considered a key input in the appraisal of transport projects. The usual interpretation has been that the larger the VTTS the more important is the reduction in trip time. After all, it represents the willingness to pay to diminish travel time by one unit and is usually estimated with some form of travel choice model. However, behind this single figure there are two elements that contribute to the size of its value: the valuation that the individual assigns to the liberated time—the value of leisure (VoL)- and the valuation that the individual assigns to the conditions of travel—the value of time assigned to travel (VTAT). For short, the VTTS increases not only with the value of time assigned to alternative (rewarding) activities but also with the unpleasantness of the trip, components that were first identified and estimated by Jara-Díaz and Guevara (2003). Identifying the VoL and VTAT “illuminates the emphasis that decision makers should put when deciding on investments in the transport sector whenever speed and comfort collide” (Jara-Diaz 2020). It is therefore vital to empirically determine which of the two components dominates, which can be achieved by estimating the VoL from time use models.¹

For more than 50 years, it has been widely agreed that time is a scarce resource and that it has value (Becker 1965; Johnson 1966; Oort 1969; DeSerpa 1971). The main two techniques for its valuation are the contingent valuation method (CVM) and time-use models (TUM). Both methods offer a way of assigning value to various types of activities such as work, travel and leisure. Only TUM, however, rely on the observed assignment of time to activities based on the assumption that behind that assignment underlies an implicit subjective valuation of the time spent on those activities, which can be revealed by modeling behavior. Since the formulation of this microeconomic model by Jara-Díaz and Guevara (2003), a series of improvements have been made in the estimation of the VoL from TUM. Nevertheless, this framework still lacks an adequate treatment of some activities: “In order to estimate more reliable VoL, there are two activity types that should be explored and studied with great care: what can be called maintenance activities (sleep, eat), and domestic work” (Jara-Diaz 2020).

Table 1 Distribution of time in different countries, %.

Domestic work (cleaning, cooking, childcare) presents various particular characteristics. First, it consumes a significant proportion of time—as shown in Table 1, certainly comparable to paid work time, and sometimes larger.² Second, in most (if not in all) countries the majority of domestic work is done by women, such that even if time assigned to paid work is lower for women, total work time is in most countries larger for them, as shown in Fig. 1. Third, domestic work is an activity that can be delegated to a third (hired) party (Reid 1934); it is not a tertiary activity (like transport) as defined by Burda et al. (2007). Several recent studies have reported gender specific differences in the VoL (e.g. Konduri et al. 2011; Verbooy et al. 2018; Hössinger et al. 2019; Jokubauskaitė et al. 2019) which we believe could be connected with an inadequate treatment of domestic work. This is what we want to examine in this paper, giving domestic work a new treatment while employing the TUM framework. As explained above, this is necessary for the estimation of a more reliable VoL and, ultimately, of better estimates of the VTAT. After all, undergoing domestic work means “[...] money saved that is traded for time assigned; the connection with the VoL is quite evident”(Jara-Diaz 2020). This paper hence focuses on the role of unpaid domestic work in explaining the gap between gender specific (monetary) values of leisure (VoL) and proposes our approach as a possible advancement in estimating the components of the VTTS.

Fig. 1

Average daily work-time by men as proportion of work-time by women. Latest year available data reported

In time use models, it is common to treat only the official (paid) work as “work” and domestic (unpaid) work as a committed activity.³ This assumption is questionable, since work is work and time is money. So far, only some studies have factored in the domestic work while estimating the value of leisure. In a recent paper by Verbooy et al. (2018), the value of unpaid work in the Netherlands was estimated with CVM (€16/h) and was shown to be close to the wage rate of housekeepers [€14/h, Hakkaart-van Roijen et al. (2015)]. However, the CVM approach is based on stated (declared) preferences and “stated behavior does not necessarily align with the actual behavior of respondents” (Verbooy et al. 2018). The TUM framework from Jara-Díaz et al. (2008) was recently extended in a related direction as well: Rosales-Salas and Jara-Díaz (2017) introduced external providers (employed personnel). The estimation of such model is, however, not always possible or efficient. Domestic chores are mostly performed by household members and not by employed personnel. Therefore, obtaining a sufficiently large sample size of households that employ personnel is likely to be difficult in most countries.

The original Jara-Díaz and Guevara (2003) framework offers a convenient way for the VoL estimation and has been used in many studies (Munizaga et al. 2008; Jara-Díaz et al. 2008, 2013, 2016; Jara-Díaz and Astroza 2013; Konduri et al. 2011). The most recent and advanced applications are Hössinger et al. (2019) and Jokubauskaitė et al. (2019), who work with the same innovative data gathered in Austria as this paper. Although, the used dataset is very informative (Aschauer et al. 2018), no information on external providers or stated preferences for time-use allocation was gathered. Thus, neither an estimation similar to the one included in Rosales-Salas and Jara-Díaz (2017) nor the application of CVM is possible.

In both recent investigations of the VTTS based on the same dataset as this paper (Hössinger et al. 2019; Jokubauskaitė et al. 2019), the VoL⁴ has been estimated for different demographic and socioeconomic segments. The papers separately but consistently report that the estimated VoL of women is only half of the VoL of men.⁵ Moreover, the largest recorded gender-specific differences in time allocation are between time spent in domestic work (men: 10.11h/week; women: 18.42 h/week) and paid work (men: 42.34 h/week; women: 33.35 h/week). This phenomenon is not unique for Austria, and has been well documented around the world. According to Alonso et al. (2019), women are typically involved in two hours more of unpaid work per day than men. Also, having a partner and/or children hampers their leisure time (Alonso et al. 2019; Wallace and Young 2010). Argyrous and Rahman (2017) have observed that regardless of their earnings and working hours, women spend more time and take on more responsibility for childcare (Heiland et al. 2017). Thus, women are involved in a “second shift” and they suffer from the resulting time poverty (Hochschild and Machung 2012; Schor 2008; Hochschild 1997; Vickery 1977). The reduction of labor market hours caused by parenthood or taking care of a dependent person (Chaykowski and Powell 1999; Bloemen et al. 2010; European Commission 2017) reduces their financial security as well.

The microeconomic theory of labor supply introduced by Becker (1965) assumes that individuals decide on the amount of time devoted to work by maximizing their utility functions subject to time and income constraints. According to Becker’s time-use model (TUM), income is defined by the time assigned to work and the hourly wage rate and the VoL is set to equal the wage rate. Thus, the gender-specific VoL gap is the difference between the corresponding wage rates. Based on Becker’s framework, Johnson (1966), DeSerpa (1971) and Jara-Díaz and Guevara (2003) provided subsequent theoretical work on the valuation of leisure and other types of time. Another evolutionary extension of TUM came with the previously mentioned introduction of external providers by Rosales-Salas and Jara-Díaz (2017). They show that the exclusion of external providers, results in an overestimation of the VoL. Yet, if nobody is hired, they treat the same work as a committed activity, pushing it to the shadows of the economic domain, as it does not generate any income. This is well reflected in the words of Margaret G. Reid written in the beginning of the 20th century: “the more we have concentrated on money values the more we have overlooked that part of our economic system which is not organized on a profit basis” (Reid 1934).

The majority of existing studies examining the economic valuation of unpaid work focuses on the inclusion of unpaid work into the calculation of the gross domestic product (GDP). Depending on methodological and geographical differences, the value of unpaid work ranges from 10% up to 60% of GDP. For instance, Bridgman et al. (2018) estimate the average value of unpaid work to be 35% of GDP for their sample of 43 countries (covering nearly a half of the world population). Payne and Vassilev (2018) have reported a 60% unpaid work value share for the UK, Schwarz and Schwahn (2016) 40% for Germany, and Schmid et al. (2002) 40–60% for Switzerland. Such a sizable contribution is certainly relevant and prompts a more careful look at the role it plays in the calculation of the values of work and leisure for men and women in the TUM framework.

In this study, we investigate the effect of the valuation (i.e. monetarization) of domestic work on gender-specific differences in the values of leisure (VoL) derived from the time-use and expenditure model (Jara-Díaz et al. 2008). This in turn will improve the VTAT estimation and will allow including a more balanced gender analysis (BGA) into the CBA of transport related projects. We estimate the TUM from Jara-Díaz et al. (2008) using a novel and very rich dataset collected in Austria in 2015, which is based on a Mobility-Activity-Expenditure Diary (MAED) described in Aschauer et al. (2018). Unlike the original framework, we consider that individuals who undertake domestic work could have hired a third person. We assume that they could have paid a market wage rate, which individuals choose not to pay avoiding expenses. In our study, different forms for the calculation of the wage rate associated with unpaid work have been analyzed in depth, with the result that we impute it using online data on the market price of various domestic work services in Austria.

The modeling framework (a system of non-linear equations) is introduced in the next section. Afterwards, in "Application" section we describe the data, offer new ways to consider a wage rate for domestic work, estimate the model using the re-calculated wage rate including a sensitivity analysis, and present the modeling results. These are then compared to the ones obtained with the original data in "Discussion and conclusions" section, where we show (a) that the gap in the VoL between genders almost disappears if the value of domestic work is considered, and (b) that the global VoL increases. This suggests an updated method to estimate time values for the analysis of transport related projects.

Theoretical model

The frameworks of Becker (1965), DeSerpa (1971) or Heckman (1974) laid the foundation of the time-use incorporation into the consumer theory. Each advancement resulted in the derivation of new indicators—value of leisure [“resource value of time”, (DeSerpa 1971)], value of travel time savings (Bates 1987; Jara-Díaz 1998), and value of time assigned to travel (Jara-Díaz et al. 2008). In this article, we use the same theoretical model as Hössinger et al. (2019) and Jokubauskaitė et al. (2019), which was first presented in Jara-Díaz and Guevara (2003) and further advanced by Jara-Díaz et al. (2008), including the same specification of the utility function such that the values of leisure and work can be readily derived as in Eqs. (10) and (11) below and the comparison of the previous results with those obtained with the reformulation presented in "Application" section below will be a fair one. The Cobb-Douglas utility function maximized by each individual is given as:

$$\begin{aligned} U = \varOmega T_w^{\theta _w} \prod _{i=1}^{n} T_i^{\theta _i}\prod _{j=1}^{m}E_j^{\phi _j} \end{aligned}$$

(1)

In Eq. (1), the utility $U$ is a function of the time assigned to work ($T_w$), the time assigned to activity $i$ ($T_i$), and the expenditure assigned to good $j$ ($E_j$). $\varOmega$ is a utility constant, the exponents $\{\theta _w$, $\theta _i$, $\phi _j\}$ represent the elasticities of utility with respect to work, activities, and expenditures on goods. By dropping out $\varOmega$ and taking a monotonous transformation of U, the maximization problem can be rewritten as:

$$\begin{aligned} \text { max}\, ln(U)= \text { max}\left( \theta _w ln(T_w)+\sum _{i=1}^{n} \theta _i ln(T_i)+\sum _{j=1}^{m} \phi _j ln(E_j) \right) \end{aligned}$$

(2)

Subject to:

$$\begin{aligned} \tau - T_w-\sum _{i=1}^{n} T_i =0\,\,(\mu )&\;\text {(time constraint)} \end{aligned}$$

(3)

$$\begin{aligned} wT_w+I-\sum _{j=1}^{m}E_j \ge 0\,\,(\lambda )&\;\text {(budget constraint)} \end{aligned}$$

(4)

$$\begin{aligned} T_i - T_i^{Min} \ge 0\,\,(\kappa _i)&\;\text {(technical constraints on activities)} \end{aligned}$$

(5)

$$\begin{aligned} E_j - E_j^{Min} \ge 0\,\,(\eta _j)&\;\text {(technical constraints on goods)} \end{aligned}$$

(6)

Here $w$ is the wage rate; $I$ is the income not related to work; $\tau$ is total available time in the work-leisure cycle (for example 168 h/week). There are $m$ expenditure groups with index set $G$ and $n$ activity categories with index set $A$. Also, goods and activities are separated into freely chosen (index set $G_f$ and $A_f$) and committed (index set $G_c$ and $A_c$). The latter goods and activities restrict their freely chosen counterparts and are deduced from the observations ($T_{g}= T_g^{Min}, g \in A_c$ and $E_{k}=E_k^{Min}, k \in G_c$). The sum of such activities and goods is introduced in the time and budget constraints as $T_c$ and $E_c$, respectively (Hössinger et al. 2019). To solve this maximization problem, we assume that individuals freely choose how much to work. After application of the Lagrange method with multipliers $\lambda$ and $\mu$, one gets an expression of optimal $T_w$, $E_{i}$ and $T_{j}$ (for more details on the derivation see Hössinger et al. 2019):

$$\begin{aligned}&T_{w}^{*}=\frac{\left( (\varPhi +\theta _w)(\tau -T_c)+(\varTheta +\theta _w)\frac{E_c}{w}\right) \pm \sqrt{D}}{2(\varTheta +\varPhi +\theta _w)} \end{aligned}$$

(7)

$$\begin{aligned}& \text {with }D=\left( (\varPhi +\theta _w)(\tau -T_c)+(\varTheta +\theta _w)\frac{E_c}{w}\right) ^{2}- 4(\varTheta +\varPhi +\theta _w)\theta _w(\tau -T_c)\frac{E_c}{w} \nonumber \\&T_{fi}^{*}=\frac{\theta _i}{\varTheta }(\tau -T_{w}^{*}-T_c) \end{aligned}$$

(8)

$$\begin{aligned}&E_{fj}^{*}=\frac{\phi _j}{\varPhi }(wT_{w}^{*}-E_c) \end{aligned}$$

(9)

Here $\varTheta =\sum _{i \in A_f} \theta _i$ and $\varPhi = \sum _{j \in G_f} \phi _j$. $T_c=\sum _{i \in A_c} T_i^{min}$ and $E_c=(\sum _{j \in G_c} E_j^{min}-I)$ correspond to total committed time and expenditures, respectively.

The model given by the nonlinear equation system (Eqs.  7–9) can be estimated using the maximum likelihood (ML) method. After the normalization of the full model (by setting $\varTheta =1$) there are at least 4 parameters left to estimate $\{\theta _w$, $\varPhi$, $\theta _1$, $\phi _1\}$ and 2 parameters to calculate ($\theta _2 = 1 - \theta _1$ and $\phi _2 = \varPhi - \phi _1$). In the original model of Jara-Díaz and Guevara (2003), a different normalization was used; the choice of normalization does not affect the estimates, as there is a direct relationship between $\{ \alpha , \beta \}$ used in Jara-Díaz and Guevara (2003) and $\{\theta _w , \varTheta , \varPhi \}$ used here [based on Jara-Díaz et al. (2008)]. In Jara-Díaz et al. (2008) (Eqs. 24, 25) it was shown that the VoL and value of time assigned to work (VTAW) can be calculated using the estimates of $\varPhi$ and $\theta _w$:

$$\begin{aligned}&VoL=\frac{\partial U \backslash \partial T_i}{\partial U \backslash \partial E_j}=\frac{\mu }{\lambda }=\frac{\varTheta (wT_w-E_c)}{\varPhi (\tau -T_w-T_c)} \overbrace{=}^{\varTheta =1} \frac{(wT_w-E_c)}{\varPhi (\tau -T_w-T_c)} \end{aligned}$$

(10)

$$\begin{aligned}&VTAW=\frac{\partial U \backslash \partial T_w}{\lambda }=\frac{\theta _w}{\varPhi }\frac{wT_w-E_c}{T_w}=VoL - w \end{aligned}$$

(11)

Here $\lambda$ and $\mu$ are marginal utilities of income and time, respectively. Thus, the VoL is calculated as a ratio between two marginal utilities. This result was derived from the First Oder Conditions (FOC) of the maximization problem for Eq. (2) and constraints of time (Eq. 3) and budget (Eq. 4). In Hössinger et al. (2019) the FOC are given as:

$$\begin{aligned}&\frac{\theta _w}{T_w}+\lambda w -\mu =0 \end{aligned}$$

(12)

$$\begin{aligned}&\frac{\theta _i}{T_i}-\mu =0,\quad \forall i \in A_f \end{aligned}$$

(13)

$$\begin{aligned}&\frac{\phi _j}{E_j}-\lambda =0,\quad \forall j \in G_f \end{aligned}$$

(14)

By solving them, one gets expressions for $\mu$ and $\lambda$:

$$\begin{aligned}&\mu =\frac{\partial U}{\partial T_i} = \frac{\varTheta }{\tau -T_w-T_c}&\lambda =\frac{\partial U}{\partial E_j} = \frac{\varPhi }{wT_w-E_c} \end{aligned}$$

(15)

Actually, $\varPhi$ and $\theta _w$ are the only parameters needed for the calculation of VoL and VTAW. Therefore, one could only estimate the labor supply defined in Eq. (7), but the estimates would be less efficient as the additional information would be ignored (Eqs.  8, 9). Many of the models based on the presented modeling framework and estimated prior to Hössinger et al. (2019) and Jokubauskaitė et al. (2019) did not use the expenditure equation (Eq. 9). As shown in Jokubauskaitė et al. (2019), the inclusion of expenditure estimation might play a crucial role. Without it, the VoL was overestimated by around 20% for Austria. The lack of other comparable estimations might be caused by the almost non-existent availability of time-use surveys with expenditure information. The MAED survey used in this study and carried out in Austria in 2015 is an exception. As advanced in the introduction, while the modeling framework is kept the same for the comparative purposes, the new treatment of unpaid labor presented in the next Section will be shown to have a relevant impact on the VoL estimated from Eq. (10).

Application

MAED data

The estimation of Eqs. (7)–(9) requires detailed information not only on time-use (activities), but also on expenditures. To facilitate this, the Mobility-Activity-Expenditure-Diary (MAED) was developed (Aschauer et al. 2018). The survey was carried out in the form of self-administered mail-back questionnaires with telephone support and incentives in Austria in spring and autumn of 2015. Participants reported their data for one week. This period was chosen as a trade-off between the hardship of response and proper portrayal of the individual’s long-term equilibrium. Diary-type information on all travel and non-travel activities as well as on any expenditures was gathered simultaneously (from the same individual at the same time) including 10 activity types, 14 expenditure groups, and 5 transport modes (walk, bike, car driver, car passenger, public transport). This makes MAED data one of a kind.

748 representatively selected Austrian workers⁶ took part in the survey. Hössinger et al. (2019) present a detailed review of plausibility checks, imputations, and error corrections done to the data. Aschauer et al. (2018, 2019) give a comprehensive overview of MAED characteristics.

Overall, the MAED data are fairly consistent with the latest Austrian Time Use Survey (ATUS; 2008/09) as well as the Austrian Consumer Expenditure Survey (ACES; 2009/10) data (see Tables 2, 3). Noticeable variations appear in expenditures on housing (ACES-16.53% and MAED-22.15%, Table 2) and savings (ACES-11.01% and MAED-4.38%, Table 2). As Hössinger et al. (2019) explains, “the original ACES data include rental equivalents (instead of reported expenses) of owner-occupied housing. The MAED data include, in contrast, only reported mortgage repayments and operating costs, which are not comparable to the (on average lower) rental equivalents. Since we found no way to make both procedures comparable, we removed the rental equivalents in the ACES, which explains the lower share.” In addition, there was an actual drop in the saving rate. According OeNB (2018) the saving rate of private households has dropped from 11.4 to 6.8 (%) between 2009 and 2015. Another divergence is the travel time. In the MAED sample, individuals devote more time to travel than in ATUS (1.23 h/week, Table 3). This might be more of a problem in ATUS than in the MAED, as time-use surveys are prone to under-report travel (Gerike et al. 2015; Aschauer et al. 2018). What is more, there is a shift in personal care and leisure, caused by the overlapping nature of such activities. In the MAED, individuals identified activities as leisure if they were performed of one’s own free will. As Hössinger et al. (2019) point out, some activities (e.g., going to church, visiting the sick) might be classified as leisure in ATUS, while in MAED they are assigned to “Personal”, as people did not perceive them as leisure.

Table 2 Distribution of expenditure in different segments, %

In terms of socio-economic segments, the biggest differences between segments in MAED expenditure categories seem to occur with respect to expenditures for housing and food. Otherwise, expenditure shares do not vary greatly within and between the segments. In contrast, time-use allocation (Table 3) varies substantially between socio-economic segments The biggest difference in time allocation by segment is in terms of the time spent on paid work and domestic work. On average, per week, women spend around nine hours less in paid work and eight hours more in the unpaid/domestic work than men (Tables 3, 5).

Table 3 Distribution of activities in different segments, h/week

To estimate the model (in particular Eqs. 7–9), activities and expenditures had to be separated into freely chosen and committed ones. Aggregation results are presented in Table 4. Unlike Hössinger et al. (2019) or Jokubauskaitė et al. (2019), we use three expenditure equations $\{E_{f1}, E_{f2}, E_{f_3}\}$ and thus we get estimates for $\{\phi _1, \phi _2\}$ and $\phi _3$ is calculated as $1 - \phi _1 - \phi _2$. This is done in order to take into account available information on the savings (S), which was previously only implicitly included into the estimation as part of $E_{f2}$. As Schmid et al. (2020) correctly points out, the estimated exponent $\phi _2$ from the previous studies was related to the estimation of $E_{f2}+S$ and not purely to $E_{f2}$. For other groups, the aggregation remained the same as in Hössinger et al. (2019) and Jokubauskaitė et al. (2019). More information on the grouping of variables can be found in Hössinger et al. (2019), Jokubauskaitė et al. (2019), Aschauer et al. (2019), Jara-Díaz et al. (2016), and Mokhtarian and Chen (2004).

Table 4 Shares and correlations of expenditure and time-use data

In the MAED data, the average share of time spent on paid work is 22.52$\%$ and to unpaid work 8.50$\%$, respectively. On average, committed activities ($T_c$) make up 53.44$\%$ of the total time budget and committed expenditures ($E_c$) 73.85$\%$ of the monetary budget. No assumptions about relationships between goods and activities are made, as the Jara-Díaz and Guevara (2003) model does not require a one-to-one mapping between them. Most empirical correlations are statistically significant (Table 5) and will be taken into account while estimating the model with maximum likelihood (ML). In addition, the aggregated modeling variables/groups are broadly defined, thus there is no danger of running into corner solutions (zero values). The gender-specific distribution of activities can be seen in Table 5. Only domestic work and paid work exhibit strong gender-specific differences.

Table 5 Distribution of activities by gender, h/week

Valuation of domestic work

Several possibilities exist for the valuation of domestic work, including the opportunity cost method [OCM; Luxton (1997)] and the replacement cost method [RCM; Folbre (2006)]. The first approach is based on the forgone value of paid employment, while the second one is based on the cost of hiring somebody to carry out the domestic work. The latter approach can be further divided into specialist (RCM-S), generalist (RCM-G), and hybrid (RCM-H) approaches. The specialist approach takes the cost of hiring a specialist to do some specific work, while the generalist approach takes an ‘all-around’ worker (such as housekeeper). RCM-H is a mix between the previous two approaches, where household activities are priced according to the generalist approach and more complex tasks (such as child or elderly care) are priced in accordance with the rate demanded by a specialist. The latter approach has been applied to, among others, data in Mexico, Canada, and Australia (UNECE 2017). Depending on which approach is chosen, the value of domestic work may vary considerably. In Jackson and William (2015), the share of unpaid work in the GDP was reported to vary between 35$\%$ and 70$\%$ when employing the OCM and between 35$\%$ and 60$\%$ with an RCM-S approach. A similarly strong variation was reported in Schmid et al. (2002), where the OCM resulted in a valuation of unpaid domestic work equal to 37.5$\%$ of GDP, while the RCM-S approach showed domestic work being valued at 57.9$\%$ of GDP in Switzerland. The authors also tried to compare Switzerland, Australia, Finland, the Netherlands, Canada and Norway, but concluded that due to the differences in data gathering (time-use survey), the comparison might not be meaningful. Reports from UNSD (2005), UN (2014), and Eurostat (2008) have proposed guidelines for the harmonization of time-use surveys and UNECE (2017) made a recommendation to use the replacement cost generalist approach, meaning to use the wage rate of an “all-round” worker/housekeeper.

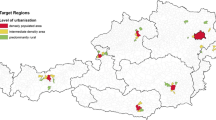
In this paper, we take an approach similar to the RCM-G, but we do not use the national account (NA) data. Instead, we use information available on the Internet, which should depict the current market situation for domestic work better. We have extracted data from two Internet platforms, where people (not companies) offer their services to perform domestic work. We will call them “Platform A” and “Platform B”. For the robustness check, data from both platforms are analyzed. On the first website, the following work categories are available: cleaning services (cleaning, ironing ...), gardening, craft-works, property management during absence, and combinations of these tasks. One person can offer more than one service and the listed price is the average of all offered categories. Thus, there is no clear separation between the prices of different services. One can only get information on so-called “all-rounders” willing to do some or all predefined tasks. In the second platform, individuals offer their work for distinct services. This allows for a clear identification of service-specific wage rates. In comparison to the first platform, one can find a wage rate for house & garden (a combination of cleaning, gardening, craft-works), childcare, elderly-care, pet-care, but no combinations for the same user. In each platform, employers can get the following information on the worker (if provided by the worker): postal code, age, years of experience, requested wage rate. In addition to this, “Platform A” makes it possible to filter workers by gender and spoken languages. New users are added each day to these platforms and prices are negotiable. The data was collected in August 2018.⁷ Average prices of services by region across Austria are presented in Fig. 2.

Fig. 2

Average wage rate of offered services by regions, €/h

Table 6 Average wage rate by service and federal state, €/h

The data collected from “Platform A” imply higher wage rates than that from “Platform B”, due to the way in which the wage on each platform is specified. On “Platform B”, people specify the minimal wage rate, while on “Platform A” workers list their desired hourly rate (“gewünschter Stundensatz”). Thus, the data from “Platform B” underestimate the actually paid wage rate and those from “Platform A” overestimate it. Both data sets exhibit a wage increase from the east to the west of Austria (Fig. 2). This might be partly explained by the spillover effects of lower wage rates of neighboring countries as well as by higher unemployment in the eastern regions. In 2017, of the nine Austrian regions, Vienna (in the East) had the highest unemployment rate (13.0%) and Vorarlberg (in the West) had one of the lowest (5.8%) (AMS 2017). To the east, Austria is surrounded by low wage countries—the Czech Republic, Slovakia, Hungary and Slovenia—and in the west by high-income countries—Italy, Switzerland, and Germany. In addition, Vienna as by far the largest city of Austria has the highest immigrant share (ÖIF 2018). This fact, in combination with the higher unemployment rate in Vienna, might explain the lower observable wage rate in this state. On “Platform B” the most expensive service is “Elderly-care”, and on “Platform A” it is “Craftworks” (Table 6). In the “Platform A” sample, around 90% of observations are identified as female. As “Platform B” does not offer gender-specific data, the gender had to be predicted. After name matching and comparison, 91% of observations were identified as female. Thus, both data sets are strongly female dominated.

Although the “Platform B” dataset might undervalue housework, it provides information on childcare, which consumes a lot of time for households with children. Thus, the “Platform B” data was ultimately chosen for the estimation. According to Ghassemi et al. (2009), in Austria working individuals spend on average around 19.5 h/week doing housekeeping and childcare as a primary activity. Childcare is also often done as a secondary activity: around 8% of women reported almost 1 h/day of talking with a child as a secondary activity, 4% of women and 2% of men played with children while being involved in another activity (Ghassemi et al. 2009). According to the same source, working men spend on average 11.4 h/week engaging in housekeeping tasks, whereas women do almost twice that (21.6 h/week). The difference in terms of the average time assigned to childcare is only 1 h/week (women: 4.2 h/week and men: 3.2 h/week.⁸)

The next step is to merge the MAED data with the “Platform B” data. As both data sets were gathered in different years (MAED in 2015, “Platform B” in 2018), the wage rates collected from “Platform B” had to be adjusted for inflation. According to Statistik Austria, the yearly inflation with basis 2015 in 2018 was 5.1%. Next, data matching between MAED and “Platform B” had to be done. From each data set it is possible to identify where individuals live according to the four-digit postal code. These areas can be further spatially aggregated to obtain larger areas approximating the nine provinces of Austria. The two data sets (MAED and “Platform B”) were merged by two-digit postal codes, which carry information on the province in which an individual lives. Merging by larger spatial area was necessary in some cases, because otherwise we would lack reliable information on some of the service types. Then for each individual included in the MAED data, filtering by four-digit postal code was done. If no “Platform B” data from the same postal code area was available, information from the two-digit postal code area (i.e. the provincial level) was used. Next, it was checked whether a person from the MAED data has children: if yes, observations from “Platform B” having the same postal region (or two-digit postal area) that offer services of childcare were identified. To get the closest match (“best approximation”) from “Platform B” for the MAED individual, the search was narrowed down by choosing individuals from “Platform B” of the same gender as the MAED individual.

For the final calculation of the domestic wage rate, two chores were used: housekeeping (house & garden) and childcare. The MAED data does not distinguish between different types of domestic work. Thus, proportions for housekeeping and childcare were chosen based on the Austrian Time Use Survey (ATUS) and considering only these two household chores (Table 7). According to these proportions, working women devote 84% of domestic work⁹ to housekeeping and 16% to childcare, whereas for men these amount to 78% and 22%, respectively. The average total chore split is 82% (housekeeping) and 18% (childcare). In order to test the robustness of our results with respect to different weights/ratios that unpaid work is assumed to be composed of, a sensitivity analysis was performed. Three different splits were used: 50–50%, 82–18% (total split), gender-specific (women split 84–16%, men split 78–22%). These weights can help to approximate the domestic wage rate—$w_D$ which is specific to a given individual in the MAED dataset.

Table 7 Distribution of domestic work according to the Austrian Time Use Survey, %

Besides treating domestic work as official (paid) work, we do not make any further changes in the theoretical model. We make the following five data adjustments for each split of household chores separately:

• 0. Calculate the average domestic wage rate: $w_D=w_{\text {housekeeping}} w_1+w_{\text {cildcare}} w_2$, $w_1 \in \{50, 82, gender\}$, $w_2 \in \{50, 18, gender\}$.

• 1. Synergy of official and domestic work wage rates: $w^{new}=(w T_w + w_{D} T_D)/(T_w+T_D)$.

• 2. Treat domestic work as official work: $T_w^{new}= T_w+T_D$.

• 3. Balance the time constraint: $T_c^{new}=T_c-T_D$.

• 4. Balance the budget constraint: $E_c^{new}=E_c + w_{D} T_D$.

Table 8 Summary statistics according to different data adjustment procedures

Results of the data adjustments are presented in Table 8. The domestic wage rate is lower than the wage rates paid on the official labor market; as a result, the “new” official wage rate is now lower for both genders. The female wage rate drops more, as women work relatively more in the domestic sector. Correspondingly, the wage gap increases from €1.25/h to €1.4/h (Table 8) when we include the valuation of unpaid work. After these adjustments, men work in total around 1 h/week more than women do (row $T_w^{new}$). There is no significant difference between the “gender-specific” and the “82–18%” split. Thus, in addition to the “50–50%” split, only the “82–18%” data adjustment, being the easier one, will be used in the further analysis. The question now is how these will affect the VoL, which was previously estimated to be €11/h for men and €6/h for women in Jokubauskaitė et al. (2019).

Estimation

The theoretical model (Eqs. 7–9) is estimated as a system of $g$ nonlinear equation with contemporaneous covariance matrix $\varSigma$:

$$\begin{aligned} Y_i= g_i(\beta )+\eta _i, \, \, \, \,\mathbf {E}(\eta _i \eta _j^\top )=\sigma _{ij}\mathbf {I}_n,\, \, \, \, \, i,j= \left\{ 1,\dots , g\right\} . \end{aligned}$$

(16)

Here $i, j$ are equation specific indices. The dependent variable $Y_i$ is modeled through the regression function $g_i$ and error term $\eta _i$, which is assumed to be normally distributed ($\eta _i \sim N(\mu _i, \sigma _i)$). $\beta$ is a vector of parameters to be estimated, $\sigma _{ij}$ is an element from the covariace matrix $\varSigma$ and $I_n$ is an $n\times n$ identity matrix. Estimation results¹⁰ can be found in Table 9.

The first model is the one estimated with the original data and modeling framework, where domestic work is treated as committed activity with no wage rate attached to it. The other model estimations presented in Table 9 correspond to different wage rates attached to domestic work. As both data adjustments (“50–50%” and “82–18%”) result in almost identical estimates and “82–18%” represents the real world situation more accurately, only the “82–18%” split will be used in the following analysis.

There is almost no change across the models in the estimated parameter $\theta _1$, which shows the elasticity of utility with respect to the first freely chosen activities group, and minimal changes in log-likelihood, adjusted $R^2$, and correlations. The FOC given by Eq. (13) defines the binding relationship between $\{\theta _i, T_i, \mu \}$. Thus, if $T_i$ does not change and $\theta _i$ does not change, the marginal utility of leisure time ($\mu$) remains constant. And if $\mu$ does not change and disposable income as well as time remain constant, the change in the VoL is caused by either $\lambda$ or $\theta _w$ (Eqs. 10, 11, Table 10). In the further analysis, we will concentrate on the FOC given by Eqs. (12)–(14). Equation (12) consists of three marginal utilities: work-time, money and leisure time.

According to the estimation results (Table 9), $\{\varPhi , \phi _1, \phi _2\}$ decrease about 20$\%$-30 $\%$. To keep the Eq. (14) valid, $\lambda$ has to decrease proportionally to this change. This decrease in turn leads to an increase in the VoL (Table 10, column “Global”). With a decreasing wage rate and a decreasing $\lambda$, the marginal utility of money ($\lambda w$) declines. The model tries to compensate the loss and equilibrate Eq. (12) by raising the marginal utility of work ($\theta _w /T_w$). Because $T_w$ increases, $\theta _w$ has to go up. Although, in comparison to the original model the estimate of $\theta _w$ almost halves, it remains statistically significant. As a result, the VTAW also almost halves, but remains negative; the marginal time spent at work generates dis-utility, but not as large as with the original data. In the new setting, work is perceived more positively and leisure is more valuable.

Table 9 Estimation results

Table (10) shows a summary of gender-specific estimation results and summary statistics. The gender-specific models were estimated using a-priori segmentation (estimation of separate models for different segments). $T_w$ increases for both genders (by 55.90$\%$ for women and 24.11$\%$ for men) and $T_c$ decreases accordingly. Through this trade-off, $T_w$ and $T_c$ are harmonized within the genders. Due to the balancing of the budget constraint, this change comes along with an analogous change in $E_c$. As the ratio between disposable income ($wT_w-E_c$) and freetime ($\tau -T_w-T_c$) remains almost the same, only the change in the modeling parameters affects the VoL and VTAW values.

A similar pattern as in the global model is observed for females (Table 10, column “Women”). Their marginal utility (MU) of leisure does not change, their MU of money decreases, and their MU of work-time increases. Due to this, their VoL and VTAW increase. In contrast, for men, the MU of money increases. To compensate this, model tries to decrease $\theta _w$ and as a consequence the VTAW decreases. With the adjusted data, men work more than women do and receive higher disutility from work, but because of the higher wage rate, their time is still a little bit “more valuable”. Without a huge decrease in the VoL of men, the gender-specific gap in the VoL is closed.

Table 10 Results by gender, estimation based on different data adjustments

As a plausibility check, additional sensitivity analyses are carried out. In the first one, we assume that each individual in the MAED data obtains the same $w_D$ per hour of domestic work (Fig. 3). The starting point is where individuals receive only €1/h for domestic work, up to €12/h. The average wage rate of domestic work from “Platform B” is around €11/h. In the second analysis, people receive a fraction ranging from 10 to 90$\%$ of the offered individual-specific wage rate for domestic work (with housekeeping and child-care distribution “82–18$\%$”, Fig. 4). In both analyses, the gender-specific VoL gap narrows as $w_D$ increases, while the VTAW ($=VoL-w$) remains almost constant.

Fig. 3

Simulation results, all get the same wage rate. Thick lines represent VoL, thin-wage rate

Fig. 4

Simulation results, different % of $w_D$. Thick lines represents VoL, thin-wage rate

Ahmad and Koh (2011) have estimated that the domestic work in Austria is worth around 24% of GDP. This share is close to the share of GDP contributed by the Austrian industrial sector. The importance of domestic work should therefore not be neglected. The monetarization of domestic work results in an increased estimate of the VoL, which has strong policy relevance. According to Schmid (2019) “Assuming a constant VTTS and decreasing marginal impacts of additional investments on user benefits, a high VoL is reflected in a high VTAT, and investing in speed might be more beneficial (by eventually decreasing the travel time), since the opportunity costs of travel are relatively high, and the conditions of travel are already at a high level (thus leaving less room for improvement).” Other situations are presented in Table 11. Jokubauskaitė et al. (2019) have reported positive values of the VTAT only for public transport. Concluding that they reflect, “the favorable public transport conditions in Austria”. Hence, the updated VoL values might give an even stronger signal for the prioritization of investment in speed rather than comfort of public transport in Austria.

Table 11 Hypothetical examples of policy recommendations when considering the VoL in addition to the VTTS under the assumption of decreasing marginal impacts of additional investments on user benefits.

Discussion and conclusions

The focus of this study was to research the possible effects of the monetary valuation of unpaid work on the gender-specific value of leisure (VoL) and in turn to offer an updated information set for policymaking based on the VTTS and its components. In many economic models, domestic work is ignored. It usually does not appear in labor statistics as work and it is not factored into the official GDP. One might thus call it the same way as Rollins (1985) did - “invisible work”, which is over-proportionally performed by females, and often associated with lower disposable incomes and as a result lower pensions. In Jokubauskaitė et al. (2019), the VoL of Austrian women is estimated to be worth only half of men’s (€11/h for men and €6/h for women). We show that this significant difference vanishes when a monetary value is assigned to domestic work. With this adjustment, the VoL was estimated to be around €9/h for both genders, which is higher than without the adjustment. As the value of travel time savings (the VTTS) increases in the VOL and decreases in the VTAT when the VTAT is estimated to be positive [which has been the case only for public transport in the earlier study based on the same data as this paper, see Jokubauskaitė et al. (2019)], the increase in the VoL reinforces that investments directed towards public transport should prioritize time saving measures over comfort enhancing measures.

The valuation of domestic work might seem to be a complicated task. On the one hand, no “best” method exists; on the other hand, the disregard of its value might lead to gender-biased economic indicators that discriminate against women and their work or anyone who is involved in domestic work. The inclusion of domestic work is important at all stages of economic calculations—from microeconomic models, such as TUM, to the calculation of the GDP. As shown in many research papers on the GDP (Alonso et al. 2019; Bridgman et al. 2018; UNECE 2017; Payne and Vassilev 2018; Schwarz and Schwahn 2016; Ahmad and Koh 2017; Hamdad 2003; Schmid et al. 2002), the inclusion of a value for unpaid work might lead up to a 60% increase in GDP, depending on which valuation method is used. For the valuation of domestic work, we have used an approach similar to the replacement cost generalist method commonly used in the re-calculation of GDP. Instead of national account data, we used data available online, which are likely to better reflect the current market situation for domestic work in Austria. Based on location and gender, each MAED individual was matched with the market wage rate for housekeeping and childcare tasks (the latter only for households with children). As both data sets were gathered in different periods, the current market wage rate of domestic work was inflation adjusted. After this modification, the average wage rate of unpaid work ($w_D$) was computed to be around €10.52/h (for men €10.78/h, for women €10.27/h). Due to the lower $w_D$ for women and higher share of time spent in this type of employment, the new average wage rate ($w^{new}$) for women decreased more than for men. Despite this, the VoL estimates are similar for both genders: for women it was estimated to be €9.00/h and for men €9.20/h. Therefore, we have shown that factoring in the domestic work reduced the gender specific VoL gap, at least for the case of Austria. The applied sensitivity analyses confirmed these results. Also, they do not seem to be overly sensitive to the different types of data adjustments that we have tested.

The theoretical model summarized by Eqs. (3)–(6) is "inherited" directly from the original specification by Jara-Díaz et al. (2008). It goes back to the reformulation of Train and McFadden (1978), following DeSerpa (1971) instead of Becker (1965). Besides the Cobb-Douglas utility function, the model carries a specific treatment of the technical relations represented by Eqs. (5) and (6). As a package, this permits the derivation of the time use and expenditures equation system (7)–(9) and the estimation of the values of leisure and work from Eqs. (10) and (11). What is obtained under this framework are the point estimates of the values of leisure and work, i.e. the model as constructed is not intended for forecasting purposes. However, note that the marginal utilities do depend on commited time and commited expenses (besides the wage rate), which make time values class-specific in spite of the constant value of the parameters in utility. Future research should include the exploration of new utility specifications from which new formulations of labor supply and values of work and leisure could emerge.

It is not possible to say which value of the VoL is the “right” one, as the VoL is a latent variable, which cannot be observed directly. Nevertheless, we believe that taking into account that engaging in domestic work means savings in term of expenses is the right way to go. Time use models at the household level like the one recently developed by Jara-Díaz and Candia (2020) should incorporate this new treatment of domestic (unpaid) labor. We have shown that the valuation of domestic work matters and that it is indeed relevant within the framework of microeconomic time use models and time valuation, which in turn is an essential input to appraisals of transport policies and investments.